Subglacial discharge effects on basal melting of a rotating, idealized ice shelf

When subglacial meltwater is discharged into the ocean at the grounding line, it acts as a source of buoyancy, enhancing flow speeds along the ice base that result in higher basal melt rates. The effects of subglacial discharge have been well studied in the context of a Greenland-like, vertical calving front, where Earth's rotation can be neglected. Here we study these effects in the context of Antarctic ice shelves, where rotation is important. We use a numerical model to simulate ocean circulation and basal melting beneath an idealized three-dimensional ice shelf and vary the rate and distribution of subglacial discharge. For channelized discharge, we find that in the rotating case, total melt-flux anomaly increases with two-thirds power of the discharge, in contrast to existing non-rotating results for which the melt-flux anomaly increases with one-third power of the discharge. The higher melt-flux anomaly with discharge is attributed to a more extensive area of the ice-shelf base being exposed to direct high melting by the rising plume as it is deflected due to Earth's rotation and its path is prolonged. For distributed discharge, we find that in both the rotating and the non-rotating cases, the melt-flux anomaly increases with two-thirds power of the discharge. Furthermore, in the rotating case, the addition of channelized, subglacial discharge can produce either a higher or a lower ice-shelf basal melt-flux anomaly than the equivalent amount of distributed discharge, depending on its location along the grounding line relative to the directionality of the Coriolis force. This contrasts with previous results from non-rotating, vertical ice-cliff simulations, where distributed discharge was always found to be more efficient than channelized discharge at enhancing the terminus-averaged melt rate. The implication, based on our idealized simulations, is that melt-rate parameterizations attempting to include subglacial discharge effects that are not geometry- and rotation-aware may produce total melt-flux anomalies that are off by a factor of 2 or more.

1 Introduction

Subglacial freshwater originates as meltwater formed at the glacier bed or as meltwater draining there from supraglacial or englacial sources. It is discharged into the ocean at the grounding line, where the ice goes afloat. Being released at depth, this freshwater is a source of buoyancy that accelerates as an ascending meltwater plume along the ice-shelf base or the vertical calving face, enhancing entrainment of ambient waters and modulating melt rates. In Alaska and Greenland, where supraglacial melting is a significant contributor to subglacial discharge, local measurements near marine-terminating glaciers have shown such high seasonal submarine melting that it could only have been driven by enhanced subglacial discharge from summer surface melt (Motyka et al., 2003; Washam et al., 2019). Circulation and renewal in some fjords have been shown to be driven almost entirely by subglacial discharge (Gladish et al., 2015; Carroll et al., 2017; Slater et al., 2018; Hager et al., 2022b). Meanwhile, the importance of subglacial discharge for sub-ice-shelf circulation and melting in Antarctica is less clear because the drainage of supraglacial meltwater to the bed is lacking, and present-day subglacial discharge is sourced only from subglacial melting that is much smaller in magnitude. However, there has been a recent surge of interest in the influence of subglacial discharge on basal melting beneath Antarctic ice shelves. Dow et al. (2022) and Hager et al. (2022a) demonstrate that the large catchment sizes in some parts of Antarctica, when combined with high subglacial melting, can lead to subglacial discharge fluxes similar in magnitude to the surface-derived melt fluxes in Greenland. Dow et al. (2022) found correspondence between elevated satellite-derived basal melt rates near grounding lines and locations of modeled subglacial meltwater discharge at some ice shelves. Pelle et al. (2023) found that it was necessary to incorporate a parameterization of subglacial discharge effects (Jenkins, 2011) on basal melting with plume theory (Jenkins, 1991; Lazeroms et al., 2018) to achieve reasonable agreement with satellite-derived basal melt rates, as two-dimensional plume theory on its own underestimated localized high melting near an inferred subglacial channel.

While several studies have implemented subglacial discharge into Antarctic regional domains and studied its effects on circulation beneath ice shelves, basal melting, and continental shelf properties (Nakayama et al., 2021; Goldberg et al., 2023; Gwyther et al., 2023), the current understanding of melt-rate sensitivities to subglacial discharge is, with exception of the work of Wekerle et al. (2024), primarily based on plume theory (Jenkins, 2011) and on idealized studies focused on a Greenland-like, vertical ice front (Xu et al., 2012, 2013; Kimura et al., 2014; Slater et al., 2015) or a narrow ice tongue (Cai et al., 2017; Wiskandt et al., 2023). Jenkins (2011) included subglacial discharge in non-rotational, one-dimensional plume theory. Using dimensional analysis, he found that the melt rate, within some distance of the freshwater source, has a linear dependence on temperature and one-third power dependence on subglacial discharge. These theoretical results were to some extent reproduced in non-rotating, idealized numerical simulations of melting, two-dimensional vertical faces (Xu et al., 2012; Sciascia et al., 2013), two-dimensional ice tongues (Cai et al., 2017; Wiskandt et al., 2023), and three-dimensional vertical faces (Xu et al., 2013; Kimura et al., 2014). These studies typically find a sub-linear, power-law relationship between melt rates ($\dot{m}$) and subglacial discharge (F_s) of the form $\dot{m}\sim F_{\mathrm{s}}^n$, with n<1. While Xu et al. (2012) found $n=\mathrm{1}/\mathrm{3}$, in line with theory, the remaining idealized, two-dimensional studies found slightly stronger melt-rate dependence on subglacial discharge; Sciascia et al. (2013) found n=0.5, Cai et al. (2017) found n=0.57, and Wiskandt et al. (2023) found n between 0.41 and 0.47 for different fjord temperatures. The three-dimensional study of Xu et al. (2013) also found a stronger melt-rate dependence on subglacial discharge, with n between 0.5–0.9, as opposed to the theoretical one-third power. Kimura et al. (2014) found a more complex functional relationship, with the melt rate saturating once a critical discharge rate has been reached and the resulting high inflow velocity forced the plume away from the ice face. Wekerle et al. (2024) found $n=\mathrm{1}/\mathrm{2}$ in a three-dimensional, global, realistic configuration focused on the 79° North Glacier Tongue that included rotation. However, in their study, shelf conditions could evolve as a function of discharge given their configuration was global and shelf conditions were not restored, allowing for conflation of the discharge and shelf temperature effects on melting. Finally, Jackson et al. (2022) addressed the relationship between basal melting and discharge observationally. Their estimates from a relatively warm Alaskan glacier showed that plume theory underestimated melting by over an order of magnitude, but the one-third power dependence of melt rate on discharge seemed to hold, albeit with substantial uncertainties.

The question of how the horizontal distribution of subglacial discharge along grounding lines affects melt rates has also been addressed before to some extent. Kimura et al. (2014) considered the case for an unstratified water column and found that two channels in close proximity produced higher melt rates than a single channel with the equivalent total discharge. Slater et al. (2015) considered a more realistic, stratified setup, in which plumes can reach neutral buoyancy, and found that distributed discharge always produces a higher total melt rate than the equivalent channelized discharge.

Crucially, what the convectively forced plume model and the existing idealized numerical studies have neglected is the effect of Earth's rotation, as have all other common basal melt-rate parameterizations used to force ice-sheet models (Burgard et al., 2022), including those that incorporate subglacial discharge (Pelle et al., 2023). The omission of Earth's rotation is typically justified based on the ratio of fjord or ice-tongue width (W) to the first-mode baroclinic deformation radius (R_d) being smaller than or close to unity. However, Jackson et al. (2018), focusing on shelf-driven forcing, show that even for $W/R_{\mathrm{d}}>\mathrm{0.5}$, which includes most of Greenland's fjords, three-dimensional dynamics are integral to understanding the fjord circulation. The omission of Earth's rotation is certainly not appropriate for Antarctic-like ice-shelf cavities, where $W/R_{\mathrm{d}}\gg \mathrm{1}$. In this paper, we revisit the relationship between the submarine melting and subglacial discharge for a rotating, Antarctic-like configuration. The simulations are idealized, and their purpose is to provide insight into melt-rate sensitivities to subglacial discharge that, in a realistic, global configuration, would be computationally expensive and potentially challenging to interpret. The idealized simulations are performed using a relatively coarse resolution compared to the Greenland-like, vertical ice-cliff studies, in line with the goal of understanding sensitivities in realistic, global model configurations.

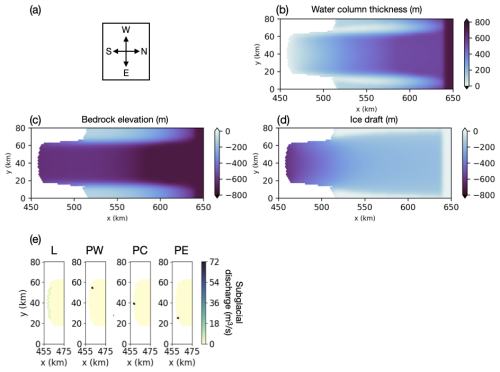
Figure 1 (a) Convention for geographic references in text. (b–d) Idealized ISOMIP+ domain setup. (b) Water column thickness. (c) Bedrock elevation. (d) Ice draft. (e) Distribution of subglacial discharge of F_s=72 m³ s⁻¹ at the grounding line along a line (L) or at point west (PW), point center (PC), or point east (PE).

2 Methods

For idealized testing, we use the ocean component of the Energy Exascale Earth System Model (E3SM), the Model for Prediction Across Scales – Ocean (MPAS-Ocean; Ringler et al., 2013). MPAS-Ocean is a finite-volume ocean model that solves the hydrostatic Boussinesq equations. It uses a horizontal mesh defined by a centroidal Voronoi tessellation. The simulations presented here use a planar mesh, rather than one on the surface of a sphere. In our experimental setup, parameterizations and coefficient choices follow the Ocean0 configuration (Fig. 1) from the second Ice Shelf-Ocean Model Intercomparison Project, ISOMIP+ (Asay-Davis et al., 2016). We use the z* vertical coordinate (Adcroft and Campin, 2004) in the open ocean. Beneath ice shelves, the coordinate follows the ice draft, and at the seafloor, layers are dropped when they intersect the bathymetry. As a result, the thickness of the top vertical layer, in contact with the ice-shelf base, varies smoothly from being thinnest near the grounding line (∼0.75 m), thickening towards the ice-shelf front (∼15 m), to being thickest in the open ocean (∼21 m). The Ocean0 experiments presented here are performed with 36 vertical levels and 2 km horizontal resolution. Sensitivity runs with 1 km and 4 km horizontal resolutions and 72 vertical levels were also run and produced qualitatively similar results. The change in resolution can be largely compensated for through an appropriate change in viscosity. For mixing, we employ horizontal and vertical Laplacian diffusivities and viscosities with values from Table 4 in Asay-Davis et al. (2016) that had been chosen to be sufficiently low not to suppress eddies but high enough to avoid numerical instabilities. There are two vertical diffusivity and viscosity values, one for a stable and one for an unstable vertical profile. Horizontal diffusivity and viscosity are constant. We use the linear equation of state. The ice-shelf geometry is static. Ice-shelf basal melting is calculated using the three-equation parameterization with standard coefficients (Jenkins et al., 2010), except for the heat transfer coefficient that was tuned to give a prescribed melt rate as per the ISOMIP+ design document (Asay-Davis et al., 2016). Following Losch (2008), temperature and salinity for calculating thermal driving for ice-shelf basal melting are found by vertically averaging over cells within 10 m of the ice base. In our vertical coordinate system, this Losch layer is necessary for melt-rate convergence with increasing vertical resolution (Gwyther et al., 2020). The Losch layer also acts as an additional source of vertical mixing near the ice base, effectively forming a mixed boundary layer of constant, spatially uniform thickness, which is used by the basal melt-rate parameterization. Heat and freshwater fluxes associated with basal melting are distributed into the ocean based on an exponential profile, with a decay length scale of 10 m, which effectively acts as enhanced vertical diffusivity near the boundary. Frazil ice is allowed to form, but it is not advected with the flow. At each time step, the model checks for frazil ice formation in the top 100 m of the water column, and any frazil mass is brought to the surface immediately and added to interfacial basal melting. The rotating cases use an f-plane configuration with the Coriolis parameter of $f=-\mathrm{1.409}\times {\mathrm{10}}^{-\mathrm{4}}$ s⁻¹, which corresponds to the latitude of 75° S.

Initially, potential temperature and salinity are prescribed as horizontally uniform and linearly increasing with depth, with surface values of $T_{\mathrm{s}}=-\mathrm{1.9}$ °C and S_s=33.8 PSU in all cases. In the base case, the properties at the deepest point are T_b=1 °C and S_b=34.7 PSU. At the northern boundary, potential temperature and salinity are restored to the initial values throughout the simulations. No slip boundary conditions are applied at the sidewalls. Subglacial discharge into the ocean at the grounding line is implemented as a volume flux of freshwater at the local pressure-dependent freezing point. Because there is no prescribed evaporation, sea level in the idealized domain increases over time due to the flux of subglacial discharge and ice-shelf basal melt into the domain. The circulation within the ice-shelf cavity is entirely driven by buoyancy forcing from ice-shelf basal melt and grounding-line freshwater flux. The simulations were run for 2 years, by which time the melt-rate pattern had developed and stabilized. Analysis is based on the last monthly mean outputs from the 2-year simulations.

In the first set of experiments, we study the melt-rate response to varying F_s, the spatially integrated subglacial freshwater flux, and how this response changes with different F_s distributions along the grounding line in a rotating framework. We prescribe the boundary shelf conditions as in the base case (T_b=1 °C and S_b=34.7 PSU). We then vary total F_s between 0 and 720 m³ s⁻¹. For each tested F_s value, we also vary its horizontal release location (Fig. 1e) as follows:

• (L) F_s is distributed along a line corresponding to the deepest part of the grounding line.

• (PW) F_s is applied at a point in the westernmost grid cell of L (in the case described immediately above).

• (PC) F_s is applied at a point in the center grid cell of L.

• (PE) F_s is applied at a point in the easternmost grid cell of L.

These experiments were also carried out in a non-rotating framework, setting f=0 s⁻¹, for comparison of our findings with those from previous studies.

The next set of experiments tests melt-rate sensitivity to varying amount of F_s across different potential temperatures. We keep the surface temperature fixed at −1.9 °C and vary the seafloor potential temperature T_b between −1.9 and 4 °C. The temperature profile was kept linear, and salinity was adjusted to keep the same density profile in all simulations. This sensitivity test was performed for a distributed discharge (L) in a rotating framework.

Simulations were run with T_b values of −1.9, −1, 0, 1, 2, and 4 °C and with F_s values of 0, 7.2, 72, 180, 360, 540, and 720 m³ s⁻¹ to capture sensitivities and regimes of interest. Not every combination of T_b and F_s was run for every horizontal release location. T_b values were chosen to include the present-day range and plausible future range of temperatures occupying the continental shelves of Antarctica. Similarly, F_s values were chosen to span the relatively wide range of modeled subglacial discharge regimes around Antarctica (e.g., Hager et al., 2022b).

By design, some models, such as MPAS-Ocean, are required to have more than a single layer at the grounding line. This then brings up the modeling choice of where to apply F_s in the vertical. In the above experiments, we chose to distribute F_s uniformly in the vertical. Melt-rate sensitivity to this modeling choice is addressed in Appendix A.

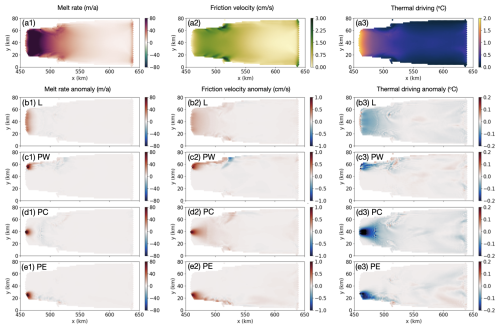
Figure 2 (a) Melt rate, friction velocity, and thermal driving for the reference case without subglacial discharge (F_s=0 m³ s⁻¹). (b–e) Melt-rate, friction-velocity, and thermal-driving anomalies when F_s=72 m³ s⁻¹ is added at various locations along the grounding line. (b) F_s is distributed along a line (L). (c–e) F_s is channelized, released at (c) point west (PW), (d) point center (PC), and (e) point east (PE).

3 Results

With F_s=0 m³ s⁻¹, the total basal melt flux over the ice shelf increases quadratically with the far-field potential temperature (Fig. A1a), in agreement with previous simulations (Holland et al., 2008) and theory (Jenkins et al., 2018). By construction, melt rates are proportional to friction velocity and thermal driving. In the rotating case, the melt-rate spatial pattern is such that melting is highest at the deepest parts of the ice shelf and enhanced at the western grounding line (Fig. 2a1). This holds as long as the thermal driving remains sufficient (Fig. 2a3) to support melting, while the ascending meltwater plume veers westward under the influence of the Coriolis force (Fig. 2a2). The friction velocity shown here in figures (e.g., Fig. 2, second column) is a good proxy for plume speed as long as the plume is attached to the ice base.

Figure 3 The same as Fig. 2 but for the non-rotating case.

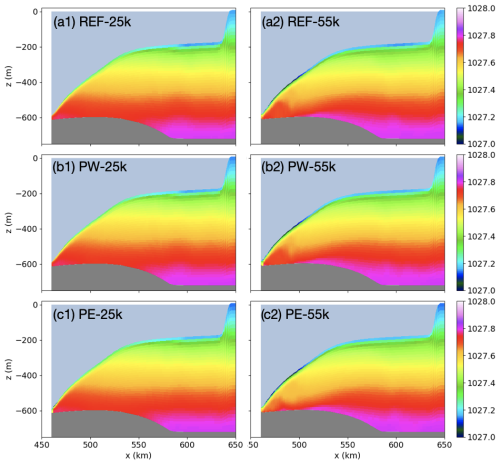
Figure 4 Potential density sections. (a) Reference case without subglacial discharge (F_s=0 m³ s⁻¹). (b) Channelized discharge (F_s=72 m³ s⁻¹) applied at point west (PW). (c) The same as (b) but for point east (PE). The sections are located at y=25 and 55 km, from left to right, corresponding to progression from east to west (Fig. 1).

The interplay between friction velocity and thermal driving, when F_s is introduced, is shown in Fig. 2 for the rotating case and in Fig. 3 for the non-rotating one. The sections shown are for the moderate discharge strength of F_s=72 m³ s⁻¹; however, the results do not change qualitatively with the strength of F_s within the tested range of values. F_s enhances friction velocities (e.g., Figs. 2e2 and 3e2) due to added buoyancy, increasing melt that cools the boundary layer (e.g., Figs. 2e3 and 3e3), which in turn suppresses melt. Near the F_s source, the friction velocity increase is so high that it dominates any cooling, producing positive melt-rate anomalies; however, with increasing distance from the source, melt-driven cooling starts compensating for the heightened friction velocity, resulting in little change in melt rates (e.g., Figs. 2e1 and 3e1). The plume slows down quickly as it rises, entrains ambient waters, and thickens. In the rotating case, the plume veers westward relative to its direct, upslope, and northward direction with no rotation. The result is meltwater accumulation near the western grounding line (Fig. 4a2), compared to the east (Fig. 4a1), and increased overall stratification with lighter waters at the surface and meltwater extending deeper into the water column in the west (Fig. 4a2). This stratification asymmetry, already present in the reference case with rotation, sets the stage for the observed qualitative differences in melt response when F_s is introduced and its release location is varied along the grounding line (Fig. 2, left column).

To quantify the rotational effects on the bulk scaling relationship between basal melting and F_s, we introduce $\mathrm{\Delta }\dot{M}$, the anomaly in spatially integrated basal melt volume flux with respect to the reference case with F_s=0 m³ s⁻¹. We use total melt-flux anomalies rather than spatially averaged melt-rate anomalies because for relatively localized anomalies, as is the case here, the latter would introduce a more evident dependence of the results on ice-shelf area. As the analysis is focused on the last monthly mean output (of 24 months of simulation) $\mathrm{\Delta }\dot{M}$ is also averaged in time. We observe that, in the presence of rotation, $\mathrm{\Delta }\dot{M}$ is strongly dependent on the horizontal release location of point source F_s (Fig. 5a), especially compared to the non-rotating case (Fig. 5b).

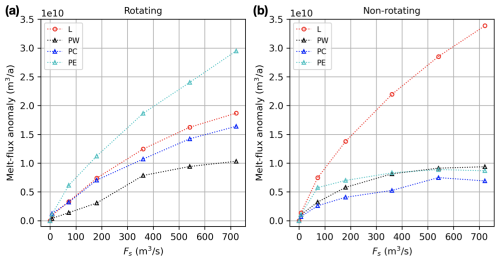
Figure 5 Total melt-flux anomaly ($\mathrm{\Delta }\dot{M}$) as a function of subglacial discharge (F_s) and its horizontal release location and distribution. (a) Rotating case, horizontal distribution sensitivity: F_s is distributed along a line (L) or released at different channelized points (west – PW, center – PC, east – PE). (b) The same as (a) but for the non-rotating case.

3.1 Melt sensitivity to horizontal discharge release location

Starting with the rotating case, the point-source experiments (PW, PC, and PE) show that the most effective location to apply F_s in terms of $\mathrm{\Delta }\dot{M}$ is at the eastern portion of the grounding line; $\mathrm{\Delta }\dot{M}$ more than doubles when F_s is applied in the east, rather than in the west (Fig. 5a). When an equivalent F_s is distributed along the grounding line (L), the resulting $\mathrm{\Delta }\dot{M}$ is approximately halfway between the $\mathrm{\Delta }\dot{M}$ in the PW and PE cases and is slightly higher than in the PC case. $\mathrm{\Delta }\dot{M}$ in the PE case is about 1.5 times higher than in the distributed (L) case. This is in part due to a larger portion of the ice-shelf area sustaining positive melt-rate anomalies when the plume is located farther east on the grounding line (Fig. 2e1) compared to its central (Fig. 2d1) or western location (Fig. 2c1). Consistent with the point-source experiment, the distributed case experiences a larger spatial extent of melt-rate increase in the east than in the west (Fig. 2b1).

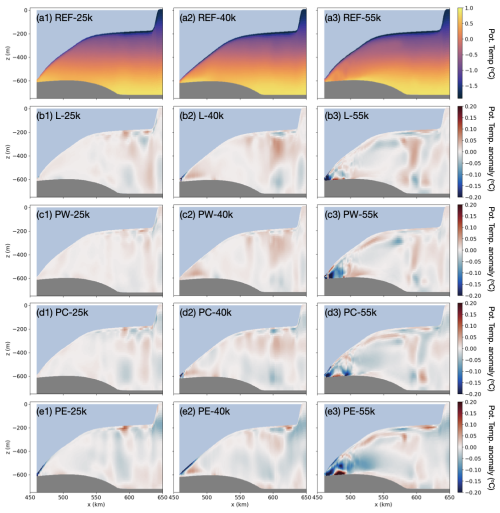
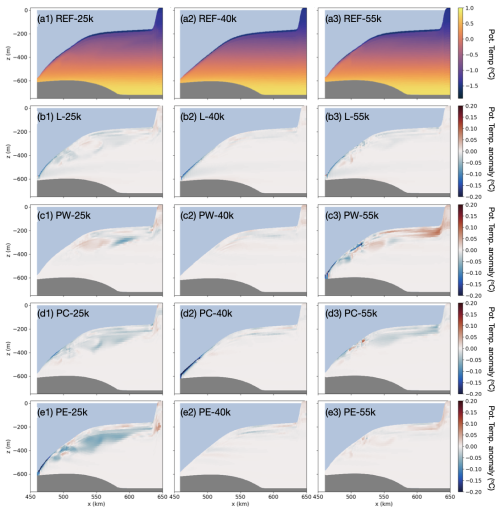
Figure 6 (a) Potential-temperature sections for the reference case without subglacial discharge (F_s=0 m³ s⁻¹). (b–e) Potential-temperature anomalies when F_s=72 m³ s⁻¹ is added at various locations along the grounding line. (b) F_s is distributed along a line (L). (c–e) F_s is channelized and released at (c) point west (PW), (d) point center (PC), and (e) point east (PE). The sections are located at y=25, 40, and 55 km, from left to right, corresponding to progression from east to west (Fig. 1).

When F_s is released at a point in the east (PE), where the water column beneath the ice shelf is less stratified compared to the west (Fig. 4c1 vs. 4c2), the added freshwater induces high flow speeds, cooling, and freshening in a thin layer near the ice base, with relative warming beneath it (Fig. 6e1). This fast, thin outflow near the ice base persists as the plume rises, spreads laterally, and turns west (Fig. 6e2). However, along the eastern and central transects, no portion of the plume has reached neutral buoyancy as it does in the non-rotating case (Fig. A2e1). Instead, the plume becomes neutrally buoyant in the western part of the domain, where the presence of the western boundary forces the plume to flow upslope, rise, and mix, as visible in the large temperature anomaly throughout the western section (Fig. 6e3). The addition of F_s has increased vertical mixing in the west, as evidenced by relative warming at the top and relative cooling at the bottom of the water column.

When F_s is released at a point in the center of the grounding line (PC), the response downstream of the release location is similar to the PE case, only weaker (Fig. 6d vs. 6e). The friction velocity increase is lower in this case (Fig. 2d2 vs. 2e2) because the water column is more stratified here, having already been freshened by meltwater coming from the east. This also means that the density difference between the subglacial discharge and the surface waters is reduced, as is the driving force for the plume ascent. Finally, the presence of the western boundary means that, the closer the discharge location is to the west, the less distance the plume is able to travel across the ice shelf before it encounters the boundary and is forced upward along the ice base (Fig. 2, second column).

When F_s is released at a point near the western boundary (PW), these tendencies are even more amplified. The water column is more stratified here, the surface water along the ice base is fresher and lighter (Fig. 4b2), and the proximity of the western boundary is closer, which forces upward flow of meltwater almost immediately upon release (Fig. 2c2). The result is that the plume has less distance to travel along the ice base and it becomes neutrally buoyant deeper in the water column. This is seen as relative warming at the top and relative cooling at the bottom of the water column, much closer to the grounding line (Fig. 6c3). Unlike in the PE and PC cases, for PW this relative warming at the top extends as far as the boundary layer, causing a warm anomaly in the thermal driving (Fig. 2c3).

In summary, the east–west asymmetry in meltwater distribution means that F_s added in the west inputs less buoyancy and therefore less available potential energy into the system than F_s added in the east. Together with the east–west asymmetry in stratification, this means that when injected in the west, the plume becomes neutrally buoyant deeper in the water column, keeping any positive melt-rate anomalies closer to the grounding line and lowering their magnitude (Fig. 2, left column).

3.2 Scaling relationships between subglacial discharge and melt

We now turn our attention to the scaling relationship between melt flux and F_s, which has been extensively studied for non-rotating scenarios. Figure 5 not only shows that $\mathrm{\Delta }\dot{M}$ depends on the horizontal distribution of F_s for the rotating case with point-source discharge, but also indicates that the functional form of the sub-linear relationship between $\mathrm{\Delta }\dot{M}$ and F_s differs depending on whether rotation is included and whether F_s is distributed or channelized (Fig. 5).

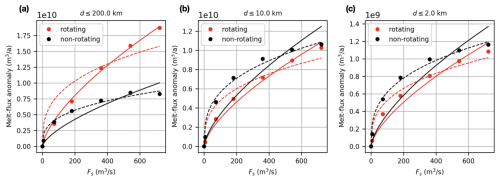
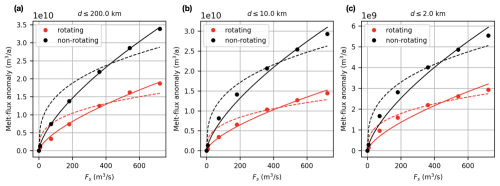
Figure 7 Scaling relationships between the integrated melt-flux anomaly ($\mathrm{\Delta }\dot{M}$) and subglacial discharge (F_s) for channelized system from averaged PW, PC, and PE experiments as in Fig. 5. The melt-flux anomaly is integrated over distance d from the discharge location. The dashed line scales with F_s to one-third power, and the solid line scales with F_s to two-thirds power.

To investigate how the functional form of the sub-linear relationship between F_s and $\mathrm{\Delta }\dot{M}$ depends on rotation for the channelized drainage system, we first remove differences associated with the domain asymmetries and the presence of boundaries. To do that, we average the $\mathrm{\Delta }\dot{M}$ results for all three point release cases separately for the rotating and the non-rotating scenarios (Fig. 5). We confirm that the non-rotating case complies with theory; that is, $\mathrm{\Delta }\dot{M}$ scales with one-third power of F_s (Fig. 7a, dashed black line), as in Jenkins (2011). However, in the rotating case, the one-third power scaling clearly overestimates $\mathrm{\Delta }\dot{M}$ for low F_s and underestimates it for high F_s (Fig. 7a, dashed red line), which means that the curvature of the one-third power scaling is incorrect. A higher power scaling seems to be a better fit for the rotating case; we find that $\mathrm{\Delta }\dot{M}$ scales well with two-thirds power of F_s. We note that the stronger $\mathrm{\Delta }\dot{M}$ scaling with F_s for the rotating case does not depend on f as long as $W/R_{\mathrm{d}}\gg \mathrm{1}$ (Fig. A1c).

Nevertheless, the theory of Jenkins (2011) should still hold in the rotating case at small distances from the source before the Coriolis effect becomes important. To test this, instead of integrating over the entire domain, we integrate melt-flux anomalies over a fixed distance from the F_s source. We compare $\mathrm{\Delta }\dot{M}$ integrated over the whole domain, over an area within 10 km of the source, and within 2 km of the source (Fig. 7a–c). We observe that, for the rotating case, the scaling between $\mathrm{\Delta }\dot{M}$ and F_s becomes closer to one-third power as melt fluxes are integrated over a smaller area nearer to the source (Fig. 7c), as expected from the non-rotating, convectively forced plume theory.

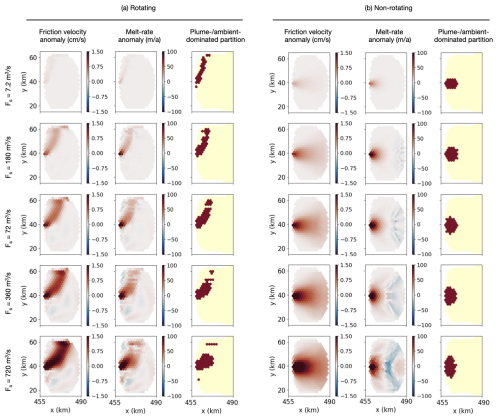
Figure 8 Friction velocity anomaly; melt-rate anomaly; and area partitioning into high-melt, plume-dominated (dark area) and low-melt, ambient-dominated (light area) regions for the (a) rotating and (b) non-rotating case. We show the ice-shelf area within 30 km of the F_s source, which is used in the analysis in Fig. 9. The rows are different values of the channelized discharge F_s released at point center (PC).

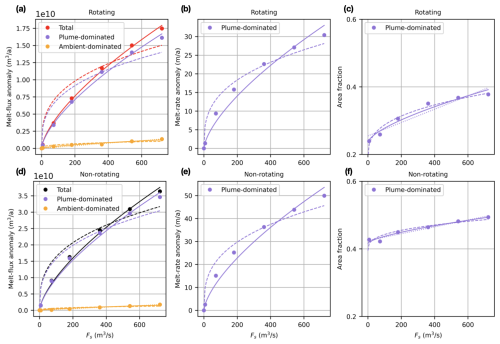
To further investigate possible causes of the power-law difference due to the inclusion of rotation, we partition the ice-shelf area into a high-melt, plume-dominated region and a low-melt, ambient-dominated region and study how each partition contributes to the overall melt-flux anomaly. To capture the high-melt region near the F_s source and along the path of the elevated plume-driven friction velocities in each case, we define the plume-dominated partition as the region where the melt-rate anomaly exceeds the threshold of 10 % of the maximum melt-rate anomaly and the ambient-dominated partition as the remainder of the ice shelf (Fig. 8). Because most of the melt-rate anomaly occurs within a few tens of kilometers of the grounding line, we restrict our attention to the area within 30 km of the F_s source (shown in Fig. 8 for the PC case). As done previously, for both the rotating and the non-rotating scenarios, we average the results from all three point release cases (PE, PC, and PW). We quantify the relative contribution of the two partitions to the total melt-flux anomaly and inspect the change in the partition area and in the mean melt-rate anomaly, averaged over each partition separately, as F_s increases. The melt-flux anomaly $\mathrm{\Delta }\dot{M}$ (e.g., Fig. 9a) is the product of the mean melt-rate anomaly (e.g., Fig. 9b) and the area over which the melt-rate anomaly is averaged (e.g., Fig. 9c). The partitioning changes from case to case (Fig. 8); therefore the melt-rate anomaly is averaged and the melt-flux anomaly integrated over a different area for each partition in each scenario.

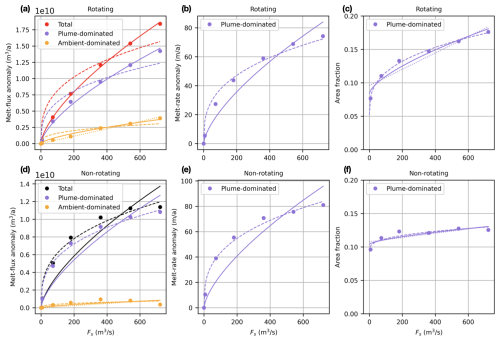
Figure 9 Scaling relationships with subglacial discharge (F_s) for different quantities evaluated over a plume-dominated or ambient-dominated partition (Fig. 8) of the ice-shelf base within 30 km of the discharge location. We consider the averaged channelized experiments. (a, d) Spatially integrated melt-flux anomaly. (b, e) Spatially averaged melt-rate anomaly. (c, f) Area fraction of an ice-shelf partition. Panels (a)–(c) show the rotating case and panels (d)–(f) the non-rotating case results. In all panels, the dashed line scales with F_s to one-third power, the solid line scales with F_s to two-thirds power, and the dotted line (where applicable) is a linear scaling with F_s.

We observe that most of the melt-flux increase with F_s occurs over the plume-dominated partition in both the rotating and the non-rotating cases (Fig. 9a, d). Therefore, explaining the melt-flux anomaly behavior of the plume-dominated partition is sufficient to the understanding of the total melt-flux anomaly behavior as F_s increases. We find that while the melt-flux anomaly respects the power-law scaling identified above, $n=\mathrm{2}/\mathrm{3}$ with rotation and $n=\mathrm{1}/\mathrm{3}$ without (Fig. 9a, d), the melt-rate anomaly averaged over the plume-dominated partition scales with one-third power of F_s both with and without rotation (Fig. 9b, e). This is reconciled by the observation that the area fraction of the plume-dominated partition scales with one-third power of F_s in the presence of rotation (Fig. 9c) but is nearly constant in the non-rotating case (Fig. 9f). This means that it is the increase in the area of the plume-dominated partition that causes stronger dependence of the melt-flux anomaly on F_s when rotation is included. By design, the plume-dominated partition (Fig. 8a, right column) closely follows the plume path identified by high friction velocities (Fig. 8a, left column). Therefore, it is clear that the higher area increase in the plume-dominated partition with F_s is related to the increasing distance over which the plume is deflected by the Coriolis force as its flow speed increases. While for the rotating case the plume path increases with the strength of F_s, this is not the case for the non-rotating case, where the flow is upward along the ice base independent of F_s. There, as the plume cools with increased melt near the discharge location, an initially sharp melt-rate increase quickly declines with distance (Fig. 8b, middle column), resulting in little area change in the plume-dominated partition (Fig. 8b, right column).

Turning to the distributed system and repeating the same analysis, we observe that $\mathrm{\Delta }\dot{M}$ scales with two-thirds power of F_s for both the rotating and the non-rotating case (Fig. A3a, solid lines). When averaged over cells within 2 km of the source, that is 1 grid-cell distance away from the F_s source, the $\mathrm{\Delta }\dot{M}$ scaling with F_s lies between one-third and two-thirds power (Fig. A3c), but already when averaged over 10 km distance from the F_s source, the scaling is much closer to two-thirds power for both cases (Fig. A3b). The analysis that partitions the ice-shelf area within 30 km of the F_s source into plume-dominated and ambient-dominated regions shows similar results for the rotating and non-rotating scenarios. Most of the melt-flux anomaly with F_s occurs over the plume-dominated partition in both the rotating and the non-rotating cases (Fig. A4a, d). In both cases, the melt-rate anomaly averaged over the plume-dominated partition (Fig. A4b, e) and the area fraction of the plume-dominated partition (Fig. A4c, f) scale with F_s similarly such that their product gives a two-third power dependence of the melt-flux anomaly on F_s (Fig. A4a, d). For the distributed system, there is some sensitivity of the exact scaling relation of both the area fraction and the associated melt-rate anomaly with F_s to the choice of the partitioning criteria, but the result – that these scalings are the same with and without rotation – is independent of the threshold.

4 Discussion

From our idealized experiments that include rotation, we found that channelized discharge can either increase or decrease the integrated melt-flux anomaly compared to the distributed system, in our particular setup by about 50 % (Fig. 5a). This contrasts with findings from non-rotating experiments by Slater et al. (2015). They modeled a Greenland-like vertical ice front and varied the distribution of freshwater discharge along the grounding line, concluding that distributed F_s is always more efficient in driving melting than channelized F_s in their simulations by up to a factor of 5. Results from our non-rotating experiments are qualitatively consistent with Slater et al. (2015), and we observe a higher $\mathrm{\Delta }\dot{M}$ for horizontally distributed than for channelized discharge. This is particularly pronounced as F_s increases, owing to the higher exponent in the power-law relationship between $\mathrm{\Delta }\dot{M}$ and F_s in the distributed case than in the channelized case (Fig. 5b). A key reason why the findings of Slater et al. (2015) – that the melt-rate response to discharge increases with the number of sources – do not apply in the rotating case is that they rely on individual plumes not interacting with each other. In the non-rotating case, individual plumes only interact when spaced sufficiently close together, but in the rotating case, the plumes interact even if spaced far from each other. Rotation eventually makes all melt from individual plumes coalesce on one side of the domain, which results in less ice-shelf area available for discharge-driven melt-rate increase compared to the non-rotating case.

The reason for the two-thirds power dependence of melt flux on F_s in the non-rotating, distributed case compared to the one-third power dependence in the channelized, non-rotating case is not clear but appears to be related to the faster growth of the area of the plume-dominated partition with F_s in the distributed case and may be related to interacting plumes. Although this difference has not been explicitly discussed in previous studies, it may be implicitly present in the work of Xu et al. (2013). They studied the relationship between submarine melt rate and discharge through three-dimensional simulations of a vertical ice front, finding a more complicated, sub-linear relationship than a simple power law, and identified two regimes, one appropriate for low F_s and the other for high F_s. In the light of our results, this difference can be attributed to the way variations in F_s magnitude were prescribed in their study: Xu et al. (2013) fixed the value of F_s in each grid cell, and, to increase total discharge, they increased the number of grid cells where this fixed F_s was applied. Thus, for lower values of F_s, they effectively simulated a channelized system and, for higher values of F_s, the system effectively became distributed. As a consequence, according to our results, the power law gradually changes from a one-third to a two-thirds power dependence, giving rise to the more complicated functional relationship reported on in Xu et al. (2013). Notably, the parameterization of Xu et al. (2013), subsequently adopted by the Ice Sheet Model Intercomparison Project for CMIP6 – Greenland Ice Sheet (ISMIP6-GIS; Slater et al., 2020), is widely used in ice-sheet models as the standard vertical ice-cliff melt-rate parameterization. While we are not able to simulate vertical cliffs, our results from non-rotating ice-shelf simulations suggest that the functional form of the melt-rate dependence on discharge from Xu et al. (2013) may need to be revised. Specifically, rather than the exponent (n) being a function of the discharge strength, our simulations indicate that n depends on whether the discharge is distributed ($n=\mathrm{2}/\mathrm{3}$) or channelized ($n=\mathrm{1}/\mathrm{3}$).

Our results have implications for melt-rate parameterizations that attempt to realistically account for the effects of subglacial discharge on ice-shelf basal melting. The same amount of total discharge can more than double $\mathrm{\Delta }\dot{M}$ if located in the east as opposed to the west of the domain (for the Southern Hemisphere). This result is based on a highly idealized ice-shelf domain and will likely change quantitatively as additional geometric complexities are included. The sensitivity of $\mathrm{\Delta }\dot{M}$ to discharge location along the grounding line is not accounted for in existing parameterizations (Jenkins, 2011; Pelle et al., 2023) and may be difficult to include accurately, especially for more complicated geometries. Our results highlight the sensitivity of melt rates to the location of channelized, submarine discharge and, therefore, also highlight the importance of accurate modeling of subglacial meltwater discharge via subglacial hydrology models.

We have primarily focused on characterizing spatially integrated melt-flux anomalies in the presence of subglacial discharge, as have previous ocean modeling studies of melting vertical cliffs and floating ice tongues. While some ice-sheet modeling studies indicate that spatially averaged melt rates are far more important for determining ice-sheet dynamics than their spatial variations (Joughin et al., 2024), a more extensive body of literature argues that melt rates near grounding lines and pinning points matter to the ice-sheet dynamics much more than melt rates elsewhere on the ice shelf (Gagliardini et al., 2010; Fürst et al., 2016; Reese et al., 2018; Zhang et al., 2020). An understanding of how the melt-rate anomalies due to subglacial discharge ultimately affect ice-sheet dynamics will require an ice-sheet model with a suitable melt-rate parameterization (e.g., Pelle et al., 2023) or a coupled ice-sheet–ocean–subglacial hydrology model.

5 Conclusions

We studied the effect of subglacial discharge on submarine melt rates for an idealized, Antarctic-like ice shelf within a rotating reference frame. This work complements existing studies focusing on non-rotating, idealized, Greenland-like vertical calving fronts and narrow ice tongues. The motivation for the study was to develop a conceptual understanding of the sensitivities and response of the system in an idealized setup before conducting global, realistic simulations. Relevant to the realistic simulations, we found that with restoring shelf conditions, the total melt-flux anomaly scales with two-thirds power of the discharge. This is a stronger melt-flux anomaly dependency on discharge than found in previously studied non-rotating cases. It results from a larger fraction of the ice-shelf base being exposed to high melt rates, locally driven by the rising plume that is deflected under rotation and whose travel path increases when forced by stronger discharge. We also found that the melt-rate response is strongly sensitive to the location of the discharge along the grounding line; the efficiency of subglacial discharge, in terms of the total melt-flux anomaly, grows with distance from the area where meltwater ultimately accumulates due to rotational effects (the western ice-shelf margin in this study). The relationship between the melt-flux anomaly and the number of sources for a given total discharge derived from non-rotating, vertical cliff experiments does not translate to the rotating ice-shelf scenario. Our results complicate the task of melt-rate parameterizations aspiring to account for subglacial discharge effects in that there is a significant additional melt-flux sensitivity to discharge location. The sensitivity to the location of discharge also lends new importance to accurate modeling of subglacial hydrology.

Appendix A

We tested the total melt-flux anomaly sensitivity to the modeling choice of F_s vertical distribution as follows:

• (T) F_s is concentrated in the top vertical layer.

• (U) F_s is uniformly mixed in the vertical.

• (B) F_s is concentrated in the bottom vertical layer.

This sensitivity test was performed for a distributed discharge in a rotating framework for three different bottom potential temperatures, −1, 0, and 1 °C. As expected, based on the different amounts of added available potential energy, the highest $\mathrm{\Delta }\dot{M}$ is produced when F_s is released at the bottom vertical layer and the lowest $\mathrm{\Delta }\dot{M}$ when F_s is released at the top layer (Fig. A1b). While the difference in $\mathrm{\Delta }\dot{M}$ caused by a choice of vertical release location can be up to 20 %, this choice does not affect the scaling relationship between $\mathrm{\Delta }\dot{M}$ and F_s.

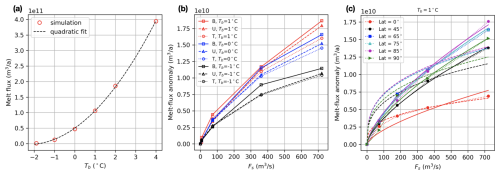
Figure A1 (a) Mean reference basal melt flux for different shelf conditions set by property restoration at the northern boundary; T_b is the restoring potential temperature at the seafloor. The dashed line shows a quadratic fit. (b) Total melt-flux anomaly ($\mathrm{\Delta }\dot{M}$) as a function of distributed subglacial discharge strength (F_s) for different vertical release locations and temperatures. The sensitivity is tested for a rotating case, and F_s is distributed along a line (L) and released at the bottom (B) layer or top (T) layer or uniformly mixed in the vertical (U). (c) $\mathrm{\Delta }\dot{M}$ as a function of F_s for varying latitude via the Coriolis parameter. The dashed line is $\mathrm{\Delta }\dot{M}$ scaling with F_s to one-third power, and the solid line is $\mathrm{\Delta }\dot{M}$ scaling with F_s to two-thirds power, using a least-squares fit. The filled dots connected by dotted lines are simulation results.

Figure A2 The same as Fig. 6 but for the non-rotating case.

Figure A3 The same as Fig. 7 but for distributed discharge.

Figure A4 The same as Fig. 9 but for distributed discharge.

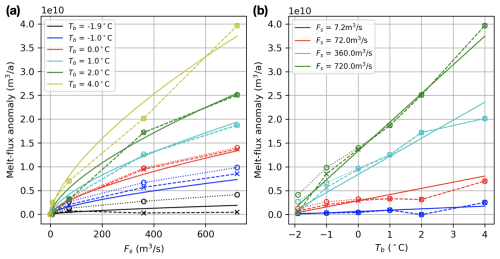
Figure A5 (a) The relationship between the total melt-flux anomaly ($\mathrm{\Delta }\dot{M}$) and distributed subglacial discharge (F_s) for different T_b values. (b) The relationship between $\mathrm{\Delta }\dot{M}$ and T_b for different F_s values. In both panels, the circles connected by dotted lines are modeled anomalies calculated from the interfacial melt rate, while the crosses connected by dashed lines are modeled anomalies calculated from the total melt rate – the sum of the interfacial melt rate and freezing rate due to frazil formation. The solid line is the fit from Eq. (A1).

We also tested the robustness of the scaling relationship between $\mathrm{\Delta }\dot{M}$ and F_s to varying latitude via the Coriolis parameter. This was tested for the PC case for latitudes of 45, 65, 85, and 90° S, in addition to the latitudes of 0 and 75° S that are the focus of the paper. We find that in cases where $W/R_{\mathrm{d}}\gg \mathrm{1}$, $\mathrm{\Delta }\dot{M}$ scales well with two-thirds power of F_s independently of latitude (Fig. A1c).

Finally, to check whether the scaling of $\mathrm{\Delta }\dot{M}$ with F_s holds across different ambient temperatures, we run temperature sensitivity experiments for the rotating, distributed case. We find that the two-thirds power scaling holds across different values of far-field bottom potential temperature (Fig. A5a), especially for interfacial melting. At colder temperatures ($T_{\mathrm{b}}=-\mathrm{1.9}$ °C), when significant quantities of frazil form and frazil freezing anomalies largely compensate for interfacial melting anomalies, the $\mathrm{\Delta }\dot{M}$ sensitivity to F_s drops and is saturated (Fig. A5a, dashed black line). Unfortunately, the representation of frazil dynamics in MPAS-Ocean is rather simplistic, so we are not in a position to investigate frazil-related dynamics in greater detail. Finally, based on the rotating, distributed case, we confirm that $\mathrm{\Delta }\dot{M}$ depends approximately linearly on ambient potential temperature (Fig. A5b) in the same way as it does in the non-rotating, convectively forced plume theory (Jenkins, 2011). The functional fit used to produce the solid curves in Fig. A5 is

$$\begin{array}{}\text{(A1)}& \mathrm{\Delta }\dot{M}=k(T_{\mathrm{b}}-T_{\mathrm{0}})F_{\mathrm{s}}^n,\end{array}$$

with $n=\mathrm{2}/\mathrm{3}$ being imposed. The remaining coefficients T₀ and k can be obtained using regression, but their values will likely depend on the ice-shelf dimensions and shape. The least-squares fit in Fig. A5 yields T₀ that is a bit lower than the freezing point, indicating that the equation does not apply well when ambient temperatures are close to the freezing point and when frazil dynamics become important (Fig. A5a, dashed black line), as already discussed.