Impact of glacial isostatic adjustment on zones of potential grounding line persistence in the Ross Sea Embayment (Antarctica) since the Last Glacial Maximum

Ice streams in the Ross Sea Embayment (West Antarctica) retreated up to 1000 km since the Last Glacial Maximum (LGM). One way that bathymetry influenced this retreat was through the presence of local bathymetric highs, or pinning points, which decreased ice flux through the grounding line and slowed grounding line retreat. During this time, glacial isostatic adjustment vertically shifted the underlying bathymetry, altering the grounding line flux. Continental-scale modeling efforts have demonstrated how solid Earth–ice sheet interactions impact the deglacial retreat of marine ice sheets; however, these models are too coarse to resolve small-scale bathymetric features. We pair a high-resolution bathymetry model with a simple model of grounding line stability in an ensemble approach to predict zones of potential grounding line persistence in the Ross Sea Embayment for given combinations of surface mass balance rate, degree of ice shelf buttressing, basal friction coefficient, and bathymetry (corrected for glacial isostatic adjustment using three different ice sheet histories). We find that isostatic depression within the interior of the Ross Sea Embayment during the LGM restricts zones where grounding lines can persist to near the edge of the continental shelf. Most grounding lines cannot persist near the present-day grounding line until sufficient uplift has occurred (mid-Holocene; ∼ 5 ka), and this uplift causes a net upstream migration of grounding line persistence zones across the deglaciation. Additionally, our results show that coarse-resolution bathymetry underpredicts possible stable grounding line positions, particularly near the present-day grounding line, highlighting the importance of bathymetric resolution in capturing the impact of glacial isostatic adjustment on ice stream stability.

1 Introduction

Since the Last Glacial Maximum (LGM) at approximately 26–19 ka (Clark et al., 2009), ice streams in the Ross Sea Embayment sector of West Antarctica have retreated up to 1000 km to their present-day grounding line position (where ice transitions from grounded to floating). Bathymetry can influence the retreat of marine ice sheets by guiding grounding lines through deep submarine troughs (Halberstadt et al., 2016; Jones et al., 2021) or by slowing retreat through local bathymetric highs known as pinning points. Pinning points, either a product of antecedent bathymetry or sediment deposited in the form of grounding zone wedges (Bart et al., 2018; Bart and Tulaczyk, 2020; Jamieson et al., 2012; Simkins et al., 2018), can slow or pause ice sheet retreat by decreasing ice flux through the grounding line (Jamieson et al., 2012; Robel et al., 2022; Schoof, 2007). Over the last deglaciation, the bathymetry underlying the marine-based (grounded below sea level) Ross Sea Embayment of the Antarctic Ice Sheet has been modulated by glacial isostatic adjustment (GIA), the solid Earth's response to ice sheet unloading through crustal deformation and perturbations to the Earth's gravitational field and rotation axis (Kendall et al., 2005). Local ice sheet retreat causes sea level to fall at the grounding line due to solid Earth rebound and a decrease in gravitational attraction, which slows the modeled retreat rate for marine sectors of the Antarctic Ice Sheet experiencing mass loss (de Boer et al., 2014; van Calcar et al., 2023; Gomez et al., 2013, 2015, 2018; Konrad et al., 2015; Pollard et al., 2017). In the Ross Sea Embayment, GIA-induced uplift is hypothesized to have stabilized the ice sheet during the Holocene by directly triggering grounding line readvance to its present-day position (Kingslake et al., 2018) or by modulating ice sheet sensitivity to ocean forcing, which similarly could have driven readvance (e.g., Lowry et al., 2024).

Although coupled GIA–ice sheet models provide valuable insight into ice sheet–solid Earth interactions across Antarctica, they are computationally expensive. As a result, ensemble runs of ice sheet or coupled GIA–ice sheet models that can encompass uncertainties in climate and glaciologic conditions are run at relatively coarse resolution (16–40 km; Albrecht et al., 2020, 2024; van Calcar et al., 2023; Gomez et al., 2018; Pollard et al., 2017) and are unable to resolve smaller-scale bathymetric features, such as pinning points (≤5 km; e.g., McKenzie et al., 2023), which influence grounding line evolution. Recent coupled GIA–ice sheet modeling showed that increasing bathymetric resolution (from 2 to 1 km) slowed predicted grounding line retreat by up to ∼ 20 % in the Amundsen Sea (Houriez et al., 2025); however, such high-resolution modeling is more appropriate for smaller regions (the Ross Sea Embayment is $\sim \mathrm{4}\times$ their model domain size) and for timescales of centuries rather than millennia. Exploring the impact of high-resolution bathymetry on grounding evolution since the LGM across a larger area, such as the Ross Sea Embayment, is still a computational challenge.

Here, we use an ensemble ($n=\mathrm{9}\times {\mathrm{10}}^{\mathrm{5}}$) of simple grounding line stability calculations to isolate how bathymetric change due to GIA impacts ice stream grounding line persistence across the deglaciation of the Ross Sea Embayment. We model possible grounding lines along 147 LGM ice stream flowlines in the Ross Sea Embayment across high-resolution models of the present day and 20 ka GIA-corrected bathymetry. Rather than reconstructing an exact history of grounding line evolution, we predict zones where a potential grounding line could persist at 20 ka and the present day. This choice allows us to produce a probability distribution of locations where past ice stream grounding lines were likely to persist, termed “zones of potential persistence”, across the entire Ross Sea Embayment. We use these predictions to explore how GIA modulates ice stream stability across the deglaciation.

2 Methods

2.1 Modeling Ross Sea Embayment paleobathymetry

To reconstruct Ross Sea Embayment 20 ka bathymetry, we modify present-day BedMachine v1.38 bathymetry (500 m horizontal resolution; Morlighem et al., 2020) for the spatiotemporal patterns of GIA caused by the deformational, gravitational, and rotational effects associated with changes in ice load (i.e., bathymetry_20 ka= bathymetry_pres – relative sea level_20 ka). Sedimentation would have also altered the 20 ka bathymetry of the Ross Sea Embayment since the LGM; however, knowledge of the timing and magnitude of sedimentation across the Ross Sea Embayment is limited to grounding zone wedges (Bart et al., 2018; Danielson and Bart, 2024), and so we focus on the role of GIA. Our simulations are based on the sea-level theory and pseudo-spectral algorithm described by Kendall et al. (2005), with a spherical harmonic truncation at degree and order 512 (spatial resolution of ∼ 40 km). This treatment includes the impact of load-induced Earth rotation changes on sea level (Milne and Mitrovica, 1996), evolving shorelines, and the migration of grounded, marine-based ice (Johnston, 1993; Kendall et al., 2005; Lambeck et al., 2003; Milne et al., 1999). Our GIA simulations require two inputs: (1) an Earth structure model with a depth-varying viscosity of the mantle along with an elastic lithospheric thickness and (2) the space–time geometry of ice sheet thickness. The resulting GIA output varies smoothly across spatial scales much broader than the spatial scales of Ross Sea Embayment bathymetric changes.

The LGM extent and deglacial history of Antarctica are uncertain due to a paucity of datasets constraining past ice thickness and sea-level change (Clark and Tarasov, 2014; Deschamps et al., 2012; Golledge et al., 2014; Gomez et al., 2018, 2020; Lambeck et al., 2014; Lin et al., 2021; Pittard et al., 2022; Simms et al., 2019; Whitehouse et al., 2012). To represent these uncertainties, we use three different ice sheet histories that span a plausible range of LGM ice sheet thickness reconstructions. The first ice history Golledge et al. (2014; henceforth Gol14) contains a deglacial Antarctic Ice Sheet volume change of ∼ 10.5 m global mean sea-level equivalent (GMSLE) and was run at 14 km resolution and 100-year time steps. Gol14 was created from the median of an ensemble of Parallel Ice Sheet Model (PISM) runs (Bueler and Brown, 2009) forced by an Earth system model and uniform sea-level changes and constrained by geologic observations such as ice-core-derived changes in regional ice thickness. The second ice history (Whitehouse et al., 2012; henceforth W12) contains a deglacial Antarctic Ice Sheet volume change of ∼ 8 m GMSLE, was created by running the GLIMMER ice sheet model (Rutt et al., 2009) for discrete time intervals (20, 15, 10, and 5 ka) with a 20 km resolution, and is constrained by glaciologic, geologic, and Antarctic relative sea-level records. The third ice history (Gomez et al., 2018; henceforth Gom18) has a deglacial Antarctic Ice Sheet volume change of ∼ 6 m GMSLE. The Gom18 model is a single model run of a coupled, gravitationally consistent GIA–dynamic ice sheet model that incorporates a 3-D Earth structure and was forced by climate via benthic δ¹⁸O records. The ice sheet model was run with 20 km resolution and 200-year time steps.

These ice sheet histories encompass a range of potential Antarctic Ice Sheet volume changes (6–10.5 m GMSLE; Supplement Fig. S1) and therefore a range of potential GIA magnitudes across the Ross Sea Embayment. To simulate GIA for W12 and Gol14, we use a 1-D, radially symmetric Earth model with a lithospheric thickness of 96 km and an upper and lower mantle viscosity of 10²¹ and 10²² Pa s, respectively. Our Earth model is similar to the best-fit 1-D Earth model used in Whitehouse et al. (2012), which was determined by inverting for the solid Earth rheology that best fit Antarctic deglacial sea-level data and is consistent with local constraints on upper mantle viscosity (Nield et al., 2016). We explore the sensitivity to our choice in Earth model by simulating GIA for W12 and Gol14 using two alternatives. One is the VM5a Earth model (lithosphere thickness of 96 km, average upper and lower mantle viscosity of 0.5×10²¹ and 1.6×10²¹, respectively (Peltier et al., 2015). Additionally, we consider a lower-viscosity Earth model representative of West Antarctica, with a 50 km lithosphere and low-viscosity zone of 10¹⁹ Pa s from 50 km to 200 km depth, a viscosity of 0.2×10²¹ Pa s to 670 km depth, and a lower mantle viscosity of 3×10²¹ Pa s (Pollard et al., 2017).

2.2 Simulating grounding line persistence

To determine the locations where grounding lines can persist in the Ross Sea Embayment, we first trace 147 LGM ice stream flowlines based on reconstructions of Anderson et al. (2014) and present-day ice sheet flow (Rignot et al., 2011). From the ice divide to the present-day grounding line, ice flowlines are based on observed ice surface velocities (Rignot et al., 2011), and from the present-day grounding line to the edge of the continental shelf, ice flowlines follow paleo-ice flow reconstructions of Anderson et al. (2014). We consider the 20 ka bathymetry and present-day bathymetry to compare LGM and interglacial (i.e., present-day) endmembers. Although Ross Sea Embayment ice stream flowlines underwent localized reorganization throughout the last deglaciation (Greenwood et al., 2018; Lee et al., 2017), we use LGM flowlines when modeling grounding line persistence for both the 20 ka and present-day bathymetry to make clear comparisons between these time periods. By using LGM flowlines for both the 20 ka and present-day bathymetry, we can track zones of grounding line persistence throughout the entire Ross Sea. Although using LGM flowlines for the present day can result in predicting steady-state stability at locations that are inconsistent with the observational record (e.g., predicting grounding line locations that do not correspond to the observed present-day grounding line), this approach expands our understanding of solid Earth–ice sheet interactions in a way that would not be possible with traditional ice sheet modeling methods.

We model the potential locations where grounding lines can persist for each ice stream flowline by first extracting its bathymetric profile for the present-day bathymetry and the 20 ka bathymetries associated with each ice history. We then use a simple differential equation for the mass balance of a marine-terminating ice stream (Eq. 1 in Robel et al., 2018, following Schoof, 2012) to test for stability along each ice stream flowline at 500 m spaced nodes.

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}L}{\mathrm{d}t}}=h_{\mathrm{g}}(PL-\mathrm{\Omega }{h}_{\mathrm{g}}^{\mathit{\beta }}),\end{array}$$

in which

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathit{\beta }={\displaystyle \frac{m+n+\mathrm{3}}{m+\mathrm{1}}},\text{(3)}& {\displaystyle }\mathrm{\Omega }={\displaystyle \frac{A{\left({\mathit{\rho }}_{i}g\right)}^{n+\mathrm{1}}{\left(\mathrm{1}-\frac{{\mathit{\rho }}_i}{{\mathit{\rho }}_w}\right)}^n}{{\left({\mathrm{4}}^{n}C\right)}^{\frac{\mathrm{1}}{m+\mathrm{1}}}}}{\mathrm{\Theta }}^{\frac{n}{m+\mathrm{1}}},\text{(4)}& {\displaystyle }{h}_{\mathrm{g}}=-b{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{i}}}},\end{array}$$

where P is the upstream averaged surface mass balance (0.01–0.3 m yr⁻¹; Buizert et al., 2015; Cavitte et al., 2018). L is the distance of the node downstream from the ice divide. t is time. b is bathymetric depth at the grounding line. h_g is ice thickness at the grounding line. Ω is a scalar that accounts for factors that affect grounding line flux such as C, the basal friction (1.62–6.62 Pa s⁻¹), and Θ ice shelf buttressing (0.5–1.0; smaller values represent more buttressing). A is the Nye–Glen law coefficient ($\mathrm{2}\times {\mathrm{10}}^{-\mathrm{24}}$ s⁻¹). n is the accompanying Nye–Glen flow law exponent (3). m is the Weertman friction law exponent ($\frac{\mathrm{1}}{\mathrm{3}})$. ρ_i is the density of ice (917 kg m⁻³). ρ_w is the density of seawater (1028 kg m⁻³). g is gravitational acceleration (9.81 m s⁻²). We consider different combinations of accumulation, basal friction, and ice shelf buttressing parameters (Table 1) by uniformly sampling the range of basal friction and ice shelf buttressing and sampling the range of accumulation rates with a non-linear spacing, since they range over an order of magnitude, resulting in an ensemble of 2000 linear stability analyses at each node along an ice stream flowline.

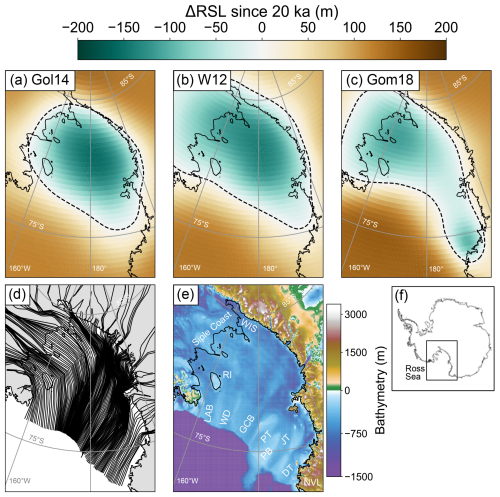
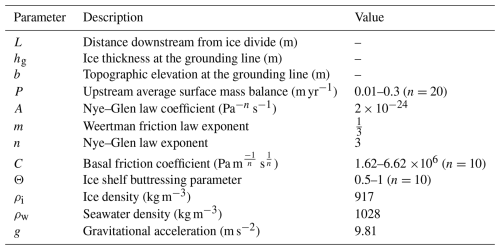
Figure 1 Change in relative sea level (ΔRSL) from 20 ka to the present day for (a) Gol14, (b) W12, and (c) Gom18. The solid black line is the present-day grounding line and the dashed black line marks the zero-contour line of ΔRSL since 20 ka. (d) Last Glacial Maximum ice stream flowlines based on Anderson et al. (2014) and Rignot et al. (2011). (e) Present-day bathymetry of the Ross Sea Embayment (Morlighem et al., 2020). LAB – Little America Basin, WD – Wales Deep, GCB – Glomar Challenger Basin, PT – Pennell Trough, PB – Pennell Bank, JT – JOIDES Trough, DT – Drygalski Trough, RI – Roosevelt Island, NVL – Northern Victoria Land, WIS – Whillans Ice Stream. (f) Inset of Antarctica. The black box shows the extent of panels (a)–(e), and the solid black line represents the present-day grounding line from MEaSUREs (Rignot et al., 2011).

We allow for ice shelf buttressing, given evidence for the formation of ice shelf embayments in both the East and West Ross Sea (e.g., Bart et al., 2018; Prothro et al., 2020), and our average upstream surface mass balance values are consistent with local ice core and ice-penetrating radar records (Buizert et al., 2015; Cavitte et al., 2018). The form of the grounding line flux ($\mathrm{\Omega }{h}_{\mathrm{g}}^{\mathit{\beta }}$) is taken from prior asymptotic approximation studies of ice flux at grounding lines (e.g., Schoof, 2007; Haseloff and Sergienko, 2018) and is appropriate to use here since we only analyze the steady state of Eq. (1). The form used here assumes a given Weertman-style basal friction law, no lateral shear stress, and buttressing from an ice shelf of fixed size. While other forms of the grounding line flux (Haseloff and Sergienko, 2018) may be used, the results here are unlikely to be strongly dependent on the particular form used, as long as there is a strong dependence on bathymetry (as occurs in existing grounding line flux approximations, e.g., Schoof, 2007).

A node is a potential “stable steady state” if two conditions are met: (1) if the ice flux into the node is equal to the ice flux out ($\frac{\mathrm{d}L}{\mathrm{d}t}=\mathrm{0}$) in Eq. (1) and (2) if the first derivative of the right-hand side of Eq. (1) with respect to L is negative (i.e., perturbations to the grounding line position return the grounding line to its original position). This is expressed as

$$\begin{array}{}\text{(5)}& P{h}_{\mathrm{g}}^{-\mathrm{1}}+\left[PL{h}_{\mathrm{g}}^{-\mathrm{2}}+\left(\mathit{\beta }-\mathrm{1}\right)\mathrm{\Omega }{h}_{\mathrm{g}}^{\mathit{\beta }-\mathrm{2}}\right]{\displaystyle \frac{{\mathit{\rho }}_w}{{\mathit{\rho }}_i}}{\displaystyle \frac{\mathrm{d}h}{\mathrm{d}L}}<\mathrm{0}.\end{array}$$

These conditions constitute a linear stability analysis of the grounding line position (Schoof, 2012; Robel et al., 2018).

Table 1 Parameters and values used for linear stability analysis.

As prior studies have argued (Robel et al., 2022; Sergienko and Haseloff, 2023), the dynamic natures of climate, ice sheets, and the solid Earth make it unlikely that grounding lines will achieve a mathematically stable steady state in the real world. However, linear stability analysis provides a useful guide to identify locations where grounding lines were likely to have persisted or slowed retreat for prolonged periods without information about where the ice margin existed geologically at any time, since information about the age and location of past grounding lines is uncertain.

Along each ice stream flowline bathymetry profile, our ensemble analysis predicts “stable steady-state” grounding line locations for different combinations of surface mass balance, ice shelf buttressing, and basal friction coefficient (P, θ, C; Table 1). Thus, our predicted stable steady-state locations are not the grounding line location at any given time, but rather where – for a combination of P, θ, and C – an ice stream grounding line could achieve mathematical stability. We interpret the parts of each flowline that contain more stable steady-state grounding line locations as being zones where the grounding line can persist across a wider range of glacial and climate conditions (zones of potential persistence, ZPP), either at the present day or 20 ka, for an extended period of time. Once we predict stable steady-state grounding lines along a bathymetric transect, we explore the impact of grid resolution by resampling the bathymetric transect at progressively coarser grid resolutions and repeating the linear stability analysis. We resample by smoothing the transect using a windowed mean of the desired resolution and then resampling the smoothed bathymetry at the desired resolution.

To validate the results from our simple model of grounding line persistence, we also modeled transient grounding line evolution with a 1-D flowline model of marine ice sheet evolution, using the shallow-shelf approximation (Robel, 2021; Schoof, 2007). This model provides an alternative method to identify the role of GIA for transient cases that do not attain a strict steady state and that do not require most of the assumptions intrinsic to Eq. (5) (e.g., grounding line dynamics are a smooth system). We calculate grounding line retreat rates and grounding line discharge over the 20 ka and present-day bathymetries and compare spatial patterns of transient grounding line retreat and discharge between the 20 ka and present-day bathymetries (Supplement). Our transient modeling mirrors our results with the stability analysis; we find that grounding line discharge decreases and grounding line retreat rates decrease at the same locations where we predict zones of potential persistence with our simpler model (Fig. S2). These similarities are not surprising since the model captured by Eqs. (1)–(3) is designed to approximate more complex ice sheet models at steady states.

3 Results and discussion

3.1 Patterns of GIA across the Ross Sea Embayment

From 20 ka to the present day, all three ice histories result in a relative sea-level (RSL) fall due to GIA uplift of the Ross Sea Embayment interior (Fig. 1a–c). The ice histories with larger excess LGM ice volume cause a larger RSL change, with a maximum RSL change of −140 to −170 m (Fig. 1a; b) for W12 (GMSLE =8 m) and Gol14 (GMSLE =10.5 m; Fig. S3), respectively. The interior of the Ross Sea Embayment, offshore of the Siple Coast (SC, Fig. 1e), experiences the maximum uplift in both of these ice histories. In contrast, Gom18 produces a smaller magnitude of uplift in the Ross Sea Embayment (RSL fall of −115 m; Fig. 1c), with two centers of maximum uplift: one offshore of the Siple Coast (Fig. 1c) and the other near Northern Victoria Land (NVL; Fig. 1c). The different pattern of GIA-induced uplift results from the lower viscosity in the Ross Sea Embayment used in Gom18 compared to the higher-viscosity 1-D Earth structure used in simulations of W12 and Gol14, in addition to differences in the ice loading history (Figs. 1a–c, S4; Gomez et al., 2018).

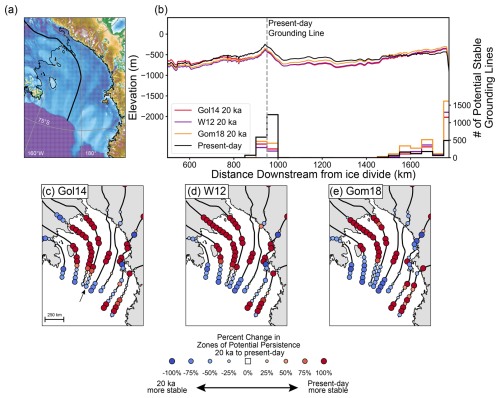
Figure 2 Zones of potential persistence (ZPP) along individual flowlines. (a) Flowline path of the paleo-Whillans ice stream and present-day bathymetry of the Ross Sea Embayment (Morlighem et al., 2020). (b) Present-day bathymetry (black) and 20 ka GIA-corrected paleobathymetry for W12 (purple), Gol14 (red), and Gom18 (orange) along the paleo-Whillans ice stream flowline with corresponding histograms of simulated stable grounding line positions. Histograms and corresponding bathymetry share colors. (c–e) Percent change in the number of modeled potential stable grounding line positions from 20 ka (LGM) bathymetry to the present-day bathymetry for Gol14 (c), W12 (d), and Gom18 (e) ice histories. The arrow in panel (c) denotes flowline used in panel (b).

3.2 The impact of GIA on grounding line persistence from 20 ka to the present day

Next, we quantify how GIA impacts where grounding lines can persist. For each ice stream, our ensemble analysis predicts the locations of stable steady-state grounding line positions for a given bathymetry (20 ka and the present day) and a set of parameter values. For example, Fig. 2b shows the count of potential stable steady-state grounding lines associated with the reconstructed bathymetric transect for the paleo-Whillans ice stream (Fig. 2a) corrected for GIA (Gom18 – orange, W12 – purple, Gol14 – red; Fig. 2b), compared to the present-day bathymetry (black; Fig. 2b). Present-day bathymetry contains a higher count of potential stable steady states upstream of the flowline, close to the present-day grounding line (black; Fig. 2b), compared to any of the 20 ka bathymetries corrected for GIA (orange, purple, and red; Fig. 2b), which contain higher counts of potential stable steady states near the edge of the continental shelf.

Zones along the transect with higher counts of potential stable grounding line locations are stable across a wider range of input parameter combinations and therefore have a relatively higher likelihood of persisting at that location, regardless of parameter uncertainty and are referred to as zones of potential persistence (ZPP). Each zone contains the count of potential stable grounding lines within a 50 km reach along a given ice stream flowline (Fig. 2b). The present-day bathymetry has zones of potential persistence near the present-day grounding line (∼ 750 km downstream, black; Fig. 2b), whereas each 20 ka bathymetry has zones of potential persistence near the continental shelf break (∼ 1600 km downstream, orange, purple, and red; Fig. 2b).

To quantify how zones of potential persistence shift across the deglaciation, we calculate the percent change in the number of stable steady-state grounding lines within a given 50 km reach of an ice stream transect from 20 ka to the present day. We calculate the percent change in zones of potential persistence along eight flowlines divided into 50 km reaches and find that, similar to predictions for the paleo-Whillans ice stream, zones of potential persistence decrease near the continental shelf break and increase further upstream from 20 ka to the present day (Fig. 2c–e).

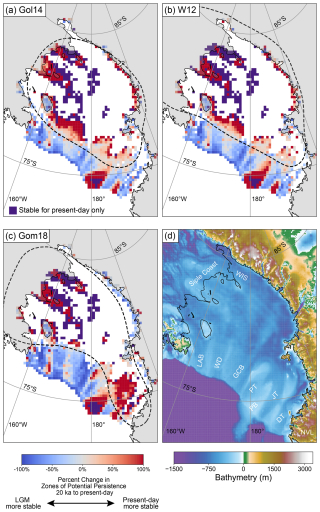
Figure 3 GIA-induced percent change in zones of potential persistence (ZPP) across 20 km × 20 km grid cells for the entire Ross Sea Embayment based on glacial isostatic adjustment simulations for (a) Gol14, (b) W12, and (c) Gom18. Grid cells that have stable steady-state grounding line positions in the present day and no stable steady-state grounding line positions at 20 ka are marked in purple. The thin black line is the present-day grounding line, and the dashed line is the zero-contour line of ΔRSL since 20 ka. (d) Present-day bathymetry of the Ross Sea Embayment (Morlighem et al., 2020).

We then expand our grounding line stability analysis to all 147 ice stream flowlines. We bin stable steady-state grounding lines within a 20 km × 20 km grid to identify zones of potential persistence for the 20 ka and present-day bathymetries and calculate the percent change in zones of potential persistence from 20 ka to the present day (Fig. 3). From 20 ka to the present day, there are fewer zones of potential persistence near the edge of the continental shelf (these locations were more stable during the LGM; blue; Fig. 3) and more zones of potential persistence upstream, suggesting these locations are more stable during the present day (red and purple; Fig. 3). The general pattern of downstream decrease in zones of potential persistence across the deglaciation is interspersed with isolated regions of increased or minimal change in zones of potential persistence, corresponding to ridges separating the Little America Basin, Wales Deep, and Glomar Challenger Basin (LAB, WD, and GCB; Figs. 4c, 1e). The Gom18 model predicts slightly different patterns compared to the Gol14 and W12 models, with the decrease in zones of potential persistence extending further upstream and a larger area of increased zones of potential persistence near the JOIDES and Drygalski troughs (JT and DT; Fig. 1e), caused by the second center of maximum uplift.

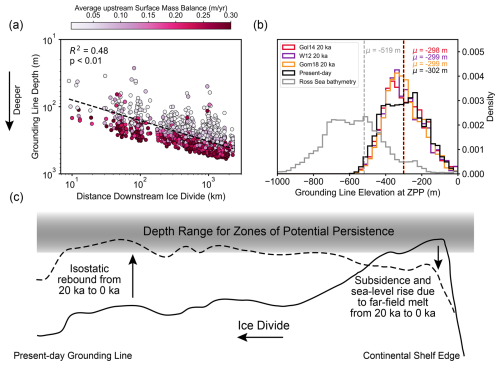
Figure 4 (a) Average upstream surface mass balance at distance downstream of the ice divide and grounding line elevation for stable steady-state grounding line positions on present-day bathymetry. (b) Histograms of elevations for the present-day bathymetry of the Ross Sea Embayment (grey), stable steady-state grounding line elevation simulated for present-day bathymetry (black), and 20 ka paleobathymetry corrected for glacial isostatic adjustment based on the ice histories of Gol14 (red), Gom18 (orange), and W12 (purple). (c) Schematic illustrating how glacial isostatic adjustment moves bathymetry into and out of the depth range for zones of potential persistence.

There are two GIA mechanisms that cause the locations of zones of potential persistence to shift upstream over the last deglaciation: (1) sea-level fall caused by rebound of the solid Earth under the locus of ice mass loss (∼ 250 m) and (2) sea-level rise caused by global ice sheet melt (∼ 130 m), as well as secondarily by the collapse of the Antarctica peripheral bulge (∼ 10 m; Fig. S3). Within the interior of the Ross Sea Embayment, relative sea-level fall caused by isostatic rebound is nearly twice the magnitude of the sea-level rise caused by global ice sheet melt. In contrast, near the continental shelf edge, relative sea-level rise is dominated by global ice sheet melt, while peripheral bulge collapse contributes <10 % to the signal.

Isostatic rebound shoals bathymetry within the interior of the Ross Sea Embayment, decreasing flux through the grounding line, thus increasing the potential for a stable steady-state grounding line at the present day. Sea-level rise caused by far-field ice sheet melt and Antarctic peripheral bulge collapse causes increased grounding line flux, which decreases the likelihood of a stable steady-state grounding line position near the edge of the continental shelf at the present day (Fig. 3).

Together, these GIA mechanisms cause a net upstream migration of zones of potential persistence. During the LGM, the grounding line was located near the edge of the continental shelf, and at the present day, the grounding line is located within the Ross Sea Embayment interior. At the present day, GIA has caused the interior of the Ross Sea Embayment to rebound, resulting in the emergence of zones of potential grounding line persistence co-located with the present-day grounding line. These zones of potential persistence located near the present-day grounding line are less prevalent at 20 ka due to isostatic depression and predominantly do not emerge until the mid-Holocene (∼ 5 ka; Fig. S5) for all ice histories, suggesting that large magnitudes of isostatic rebound over a prolonged period (i.e., deglacial timescale) provide persistence at the present-day grounding line location.

Our analysis shows that GIA promotes grounding line stability near the edge of the continental shelf during the LGM, and it promotes grounding line stability within the Ross Sea Embayment interior at the present day. The co-occurrence of inferred locations of the grounding line for the present day and LGM suggests GIA stabilizes the grounding line at both the glacial maximum climate states and interglacial climate states.

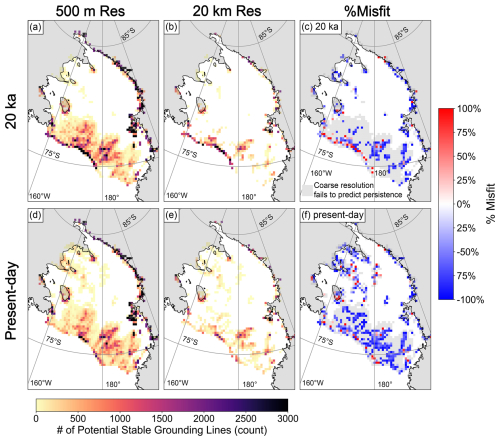
Figure 5 Zones of potential persistence for Gom18 Last Glacial Maximum (20 ka) (a–c), the present day (d–f), for high-resolution (50 m; a, d) and low-resolution (20 km; b, e) percent misfit for 20 ka (c) and the present day (f). Defined as the difference between zones of potential persistence calculated using high-resolution and coarse-resolution bathymetry divided by zones of potential persistence calculated using high-resolution bathymetry $\left(\frac{{\mathrm{ZPP}}_{\mathrm{500}\mathrm{m}}-{\mathrm{ZPP}}_{\mathrm{20}\mathrm{km}}}{{\mathrm{ZPP}}_{\mathrm{500}\mathrm{m}}}\right)$. Light grey shows where coarse resolution fails to predict persistence.

Global-scale ice sheets reinforce zones of potential persistence at the LGM grounding line. The occurrence of zones of potential persistence at 20 ka within the deep submarine troughs of the Ross Sea Embayment (Fig. 3) is due to lower LGM relative sea level caused by Northern Hemisphere ice sheet growth and the resulting global sea-level lowstand. Simulations that ignore Northern Hemisphere ice sheets underestimate zones of potential persistence at 20 ka by up to 100 % (Fig. S4), emphasizing the importance of large Northern Hemisphere ice sheets for stabilizing the LGM grounding line at the continental shelf edge and potentially driving larger LGM ice volume in the Ross Sea Embayment.

Our finding that zones of potential persistence increase at the Ross Sea Embayment LGM grounding line due to GIA parallels the finding that far-field ice sheet retreat has an important feedback on Antarctic Ice Sheet deglaciation (Gomez et al., 2020). While previous studies focused on the influence of GIA on transient grounding line retreat (solid Earth feedbacks due to ice mass loss at a given time step; de Boer et al., 2014; van Calcar et al., 2023; Gomez et al., 2013, 2015, 2018; Konrad et al., 2015; Pollard et al., 2017), our analysis instead provides a window into how GIA reinforces the grounding line at endmember glacial–interglacial time frames.

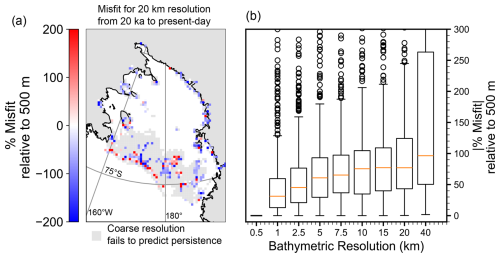
Figure 6 (a) Misfit of 20 km resolution compared to 500 m resolution for predicted zones of potential persistence from 20 ka to the present day. Percent misfit defined as the difference between zones of potential persistence calculated using high-resolution and coarse-resolution bathymetry divided by zones of potential persistence calculated using high-resolution bathymetry $\left(\frac{\mathrm{\Delta }{\mathrm{ZPP}}_{\mathrm{500}\mathrm{m}}-\mathrm{\Delta }{\mathrm{ZPP}}_{\mathrm{20}\mathrm{km}}}{\mathrm{\Delta }{\mathrm{ZPS}}_{\mathrm{500}\mathrm{m}}}\right)$. Light grey shows where coarse resolution fails to predict stability. (b) Magnitude distribution of percent misfit between zones of potential persistence calculated with 500 m resolution bathymetry and coarser bathymetry resolutions.

3.3 Characteristic stable grounding line depths for the Ross Sea Embayment

GIA moves zones of potential persistence by modulating the bathymetry of the Ross Sea Embayment. However, bathymetry is only one of the parameters that determines where grounding line persistence occurs. Grounding line persistence is a function of surface mass balance (P), ice shelf buttressing (Θ), basal friction (C), distance downstream from the ice divide (L), and ice thickness at the grounding line (h_g). Therefore, for a given combination of input parameters (Table 1), there is an ice thickness h_g (and equivalent grounding line depth b) that produces a stable grounding line position (Figs. 4a and S5). Our linear stability analysis shows that stable grounding line depth is a function of the other input parameters (Figs. 4a and S6). For instance, distance downstream from the ice divide and average upstream surface mass balance rate are both negatively correlated with grounding line depth (Fig. 4a). Therefore, the depths at which we predict stable grounding lines are a function of both the deglacial climate system and the geometry of the Antarctic Ice Sheet. As a result, the mean stable grounding line depths for the 20 ka bathymetry and present-day bathymetry are similar (Fig. 4a). These mean depths are significantly different from the bathymetry we input into the simple model of grounding line persistence (Fig. 4; grey, t test, p_{present day}, p_W12, p_Gol14, and p_Gom18<0.001), showing that the depth range at which our simple model finds persistence depends on our input parameters and the ice flowline geometry of the Ross Sea Embayment. Therefore, we infer that zones of potential persistence migrate spatially due to GIA by causing bathymetry to be uplifted or subsided into and out of this characteristic depth range (Fig. 4c).

3.4 Influence of grid resolution on predicted zones of potential persistence

To explore the effects of grid resolution, we use high-resolution (500 m; Morlighem et al., 2020) bathymetry and resample to coarser resolution (up to 40 km) to compare how predicted zones of potential persistence vary across the Ross Sea (Fig. 5). Some of the datasets constraining bathymetry in the Ross Sea Embayment are gravity based and therefore have a true resolution coarser than the 500 m output resolution of BedMachine. Nonetheless, we decide to treat BedMachine as 500 m resolution in the Ross Sea Embayment to explore the potential impacts of grid resolution. We predict fewer zones of potential persistence across the Ross Sea Embayment at 20 ka and the present day when using the coarse grid resolution (20 km; Fig. 5b, c). Predictions with coarse-resolution bathymetry largely fail to produce zones of potential persistence near the edge of the continental shelf (Fig. 5c). Furthermore, the coarse-resolution prediction fails to predict zones of potential persistence near the present-day grounding line on the present-day bathymetry (Fig. 5f).

Since coarse grid resolution underpredicts zones of potential persistence for 20 ka and present-day bathymetry, coarse-grid resolution will also underpredict how GIA migrates zones of potential persistence across the deglaciation. We quantify how coarse grid resolution underpredicts the impact of GIA by calculating the change in zones of potential persistence from 20 ka to the present day (Fig. 3) but with coarser grid bathymetric resolution (20 km). Figure 6a shows the percent misfit for change in zones of potential persistence from 20 ka to the present day of 20 km resolution compared to 500 m resolution $\left(\frac{\mathrm{\Delta }{\mathrm{ZPP}}_{\mathrm{500}\mathrm{m}}-\mathrm{\Delta }{\mathrm{ZPP}}_{\mathrm{20}\mathrm{km}}}{\mathrm{\Delta }{\mathrm{ZPP}}_{\mathrm{500}\mathrm{m}}}\right)$.

We find that the coarse-resolution bathymetry underpredicts the impact of GIA near the present-day grounding line (blue; Fig. 6a) and fails to capture the impact of GIA within most of the deep submarine troughs (grey; Fig. 6a), suggesting that high-resolution bathymetry may be necessary to fully quantify the role of GIA in potential retreat and readvance scenarios in the Ross Sea Embayment (Balco et al., 2023; Kingslake et al., 2018; Lowry et al., 2024; Neuhaus et al., 2021; Nichols et al., 2024; Venturelli et al., 2020). We also vary the coarseness of the grid resolution and find that, as grid resolution coarsens, percent misfit converges towards ∼ 80 %–90 % (compared to 500 m bed resolution; Fig. 6b), highlighting the need for fine grid resolution to capture interactions between GIA and bathymetry. The importance of bed resolution is, in part, due to the broad-scale retrograde slope of the Ross Sea Embayment bathymetry. In our linear stability analysis, local prograde slope is one of the two conditions needed to achieve linear stability (Eq. 5). A coarse grid resolution smooths over small-scale (≤5 km) bathymetric pinning points, which provide local prograde slope in addition to smoothing over regions of locally shallower grounding line depth. Based on our analysis, compared to 500 m grid resolution, a grid resolution of 40 km leads to a ∼ 95 % misfit, while a grid resolution of 1 km leads to a ∼ 25 % misfit (Fig. 6b).

3.5 Comparisons with the geologic record of grounding line retreat

The Ross Sea Embayment geologic record suggests a complex pattern of asynchronous retreat over the last deglaciation. In the western Ross Sea Embayment, retreat began in the Pennell Trough (PT; Fig. 1e) at ∼ 15 ka and in the JOIDES Trough (JT; Fig. 1e) at ∼ 13 ka (Prothro et al., 2020). Meanwhile, in the eastern Ross Sea Embayment, small-scale retreat in Wales Deep (WD; Fig. 1e) also began at ∼ 15 ka and increased during the early Holocene (Bart et al., 2018). Across the west and east Ross Sea Embayment, the ice sheet remained grounded to the trough banks as the ice sheet retreated through submarine troughs, forming embayments (Halberstadt et al., 2016). The grounding line then retreated throughout the Holocene (Bart et al., 2018; Halberstadt et al., 2016; Prothro et al., 2020). Prior to ∼ 8.6 ka, ice stream flow paths changed direction and readvanced near Drygalski Trough (DT; Fig. 1e; Greenwood et al., 2018; Lee et al., 2017). It is possible that local GIA uplift played a role in this ice stream reorganization as ∼ 60 m of uplift occurred in this region from the LGM to the early Holocene (Fig. S7).

A common pattern across ice sheet histories is a decrease in zones of potential persistence within the deep submarine troughs near the edge of the continental shelf (Fig. 3), which occurs due to sea-level rise driven by far-field ice sheet melt (Fig. S4). The ridges separating the submarine troughs are shallow enough to stabilize the grounding line, despite relative sea-level rise during the deglaciation (Fig. 4c), which prevents a decrease in zones of potential persistence along these ridges. In the geologic record, geomorphic features suggest that the grounding line back-steps up these banks throughout the deglaciation (Halberstadt et al., 2016). Our modeling suggests this back-stepping may be caused by sea-level rise driven by Northern Hemisphere ice sheets, which forces the grounding line to shallower depths in addition to other drivers of retreat, such as ocean forcing.

4 Conclusions

Over the deglaciation, the Ross Sea Embayment experienced sea-level fall within its interior due to glacial isostatic rebound and sea-level rise near the edge of the continental shelf due to far-field sea-level rise and secondarily due to peripheral bulge collapse. We use a simple model of grounding line stability to show that glacial isostatic adjustment promotes grounding line persistence near the edge of the continental shelf at the Last Glacial Maximum and near the present-day grounding line at the present day, resulting in a net upstream migration of zones of potential persistence across the deglaciation. We also show that coarse bathymetric resolution underpredicts grounding line persistence near the present-day grounding line and within the deep submarine troughs of the Ross Sea, thereby underestimating the impact of glacial isostatic adjustment. This finding highlights the importance of resolving small-scale bathymetric features when modeling deglacial and potential grounding line readvance scenarios in the Holocene. In this study, we have shown that, in addition to impacting transient grounding line retreat, glacial isostatic adjustment promotes stability across ice-age timescales by shifting zones of potential grounding line persistence from near the edge of the continental shelf toward the present-day grounding line across the deglaciation. Our results highlight the role of bathymetry, as modulated by solid Earth processes, in shaping the history of ice sheet advance and retreat on glacial–interglacial timescales.