Long-term development of a perennial firn aquifer on the Lomonosovfonna ice cap, Svalbard

An uncertain factor in assessing future sea level rise is the meltwater runoff buffering capacity of snow and firn on glaciers and ice caps. Field studies have resulted in observations of perennial firn aquifers (PFAs), which are bodies of water present deep in the firn layer and sheltered from cold surface conditions. PFAs can store surface melt, thereby acting as a buffer against sea level rise, and influence the thermodynamics of the firn layer. Furthermore, ice dynamics might be affected by the presence of liquid water through hydrofracturing and water transport to the bed, influencing bed properties and ice flow. In this study, we present results of applying the US Geological Survey (USGS) Modular Hydrological Model MODFLOW 6 to an observed perennial firn aquifer on the Lomonosovfonna ice cap in central Svalbard. The observations span a 3-year period, where a ground-penetrating radar (GPR) was used to measure the water table depth of the aquifer. We calibrate our model against these observations to infer a hydraulic conductivity of firn snow of $\mathrm{6.4}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹ and then use the model to project the aquifer evolution over the period 1957–2019. We find that the aquifer was present in 1957 and that it steadily grew over the modeled period with a relative increase of about 15 % in water table depth. On an annual basis, the aquifer exhibits sharp water table increases during the melt season, followed by slow seepage through the cold season.

1 Introduction

Aquifers, defined in groundwater analysis as an underground layer of permeable material that traps liquids in its pore spaces, can hold substantial volumes of water. Firn, defined as multi-year snow with a lower density than ice, contains pore spaces and can therefore also contain water. Kuipers Munneke et al. (2014) found that aquifers can form in firn layers of ice caps or glaciers, given certain meteorological conditions. If a firn aquifer persists for multiple years, i.e., in case it does not entirely drain of refreeze in the cold season, it is referred to as a perennial firn aquifer (PFA).

PFAs can form (i) when there is enough water input into the firn, either by rain or surface melting, and (ii) when there is enough pore space at depth to accommodate the percolated water and to shelter the PFA from refreezing during (winter) cold periods (Kuipers Munneke et al., 2014). Future climate warming introduces both positive and negative effects on PFA extent and volume. On the one hand, increased (atmospheric) temperatures lead to more meltwater and/or rain as input to a PFA, and a less cold winter period reduces conductive cooling and refreezing of a PFA from above. On the other hand, higher firn temperatures lead to a denser firn pack (Brils et al., 2022; van Pelt et al., 2019; Kuipers Munneke et al., 2014) and less firn air content or pore space (Veldhuijsen et al., 2023), lowering the potential of the firn to retain meltwater and thereby preventing volume growth of the aquifer. Regions in which PFAs are already present, such as on the Greenland ice sheet (GrIS) and Svalbard, might disappear or move up-glacier once the firn is too dense to foster a PFA. In other areas that were too cold for PFA formation in the past but have a deep and airy firn layer, PFA formation may be initiated. This could happen, for example, on the Antarctic ice sheet (Veldhuijsen et al., 2024).

A key requirement for PFAs to form is temperate conditions at depths >∼ 10 m below the surface (in addition to a lack of options for the water to drain supraglacially and englacially via streams, crevasses, and moulins). In Svalbard, temperate firn at such depths exists across nearly all accumulation zones (van Pelt et al., 2019), and previous work has already shown PFA existence on the Holtedahlfonna ice cap (Christianson et al., 2015) and on the Lomonosovfonna ice cap (Hawrylak and Nilsson, 2019). Furthermore, PFAs have been found in Greenland (Forster et al., 2014; Koenig et al., 2014) and on mountain glaciers in other Arctic regions, e.g., in Canada (Ochwat et al., 2021) or the USA (Fountain, 1989). Miller et al. (2020) found that the residence time of water in the Greenland PFA is about 6.5 years, and Poinar et al. (2017) found that aquifer flow enhanced the formation of deeper crevasses. Recently, surface meltwater streams have been identified on the Antarctic ice sheet that are said to be able to form firn aquifers (Kingslake et al., 2017). Modeling studies have already shown that perennial firn aquifers can form on the Antarctic Peninsula (van Wessem et al., 2021) and on the rest of the Antarctic ice sheet (van Wessem et al., 2021). Radar observations of an East Antarctic outlet glacier indicate the possible presence of a PFA, comparable to the one found on the Greenland ice sheet (Lenaerts et al., 2017; Lenaerts et al., 2018; Schaap et al., 2020).

Previous efforts have been made to model the formation and development of PFAs. Kuipers Munneke et al. (2015) present a 1D aquifer model, which is designed to assess under what climatic conditions an aquifer will form and how wet firn responds to climate change compared to dry firn. While previous efforts have primarily focused on simulating vertical meltwater percolation (Marchenko et al., 2017a; Steger et al., 2017; Vandecrux et al., 2020), attempts to model water flow in PFAs are scarce. Recently, Miller et al. (2023) modeled a PFA on Helheim Glacier in Greenland using SUTRA-ICE, a 2D model combining groundwater flow with a subsurface energy balance model to calculate freeze–thaw cycles. The model SUTRA-ICE is comprehensive: it contains water flow through the unsaturated zone and water movement within the saturated zone. Freeze–thaw cycles are modeled, so potential winter refreezing of (a part of) the modeled PFA is included. The model is tested on a 2D flowline of Helheim Glacier, with constant recharge rates; 3D flow and realistic meltwater input from a (downscaled) climate or energy balance model are missing. For an extensive comparison of firn models and their components, the reader is referred to Vandecrux et al. (2020) and Stevens et al. (2020).

A key parameter needed to accurately model a PFA is the hydraulic conductivity of firn and snow, being the main control on water flow rates. Fountain and Walder (1998) examined field tests of five different glaciers and found a range of 1–5×10⁻⁵ m s⁻¹. They argue that firn conditions are therefore uniform between glaciers because of the low range in measured hydraulic conductivity. Miller et al. (2017) performed slug tests on the Greenland ice sheet (GrIS) and found hydraulic conductivities ranging between 2.5 × 10⁻⁵ and 1.1 × 10⁻³ m s⁻¹. Stevens et al. (2018) found a range of 10⁻⁶–10⁻² m s⁻¹ in their literature review, using similar techniques to Miller et al. (2017) on 10 Northern Hemisphere glaciers (in Canada, Svalbard, northern Sweden, Greenland, and the Alps).

In this study, we combine 3 years of field data (2017–2019), a state-of-the-art firn model, and a 3D groundwater flow model to simulate the evolution of a PFA found on the Lomonosovfonna ice cap on Svalbard from 1957–2019. We approach the PFA as a classical groundwater system of flow through a porous medium, with meltwater input at the top and outflow through the boundaries. Surface and firn processes, such as melt, water percolation, refreezing, heat diffusion, and firn densification, are resolved by the Energy Balance Firn Model (EBFM; van Pelt et al., 2019), which provides input to the PFA model. The PFA model is calibrated using the hydraulic conductivity, pore close-off depth, and seepage rate to fit with in situ observations of 3 consecutive years, obtained with ground-penetrating radar (GPR) measurements. Our objective with this work is to add to the knowledge of the dynamics of firn aquifers and, in particular, how changes in the aquifer can be described numerically by a hydrogeological model. Furthermore, the modeling gives a long-term perspective of how the thermal regime and water storage have changed on an Arctic ice cap since the 1950s.

2 Study area

The Lomonosovfonna ice cap is situated in central eastern Spitsbergen, the largest island of the Svalbard archipelago; see Fig. 1. It is the highest ice cap of Svalbard, reaching up to 1250 m a.s.l. The Lomonosovfonna ice cap is about 600 km² and feeds into several outlet glaciers. Two of these outlet glaciers, Tunabreen and Negribreen, have surged over the last 20 years (Flink et al., 2015; Haga et al., 2020; Koch et al., 2023).  Nordenskiöldbreen and the Lomonosovfonna ice cap have been monitored since 1997 by Uppsala University and Utrecht University (Marchenko et al., 2019; Marchenko et al., 2017b; Marchenko et al., 2021; Van de Wal et al., 2002). The monitoring program consists of mass balance monitoring, ice velocity measurements, ice thickness measurements, and meteorological observations. A map of the Lomonosovfonna ice cap, showing the locations where the observations took place, is presented in Fig. 1b. Previous glaciological studies on Nordenskiöldbreen and the Lomonosovfonna ice cap, using the data from the monitoring program, have assessed climatic mass balance (van Pelt et al., 2012), snow and firn conditions (Marchenko et al., 2019; Marchenko et al., 2017a; Pohjola et al., 2002), and ice dynamics and thickness (van Pelt et al., 2013, 2018). The modeled grid in this study, together with the areas where GPR observations were made each year, is shown in Fig. 1b (light-blue box).

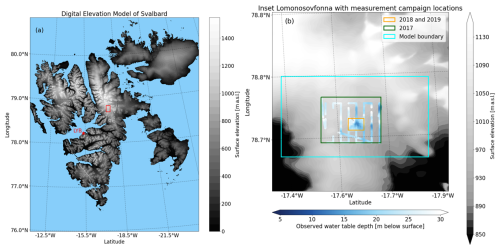
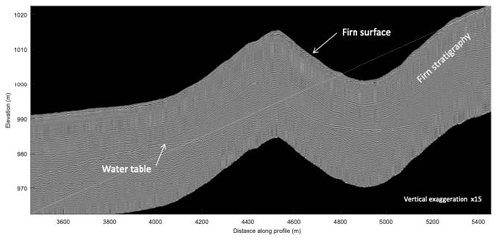
Figure 1 (a) The Svalbard archipelago, plotted from the digital elevation of the Norwegian Polar Institute (2014) model, with Longyearbyen airport (LYB) shown with a red star. Panel (b) is a close-up of the red rectangle in panel (a), showing the location and the observed depth of the water table observations over the years 2017 (green), 2018, and 2019 (orange; same location in both years). The rectangles correspond to the minimum and maximum coordinates of the observations in those years and thus show the extent of the PFA measurements. The model boundary in this study is shown in cyan, with a buffer zone around the observation campaign, The data points obtained in these campaigns are turned to water depths (using the methods described in the next section). The data points and extent of the observation campaign of the years 2018 and 2019 overlap and therefore are nearly identical.

3 Data and methods

3.1 Water table height data

We use water table depth observations obtained at the Lomonosovfonna ice cap as our main tuning data for the ground water flow model. The water table depth was obtained from ground-penetrating radar data, where the water table stands out clearly due to the large permittivity difference between liquid water and air-saturated firn (Fig. 2). The GPR data were collected with a MALÅ ProEx radar system with a 250 MHz antenna pulled behind a snowmobile. The positioning of the radar profiles was done with a two-frequency geodetic GNSS receiver. The GPR profiles followed a grid pattern over the study area (Fig. 1) and were collected during March–April in 2017, 2018, and 2019. The average length of the radar profiles during one season is ∼ 40 km.

The raw GPR data were minimally processed with zero-time adjustment and a low-pass filter (300 MHz cut-off frequency). An example radargram is shown in Fig. 2. The water table is semi-automatically picked from a radargram (example in Fig. 2). Firstly, the reflective surface of the water table is manually found in a single data point. Next, a tracing algorithm is used to track the reflective surface through adjacent points. This results in the two-way travel times (TWTTs) per data point. Then, the velocity of the radar wave in the firn is used to calculate the distance to the water table from the surface. For this, the dielectric constant of firn is required, which is calculated according to Kovacs et al. (1995), where ρ_f is the density of the firn layer and ρ_w the density of water:

$$\begin{array}{}\text{(1)}& {\mathit{ϵ}}_{\mathrm{f}}={\left(\mathrm{1}+\mathrm{0.845}\times {\displaystyle \frac{{\mathit{\rho }}_{\mathrm{f}}}{{\mathit{\rho }}_{\mathrm{w}}}}\right)}^{\mathrm{2}}.\end{array}$$

The density of the firn ρ_f at the location of the observations is obtained from the Energy Balance Firn Model (EBFM; van Pelt et al., 2019), of which a description is given in the next section.

Figure 2 An example of a topographically corrected (×15 exaggeration) radargram. The water table of the firn aquifer is clearly visible and cuts the general firn stratigraphy. The resulting observed water table depth is shown in Fig. 1.

3.2 Water input and firn density from the Energy Balance Firn Model

In this model study, time-dependent firn density and meltwater input are the primary input variables used to model the PFA found at the Lomonosovfonna ice cap. This is retrieved from the Energy Balance Firn Model (EBFM) (Marchenko et al., 2019; van Pelt and Kohler, 2015; van Pelt et al., 2012). Here, we use output from the model version of the EBFM presented in van Pelt et al. (2019), which was previously calibrated and validated against stake measurements, weather station data, and observed firn density profiles from shallow firn cores. For more details, refer to van Pelt et al. (2019) and references therein. A summary of the EBFM components that are most relevant for this study is given below.

Firstly, the EBFM solves the surface energy balance equation:

$$\begin{array}{}\text{(2)}& Q_{\mathrm{melt}}={\mathrm{SW}}_{\mathrm{net}}+{\mathrm{LW}}_{\mathrm{net}}+Q_{\mathrm{sens}}+Q_{\mathrm{lat}}+Q_{\mathrm{sub}}.\end{array}$$

Energy fluxes at the surface that are part of this model are net shortwave radiation flux (SW_net), net longwave radiation flux (LW_net), turbulent heat exchange flux through latent and sensible heat (Q_lat and Q_sens, respectively), and the conductive heat flux into the ice (Q_sub). Equation (2) is solved for the surface temperature with a melt energy flux (Q_melt) set to zero. If the resulting surface temperature is higher than 0 °C, the surface temperature is set at 0 °C and the energy fluxes in Eq. (2) are recomputed, resulting in a value for Q_melt>0. The EBFM requires air temperature, pressure, relative humidity, cloud cover, and precipitation as input to solve the surface energy balance, which comes from the downscaled Norwegian Hindcast Archive (NORA10) regional climate model dataset (Haakenstad et al., 2020).

Below the surface, the EBFM solves the thermodynamic equation and the densification equation. The thermodynamic equation, in which ρ is the firn density, c_p(T) is the temperature-dependent heat capacity of the firn, κ(ρ) is the firn-density-dependent effective conductivity of the firn, F is the refreezing rate (in kg m⁻³ s⁻¹), and L_m is the latent heat of melting ice (3.34×10⁵ J kg⁻¹), describes the temporal change in the temperature–depth profile due to heat conduction and refreezing of percolating and stored meltwater and rainwater.

$$\begin{array}{}\text{(3)}& \mathit{\rho }{c}_{\mathrm{p}}\left(T\right){\displaystyle \frac{\mathit{\delta }T}{\mathit{\delta }t}}={\displaystyle \frac{\mathit{\delta }}{\mathit{\delta }z}}\left(\mathit{\kappa }\left(\mathit{\rho }\right){\displaystyle \frac{\mathit{\delta }T}{\mathit{\delta }z}}\right)+F{L}_{\mathrm{m}}\end{array}$$

The densification equation describes the change in firn density due to gravitational compaction and refreezing.

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\mathit{\delta }\mathit{\rho }}{\mathit{\delta }t}}=K_{\mathrm{g}}\left(\mathit{\rho },T\right)+F\end{array}$$

The firn density of fresh deposited snow is fixed at 350 kg m⁻³. Gravitational compaction K_g(ρ,T) follows Ligtenberg et al. (2011):

$$\begin{array}{}\text{(5)}& K_{\mathrm{g}}\left(\mathit{\rho },T\right)=C\left(b\right)bg\left({\mathit{\rho }}_{\mathrm{ice}}-\mathit{\rho }\right)\exp \left(-{\displaystyle \frac{E_{\mathrm{c}}}{RT}}+{\displaystyle \frac{E_{\mathrm{g}}}{R{T}_{\mathrm{avg}}}}\right),\end{array}$$

in which C(b) is an accumulation-dependent parameter (Ligtenberg et al., 2011), b is the accumulation rate, ρ_ice is the density of ice (typically 917 kg m⁻³), E_c is the activation energy of creep by lattice diffusion (typically 60 kJ mol⁻¹), E_g is the activation energy of gain growth (typically 42.4 kJ mol⁻¹), R is the gas constant, T is the temperature of the firn, and T_avg is the temporal mean subsurface temperature.

Water in the EBFM originates from surface melt and rain and percolates down from the surface into the firn. This happens in two ways: by using the fast deep-percolation statistical parameterization from Marchenko et al. (2017a) for the instantaneous vertical distribution of available melt and rain and by applying the “tipping-bucket” scheme for subsequent vertical transport. The fast percolation instantaneously distributes water in the vertical model according to a normal distribution with a peak at the surface. Further water transport is modeled with a tipping-bucket approach. Firstly, the water refreezes when the conditions in a model layer are sufficient, namely when the temperature is below melting point and the firn density is below the firn density of ice. Refreezing raises the temperature and firn density. In cases where not all water refreezes, a small portion will be stored in the layer as irreducible water content. The remaining water will percolate down to the next layer, where the process repeats. This continues until the water encounters impermeable ice, in which case the water becomes runoff, i.e., water input in the Lomonosovfonna Perennial Firn Aquifer Model (LPFAM).

3.3 Firn aquifer modeling

The US Geological Survey (USGS) Modular Hydrological Model MODFLOW 6 is chosen in this research to model the horizontal and vertical water flows in the PFA on the Lomonosovfonna ice cap. For extensive documentation, the reader is referred to Bakker et al. (2016) and Langevin et al. (2017).

Liquid flow in porous media is governed by Darcy's law, which states that a liquid will flow from areas with a higher water table height towards areas with a lower water table height. It was found experimentally by Miller et al. (2020), by using salt injection in boreholes in an aquifer on the Greenland ice sheet, that water flow in a firn aquifer generally obeys Darcy's Law and can therefore be approached as a groundwater flow problem. The simplest form of the Darcy equation is given in Eq. (6), in which q is the flow per unit area (m s⁻¹), k is the hydraulic permeability (m²), μ is the dynamic viscosity of the fluid (Pa s), and ∇p is the pressure gradient vector (Pa m⁻¹).

$$\begin{array}{}\text{(6)}& q=-{\displaystyle \frac{k}{\mathit{\mu }}}\mathrm{\nabla }p\end{array}$$

The hydraulic permeability is a measure of how easily a fluid moves through a medium. A higher k indicates less resistance from the medium to the flow. Often, hydraulic conductivity and hydraulic permeability are interchangeably used. Hydraulic conductivity and hydraulic permeability are linked in Eq. (7), in which K is the hydraulic conductivity, k is the hydraulic permeability, ρ is the firn density of the fluid, g is the gravitational acceleration, and μ is the viscosity of the fluid.

$$\begin{array}{}\text{(7)}& K={\displaystyle \frac{k\mathit{\rho }g}{\mathit{\mu }}}\end{array}$$

Equation (6) assumes that the hydraulic permeability remains spatially constant, and all sources and sinks of the water are summarized in the ∇p term. A more comprehensive Darcy equation, adapted from Langevin et al. (2017), is

$$\begin{array}{}\text{(8)}& \begin{array}{rl}{\displaystyle \frac{\mathit{\delta }}{\mathit{\delta }x}}\left(K_{xx}{\displaystyle \frac{\mathit{\delta }h}{\mathit{\delta }x}}\right)& +{\displaystyle \frac{\mathit{\delta }}{\mathit{\delta }y}}\left(K_{yy}{\displaystyle \frac{\mathit{\delta }h}{\mathit{\delta }y}}\right)+{\displaystyle \frac{\mathit{\delta }}{\mathit{\delta }z}}\left(K_{zz}{\displaystyle \frac{\mathit{\delta }h}{\mathit{\delta }z}}\right)\\ & =\mathrm{SS}{\displaystyle \frac{\mathit{\delta }h}{\mathit{\delta }t}}+Q_{\mathrm{S}}.\end{array}\end{array}$$

The first three terms on the left-hand side of Eq. (8) represent the flow due to differences in water table height, with a spatially varying and direction-dependent hydraulic conductivity. Q_S represents different sources and sinks, such as surface runoff, evapotranspiration, wells, and precipitation. Note that those sinks and sources can be space- and time-dependent. The SS term on the right-hand side refers to specific storage, which is the water released or stored per drop of head from the pore storage. K_xx, K_yy, and K_zz are the hydraulic conductivities that control the speed of the water flow in the x, y, and z direction, respectively.

The standard packages that regulate the firn density are time-independent in MODFLOW 6, which means that the density of the modeled medium typically does not change during a (regular) MODFLOW simulation. In groundwater modeling, with, for example, solid porous media like rocks and sand, this can be a justifiable simplification. In the case of modeling a PFA, this is not desired, as the firn density changes significantly during a multi-decadal simulation.

It is therefore necessary to make separate MODFLOW iterations at every time step when the steady packages need to change. To connect these separate MODFLOW iterations into one model, the head heights of run t are used as initial conditions for run t+1. This makes the model slower compared to a default MODFLOW 6 run. However, all runs in this study take approximately 3 h to run on a single processor (approximately 60 model years with weekly resolution). A schematic overview of the modeling process is presented in Fig. 3.

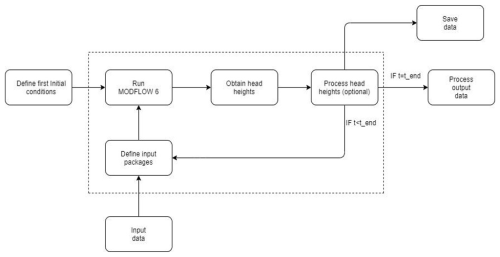
Figure 3 The modeling process, in which a new MODFLOW model is used every time step, using the water table height from the previous time step as initial conditions. The dotted lines indicate the loop, for which every loop is a new MODFLOW model, that uses the head height output of the previous loop as initial conditions. Note that input data can be read in every loop, instead of all at once, and that output data can be stored after each loop.

We run the Lomonosovfonna Perennial Firn Aquifer Model (LPFAM) on a grid of 100 by 100 cells, with 96 m resolution in the y direction and 72 m in the x direction. The vertical grid consists of five layers with a thickness of 1.4, 3.8, 10, 24.8, and 49.8 m, respectively. Average densities for the vertical layers are extracted from the EBFM output. The water table height is resolved on a continuous vertical scale, providing more spatial (vertical) detail. We choose the model domain such that it extends several kilometers beyond the largest observational grid (2017; see Fig. 1) and that the areas with the most data points (2018 and 2019) are roughly in the middle of the grid. This reduces the effects of the lateral boundary conditions. At the start of a spin-up routine, we fix the water table height at 10 m above the bottom of the deepest model layer at the boundaries. This is the approximate depth at which the firn density reaches the density of glacial ice.

We perform a spin-up of 20 years, where we run 1957–1977, with an arbitrary initialized state of 10 m water column above the bottom of the model domain in 1957. The resulting water table profile at the end of the spin-up (in 1977) is used as the initial conditions for historical runs from 1957–2019. We manually tune uncertain parameters to match the GPR observations in the years 2017–2019, as described in the next section. When changing parameter values, spin-up is always repeated.

4 Results and discussion

4.1 Model calibration and inference of hydraulic properties

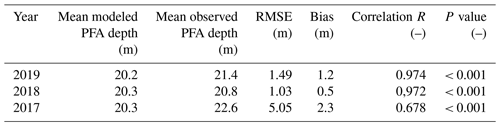
In this study, three steps were performed to tune the LPFAM to reproduce a water table close to observations in the years 2017–2019. Three uncertain parameters were manually optimized, starting with the parameter K (hydraulic conductivity), to which water table height was found to be most sensitive. Remaining errors of the modeled water table versus observations are quantified by calculating the RMSE and bias.

Firstly, we took a vertically and horizontally uniform hydraulic conductivity and varied it between 10⁻⁵–10⁻³ m s⁻¹ in 100 steps. The uniform hydraulic conductivity we found is referred to as K_u. In a next step, a pore close-off depth is introduced. Below the pore close-off, depth porosity is low, causing water to be immobile (Humphrey et al., 2021; Koenig et al., 2014). We varied the pore close-off depth on a layer basis: we tried putting the close-off depth at the fifth, fourth, and third layers. However, it is still expected that the water can dissipate with an unknown rate from this layer, for example, by entering crevasses or by slow horizontal flow. This process is not explicitly modeled, so the pore close-off hydraulic conductivity is used as a final tuning parameter. We varied the pore close-off hydraulic conductivity to be between 10⁻¹–10⁻⁶ times the hydraulic conductivity found in the first tuning step. The pore close-off hydraulic conductivity we found is referred to as K_c. The optimal set of parameters is presented in Table 1. A summary of performance statistics for the years with observations is shown in Table 2. We find an average close-off firn density of 804 kg m⁻³, happening at an average depth of 52.9 m below the surface. Our pore close-off firn density is well within the range of field studies (Gregory et al., 2014) and other modeling studies (e.g., Huss, 2013; Ligtenberg et al., 2011; Brils et al., 2022; Herron and Langway, 1980), which typically fix the pore close-off firn density at 800–830 kg m⁻³. Our hydraulic conductivity is also in the range of $\mathrm{1}\times {\mathrm{10}}^{-\mathrm{3}}$–$\mathrm{1}\times {\mathrm{10}}^{-\mathrm{5}}$ m s⁻¹ found by Miller et al. (2020), Miller et al. (2023), Miller et al. (2017), and Stevens et al. (2018).

Table 1 Optimal values found in the three consecutive tuning steps.

4.2 Validation of modeled water table depth

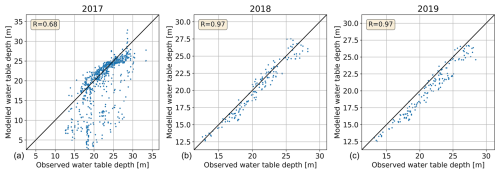
Figure 4 shows the modeled water table depth and the comparison with observations for the 3 observation years (2017–2019). The LPFAM maximum vertical depth (∼ 50 m, dependent on the thickness of the firn package) is deeper than what the GPR can observe (up to ∼ 40 m). All radar observations with no detected water table are excluded from the comparison and cause interruptions in the tracks in Fig. 4, which does not mean that the water table is absent.

In 2017, observations covered the largest area (Fig. 1b). The modeled water table depth is overestimated in the southeastern corner of the grid. Although the modeled and observed spatial variations are comparable (R=0.68), the LPFAM has a water table significantly closer to the surface (bias = 2.3 m). This could be because there are missing sinks in the LPFAM in that region. During observational campaigns, the GPR could not measure beyond the southwestern corner because of the presence of a crevasse field; see, for example, Hawrylak (2021). These crevasses could very well act as a sink that is currently unaccounted for in the model. As a result, the root-mean-square error (RMSE) is significantly larger for the large grid observed in 2017 (5.05 m) than for the small grid in 2018 (1.03 m) and 2019 (1.49 m), where vertical drainage is likely small or absent.

The modeled water table depth agrees very well with the in situ observations on the smaller grid during the years 2018 (RMSE = 1.03 m; bias = 0.5 m; R = 0.97; maximum error: 3.2 m) and 2019 (RMSE = 1.49 m; bias = 1.23 m; R = 0.97; maximum error: 4.3 m). Within the observation grid in 2018 and 2019 (Fig. 4), the northwestern, southwestern, and northeastern corners contain little water according to model and observations, whereas water flow is steered by the surface topography to the flatter central part and southeastern corner before leaving the observational grid.

In Fig. 5, the modeled water table depth and the nearest observed water table depth are compared. The modeled water table depth patterns in 2018 and 2019 correlate very well with the observations (Table 2). In 2017, the outliers in the modeled water table depth are mostly below the 1:1 line; i.e., the modeled water table depth is locally underestimated and the water table height is overestimated compared to the observations, confirming the missing sinks in the southwestern corner of the model grid. Adding sinks would lower the modeled water table height and possibly remove the outliers.

From the height contours and water table height pattern, it can be inferred that water table height variations are steered by surface topography rather than lateral firn density variations. Locally elevated (convex) areas are often modeled and observed to have a deeper water table, whereas local depressions (concavities) in the terrain are associated with a water table close to the surface. This applies to both the smaller grid (2018 and 2019) and the larger grid (2017).

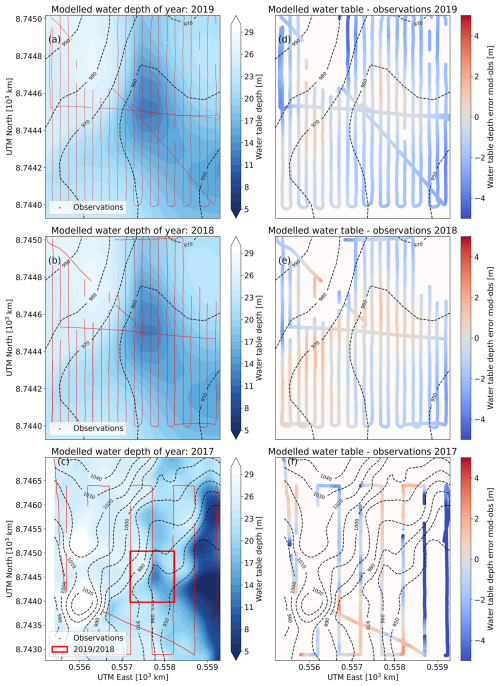
Figure 4 Modeled water table depth and the difference with regard to observations. (a, b, c) Modeled water table depth for the years with the most observational coverage (2017, 2018, and 2019). The observational data point locations are shown in red. The surface height contours, taken from the NPI DEM per 10 m a.s.l., are shown with dashed black lines. (d, e, f) Modeled water table depth minus observed water table depth, where modeled values are interpolated to the locations of the observations. The performance statistics are shown in Table 2. In the bottom-left panel, the studied area in 2018 and 2019 is marked by a red rectangle.

Table 2 Performance indicators of the perennial firn aquifer depth from the model and compared to observed firn aquifer depth. The RMSE and bias are determined by comparing all modeled points within the observational grid of a given year with the closest observed location. This results in 145, 143, and 835 data points, respectively, in the years 2019, 2018, and 2017. The mean modeled and mean observed depths are the arithmetic means of the aforementioned matched data points.

Figure 5 Scatter plots of the modeled and observed water table depths in 2017 (a), 2018 (b), and 2019 (c). The black line is the 1:1 line, and the calculated correlation is shown in the top-left corner of each panel.

4.3 Multi-decadal PFA development

At the end of our spin-up routine in 1977, a PFA is present in the firn. The time series in Nordli et al. (2020) show homogenized observational time series for Svalbard (Longyearbyen) back to 1898. Figure 3 in Nordli et al. (2020) reveals that the decades before 1957 (∼ 1930–1957) were warmer than the period 1957–1977. Even though these time series apply to sea level, we argue it is unlikely that an opposite temperature trend applies at high elevations. Since we used the colder period 1957–1977 to initialize our model, the presence of a perennial firn aquifer at the end of the spin-up period is a strong indication that a perennial firn aquifer would also have been present in 1957. We argue that higher temperatures imply more surface melt and likely growth of the PFA (assuming snow accumulation does not drop markedly during warm periods). Figure 6 confirms that warm (high-melt) years typically induce an increase in water table height. Furthermore, high melt (and accumulation) rates were also listed as a requirement for firn aquifer formation in Kuipers Munneke et al. (2014). Based on the likely warmer temperatures prior to 1957 than the period that was used for model spin-up, we argue that the perennial firn aquifer may have been larger at the start of the simulation in 1957 than it is currently.

It is worth noting that initial PFA water table depth perturbations only affect simulated water table depths in the first 10–20 years, which is the typical response time of the PFA. However, when starting a simulation with no perennial firn aquifer, we find an unphysical increase in water table depth even during the cold season for the first 10 years of the simulation (not shown). This modeled behavior and the temperature dataset of Nordli et al. (2020) make it very likely that the PFA was already present well before 1957.

The water table height at a central location in the model domain is plotted together with the meltwater input from the EBFM for the whole run and for the last years in Fig. 6. There is in general a positive trend, both in modeled average water table depth and meltwater input. It can clearly be seen that the PFA reacts quickly to a meltwater input peak. There is a time delay between a peak in meltwater input and aquifer water table height in the order of weeks. This delay is likely caused because this location is in the center of a topographic low. It can therefore receive water from all sides, which extends the growing phase of the aquifer in this location beyond the initial pulse. The strongest meltwater peaks coincide with sharp water table height increases. Once the water table depth peak has passed, the water table decreases again with a rate dependent on the peak magnitude but following the same smooth pattern every year. Large rapid jumps in the water table height occur during high-melt summers, such as in 1998 and 2016, while gradual decreases in the water table height occur during multi-year cold periods, e.g., 1962–1966 or 1994–1997.

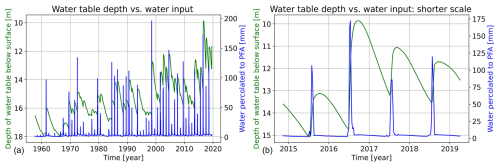
Figure 6 Water table depth from the LPFAM versus meltwater input from the EBFM for the whole simulation (a) and for the final years (b).

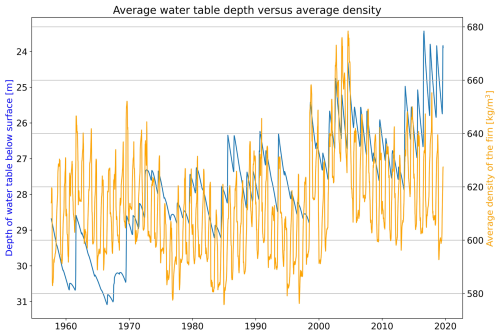
Figure 7 Average density of the firn from the EBFM (orange) with the average water table height from the LPFAM (blue).

In Fig. 7, the average firn density on the model grid versus the average water table depth (for the whole model grid) is shown. The correlation between water table depth and average firn density is −0.41 (negative, as a higher firn density corresponds to a lower water table depth). Firn compaction hence contributes significantly to the modeled increases in water table height, although most of the water table height variations are related to the total water content ($R=-\mathrm{0.75}$).

4.4 Uncertainties

Although the LPFAM captures the main processes to describe PFA formation and development, some processes or interactions are not accounted for, thereby inducing uncertainties. A main source of uncertainty is that there is only a one-way coupling from the EBFM to the LPFAM. Two-way coupling would be more physically desirable. For example, the extra weight of water in saturated firn will induce faster densification by the gravitational overburden pressure, a process currently not incorporated in the EBFM. Furthermore, as soon as the aquifer reaches closer to the surface, the overlaying firn may not be able to protect the water from refreezing. The observed water table does not reach closer than 10 m below the surface, so, in the present-day conditions, this is unlikely to happen. However, in the future, with less pore space and more meltwater production, refreezing of the water table might occur. Meltwater refreezing creates an ice layer in the firn. This ice lens, when thick enough, can impede free vertical movement of the water table and prevent meltwater from the surface from reaching the aquifer. Hence, under such conditions, the PFA is no longer entirely unconfined. A two-way coupled EBFM–LPFAM, where, on top of the current couplings, refreezing of PFA water and densification of saturated firn are accounted for, could be the scope of future work.

Another source of modeling errors is vertical water drainage through local sinks, such as crevasses and moulins, which is not accounted for. Instead, all water drains through the lateral boundaries of the grid. No data are available on the existence, location, size, and capacity of the sinks within our modeled grid on Lomonosovfonna, so they could not be incorporated into the LPFAM. As can be seen in the results for 2017, the LPFAM overestimates the water table height in the southeastern corner of the model grid. There is likely a crevasse field there, but we do not know the specific locations and dimensions of the crevasses. Also, the interactions between the aquifer and crevasses, particularly the drainage rates, are unknown. Preliminary tests with artificial drains with almost instant drainage in 40 grid cells positioned north–south 50 m east of the of the observation grid improved the results (RMSE decreases from 5.05 to 3.24 m in 2017, from 1.03 to 0.89 m in 2018, and from 1.49 to 1.10 in 2019). Identification of crevasse fields in satellite products, e.g., Sentinel-1 or Sentinel-2, is challenging in accumulation zones but could provide important data on PFA sinks in the area.

There are uncertainties in the observed water table depth shown in this study. The system-specific uncertainty (related to the sampling frequency, the cable length, and the GPR used) is small, about ± 0.02 m. The largest source of uncertainty stems from the calculation of the velocity of the radar wave, which is calculated using a modeled density profile of the firn. When changing the firn density arbitrarily with ± 10 %, this resulted in a spread of ± 0.21 m in calculated water table depths. The uncertainty arising from digitizing the water table, quantified by performing cross-analysis of double-measured points during the same field season, results in ± 0.03 m.

In a future climate, increased melting and rainfall (Hansen et al., 2014; Bintanja and Andry, 2017) will lead to less deep and higher firn densities and to a water table depth that reaches closer to the surface. This will simultaneously increase the likelihood for wintertime freezing of the water table in places where the water table is close enough to the surface (< 8–10 m). During the modeled period (1957–2019), this did not occur, as the water table depth did not reach closer than 12 m below the surface in the observations in 2012 and 2013. The firn temperature at the Lomonosovfonna ice cap was measured with thermistor strings, and the cold wave did not penetrate to below approximately 10 m (Marchenko et al., 2017b). For the future development of the PFA, and for the formation of surface streams or meltwater lakes, this could become important if the surface topography allows it.

The hydraulic conductivity we find by calibrating the LPFAM ($\mathrm{6.4}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹) is in between the values of 10⁻⁵–10⁻³ m s⁻¹ (Fountain and Walder, 1998; Miller et al., 2020; Miller et al., 2023; Miller et al., 2017; Stevens et al., 2018). We find this uniform hydraulic conductivity by manually tuning our model until it fits with observations. A tuned variable can only represent a real parameter if all other processes at play are perfectly represented, so our tuned variable can compensate for errors in the firn conditions from the EBFM, uncertainties in observations, and/or missing processes. Furthermore, the hydraulic conductivity of horizontal water flow above the pore close-off depth is assumed to be a constant in this study but in reality likely depends on the porosity of the firn. In future work, the porosity dependence of hydraulic conductivity could be inferred using PFA modeling of higher (vertical) resolution, more extensive water table depth data, borehole pressure data, and/or pump or slug tests.

5 Conclusions

In this study, we adapted an existing groundwater flow model MODFLOW6 so that it could be applied to model a perennial firn aquifer. We tested the model setup on a PFA that has been observed on the Lomonosovfonna ice cap in central Svalbard. We used in situ measurement campaigns of 3 consecutive years to tune uncertain parameters so that the modeled water table height fitted with observations. From the calibration, we inferred a hydraulic conductivity of the PFA of $\mathrm{6.4}\times {\mathrm{10}}^{-\mathrm{4}}$ m s⁻¹. After spin-up, we ran the PFA model from 1957–2019 and found a general increase in water table height over the modeled period, with large jumps during high-melt summers. We found that the PFA likely already existed before 1957. The height of the water table reacts quickly to meltwater input, in the order of weeks, and long-term water table depth variations further depend on long-term firn density changes. During the cold season, the water table decays steadily to a minimum prior to the new melt season. The water table is likely to rise further in the future, as more melt/rain and a denser firn pack are expected in a warmer climate. This may newly induce refreezing of the PFA from above. With continued firn densification, the water table in our study area is likely to reach the surface locally in the coming decades.