The influence of firn layer material properties on surface crevasse propagation in glaciers and ice shelves

Linear elastic fracture mechanics (LEFM) models have been used to estimate crevasse depths in glaciers and to represent iceberg calving in ice sheet models. However, existing LEFM models assume glacier ice to be homogeneous and utilize the mechanical properties of fully consolidated ice. Using depth-invariant properties is not realistic as the process of compaction from unconsolidated snow to firn to glacial ice is dependent on several environmental factors, typically leading to a lower density and Young's modulus in upper surface strata. New analytical solutions for longitudinal-stress profiles are derived using depth-varying properties based on borehole data from the Ronne Ice Shelf and are used in an LEFM model to determine the maximum penetration depths of an isolated crevasse in grounded glaciers and floating ice shelves. These maximum crevasse depths are compared to those obtained for homogeneous glacial ice, showing the importance of including the effect of the upper unconsolidated firn layers on crevasse propagation. The largest reductions in the penetration depth ratio were observed for shallow grounded glaciers, with variations in Young's modulus being more influential than firn density (maximum differences in crevasse depth of 46 % and 20 %, respectively), whereas firn density changes resulted in an increase in penetration depth for thinner floating ice shelves (95 %–188 % difference in crevasse depth between constant and depth-varying properties). Thus, our study shows that the firn layer can increase the vulnerability of ice shelves to fracture and calving, highlighting the importance of considering depth-dependent firn layer material properties in LEFM models for estimating crevasse penetration depths and predicting rift propagation.

1 Introduction

The formation of surface and basal crevasses as a consequence of deformation in ice sheets plays an influential role in glacial mass balance (Colgan et al., 2016). Crevasses are predominantly mode-I (tensile) fractures that propagate vertically downwards to the depth at which they stabilize (i.e. maximum crevasse depth), depending on the longitudinal-stress state normal to the fracture surface (Enderlin and Bartholomaus, 2020). Fracture propagation can be further aided by the accumulation of meltwater within surface crevasses, the supply and storage of which can be attributed to supraglacial lakes and firn aquifers (Poinar et al., 2017). This can trigger a process called hydrofracture, wherein the meltwater in the crevasse exerts additional opening stress on the crevasse walls (Weertman, 1973). If the volume of meltwater is sufficiently large, hydrofracture can cause full-thickness crevasse propagation and lead to large-scale iceberg calving events from ice shelves (Scambos et al., 2009) and to increases in basal sliding rates (Selmes et al., 2011). Glacial mass loss caused by the calving events represents one of the leading contributors to global sea level rise (Rignot et al., 2013; Frederikse et al., 2020; Siegert et al., 2020).

The first study to examine crevasse propagation in glaciers and ice sheets was conducted by Nye (1957), who proposed an analytical zero-stress model. The so-called Nye zero-stress model assumed that crevasses are dry and that ice has no resistance to fracturing; thus, a crevasse will propagate to a depth at which tensile stresses are completely offset by the compressive overburden pressure due to gravitational self-weight. The zero stress was later adapted by Benn et al. (2007) to accommodate for the presence of meltwater in crevasses. Nevertheless, this simplistic model agreed well with observational results for fields of closely spaced crevasses (Mottram and Benn, 2009), where neighbouring crevasses provide shielding effects in relation to crack tip singularities (Weertman, 1974). However, it underestimates the depths of isolated crevasses, where this shielding effect is not present. Therefore, linear elastic fracture mechanics (LEFM) models were introduced by van der Veen (1998a, b) to model these isolated surface and basal crevasses.

LEFM models capture the effects of the stress singularity (assuming that the resulting plastic zone around the crack tip is sufficiently small) by evaluating the stress intensity factor at the crack tip. The role of crack size and orientation, ice thickness, and applied loading conditions can be captured through the evaluation of the stress intensity factor (Jiménez and Duddu, 2018). Using the principle of superposition, the LEFM models include the contributions from the tensile normal stress, the lithostatic compressive stress, and the meltwater pressure. The LEFM approach has been combined with full-Stokes models to study surface and basal crevasse propagation in Thwaites Glacier, with results agreeing well with NASA's radar penetration depths (Yu et al., 2017). In addition, LEFM models have been used to map the vulnerability of Antarctic ice shelf crevasses subject to meltwater-driven hydrofracture, with projections agreeing well with existing fractures being mapped by neural networks (Lai et al., 2020). The LEFM approach has been successfully combined with boundary element methods, capturing the interactions between basal and surface crevasses and providing estimates regarding the stability (Zarrinderakht et al., 2024) and evolution of crevasse shape (Zarrinderakht et al., 2022). However, while analytical LEFM models are computationally efficient and can be implemented into numerical ice sheet models (Krug et al., 2014), they do not account for the role of creep deformation or of depth-varying ice material properties in crevasse propagation (Gao et al., 2023).

In recent years, several studies focused on the development of computational approaches for modelling crevasse propagation in grounded glaciers and floating ice shelves. Notably, continuum damage mechanics (CDM) approaches were developed to describe more complex thermo-hydro-mechanical phenomena, but they are computationally more intensive compared to zero-stress and LEFM approaches. Such approaches can capture the effects of viscous deformation and long-term stress states on crevasses (Duddu and Waisman, 2012; Jiménez et al., 2017; Duddu et al., 2020) and can be readily implemented into Stokes-based ice flow models (Pralong and Funk, 2005; Sun et al., 2017). Recent studies have developed phase field fracture models that formulate LEFM crack propagation criteria within the CDM framework, thus unifying the two approaches (Sun et al., 2021; Clayton et al., 2022). Additionally, CDM-based models can be useful in assessing the accuracy of LEFM and zero-stress models and in understanding the conditions under which their predictions are valid (Duddu et al., 2020).

While the above-mentioned LEFM and CDM studies capture a range of mechanical interactions, they assume glacial ice to be a homogeneous material, with the values of mechanical properties taken as constants equal to those of fully consolidated ice. In reality, glacial ice forms from the accumulation of snowfall at the upper surface and undergoes compaction as a result of the overburden pressure, the rate of which is dependent on accumulation rates and surrounding temperatures (Veldhuijsen et al., 2023). Moreover, snowflakes are restructured into smaller ice crystals due to wind, which then deform into more stable, compact crystal arrangements (Benn and Evans, 2010); this causes large differences in the porosity, density, and strength of these top snow layers, referred to as firn, and the deeper glacial ice. Neglecting firn layers leads to an overestimation of mechanical properties in the upper strata (Rist et al., 2002, 1996). This is of particular importance for geological media subject to self-gravitational loading (Paterson, 1994) because the driving stresses are dependent on the mechanical properties in such layered or vertically graded materials. The main hypothesis of this study is that accounting for these depth-dependent material parameters in the LEFM framework would alter the crevasse penetration depths in glaciers and ice shelves.

The aim of this article is to explore the importance of including firn layer effects on surface crevasse propagation. To this end, we determine the maximum crevasse depths in idealized glaciers and ice shelves assuming two different material conditions: fully consolidated homogeneous ice and vertically graded ice as reported from ice core samples, with depth-varying material properties. We derive the analytical solution for the far-field longitudinal stress σ_xx with depth-dependent properties, which primarily drives the vertical propagation of mode-I crevasses. Next, we systematically investigate the effect of varying each material property in the unconsolidated firn layers through parametric studies as follows: using only the depth-variant density in Sect. 2.1, using only the depth-variant Young's modulus in Sect. 2.2, and using both the depth-variant density and depth-variant Young's modulus in Sect. 2.3. We then conduct fracture mechanics studies in Sect. 3 for a grounded glacier using the analytical LEFM models presented in Jiménez and Duddu (2018) and verify the models' accuracy with the stress-based phase field fracture model of Clayton et al. (2022). Through variations in meltwater depth ratios in water-filled surface crevasses and in ocean water heights in marine-terminating glaciers, the conditions under which depth-dependent material properties are influential are explored. In Sect. 4, these studies are extended to floating ice tongues. Sect. 5 considers the effects of assuming that crevasses develop rapidly (as linear elastic) versus slowly (as non-linear viscous), and we summarize all the findings in Sect. 7.

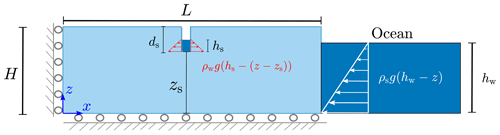
Figure 1 Schematic diagram showing the geometry and boundary conditions of a grounded glacier containing a single surface crevasse.

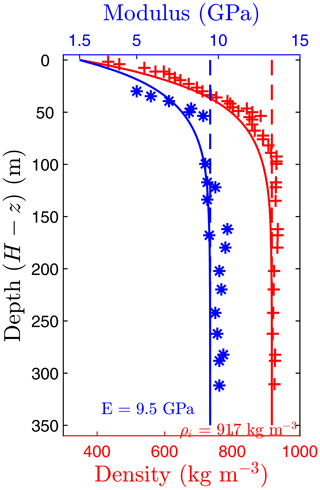
Figure 2 Profile of depth-dependent mechanical properties for ice density (red, bottom axis) and Young's modulus (blue, top axis). Data extracted from ice core specimens from the Ronne Ice Shelf by Rist et al. (2002) are displayed as markers. Isotropic properties are displayed with the dotted lines.

2 Analytical solutions for the longitudinal stress

We consider a grounded glacier with an idealized rectangular geometry of height H and length L. We neglect lateral shear and restrict the domain to a flow line near the terminus, with x and z representing the along-flow and vertical coordinates. As the out-of-plane length of the glacier is typically much longer than its length, the plane strain assumption is exploited to reduce the three-dimensional glacier geometry to a two-dimensional (height and length) representation. A visual representation of the geometry and boundary conditions can be found in Fig. 1. Horizontal displacements are restrained in the far left of the domain to prevent rigid body motion, and a free-slip boundary condition is applied by restraining vertical displacements at the base (represented by rollers). The upper surface is defined as a traction-free surface, representing the atmosphere–ice interface. The load contributions considered are the gravitational self-weight, ocean water pressure at the far-right terminus, and meltwater pressure in the crevasse. Note that, under the small-deformation assumption, this representation of the grounded glacier is identical to that of a floating ice shelf (Weertman, 1957) in the far-field region.

The far-field longitudinal stress (based on the long-wavelength approximation) within the grounded glacier or ice shelf was derived for the case of steady-state creep with constant (i.e. depth-independent) and homogeneous material properties by Weertman (1957). Recently, this longitudinal stress was derived for compressible linear elasticity by Sun et al. (2021) as follows:

$$\begin{array}{}\text{(1)}& {\mathit{\sigma }}_{xx}={\displaystyle \frac{\mathit{\nu }}{(\mathrm{1}-\mathit{\nu })}}{\mathit{\rho }}_{\text{i}}g\left(z-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}H\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}}{H}},\end{array}$$

where ν=0.35 is the Poisson's ratio, assumed to be equal for firn and ice; g is gravitational acceleration; ρ_i=917 kg m⁻³ is the density of fully consolidated glacial ice; ρ_s=1020 kg m⁻³ is the seawater density; and h_w is the seawater height above the glacier bed. We use the convention that positive σ_xx corresponds to tensile stresses, creating and propagating crevasses, whereas negative σ_xx is compressive, thus stabilizing the glacier and preventing the formation of crevasses. This analytical stress will be used throughout this paper to compare between the cases with homogeneous (given by the above equation) and depth-dependent (derived in the remainder of this section) material properties. The Poisson ratio ν used within our results represents ice as a linear elastic compressible solid, which is a common assumption for rapidly propagating cracks. If the crevassing process occurs on a timescale well below the Maxwell timescale, ranging from hours to days depending on the strain rate due to the non-linear viscous nature, the assumption of compressibility would be valid. If, instead, the crevassing process occurs slowly, over the span of weeks, the assumption of incompressibility would be valid; thus, a Poisson ratio of ν=0.5 will allow for the model derived here to be applicable over longer timescales. Results for this incompressible case are given in Sect. 5, whilst results for a depth-dependent Poisson ratio are presented in Appendix E.

As shown in Fig. 2, ice core sample data from the Ronne Ice Shelf, gathered and presented by Rist et al. (2002), indicate large variations in material properties within the firn and meteoric ice layers forming the upper 150 m of the ice core. The ice core data for density can be fitted using the following exponential equation (Paterson, 1994; van der Veen, 1998a):

$$\begin{array}{}\text{(2)}& \mathit{\rho }\left(z\right)={\mathit{\rho }}_{\text{i}}-({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})e^{-(H-z)/D},\end{array}$$

where ρ_f=350 kg m⁻³ is the density of the unconsolidated upper surface firn layers, H is the height of the glacier, z is the vertical coordinate (z=0 at the base of the glacier, z=H at the surface), and D is a constant taken as D=32.5 m (Rist et al., 2002). This constant gives an indication of the thickness of the firn layer: at the surface z=H, the density of the glacier is equal to that of the unconsolidated firn; at a depth of $H-z=D$ below the surface, the density is in between that of firn and ice at 75 % of the density of ice; and at a depth of $H-z=\mathrm{2.5}D$ below the surface, the density of the glacier is 95 % the density of consolidated ice.

The ice core sample data for elastic modulus from Fig. 2 can be fitted using a similar function as that used for the density, including the depth-dependent Young's modulus:

$$\begin{array}{}\text{(3)}& E\left(z\right)=E_{\text{i}}-\left(E_{\text{i}}-E_{\text{f}}\right)e^{-\left(H-z\right)/D},\end{array}$$

where E_i=9.5 GPa is Young's modulus for solid ice, E_f=1.5 GPa is Young's modulus for unconsolidated upper surface firn layers, and D=32.5 m is a tuned constant. Here, we have chosen to use a single constant D to describe the depth variations in both density and Young's modulus. While this is not necessary for the derivation of the analytic solutions, the interpretation of D as a length scale of the firn layer thickness indicates that Young's modulus is directly proportional to density and is inherently related to porosity, similarly to porous metallic foams (Ashby et al., 2000).

In the remainder of this section, analytical expressions are derived for the longitudinal stresses driving the creation of crevasses. We first consider two cases wherein only the density or Young's modulus is depth-varying so as to isolate and examine the influence of each property on the maximum crevasse penetration depth. For the third and final case, we consider both properties to be depth-varying, which is the real-case scenario.

2.1 Depth-varying density

We consider it to be that only the density is depth-dependent following Eq. (2), while Young's modulus is constant throughout the full thickness (van der Veen, 1998a). The lithostatic compressive stress for this density distribution is

$$\begin{array}{}\text{(4)}& {\displaystyle \frac{\partial {\mathit{\sigma }}_{zz}}{\partial z}}=-\mathit{\rho }\left(z\right)g,\end{array}$$

with g denoting the gravitational acceleration. By substituting Eq. (2) for the depth-dependent density and integrating over the depth, the vertical stress component is obtained as follows:

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}_{zz}=-{\mathit{\rho }}_{\text{i}}g\left(H-z\right)+({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})Dg\left(\mathrm{1}-e^{-(H-z)/D}\right).\end{array}$$

The above relation consists of a linear stress contribution from ρ_i and an exponential term that reduces the net lithostatic stress when considering the effects of firn density ρ_f. This solution can be simplified to the homogeneous ice case when considering ρ_i=ρ_f.

Exploiting the plane strain assumption ε_yy=0 allows for the out-of-plane stress σ_yy to be found in terms of longitudinal stress σ_xx and lithostatic stress σ_zz:

$$\begin{array}{}\text{(6)}& {\mathit{\sigma }}_{yy}=\mathit{\nu }\left({\mathit{\sigma }}_{xx}+{\mathit{\sigma }}_{zz}\right).\end{array}$$

Assuming small strains and small rotations, the longitudinal strain can then be written in terms of σ_xx and σ_zz by using Hooke's law and Eq. (6):

$$\begin{array}{}\text{(7)}& {\mathit{\epsilon }}_{xx}={\displaystyle \frac{\mathrm{1}}{E}}\left((\mathrm{1}-{\mathit{\nu }}^{\mathrm{2}}){\mathit{\sigma }}_{xx}-\mathit{\nu }(\mathrm{1}+\mathit{\nu }){\mathit{\sigma }}_{zz}\right).\end{array}$$

Following this, the membrane strain assumption is adopted due to the thickness of the glacier being several orders of magnitude smaller than the length. The longitudinal strain is therefore invariant with depth (Sun et al., 2021):

$$\begin{array}{}\text{(8)}& {\displaystyle \frac{\partial {\mathit{\epsilon }}_{xx}}{\partial z}}=\mathrm{0}.\end{array}$$

Note that the above condition can be derived using Föppl–von Kármán equations describing the large deflections of thin flat plates. Applying this constraint to Eq. (7) allows for the derivative of the horizontal stress to be found:

$$\begin{array}{}\text{(9)}& {\displaystyle \frac{\partial {\mathit{\sigma }}_{xx}}{\partial z}}={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\displaystyle \frac{\partial {\mathit{\sigma }}_{zz}}{\partial z}},\end{array}$$

leading to a far-field longitudinal stress of

$$\begin{array}{}\text{(10)}& {\mathit{\sigma }}_{xx}={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\mathit{\sigma }}_{zz}+R_{xx},\end{array}$$

where R_xx is an integration constant that can be interpreted as the depth-invariant tensile resistive stress. Substituting the lithostatic compressive stress σ_zz from Eq. (5) gives the following:

$$\begin{array}{}\text{(11)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}(-{\mathit{\rho }}_{\text{i}}g(H-z)\\ +& ({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})Dg(\mathrm{1}-e^{-(H-z)/D}))+R_{xx}.\end{array}\end{array}$$

It can be observed that the far-field longitudinal stress is composed of two components: the lithostatic compressive-stress component, which is always negative and thus is responsible for crevasse closure, and the resistive tensile stress R_xx, which is responsible for crevasse opening. van der Veen (1998a) conjectured that the inclusion of firn density into the LEFM model would lead to deeper crevasse propagation because the magnitude of the lithostatic compressive stress would be reduced; however, the reduction in tensile resistive stress was not considered. van der Veen (1998b) stated that “accounting for the lower firn density almost doubles the penetration depth of surface crevasses compared to the constant density model”. To properly account for the influence of firn density, we evaluate the indefinite integration constant R_xx, appearing in Eq. (10), by considering force equilibrium over the entire thickness in the longitudinal direction as follows:

$$\begin{array}{}\text{(12)}& \underset{\mathrm{0}}{\overset{H}{\int }}{\mathit{\sigma }}_{xx}\text{d}z+F_{\text{w}}=\mathrm{0},\end{array}$$

where $F_{\text{w}}=\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}$ is the hydrostatic force as a result of the ocean water pressure at the glacier front. From this equilibrium between the glaciological longitudinal stress and the ocean water pressure at the terminus, we find the resistive tensile stress as follows:

$$\begin{array}{}\text{(13)}& \begin{array}{rl}{R}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\displaystyle \frac{{\mathit{\rho }}_{\text{i}}gH}{\mathrm{2}}}-{\mathit{\rho }}_{\text{s}}g{\displaystyle \frac{h_{\text{w}}^{\mathrm{2}}}{\mathrm{2}H}}-{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})gD\\ & +{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\displaystyle \frac{({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})g{D}^{\mathrm{2}}}{H}}(\mathrm{1}-e^{-H/D}).\end{array}\end{array}$$

Negative values of R_xx, together with the lithostatic compressive stress, prevent crevasse propagation, whereas crevasses can only nucleate when R_xx exceeds the lithostatic stress.

Substituting the value of R_xx into the far-field longitudinal stress of Eq. (11) gives the following analytical solution:

$$\begin{array}{}\text{(14)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\mathit{\rho }}_{\text{i}}g\left(z-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}H\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\displaystyle \frac{{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}}{H}}\\ & +{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})gD\left(-e^{-(H-z)/D}+{\displaystyle \frac{D}{H}}(\mathrm{1}-e^{-H/D})\right)\end{array}.\end{array}$$

This solution can be simplified to the one for the far-field longitudinal stress in the depth-invariant case, as in Eq. (1), when considering ρ_i=ρ_f. The first term indicates that homogeneous land-terminating glaciers develop crevasses up to half their thickness (based on the zero-stress model), whereas the second (negative) term due to the ocean water height reduces the crack-driving stress, thereby providing a stabilizing effect. The third term includes the influence of the depth-dependent density over the stress that is a function of the vertical coordinate z; this term is negative near the top surface, thus stabilizing the top firn layers, but it tends toward a positive constant in the bottom regions of the glacier, thus increasing the propensity for deeper crevasse propagation below a certain depth. Thus, the inclusion of depth-dependent density can thwart or promote deeper crevasse propagation depending on the glacier and ocean water heights, which is more nuanced than the description by van der Veen (1998a), who neglected any influence of depth-varying density on resistive stress R_xx.

2.2 Depth-varying Young's modulus

We next derive the relation for far-field longitudinal stress considering a depth-variant elastic modulus E(z). The depth-dependent longitudinal strain is given by

$$\begin{array}{}\text{(15)}& {\mathit{\epsilon }}_{xx}={\displaystyle \frac{\mathrm{1}}{E\left(z\right)}}\left((\mathrm{1}-{\mathit{\nu }}^{\mathrm{2}}){\mathit{\sigma }}_{xx}\left(z\right)-\mathit{\nu }(\mathrm{1}+\mathit{\nu }){\mathit{\sigma }}_{zz}\left(z\right)\right),\end{array}$$

with E(z) given by Eq. (3). In the depth-invariant modulus cases, E simply gets eliminated with Eq. (8), leading to a horizontal stress that is independent of Young's modulus, as given by Eqs. (1) and (14). However, in the depth-dependent modulus case, E does not get eliminated from the far-field longitudinal stress with the membrane strain assumption. However, the longitudinal strain must be depth invariant, as required by Eq. (8), and so we get

$$\begin{array}{}\text{(16)}& (\mathrm{1}-{\mathit{\nu }}^{\mathrm{2}}){\displaystyle \frac{E{\displaystyle \frac{\partial {\mathit{\sigma }}_{xx}}{\partial z}}-{\mathit{\sigma }}_{xx}{\displaystyle \frac{\partial E}{\partial z}}}{E^{\mathrm{2}}}}-\mathit{\nu }(\mathrm{1}+\mathit{\nu }){\displaystyle \frac{E\frac{\partial {\mathit{\sigma }}_{zz}}{\partial z}-{\mathit{\sigma }}_{zz}{\displaystyle \frac{\partial E}{\partial z}}}{E^{\mathrm{2}}}}=\mathrm{0}.\end{array}$$

This can then be rearranged to obtain the following expression for the horizontal stress derivative:

$$\begin{array}{}\text{(17)}& {\displaystyle \frac{\partial {\mathit{\sigma }}_{xx}}{\partial z}}={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\displaystyle \frac{\partial {\mathit{\sigma }}_{zz}}{\partial z}}-{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\displaystyle \frac{{\mathit{\sigma }}_{zz}}{E}}{\displaystyle \frac{\partial E}{\partial z}}+{\displaystyle \frac{{\mathit{\sigma }}_{xx}}{E}}{\displaystyle \frac{\partial E}{\partial z}}.\end{array}$$

This derivation can be simplified to the depth-invariant case if $\partial E/\partial z=\mathrm{0}$. Solving the above ordinary differential equation yields the following longitudinal stress for constant density:

$$\begin{array}{}\text{(18)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\mathit{\rho }}_{\text{i}}g\left(z-{\displaystyle \frac{\left(E_{\text{i}}-E_{\text{f}}\right)}{E_{\text{i}}}}H{e}^{-(H-z)/D}\right)\\ & +C_{\mathrm{1}}\left(E_{\text{i}}{e}^{\left(H/D\right)}-\left(E_{\text{i}}-E_{\text{f}}\right)e^{\left(z/D\right)}\right),\end{array}\end{array}$$

where C₁ is an integration constant that can be determined using force equilibrium in the longitudinal direction, as defined by Eq. (12), which yields

$$\begin{array}{}\text{(19)}& \begin{array}{rl}{C}_{\mathrm{1}}& ={\displaystyle \frac{\mathrm{1}}{E_{\text{i}}H{e}^{H/D}-\left(E_{\text{i}}-E_{\text{f}}\right)D\left(e^{H/D}-\mathrm{1}\right)}}\left({\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}\right.\\ & \cdot \left(\left.{\displaystyle \frac{E_{\text{i}}-E_{\text{f}}}{E_{\text{i}}}}D{\mathit{\rho }}_{\text{i}}gH\left(\mathrm{1}-e^{-H/D}\right)-{\displaystyle \frac{{\mathit{\rho }}_{\text{i}}g{H}^{\mathrm{2}}}{\mathrm{2}}}\right)-{\displaystyle \frac{{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}}{\mathrm{2}}}\right).\end{array}\end{array}$$

Substituting the above into Eq. (18), we obtain the longitudinal-stress distribution for the depth-varying Young's modulus and constant-density case as follows:

$$\begin{array}{}\text{(20)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\mathit{\rho }}_{\text{i}}g\left(z-{\displaystyle \frac{\mathrm{1}-E^{*}}{\mathrm{2}}}H\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}+E^{*}){\displaystyle \frac{{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}}{H}},\\ & \text{where }{E}^{*}={\displaystyle \frac{\left(E_{\text{i}}-E_{\text{f}}\right)}{E_{\text{i}}}}{\displaystyle \frac{(\mathrm{1}-e^{-H/D})\frac{D}{H}-e^{-(H-z)/D}}{\mathrm{1}-(\mathrm{1}-e^{-H/D})\frac{\left(E_{\text{i}}-E_{\text{f}}\right)D}{E_{\text{i}}H}}}.\end{array}\end{array}$$

As expected, the solution for the variable Young's modulus case can be simplified to the far-field longitudinal stress for the depth-invariant case, where E_i=E_f ($E^{*}=\mathrm{0}$). Notably, the variable density only provided an additional term to the homogenous case, but the variable Young's modulus also alters all the terms in the longitudinal-stress relation. Including the effects of the firn layer's modulus redistributes the contribution of the horizontal ocean water pressure, where its contribution is less near the surface ($E^{*}<\mathrm{0}$) and greater near the base ($E^{*}>\mathrm{0}$).

2.3 Depth-varying Young's modulus and density

The final stress relationship we derive is for the case with the depth-varying density and Young's modulus using Eqs. (2) and (3), respectively. We do not show the full details of the derivation as it is similar to that in the previous sections. We use the horizontal stress derivative given in Eq. (17) and substitute the lithostatic compressive stress and derivative from Eqs. (4) and (5). This gives us an ordinary differential equation that is solved using MATLAB's symbolic toolkit to obtain the longitudinal stress σ_xx as follows:

$$\begin{array}{}\text{(21)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}g\left(-{\mathit{\rho }}_{\text{i}}(H-z)+\left({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}}\right)D(\mathrm{1}-e^{-(H-z)/D})\right)\\ & +(E_{\text{i}}{e}^{H/D}-\left(E_{\text{i}}-E_{\text{f}}\right)e^{z/D})C_{\mathrm{2}},\end{array}\end{array}$$

where C₂ is the indefinite integration constant, which can be found using force equilibrium.

$$\begin{array}{}\text{(22)}& \begin{array}{rl}{C}_{\mathrm{2}}& ={\displaystyle \frac{\mathrm{1}}{E_{\text{i}}H{e}^{H/D}-\left(E_{\text{i}}-E_{\text{f}}\right)D\left(e^{H/D}-\mathrm{1}\right)}}\left({\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}\left({\displaystyle \frac{{\mathit{\rho }}_{\text{i}}g{H}^{\mathrm{2}}}{\mathrm{2}}}\right.\right.\\ & \left.\left.-({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})gHD+({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})g{D}^{\mathrm{2}}(\mathrm{1}-e^{-H/D})\right)-{\displaystyle \frac{{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}}{\mathrm{2}}}\right)\end{array}\end{array}$$

Substituting C₂ back into σ_xx gives the final expression:

$$\begin{array}{}\text{(23)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\mathit{\rho }}_{\text{i}}g\left(z-{\displaystyle \frac{\mathrm{1}-E^{*}}{\mathrm{2}}}H\right)-{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}(\mathrm{1}+E^{*}){\displaystyle \frac{{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}}{H}}\\ & +{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})gD\left(\right(\mathrm{1}-e^{-(H-z)/D})\\ & +(\mathrm{1}+E^{*})(-\mathrm{1}+{\displaystyle \frac{D}{H}}(\mathrm{1}-e^{-H/D}\left)\right)),\end{array}\end{array}$$

where Young's modulus ratio E^* is defined in Eq. (20). The above equation can be reduced to the analytic relation for depth-dependent density in Eq. (14) if Young's modulus is constant ($E^{*}=\mathrm{0}$) and can be reduced to the analytical relation for the depth-dependent Young's modulus, as in Eq. (20), if the density is constant (${\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_f=\mathrm{0}$).

2.4 Limitations of analytical LEFM models

There are a few limitations to be noted regarding the outcomes of the LEFM models used in this study (refer to the Appendices). First, the depth variations of the mechanical properties are assumed based on borehole samples from ice cores in the Ronne Ice Shelf; therefore, they may not be fully representative of other Antarctic ice shelves or glaciers elsewhere. For example, temperate glaciers that are subject to higher rates of melting and refreezing will undergo a faster rate of densification due to meltwater percolating into pore spaces and refreezing (Wakahama et al., 1976). Thus, the process of firn densification is dependent on environmental factors including accumulation rates, overburden pressure, temperature, and local strain rates (Oraschewski and Grinsted, 2022). For instance, Seward Glacier, Yukon, Canada, is fully consolidated at a depth of 13 m in contrast to sites on the Greenland Ice Sheet where transitions from firn to glacial ice occur at depths of ≈66 m (Paterson, 1994). Data from surrounding borehole samples should therefore be considered when assessing the depth to which crevasses propagate to include the effects of firn layer properties.

The fracture analysis used in the following sections also assumes that, over short timescales, ice behaves as an elastic compressive material (ν=0.35), with crevasses propagating rapidly in a brittle manner. However, in reality, ice behaves like an incompressible fluid over longer timescales, with viscous deformation being described using Glen's flow law (Glen, 1955). The effects of time-dependent deformation can be included in an ad hoc manner by taking the stress from Stokes-based formulations and using LEFM to propagate crevasses in a staggered manner (Yu et al., 2017). Furthermore, the cracking conditions can be more complex than those that can be addressed with a simple analytical model (e.g. multiple crevasse interactions). To account for non-linear behaviour and problems of arbitrary complexity, one can utilize phase field fracture (Clayton et al., 2022), cohesive zone (Gao et al., 2023), or nonlocal creep damage (Huth et al., 2021, 2023) models. However, these non-linear models are computationally costly and not so easy to implement within numerical ice sheet models, and so analytical LEFM models are desirable.

3 Results for grounded glaciers

Figure 3 shows the analytical solutions of the far-field longitudinal stress σ_xx in a land-terminating grounded glacier (h_w=0 m) of height H=125 m. Each subfigure includes the longitudinal stress versus depth profiles for depth-varying properties (derived in the previous section) and those of the homogeneous case. In addition to the analytical solutions, numerical results from the finite-element solver COMSOL Multiphysics are plotted for the verification of our analytic expressions. The analytical solutions derived are identical to the numerical results, confirming the correctness of the presented expressions along with the appropriateness of the membrane strain assumption.

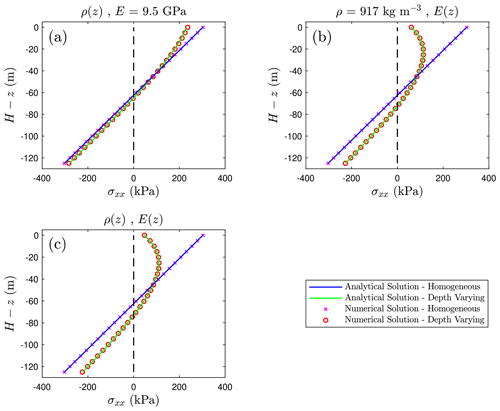
Figure 3 Far-field longitudinal stress σ_xx throughout the depth of a land-terminating glacier (h_w=0), showing the effects of the (a) depth-varying density ρ(z); (b) depth-varying Young's modulus E(z); and (c) depth-varying density and Young's modulus ρ(z),E(z). Numerical results are obtained from COMSOL Multiphysics for constant (crosses) and depth-varying properties (circles). The analytical solutions for depth-varying properties are given in Eqs. (14), (20), and (23) and are represented by the green lines. The vertical dashed line indicates the zero-stress level.

Using these stress solutions, we predicted crevasse depths based on an analytical LEFM model, as described in the Appendices. For grounded glaciers with free tangential slip at the base, we use the “double-edge crack” weight functions (refer to Appendix B) as this was shown to yield stress intensity factors that are consistent with those calculated using the displacement correlation method (Jiménez and Duddu, 2018). Specifically, we consider the evolution of an isolated surface crevasse within a grounded glacier of height H=125 m, assuming damage to initialize beneath a pre-specified surface crack of depth d_s=10 m. To further verify the LEFM results, we conducted phase field fracture (PFF) simulations with the same configuration used for LEFM studies but with a pre-existing surface notch of depth d_s=10 m and width b=2.5 m. The PFF model simulations capture the non-linear propagation of the crack driven by the mechanical stress beneath the notch until it reaches a final and/or stabilized crevasse depth. For a full description of this PFF model, we refer the reader to our recent work (Clayton et al., 2022).

The comparison of the crevasse depth ratios (i.e. the final crevasse depth normalized with the ice thickness) obtained from LEFM and PFF models is shown in Fig. 4. As the ocean water depth is increased, the glacier is subjected to increased compressive hydrostatic pressure at the glacier terminus, which suppresses crevasse growth. The surface crevasse depth ratio decreases non-linearly with the ocean water depth ratio, which is consistent with previous research works (Bassis and Walker, 2012; Duddu et al., 2013). In each of the depth-varying-property cases in Fig. 4, we obtained excellent agreement between LEFM and PFF models, which serves as a verification of our LEFM implementation. However, the nuanced differences in crevasse propagation results for each of the cases are discussed in the sections below.

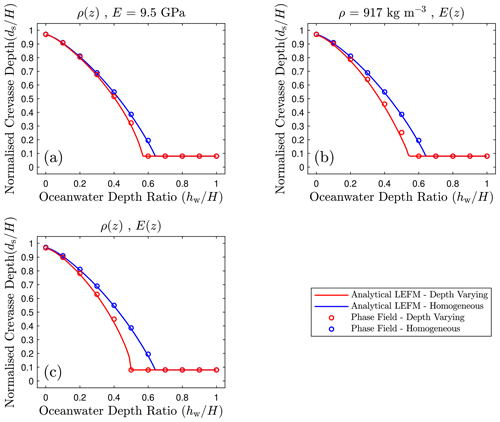
Figure 4 Normalized crevasse depth predictions versus ocean water height ratio for a single isolated dry crevasse in a linear elastic ice sheet considering homogeneous and depth-dependent mechanical properties.

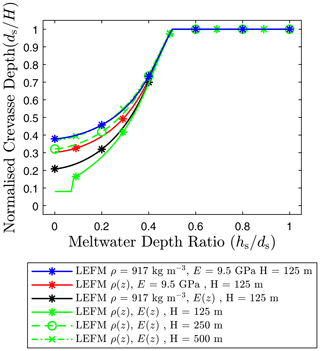
Figure 5 Normalized crevasse depth predictions versus meltwater depth ratio for a single isolated crevasse in a linear elastic ice sheet considering homogeneous and depth-dependent mechanical properties for an ocean water height h_w=0.5H.

3.1 Influence of depth-varying density

If the material properties of ice are assumed to be depth-independent then the longitudinal stress σ_xx varies linearly with depth according to Eq. (1). In the case of a land-terminating glacier (h_w=0) with free tangential slip at the base, the σ_xx profile is symmetrical about the centre line ($z=H/\mathrm{2}$). This stress is tensile in the regions above the centre line, with a maximum value of σ_xx≈300 kPa at the top surface for ice thickness H=125 m (blue line in Fig. 3). If a depth-dependent density is incorporated (green line in Fig. 3a), the maximum value of σ_xx is reduced to ≈235 kPa, with a non-linear distribution in the upper region. Approximately 50 m below the top surface, σ_xx tends towards a linear distribution, with the compressive stress nearer to the base being slightly less than that compared to the homogeneous case due to the reduced weight of the ice. We next discuss parametric studies to explore the effect of depth variations on crevasse propagation.

The first parametric study considers a dry (air-filled) crevasse, with different values of ocean water height h_w. The normalized crevasse depths ($d_{\text{s}}/H$) obtained using LEFM for this case are presented in Fig. 4a. For land-terminating glaciers (h_w=0 m), the crevasse propagates to the full thickness of the glacier for both the homogeneous and depth-varying cases because there is no compressive ocean water pressure to arrest crevasse growth. However, as ocean water height is increased, the stabilized crevasse depth is reduced, and the inclusion of the depth-varying density comes into effect and further reduces the stabilized crevasse depth. With ocean water heights of h_w>0.7H, the longitudinal stress is compressive enough that the crevasse will not grow beyond the initial specified depth of 10 m. To verify the accuracy of the LEFM model (solid line) results presented here, we also show the results obtained from the phase field fracture model (markers) in Fig. 4 (Clayton et al., 2022).

In Fig. 5, the relation between the crevasse depth ratio ($d_{\text{s}}/H$) and the meltwater depth ratio ($h_{\text{s}}/d_{\text{s}}$) for the thinner glacier (H=125 m) is shown. The ocean water height is fixed at h_w=0.5H for both the homogeneous-density (blue line) and depth-varying-density (red line) scenarios. The largest reduction of 20 % in the stabilized crevasse depth is observed for a dry crack (h_s=0) when considering the effect of depth-varying density. The additional tensile stress provided by the presence of meltwater allows the surface crevasse to penetrate deeper into the strata, with full fracture occurring for meltwater depth ratios greater than 0.5 in both scenarios.

As shown in Fig. 3a, the inclusion of the firn layer reduces the longitudinal stress in the upper regions of the glacier and tends towards the homogeneous-stress profile in the consolidated strata. The effect of this stress variation can be understood from Fig. 5. As the meltwater depth ratio is increased, the crevasse penetrates deeper into the glacier, and the influence of the firn layer on the stress state disappears; thus, the crevasse depth for the depth-varying case agrees with the homogeneous case for all $h_{\text{s}}/d_{\text{s}}>\mathrm{0.4}$. We found that the normalized crevasse depth ratio is insensitive to the glacier thickness H in the homogeneous case because the thickness only controls the magnitude of the longitudinal stress but not the depth at which the stress becomes compressive. However, in the depth-varying case, the normalized crevasse depth ratio is sensitive to the glacier thickness but converges with the homogeneous case for thicker glaciers. For example, the maximum percentage difference in the crevasse depth ratio between the depth-varying and homogeneous cases is 20 %, 4.5 %, and 1 % for H=125 m, H=250 m, and H=500 m, respectively.

3.2 Influence of depth-varying Young's modulus

The influence of a variable Young's modulus on the far-field longitudinal stress is shown in Fig. 3b. It can be observed that there is a greater deviation from the homogeneous case relative to the depth-varying density case. In the upper regions, σ_xx is further reduced to ≈60 kPa, and the stress profile is highly non-linear. However, at lower depths where the firn is fully consolidated into ice, the stress profile becomes linear. The maximum compressive stress at the glacier base is less due to the reduction in overburden pressure in the upper strata. Notably, the depth at which the stress becomes zero increases from 62.5 m in the homogeneous case to 72.3 m in the variable Young's modulus case. However, the stress intensity factor at the crevasse tip decreases due to a reduction in the magnitude of longitudinal stress; thus, the firn layer causes a reduction in crevasse penetration depth.

We now consider the propagation of an isolated dry crevasse for the depth-varying Young's modulus scenario using the LEFM model and the longitudinal-stress relation derived in Eq. (20). The results for the parametric study evaluating the normalized crevasse depths for various ocean water heights h_w are presented in Fig. 4b. Similarly to the results in Fig. 4a, the dry crevasse propagates to the same depth in the depth-varying and homogeneous cases for low ocean water heights. Because the crevasse propagates deeper into the fully consolidated ice regions, the properties of the firn layer have little impact on crevasse depth. As the ocean water height increases, the compressive-stress-resisting crevasse propagation increases, and so the crevasse growth is arrested at a shallower depth. The influence of the variable Young's modulus can be observed in these intermediate ocean water heights ($h_{\text{w}}/H=\mathrm{0.2}-\mathrm{0.6}$) as the crevasse depth is reduced when accounting for the firn layers. The maximum difference in crevasse depth is ≈0.2H at an ocean water height of h_w=0.55H. For ocean water heights greater than h_w=0.55H, the crevasse does not propagate beyond the initial specified depth of 10 m.

In Fig. 5, we report the normalized crevasse depth ratio versus the meltwater depth ratio considering the depth-varying Young's modulus (black line). The largest reductions in crevasse depth are observed for the thinner glacier (H=125 m) with a dry crevasse, where $d_{\text{s}}/H$ is reduced from 0.378 in the homogeneous case to 0.209 in the depth-varying case. The difference in normalized crevasse depth is reduced as the meltwater depth ratio increases because the crevasse penetrates deeper into the fully consolidated strata, thus reducing the influence of firn properties. For thicker glaciers, the difference between the homogeneous and depth-varying Young's modulus cases is smaller, which is attributed to the increase in magnitude of far-field longitudinal stress based on our stress analysis. The maximum percentage difference in crevasse depths for H=125 m is 44.9 %, while for H=250 m it is 16.5 %, and for H=500 m it is 6.0 %.

3.3 Influence of depth-varying Young's modulus and density

The next set of results entails the propagation of an isolated surface crevasse driven by the longitudinal stress considering both the depth-varying Young's modulus and the depth-varying density shown in Eq. (23). The stabilized crevasse depths for a dry crevasse in a grounded glacier of height H=125 m, calculated using LEFM and the phase field method for various ocean water heights h_w, are presented in Fig. 4c. As expected, for lower ocean water heights, the crevasse depths are in agreement with the homogeneous case due to the crevasse penetrating deeper into the compressive regions of the glacier. We observe the largest reductions in crevasse depths for intermediate values of ocean water height ($h_{\text{w}}=\mathrm{0.2}-\mathrm{0.4}H$), whereas the crevasse does not propagate beyond the initially specified depth for ocean water heights greater than 0.4H in this case (red line in Fig. 4c).

The relationship between stabilized crevasse depth ratios and meltwater depth ratios is presented in Fig. 5 for three different glacier thicknesses (green lines). For the thinnest glacier (H=125 m), the longitudinal stress is significantly reduced in the upper regions due to the lower stiffness and density of the firn layer, which prevents the dry crevasse from propagating beyond the initially specified depth of 0.08 compared to a crevasse depth ratio of 0.378 for the homogeneous case. The difference in crevasse depth ratios is reduced with increasing meltwater depth ratios because the crevasse propagates deeper into the consolidated ice strata. Full-depth propagation is achieved for meltwater depth ratios $h_{\text{s}}/d_{\text{s}}\ge \mathrm{0.5}$. The percentage difference in penetration depth for the dry crevasse is 18.0 % for H=250 m and 6.21 % for H=500 m. Overall, we find that the influence of depth-varying firn material properties is less in thicker glaciers; however, the effect is more prominent if the variation in both Young's modulus and density with depth is considered.

Figure 6 Schematic diagram showing the applied boundary conditions of a floating ice shelf containing an isolated surface crevasse.

4 Results for floating ice shelves

The final set of results entails the propagation of surface crevasses in floating ice shelves. We consider an idealized rectangular ice shelf geometry of variable height H and length L=5000 m. Three types of external loads act on the ice shelf: gravitational self-weight, causing a body force, and ocean water pressure and meltwater pressure in the crevasse, causing surface forces. A Robin-type boundary condition is applied at the base of the ice shelf because the buoyancy pressure is a function of the vertical displacement u_z, as given by ρ_sg(h_w−u_z). The far-left terminus is constrained to prevent free body motion; the top surface is considered to be traction-free; and the Neumann boundary condition is applied on the right edge to account for the ocean water pressure, similarly to the grounded-glacier case. A schematic diagram representing the applied boundary conditions is shown in Fig. 6.

The floatation heights for the buoyancy pressure are found by assuming local hydrostatic equilibrium. For the homogeneous ice case, this can be simplified to the ratio of ice density to ocean water density – that is, $h_{\text{w}}/H={\mathit{\rho }}_{\text{i}}/{\mathit{\rho }}_{\text{s}}\approx \mathrm{0.9}$. However, the inclusion of the depth-varying density profile leads to a reduction in the applied gravitational body force, causing a decrease in the floatation height. We evaluate the reduced floatation heights for each ice shelf thickness by integrating the depth-varying density profile over the entire ice shelf thickness and dividing by the thickness and ocean water density. Thus, we find that $h_{\text{w}}/H$ is equal to 0.7560 for H=125 m, 0.8268 for H=250 m, 0.8629 for H=500 m, and 0.8809 for H=1000 m. For deeper ice shelves, the material properties of the firn layer become less significant as its thickness is small relative to ice shelf thickness; therefore, the floatation depth tends towards the homogeneous case for thicker ice shelves.

Because of the buoyancy condition at the base and the dependence on ice shelf deflection, the analytical solutions for longitudinal stress derived in Sect. 2.1, 2.2, and 2.3 are not appropriate in the regions closer to the terminus. In Clayton et al. (2022), we showed that, faraway from the terminus, the longitudinal stress in the ice shelf agreed well with analytical solutions for grounded glaciers. Therefore, we use finite-element analysis to extract the longitudinal-stress data as a function of the vertical coordinate z at the horizontal position x=4750 m (i.e. 250 m from the ice shelf terminus). The data are fitted to a sixth-order polynomial equation, with coefficients presented in Table C1 in the Appendix, which defines the stress function σ_xx(z). Surface crevasses in the far-field region are ignored because the longitudinal stress is significantly compressive, preventing their propagation, regardless of whether the crevasses were filled with meltwater or not. The propagation of surface crevasses close to the terminus (ice–ocean front) is investigated by estimating the final and/or stabilized crevasse depth using LEFM. The LEFM model used in Krug et al. (2014) (see Appendix A) is appropriate for floating ice shelves as this was shown to match numerically calculated stress intensity factors using the displacement correlation method (Jiménez and Duddu, 2018).

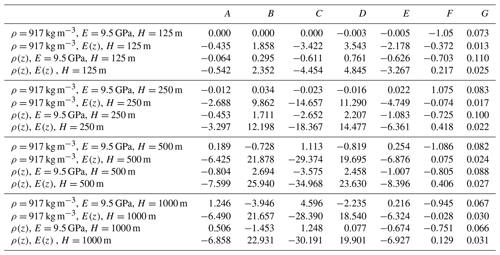
Table 1 Normalized crevasse depths for a dry ($h_{\text{s}}/d_{\text{s}}=\mathrm{0.0}$) isolated surface crevasse within a floating ice shelf close to the front (x=4750 m), calculated using the LEFM method in Krug et al. (2014). Bracketed values represent the difference in crevasse depth between the variational and homogeneous cases normalized by the crevasse depth for homogeneous ice, $(d_{\text{s}}^{\text{depth-dep}}-d_{\text{s}}^{\text{uniform}})/d_{\text{s}}^{\text{uniform}}\cdot \mathrm{100}\mathit{\%}$.

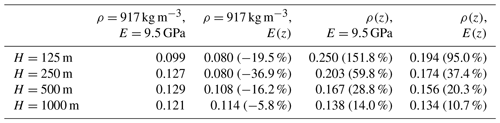
Table 2 Normalized crevasse depths for an isolated surface crevasse with a meltwater depth ratio of h_s/d_s=0.75 within a floating ice shelf close to the front (x=4750 m), calculated using the LEFM method in Krug et al. (2014). Bracketed values represent the difference in crevasse depth between the variational and homogeneous cases normalized by the crevasse depth for homogeneous ice, $(d_{\text{s}}^{\text{depth-dep}}-d_{\text{s}}^{\text{uniform}})/d_{\text{s}}^{\text{uniform}}\cdot \mathrm{100}\mathit{\%}$.

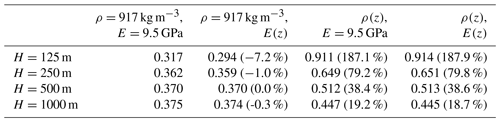
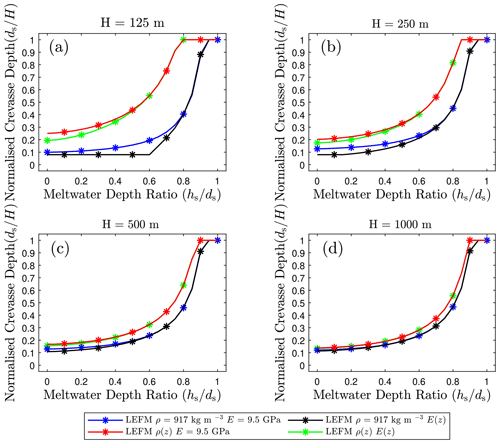
Figure 7 Normalized crevasse depth predictions versus meltwater depth ratio for an isolated surface crevasse close to the front in a floating ice shelf.

Crevasse penetration depths versus meltwater depth ratios $h_{\text{s}}/d_{\text{s}}$ from the LEFM model are presented graphically in Fig. 7. Penetration depths for the dry crevasse ($h_{\text{s}}/d_{\text{s}}=\mathrm{0}$) and for $h_{\text{s}}/d_{\text{s}}=\mathrm{0.75}$ are also reported in Tables 1 and 2, respectively, for ease of comparing data points. For the homogeneous ice case, there is minimal influence over the normalized crevasse depth by increasing glacier thickness (blue lines); for example, the maximum difference in penetration depth for the dry crevasse is 0.022H when increasing the ice shelf thickness. Surface crevasses with low levels of meltwater only penetrate a few metres below the surface due to the longitudinal-stress profile being predominantly compressive due to the high ocean water pressure. For $h_{\text{s}}/d_{\text{s}}<\mathrm{0.6}$, an incremental increase in meltwater does not result in significant crevasse growth. Full-fracture propagation is only observed when crevasses are almost fully filled with meltwater ($h_{\text{s}}/d_{\text{s}}>\mathrm{0.9}$), where the meltwater pressure is sufficient to overcome the compressive longitudinal stress.

Considering the depth-varying Young's modulus leads to a minor reduction in stabilized crevasse depth (black lines), with no growth occurring beyond the initial notch for meltwater depth ratios of $h_{\text{s}}/d_{\text{s}}<\mathrm{0.6}$ for H=125 m. Penetration depths match with the homogeneous case for meltwater depth ratios of $h_{\mathrm{s}}/d_{\mathrm{s}}\ge \mathrm{0.8}$ as the crevasse penetrates deeper into the ice strata. The influence of the depth-varying Young's modulus is reduced with increasing ice shelf thickness. This is the most noticeable for the crevasse depths reported in Table 2 as the percentage difference between the depth-varying modulus and homogeneous cases is reduced to 1 % for H=250 m.

Considering the depth-varying density in the fracture analysis results in surface crevasses propagating deeper into the ice strata (red lines), with a dry crevasse propagating to a depth of 0.250H compared to a depth of 0.099H for homogeneous ice within an ice shelf of thickness H=125 m. This is in contrast to the grounded-glacier case (where crevasse depth decreased) and can be attributed to the reduction in overburden pressure and the reduced buoyancy height specific to ice shelves. The inclusion of meltwater within the crevasse results in an increased penetration depth, and full-thickness fracture is achieved for meltwater depth ratios of $h_{\text{s}}/d_{\text{s}}\ge \mathrm{0.8}$. The largest differences in penetration depth for the depth-varying density compared to in the homogeneous case are observed in Table 2. For thin ice shelves (H=125 m) and a meltwater depth ratio of $h_{\text{s}}/d_{\text{s}}=\mathrm{0.75}$, the crevasse propagates approximately 3 times deeper when accounting for the depth-varying density. Similarly to the grounded-glacier case, the influence of the depth-varying density is reduced when the ice shelf thickness increases due to a larger proportion of ice being fully consolidated. However, there are still some differences in penetration depth compared to the homogeneous case for thick ice shelves (H=1000 m), with a percentage difference of 14.0 % for the dry crevasse and of 19.2 % for $h_{\text{s}}/d_{\text{s}}=\mathrm{0.75}$.

Including the effects of both depth-varying density and depth-varying modulus highlights that density is the more prominent property influencing surface crevasse propagation in ice shelves. It is observed in Fig. 7 that the majority of results for depth-varying density and modulus (green lines) overlap with the depth-varying density results (red lines). The exception to this is for dry crevasses in thin ice shelves, where the stabilized penetration depth is 0.194H compared to 0.25H when considering only the depth-varying density.

5 Non-linear viscous incompressible rheology

The above analysis has considered ice to behave as a linear elastic compressible solid, with a Poisson ratio of ν=0.35. This is based on the assumption that crevasse propagation occurs in a rapid brittle manner, such that the cracking occurs on a timescale well below the Maxwell time (typically on the order of hours to days for glacial ice). However, it is more common in the glaciology literature to assume that glacier ice deformed over long timescales well before the nucleation and propagation of crevasses. Also, if the slow development of crevasses is considered, with crevasse depths stabilizing over a span of weeks (Duddu et al., 2013), then ice should be considered to be a viscous material. The analytical solution (see Appendix A in Sun et al., 2021) for the stress state of a grounded glacier with incompressible linear elastic rheology and that of one with an incompressible non-linear viscous rheology are the same. Therefore, in this study, we simply set the Poisson ratio to ν≈0.5 (using ν=0.49 to prevent numerical issues) to obtain the background stress. In addition, we conduct finite-element simulations for a grounded glacier, including the viscoelastic contributions (with ν=0.35) of ice flow modelled through Glen's flow law, and extract numerical values of the longitudinal stress. To illustrate that the stress state is only sensitive to the incompressibility assumption and not to the linear elastic or non-linear viscous rheology, we plot the longitudinal-stress profile for a land-terminating (h_w=0) grounded glacier considering linear elastic compressibility (ν=0.35), linear elastic incompressibility (ν≈0.5), and a non-linear viscous rheology in Fig. 8.

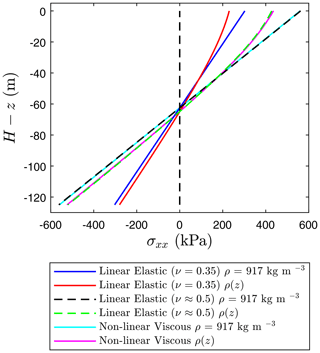
Figure 8 Far-field longitudinal stress σ_xx throughout the depth of a land-terminating glacier (h_w=0), showing the effects of depth-varying density ρ(z) considering linear elastic compressibility (ν=0.35), linear elastic incompressibility (ν≈0.5), and a non-linear viscous rheology.

Figure 8 shows that if ice is considered to be linear elastic incompressible (ν≈0.5), the obtained stress solution matches with the steady-state creep stress state derived by Weertman (1957) for depth-independent density and matches stress profiles obtained through simulations using a visco-elastic rheology. We observe that stresses are more extensional in the upper surface and more compressive at the base when considering incompressibility and that the stress obtained through simulations is independent of ice rheology (Glen's law creep coefficients) once a sufficiently long time has passed. For the homogeneous case, the longitudinal stress varies linearly with depth and is symmetrical about the centre line $z=H/\mathrm{2}$. Similarly to the linear elastic compressible case, the inclusion of depth-dependent density results in a reduction in both the lithostatic stress contribution σ_zz and the resistive stress R_xx for both material rheologies.

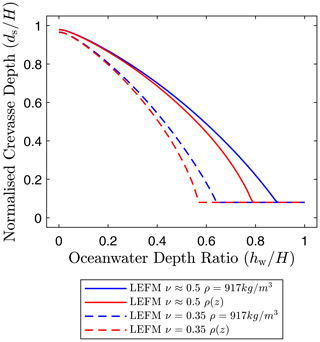
Figure 9 Normalized crevasse depth predictions versus ocean water height ratio for a single isolated dry crevasse in a grounded glacier considering compressible (ν=0.35) and incompressible (ν≈0.5) homogeneous and depth-dependent mechanical properties of ice.

The longitudinal-stress profiles presented in Fig. 8 are used to drive crevasse propagation in the linear elastic fracture mechanics study. Values of crevasse penetration depth for an isolated dry crevasse in a grounded glacier, subject to different values of ocean water height h_w, are presented in Fig. 9. The solid-line curves represent incompressible ice, whilst the dashed lines represent compressible ice of Poisson ratio ν=0.35. Considering ice to be an incompressible solid leads to deeper crevasse penetration depths compared to linear elastic compressibility, but these crevasses follow a similar trend as that observed for the compressible case. Accounting for the depth-varying properties of the firn layer in grounded glaciers leads to two different regimes of crevasse growth behaviour. If the resistive stress R_xx is large (e.g. a low ocean water height), the firn layer promotes crevasse propagation, and the crevasse penetrates to a slightly greater depth than in the constant-density case; this result is in agreement with the van der Veen (1998a) study. In contrast, if the resistive stress is small (e.g. high ocean water height) then the firn layer stunts crevasse propagation, and the crevasse depth would be greater in the constant-density case; this result contradicts the van der Veen (1998a) study. We note that, even if the Nye zero-stress criterion is used (assuming densely spaced cracks) instead of using LEFM to consider a single isolated crevasse, this finding of the two different crevasse growth regimes holds true.

Comparing the effects of assuming an incompressible and/or viscous rheology, the percentage difference in penetration depth when considering depth-dependent density for a dry crevasse of ocean water height h_w=0.5H is reduced to 4 % compared to 20 % for linear elastic compressibility. The ocean water height required to prevent any development of dry crevasses differs, with values of h_w=0.55H being sufficient for compressible depth-dependent density cases, whereas ocean water levels of h_w=0.8H are required for the incompressible case. Comparing this to the cases in which no density variations are considered still shows a similar trend, with higher ocean water levels being needed to stabilize crevasses when density variations are not considered.

Finally, we consider water-filled surface crevasses in floating ice shelves of height H=125 m and length L=5000 m using a non-linear viscous ice rheology. Similarly to the linear elastic compressible case, we consider surface crevasses at the horizontal position x=4750 m (250 m from the ice shelf terminus) and extract the longitudinal-stress profiles from the finite-element analysis. We plot the stabilized crevasse depth versus meltwater depth ratio for the non-linear viscous (NLV) rheology in Fig. 10 along with the results for linear elastic (LE) compressibility (ν=0.35) and incompressibility (ν=0.49).

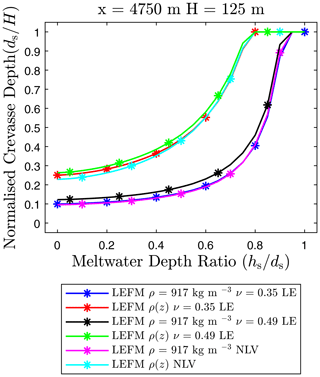
Figure 10 Normalized crevasse depth predictions versus meltwater depth ratio for a single isolated surface crevasse located close to the ice shelf front (x=4750 m) considering a linear elastic (LE) and non-linear viscous (NLV) rheology.

When comparing the stabilized crevasse depths close to the front, we note that the penetration depth is independent of ice rheology, which is in contrast to the grounded-glacier case. For the homogeneous density, minimal crevasse propagation is observed for meltwater depth ratios below $h_{\text{s}}/d_{\text{s}}<\mathrm{0.6}$, with full-thickness propagation only occurring when fractures are close to saturation. The inclusion of the depth-dependent density results in deeper crevasse penetration depths, with minimal differences in penetration depth between the linear elastic cases and the non-linear viscous rheology. This likely indicates that, for crevasses close to the front, fracture is driven by the flotation height and the bending stresses due to the floating condition. For depth-dependent density, the reduction in flotation height leads to an increase in tensile stress in the upper surface due to increases in R_xx and increased bending stress. In addition, the lithostatic component of longitudinal stress is reduced, leading to deeper crevasse propagation when including firn density.

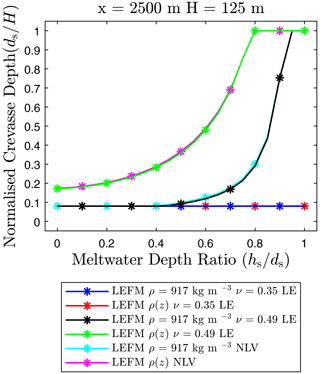
Figure 11 Normalized crevasse depth predictions versus meltwater depth ratio for a single isolated surface crevasse located in the far-field region (x=2500 m) considering a linear elastic (LE) and non-linear viscous (NLV) rheology.

We also consider the propagation of an isolated surface crevasse located in the far-field region (x=2500 m) of a floating ice shelf, with results presented in Fig. 11. As shown previously, for the linear elastic compressible rheology, the stress state is fully compressive for both the homogeneous- and the depth-dependent-density case; thus, no crevasse propagation is observed regardless of the meltwater depth ratio. By contrast, when considering the non-linear viscous rheology of ice, surface crevasses may propagate in the far-field region if there is sufficient meltwater pressure present. Large increases in crevasse penetration depth are observed for meltwater depth ratios greater than $h_{\text{s}}/d_{\text{s}}=\mathrm{0.50}$, with full-thickness propagation being observed close to crevasse saturation at $h_{\text{s}}/d_{\text{s}}=\mathrm{0.95}$. Similarly to crevasses near the front, the inclusion of depth-dependent density results in increased crevasse penetration depths compared to the homogeneous-density scenario. Thus, similar conclusions can be drawn for both elastic and viscous rheologies.

6 Discussion

An important finding of this paper is that the inclusion of the depth-varying mechanical properties of unconsolidated ice strata results in a reduction in both the lithostatic compressive-stress component and the resistive tensile-stress component. Contrarily to the conventional understanding (van der Veen, 1998a), we find that accounting for depth-varying density and modulus can lead to an overall reduction in surface crevasse depths in grounded glaciers. This is because, in some scenarios, the reduction in resistive stress can hinder crevasse propagation more than the increase in crevasse propagation resulting from the reduction in lithostatic stress. Thus, our study suggests that firn layers can have a stabilizing effect by curtailing surface crevasse growth in grounded glaciers.

Assuming ice to be a linear elastic compressible material, we find that considering depth-varying Young's modulus has a greater influence on crevasse depths than density in thinner glaciers. For example, considering depth-varying density results in a maximum percentage difference of 20 % in the penetration depth of dry crevasses compared to a maximum percentage difference of 45 % when considering the depth-varying Young's modulus. The largest reductions in crevasse depths are observed in thinner glaciers (depths of approximately 100–150 m), where the stabilizing effects of the firn layers seem to be more prominent. Larger meltwater depth ratios are required to propagate surface crevasses in thinner ice shelves, whereas, in thicker glaciers, the influence of firn density is less (in some cases negligible), and so surface crevasses propagate deeper into the fully consolidated strata. Thus, our study reveals that LEFM models assuming homogeneous ice properties are valid for crevasse depth estimation in thicker glaciers with ice thickness H>250 m.

Accounting for depth-varying density in the floating-ice-shelf case increases the penetration depth of surface crevasses close to the ice–ocean front, with this increase being caused by reductions in buoyancy height and lithostatic compressive stresses. The effect of depth-varying density is dominant in thinner ice shelves, but it can still impact surface crevasse propagation in ice shelves as thick as H=1000 m, although this would be to a lesser extent. For instance, the crevasse depth ratio increases to d_s=0.91H (188 % increase compared to homogeneous case) for thin ice shelves (H=125 m), whereas a 19 % increase is observed for 1 km thick ice (d_s=0.45H). Considering the depth-varying Young's modulus in the floating-ice-shelf case reduces surface crevasse depth for low meltwater depths slightly, and the effect becomes less significant in thicker ice shelves. This study suggests that, as the ice shelves become thinner due to increased basal melting in warmer oceans, the effects of the firn layer can make them more vulnerable by allowing deeper crevasse propagation. However, without the presence of any meltwater, full-depth penetration of surface crevasses in ice shelves may not be possible. Therefore, an important aspect to explore in a future study is the effect of the firn layer on basal crevasse propagation in ice shelves, which likely controls rift formation and iceberg calving.

The analytical (closed-form) and numerical (polynomial-fitted) solutions developed in this paper provide a more realistic description of the longitudinal stress in glaciers and ice shelves. The effect of depth-varying firn and/or ice properties could be accounted for in the shallow-shelf approximation (SSA) and could be coupled with LEFM models to potentially enable the prediction of rift propagation. Krug et al. (2014) proposed a simple method for estimating crevasse depths in an ice shelf, wherein the longitudinal stress calculated from the full-Stokes model was used to evaluate the stress intensity factors based on an LEFM model. A similar approach can be developed to estimate crevasse depths from shallow-shelf models or remote sensing data. In Appendix D, we discuss how the 2D stress fields obtained from a shallow-ice-shelf model can be augmented to include the depth-dependent density and Young's modulus. This stress can then be used within an analytical LEFM model to predict crevasse depth and calving.

We acknowledge that there are a few limitations in the current study. Firstly, we assume our glacier and/or ice shelf geometry to be a 2D rectangle with the free-slip condition at the base, which is highly idealized and does not consider any contributions from frictional sliding at the base for the grounded case or buttressing stresses for floating ice shelves (Buck, 2023; Buck and Lai, 2021). Another limitation of the current model is that the rate of firn consolidation is assumed to be uniform, with a horizontal position, and is assumed to be unaffected by glacier thickness H. However, firn densification is dependent on environmental factors including accumulation rates, overburden pressure, temperature, and local strain rates (van den Broeke, 2008; Amory et al., 2024). Firn densification near terminus regions or in thinner glaciers potentially results in a thinner firn layer and thus a reduced value of the parameter D, indicating a shorter length scale for the transition between firn and dense ice properties. However, while the findings presented here are all based on the density profiles from the Ronne Ice Shelf (Rist et al., 2002), the analytic models (and provided MATLAB code) allow for an easy way to evaluate the impact for specific firn heights. This makes it possible to estimate the impact of including firn properties on the crevasse depth for specific locations.

One final limitation of our analytic models is related to water-filled crevasses. While we investigate the effects of including the effect of firn on the density and Young's modulus, both these effects are (partially) driven by the porosity of the firn. However, when water-filled crevasses are considered, no model is included to account for water leaking from the crevasse into the surrounding firn. For colder ice sheets and deeper crevasses, where the full water contents are surrounded by ice of sub-zero temperatures, this assumption is reasonable: any water that seeps into the surrounding ice or firn will freeze, creating an impermeable ice layer surrounding the crevasse, which will prevent water from permeating further into the firn (Buzzard et al., 2018; Amory et al., 2024). As these ice layers are typically very thin, they do not alter the mechanical properties of the ice. However, if more temperate glaciers are considered or if one considers conditions where water-filled crevasses do not penetrate to a considerable depth, the firn and/or ice surrounding the crevasse might not be sufficiently cold to cause this ice layer to form. In such circumstances, the presented model will overestimate the crevasse depths obtained as the saturated firn will reduce the effects of the water pressure within the crevasse by re-distributing this pressure over a larger region surrounding the crevasse.

7 Conclusions

In this paper, we derived analytical equations for the far-field longitudinal stress, including the effects of surface firn layers, described by depth-varying density and Young's modulus profiles based on field data. These analytic expressions were used to perform fracture propagation studies on isolated air- and/or water-filled surface crevasses in grounded glaciers and ice shelves for the homogeneous (assuming fully consolidated glacial ice) and depth-varying ice cases. The derived analytical equations for the far-field longitudinal stress in grounded glaciers were verified with the stress profiles obtained through finite-element analysis. We also used the phase field fracture model to validate the crevasse depths predicted by the LEFM model. The LEFM model results demonstrate the potentially large impact of including the properties of unconsolidated firn layers within the predictions of crevasse depths. For grounded glaciers, depth-varying firn properties inhibit crevasse propagation, requiring lower ocean water heights and larger meltwater depth ratios for full-depth propagation. In contrast, for floating ice shelves and/or tongues, the consideration of depth-varying firn properties promoted crevasse propagation, in some cases up to 3 times as deep. Thus, with regard to fracture and calving, the firn layer may have a stabilizing effect on grounded glaciers, whereas it may have a destabilizing effect on ice shelves. Overall, this study establishes the importance of including the depth dependence of firn layer material properties in crevasse models using LEFM. Additionally, we propose a simple scheme to integrate our analytical solutions with the stresses obtained from the shallow-shelf approximation, which can allow us to assess the vulnerability of ice shelves to calving, accounting for firn layer effects.

Appendix A: Analytical LEFM model

We evaluate the stress intensity factor (SIF) considering the contributions of normal tensile stress, lithostatic compressive stress, and meltwater pressure using an iterative code in MATLAB. An initial crevasse depth d is suggested, and the net SIF is found by integrating over the crevasse depth due to the varying stress field with depth. The crevasse will continue to propagate if $K_{\text{I}}^{\text{net}}$ is larger than the fracture toughness K_IC, which, for glacial ice, is taken as K_IC=0.1$\mathrm{MPa}{\mathrm{m}}^{\mathrm{1}/\mathrm{2}}$, found from experimental data (Fischer et al., 1995). Since $K_{\text{I}}^{\text{net}}$ is proportional to the net longitudinal stress σ_net, the SIF will begin to be reduced once the crevasse penetrates into the compressive region of the ice. The net longitudinal stress σ_net is defined as the sum of the longitudinal stress σ_xx and the meltwater pressure in the crevasse p_w:

$$\begin{array}{}\text{(A1)}& {\mathit{\sigma }}_{\text{net}}\left(z\right)={\mathit{\sigma }}_{xx}\left(z\right)+p_{\text{w}}\left(z\right),\end{array}$$

where

$$\begin{array}{}\text{(A2)}& p_{\text{w}}={\mathit{\rho }}_{\text{w}}g〈h_{\text{s}}-\left(z-z_{\text{s}}\right)〉.\end{array}$$

In the above, ρ_w is the meltwater density, z_s is the elevation of the crevasse tip above the glacier base, and h_s is the meltwater height in the crevasse. The presence of the Macaulay brackets in Eq. (A2) indicates that the pressure is zero above the water surface.

The SIF $K_{\text{I}}^{\text{net}}$ is calculated using the following equation:

$$\begin{array}{}\text{(A3)}& K_{\text{I}}^{\text{net}}=\underset{\mathrm{0}}{\overset{d}{\int }}{M}_{\text{D}}\left(\mathit{\chi },H,d\right){\mathit{\sigma }}_{\text{net}}\left(\mathit{\chi }\right)\text{d}\mathit{\chi },\end{array}$$

where M_D is a weight function dependent on the applied boundary conditions and domain geometry, and $\mathit{\chi }=H-z$ and d represent the trial crevasse depth. This selection has been debated in various literature sources (van der Veen, 1998a; Krug et al., 2014).

Appendix B: Weight function for grounded glaciers with free tangential slip

For a grounded glacier undergoing free slip, we follow the double-edge crack formulation as this gives good agreement with SIFs calculated using the displacement correlation method with finite-element method (FEM) simulations (Jiménez and Duddu, 2018). The weight function is taken from Tada et al. (1985) and takes the following form:

$$\begin{array}{}\text{(B1)}& M_{\text{D}}={\displaystyle \frac{\mathrm{2}}{\sqrt{\mathrm{2}H}}}\left(\mathrm{1}+f_{\mathrm{1}}\left({\displaystyle \frac{\mathit{\chi }}{d}}\right)f_{\mathrm{2}}\left({\displaystyle \frac{d}{H}}\right)\right)\mathit{\theta }\left({\displaystyle \frac{d}{H}},{\displaystyle \frac{\mathit{\chi }}{H}}\right),\end{array}$$

where the functions f₁,f₂, and θ are defined as

$$\begin{array}{}\text{(B2)}& {\displaystyle }{f}_{\mathrm{1}}=\mathrm{0.3}\left(\mathrm{1}-{\left({\displaystyle \frac{\mathit{\chi }}{d}}\right)}^{\frac{\mathrm{5}}{\mathrm{4}}}\right),\text{(B3)}& {\displaystyle }{f}_{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left(\mathrm{1}-\sin \left({\displaystyle \frac{\mathit{\pi }d}{\mathrm{2}H}}\right)\right)\left(\mathrm{2}+\sin \left({\displaystyle \frac{\mathit{\pi }d}{\mathrm{2}H}}\right)\right),\text{(B4)}& {\displaystyle }\mathit{\theta }={\displaystyle \frac{\sqrt{\tan \left(\frac{\mathit{\pi }d}{\mathrm{2}H}\right)}}{\sqrt{\mathrm{1}-{\left(\frac{\cos \left(\frac{\mathit{\pi }d}{\mathrm{2}H}\right)}{\cos \left(\frac{\mathit{\pi }\mathit{\chi }}{\mathrm{2}H}\right)}\right)}^{\mathrm{2}}}}}.\end{array}$$

Appendix C: Weight function for floating ice shelves

For the floating-ice-shelf condition, it was found that the SIFs calculated using the weight function presented in Krug et al. (2014) gave better agreement with SIFs using the displacement correlation method (Jiménez and Duddu, 2018). Therefore, the penetration depths in Sect. 4 were calculated using the formulation below:

$$\begin{array}{}\text{(C1)}& K_{\mathrm{1}}^{\text{net}}=\underset{\mathrm{0}}{\overset{d}{\int }}\mathit{\beta }\left(z,H,d\right){\mathit{\sigma }}_{\text{net}}\left(\mathit{\chi }\right)\text{d}\mathit{\chi },\end{array}$$

where

$$\begin{array}{}\text{(C2)}& {\displaystyle }\begin{array}{rl}\mathit{\beta }\left(z,H,d\right)& ={\displaystyle \frac{\mathrm{2}}{\sqrt{\mathrm{2}\mathit{\pi }\left(d-z\right)}}}\left(\mathrm{1}+M_{\mathrm{1}}{\left(\mathrm{1}-{\displaystyle \frac{z}{d}}\right)}^{\mathrm{0.5}}\right.\\ & \left.+M_{\mathrm{2}}\left(\mathrm{1}-{\displaystyle \frac{z}{d}}\right)+M_{\mathrm{3}}{\left(\mathrm{1}-{\displaystyle \frac{z}{d}}\right)}^{\mathrm{1.5}}\right),\end{array}\text{(C3)}& {\displaystyle }\begin{array}{rl}{M}_{\mathrm{1}}& =\mathrm{0.0719768}-\mathrm{1.513476}\mathit{\lambda }-\mathrm{61.1001}{\mathit{\lambda }}^{\mathrm{2}}+\mathrm{1554.95}{\mathit{\lambda }}^{\mathrm{3}}\\ & -\mathrm{14}\mathrm{583.8}{\mathit{\lambda }}^{\mathrm{4}}+\mathrm{71}\mathrm{590.7}{\mathit{\lambda }}^{\mathrm{5}}-\mathrm{205}\mathrm{384}{\mathit{\lambda }}^{\mathrm{6}}+\mathrm{356}\mathrm{469}{\mathit{\lambda }}^{\mathrm{7}}\\ & -\mathrm{368}\mathrm{270}{\mathit{\lambda }}^{\mathrm{8}}+\mathrm{208}\mathrm{233}{\mathit{\lambda }}^{\mathrm{9}}-\mathrm{49}\mathrm{544}{\mathit{\lambda }}^{\mathrm{10}},\end{array}\text{(C4)}& {\displaystyle }\begin{array}{rl}{M}_{\mathrm{2}}& =\mathrm{0.246984}+\mathrm{6.47583}\mathit{\lambda }+\mathrm{176.456}{\mathit{\lambda }}^{\mathrm{2}}-\mathrm{4058.76}{\mathit{\lambda }}^{\mathrm{3}}\\ & +\mathrm{37}\mathrm{303.8}{\mathit{\lambda }}^{\mathrm{4}}-\mathrm{181}\mathrm{755}{\mathit{\lambda }}^{\mathrm{5}}+\mathrm{520}\mathrm{551}{\mathit{\lambda }}^{\mathrm{6}}-\mathrm{904}\mathrm{370}{\mathit{\lambda }}^{\mathrm{7}}\\ & +\mathrm{936}\mathrm{863}{\mathit{\lambda }}^{\mathrm{8}}-\mathrm{531}\mathrm{940}{\mathit{\lambda }}^{\mathrm{9}}+\mathrm{12}\mathrm{729}{\mathit{\lambda }}^{\mathrm{10}},\end{array}\text{(C5)}& {\displaystyle }\begin{array}{rl}{M}_{\mathrm{3}}& =\mathrm{0.529659}-\mathrm{22.3235}\mathit{\lambda }+\mathrm{532.074}{\mathit{\lambda }}^{\mathrm{2}}-\mathrm{5479.53}{\mathit{\lambda }}^{\mathrm{3}}\\ & +\mathrm{28}\mathrm{592.2}{\mathit{\lambda }}^{\mathrm{4}}-\mathrm{81}\mathrm{388.6}{\mathit{\lambda }}^{\mathrm{5}}+\mathrm{128}\mathrm{746}{\mathit{\lambda }}^{\mathrm{6}}-\mathrm{106}\mathrm{246}{\mathit{\lambda }}^{\mathrm{7}}\\ & +\mathrm{35}\mathrm{780.7}{\mathit{\lambda }}^{\mathrm{8}},\end{array}\end{array}$$

and $\mathit{\lambda }=d/H$.

The longitudinal stress in the ice shelf cannot be determined analytically due to the bending-stress contribution from the floatation pressure at the base. The stress profiles at the front are obtained numerically (normalized with respect to ρ_igH) and are fitted to a sixth-order polynomial equation, taking the general form below:

$$\begin{array}{}\text{(C6)}& \begin{array}{rl}{\displaystyle \frac{{\mathit{\sigma }}_{xx}}{{\mathit{\rho }}_{\text{i}}gH}}& =A{\left({\displaystyle \frac{\mathit{\chi }}{H}}\right)}^{\mathrm{6}}+B{\left({\displaystyle \frac{\mathit{\chi }}{H}}\right)}^{\mathrm{5}}+C{\left({\displaystyle \frac{\mathit{\chi }}{H}}\right)}^{\mathrm{4}}\\ & +D{\left({\displaystyle \frac{\mathit{\chi }}{H}}\right)}^{\mathrm{3}}+E{\left({\displaystyle \frac{\mathit{\chi }}{H}}\right)}^{\mathrm{2}}+F\left({\displaystyle \frac{\mathit{\chi }}{H}}\right)+G,\end{array}\end{array}$$

where $A,B,C,D,E,F$, and G are non-dimensionalized stress coefficients that are presented in Table C1.

Table C1 Coefficients of normalized longitudinal stress in Eq. (C6) for a floating ice shelf at horizontal position x=4750 m.

The net SIFs from Eqs. (A3) and (C1) are numerically integrated over the crevasse depth, taking into account the variations in net longitudinal stress with depth. As the crevasse propagates into deeper strata, $K_{\text{I}}^{\text{net}}$ is reduced, and the crevasse stabilizes once $K_{\text{I}}^{\text{net}}=K_{\text{IC}}$.

Appendix D: Linking with shallow-ice-shelf models

Over longer timescales, ice sheet flow is described as an incompressible non-linear viscous-fluid-like model, where the elastic deformations are negligible compared to the viscous deformation. Therefore, the incompressible Stokes equations are used to solve for mass and momentum balance, wherein the volumetric stress or pressure p is constitutively indeterminate, and the deviatoric stress tensor σ^′ is defined by a non-linear viscous constitutive law as follows:

$$\begin{array}{}\text{(D1)}& {\mathit{\sigma }}^{\prime }=\mathit{\sigma }-p\mathbf{I}=\mathrm{2}\mathit{\mu }\left({\dot{\mathit{\epsilon }}}_{\text{eq}}\right)\dot{\mathit{\epsilon }},\end{array}$$

where $\dot{\mathit{\epsilon }}$ is the strain rate tensor given by the symmetric part of the velocity gradient tensor, I is the second-order identity tensor, and the viscosity μ is determined using a Bingham–Norton–Maxwell-type relation (Glen, 1955) that accounts for shear-thinning behaviour.

$$\begin{array}{}\text{(D2)}& \mathit{\mu }=A(T{)}^{-\mathrm{1}/n}{\dot{\mathit{\epsilon }}}_{\text{eq}}^{\frac{\mathrm{1}-n}{n}}\end{array}$$

In the above equation, A(T) is the temperature-dependent creep coefficient, n is the creep exponent, and ${\dot{\mathit{\epsilon }}}_{\text{eq}}$ is the second invariant of the strain rate tensor. Notably, the strain rate tensor can be calculated using surface velocity obtained from remote sensing observations (Chudley et al., 2022).

While it may not be impossible to simulate ice sheet flow using a full-Stokes model, this is currently too computationally expensive. The spatial discretization in the full-Stokes model is dictated by the ice thickness, which is much smaller than the in-plane dimensions of ice sheet–ice shelf systems, thus leading to an excessively refined mesh for resolving in-plane ice velocity. The shallow-ice-shelf approximation (SSA) simplifies the full-Stokes model by assuming that vertical shear is zero (MacAyeal, 1989), leading to the following depth-averaged governing equations in the horizontal x and y directions:

$$\begin{array}{}\text{(D3)}& \begin{array}{rl}{\displaystyle \frac{\partial }{\partial x}}\left(\mathrm{4}\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{u}}{\partial x}}+\mathrm{2}\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{v}}{\partial y}}\right)+{\displaystyle \frac{\partial }{\partial y}}\left(\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{u}}{\partial y}}+\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{v}}{\partial x}}\right)& =\mathit{\rho }gH{\displaystyle \frac{\partial s}{\partial x}},\\ {\displaystyle \frac{\partial }{\partial y}}\left(\mathrm{4}\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{v}}{\partial y}}+\mathrm{2}\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{u}}{\partial x}}\right)+{\displaystyle \frac{\partial }{\partial x}}\left(\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{v}}{\partial x}}+\stackrel{\mathrm{‾}}{\mathit{\mu }}{\displaystyle \frac{\partial \stackrel{\mathrm{‾}}{u}}{\partial y}}\right)& =\mathit{\rho }gH{\displaystyle \frac{\partial s}{\partial y}},\end{array}\end{array}$$

where $\stackrel{\mathrm{‾}}{\mathit{\mu }}={\int }_{\mathrm{0}}^H\mathit{\mu }\text{d}z$ is the depth-integrated viscosity, and s is the upper surface elevation. Together with appropriate boundary conditions (e.g. velocity and terminus ocean water pressure), solving this equation provides an excellent approximation of the flow of ice sheets. Using the velocity components, we can determine the deviatoric stress components according to Eq. (D1). Based on the assumption that the vertical stress σ_zz is hydrostatic, we can determine the stress components in the plane of the ice shelf as follows (Greve and Blatter, 2009):

$$\begin{array}{}\text{(D4)}& \begin{array}{rl}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xx}& =\mathrm{2}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xx}^{\prime }+{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{yy}^{\prime }-{\mathit{\rho }}_{\text{i}}g(H-z),\\ {\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{yy}& =\mathrm{2}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{yy}^{\prime }+{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xx}^{\prime }-{\mathit{\rho }}_{\text{i}}g(H-z),\\ {\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xy}& ={\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xy}^{\prime },\end{array}\end{array}$$

where $\stackrel{\mathrm{‾}}{\mathit{\sigma }}$ represents the height-averaged stresses. Here, we propose an approximate way of linking the LEFM model for crevasse depth estimation with the SSA. Using the in-plane stresses in Eq. (D4), we can determine the principal values which correspond to the maximum and minimum normal stresses in the plane of the ice shelf. Assuming that crevasses open perpendicularly to the maximum principal stress ${\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\text{max}}$, we can determine the net force F_w (per unit width out of plane) acting on the boundary as follows:

$$\begin{array}{}\text{(D5)}& \begin{array}{rl}{F}_{\text{w}}=H{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{\text{max}}& =H\left({\displaystyle \frac{{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xx}+{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{yy}}{\mathrm{2}}}\right.\\ & \left.+{\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\sqrt{({\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xx}-{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{yy}{)}^{\mathrm{2}}+\mathrm{4}{\stackrel{\mathrm{‾}}{\mathit{\sigma }}}_{xy}^{\mathrm{2}}}\right).\end{array}\end{array}$$

The force F_w, if compressive, would have a similar effect as the ocean water pressure term in Eq. (23), and so it can be used to replace the term $\frac{\mathrm{1}}{\mathrm{2}}{\mathit{\rho }}_{\text{s}}g{h}_{\text{w}}^{\mathrm{2}}$. Thus, the SSA stress solution can be augmented to include the effect of depth-varying density and modulus as follows:

$$\begin{array}{}\text{(D6)}& \begin{array}{rl}{\mathit{\sigma }}_{xx}& ={\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}{\mathit{\rho }}_{\text{i}}g\left(z-{\displaystyle \frac{\mathrm{1}-E^{*}}{\mathrm{2}}}H\right)-(\mathrm{1}+E^{*}){\displaystyle \frac{F_{\text{w}}}{H}}\\ & +{\displaystyle \frac{\mathit{\nu }}{\mathrm{1}-\mathit{\nu }}}({\mathit{\rho }}_{\text{i}}-{\mathit{\rho }}_{\text{f}})gD\left(\right(\mathrm{1}-e^{-(H-z)/D})\\ & +(\mathrm{1}+E^{*})(-\mathrm{1}+{\displaystyle \frac{D}{H}}(\mathrm{1}-e^{-H/D}\left)\right)).\end{array}\end{array}$$

The above stress can be used as the net stress to determine the stress intensity factor and to estimate the crevasse depth. We note that, depending on the discretization used for the numerical solution of the SSA, some of the details of the scheme would need modifications. In future work, we will establish the viability of coupling this scheme with the LEFM model with the shallow-shelf and other depth-integrated approximations.

Appendix E: Influence of depth-variable Poisson ratio ν

For the crevasse propagation studies previously presented, a depth-invariant Poisson's ratio of ν=0.35 was assumed. However, it has been suggested that Poisson's ratio also exhibits a linear dependency on ice density and therefore leads to a depth-dependent profile (Smith, 1965). Furthermore, King and Jarvis (2007) and Schlegel et al. (2019) provide a depth-dependent Poisson's ratio profile based on seismic velocity measurements conducted on ice cores. To study the effect of this depth-dependent Poisson ratio, a linear elastic fracture mechanics study is performed. We assume an exponential distribution of Poisson's ratio with depth, similarly to the density and Young's modulus distributions.

$$\begin{array}{}\text{(E1)}& \mathit{\nu }\left(z\right)={\mathit{\nu }}_{\text{i}}-({\mathit{\nu }}_{\text{i}}-{\mathit{\nu }}_{\text{f}})e^{-(H-z)/D}\end{array}$$

In the above, ν_f=0.07 is the Poisson's ratio of firn in the upper surface, ν_i=0.35 is the Poisson's ratio of fully consolidated ice, and D=32.5 is the tuned constant. This profile approximates the observations from Schlegel et al. (2019), where we have scaled the length parameter D to match our density and Young's modulus profiles as this profile was obtained at a different location (with significantly different ice sheet and firn thickness). As it is not possible to derive a fully analytic expression for the stress profiles with this depth-dependent Poisson's ratio, the longitudinal-stress profiles are obtained numerically using the finite-element method. The numerical stresses are then used to drive the propagation of the surface crevasse using LEFM.

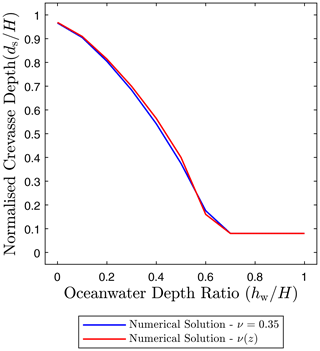
Figure E1 Normalized crevasse depth predictions versus ocean water height ratio for a single isolated dry crevasse in a linear elastic ice sheet considering homogeneous and depth-dependent Poisson ratios.

We consider a dry (air-filled) crevasse, with different values of ocean water height h_w, and plot the normalized crevasse penetration depth versus ocean water height h_w in Fig. E1. This figure shows that including variations in Poisson's ratio has a negligible effect as compared to density and Young's modulus variations. The largest percentage difference in crevasse depth was observed for intermediate ocean water levels, with an increase of 6 % in crevasse depth with respect to the homogeneous case when considering a depth-dependent Poisson's ratio for an ocean water height of h_w=0.5H. The effect of including a depth-dependent Poisson's ratio is less influential compared to density and Young's modulus as depth-dependent density resulted in a reduction of 20 % in the crevasse depth, and the depth-dependent Young's modulus resulted in a reduction of 45 % in the crevasse depth. This study suggests that the inclusion of variations in Poisson ratio does not play a significant role in crevasse propagation.