the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Contribution of blowing-snow sublimation to the surface mass balance of Antarctica
Srinidhi Gadde
Willem Jan van de Berg
Blowing-snow sublimation is a key boundary layer process in polar regions and is the major ablation term in the surface mass balance (SMB) of the Antarctic ice sheet. This study updates the blowing-snow model in the Regional Atmospheric Climate Model (RACMO), version 2.3p3, incorporating blowing-snow sublimation into the prognostic equations for temperature and water vapour. These updates address numerical artefacts in the previous model version by replacing the uniformly discretised ice particle radius distribution, which limited the maximum ice particle radius to ≤ 50 µm, with a non-uniform distribution covering radii from 2 to 300 µm without additional computational overhead. The improved model is validated against meteorological observations from site D47 in Adélie Land, East Antarctica. The updates fix the numerical artefacts, successfully predicting the power-law variation in the blowing-snow flux with wind speed while improving the prediction of its magnitude. Additionally, a qualitative comparison with CALIPSO (Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation) satellite data shows that RACMO accurately forecasts the spatial pattern of monthly blowing-snow frequencies. The model also yields an average blowing-snow layer depth of 230±116 m at D47, matching typical satellite observation values. Results reveal that, without blowing snow, sublimation in Antarctica mainly occurs in summer (October–March), with minimal surface sublimation in winter (April–September). Introducing the blowing-snow model creates an additional sublimation mechanism primarily contributing in winter. From 2000–2012, model-integrated blowing-snow sublimation averaged 175±7 Gt yr−1, a 52 % increase from the previous version. Total sublimation, summing blowing-snow and surface sublimation, reached 234±10 Gt yr−1, 47 % higher than in simulations without the blowing-snow model. This increase leads to a 1.2 % reduction in the Antarctic ice sheet's integrated SMB. Additionally, changes in sublimation in coastal and lower escarpment zones underscore the importance of the model updates for Antarctic climatology.
- Article
(9671 KB) - Full-text XML
- BibTeX
- EndNote
In the coastal regions of Antarctica, strong katabatic winds lift loose snow off the ground, causing drifting snow (e.g. Kodama et al., 1985). When this snow rises further and is suspended in the atmospheric boundary layer, it is called blowing snow. This wind-driven transport can be categorised as drifting (<1.8 m a.g.l.) and blowing (>1.8 m a.g.l.) snow (Serreze and Barry, 2005, p. 54). It redistributes the snow on the surface of an ice sheet and can also give rise to black-ice areas, affecting the local surface energy balance (SEB) (van den Broeke and Bintanja, 1995). Furthermore, it is well known that the suspended snow particles are more prone to sublimation than surface snow (Schmidt, 1972; Bintanja, 2001). Therefore, drifting- and blowing-snow transport and sublimation are important factors contributing to Antarctica's surface mass balance (SMB), particularly in coastal regions (Bintanja, 1998). For brevity, from hereon, both drifting and blowing snow are combined and referred to as blowing snow.
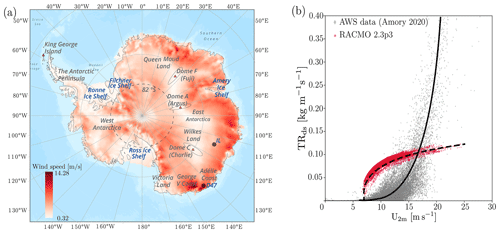
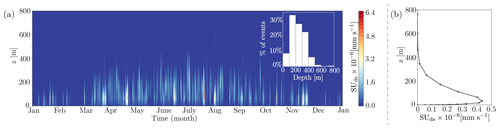
Figure 1(a) Yearly average (2000–2012) 10 m wind speed (m s−1). Location of observational site D47 in Adélie Land, East Antarctica. IL represents an interior location (71.1° S, 111.7° E), and dashed lines represent the latitude of 82° S, north of which CALIPSO (Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation) satellite data are available. (b) Variation in near-surface blowing-snow flux TRds () vs. 2 m wind speed U2 m (m s−1). Solid and dashed lines represent the variation in observed and simulated (RACMO2.3p3) near-surface snowdrift fluxes, respectively.
Blowing snow is a significant contributor to the (local) SMB of the polar regions and plays a crucial role in the climate system of Antarctica. While there have been automatic weather station (AWS) observations of blowing-snow-related processes from Antarctica (van den Broeke et al., 2004; Thiery et al., 2012; Barral et al., 2014; Amory, 2020), continent-wide estimates of blowing snow are difficult to obtain from such observations. Though continent-wide estimates derived from satellite-based products are available (Palm et al., 2017), they are restricted to optically thin cloud conditions and snow suspended in upper layers of the boundary layer (>30 m a.g.l.) (Palm et al., 2011) and therefore are not suitable for estimates of near-surface blowing snow and its contribution to SMB. Hence, the continent-wide estimates can only be obtained by parameterising blowing-snow processes and embedding these parameterisations in regional climate models (RCMs) (Bintanja, 1998; Déry and Yau, 2001; Lenaerts and van den Broeke, 2012; Amory et al., 2021; Toumelin et al., 2021). However, the representation of blowing snow in RCMs is challenging due to the complex and dynamic nature of the phenomenon involving multiple feedbacks with related processes such as snow precipitation and surface sublimation.
Including a blowing-snow model in RCMs has been found to improve the SMB estimates in the regions where katabatic winds form (Mottram et al., 2021). Specifically, without modelling blowing-snow processes, it is difficult to capture the spatial gradients in the sublimation of snow accurately (Agosta et al., 2019), which is particularly important in the escarpment regions of Antarctica. To improve our understanding of the Antarctic climate, it is crucial to accurately model the occurrence and impacts of blowing snow in RCMs. However, due to the coupled nature of blowing snow and the high sensitivity of the model to parameters, it is difficult to obtain a perfect agreement between observed and RCM estimates of blowing-snow flux (Lenaerts et al., 2014; van Wessem et al., 2018; Amory et al., 2015, 2021).
The polar version of the Regional Atmospheric Climate Model (RACMO) (van Wessem et al., 2018; van Dalum et al., 2022) is coupled with a blowing-snow scheme based on the PIEKTUK model (Déry and Yau, 2001; Lenaerts et al., 2012) to represent snow transport in polar regions.
Evaluation of RACMO against snow particle counter (SPC) observations from Greenland showed that RACMO2.3p1 (hereafter Rp1) overestimated the snow particle transport (Lenaerts et al., 2014). Therefore, in RACMO2.3p2 (hereafter Rp2) (van Wessem et al., 2018), the linear saltation coefficient was subsequently halved to match the SPC observations from Greenland.
Recently, we evaluated blowing-snow fluxes from RACMO2.3p3 (hereafter Rp3) against the SPC observational data at site D47 (location: 67.4° S, 138.7° E), Adélie Land, East Antarctica (Amory, 2020). Figure 1a shows the yearly (2000–2012) average 10 m wind speed obtained by Rp3 and the location of observation site D47. Since the coastal regions of Antarctica witness very high wind speeds (Fig. 1a) and the concentration of blowing-snow particles increases with the wind speed (Radok, 1977; Budd, 1966; Amory, 2020), the blowing-snow transport (TRds; ) is expected to increase in a power-law fashion with velocity. However, Fig. 1b shows that TRds from Rp3 does not show a rapid increase with velocity as expected. Evaluation of Rp3 blowing-snow flux with observations also revealed that it consistently underestimates the magnitude of the observed flux. The evaluation shows the need to improve the blowing-snow model in Rp3 and systematic comparison of blowing-snow fluxes against observations to obtain reliable estimates of Antarctic SMB.
In this study, several updates to the blowing-snow scheme in Rp3 are presented. The updates aim to improve the coupling of the blowing-snow processes with Rp3 atmospheric physics. Next, near-surface blowing-snow fluxes obtained from Rp3 are compared against the observed fluxes from site D47, Adélie Land, East Antarctica (Amory, 2020). The observations from site D47 are particularly suitable for evaluations since the region experiences frequent blowing snow, and the observations employ second-generation FlowCapt™ sensors, which have been found to predict the blowing-snow fluxes with reasonable accuracy (Amory, 2020). The details of RACMO and the modifications to the blowing-snow scheme in Rp3 are presented in Sect. 2, and details of the observational site and available data are presented in Sect. 3. Blowing-snow frequency and fluxes from the updated RACMO are evaluated against the observations in Sect. 4, followed by a comparison of results against version Rp3. Furthermore, we discuss the impact of the snowdrift updates on the continent-wide estimates of SMB for Antarctica by comparing the modelled SMB for 2000–2012 with a no-blowing-snow case and model results from CRYOWRF (Gerber et al., 2023), followed by conclusions in Sect. 5.
2.1 Regional Atmospheric Climate Model (RACMO)
RACMO is built on the semi-implicit semi-Lagrangian dynamics kernel of the numerical weather prediction model HIRLAM (High Resolution Limited Area Model; Undén et al., 2002), version 5.0.3, with the European Centre for Medium-Range Weather Forecasts (ECMWF) physics package, including both surface and atmospheric processes, from cycle 33r1 (ECMWF, 2009). The model assumes hydrostatic equilibrium, and the operational polar version, Rp2, has been verified to produce realistic results at the resolutions used in this study (van Wessem et al., 2015, 2016). This polar (p) version of RACMO2 includes a multilayer snow model that calculates the snow albedo evolution, melt, refreezing, percolation, and run-off of meltwater (Greuell and Konzelmann, 1994; Ettema et al., 2010; Kuipers Munneke et al., 2011). It also includes a blowing-snow scheme based on the PIEKTUK model (Déry and Yau, 1999; Lenaerts et al., 2012).
In the newer version, Rp3, the snow and ice albedo parameterisations were updated using the Two-streAm Radiative TransfEr in Snow (TARTES) model (Libois et al., 2013) coupled with the Spectral-to-NarrOWBand ALbedo (SNOWBAL) module, version 1.2 (van Dalum et al., 2019). Rp3 has produced results that compare well with both in situ and remote sensing observations of SMB from Antarctica (van Dalum et al., 2022). Rp2 and Rp3 are introduced in detail in Noël et al. (2018) and van Dalum et al. (2019), respectively. At the lateral boundaries, the simulations presented here are forced with ECMWF ERA5 reanalysis data (Hersbach et al., 2020) with an update interval of 3 h.
2.2 Blowing-snow model
In Rp3, we use the bulk (non-spectral) version of the PIEKTUK model (Déry and Yau, 1999), which employs an evolution equation for the mixing ratio of blowing snow qb (kg kg−1) and an additional equation for the evolution of snow particle number concentration N, which is the double-moment version of the model (hereafter PIEKTUK-D; Déry and Yau, 2001). Here, we introduce only the essential features of the PIEKTUK model, and additional details can be found in Déry and Yau (2001). PIEKTUK is an Inuktitut word for blowing snow (Déry et al., 1998).
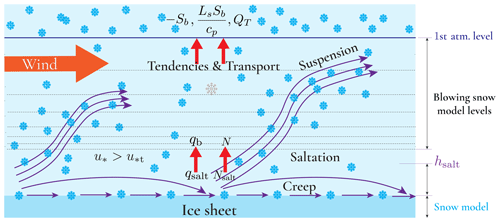
Figure 2Schematic showing the blowing-snow model levels, Rp3 model levels, and key processes involving blowing snow. QT represents the snow transport due to blowing snow. The figure shows that the model level of blowing snow is above the saltation height. In the schematic, qb (mixing ratio) and N (number concentration) represent the boundary conditions for the blowing-snow model calculated from qsalt and Nsalt using the classical equation for suspended particle concentration.
Figure 2 shows the blowing-snow processes and the coupling between PIEKTUK-D and Rp3, presenting the important snow transport mechanisms over an ice sheet. When the friction velocity, a measure of the wind shear at the surface, exceeds the threshold friction velocity, the snow particles perform a downwind motion of a series of jumps or skips, a process called saltation. When the saltating snow particles get suspended in the boundary layer due to turbulent mixing, they form the blowing snow. In PIEKTUK-D, this transition from saltation to suspension, governed by different physical mechanisms, is assumed to happen at elevation hsalt.
To calculate the sublimation and transport of blowing snow, the evolution equation for the blowing-snow mixing ratio qb (kg kg−1) is written as
where t (s) denotes time, z (m) is the vertical coordinate, vb (m s−1) is the bulk terminal velocity, Kb (m2 s−1) represents turbulent eddy diffusivity for blowing snow, and Sb () is the bulk sublimation rate. The lowest blowing-snow model level is set to 0.1 m, at the top of the saltation layer at height hsalt. The boundary condition for solving Eq. (1) is given by relating the blowing-snow mixing ratio qb at the lowest model level with the mixing ratio at the top of the saltation layer qsalt (kg kg−1). There exist several empirical formulations for erosion of the snow particles in the saltation layer. In Rp1, saltation flux was parameterised using (Déry and Yau, 1999)
in which csalt is a constant, initially set to 0.385 and retuned to 0.192 in Rp2 and Rp3, respectively. Furthermore, uthr represents the threshold wind velocity (m s−1), and Ufml represents wind speed at the first model level (m s−1). The threshold wind velocity is defined by with T2 m in degrees Celsius (°C) (Déry and Yau, 1999).
In Rp3, we update the saltation parameterisation (Pomeroy, 1989):
where the saltation efficiency esalt is set to , u* (m s−1) is the friction velocity, represents the thickness of the saltation layer (m) according to the relation of Pomeroy and Male (1992), g=9.81 is the gravitational acceleration (m s−2), and u*t represents the threshold friction velocity (m s−1).
The parameterisation of the threshold friction velocity in Eq. (3) is given by Gallée et al. (2001):
where is the snow porosity and , with ρs as the actual mean snow density of the upper 5 cm and ρi as the density of ice. n0 is the porosity of fresh snow with ρ0=300 kg m−3. The reference threshold friction velocity u*t0 is calculated based on the potential for snow erosion by the wind. u*t0 is characterised by a snow mobility index of , where the variables d and s represent the snow grain dendricity and sphericity, respectively. However, dendricity and sphericity are not modelled in RACMO. Therefore, we take , hence setting Mo to 0.625. The threshold friction velocity based on Gallée et al. (2001) depends on the snow mobility index, which denotes the potential for snow erosion by the wind. Gallée et al. (2001) mention that the crystal shape of freshly fallen snow does not allow for large grain cohesion in the snowpack. Therefore, this allows for relatively high snow mobility index Mo values for large d values. Sintering is enhanced when the number of rounded shapes increases so that Mo decreases when s decreases. Explicitly modelling the snow mobility index requires solving prognostic equations for snow particle characteristics. Without sophisticated models for snow particle characteristics, the snow mobility index was set to 0.625 (d=0.5 and s=0.5) to match blowing-snow frequency observations. A detailed discussion is available in Lenaerts et al. (2012). A parametric study of the snow particle characteristics is out of the scope of the present study.
Finally, u*t0 is defined by Gallée et al. (2001) as
where represents the drag coefficient of momentum.
The governing equation for the evolution of the concentration of particles (N) is
Here, KN (m2 s−2) is the eddy diffusivity for N and SN (m3 s−1) denotes the rate of change in particle numbers due to the sublimation process. The lower boundary condition for solving Eq. (6) here is also the particle concentration at the top of the saltation layer (Nsalt) (Déry and Yau, 1999), which will be defined below.
In PIEKTUK-D, the bulk blowing-snow mixing ratio qb is related to N via the spectral number density F(r), following Schmidt (1982):
where the distribution of F(r) follows a two-parameter gamma distribution (Budd, 1966; Schmidt, 1982) with the relation
where r represents the radius of ice particles and α (dimensionless) and β (m) are the shape and scale parameters of the gamma distribution Γ. Substituting Eq. (8) for Eq. (7), we obtain the particle number concentration Nsalt at the saltation layer:
with α=4.0, (μm), and density of ice ρice=917 kg m−3. Equation (7) is discretised with the hypothesis that ice particle size follows a two-parameter gamma distribution, with particle size bins covering particles with a radius of 2 to 300 µm (Déry et al., 1998).
Finally, in the blowing-snow model, the mass change in an ice particle due to the blowing-snow sublimation is given by the model of Thorpe and Mason (1966):
where σ (dimensionless and negative) is the water vapour deficit with respect to ice , where e and ei are the vapour pressure and its value at saturation over ice; Ta is the ambient air temperature (K); K is the thermal conductivity of air (); Ls is the latent heat of sublimation (); Rv is the gas constant for water vapour; D is the molecular diffusivity of water vapour in air (m2 s−1); Qr is the net radiation transferred to the ice particle (W); and NNu and NSh are the Nusselt and Sherwood numbers.
2.3 Major changes to the blowing-snow model in RACMO
Six major updates in the implementation of PIEKTUK-D in Rp3 are summarised below.
-
In Rp3, uniformly discretised 12-particle size bins were used, with a constant particle bin size Δr=4 µm. Therefore, size bins with a mean particle radius greater than 50 µm were excluded, which caused the unexpected variation in TRds observed in Fig. 1b. To solve the issue, we use a grid-stretching technique similar to direct numerical simulations (DNSs) of channel flows to obtain non-uniform distribution with smooth stretching following a tangent hyperbolic function (Vinokur, 1983). We now use 16-particle size bins with varying Δr values to include all relevant particle size classes with particles with a mean radius for each bin from 2 to 300 µm while keeping the computational overhead the same as before. Déry et al. (1998) report convincing results by including particles with a mean radius for each bin from 2 to 254 µm.
-
Previously, in the blowing-snow model of Rp3, 32 vertical levels equidistant on a logarithmic scale were used. The blowing-snow model was not fully coupled to the boundary layer model as the blowing-snow grid levels did not match the model atmospheric levels. Specifically, instead of the actual velocity profiles, temperature and velocity profiles were reconstructed using logarithmic relations from the first model atmospheric level. In addition, the friction velocity (u*) was recalculated in the blowing-snow model, assuming near-neutral conditions. These inconsistencies have now been resolved, and actual velocity and temperature profiles and friction velocities from the boundary layer model are used, which constitutes another major improvement. We have reduced the vertical levels to 16 to reduce computational expenses, with 8 logarithmically varying levels up to the lowest model level (dashed lines in Fig. 2). Furthermore, above the lowest atmospheric level, the PIEKTUK-D model levels coincide with the model atmospheric levels, and this facilitates easier coupling of blowing-snow sublimation as tendencies in the prognostic equations.
-
We found that PIEKTUK-D, when coupled to Rp3, is highly sensitive to the model time step. In PIEKTUK-D, the integrated blowing-snow flux quickly reaches equilibrium, and it depends on the time step used to solve the evolution equations. While Déry and Yau (1999) specify a model time step of 2 s for PIEKTUK-D, in Rp3, the model time step was of the order of 300–600 s. This time step was too large to predict the drift fluxes reliably. To overcome this, we introduce sub-stepping in the blowing-snow model. We ran the model with different Δt values and different time step sizes. We found a large difference between the values of integrated blowing-snow flux for Δt=600, 300, 100, 50, 20, 10, and 5 s. For Δt=10 and Δt=5, the magnitude of blowing-snow flux was nearly the same, so we choose Δt=10 s. Furthermore, the model quickly reaches a steady state in five sub-steps. Therefore, we use five sub-steps with a time step of 10 s, and the fluxes from the last sub-step are taken as the representative flux for the full Rp3 model step.
-
In the original PIEKTUK model implementation by Déry and Yau (1999), the blowing-snow mixing ratios are reset to zero only if the friction velocity is lower than the threshold friction velocity in two consecutive time steps, providing a realistic initial approximation of blowing-snow quantities in each time step. However, previously in Rp3, N and qb were reset to zero after every model time step, though in reality, the blowing-snow events last for hours. Resetting the flux to zero is unrealistic and calls for a proper initialisation of the variables. Therefore, we now initialise N and qb from the previous time step if two consecutive time steps satisfy the condition ; otherwise, the values are reset to zero, indicating the end of the blowing-snow event.
-
In Rp3, the bulk sublimation rate Sb was used to calculate an integrated blowing-snow sublimation flux, and this integrated moisture flux was added to the surface. While this approach works reasonably in obtaining SMB estimates, it is not realistic since it limits the effect of blowing-snow sublimation to the surface. To rectify this error in representation, we now add the blowing-snow sublimation rate (−Sb) and latent heat due to blowing snow (), where cp is the specific heat capacity of air, as tendencies for the prognostic equations of atmospheric water vapour and temperature, respectively.
-
In Rp3, snowdrift was modelled if and Eq. (2) was used to estimate the saltation flux. This parameterisation caused sharp variations in the saltation flux in Rp3 and was not optimal. Therefore, the saltation flux is now derived with Eq. (3), which produces smooth variations in qsalt. Furthermore, Eq. (3) is also used in the MAR model to parameterise saltation flux (Amory et al., 2021). Finally, the formula to derive the vapour saturation pressure to ice (ei) in Eq. (10) has been updated to the AERKi formula (Alduchov and Eskridge, 1996; CY45R1–Part IV, 2018), as this formula is used in Integrated Forecasting System (IFS) code in which the blowing-snow module is embedded.
3.1 In situ snowdrift observations
The in situ observations used for evaluation are presented and discussed in detail by Amory (2020) and Amory et al. (2020a); here, we summarise the key information. The observational site D47 (location: 67.4° S, 138.7° E; Fig. 1a) is located at an elevation of 1560 m and at a distance of 105 km from the shore. Due to its topographical situation, the site experiences strong katabatic winds with a strong directional consistency (Amory, 2020). Due to the high surface winds, the site experiences frequent blowing-snow events and is ideally suited for evaluating RACMO results. For evaluation, observations of near-surface quantities such as 2 m wind speed, temperature, and air relative humidity are used, complemented with half-hourly drifting-snow transport fluxes. These observations are available for 2010–2012 with half-hourly temporal resolution. The drifting-snow transport fluxes are measured with second-generation FlowCapt™ sensors. The sensors convert the acoustic vibration caused by blowing-snow particles into integrated snow mass flux. The equipment consists of two 1 m length acoustic tubes, superimposed vertically to measure snow flux in the first 2 m above the ground.
The blowing-snow scheme in Rp3 has multiple levels, with the lowest vertical level set at 0.1 m. For comparison with observations, we obtain an average vertically integrated blowing-snow flux QT,RACMO () from the lowest model level up to 2 m height. Following Amory et al. (2021), since there are two acoustic tubes for measurement, we combine snow mass flux from both the tubes into an average near-surface mass flux QT,OBS ():
where QT,1 is the observed snow mass flux integrated over the exposed length of hi of the corresponding second-generation FlowCapt™ sensor. The height of the sensor at D47 is 2.8 m. However, Amory (2020) mentions that, due to harsh weather conditions at D47, it was difficult to reset the height of the sensors owing to the elevation changes due to snow. As a result, by late December 2012, the measurement heights decreased from their initial values to 1.5 m for wind speed and direction and 0.9 m for temperature and relative humidity. Therefore, we compare the instantaneous fluxes for the year 2011. The data are made available on Zenodo as quantities at 2 m height (Amory et al., 2020b). Since the first atmospheric level in RACMO (approximately 8–10 m) is above this height, we obtain the 2 m wind speed using the Monin–Obukhov similarity theory.
3.2 Satellite data for evaluating monthly blowing-snow frequency
We compare model results with lidar data from CALIPSO (Cloud-Aerosol Lidar and Infrared Pathfinder Satellite Observation; Palm et al., 2017), which measures blowing-snow quantities for the Antarctic ice sheet north of 82° S (Palm et al., 2017, 2018). These satellite observations include only those blowing-snow layers deeper than 30 m and only those events without clouds. Making an accurate one-to-one comparison of the model results with the satellite observations requires filtering of the model results to layers deeper than 30 m and for cases with no or optically thin cloud conditions, of which the former is not possible with the data exported from the current RACMO simulations. Therefore, we use the satellite observations to look at the seasonal patterns and only qualitatively compare the model results.
Three Rp3 simulations for 2000–2012, forced by ERA5 reanalysis data, were run for the evaluation presented here. The first one, from hereon referred to as RpNew, employed all updates listed in Sect. 2.3. A second simulation was carried out with the blowing-snow scheme switched off, from hereon referred to as the NO-DRIFT simulation, to study the effects of blowing snow compared to the no-blowing-snow scenario. Finally, a simulation with the original blowing-snow code of Rp3 has been carried out to compare the change in SMB estimates and related quantities.
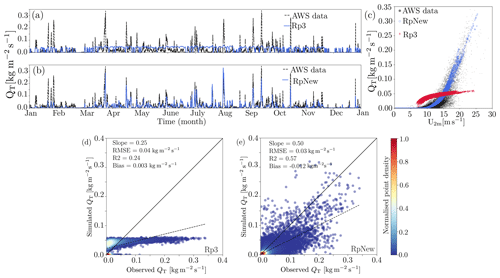
Figure 3Comparison of simulated instantaneous near-surface blowing-snow flux QT () with observations for the year 2011: (a) Rp3, (b) RpNew, and (c) variation in near-surface blowing-snow flux QT with 2 m wind speed U2 m (m s−1). Open circular, filled red diamond, and filled circular markers represent data from RpNew, Rp3, and AWS data, respectively. Observed and simulated blowing-snow fluxes (): (d) Rp3 and (e) RpNew. Solid lines represent the 1:1 line, and the dashed lines represent the best-fit line. The colours represent the normalised point density from low (0.0, black) to high (1.0, red).
4.1 Model evaluation with observations at site D47
4.1.1 Blowing-snow flux and near-surface relative humidity
Figure 3a presents the instantaneous blowing-snow mass flux obtained from Rp3 compared with the observations for the year 2011. As can be seen in the figure Rp3 fails to predict the peaks of blowing-snow magnitude when compared with observations and as such does not reliably predict the magnitude of the blowing snow. In Rp3, the linear saltation coefficient csalt (Eq. 2) was reduced (van Wessem et al., 2018), which resulted in the low, limited snow transport flux seen in Fig. 3a. As halving csalt roughly led to halving the snowdrift flux, the RACMO versions preceding version 2.3p2, with doubled csalt, overestimated QT for most of the time (not shown).
Figure 3b presents the instantaneous blowing-snow mass flux obtained with RpNew. We observe that RpNew works well in predicting the magnitude of the blowing-snow flux. Specifically, the magnitude of the blowing-snow flux matches the observations reasonably well in the Antarctic winter (April–September). However, it is underestimated in the Antarctic summer (October–March). The underestimation might be related to the amount of loose snow available at the surface, possibly due to inaccuracies of the modelled surface snow compaction in summer or the direct interaction between precipitation and snowdrift, which Rp3 does not resolve. As we found no clear cause for the underestimation of snowdrift during summer, further study is necessary to uncover the seasonal differences in the blowing-snow flux.
Figure 3c presents the variation in blowing-snow mass flux with the near-surface wind speed. Flux from Rp3 fails to produce power-law variation with the wind speed; however, RpNew successfully predicts it. The primary reason for this improvement is the non-uniform ice particle radius distribution, allowing us to include all relevant ice particles in the range between 2 and 300 µm. Coupled with the better coupling with RACMO prognostic variables and sub-stepping, the behaviour of the flux follows the expected power-law variation seen in Fig. 3c.
In Fig. 3d and e, we present the comparison of simulated near-surface blowing-snow mass flux with observed flux for Rp3 and RpNew, respectively. Simulated flux from Rp3 has a positive bias, with a very low R2 (p value <0.01), indicating that Rp3 fails to capture the variability in the blowing-snow flux observations. The predictions with Rp3 also have a higher RMSE of 0.035 . Also, it is apparent from Fig. 3d that Rp3 fails to predict the blowing-snow fluxes reliably when compared with the observations. In contrast, with RpNew, we have a reasonable agreement between the observed and simulated fluxes (Fig. 3e) with R2=0.56 (p value <0.01). The agreement indicates that the changes introduced significantly improve its ability to predict the blowing-snow fluxes. Though the predictions are considerably improved compared to the observations, both Rp3 and RpNew underestimate the blowing-snow fluxes. The underestimation is mostly due to the underestimation of velocities reported in Table A1 and the model sensitivity to the chosen parameters. Since the snow transport flux varies in a power-law fashion with the wind speed (Radok, 1977; Budd, 1966; Amory, 2020), the flux is highly sensitive to the wind-speed predictions; even a slight underestimation in the velocity introduces a significant difference in the blowing-snow mass flux.
Though RpNew results show the desired behaviour, it fails to capture the spread in the observational data (Fig. 3c). Through sensitivity analysis of the data, we found that the spread in the data depends on the modelling choices made, e.g. the parameter α in two-parameter gamma distribution (Eq. 8) and the threshold friction velocity. Budd (1966) and Schmidt (1982) report that the distribution of ice particle diameters follows a two-parameter gamma function that varies with height from the ground, with the α value varying between 2 and 14. However, for simplified implementation, following Déry and Yau (2002), we used a constant α=4, which does not vary with height; this influences the modelled snow mass flux at different heights. Furthermore, the use of constant snow grain properties in the calculation of the snow mobility index used in the calculation of the threshold friction velocity (Eq. 4) can influence the spread in the data. Irrespective of these simplifications, RpNew reasonably accurately predicts the blowing-snow fluxes.
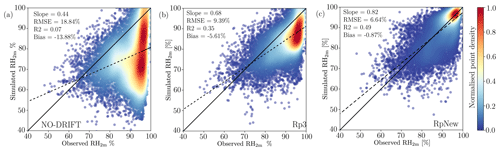
Figure 4Density scatter plots of observed and simulated near-surface relative humidity with respect to ice at site D47, for the (a) NO-DRIFT, (b) Rp3, and (c) RpNew cases. Solid lines represent the 1:1 line, and the dashed lines represent the best-fit line. The colours represent the normalised point density from low (0.0, black) to high (1.0, red).
Improving the blowing-snow prediction is expected to improve the near-surface humidity predictions. Figure 4a, b, and c present a comparison of observed relative humidity with respect to ice against the simulated relative humidity for the three experiments. Figure 4a shows that the NO-DRIFT case shows a negative bias in the moisture, with low R2 of 0.07 (p value <0.01) and a high error indicated by an RMSE of 18.84 %. With Rp3, the results are slightly improved with a lower negative bias and a higher R2 of 0.35 (p value <0.01). However, Fig. 4c shows that, with RpNew, the modelled results show an improved correlation with the observations (R2=0.49, p value <0.01). Though the data have a large spread, the RMSE is 6.6 %, and the figure shows an improved match between the observed and simulated data. It is evident from Fig. 4a, b, and c that the updates improve the moisture prediction when compared with the observations.
4.1.2 Blowing-snow events at site D47
To quantify the ability to model the blowing-snow events, we follow Amory et al. (2017, 2021) and classify blowing-snow events as the occurrences when the blowing-snow mass flux is greater than 10−3 . Subsequently, we create confusion matrices comparing the blowing-snow events from observed and simulated data. The diagonal entries in the confusion matrix represent the events correctly predicted by the simulations, and the off-diagonal entries represent the remaining events.
Table 1a represents the confusion matrix, presenting the percentage of blowing-snow events observed and simulated by RpNew and Rp3, respectively. In Table 1a, we see that out of the total observations, 80 % are observed blowing-snow events, and RpNew manages to predict 54 % of these events. In contrast, Rp3 predicts 63 % of the total blowing-snow events. We calculate the blowing-snow frequency as the ratio of correctly simulated blowing-snow events and the total number of observed blowing-snow events. For RpNew, we obtain a blowing-snow frequency of 0.68, and Rp3 has a blowing-snow frequency of 0.79. Rp3 performs comparatively better in predicting the blowing-snow events as the threshold friction velocity calculated in Rp3 is lower than RpNew. As mentioned previously, in Rp3, u* was recalculated in every step with a simple logarithmic-law assumption, which reduced the threshold friction velocity used in the model to trigger a blowing-snow event. Since the assumption was not correct, we changed it and used the friction velocity calculated from the physics module. With RpNew, the model's friction velocity is consistently higher than Rp3 (not shown here). This can be tuned in future versions to match the observations better. Furthermore, we do not observe any seasonality in the underestimation of blowing-snow events; we observe only marginal differences in the blowing-snow frequency of RpNew over Antarctica summer (October–March) and winter (April–September) months. Clearly, Rp3 does a better job at identifying the blowing-snow events; however Fig. 3a shows that it does not capture any peaks in the blowing-snow fluxes.
To evaluate the performance of RpNew in identifying the higher-magnitude blowing-snow fluxes, we create another confusion matrix where we compare the blowing-snow events with blowing-snow mass flux QT>0.05 . Table 1b presents a comparison of the observed and simulated blowing-snow fluxes for events with QT>0.05 . The tables show that 14 % of the observed events account for events with high blowing-snow mass flux. While RpNew captures 5 % out of the 14 % of high blowing-snow flux events, Rp3 does not capture any of these events. Therefore, RpNew shows a marked improvement in predicting blowing-snow peaks compared to Rp3. However, RpNew still underestimates the number of strong blowing-snow events, which is closely related to the underestimation of the wind speed (Table A1) in RpNew and Rp3. The results show that RpNew provides reasonable estimates of low- and high-magnitude blowing-snow events, while future improvements are needed.
Table 1Confusion matrix presenting the comparison between observed (OBS) and simulated (SIM) blowing-snow events: (a) all snowdrift events and (b) strong snowdrift events. In (a), the DRIFT case represents the events where and the NO-DRIFT case represents the remaining events. In the tables below, the first number in each cell represents events from RpNew and the second number represents those from Rp3.

4.1.3 Blowing-snow sublimation at site D47
Figure 5a shows the modelled instantaneous profiles of the blowing-snow sublimation rate for 2011 at site D47. In the Antarctic winter (April–September), deep blowing-snow layers are modelled, with a typical range of blowing-snow layer heights and snow sublimation between 100 and 500 m. A shallower blowing-snow layer is observed in Antarctic summer (October–March). The figure shows multiple events with continuous blowing-snow storms in winter, indicating a significant contribution of blowing snow to Antarctic sublimation. Although sublimation over a thick layer coincides with blowing-snow events (Fig. 3b), we do not see a direct relation between the near-surface snowdrift flux and the intensity or total magnitude of blowing-snow sublimation. This shows the necessity to explicitly couple the blowing-snow model to the atmospheric model layers, as the modelled temperatures, humidities, and wind speeds of the lowermost model level are unlikely to be representative of the whole boundary layer.
Figure 5b presents the yearly average blowing-snow sublimation rate profile for 2011 at site D47. The average blowing-snow layer depth is 230±116 m. As the air is saturated at the surface, the sublimation at the surface is negligible, with sublimation increasing away from the ground and maximum sublimation above. Déry and Yau (2002) and Toumelin et al. (2021) have reported a similar variation in blowing-snow sublimation. It is worth noting here that both the drifting-snow concentration and horizontally drifting-snow transport peak even close to the ground (not shown). As depicted in Fig. 5a, blowing-snow sublimation starts below the model's first atmospheric level (approximately 8–10 m). Previously in Rp3, this vertical profile of sublimation was not represented as blowing-snow sublimation was added to the surface.
Based on lidar data from CALIPSO observations, Palm et al. (2017) report for the Antarctic ice sheet north of 82° S an average snow layer depth of 120 m, with typical blowing-snow layers of 200 m all along the coastal katabatic wind regions (see Fig. 5 in Palm et al., 2018). For site D47, RpNew shows a similar mean layer depth of 230±116 m and a similar typical range (inset Fig. 5a). This analysis shows that RpNew satisfactorily reproduces all the necessary features of blowing-snow sublimation and can be used to obtain continent-wide estimates. However, it is worth mentioning that total blowing-snow sublimation is sensitive to horizontal resolution. At the 27 km resolution employed in the study, strong spatial gradients near the coast would not be accurately captured. Subsequently, the impact of blowing snow on sublimation and horizontal transport of mass can be underestimated.
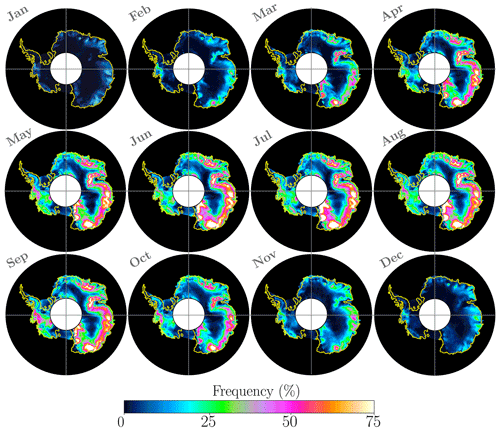
Figure 6Blowing-snow frequency visualised to provide a qualitative comparison with satellite measurements of Palm et al. (2018). The panels show average blowing-snow frequency over the decade 2001–2010 and use the same colour scale as Palm et al. (2018). A colour-blind-friendly version of this figure is given in Appendix B (Fig. B1).
4.2 Continental blowing-snow frequency
Figure 6 gives the monthly variation in the mean blowing-snow frequency from RpNew over Antarctica for the decade 2001–2010. Blowing-snow frequency is obtained by calculating all the blowing-snow events with the blowing-snow mixing ratio . The cutoff qb, the limits, and the colour map in Fig. 6 are chosen to facilitate a qualitative comparison with the satellite observations presented in Fig. 3 in Palm et al. (2018). We observe that the monthly blowing-snow frequency largely follows the seasonal trend in the surface wind patterns over Antarctica, with high-frequency blowing snow in winter compared to summer. Despite the differences between the two approaches, the simulated blowing-snow frequency is qualitatively similar to that obtained from the CALIPSO satellite observations (Palm et al., 2017, 2018). The results show a persistent blowing-snow hotspot in East Antarctica near Adélie Land, observed in satellite observations and our simulations. We can also infer that the satellite observations slightly underestimate the frequencies compared with the simulations due to the reasons mentioned in Sect. 3.2.
Our results are also qualitatively similar to the simulations with the CRYOWRF model carried out by Gerber et al. (2023), although the simulated periods are different. Specifically, Gerber et al. (2023) report a zone of the strongest blowing snow along the coast of East Antarctica with the highest values of blowing-snow frequency slightly inland. Zones with reduced blowing snow are found over the Amery Ice Shelf, toward western Queen Maud Land. RpNew shows similar qualitative trends. Most of the blowing-snow hotspots observed in our simulations also correspond to the “wind glaze” areas in East Antarctica reported by Scambos et al. (2012). Scarchilli et al. (2010) report blowing-snow frequencies of 80 % at the wind convergence zone of Terra Nova Bay (East Antarctica); we observe approximately 80 %–90 % blowing-snow frequency in the area during the Antarctic winter months.
4.3 Continent-wide estimates of blowing-snow climate over Antarctica
Figure 7 presents the updated continent-wide estimates of the blowing-snow climate of Antarctica by comparing the yearly average (2000–2012) quantities of RpNew and NO-DRIFT simulations. Similar to previous model results (Lenaerts and van den Broeke, 2012), we observe negligible blowing-snow sublimation (Fig. 7a) in the interior parts of Antarctica with maximum sublimation towards the coast. Model results show blowing-snow sublimation hotspots () in George V Land, Adélie Land, Wilkes Land, and Queen Mary Land in East Antarctica with non-zero sublimation all along the coast of Antarctica. RACMO shows negligible sublimation over Dome Fuji, Dome Argus, and Dome Charlie, which form the interior parts of East Antarctica, due to the lower wind speed and low temperatures in these regions (Fig. 1a). Similarly, we observe negligible sublimation over the Ronne and Ross ice shelves, which also experience low wind speeds. This shows that blowing-snow sublimation is mostly limited to the katabatic wind regions of Antarctica. Maximum blowing-snow sublimation of 335±30 mm w.e. yr−1 occurs in Adélie Land at the location of 66.9° S, 130.4° E. Palm et al. (2017), based on the CALIPSO lidar observations, report a maximum blowing-snow sublimation of 250±125 mm w.e. yr−1 near the coast between longitudes of 140 and 150° E. A slight shift in the location of the maximum blowing-snow sublimation between the satellite and model results can be related to the fact that CALIPSO observes moderate and strong events without thick cloud cover, while Fig. 7 displays all snowdrift events (see Sect. 3.2). Both spatial distribution and the magnitude of blowing-snow sublimation from RpNew match reasonably well with CALIPSO observations of Palm et al. (2017).
Figure 7b provides the difference between the 2 m temperature for the RpNew and NO-DRIFT cases. The figure shows that blowing-snow sublimation reduces the near-surface temperature. At blowing-snow sublimation hotspots, we observe a cooling of 0.1–0.3 K, with negligible change in the temperature over most of interior Antarctica. It is worth mentioning here that, with Rp3, we observed a slight warm bias compared to the NO-DRIFT case (not shown); this shows that the coupling was previously incorrect. The results have appreciably improved with RpNew. However, the overall effect of blowing-snow sublimation on the yearly average near-surface temperature in Antarctica seems marginal, similar to previous model results.
Higher sublimation due to blowing snow in RpNew leads to higher near-surface relative humidity (Fig. 7c) when compared to NO-DRIFT simulations. We observe higher relative humidity along the Antarctic coast with a maximum of 10 % in coastal George V Land and Adélie Land. This increase in relative humidity is higher than what was previously observed with Rp3. Similar to sublimation, blowing-snow transport TRds () (Fig. 7d) is negligible over interior Antarctica. We observe a strong blowing-snow transport near coastal George V Land with maximum transport of 9×106 . Along the rest of the Antarctic coast, blowing-snow transport is approximately 2×106–3×106 . Blowing-snow erosion ERds () (Fig. 7e), which is a contributor to Antarctic SMB, shows complex convergence and divergence patterns all along the Antarctic coast. Similar to Bromwich et al. (2004) and Lenaerts and van den Broeke (2012), we observe large blowing-snow divergence near escarpment areas with significant katabatic wind acceleration. Furthermore, areas with blowing-snow convergence are near blowing-snow divergence, which indicates that blowing snow is important for redistributing the precipitation in the coastal areas of Antarctica. However, the magnitude of ERds is not significant enough for a major contribution to SMB, as only the snow blown off Antarctica counts for the integrated SMB.
Total sublimation SUtotal (), the sum of blowing-snow and surface sublimation (SUds+SUs), follows the spatial distribution of blowing-snow sublimation. The maximum total sublimation of 396 is observed at the same location as the maximum blowing-snow sublimation, indicating the leading contribution of blowing-snow sublimation to total sublimation. Total sublimation is higher in the RpNew simulations when compared to NO-DRIFT simulations (Fig. 7f); in the regions near Adélie Land, the difference in total sublimation is as high as 200 .
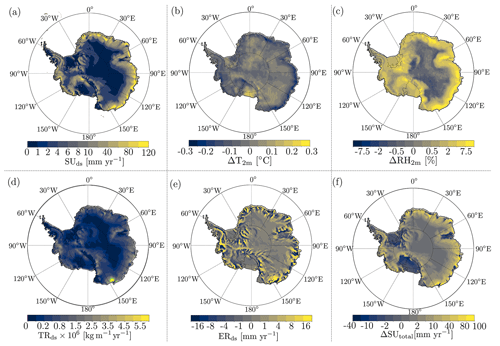
Figure 7Yearly mean (2000–2012) (a) blowing-snow sublimation SUds (mm w.e.); (b) difference in near-surface temperature ΔT2 m between the RpNew and NO-DRIFT simulations; (c) difference in relative humidity ΔRH2 m; (d) blowing-snow flux (); (e) erosion due to blowing snow ERds or the divergence due to blowing snow (); and (f) total sublimation SUtotal, including surface and blowing-snow sublimation ().
4.4 Seasonal variation in integrated sublimation
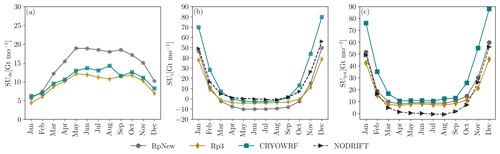
In Fig. 8 we present the different components of sublimation from the RpNew, NO-DRIFT, Rp3, and CRYOWRF cases (Gerber et al., 2023). The monthly contribution to the yearly average integrated blowing-snow sublimation (Fig. 8a) shows that lowing-snow sublimation in the Antarctic summer (October–March) is lower than in Antarctic winter (April–September) due to higher temperatures and summer snow densities, making it difficult for the snow to lift off from the ground. Blowing-snow sublimation SUds increases with the onset of winter and remains relatively constant over winter, with an approximate contribution of 15–20 Gt per month in winter. For RpNew blowing-snow sublimation contributes 108 Gt during winter out of the total sublimation of 175 Gt yr−1. This amounts to 62 % of the total blowing-snow sublimation. Constant blowing snow indicates that blowing-snow sublimation is a major contributor to total sublimation in winter. Due to the updates made in RpNew, the blowing-snow sublimation has nearly doubled throughout the winter compared to Rp3. CRYOWRF produces blowing-snow sublimation which is comparable in magnitude to Rp3. Surface sublimation SUs dominates the sublimation in summer due to higher temperatures (Fig. 8b) and reaches a relatively constant value in winter. We observe that surface sublimation in Antarctic summer with CRYOWRF is nearly 1.5 times the surface sublimation observed with RpNew, while winter sublimation is comparable. SUs is negligible in Antarctic winter, and it is nearly zero. Interestingly, with the introduction of blowing-snow sublimation in Rp3 and RpNew, we observed negative surface sublimation, indicating the deposition of water vapour onto the snow surface in winter. This deposition agrees with the measurements of King et al. (1996), who measured small, downward water vapour fluxes in the winter of 1991 at Halley Station, East Antarctica. A similar seasonal cycle in surface sublimation with negative surface sublimation in winter has been reported by King et al. (2001). While blowing-snow sublimation is increased in RpNew, negative surface sublimation also increases, balancing the net change in total sublimation. The deposition follows the same spatial and seasonal pattern as blowing-snow sublimation. Since the condensation is directly proportional to the difference between the vapour pressure of water at the surface and above the surface, with RpNew, which has better coupling with the atmosphere, there is more condensation in winter compared to Rp3. Specifically, condensation in winter is nearly doubled with RpNew compared to Rp3.
However, we do not see such negative surface sublimation with CRYOWRF.
Total sublimation SUtotal (Fig. 8c) follows a pattern similar to surface sublimation, with higher values during Antarctic summer and relatively constant values in winter. It is clear from the NO-DRIFT case that surface sublimation is negligible in Antarctic winter. The magnitude of total sublimation is comparable between RpNew and CRYOWRF in the Antarctic winter (March–September); the difference in sublimation between different models is mostly a summer phenomenon. CRYOWRF consistently produces higher summer sublimation values than RpNew. While the seasonal trends of sublimation remain unaltered between Rp3 and RpNew, interestingly, we observe that an increase in blowing-snow sublimation in RpNew in winter leads to an increase in deposition, leading to limited overall changes in total sublimation.
Table 2Total ice sheet, including ice shelves, integrated SMB mean 2000–2012 values (Gt yr−1) with interannual variability σ: total (snow and rain) precipitation (Ptot), total sublimation (SUtot), surface sublimation (SUs), blowing-snow sublimation (SUds), blowing-snow erosion (ERds), and run-off (RU). ERds only considers the transport aspect of blowing snow. ERds is positive in the case of erosion due to divergence of the blowing-snow flux and negative if convergence of the blowing-snow flux brings snow to a grid box. Furthermore, as ERds only considers the snow redistribution, the spatially integrated impact on the SMB is zero as long as drifting snow is not blown off the ice sheet. Integrated surface mass balance is given by . (a) Change between the RpNew and NO-DRIFT cases. Percentage change is calculated as (RpNew − NO-DRIFT) NO-DRIFT. (b) SMB difference between RpNew (2000–2012) with CRYOWRF (2010–2020) (Gerber et al., 2023).
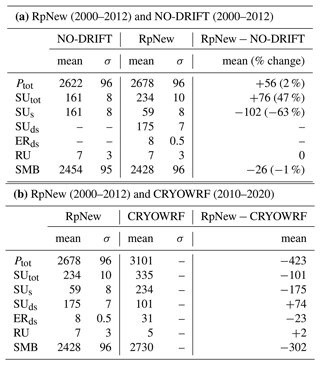
4.5 Changes in integrated SMB
Table 2a presents the SMB and its components integrated over the whole ice sheet (including ice shelves) for the years 2000–2012 (Gt yr−1) along with their interannual variability. Compared to the NO-DRIFT case, RpNew has an increased precipitation of 56 Gt yr−1 caused by the higher moisture content in the atmosphere due to blowing-snow sublimation. Total sublimation is increased by 76 Gt yr−1, with blowing-snow sublimation being the major contributor. There is a decrease in surface sublimation of 102 Gt yr−1, as blowing-snow sublimation is now the dominant mechanism of sublimation. With blowing-snow transport fluxes, we have a snow erosion increase of 8 Gt yr−1. Overall, the integrated SMB is reduced by 26 Gt yr−1, due to a net increase in blowing-snow sublimation. The change amounts to only a 1 % decrease in SMB compared to the NO-DRIFT case. Since the change in SMB with the updates is minor and the SMB results from RACMO have been previously evaluated against several in situ and remote sensing observations, we refer to Noël et al. (2018) and van Wessem et al. (2018) for the SMB evaluation. Though there is negligible change in the overall SMB, blowing-snow sublimation is very important to local SMB, especially in the escarpment areas in East Antarctica.
Table 2b compares the integrated quantities obtained from RpNew with the results from CRYOWRF from 2010–2020. While the period is different, the study of Gerber et al. (2023) is the only other one (other than RACMO studies) that reports SMB results of all of Antarctica with a blowing-snow model, making these results interesting to compare. Our experience with RACMO runs suggest that the total sublimation from Rp3 does not vary much between 2000–2020. Therefore, we do not expect a large difference in sublimation during this time period, and therefore, the results are comparable. Table 2b shows that there is a large difference in SMB (11 %) and precipitation (14 %) between RpNew and CRYOWRF. While precipitation and SMB are comparably higher in CRYOWRF, the ablation terms of CRYOWRF, especially sublimation, are more interesting. Specifically, CRYOWRF produces higher total sublimation (+101 Gt yr−1) when compared to RpNew. From monthly average sublimation (Fig. 8) we observed that CRYOWRF produces higher surface sublimation in Antarctic summer (October–March), when compared to winter.
In this study, we updated the blowing-snow model in the regional climate model RACMO, version 2.3p3 (Rp3), to better represent the blowing-snow phenomenon, the major ablation term in the SMB of the Antarctic ice sheet. As observed in the limited number of available observations, the unaltered version of the Rp3 model failed to accurately predict the power-law variation in blowing-snow mass flux with wind speed. Furthermore, choices made in the unaltered version to reduce the blowing-snow model's computational expenses led to simplifications and assumptions that affected the model results. In the present work, we updated the empirical formulation of saltation flux used as the boundary condition for the blowing-snow model. We increased the number and distribution of ice-particle radius classes to cover all the relevant blowing-snow radius classes. We also improved the coupling of the blowing-snow model with RACMO by providing velocity, temperature profiles, and friction velocities from RACMO to the blowing-snow model, which was previously modelled as logarithmic-law velocity, with the friction velocity being based on the velocities of the first model level. In addition, we found that the blowing-snow model was very sensitive to its time step and introduced sub-stepping for the blowing-snow model, which significantly improved the results.
We ran the original blowing-snow model (Rp3) and the updated code (RpNew) for Antarctica on a 27 km grid laterally forced by 3-hourly ERA5 data. We performed three experiments for 2000–2012: the NO-DRIFT, RpNew, and Rp3 experiments. In the NO-DRIFT experiment, RACMO was run without the blowing-snow model. The results from the updated model were evaluated against in situ observations from site D47, Adélie Land, Antarctica (Amory, 2020). Important surface quantities such as the near-surface wind, temperature, humidity, and blowing-snow fluxes were compared. We found that RpNew results compared well against the blowing-snow observations, successfully predicting both blowing-snow frequency and magnitude. Furthermore, RpNew also successfully predicts the power-law variation in the blowing-snow transport fluxes with wind speed. Comparison of continental blowing-snow frequency obtained from RpNew with CALIPSO satellite observations (Palm et al., 2018) shows that, qualitatively, RpNew predicts the blowing-snow frequency over Antarctica reasonably well.
The updated estimates of blowing-snow sublimation from RpNew also agree well with the continent-wide estimates of blowing-snow sublimation from satellite observations. An average blowing-snow depth of 230±116 m obtained from RpNew matches reasonably well with the satellite observations from Palm et al. (2017). Furthermore, Palm et al. (2017), from CALIPSO lidar observations, report a maximum blowing-snow sublimation of 250±125 near the Antarctic coast around 140° E longitude. We observe a maximum blowing-snow sublimation of 335±30 at the location of 66.9° S, 130.4° E. CALIPSO satellite observations indicate blowing-snow sublimation could be as high as 393±196 Gt yr−1. We observe a blowing-snow sublimation of 176±10 Gt yr−1 with RpNew, which shows there is a significant difference between model results and satellite observations. Palm et al. (2018) attribute the high blowing-snow sublimation estimates to the errors associated with MERRA-2 reanalysis data (Gelaro et al., 2017) used for calculating sublimation, particle radius error, and extinction errors, and, therefore, the satellite estimates involve a large error. However, without other continental-scale estimates of blowing-snow sublimation, future studies must properly document the differences between different methods.
In the absence of blowing-snow sublimation, sublimation in Antarctica is mostly a summertime phenomenon (October–March), shown by the NO-DRIFT experiment, with negligible surface sublimation in winter. However, with the introduction of the blowing-snow model, total sublimation increases with a large contribution of blowing-snow sublimation in the Antarctic winter (April–September). We observe an interesting self-limiting nature of total sublimation from RpNew model results. Specifically, while RpNew leads to an increase in blowing-snow sublimation, we observed a corresponding decrease in surface sublimation and a non-negligible increase in deposition, balancing the total sublimation in Antarctic winter. In RpNew, sublimation in Antarctica is a self-limiting mechanism, where large blowing-snow sublimation saturates the near-surface layers, limiting the potential for surface sublimation. Future intercomparison studies with other models are necessary to test this hypothesis. We also compared the RpNew result with the simulation results from CRYOWRF (Gerber et al., 2023). While blowing-snow sublimation is the major contributor to total sublimation in RpNew, surface sublimation is the dominant contributor to total sublimation in CRYOWRF. Furthermore, sublimation in CRYOWRF is nearly 4 times higher than RpNew surface sublimation. The difference shows that future intercomparison studies are necessary to identify the major contributor to total sublimation.
In conclusion, the updates introduced to the regional climate model RACMO in this study significantly improve the representation of blowing-snow physics within the model. Blowing-snow and surface sublimation are the major mass loss terms in Antarctica's SMB, and, locally, this leads to a negative SMB, which results in the formation of blue-ice areas. This study presents a step forward in modelling blowing snow to produce a physically sound and reliable estimate of Antarctica's SMB. However, some limitations and simplifications exist in the model, which could be further improved. Currently, snow properties such as dendricity and helicity are assumed to be constant. As a result, the model does not capture variance in the observational data accurately; fixing this simplification would be a major improvement. In addition, the blowing-snow model is not coupled with the radiation model, and, as such, the effect of blowing snow on radiative transfer is not considered, which could be further improved. Finally, the modelling of surface snow density and wind packing should be improved, as we have observed that the poor representation of the temporal and spatial variability in the surface snow density gives the largest uncertainties and model deviations in the modelled firn densification and firn air content.
We evaluate the performance of RpNew in predicting the near-surface wind speed, temperature, relative humidity, and snow transport fluxes for 2010–2012 compared to the Rp3 and NO-DRIFT experiments. Table A1 presents the statistics comparing observed near-surface quantities against simulated results from the three experiments. We observe that the model underestimates the near-surface wind speed in all three experiments; however, with the current updates, the model bias is slightly decreased from −3.34 m s−1 in the NO-DRIFT case to −2.72 m s−1 in the case of RpNew. The model captures the variability in the data reasonably well, with negligible differences between the three experiments. The coefficient of determination (R2) is approximately 0.76, indicating that model results resemble the synoptic evolution of the wind strength well. An RMSE of approximately 3.88 m s−1 indicates that there are still significant differences between the model results and observations. As all three simulations underestimate the wind speed, we also performed tests with a dual mass flux–turbulent kinetic energy (TKE) scheme (van Meijgaard et al., 2012), which allows for better modelling of the turbulent boundary layer processes. However, it did not improve the wind-speed predictions appreciably (not shown). Therefore, this scheme was not used further. The underprediction of simulated wind speed is likely due to the lower vertical resolution of the model, wherein the first atmospheric level is approximately 8 to 10 m above the surface, and the 2 m wind speed is calculated based on the similarity theory and is not simulated.
In the blowing-snow model, the mass change in an ice particle due to blowing-snow sublimation is given by the model of Thorpe and Mason (1966) (Eq. 10). Since the mass change depends on the water vapour deficit and air temperature, accurate prediction of these quantities is necessary to obtain reliable estimates of blowing-snow sublimation. Table A1 shows that the near-surface temperature is overpredicted for all three experiments, and all simulations have a slight positive temperature bias. However, with the updates to the model, the bias in the model is improved from 1.61 °C for the NO-DRIFT case to 1.45 °C for the RpNew case. RpNew also shows an improved temperature prediction with a lower bias of 0.3 °C compared to Rp3. The variability is modelled well, with an RMSE of 3 °C and a high R2 of 0.91. The numbers show that RpNew predicts the near-surface wind and temperature better than the other two experiments.
Table A1Root mean square error (RMSE), slope, intercept, bias, and coefficient of determination (R2) for comparison of the NO-DRIFT, Rp3, and RpNew simulations against observations at site D47. Statistics are reported for 2 m wind speed (m s−1), 2 m temperature (°C), 2 m relative humidity with respect to ice (%), and the near-surface blowing-snow flux (kg m−2 s−1).
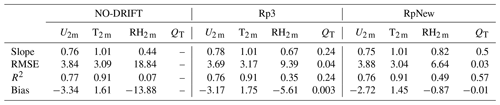
Figure B1 provides a colour-blind-friendly version of the blowing-snow frequency.
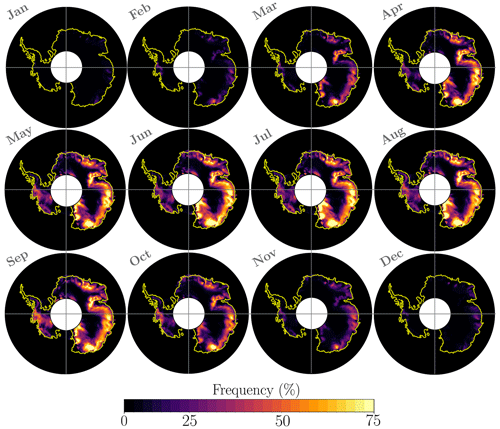
Figure B1Blowing-snow frequency visualised to provide a qualitative comparison with satellite measurements of Palm et al. (2018). Figures show the average blowing-snow frequency from 2000 to 2012.
In Fig. C1, we present the difference in some important variables between RpNew and Rp3 to quantify the magnitude of change between the two versions. The blowing-snow transport TRds (Fig. C1b) decreased somewhat over most of Antarctica, with significant but localised increases in transport along George V Land, Adélie Land, and Queen Maud Land. At these locations, the blowing-snow transport is increased by 2–3 times compared to Rp3 due to better modelling of snow particle distribution, which includes more particles with well-distributed ice particle radii and particle initialisation. As visualised in Fig. C1g, as an example, however, for most of Antarctica, most blowing-snow events are reduced in intensity by the model updates. Only for a few instances per year does the wind speed exceed the threshold for which the updated blowing-snow model simulates higher blowing-snow transport.
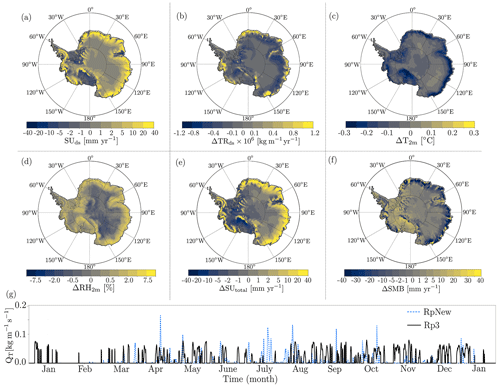
Figure C1Yearly average (2000–2012) difference between RpNew and Rp3 quantities: (a) blowing-snow sublimation (mm yr−1), (b) blowing-snow transport (), (c) near-surface temperature T2 m (°C), (d) relative humidity in percentage, (e) total sublimation (mm yr−1), and (f) SMB (mm yr−1). SUds, SUtotal, and SMB are in millimetres of water equivalent (mm w.e.). (g) Instantaneous drifting-snow flux at an interior region of East Antarctica (71.1° S, 111.7° E).
Conversely, for most of Antarctica, we observe higher blowing-snow sublimation (Fig. C1a) due to the ability of RpNew to capture the peaks in blowing-snow fluxes and the change in initialisation employed for the blowing-snow model. This increase indicates the necessity of a direct two-way coupling of the atmosphere with the blowing-snow model. In RpNew, the snow particles are lifted into the warmer and drier air of the upper part of the stable boundary layer. In Rp3, particles were not lifted that high – due to errors in the particle size distribution. The larger ice shelves are the only regions of Antarctica where blowing-snow sublimation decreases. Here, the stable boundary layer is generally very thick (e.g. van den Broeke and Van Lipzig, 2003, Fig. 10), inhibiting the blowing-snow from reaching the warmer air above the surface layer.
Results show that RpNew is slightly colder by 0.3–0.4 K (Fig. C1c) along the coastal areas when compared to Rp3. This results from a better coupling of blowing-snow sublimation to the tendencies of temperature, which allows for the removal of latent heat from upper vertical levels of Rp3. Compared to Rp3, RpNew also has higher relative humidity (Fig. C1d); due to better coupling of blowing-snow moisture tendencies, the change in moisture leads to an increase in the dew-point temperature of 2–4 K (not shown here) in the first few vertical layers of Rp3. Furthermore, total sublimation is higher in RpNew (Fig. C1e) when compared to Rp3. Along the coast, the difference is as high as 100 . Overall, the average surface mass balance (Fig. C1f) changes mostly along the coastal Antarctica with a reduction of approximately 30–40 . Since there is an increase in the moisture availability, there is relatively higher precipitation over the Ronne and Ross ice shelves, with a corresponding increase in SMB of approximately 20 .
In conclusion, changes introduced in RpNew greatly influence the overall sublimation pattern in Antarctica and moisture content in lower levels of the atmosphere. In RpNew, blowing snow's impact is more regional than in Rp3. However, the overall impact on SMB is limited, with a decrease in SMB on the East Antarctic coast and a slight increase in SMB in West Antarctica due to higher moisture content created by blowing-snow sublimation.
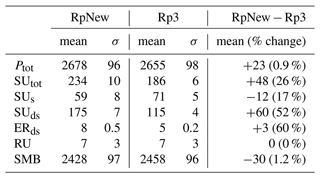
Table D1 presents the SMB and its components integrated over the whole ice sheet (including ice shelves) for the years 2000–2010 in Gt yr−1 along with their interannual variability. Compared to Rp3, RpNew has an increased precipitation of 23 Gt yr−1, caused by the higher moisture content in the atmosphere due to higher blowing-snow sublimation. Total sublimation is increased by 48 Gt yr−1, with blowing-snow sublimation being the major contributor. There is a slight decrease in surface sublimation (12 Gt yr−1) as air in the boundary layer is saturated more efficiently with RpNew compared to Rp3, which causes a reduction in the potential for surface sublimation. With higher blowing-snow transport fluxes, we have a higher snow erosion increase of 3 Gt yr−1. This number remained small as snow erosion only influences the integrated SMB once the snow is blown off the ice sheet. Overall, the integrated SMB is reduced by 30 Gt yr−1, due to a net increase in blowing-snow sublimation. The change amounts to only a 1.2 % decrease in SMB compared to Rp3. Since the SMB changes with the updates are minor and the SMB results from Rp2 have been previously evaluated against several in situ and remote sensing observations, we refer to Noël et al. (2018) and van Wessem et al. (2018) for the SMB evaluation. Though there is negligible change in the overall SMB, blowing-snow sublimation is highly important to local SMB, especially in the escarpment areas in East Antarctica.
Table D1Total ice sheet, including ice shelves, integrated SMB mean 2000–2012 values (Gt yr−1) with interannual variability σ: total (snow and rain) precipitation (Ptot), total sublimation (SUtot), surface sublimation (SUs), blowing-snow sublimation (SUds), blowing-snow erosion (ERds), and run-off (RU). Integrated surface mass balance is given by .
Monthly accumulated sublimation and yearly accumulated SMB components for the NO-DRIFT, Rp3, and RpNew cases are publicly available on Zenodo (https://doi.org/10.5281/zenodo.12509004, Gadde and van de Berg, 2024) for the years 2000–2012. Observational data were downloaded from Amory et al. (2020b) (https://doi.org/10.5281/zenodo.3630497). CRYOWRF results were downloaded from Gerber et al. (2022) (https://doi.org/10.16904/envidat.347).
SG and WJvdB conceived this study and decided on the new model settings. SG performed the code development, performed the model simulations, and led the writing of the manuscript.
The contact author has declared that neither of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
We would like to thank Charles Amory for the discussion about the observational dataset from site D47, East Antarctica. We would also like to thank Melchior van Wessem and Christiaan van Dalum for discussions about RACMO model development. This project has received funding from the European Union's Horizon 2020 research and innovation programme (PolarRES; grant agreement no. 101003590). We also acknowledge the ECMWF for the use of archiving facilities and computational time on their supercomputers.
This research has been supported by the EU Horizon 2020 programme (grant no. 101003590).
This paper was edited by Jürg Schweizer and reviewed by two anonymous referees.
Agosta, C., Amory, C., Kittel, C., Orsi, A., Favier, V., Gallée, H., van den Broeke, M. R., Lenaerts, J. T. M., van Wessem, J. M., van de Berg, W. J., and Fettweis, X.: Estimation of the Antarctic surface mass balance using the regional climate model MAR (1979–2015) and identification of dominant processes, The Cryosphere, 13, 281–296, https://doi.org/10.5194/tc-13-281-2019, 2019. a
Alduchov, O. A. and Eskridge, R. E.: Improved Magnus form approximation of saturation vapor pressure, J. Appl. Meteorol. Climatol., 35, 601–609, https://doi.org/10.1175/1520-0450(1996)035<0601:IMFAOS>2.0.CO;2, 1996. a
Amory, C.: Drifting-snow statistics from multiple-year autonomous measurements in Adélie Land, East Antarctica, The Cryosphere, 14, 1713–1725, https://doi.org/10.5194/tc-14-1713-2020, 2020. a, b, c, d, e, f, g, h, i, j
Amory, C., Trouvilliez, A., Gallée, H., Favier, V., Naaim-Bouvet, F., Genthon, C., Agosta, C., Piard, L., and Bellot, H.: Comparison between observed and simulated aeolian snow mass fluxes in Adélie Land, East Antarctica, The Cryosphere, 9, 1373–1383, https://doi.org/10.5194/tc-9-1373-2015, 2015. a
Amory, C., Gallée, H., Naaim-Bouvet, F., Favier, V., Vignon, E., Picard, G., Trouvilliez, A., Piard, L., Genthon, C., and Bellot, H.: Seasonal variations in drag coefficient over a sastrugi-covered snowfield in coastal East Antarctica, Bound.-Lay. Meteorol., 164, 107–133, https://doi.org/10.1007/s10546-017-0242-5, 2017. a
Amory, C., Genthon, C., and Favier, V.: A drifting snow data set (2010–2018) from coastal Adelie Land, eastern Antarctica, Zenodo [data set], https://doi.org/10.5281/zenodo.3630496, 2020a. a
Amory, C., Genthon, C., and Favier, V.: A drifting snow data set (2010-2018) from coastal Adelie Land, Eastern Antarctica, Zenodo [data set], https://doi.org/10.5281/zenodo.3630497, 2020b. a, b
Amory, C., Kittel, C., Le Toumelin, L., Agosta, C., Delhasse, A., Favier, V., and Fettweis, X.: Performance of MAR (v3.11) in simulating the drifting-snow climate and surface mass balance of Adélie Land, East Antarctica, Geosci. Model Dev., 14, 3487–3510, https://doi.org/10.5194/gmd-14-3487-2021, 2021. a, b, c, d, e
Barral, H., Genthon, C., Trouvilliez, A., Brun, C., and Amory, C.: Blowing snow in coastal Adélie Land, Antarctica: three atmospheric-moisture issues, The Cryosphere, 8, 1905–1919, https://doi.org/10.5194/tc-8-1905-2014, 2014. a
Bintanja, R.: The contribution of snowdrift sublimation to the surface mass balance of Antarctica, Ann. Glaciol., 27, 251–259, https://doi.org/10.3189/1998AoG27-1-251-259, 1998. a, b
Bintanja, R.: Snowdrift sublimation in a katabatic wind region of the Antarctic ice sheet, J. Appl. Meteorol. Climatol., 40, 1952–1966, https://doi.org/10.1175/1520-0450(2001)040<1952:SSIAKW>2.0.CO;2, 2001. a
Bromwich, D. H., Guo, Z., Bai, L., and Chen, Q.-S.: Modeled Antarctic precipitation. Part I: Spatial and temporal variability, J. Climate, 17, 427–447, https://doi.org/10.1175/1520-0442(2004)017<0427:MAPPIS>2.0.CO;2, 2004. a
Budd, W. F.: The drifting of nonuniform snow particles, Studies in Antarctic meteorology, 9, 59–70, https://doi.org/10.1029/AR009p0059, 1966. a, b, c, d
CY45R1–Part IV, I. D.: Physical processes, IFS Documentation CY45R1, 2018. a
Déry, S. J. and Yau, M. K.: A bulk blowing snow model, Bound.-Lay. Meteorol., 93, 237–251, https://doi.org/10.1023/A:1002065615856, 1999. a, b, c, d, e, f, g
Déry, S. J. and Yau, M. K.: Simulation of blowing snow in the Canadian Arctic using a double-moment model, Bound.-Lay. Meteorol., 99, 297–316, https://doi.org/10.1023/A:1018965008049, 2001. a, b, c, d
Déry, S. J. and Yau, M. K.: Large-scale mass balance effects of blowing snow and surface sublimation, J. Geophys. Res.-Atmos., 107, ACL–8, https://doi.org/10.1029/2001JD001251, 2002. a, b
Déry, S. J., Taylor, P. A., and Xiao, J.: The thermodynamic effects of sublimating, blowing snow in the atmospheric boundary layer, Bound.-Lay. Meteorol., 89, 251–283, https://doi.org/10.1023/A:1001712111718, 1998. a, b, c
ECMWF: IFS Documentation CY33R1 – Part IV: Physical Processes, 4, ECMWF, https://doi.org/10.21957/8o7vwlbdr, 2009. a
Ettema, J., van den Broeke, M. R., van Meijgaard, E., van de Berg, W. J., Box, J. E., and Steffen, K.: Climate of the Greenland ice sheet using a high-resolution climate model – Part 1: Evaluation, The Cryosphere, 4, 511–527, https://doi.org/10.5194/tc-4-511-2010, 2010. a
Gadde, S. and van de Berg, W. J.: Monthly accumulated sublimation and yearly accumulated surface mass balance (SMB) components RACMO model simulations for Antarctica on 27 km grid for 2000–2012 (Version v1), Zenodo [data set], https://doi.org/10.5281/zenodo.12509005, 2024. a
Gallée, H., Guyomarćh, G., and Brun, E.: Impact of snow drift on the Antarctic ice sheet surface mass balance: possible sensitivity to snow-surface properties, Bound.-Lay. Meteorol., 99, 1–19, https://doi.org/10.1023/A:1018776422809, 2001. a, b, c, d
Gelaro, R., McCarty, W., Suárez, M. J., Todling, R., Molod, A., Takacs, L., Randles, C. A., Darmenov, A., Bosilovich, M. G., Reichle, R., Wargan, K., Coy, L., Cullather, R., Draper, C., Akella, S., Buchard, V., Conaty, A., da Silva, A. M., Gu, W., Kim, G.-K., Koster, R., Lucchesi, R., Merkova, D., Nielsen, J. E., G., P., Pawson, S., Putman, W., Rienecker, M., Schubert, S. D., Sienkiewicz, M., and Zhao, B.: The modern-era retrospective analysis for research and applications, version 2 (MERRA-2), J. Climate, 30, 5419–5454, https://doi.org/10.1175/JCLI-D-16-0758.1, 2017. a
Gerber, F., Sharma, V., and Lehning, M.: Reproducibility dataset for CRYOWRF validation, EnviDat [data set], https://doi.org/10.16904/envidat.347, 2022. a
Gerber, F., Sharma, V., and Lehning, M.: CRYOWRF–Model Evaluation and the Effect of Blowing Snow on the Antarctic Surface Mass Balance, J. Geophys. Res.-Atmos., 128, e2022JD037744, https://doi.org/10.1029/2022JD037744, 2023. a, b, c, d, e, f, g
Greuell, W. and Konzelmann, T.: Numerical modelling of the energy balance and the englacial temperature of the Greenland Ice Sheet. Calculations for the ETH-Camp location (West Greenland, 1155 m asl), Global Planet. Change, 9, 91–114, https://doi.org/10.1016/0921-8181(94)90010-8, 1994. a
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., Chiara, G. D., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Holm, E., Janiskova, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thepaut, J.-N.: The ERA5 global reanalysis, Q. J. Roy. Meteor. Soc., 146, 1999–2049, https://doi.org/10.1002/qj.3803, 2020. a
King, J. C., Anderson, P. S., Smith, M. C., and Mobbs, S. D.: The surface energy and mass balance at Halley, Antarctica during winter, J. Geophys. Res.-Atmos., 101, 19119–19128, https://doi.org/10.1029/96JD01714, 1996. a
King, J. C., Anderson, P. S., and Mann, G. W.: The seasonal cycle of sublimation at Halley, Antarctica, J. Glaciol., 47, 1–8, https://doi.org/10.3189/172756501781832548, 2001. a
Kodama, Y., Wendler, G., and Gosink, J.: The effect of blowing snow on katabatic winds in Antarctica, Ann. Glaciol., 6, 59–62, https://doi.org/10.3189/1985AoG6-1-59-62, 1985. a
Kuipers Munneke, P., Van den Broeke, M., Lenaerts, J., Flanner, M., Gardner, A., and Van de Berg, W.: A new albedo parameterization for use in climate models over the Antarctic ice sheet, J. Geophys. Res.-Atmos., 116, D05114, https://doi.org/10.1029/2010JD015113, 2011. a
Lenaerts, J. T. M. and van den Broeke, M. R.: Modeling drifting snow in Antarctica with a regional climate model: 2. Results, J. Geophys. Res.-Atmos., 117, D05109, https://doi.org/10.1029/2010JD015419, 2012. a, b, c
Lenaerts, J. T. M., van den Broeke, M. R., Déry, S. J., van Meijgaard, E., van de Berg, W. J., Palm, S. P., and Rodrigo, J. S.: Modeling drifting snow in Antarctica with a regional climate model: 1. Methods and model evaluation, J. Geophys. Res.-Atmos., 117, D05108, https://doi.org/10.1029/2011JD016145, 2012. a, b, c
Lenaerts, J. T. M., Smeets, C. J. P. P., Nishimura, K., Eijkelboom, M., Boot, W., van den Broeke, M. R., and van de Berg, W. J.: Drifting snow measurements on the Greenland Ice Sheet and their application for model evaluation, The Cryosphere, 8, 801–814, https://doi.org/10.5194/tc-8-801-2014, 2014. a, b
Libois, Q., Picard, G., France, J. L., Arnaud, L., Dumont, M., Carmagnola, C. M., and King, M. D.: Influence of grain shape on light penetration in snow, The Cryosphere, 7, 1803–1818, https://doi.org/10.5194/tc-7-1803-2013, 2013. a
Mottram, R., Hansen, N., Kittel, C., van Wessem, J. M., Agosta, C., Amory, C., Boberg, F., van de Berg, W. J., Fettweis, X., Gossart, A., van Lipzig, N. P. M., van Meijgaard, E., Orr, A., Phillips, T., Webster, S., Simonsen, S. B., and Souverijns, N.: What is the surface mass balance of Antarctica? An intercomparison of regional climate model estimates, The Cryosphere, 15, 3751–3784, https://doi.org/10.5194/tc-15-3751-2021, 2021. a
Noël, B., van de Berg, W. J., van Wessem, J. M., van Meijgaard, E., van As, D., Lenaerts, J. T. M., Lhermitte, S., Kuipers Munneke, P., Smeets, C. J. P. P., van Ulft, L. H., van de Wal, R. S. W., and van den Broeke, M. R.: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 1: Greenland (1958–2016), The Cryosphere, 12, 811–831, https://doi.org/10.5194/tc-12-811-2018, 2018. a, b, c
Palm, S. P., Yang, Y., Spinhirne, J. D., and Marshak, A.: Satellite remote sensing of blowing snow properties over Antarctica, J. Geophys. Res.-Atmos., 116, D16123, https://doi.org/10.1029/2011JD015828, 2011. a
Palm, S. P., Kayetha, V., Yang, Y., and Pauly, R.: Blowing snow sublimation and transport over Antarctica from 11 years of CALIPSO observations, The Cryosphere, 11, 2555–2569, https://doi.org/10.5194/tc-11-2555-2017, 2017. a, b, c, d, e, f, g, h, i
Palm, S. P., Kayetha, V., and Yang, Y.: Toward a satellite-derived climatology of blowing snow over Antarctica, J. Geophys. Res.-Atmos., 123, 10–301, https://doi.org/10.1029/2018JD028632, 2018. a, b, c, d, e, f, g, h, i
Pomeroy, J. W.: A process-based model of snow drifting, Ann. Glaciol., 13, 237–240, https://doi.org/10.3189/S0260305500007965, 1989. a
Pomeroy, J. W. and Male, D. H.: Steady-state suspension of snow, J. Hydrol., 136, 275–301, https://doi.org/10.1016/0022-1694(92)90015-N, 1992. a
Radok, U.: Snow drift, J. Glaciol., 19, 123–139, https://doi.org/10.3189/S0022143000215591, 1977. a, b
Scambos, T. A., Frezzotti, M., Haran, T., Bohlander, J., Lenaerts, J., Van Den Broeke, M., Jezek, K., Long, D., Urbini, S., Farness, K., Neumann, T., Albert, M., and Winther, J.-G.: Extent of low-accumulation'wind glaze'areas on the East Antarctic plateau: implications for continental ice mass balance, J. Glaciol., 58, 633–647, https://doi.org/10.3189/2012JoG11J232, 2012. a
Scarchilli, C., Frezzotti, M., Grigioni, P., Silvestri, L. D., Agnoletto, L., and Dolci, S.: Extraordinary blowing snow transport events in East Antarctica, Clim. Dynam., 34, 1195–1206, https://doi.org/10.1007/s00382-009-0601-0, 2010. a
Schmidt, R. A.: Sublimation of wind-transported snow: a model, vol. 90, Rocky Mountain Forest and Range Experiment Station, Forest Service, US …, 1972. a
Schmidt, R. A.: Vertical profiles of wind speed, snow concentration, and humidity in blowing snow, Bound.-Lay. Meteorol., 23, 223–246, https://doi.org/10.1007/BF00123299, 1982. a, b, c
Serreze, M. C. and Barry, R. G.: The Arctic climate system, Cambridge University Press, 2005. a
Thiery, W., Gorodetskaya, I. V., Bintanja, R., Van Lipzig, N. P. M., Van den Broeke, M. R., Reijmer, C. H., and Kuipers Munneke, P.: Surface and snowdrift sublimation at Princess Elisabeth station, East Antarctica, The Cryosphere, 6, 841–857, https://doi.org/10.5194/tc-6-841-2012, 2012. a
Thorpe, A. and Mason, B.: The evaporation of ice spheres and ice crystals, British J. Appl. Phys., 17, 541, https://doi.org/10.1088/0508-3443/17/4/316, 1966. a, b
Le Toumelin, L., Amory, C., Favier, V., Kittel, C., Hofer, S., Fettweis, X., Gallée, H., and Kayetha, V.: Sensitivity of the surface energy budget to drifting snow as simulated by MAR in coastal Adelie Land, Antarctica, The Cryosphere, 15, 3595–3614, https://doi.org/10.5194/tc-15-3595-2021, 2021. a, b
Undén, P., Rontu, L., Jarvinen, H., Lynch, P., Calvo Sánchez, F. J., G., C., Cuxart, J., Eerola, K., Fortelius, C., García-Moya, J. A., Antonio, J., Jones, C., Lenderink, G., McDonald, A., McGrath, R., Navascués, B., Woetman-Nielsen, N., Odegaard, V., Rodríguez, C., Ernesto, C., Rummukainen, M., Room, R., Sattler, K., Hansn Sass, B., Savijärvi, H., Wichers Schreur, B., Sigg, R., Han, T., and Tijm, A.: HIRLAM-5 scientific documentation, http://hdl.handle.net/20.500.11765/6323 (last access: 23 October 2024), 2002. a
van Dalum, C. T., van de Berg, W. J., Libois, Q., Picard, G., and van den Broeke, M. R.: A module to convert spectral to narrowband snow albedo for use in climate models: SNOWBAL v1.2, Geosci. Model Dev., 12, 5157–5175, https://doi.org/10.5194/gmd-12-5157-2019, 2019. a, b
van Dalum, C. T., van de Berg, W. J., and van den Broeke, M. R.: Sensitivity of Antarctic surface climate to a new spectral snow albedo and radiative transfer scheme in RACMO2.3p3, The Cryosphere, 16, 1071–1089, https://doi.org/10.5194/tc-16-1071-2022, 2022. a, b
van den Broeke, M. and Bintanja, R.: The interaction of katabatic winds and the formation of blue-ice areas in East Antarctica, J. Glaciol., 41, 395–407, https://doi.org/10.3189/S0022143000016269, 1995. a
van den Broeke, M. and Van Lipzig, N.: Factors controlling the near-surface wind field in Antarctica, Mon. Weather Rev., 131, 733–743, 2003. a
van den Broeke, M. R., Reijmer, C. H., and van de Wal, R. S. W.: A study of the surface mass balance in Dronning Maud Land, Antarctica, using automatic weather stations, J. Glaciol., 50, 565–582, https://doi.org/10.3189/172756504781829756, 2004. a
van Meijgaard, E., van Ulft, L., Lenderink, G., de Roode, S. R., Wipfler, E. L., Boers, R., and van Timmermans, R. M. A.: Refinement and application of a regional atmospheric model for climate scenario calculations of Western Europe, KVR 054/12, KvR, https://library.wur.nl/WebQuery/wurpubs/427097 (last access: 23 October 2024), 2012. a
van Wessem, J. M., Ligtenberg, S. R. M., Reijmer, C. H., van de Berg, W. J., van den Broeke, M. R., Barrand, N. E., Thomas, E. R., Turner, J., Wuite, J., Scambos, T. A., and van Meijgaard, E.: The modelled surface mass balance of the Antarctic Peninsula at 5.5 km horizontal resolution, The Cryosphere, 10, 271–285, https://doi.org/10.5194/tc-10-271-2016, 2016. a
van Wessem, J. M., van de Berg, W. J., Noël, B. P. Y., van Meijgaard, E., Amory, C., Birnbaum, G., Jakobs, C. L., Krüger, K., Lenaerts, J. T. M., Lhermitte, S., Ligtenberg, S. R. M., Medley, B., Reijmer, C. H., van Tricht, K., Trusel, L. D., van Ulft, L. H., Wouters, B., Wuite, J., and van den Broeke, M. R.: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 2: Antarctica (1979–2016), The Cryosphere, 12, 1479–1498, https://doi.org/10.5194/tc-12-1479-2018, 2018. a, b, c, d, e, f
van Wessem, M. J., Reijmer, C. H., van de Berg, W. J., van den Broeke, M. R., Cook, A. J., van Ulft, L. H., and van Meijgaard, E.: Temperature and wind climate of the Antarctic Peninsula as simulated by a high-resolution regional atmospheric climate model, J. Climate, 28, 7306–7326, https://doi.org/10.1175/JCLI-D-15-0060.1, 2015. a
Vinokur, M.: On one-dimensional stretching functions for finite-difference calculations, J. Comput. Phys., 50, 215–234, https://doi.org/10.1016/0021-9991(83)90065-7, 1983. a
- Abstract
- Introduction
- Model descriptions
- Datasets for model evaluation
- Results and discussion
- Summary and conclusions
- Appendix A: Near-surface climate
- Appendix B: Blowing-snow frequency
- Appendix C: Difference between RpNew and Rp3
- Appendix D: Changes in integrated SMB between RpNew and Rp3
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Model descriptions
- Datasets for model evaluation
- Results and discussion
- Summary and conclusions
- Appendix A: Near-surface climate
- Appendix B: Blowing-snow frequency
- Appendix C: Difference between RpNew and Rp3
- Appendix D: Changes in integrated SMB between RpNew and Rp3
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References