Characterization of in situ cosmogenic ¹⁴CO production, retention and loss in firn and shallow ice at Summit, Greenland

Measurements of carbon-14-containing carbon monoxide (¹⁴CO) in glacial ice are useful for studies of the past oxidative capacity of the atmosphere as well as for reconstructing the past cosmic ray flux. The ¹⁴CO abundance in glacial ice represents the combination of trapped atmospheric ¹⁴CO and in situ cosmogenic ¹⁴CO. The systematics of in situ cosmogenic ¹⁴CO production and retention in ice are not fully quantified, posing an obstacle to interpretation of ice core ¹⁴CO measurements. Here we provide the first comprehensive characterization of ¹⁴CO at an ice accumulation site (Summit, Greenland), including measurements in the ice grains of the firn matrix, firn air and bubbly ice below the firn zone. The results are interpreted with the aid of a firn gas transport model into which we implemented in situ cosmogenic ¹⁴C. We find that almost all (≈ 99.5 %) of in situ ¹⁴CO that is produced in the ice grains in firn is very rapidly (in <1 year) lost to the open porosity and from there mostly vented to the atmosphere. The timescale of this rapid loss is consistent with what is expected from gas diffusion through ice. The small fraction of in situ ¹⁴CO that initially stays in the ice grains continues to slowly leak out to the open porosity at a rate of ≈ 0.6 % yr⁻¹. Below the firn zone we observe an increase in ¹⁴CO content with depth that is due to in situ ¹⁴CO production by deep-penetrating muons, confirming recent estimates of ¹⁴CO production rates in ice via the muon mechanisms and allowing for narrowing constraints on these production rates.

1 Introduction to ¹⁴C in glacial ice and firn and motivation for studies of ¹⁴CO in ice

Measurements of carbon-14 (¹⁴C) in ice cores have been explored in a number of applications, including the determination of glacial ablation rates (e.g., Lal et al., 1990) and ice core dating (e.g., van de Wal et al., 2007; Wilson and Donahue, 1992). More recently, they have been used for characterization of the fossil fraction of the paleoatmospheric methane budget (Petrenko et al., 2017; Dyonisius et al., 2020; Hmiel et al., 2020). The ¹⁴C is included in glacial ice via two separate mechanisms: trapping of carbon-containing atmospheric gases (mainly carbon dioxide, CO₂; carbon monoxide, CO; and methane, CH₄) into air bubbles in ice and in situ production directly from ¹⁶O within the ice crystal lattice via neutron-induced spallation (e.g., Lal et al., 1987), negative muon capture (van der Kemp et al., 2002) and interactions with fast muons (Petrenko et al., 2016). The in situ produced ¹⁴C in the gas phase mainly forms ¹⁴CO₂ and ¹⁴CO, with a smaller fraction forming ¹⁴CH₄; other simple organics may account for up to 25 % of total in situ ¹⁴C (Dyonisius et al., 2023; Hoffman, 2016; van der Kemp et al., 2002; Fang et al., 2021).

Applications of ice core ¹⁴C measurements depend on the ability to separately characterize the contributions from the in situ and trapped atmospheric components. However, in glacial ice, these two ¹⁴C components exist in a combined form and cannot be separated analytically. Therefore, for applications where the trapped atmospheric ¹⁴C component is of interest, the in situ component must be independently constrained and corrected for and vice versa. The in situ ¹⁴C content in ice at a snow accumulation site is influenced by both the production of ¹⁴C and its retention in the firn grains. In situ production rates are highest near the surface (Fig. 1), but ¹⁴C produced in the firn layer can be lost to the atmosphere via the interconnected porosity (e.g., Petrenko et al., 2013b; van der Kemp et al., 2000). While the balance of evidence now indicates that most in situ ¹⁴C produced in the firn is not retained (Petrenko et al., 2013b, and references therein), there has been no work to date that has been able to fully characterize the production and movement of in situ ¹⁴C throughout the entire firn column.

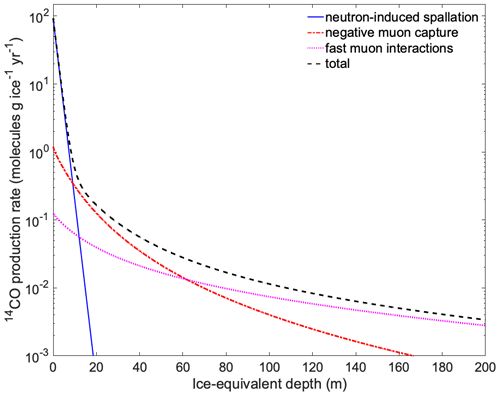
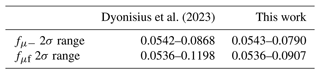
Figure 1 Predicted ¹⁴CO production rate versus depth. The ¹⁴CO production rates versus depth in ice by the neutron and muon mechanisms, calculated for the Greenland Summit location. Production rate from neutrons is calculated using Eq. (3) as described in Sect. 3.2.1. Production rates for the muon mechanisms are calculated using Eqs. (6) and (7) as described in Sect. 3.2.2, using best-estimate f_μ values from Dyonisius et al. (2023).

Of the trace gas species known to be affected by in situ ¹⁴C in ice (CO₂, CO and CH₄), the ratio of in situ to trapped atmospheric ¹⁴C is highest for ¹⁴CO, making this the best target for studies of in situ ¹⁴C processes. One of the main aims of this study is therefore to use new measurements of ¹⁴CO in the firn matrix (ice grains) and open porosity (firn air) to provide a detailed quantitative characterization of in situ ¹⁴C retention in and leakage from the ice grains in firn. In ice below the firn zone, ¹⁴CO is also of interest for paleoenvironmental applications. The trapped atmospheric component of ¹⁴CO can provide information about the past atmospheric oxidative capacity because atmospheric ¹⁴CO serves as an integrating proxy for hydroxyl radical abundance (e.g., Jöckel and Brenninkmeijer, 2002; Petrenko et al., 2021). The in situ component of ¹⁴CO in ice is also of interest for studies of the past galactic cosmic ray (GCR) flux because, at sites with low snow accumulation rates, the in situ component is much larger than the trapped atmospheric component and has the potential to record GCR changes without the confounding influences of solar, geomagnetic, climate and carbon cycle variations (Petrenko et al., 2024).

All in situ cosmogenic ¹⁴C (including ¹⁴CO) that is produced below the firn zone is retained in the ice, and at these larger depths the ¹⁴C production occurs via the muon mechanisms only (Fig. 1). The interpretation of ice core ¹⁴CO measurements for the above applications therefore requires a good understanding of the muogenic ¹⁴CO production rates. Dyonisius et al. (2023) and Petrenko et al. (2016) made measurements of ¹⁴CO in relatively shallow (0–72 m) ice obtained from the ablation zone of Taylor Glacier, Antarctica. The relatively old age (>50 ka) of this ice ensured that ¹⁴CO in the samples originated exclusively from in situ cosmogenic production during ice transport within the glacier, allowing for constraints on muogenic ¹⁴CO production rates. However, relatively large uncertainties in ice flow trajectories within the glacier translated into relatively large uncertainties in ¹⁴CO production rates (up to 30 % for the fast muon mechanism). Dyonisius et al. (2023) measured ¹⁴CO₂ and ¹⁴CH₄ in addition to ¹⁴CO and found that the overall in situ cosmogenic ¹⁴C production rate for these species in ice by muons is 4–5 times smaller than the total ¹⁴C production rate predicted from prior laboratory and field studies for quartz (Heisinger et al., 2002a; Heisinger et al., 2002b; Lupker et al., 2015). The second main aim of this study is therefore to test the Dyonisius et al. (2023) muogenic ¹⁴CO production rates in ice at a site with very different characteristics and to place tighter constraints on these production rates.

2 Sample collection, analyses and calculation of ¹⁴CO concentration

2.1 Overview of samples

The study site (72.66° N, 38.58° W; 3214 m above sea level) was located ≈ 10 km to the NW of Summit Station in central Greenland. Four different types of samples were collected for use in this study: (1) firn air samples, (2) firn matrix samples containing only negligible amounts of trapped air, (3) combined firn matrix and bubbly-ice samples within the lock-in zone (LIZ; the depth range where most of the bubble trapping process happens, e.g., Buizert, 2013; ≈ 68–80 m at Summit), and (4) samples of bubbly ice below the LIZ to ≈ 135 m depth.

2.2 Firn air sample collection and analyses

Firn air samples were collected in May 2013 from a borehole drilled with a 3 in. (7.62 cm) electromechanical ice core drill at depth levels between 0 and 80 m (Table S1). Firn air was sampled using the US firn air sampling device (FASD; Battle et al., 1996) following established techniques (Buizert et al., 2012). For the purposes of ¹⁴CO measurements, air samples and accompanying procedural blanks were collected into 35 L electropolished stainless steel canisters. For the ¹⁴CO procedural blanks, clean ambient air from a cylinder was run into the FASD through a tube containing a Sofnocat 423 reagent (Molecular Products) to remove all CO, including ¹⁴CO. CO dry-air mole fraction (x_CO) in the ¹⁴CO samples was measured at the University of Rochester (UR) by gas chromatography (GC) with hot mercuric oxide reduction and photometric absorption (Peak Performer 1 from Peak Labs), and δ¹³C-CO was measured at the Institute of Arctic and Alpine Research (INSTAAR) (Vimont et al., 2017; Table S1). Additional firn air samples were also collected into 2.5 L glass flasks and 34 L stainless steel canisters for a range of supporting measurements (not shown) that allowed for characterizing firn gas transport at this site. Further details on firn air samples and associated analyses were presented in the “Supplementary information” of Hmiel et al. (2020).

2.3 Firn matrix and LIZ sample collection

Samples for investigating the in situ cosmogenic ¹⁴CO content in the firn matrix (ice grains) at shallower than 60 m (Table S2) were collected in May–June 2014 and 2015 using techniques similar to prior large-volume firn and ice core ¹⁴CO measurements (Petrenko et al., 2016, 2013b). Firn for the surface sample was cut in a snow pit with clean handsaws, while for deeper samples it was recovered from multiple adjacent boreholes using the 24 cm diameter Blue Ice Drill (Kuhl et al., 2014). The firn was loaded into a large 670 L ice melter (Petrenko et al., 2008, 2013b), the melter was evacuated to ≈ 3 mbar and then ≈ 130 mbar of ultrapure N₂ was added as a flush gas. The evacuate–flush sequence was then repeated, followed by a final evacuation to 1–2 mbar and a subsequent injection of a standard gas into the melter. The standard gas is needed as a carrier because the shallow firn matrix contains very little trapped air. The standard gas was passed through Sofnocat to remove all CO (including ¹⁴CO) for samples collected in 2015 (36 and 53 m samples) but not for samples collected in 2014 (surface to 20 m; Table S3). The firn was then melted, the gases were equilibrated between the headspace and the water by recirculating the air through the water via a bubbler manifold at the melter bottom for 30 min, and the headspace air was then transferred to 35 L electropolished stainless steel canisters using diaphragm pumps.

Samples from the LIZ (Table S2) were obtained in May–June 2015 from two adjacent boreholes using the Blue Ice Drill. These samples contain more trapped air than shallower firn but less than bubbly ice below the firn zone. While the procedure for the melt extraction of gases for LIZ samples was almost identical to the procedure for firn matrix samples, the amount of standard gas added to the ice melter (via Sofnocat to remove CO and ¹⁴CO) for each melt extraction was adjusted so that the effective total air content for these samples approximately matched the effective total air content from the firn matrix and bubbly-ice samples (Table S2). Additionally, the standard gas used for the LIZ samples contained an artificially high mole fraction of Ne (≈ 1800 µmol mol⁻¹) to help constrain the fraction of the collected sample air originating from the standard gas.

Several procedural blank tests (“water blanks” in Tables S2–S4) were collected in both the 2014 and 2015 seasons as follows. Following a sample melt extraction, the meltwater was purged with ultrapure air at ≈ 2 L STP min⁻¹ (standard temperature and pressure) flow via Sofnocat and the bubbler manifold for ≈ 75 min to remove any remaining dissolved ¹⁴CO. Next, a standard gas was introduced to the melter headspace, approximately matching the volume of air obtained in real melt extractions. For the 2014 field campaign, the same standard gas was used for the water blanks as for the firn matrix samples, without flowing the gas through Sofnocat in both cases (Table S3). This standard gas also contained ≈ 100 µmol mol⁻¹ of Kr and ≈ 50 µmol mol⁻¹ of Xe. For the 2015 campaign, two different standard gases were used for the water blanks, both of which were passed through Sofnocat when introduced to the melter (same as for all 2015 firn matrix and LIZ samples). The standard gas used for 2015 water blank 1 was the same standard gas as was used for the 2015 firn matrix samples and also contained ≈ 100 µmol mol⁻¹ of Kr and ≈ 50 µmol mol⁻¹ of Xe. The artificially high Kr and Xe allow for accurate characterization of gas partitioning between the water and headspace in the ice melter (Petrenko et al., 2016, 2013b). The standard gas used for 2015 water blank 2 was the same standard gas as was used for the 2015 LIZ samples.

2.4 Bubbly-ice sample collection and analyses of air from firn matrix, LIZ and bubbly-ice samples

Samples of bubbly ice (ice below the LIZ) were collected in May–June 2015 from two to three adjacent boreholes using the Blue Ice Drill (Table S2). Sample handling and melt extraction of air for bubbly-ice samples were very similar to the procedures for firn matrix samples and LIZ samples described above, except that no standard gas was added to the melter as a carrier.

Air samples obtained from melt extractions of firn matrix, LIZ and bubbly ice and accompanying procedural blanks were measured for δ¹³C-CO at INSTAAR (Table S3) (Vimont et al., 2017), as well as for mole fractions of SF₆, CFC-11 and CFC-12 at the Scripps Institution of Oceanography (SIO; not shown) to confirm the absence of significant contamination by ambient air. The x_CO in 2014 samples was measured by gas chromatography (GC) with hot mercuric oxide reduction and photometric absorption (Peak Performer 1 from Peak Labs), and that in 2015 samples was measured by cavity ring-down spectroscopy (Picarro G2401) at UR (Table S3). $\mathit{\delta }\mathrm{Xe}/\mathrm{Kr}$, $\mathit{\delta }\mathrm{Xe}/\mathrm{Ar}$, $\mathit{\delta }\mathrm{Kr}/\mathrm{Ar}$ and $\mathit{\delta }\mathrm{Ar}/{\mathrm{N}}_{\mathrm{2}}$ were measured at SIO (Bereiter et al., 2018; not shown) for all samples and blanks that were collected with the use of standard gases that contained high Kr and Xe. $\mathit{\delta }\mathrm{Ne}/{\mathrm{N}}_{\mathrm{2}}$ was also measured at SIO in 2015 LIZ samples and 2015 water blank 2, which were all collected with the use of the high-Ne standard gas (not shown).

2.5 Sample processing and measurement for ¹⁴CO

Methods used for processing and measurements of ¹⁴CO in ambient air (Petrenko et al., 2021), firn air (Hmiel et al., 2020) and ice core air samples (Dyonisius et al., 2020; Hmiel et al., 2020) have been previously described; here we provide a brief summary and details specific to the samples presented in this study. In a first step, air in the 35 L canisters containing samples and field procedural blanks is diluted at UR to reduce the ¹⁴C activity of CO, bringing the ¹⁴C activity into the range of commonly used ¹⁴C measurement standards (0–135 pMC, percent modern carbon). This is accomplished via the addition of a standard gas (“dilution gas” in Tables S1 and S3) that has high x_CO (10.29 ± 0.13 µmol mol⁻¹) and low ¹⁴C (<1 pMC) activity. The dilution also increases the CO carbon mass (to ≈ 33 µg C for 2013 samples and ≈ 18 µg C for 2014 and 2015 samples), which is needed for precise ¹⁴C measurements. The diluted samples and blanks are then run through an air-processing system at UR that cryogenically dries the air and removes carbon-containing trace gases other than CO and CH₄, followed by CO oxidation over platinized quartz wool at 175 °C (CH₄ passes through unaffected) and cryogenic trapping and purification of CO-derived CO₂. This CO₂ is subsequently converted to graphite at the Australian Nuclear Science and Technology Organisation (ANSTO), and ¹⁴C activity is measured on the 10MV ANTARES (Australian National Tandem Research Accelerator) accelerator mass spectrometer (AMS) (Smith et al., 2010; Tables S1 and S3). Sets of commensurately sized ¹⁴C standards and blanks are prepared at ANSTO and accompany the samples through graphitization and measurement. Two to three larger (≈ 100 µg C) samples of the high-x_CO dilution gas were also processed and measured together with each sample set. This allowed for characterizing the slight growth of ¹⁴CO in the dilution gas over the years (Tables S1 and S3) resulting from in situ cosmogenic ¹⁴CO production in the air cylinder (Lowe et al., 2002).

2.6 Corrections for procedural effects and calculation of sample [¹⁴CO]

The detailed approaches for calculating ¹⁴CO concentration ([¹⁴CO]) and for correcting for procedural effects have been previously presented (Dyonisius et al., 2020; Hmiel et al., 2020; Petrenko et al., 2016, 2013b, 2021). For the reader's convenience we also provide a brief description here. The [¹⁴CO] in firn matrix and bubbly-ice samples is calculated using

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\left[{}^{\mathrm{14}}\mathrm{CO}\right]& ={\displaystyle \frac{\mathrm{pMC}}{\mathrm{100}}}\times e^{-\mathit{\lambda }\left(y-\mathrm{1950}\right)}\times {\displaystyle \frac{{\left(\mathrm{1}+\frac{{\mathit{\delta }}^{\mathrm{13}}C}{\mathrm{1000}}\right)}^{\mathrm{2}}}{{\mathrm{0.975}}^{\mathrm{2}}}}\\ & \times \mathrm{1.1694}\times {\mathrm{10}}^{-\mathrm{12}}\times x_{\mathrm{CO}}\times {\displaystyle \frac{\mathrm{1}}{\mathrm{22}\mathrm{400}}}\times N_{\mathrm{A}}\times V,\end{array}\end{array}$$

where [¹⁴CO] is the number of ¹⁴CO molecules g⁻¹ ice, pMC is the sample or blank ¹⁴C activity in percent modern carbon (Stuiver and Polach, 1977), λ is the ¹⁴C decay constant (1.216 × 10⁻⁴ yr⁻¹), y is the year of measurement, δ¹³C is the δ¹³C of CO in the sample or blank, 0.975 is a factor arising from ¹⁴C activity normalization to δ¹³C of −25 ‰ associated with pMC, 1.1694 × 10⁻¹² is the ${}^{\mathrm{14}}\mathrm{C}/({}^{\mathrm{13}}\mathrm{C}+{}^{\mathrm{12}}\mathrm{C})$ ratio corresponding to the absolute international ¹⁴C standard activity (Hippe and Lifton, 2014), 22 400 is the number of cubic centimeters STP of gas per mole, N_A is the Avogadro constant and V is the air content in cubic centimeters STP per gram of ice. For firn air samples and blanks, the air content term does not apply and [¹⁴CO] is given in units of ¹⁴CO molecules per cubic centimeter STP of air instead.

As the ¹⁴C measurements are made on diluted samples, it is [¹⁴CO] in the diluted sample air that is initially calculated using x_CO and δ¹³C of CO in diluted samples. The pMC values used for this calculation (Tables S1 and S3) are values that have been empirically corrected for processing effects at ANSTO using measurements of commensurately sized ¹⁴C standards and blanks (Petrenko et al., 2021); this correction has a 0 %–2 % effect for samples in this study. The calculation is then repeated to determine the [¹⁴CO] contribution in the diluted samples that is due to the high-x_CO, low-¹⁴C dilution gas, and this contribution is then subtracted from the total. The remaining [¹⁴CO] is further corrected for the effect of air dilution associated with adding the dilution gas to the samples (Petrenko et al., 2021; Tables S1 and S4).

The field procedural blanks collected during each season (Tables S1–S4) characterize all or most of the extraneous [¹⁴CO] in the samples, which is mainly due to in situ ¹⁴CO production in the canisters containing sample air during storage and transport prior to sample processing. For 2013 firn air samples, the procedural blanks are fully representative of all extraneous ¹⁴CO in the samples. However, the blanks were collected 11 d apart, and procedural blank 1 shows significantly higher [¹⁴CO] due to the 11 extra days of in situ ¹⁴CO production in the canister during storage at the high-altitude Summit site (Table S1). The procedural blank correction for the 2013 samples therefore accounted for differences in exposure time at Summit based on the sample collection date and in situ ¹⁴CO growth rate at Summit as determined from the two procedural blanks. Fully corrected firn air sample ¹⁴CO values are shown in Table S1 and Fig. 3.

For 2014 and 2015 samples, several corrections are needed beyond the dilution correction. First, [¹⁴CO] for both samples and blanks is corrected for the effect of gas dissolution in the ice melter (<1 % effect; Table S4) using solubility equilibrium parameters determined from $\mathit{\delta }\mathrm{Xe}/\mathrm{Kr}$. The samples are next corrected for extraneous [¹⁴CO] as characterized by procedural blanks from the same field campaign (Table S4). For 2014, the same standard gas was used in all sample and blank extractions, and this gas was not passed through Sofnocat to remove ¹⁴CO. For this set of samples, there was no significant difference in [¹⁴CO] between procedural blank 1 (start of season) and procedural blank 2 (end of season). This is because ¹⁴CO was being produced in situ in the sample and blank canisters at the same rate as it was being produced in the 2014 standard gas cylinder. For this reason, for 2014 samples the average [¹⁴CO] for procedural blanks was subtracted from sample [¹⁴CO]. For 2015, the standard gases used for samples and blanks were passed through Sofnocat, removing all ¹⁴CO. Because of this, the blank correction for 2015 samples accounted for differences in exposure time at Summit using the same approach as for 2013 samples.

There are two additional sources of extraneous ¹⁴CO in the 2014 and 2015 samples that the field procedural blanks do not characterize. First, the field procedural blanks do not properly mimic heating of the ice melter walls and associated CO outgassing. Second, x_CO in trapped air in Greenland ice is known to be affected by (non-cosmogenic) in situ production in the ice likely originating from organic impurities (Faïn et al., 2014, 2022). Both the x_CO contribution and the ¹⁴C activity of this extraneous CO are needed to estimate the contribution to [¹⁴CO]. This extraneous x_CO contribution for firn matrix samples (Table S3) is calculated by subtracting the average x_CO of the field procedural blanks for the same season from sample x_CO. For LIZ and bubbly-ice samples (which do contain trapped air), we use a Northern Hemisphere high-latitude x_CO history compiled by Hmiel et al. (2020) based on direct atmospheric observations as well as firn air and ice core measurements (Haan and Raynaud, 1998; Petrenko et al., 2013a, and references therein) to predict expected x_CO in trapped air. For bubbly ice, the additional extraneous x_CO contribution from outgassing from hot melter walls and in situ CO production in the ice (Table S3) is estimated as follows:

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{x}_{\mathrm{CO},\mathrm{extraneous}}& =x_{\mathrm{CO},\mathrm{measured}}-x_{\mathrm{CO},\mathrm{2015}\mathrm{field}\mathrm{blank}\mathrm{average}}\\ & -x_{\mathrm{CO},\mathrm{expected}\mathrm{from}\mathrm{trapped}\mathrm{air}}.\end{array}\end{array}$$

For LIZ samples, the calculation is similar but with the expected x_CO from trapped air estimated based on the x_CO atmospheric history and the fraction of air in the sample arising from air bubbles as determined from $\mathit{\delta }\mathrm{Ne}/{\mathrm{N}}_{\mathrm{2}}$ measurements (more trapped air lowers the $\mathrm{Ne}/{\mathrm{N}}_{\mathrm{2}}$ ratio in these samples that used a high-Ne standard gas to supplement air content). The ¹⁴C activity of the extraneous CO is uncertain; we thus use a value of 50 pMC and a 2σ uncertainty of 50 pMC, allowing for the full range from ¹⁴C-free to ¹⁴C-modern. The relative effect of the correction for this extraneous ¹⁴CO is large for the surface sample (39 %), small for bubbly-ice samples (2 %–3 %) and intermediate (3 %–11 %) for other samples; this correction contributes significantly to overall uncertainty (Table S4).

Shallow firn above the LIZ contains a small amount of trapped air, possibly in microbubbles (e.g., Siegenthaler et al., 2005). As this microbubble air is not well understood and is not included in the closed porosity parameterization we use in our model (Sect. 3.1), we further correct [¹⁴CO] in the firn matrix samples for microbubble air. The amount of microbubble air is estimated from the comparison of measured $\mathit{\delta }\mathrm{Xe}/\mathrm{Ar}$ and $\mathit{\delta }\mathrm{Kr}/\mathrm{Ar}$ values with those expected from the solubility equilibrium in the ice melter (addition of trapped air lowers the $\mathrm{Xe}/\mathrm{Ar}$ and $\mathrm{Kr}/\mathrm{Ar}$ ratios in these samples that use a high-Kr, high-Xe gas as a carrier). The magnitude of the correction for ¹⁴CO from microbubbles is 0.6 %–2 % (Table S4). As a final step in the calculation for 2014 and 2015 samples, the fully corrected [¹⁴CO] (in units of ¹⁴CO molecules cm⁻³ STP) is converted to ¹⁴CO content g⁻¹ ice (Table S4; Fig. 3) via multiplying by the effective air content in the samples (V in Eq. 1; in cm³ STP g⁻¹ ice; Table S2). For the firn matrix and LIZ samples, the air content is determined based on the sampled ice mass and recovered amount of air. For bubbly-ice samples, the air content is taken as 0.0904 cm³ STP g⁻¹ ice, which is the average value for the last 2000 years from the nearby Greenland Ice Core Project (GRIP) ice core (Raynaud et al., 1997). The firn model is tuned to match the same air content in ice below the LIZ.

3 Model characterization of firn and ice ¹⁴CO

3.1 Overview of the firn model used for the Greenland Summit site

Interpretation of ¹⁴CO results is done using an established firn gas transport model – the Centre for Ice and Climate (CIC) model from Buizert et al. (2012), which has been modified for this study to include production and movement of in situ ¹⁴C (Sect. 3.2); herein referred to as the “firn model”. The model assumes a steady-state, isothermal firn column with an accumulation rate of 0.235 m ice equivalent yr⁻¹, a temperature of −31 °C, firn densities based on a fit to the Summit density measurements by Adolph and Albert (2014), and a vertical diffusivity profile that is calibrated using firn air measurements of several traces gases with known atmospheric histories. The model simulates transport of trace gas mole fractions in the open and closed porosity (air bubbles) and can extend to depths below the firn zone. The total air content in the firn model below close-off (where all the air has been trapped into bubbles) is tuned to match the value of 0.0904 cm³ STP g⁻¹ ice from Raynaud et al. (1997) as mentioned above.

The method for tuning the depth–diffusivity profile is as described in the Supplement to Buizert et al. (2012), with a few modifications for the Summit site as follows. (1) The ¹⁴CO₂ was not used as a tracer gas due to uncertainty about the magnitude of in situ cosmogenic ¹⁴CO₂ production. (2) δ¹⁵N₂ was also not used due to an observed thermal-fractionation signal from recent warming and seasonal temperature gradients (e.g., Severinghaus et al., 2001) that are not well captured by the steady-state model. (3) N₂O was included as a tracer gas using a recently developed multi-site reconstruction from firn air (Prokopiou et al., 2017). (4) All Northern Hemisphere atmospheric histories for trace gases used in model tuning were updated through December 2015 with monthly mean flask measurements from Summit Station by NOAA Earth System Research Laboratories (ESRL) (Dlugokencky et al., 2018; Petron et al., 2018) and converted to the most recent NOAA measurement scales (Hall et al., 2014).

Firn gas transport models consider layer thinning by densification but do not normally consider additional ice thinning related to deformation by ice flow because such thinning effects are typically very small in the firn column. As our measurements extend to ≈ 130 m, however, the effects of flow-related thinning do need to be considered for the deepest samples. Measurements that could provide a complete ice age–depth scale (and a complete empirical thinning function) are unfortunately not available at our site. However, Hmiel et al. (2020; see their “Supplementary information”) used age tie points from continuous flow chemistry analyses on sections of ice cores from our site between 67–98 m depth to show that a constant accumulation rate of 0.235 m ice equivalent yr⁻¹ in the model yields an excellent match to these tie points. Hmiel et al. (2020) further showed that these same age–depth tie points can be matched well in a Dansgaard–Johnsen (DJ) thinning model (Dansgaard and Johnsen, 1969) that uses a constant accumulation rate of 0.246 m ice equivalent yr⁻¹. For the purposes of the firn model, we use the accumulation rate of 0.235 m ice equivalent yr⁻¹, as this also yields a good match to trace gas measurements. However, we apply a small depth correction for ice deeper than 112 m, where the age–depth scales for the scenario with a constant accumulation rate of 0.235 m ice equivalent yr⁻¹ and the DJ model scenario with 0.246 m ice equivalent yr⁻¹ start to diverge significantly. This correction adjusts the depths used for in situ ¹⁴CO calculations to those predicted by the DJ model scenario, resulting in a 1.25 m shallower depth in the model for the range of the deepest (130 m) sample and a ≈ 1 % increase in model-calculated ¹⁴CO content for that sample.

3.2 Parameterization of in situ cosmogenic ¹⁴CO in the firn model

The firn model accounts for in situ ¹⁴C production in the ice grains by secondary cosmic ray neutrons and muons, for the fraction of this ¹⁴C that forms ¹⁴CO as well as for any loss of this ¹⁴C from the ice grains via leakage into the open porosity (firn air) or closed porosity (air bubbles). Figure 1 illustrates ¹⁴CO production rates by secondary cosmic ray neutrons and muons versus depth at Summit, and the following sections describe how in situ cosmogenic ¹⁴CO was implemented in the model for the purposes of this study, with an overview of the relevant model parameters presented in Table 1.

Table 1 Summary of model parameters involved in calculations of ¹⁴CO.

3.2.1 ¹⁴CO production by neutrons

In situ ¹⁴C production rate by neutron-induced spallation of ¹⁶O has been well constrained from measurements in near-surface quartz samples (Borchers et al., 2016; Young et al., 2014); these ¹⁴C production rates for a sea level high-latitude (SLHL) site ($P_{\mathrm{n},\mathrm{SLHL}}^{\mathrm{Qtz}}\left(\mathrm{0}\right)$) can be translated to ice ($P_{\mathrm{n},\mathrm{SLHL}}^{\mathrm{Ice}}\left(\mathrm{0}\right)$) by accounting for the difference in oxygen atom density (atoms g⁻¹) between quartz and ice (Q_c, factor of 1.667). The subscript n denotes the neutron mechanism for ¹⁴C production. Surface production rates at different locations are estimated as a function of surface pressure and geomagnetic latitude using established “scaling models” (e.g., Desilets et al., 2006; Lifton et al., 2014; Stone, 2000) which use measurements and/or models of the secondary cosmic ray flux in the atmosphere. In this study, we use the scaling model of Lifton et al. (2014) for neutron-induced ¹⁴C production to determine the scaling factor for our site (S_n,Sum). The SLHL production rate of 12.76 molecules g⁻¹ Qtz yr⁻¹ from the CRONUS-Earth project (Cosmic Ray produced Nuclides on Earth; Borchers et al., 2016) is used for $P_{\mathrm{n},\mathrm{SLHL}}^{\mathrm{Qtz}}\left(\mathrm{0}\right)$. This value was chosen as it was calculated using the same scaling model (Lifton et al., 2014) as used in this study; production rate differences between scaling models are on the order of ±10 % and generally agree within measurement uncertainty for high-latitude locations.

We use a value of Ω^CO=0.31 for the fraction of total in situ ¹⁴C in ice that forms ¹⁴CO (Dyonisius et al., 2023; van der Kemp et al., 2002). We note that this value is based on prior measurements in ice where part or all of the in situ ¹⁴C originated from production via the muon mechanisms. However, since all newly produced “hot” in situ ¹⁴C atoms have to lose most of their energy prior to reacting (regardless of production mechanism), there is no a priori reason why the partitioning of in situ ¹⁴C would be different for different production mechanisms.

The ¹⁴C production from neutrons declines exponentially with increasing mass depth (h, in g cm⁻²); we use a value of 150 g cm⁻² for the absorption mean free path Λ_n of neutrons in ice (e.g., Lal et al., 1987; van de Wal et al., 2007). The model also includes an adjustable parameter F_n that allows for tuning the model production rate within uncertainties. These parameters are combined to calculate the ¹⁴CO production rate by neutrons (in ¹⁴CO molecules g⁻¹ ice yr⁻¹) as a function of mass depth h:

$$\begin{array}{}\text{(3)}& P_{\mathrm{n}}^{\mathrm{CO}}\left(h\right)={\mathrm{\Omega }}^{\mathrm{CO}}\cdot F_{\mathrm{n}}\cdot S_{\mathrm{n},\mathrm{Sum}}\cdot Q_{\mathrm{C}}\cdot P_{\mathrm{n},\mathrm{SLHL}}^{\mathrm{Qtz}}\left(\mathrm{0}\right)\cdot e^{-h/{\mathrm{\Lambda }}_{\mathrm{n}}}.\end{array}$$

As can be seen in Fig. 1, ¹⁴CO production by neutrons is only significant in the top ≈ 10 m ice equivalent depth. Neutron fluxes at high-latitude sites are modulated by the heliospheric magnetic field, and over the range of ice ages (≈ 500 years) that correspond to the sampled depth range (≈ 0–130 m), the Lifton et al. (2014) model predicts variability in P_n(0) at Summit of up to ≈ 25 %. However, for deeper ice samples (which would have been most affected by the temporal P_n(0) change), the neutron-produced contribution to total ¹⁴CO is 20 % or less. As temporal variations in P_n(0) have a much smaller effect on total ¹⁴CO than uncertainties in other parameters such as muogenic production rates and the atmospheric [¹⁴CO] history, we assume no temporal variability in P_n(0) for the purposes of this study.

3.2.2 ¹⁴CO production by muons

For in situ ¹⁴C production from ¹⁶O via the muon mechanisms, we use the parameterizations developed by Heisinger et al. (2002a, b) as implemented in MATLAB by Balco et al. (2008) (also Model 1A in Balco, 2017), herein referred to as the “Balco model”, with all relevant parameters adjusted for ice. Briefly, the Heisinger et al. (2002a) production rate (in ¹⁴C atoms g⁻¹ yr⁻¹) parameterization for the negative muon capture mechanism is

$$\begin{array}{}\text{(4)}& P_{\mathit{\mu }-}\left(h\right)=R_{\mathit{\mu }-}\left(h\right)\cdot f_{\mathrm{C}}\cdot f_{\mathrm{D}}\cdot f^{\ast },\end{array}$$

where R_μ−(h) is the stopping rate of negative muons (muons g⁻¹ yr⁻¹) at mass depth h, f_C is the chemical compound factor representing the probability that the stopped muon is captured by one of the target atoms, f_D is the probability that the negative muon does not decay in the K shell before nuclear capture and f^∗ is the effective probability for production of the cosmogenic nuclide of interest after μ⁻ capture by the target nucleus. We use the f values given by Heisinger et al. (2002a) for production of ¹⁴C from ¹⁶O in ice.

Heisinger et al. (2002b) parameterizes production rate from fast muons as

$$\begin{array}{}\text{(5)}& P_{\mathit{\mu }\mathrm{f}}\left(h\right)={\mathit{\sigma }}_{\mathrm{0}}\cdot \mathit{\beta }\left(h\right)\cdot \mathit{\varphi }\left(h\right)\cdot \stackrel{\mathrm{‾}}{E}(h{)}^{\mathit{\alpha }}\cdot N,\end{array}$$

where σ₀ is the reference nuclear-reaction cross section at a muon energy of 1 GeV (cm²), ϕ(h) is the total muon flux at mass depth h (muons cm⁻² yr⁻¹ sr⁻¹), β(h) is a unitless mass-depth dependence factor, $\stackrel{\mathrm{‾}}{E}\left(h\right)$ is the mean muon energy at mass depth h (GeV), α is a power factor that describes the energy dependence of the cross section (we use α=0.75, consistent with Dyonisius et al., 2023, and Heisinger et al., 2002b) and N is the number of target nuclei per gram target mineral.

The above muogenic production rate parameterizations are incorporated within the Balco model, which also provides the needed altitude scaling of muon fluxes and energies based on atmospheric pressure at Summit. The ¹⁴CO production rate via the negative muon and fast muon mechanisms as a function of mass depth h is then calculated as

$$\begin{array}{}\text{(6)}& {\displaystyle }{P}_{\mathit{\mu }-}^{\mathrm{CO}}\left(h\right)=f_{\mathit{\mu }-}\cdot P_{\mathit{\mu }-}^{\mathrm{Balco}}\left(h,P\right),\text{(7)}& {\displaystyle }{P}_{\mathit{\mu }\mathrm{f}}^{\mathrm{CO}}\left(h\right)=f_{\mathit{\mu }\mathrm{f}}\cdot P_{\mathit{\mu }\mathrm{f}}^{\mathrm{Balco}}\left(h,P\right),\end{array}$$

where $P_{\mathit{\mu }}^{\mathrm{Balco}}\left(h,P\right)$ is the total ¹⁴C production rate (in atoms g⁻¹ yr⁻¹) from the respective muon mechanism at mass depth h and surface pressure P and f_μ− and f_μf are dimensionless tuning factors that account for (1) the fraction of total ¹⁴C that forms ¹⁴CO (Ω^CO) and (2) the adjustment factor for the production rate. This definition of f_μ− and f_μf is consistent with the Dyonisius et al. (2023) study of muogenic ¹⁴CO production rates in ice at Taylor Glacier, Antarctica. Figure 1 illustrates the predicted muogenic ¹⁴CO production rates at a range of depths at Summit.

Only muons with sufficiently high energy can penetrate the Summit firn column to the depths (70–80 m) where the first impermeable ice layers start to form and in situ ¹⁴C retention in the ice/firn starts to increase. The primary cosmic rays responsible for the production of such higher-energy muons are of a sufficiently high energy so as to be insensitive to solar modulation (Petrenko et al., 2024). We therefore do not assume any temporal variability in muon fluxes.

3.2.3 ¹⁴C retention, leakage and decay

The firn model defines two reservoirs within the ice grains to contain the in situ produced ¹⁴C (Fig. 2). The partitioning of ¹⁴C between these reservoirs is numerically defined by coefficients R₀ and R₁, representing the fraction of in situ produced ¹⁴C entering each reservoir. For each reservoir, the model also defines leakage coefficients L₀ and L₁ which represent the fraction of total in situ ¹⁴C that leaks out of the respective reservoir per year (for L₁) or per time step (for L₀). We introduce these two reservoirs because a preliminary analysis showed that using a single ice grain reservoir does not provide a good fit to the observations; physical justification for these two reservoirs is discussed in Sect. 4.2. The relative partitioning of leaked ¹⁴C between open and closed porosity scales with the relative volumes of open and closed porosity in the model at a given depth such that the fraction leaked into the open pores equals $L_i\times \frac{s_{\mathrm{op}}}{s}$ and the fraction leaked into the closed pores is $L_i\times \frac{s_{\mathrm{cl}}}{s}$, where s_op and s_cl are the open and closed porosity, respectively, and the total porosity is $s=s_{\mathrm{op}}+s_{\mathrm{cl}}$ (Fig. 2). Any ¹⁴CO that leaks into the closed porosity is retained permanently, and ¹⁴CO that leaks into the open pores can escape the firn via upward diffusion into the atmosphere.

Figure 2 Conceptual diagram of model parameterization of in situ ¹⁴C partitioning between ice grain reservoirs and leakage into porosity.

Prior studies have found that the majority of in situ cosmogenic ¹⁴C produced in the upper firn column is lost to the atmosphere and not retained through firn densification into ice (e.g., de Jong et al., 2004; Petrenko et al., 2013b; Smith et al., 2000). The model accounts for the rapid loss of most ¹⁴C from ice grains by defining the leakage coefficient L₀ of the primary reservoir so that all ¹⁴C in this reservoir is lost to porosity at every model time step (time step of 0.5 years). In tuning the model, we find that the partitioning coefficient R₀ is close to 1, which means that for a given model time step the majority of the in situ ¹⁴C produced at all depths is sorted into the primary reservoir, and all of it leaks from the ice grains into the porosity. In the upper firn, which is dominated by open porosity, this ¹⁴C typically escapes to the atmosphere, whereas in the LIZ the in situ ¹⁴C that leaks from the grains into the open and closed porosity is inhibited from exchange with the atmosphere due to limited vertical diffusion. For ice below bubble close-off (∼ 80 m at Summit), there is no longer any open porosity in the model, and thus any in situ ¹⁴C that leaks out of the ice grains must leak into the closed porosity.

This parameterization enables tuning of the in situ ¹⁴C content in the firn matrix to match the observations by specifying the secondary reservoir partitioning and leakage coefficients (R₁, L₁), while the primary reservoir partitioning coefficient is determined from the conservation of mass ($R_{\mathrm{0}}=\mathrm{1}-R_{\mathrm{1}}$) and its leakage coefficient L₀ is fixed as described above.

Radioactive decay of ¹⁴C is considered using the standard exponential decay equation with a decay constant of 1.210 × 10⁻⁴ yr⁻¹, corresponding to a ¹⁴C half-life of 5730 years (Godwin, 1962). Finally, the downward advection of ice is considered at each time step by adding a new ice parcel (with no in situ ¹⁴C content) at the uppermost box of the model, shifting each ice parcel downwards by one box of the depth resolution and removing the bottommost ice parcel.

As is described in Sect. 4 below, the firn model is used in combination with the measurements to constrain the possible ranges of four parameters relevant to production and retention of ¹⁴CO in the firn and ice (R₁, L₁, f_μ− and f_μf). While the model has a large number of parameters, we note that for most of these parameters the values are either available from prior studies or determined outside of the model (Table 1). We note further that we only constrain/tune two model parameters at once ([R₁, L₁] or [f_μ−, f_μf]).

4 Results and discussion

4.1 Main features of results and overview of the approach for constraining in situ ¹⁴CO parameters

Figure 3 shows the measurements after all corrections in ice grains + closed porosity (Fig. 3a) and in firn air (Fig. 3b) together with an example of a firn model fit. First, we discuss [¹⁴CO] in the ice grains and closed porosity (Fig. 3a). In the shallow firn (0–60 m), the amount of closed porosity is very small and both the measurements and the model represent [¹⁴CO] in the ice grains only. The [¹⁴CO] first increases rapidly with depth to a peak in the 10–20 m depth range, mainly due to ¹⁴CO production by the neutron mechanism. The [¹⁴CO] then declines gradually with depth through the shallow firn to a minimum at ≈ 60 m. As firn layers move downwards via the processes of continued snow accumulation at the surface, densification and ice flow, the layers carry with them the ice grain ¹⁴CO content they acquired above. Further, ¹⁴CO production continues (by muons) at intermediate firn depths (20–60 m). Therefore, the fact that ¹⁴CO content in the ice grains decreases rather than increases with increasing depth between 20 and 60 m indicates slow ¹⁴CO leakage out of the ice grains. The ¹⁴C radioactive decay is far too slow to explain this, as the ice layers traverse the entire firn column at the Greenland Summit site in only ≈ 200 years. The [¹⁴CO] then increases rapidly with depth in the LIZ (≈ 69–80 m), mainly reflecting the air-trapping process that moves ¹⁴CO from the open into the closed pores. Below ≈ 80 m, no further air trapping takes place (air is already all in trapped bubbles) and the continued more gradual increase in [¹⁴CO] with depth is due to production by deep-penetrating muons.

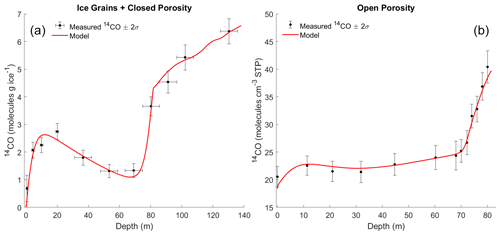
Figure 3 ¹⁴CO measurements at Summit. The [¹⁴CO] measured at Summit in ice grains + closed porosity (a) and in open porosity (firn air) (b), together with an example of our firn model fit to the data. Measured values are after all corrections (Table S4).

Second, we look at the open porosity [¹⁴CO] profile (Fig. 3b). It shows a small peak at ≈ 10 m, representing the previous winter's seasonal maximum in atmospheric [¹⁴CO]. Firn air [¹⁴CO] increases gradually with depth between 30–70 m. This reflects the fact that at deeper levels in the firn, the diffusive gas exchange with the atmosphere is relatively slower, allowing some of the ¹⁴CO produced by the muon mechanisms to accumulate. Firn air [¹⁴CO] increases rapidly in the LIZ, as the impermeable ice layers present in the LIZ almost completely stop vertical gas diffusion, trapping all ¹⁴CO that is produced by muons at these depth levels.

The different tuning parameters in the firn model are each constrained most strongly by different depth ranges of the [¹⁴CO] profile. Because firn shallower than ≈ 60 m contains almost no closed porosity, [¹⁴CO] in the firn matrix in this depth range is sensitive only to in situ production, retention and leakage rates. Further, production rates in the shallowest firn (≈ 0–10 m) are 1–2 orders of magnitude higher than rates in mid-depth firn (≈ 40 m), and in the shallowest firn production is dominated by the neutron mechanism (Fig. 1). As neutron ¹⁴C production rates as well as the ¹⁴CO fraction of total ¹⁴C are well constrained (Sect. 3.2.1), this allows us to use measurements in the 0–60 m depth range to constrain the key relevant parameters in the firn model: R₁, the fraction of produced ¹⁴CO that initially stays in the ice grains, and L₁, the leakage rate of this initially retained ¹⁴CO into porosity (Fig. 2). As mentioned above, $R_{\mathrm{0}}=\mathrm{1}-R_{\mathrm{1}}$ and L₀=1, so these parameters are not tuned in the model.

The [¹⁴CO] in LIZ firn air and in bubbly ice below the LIZ is mainly sensitive to muogenic production rates and to a lesser extent the atmospheric [¹⁴CO] history. We therefore use the [¹⁴CO] measurements in this depth range to provide improved constraints on the muogenic ¹⁴CO production rates. Model [¹⁴CO] in ice grains and closed porosity in the LIZ is extremely sensitive to model characterization of the air-bubble-trapping process. As this characterization is imperfect, we do not use firn/ice samples from the LIZ (70 and 80 m samples in Tables S2–S4) for constraining in situ ¹⁴CO parameters.

4.2 Retention and leakage of in situ cosmogenic ¹⁴CO in the firn

To constrain the best-estimate and possible range of values of the R₁ and L₁ parameters, we employ a grid search approach that involves repeated runs of the firn model while varying these parameters within reasonable ranges determined from preliminary manual tuning of the model to observations. In addition to varying R₁ and L₁, the grid search also varies F_n (the adjustment factor for production rate from neutrons; Sect. 3.2.1). The grid search scans over values for F_n ranging from 0.9 to 1.1 at an interval of 0.01, for R₁ ranging from 0.3 % to 0.7 % at an interval of 0.02 % and for L₁ ranging from 0.3 % yr⁻¹ to 1.3 % yr⁻¹ at an interval of 0.05 %. For the purposes of this grid search, the muogenic ¹⁴CO production rate adjustment factors f_μ− and f_μf are 0.068 and 0.085, respectively, following the best-estimate values from Taylor Glacier measurements (Dyonisius et al., 2023). We also trialed lower f_μ− and f_μf values of 0.0584 and 0.0633 that are more consistent with ¹⁴CO observations in ice below the LIZ (Sect. 4.3); this did not affect the results of this grid search for optimization of the R₁ and L₁ parameters. In total, the grid search amounts to all permutations of 21 different values for each of F_n, L₁ and R₁, resulting in 21³=9261 simulations.

The best-estimate set of parameters minimizes the model–data mismatch for the firn matrix samples (0–60 m depth range; mismatch defined by the reduced χ² value) for the case where F_n=1 (Fig. 4a, purple trace). The best-estimate value for R₁ is 0.46 %, and the best-estimate value for L₁ is 0.60 % yr⁻¹. To define an uncertainty range of these parameters, we accept all solutions from the grid search where the model calculates ¹⁴CO within a 2σ bound of the best solution. The 2σ bound is the mean 2σ analytical uncertainty for the firn matrix ¹⁴CO measurements, and the range of these accepted solutions is represented by the blue shading in Fig. 4a. The contour of accepted solutions in the R₁–L₁ space is shown in Fig. 4b. We also determined which combinations of parameters (from the accepted set of solutions) result in the minimum and maximum ¹⁴CO content in ice below the LIZ, as this is important for constraining f_μ− and f_μf values (Sect. 4.3). The results of the grid search are summarized in Table 2.

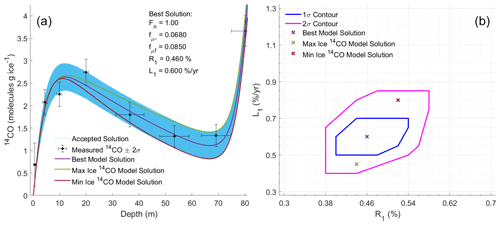
Figure 4 Constraints on ¹⁴CO retention and leakage in Summit firn. Panel (a) shows results for the firn matrix samples that were used to provide the constraints, together with the set of accepted solutions (blue envelope), as well as the best-fit (minimum χ²) solution and the accepted solutions that yield minimum (“Min Ice”) or maximum (“Max Ice”) ¹⁴CO content in ice below the LIZ. Panel (b) shows the set of accepted solutions as well as the best, Min Ice and Max Ice solutions in R₁–L₁ space. R₁ is the fraction of produced ¹⁴CO that initially stays in the ice grains, and L₁ is the leakage rate of this initially retained ¹⁴CO.

Table 2 Results of the grid search for R₁ and L₁ parameters in the firn matrix. Note that the values listed for F_n under the 2σ range column are not determined from the grid search but rather assumed based on published uncertainty estimates for ¹⁴C production rates by neutrons (Sect. 3.2.1.).

Previous discussions of low retention of in situ cosmogenic ¹⁴C in the firn focused on mechanisms such as firn sublimation and recrystallization in combination with wind ventilation (e.g., Lal et al., 2001; Petrenko et al., 2013b). However, our results are quantitatively consistent with a mechanism that involves a very rapid (<1 year) loss from the ice grains of >99 % of produced ¹⁴C, which is too fast to be explained by recrystallization or ventilation. The observation of the rapid loss of almost all in situ ¹⁴C from the ice grains is also consistent with the results of the in situ ¹⁴C production rate comparison between the Antarctic blue-ice areas of Taylor Glacier (Dyonisius et al., 2023; Petrenko et al., 2016) and Scharffenbergbotnen (van der Kemp et al., 2002) that Dyonisius et al. (2023) conducted. The Taylor Glacier results included ¹⁴CO measurements that were obtained with the same method as this study as well as ¹⁴CO₂ measurements that used an ice sublimation technique, while the Scharffenbergbotnen ¹⁴CO and ¹⁴CO₂ measurements were made using a dry-extraction technique. There has been concern with dry-extraction measurements with regard to an incomplete release of in situ ¹⁴C from the ice grains (Smith et al., 2000; van der Kemp et al., 2002). However, if almost all in situ ¹⁴C is rapidly transferred to the air porosity after production, then the dry-extraction technique would be expected to give equivalent results.

We hypothesize that the rapid loss of in situ ¹⁴C from ice grains is mainly driven by diffusion of the ¹⁴C-containing gas molecules (¹⁴CO, ¹⁴CH₄, ¹⁴CO₂). While we are not aware of prior estimates of CO diffusivity through ice, both measurement-based estimates and estimates based on molecular dynamics simulations indicate that gases with smaller molecular diameters diffuse faster through ice than gases with larger molecular diameters (e.g., Patterson and Saltzman, 2021, and references therein). There are estimates of gas diffusivity through ice available for CH₄ (Ikeda-Fukazawa et al., 2004; Noguchi et al., 2019) and O₂ (Ikeda-Fukazawa et al., 2005). CH₄ has a slightly larger molecular diameter than CO, while O₂ has a slightly smaller molecular diameter (Severinghaus and Battle, 2006); thus diffusivity estimates for CH₄ and O₂ should be indicative of the possible range for CO diffusivity through ice. Noguchi et al. (2019) experimentally determined the diffusivity of CH₄ through ice at 257 K, with $D_{{\mathrm{CH}}_{\mathrm{4}},\mathrm{257}\mathrm{K}}=(\mathrm{5.2}\pm \mathrm{1.4})\times {\mathrm{10}}^{-\mathrm{11}}$ m² s⁻¹. Ikeda-Fukazawa et al. (2004) used molecular dynamics simulations to estimate CH₄ diffusivity, with average of $D_{{\mathrm{CH}}_{\mathrm{4}},\mathrm{257}\mathrm{K}}=\mathrm{3.6}\times {\mathrm{10}}^{-\mathrm{11}}$ m² s⁻¹, in fairly good agreement with the experimental estimate. To be conservative, we take the lower estimate (Ikeda-Fukazawa et al., 2004) and recalculate it (following the temperature dependence in Ikeda-Fukazawa et al., 2004) for the temperature of the Greenland Summit site (−31 °C; Buizert, 2013). This yields $D_{{\mathrm{CH}}_{\mathrm{4}},\mathrm{242}\mathrm{K}}=\mathrm{1.2}\times {\mathrm{10}}^{-\mathrm{11}}$ m² s⁻¹.

For O₂, Ikeda-Fukazawa et al. (2005) used molecular dynamics simulations to estimate the diffusivity through ice as a function of temperature. This relationship yields $D_{{\mathrm{O}}_{\mathrm{2}},\mathrm{242}\mathrm{K}}=\mathrm{2.8}\times {\mathrm{10}}^{-\mathrm{11}}$ m² s⁻¹. The Ikeda-Fukazawa et al. (2005) estimates were recently called into question by Oyabu et al. (2021), who used observations of diffusive smoothing of the $\mathit{\delta }{\mathrm{O}}_{\mathrm{2}}/{\mathrm{N}}_{\mathrm{2}}$ signal with depth in the Dome Fuji ice core to show that the permeation coefficients (product of diffusivity and solubility) of O₂ as estimated by Ikeda-Fukazawa et al. (2005) are likely too high (by a factor of ≈ 5 at 242 K). If we assume that this difference in permeation coefficients is due to overestimates of diffusivity, we can lower the Ikeda-Fukazawa et al. (2005) value by a factor of 5 to yield $D_{{\mathrm{O}}_{\mathrm{2}},\mathrm{242}\mathrm{K},\mathrm{adjusted}}=\mathrm{5.6}\times {\mathrm{10}}^{-\mathrm{12}}$ m² s⁻¹. As we consider the question of whether gas diffusion can be fast enough to explain the observed rapid loss of in situ ¹⁴CO from ice grains at Summit, we use this diffusivity estimate (lowest of the set of values discussed above) to be conservative. The characteristic timescale for diffusion can be estimated as $t=L^{\mathrm{2}}/D$, where L is the diffused distance and D is the diffusivity. Taking a typical firn grain radius as 3 mm (Linow et al., 2012), the timescale for diffusion out of the firn grain is then 0.05 years (18 d), which is sufficiently fast to be consistent with our observations.

If our hypothesis is correct, then the rate of rapid loss of in situ ¹⁴C from the firn grains would be site dependent, with less rapid loss predicted at colder sites. If we use the temperature dependence of CH₄ diffusivity from Ikeda-Fukazawa et al. (2004), then the diffusivity in ice at a very cold ice core site such as Dome C ($T=-\mathrm{54}$ °C) would be ≈ 7 times lower than at the Greenland Summit site. However, this lower diffusivity would still be sufficient to allow for complete loss of in situ ¹⁴C from firn grains on a timescale of faster than 1 year. The lack of retention of in situ ¹⁴C in the firn even at cold sites is consistent with findings from prior measurements of ¹⁴CO and ¹⁴CO₂ in the Dome C ice core using a dry-extraction technique (de Jong et al., 2004).

Regarding the ≈ 0.5 % of in situ produced ¹⁴CO that is not lost rapidly from the firn matrix, it may be possible that this ¹⁴CO becomes trapped in microbubbles or at dislocations or grain boundaries in the ice lattice. Microbubbles (closed porosity in firn above the lock-in zone) have been observed at ice core sites in both Antarctica (e.g., Siegenthaler et al., 2005) and Greenland (Petrenko et al., 2013b; this study; see Table S2) and would be expected to retain ¹⁴CO in the same way as bubbles in deeper ice. Further movement of ¹⁴CO from microbubbles to open porosity would be controlled by the gas permeation coefficient (product of diffusivity and solubility). As solubility of gases in ice is very low (e.g., Patterson and Saltzman, 2021, and references therein), this process is slow. This is different from the situation of ¹⁴CO immediately following in situ production, as in this case ¹⁴CO is already in the ice lattice and only diffusivity matters. Dislocations and grain boundaries tend to concentrate impurities (e.g., Stoll et al., 2021, and references therein), and it may be possible that interactions with other impurities help to retain ¹⁴CO molecules. This trapped ¹⁴CO could then be released more slowly (as mentioned above, our best-estimate leakage rate for this slow process is 0.6 % yr⁻¹) as the microbubbles disintegrate or as dislocations and grain boundaries come in contact with porosity via the relatively slow process of recrystallization.

4.3 Production rates from muon mechanisms

4.3.1 Approach for constraining production rates from muon mechanisms

In this study, we require the determined muogenic ¹⁴CO production rates to be consistent with both Taylor Glacier (Dyonisius et al., 2023) and Summit measurements. Dyonisius et al. (2023) determined the possible set of f_μ−–f_μf pairs via comparison of predictions from an ice flow model for Taylor Glacier that included in situ ¹⁴CO production with Taylor Glacier measurements. We take the set of f_μ−– f_μf pairs from Dyonisius et al. (2023) that represents the 2σ range (3851 pairs) and perform repeated runs of the model, comparing the model ¹⁴CO results with measurements in ice below the LIZ and in firn air in the LIZ. As different sets of f_μ−– f_μf pairs yield optimal solutions for ice and LIZ firn air, we define the “best” and accepted range of f_μ−–f_μf pairs separately for ice and LIZ air. In each case, the reduced χ² value is once again used to define the best f_μ−–f_μf pair. The accepted sets of f_μ−–f_μf pairs are those that yield model solutions that fall within the 2σ uncertainty bound from the best solution. The 2σ uncertainty bound is defined separately for ice and LIZ firn air and is equal to the mean 2σ measurement uncertainty for samples within the depth range used for the model–data comparison. The final accepted set of f_μ−–f_μf pairs represents the overlap between the sets accepted for ice and for LIZ firn air.

As discussed above, the ¹⁴CO content in bubbly ice below the LIZ and in LIZ firn air is sensitive to the atmospheric [¹⁴CO] history in addition to muogenic ¹⁴C production rates. We use several possible atmospheric [¹⁴CO] scenarios (Sect. 4.3.2) to ensure that we are capturing the full possible range of accepted of f_μ−–f_μf pairs. For each [¹⁴CO] scenario, we repeat the firn model runs for each f_μ−–f_μf pair from Dyonisius et al. (2023). Finally, the choice of retention and leakage parameters does have a small impact on the ¹⁴CO content in bubbly ice below the LIZ. We therefore also repeat the above sets of firn model runs with R₁, L₁ and F_n parameters set to either the best-estimate values or the min or the max values in Table 2.

4.3.2 Atmospheric [¹⁴CO] history scenarios

The “baseline” atmospheric [¹⁴CO] history for the Greenland Summit site used in this study (Fig. 5, scenario 1) was developed by Hmiel et al. (2020) and discussed in their “Supplementary information”. This history is based on atmospheric ¹⁴C production as indicated by the sunspot group number and was constructed as follows. We used the longest available record of atmospheric [¹⁴CO] measurements from Manning et al. (2005) (from New Zealand and Antarctica) and the sunspot group number record from Svalgaard and Schatten (2016). For the period of overlap between these two records, we applied a linear regression of the annual sunspot group number and a 12-month moving average of the Southern Hemisphere (SH) [¹⁴CO] measurements corrected for the secondary [¹⁴CO] component (∼ 10 %) that arises from CH₄ and non-CH₄ hydrocarbon oxidation and biomass burning (Manning et al., 2005). This yields the Southern Hemisphere (SH) [¹⁴CO]–sunspot group number relationship, which is then applied to the earlier part of the sunspot group number record to construct a SH cosmogenic [¹⁴CO] history. A constant offset of +6.98 molecules cm⁻³ STP is then applied to the SH [¹⁴CO] history to account for the higher mean annual [¹⁴CO] at the Greenland Summit site as compared to the SH as well as for the secondary component of [¹⁴CO] (e.g., Jöckel and Brenninkmeijer, 2002). Lastly, the seasonal cycle in [¹⁴CO] (not shown in Fig. 5) is developed from fitting a harmonic function to the available records of Northern Hemisphere [¹⁴CO] from the high-latitude sites of Alert, Ny-Ålesund and Barrow (Jöckel and Brenninkmeijer, 2002). The [¹⁴CO] seasonal cycle amplitude and the constant Greenland–SH offset were optimized by trialing a range of values in the firn model to minimize the reduced χ² metric for the difference between model and firn air [¹⁴CO] observations in the 0–60 m depth range.

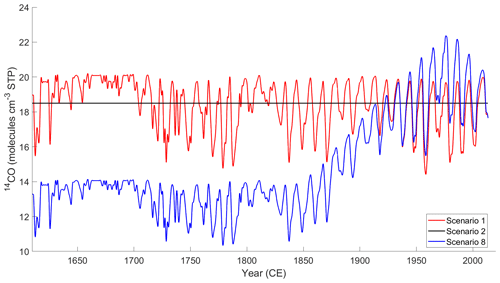
Figure 5 Paleoatmospheric [¹⁴CO] scenarios. Visualization of some of the paleoatmospheric ¹⁴CO history scenarios used in constraining muogenic ¹⁴CO production tuning factors f_μ− and f_μf. Scenario names in the figure caption correspond to the list in Sect. 4.3.2.

While the baseline atmospheric [¹⁴CO] history at Summit described above takes into account variations in the atmospheric ¹⁴C production rate, atmospheric [¹⁴CO] is also sensitive to variations in hydroxyl radical concentrations ([OH]); stratosphere-to-troposphere transport (STT); and, to a lesser extent, changes in secondary ¹⁴CO sources such as CH₄ and volatile organic compound (VOC) oxidation and biomass burning (e.g., Jöckel and Brenninkmeijer, 2002). Variability in global [OH] is relatively well constrained via observations of methyl chloroform back to the mid-1990s (e.g., Montzka et al., 2011; no large changes) but more uncertain further back in time. With regard to STT, we investigated the sensitivity of [¹⁴CO] over Greenland to changes in the Brewer–Dobson circulation using a preliminary implementation of ¹⁴CO in the GEOS-Chem chemical transport model. A preindustrial run was compared with a 4xCO₂ run in GEOS-Chem (the Brewer–Dobson circulation is expected to intensify with warming), and no significant change in [¹⁴CO] over Greenland was found.

However, to ensure that plausible f_μ−–f_μf pairs were not excluded, we still allowed for relatively large (up to 30 %) variability in [¹⁴CO] as compared to the baseline scenario to account for possibilities such as Northern Hemisphere [OH] variations prior to the 1990s in response to large changes in emissions of reactive species, increasing uncertainty in the atmospheric ¹⁴C production rates further back in time and possible changes in the frequency of stratospheric air intrusions. The [¹⁴CO] atmospheric history scenarios we trialed differed as follows from the baseline scenario:

1. baseline scenario

2. constant [¹⁴CO] at all times at 18.5 molecules cm⁻³ STP

3. +15 % change from the baseline at all times

4. −15 % change from the baseline at all times

5. −30 % change from the baseline at all times

6. a linear increase in [¹⁴CO] back in time from baseline [¹⁴CO] in 2013, reaching +15 % at 1980, then a linear decrease further back in time, reaching −15 % at 1850 as compared to the baseline, with −15 % from the baseline for ages older than 1850

7. same temporal structure as 6, except for variations of +30 % in 1980 and −30 % at 1850 and older

8. same temporal structure as 6, except for variations of +15 % in 1980 and −30 % at 1850 and older.

4.3.3 Results for muogenic ¹⁴CO production rate tuning factors f_μ− and f_μf

Figure 6 shows the results for the trialed combination of atmospheric [¹⁴CO] history and R₁, L₁ and F_n parameters that yields the largest accepted set of f_μ−–f_μf pairs. This set, which yields solutions that give a good fit to the measurements in both bubbly ice and LIZ firn air, is bounded by the blue contour in Fig. 6c. Table 3 compares the 2σ ranges for f_μ− and f_μf values between this study and Dyonisius et al. (2023). As can be seen, the Summit results are consistent with most of the f_μ− range from the Taylor Glacier (TG) study but only with approximately the lower half of the f_μf range. This is not surprising – the Taylor Glacier results for f_μf had larger relative uncertainties, due mainly to uncertainties in the depth of ice transport in the glacier over the last few thousand years. Our results are consistent with the relatively shallower Taylor Glacier flowlines considered in Dyonisius et al. (2023).

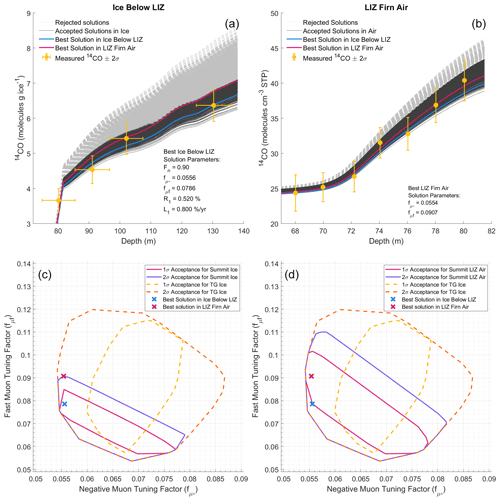
Figure 6 Constraints on f_μ− and f_μf values. Results from repeated runs of the firn model with the full set of f_μ−–f_μf pairs from Dyonisius et al. (2023). In the shown model runs, atmospheric [¹⁴CO] history scenario 8 (see Sect. 4.3.2) was used, along with the set of F_n, R₁ and L₁ values that yield minimum ¹⁴CO content in ice below the LIZ (Table 2). Panel (a) shows the model run results for ¹⁴CO content in ice below the LIZ, and panel (b) shows the results for LIZ firn air. Panels (c) (ice) and (d) (LIZ firn air) show the corresponding contours of accepted sets of f_μ−–f_μf values.

Table 3 Comparison of f_μ ranges from Dyonisius et al. (2023) and this work.

We note that the atmospheric [¹⁴CO] history scenarios that result in the best model fit to both the bubbly-ice and LIZ firn air measurements all contain significant temporal variability, with [¹⁴CO] around 1980 that is higher than predicted from estimated atmospheric ¹⁴CO production rates and [¹⁴CO] prior to ≈ 1920 that is lower than predicted (Sect. 4.3.2 and Fig. 5). Such variability, if real, may be indicative of long-term changes in Northern Hemisphere hydroxyl radical concentrations and could be investigated more effectively at a site with a very high accumulation rate (e.g., southeastern Greenland dome; Iizuka et al., 2017) where the in situ ¹⁴CO component would be minimized.

4.3.4 Discussion of implications for muogenic ¹⁴C production rates

Because Dyonisius et al. (2023) observed a constant in situ ${}^{\mathrm{14}}\mathrm{CO}{/}^{\mathrm{14}}{\mathrm{CO}}_{\mathrm{2}}$ production ratio, our results also indirectly confirm their finding that muogenic ¹⁴C production rates for ¹⁴C-bearing gases in ice appear to be much lower than total ¹⁴C production rates predicted from studies of quartz. Dyonisius et al. (2023) considered this discrepancy and were able to rule out the following as possible explanations: (1) analytical issues with ice core ¹⁴C measurements (good agreement between independent methods), (2) much higher historical ice ablation rates as compared to modern ones (not supported by paleoclimate data; also for the Greenland Summit site the ice chronology is very well determined, so the accumulation rate is not in question), (3) f_μf of 0 and a much higher f_μ− (this would be consistent with ¹⁴C results from a rock core but is not consistent with ice core data), (4) the unmeasured organic fraction of in situ ¹⁴C in ice explaining the difference (organic fraction is <25 %, so this is too small), and (5) a value used for α (0.75; see Eq. 5) which is too small (using an upper-end value for α does not change the results appreciably).

If there was a process that destroyed ¹⁴CO to a significant extent in ice at the Greenland Summit site and other previously sampled locations, biasing the ice core measurements low, this could help to reconcile the observed muogenic ¹⁴C production rate difference between ice and quartz. Such a chemical or biological process would very likely be temperature and/or impurity dependent and, therefore, site dependent. There are two previously published ice core ¹⁴CO data sets using different methodology from two different locations in Antarctica, Scharffenbergbotnen (van der Kemp et al., 2002) and Taylor Glacier (Dyonisius et al., 2023), and these agree with each other with regard to production rates within uncertainties, as do the Greenland Summit site and Taylor Glacier. An additional new ¹⁴CO data set from Law Dome, Antarctica, is also consistent with the muogenic production rates determined here (Petrenko et al., 2023). Further, while CO in Greenland ice cores is known to be affected by in situ production, CO in Antarctic ice cores appears to be generally well preserved, and there is no evidence of CO destruction in either Greenland or Antarctic ice cores (e.g., Faïn et al., 2022, 2023; Haan et al., 1998). This process therefore seems highly unlikely to explain the ice–quartz disagreement.

Partitioning of hot in situ ¹⁴C atoms among different species in the polar ice cores is unlikely to be site dependent because impurities are present in Greenland and Antarctic ice cores at trace levels (on the order of parts per million or lower), so the probability of a hot ¹⁴C atom bonding with atoms other than O and H is very low. The agreement among different ice core sites with regard to ¹⁴CO production rates suggests constant partitioning of muogenic in situ ¹⁴C. Variations in hot ¹⁴C partitioning in ice therefore also seem unlikely to explain the ice–quartz disagreement.

It may in principle be possible that gas-phase ice core ¹⁴C measurements (¹⁴CO + ¹⁴CO₂ + ¹⁴CH₄) are missing the majority of in situ ¹⁴C if the majority of this ¹⁴C is present as non-gas species. While the organic fraction of ¹⁴C mentioned above seems too small to be the main explanation, it may be possible that other forms of inorganic carbon (HCO${}_{\mathrm{3}}^{-}$, CO${}_{\mathrm{3}}^{\mathrm{2}-}$) play a role.

5 Conclusions

This study has provided the most comprehensive characterization to date of the production, movement and retention of in situ cosmogenic ¹⁴CO in the firn layer of an accumulation site. Our results conclusively show that only a very small fraction (<0.6 %) of total in situ cosmogenic ¹⁴CO that is produced in the ice grains initially stays in the ice grains. Measurements in the firn matrix indicate that the vast majority of in situ ¹⁴CO is lost very rapidly to the open porosity in the firn. Gas diffusion through ice appears to be the most likely process responsible for this rapid loss. Our firn matrix measurements also conclusively demonstrate that there is a second, much slower process for loss of in situ ¹⁴CO from the ice grains that occurs on timescales that could be consistent with the process of firn recrystallization. More measurements from different ice core sites would provide further insight into ¹⁴C loss and retention processes and would allow for explicit inclusion of these physical processes into future models of in situ ¹⁴C in the firn.

While the uncertain atmospheric [¹⁴CO] history over Greenland translates into increased uncertainties in the determination of muogenic ¹⁴CO production rates in ice, we were nevertheless able to further narrow the possible range of these production rates. These findings help to lay the groundwork for ice core studies of past atmospheric [¹⁴CO] and past cosmic ray flux, as well as for ice core studies that use other ¹⁴C-containing gases for applications such as examining the past atmospheric methane budget (using ¹⁴CH₄) and the past carbon cycle (using ¹⁴CO₂). Finally, our results continue to highlight the apparent discrepancy in muogenic ¹⁴C production rates determined from studies of gases in ice versus those determined from studies of quartz. No clear explanation for this discrepancy currently exists, although it is possible that studies of ice to date have missed some of the species that in situ ¹⁴C partitions into. Future studies that provide more comprehensive characterization of ¹⁴C in ice cores (including gas species and non-gas organic and inorganic carbon species) as well as laboratory studies involving muon irradiation of ice samples may be helpful in resolving this disagreement. For completeness, future studies could also explicitly consider uncertainties in all muogenic ¹⁴C production parameters, such as muon fluxes and energies.