the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Brief communication: A continuous formulation of microwave scattering from fresh snow to bubbly ice from first principles
Ghislain Picard
Henning Löwe
Christian Mätzler
Microwave remote sensing of the cryosphere demands a formulation of the scattering coefficient which can be applied over the entire range of relevant densities, from fresh snow to bubbly ice, at all frequencies and for any grain size and snow type. Most challenging are intermediate densities (450–550 kg m−3) and high frequencies (or coarse-grained snow) where current scattering formulations break down. In this brief communication we demonstrate that the strong contrast expansion method recently developed for heterogeneous, dielectric media can be applied to microwave scattering in snow, firn and ice to solve these problems.
- Article
(917 KB) - Full-text XML
- BibTeX
- EndNote
Optimal use of satellite observations to retrieve information from the snowpack requires a precise understanding of the interaction between electromagnetic waves and snow. In the microwave domain, a thorough model for the radiation emitted or reflected by a snowpack involves three main ingredients: (1) a snow microstructure representation, which determines the input parameters that must be collected in the field or obtained from a snowpack evolution model; (2) an electromagnetic theory to compute the scattering and absorption coefficients in each snow layer from the given microstructure parameters; (3) a method to solve the radiative transfer equation that describes the propagation of the radiation from layer to layer up to the surface. Well-established and accurate methods exist for the last ingredient as long as the snowpack has a plane-parallel layered structure (e.g., Tsang et al., 2000; Jin, 1994). The first ingredient is an active research topic that has received much attention in the last decades (e.g., Mätzler, 2002; Royer et al., 2017; Sandells et al., 2021; Picard et al., 2022a) because it is a major source of uncertainties. The second ingredient is the topic of this communication.
Established rigorous and empirical electromagnetic theories have been used for decades by the snow community. The most popular ones are the Helsinki University of Technology (HUT) empirical relationship (Pulliainen et al., 1999), the improved Born approximation (IBA) (Mätzler, 1998) and dense-media radiative transfer quasi-crystalline approximation (DMRT-QCA) theory (Tsang et al., 1985). Despite being used with reasonable success, all of these formulations have some fundamental, and therefore practical, limitations. These limitations originate from restricting assumptions in these theories about the grain size, grain shape and snow density which prevent consistent microwave modeling of snow, firn and ice in the entire range of density and microstructures found throughout the cryospheric regions. The development of robust retrieval algorithms of snow properties requires improved consistent scattering theories.
In what follows, we shall pinpoint these limitations and their implications and demonstrate how they can be simultaneously overcome by employing new, theoretical results on the effective permittivity of random porous media. In a recent paper, Torquato and Kim (2021) (hereinafter TK21) propose the non-local, strong contrast expansion (SCE) as a generic homogenization theory to compute effective wave propagation in any random two-phase medium. A careful inspection of the comprehensive (54-page) derivation and of two precursor papers (Rechtsman and Torquato, 2008; Kim and Torquato, 2020) reveals that it sheds new light on three key problems regarding snow, concerning the grain size, grain shape and density. The objective of this communication is to relate this new theory to existing ones and to feature the powerful approach (Torquato and Kim, 2021) through its implementation in the Snow Microwave Radiative Transfer model (SMRT, Picard et al., 2018).
Our starting point is the main result of the strong contrast expansion (Rechtsman and Torquato, 2008; Kim and Torquato, 2020; Torquato and Kim, 2021), which expresses the dielectric polarizability of an effective medium (in any dimension d) with respect to the background material as an exact infinite series in the dielectric polarizability of the foreground material with respect to the background. Here, we consider the particular case of snow, assumed to be an isotropic three-dimensional medium composed of ice (foreground) and air (background). The effective polarizability βeff-air reads (Eq. 54 in TK21) as
where ϕice is the fractional volume of ice and keff0 the wave number in the effective medium in the static approximation (this version is referred as to “scaled SCE” in TK21 section VI.B.2 and is used here for consistency with the other theories). The terms are discussed below. The polarizability for the effective medium (eff) or material (air or ice) denoted as 1 and 2 is defined as
To simulate the snow electromagnetic properties, a model will first deduce the effective permittivity ϵeff of the ice and air mixture using Eq. (2) from calculated with Eq. (1) once the other terms are calculated. The extinction coefficient is deduced from the imaginary part of the effective dielectric constant Ke=2k0ℑϵeff, where k0 is the wave number in the vacuum and ℑ takes the imaginary part. While not considered in TK21, the absorption coefficient is obtained here in the static regime (k0=0 or formally by setting An=0 for all n). The scattering coefficient is finally obtained by .
The terms are complicated expressions (Eqs. 51–53 in TK21) but only depend on the microstructure and the wave number. They carry all the geometrical information of the medium microstructure (only the fractional volume appears in other parts of the theory) and are thereby the main driver of the scattering signature of the medium. is an integral over space of the two-point correlation function (Eqs. 51 in the general case and 67–69 for the isotropic case in TK21). Roughly speaking, this function accounts for the size, shape and relative arrangement in space of the ice crystals (Picard et al., 2022a). It can be obtained by computing the auto-covariance of three-dimensional images of the snow (Sandells et al., 2021). This term is similar to the I integral in the IBA (Mätzler, 1998) and is linked to the pair correlation in DMRT (Tsang and Kong, 2001; Löwe and Picard, 2015).
For a given order n, the term depends on all n-point correlation functions up to that order. This implies that the calculation of the terms n>2 would require increasingly more detailed information on the microstructure (e.g., larger and more resolved three-dimensional images of the snow microstructure), which has hitherto not been available for snow in practice (Sandells et al., 2021). Not mentioning the difficulty of the numerical computation of these complex terms, we thereby consider the term n=2 only at this stage. The numerical implementation of SCE and of the other approximations presented below have been done in the SMRT model, an open-source, active and passive microwave radiative transfer model (Picard et al., 2018).
As stated in its title, TK21 develops the “non-local” SCE, extending former work on the “local” SCE (RT08). The latter requires very small-sized scatterers with respect to the wavelength (i.e., the quasi-static approximation) and the absence of large aggregates of scatterers, which makes it more suitable for low microwave frequencies (the equivalent terminology in DMRT is long- and short-range approximations, Tsang and Kong, 2001, which was adopted in SMRT). The main difference between the two versions appears in the term and implies a numerical integration accounting for the surrounding microstructure in the non-local SCE instead of a simple function evaluation in the local version. The extra computational cost and risk of numerical instability are to be balanced with the gain in accuracy. To assess this gain for snow, Fig. 1 presents the scattering coefficient for sticky spheres of radius a as a function of k0a (the simulations are run with a fixed radius of 0.5 mm, stickiness of 0.2 and varying frequency of up to 150 GHz). The results for a density of 300 kg m−3 show a sharp increase as a function of k0a for several of the models. This increase indeed follows a power law in at low frequencies which tend to slow down in the case of the long-range theories (TK21, IBA, and the Mie DMRT version implemented in the DMRT-QMS model, Tsang et al., 2007) when k0a is increasing (e.g., we found an apparent relationship for SymSCE when fitted around k0a=1). These results also indicate that the short-range theories (SCE RT08 and the two DMRT flavors available in SMRT) diverge for k0a⪆0.6 from the long-range theories. Additionally, the long-range theories remain close to each other up to k0a≈1.5, and they diverge for even larger grain sizes. While including additional terms (with n>2) extends in principle the SCE capability to work beyond this range, we note that TK21 indicates an upper bound of the order of the wavelength (i.e., k0a⪅1) for their general theory.
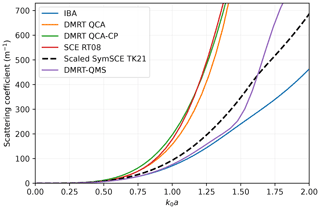
Figure 1Scattering coefficient as a function of the product of wave number and radius (k0a) for a variety of electromagnetic theories. The microstructure is made of sticky hard spheres with radius 0.5 mm, stickiness 0.2 and density 300 kg m−1.
Overall, these results give additional confidence in the three long-range theories, even with the n=2 truncation, being applicable for most snows in the microwave range. Moreover, TK21 conducted numerical electromagnetic simulations using the finite-difference time-domain method that compare favorably with SCE for a dielectric contrast comparable to that of ice and air and up to ka≈1 (Fig. 9 in TK21). These results also highlight the equivalence between SCE, IBA and DMRT-QMS up to about k0a≈1.5. Based on these results, our main practical recommendation is limiting the size in the range where these three theories agree.
The different scattering theories require some assumptions about how the medium microstructure is prescribed, and these assumptions have a critical impact on the scattering signature. In the original DMRT (Tsang et al., 1985; Tsang and Kong, 2001), spherical particles are assumed, with their relative positions determined by the sticky hard-sphere model. Despite the success of this theory, snow is composed of diverse shapes interconnected in a complex manner that prevents successful mapping onto the sticky hard-sphere model (Löwe and Picard, 2015). In the IBA, this restrictive assumption about the shape of the scatterers is partially removed. While IBA still assumes a particular shape to compute the internal field ratio in the scatterers, it leaves free the choice of the two-point correlation function that can be accurately constrained by data (Sandells et al., 2021). However, technically it is possible (and practically done) to select a shape and form of correlation function independently and inconsistently (e.g., spherical scatterers and an exponential correlation function). The internal field ratio can also be optimized from experimental data (Mätzler, 1996, 1998) without explicitly assuming a geometrical shape.
The SCE derivation does not rely on the scatterer concept, the medium is exhaustively described by the n-point correlation functions and the electromagnetic derivation uses the Green function formalism (Tsang and Kong, 2001). Nevertheless, an infinitesimal exclusion volume is required to integrate the Green function, and its shape determines the form of the final SCE equations. TK21 chooses a sphere for this volume (Eq. 25 in TK21) in the main text and illustrates the results for two alternative shapes (Appendix A in TK21, Eqs. A1 and A2). These three equations constitute different forms but are strictly equal in the infinite series. However, in practice, the necessary truncation breaks this equality. Further noting that the spherical exclusion volume provides a faster convergence (TK21 Sect. III B) as a function of the dielectric contrast in the case of isotropic media, the conclusion is that a spherical exclusion volume is recommended for any isotropic microstructure, i.e., independently of the existence (and shape) of individual scatterers.
Interestingly, by analyzing the similarities between IBA and SCE expressions, it appears that choosing the scatterer shape in the IBA and the exclusion volume in SCE leads to similar analytical polarizability equations. The numerical results also highlight the similarity between both theories (Fig. 2). We conclude that, while getting rid of the scatterer concept is a theoretical advance of SCE, it does not lead to numerical improvements in practice.
Despite being developed for dense media, the existing theories used for snow actually become inaccurate at high density. The DMRT theory was shown to degrade for fractional volume ϕice>0.3 (Liang et al., 2006) when compared to exact electromagnetic calculations, possibly because of the limitation of the Percus–Yevick approximation applied for solving the sticky hard-sphere model. The SCE theory is invalid when the ice phase is percolating (RT08), which also occurs from ϕice around 0.3 for many microstructures. Regarding IBA, the apparent permittivity is valid for ϕice⪅0.5, and little is known about the other parts of this theory. This general limitation is severely restrictive for application to snow, where density is often larger than 300 kg m−3, especially on glaciers and in the firn.
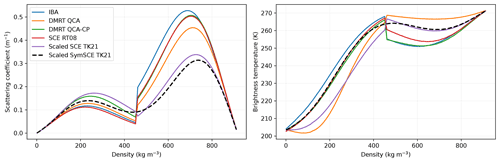
For very high density, when the fractional volume of air is <0.3, a possible workaround is to “invert” ice and air in the equations. No theoretical limitation forbids this inversion. In any case, a wide range of common intermediate densities remains inaccessible (≈ 300–700 kg m−3). RT08 and Dierking et al. (2012) independently suggest the following method: the theory is applied up to the percolation limit on both sides (ϕice=0–0.3 and 0.7–1), and spline interpolation is used in between. This ad hoc correction is effective in smoothening the discontinuity that appears when using medium inversion at ϕice=0.5 (Fig. 2), but it lacks a physical basis.
An alternative rigorous approach is proposed in TK21. Considering that (i) the infinite expansion Eq. (1) is exact and that (ii) the same expansion applied with ice and air switched is exact as well, then any combination of both expansions will be exact as well. Let us choose a linear combination weighted by 1−ϕice and ϕice for the normal and inverted media, respectively, so that a higher weight is given to the normal medium at low ϕice and to the inverted medium at high ϕice. Once truncated at n=2, this combination yields a quadratic equation in ϵeff that is solved analytically (Eq. D2 in TK21). This provides a new approximation of the scaled SCE that we call scaled SymSCE.
Figure 2 shows the scattering coefficient computed for several theories and approximations as a function of snow density. Sticky hard spheres with a radius of 0.4 mm and a stickiness of 0.2 are used for all the simulations. For very low and very high ice fractional volumes, all theories give similar results showing an excellent agreement between the new SymSCE theory and the established ones. They however all differ in the intermediate range (150–800 kg m−3, often moderately, but by a factor of up to 2 around ϕice=0.5 (458 kg m−3). For comparison, this value can be compared to the 1.5-fold uncertainty in scattering resulting from the typical 15 % uncertainty in the measured optical radius of snow (Gallet et al., 2009). As expected, all but SymSCE are affected by a discontinuity around ϕice=0.5, where we chose to invert the materials. Despite this nice and improved behavior, it still remains to prove that SymSCE is more accurate than the other theories. Figure 2 also shows the consequences for the brightness temperature for a hypothetical semi-infinite single homogeneous layer of snow (at 273 K). Note that, for this calculation, the phase matrix of the radiative transfer equation is needed. It is not available for the SCE theory, and we assumed that its angular variations are the same as predicted by IBA. The overall trend is an increasing function, mainly driven by the monotonous increase in the absorption with density. Scattering modulates this overall trend. Despite this secondary role, the differences between the theories reach 15 K in a wide range of densities, a significant uncertainty.
SymSCE is not the unique possible combination of SCE equations to yield a symmetrical behavior (e.g., and are possible). However, there is one reason to prefer this particular definition. In the static regime, only the SymSCE reduces to the Polder and van Santen mixing formula (Polder and van Santen, 1946), which is the most accurate theoretical equation for predicting the real part of snow permittivity (Mätzler, 1996; Olmi et al., 2021). It is worth noting that the procedure of linear combination is not specific to SCE: it was previously proposed to symmetrize the Maxwell Garnett mixing formula, yielding the Polder and van Santen mixing formula (Sihvola, 1999), and it could be applied to IBA and DMRT equations to remove the discontinuity.
The non-local symmetrized SCE theory presented in TK21 and featured in this brief communication provides several conceptual remedies to long-standing problems in other theories commonly used to compute snow scattering from microstructure information. The key point is that the strong contrast expansion is exact and does not require any assumption until the truncation at the end of the development. The actual accuracy of this theory for practical snow simulations is however not known and could only be assessed with detailed ground truth after eliminating other major uncertainties like the snow microstructure, soil parameters, or surface roughness.
Nevertheless, the SCE as presented in TK21 is even more general than applied here (isotropic medium and truncation at n=2), paving the way for further improvements. For instance, the calculations of the higher terms of the series (n>2) is complicated but should extend the validity range to higher frequencies and/or coarser-grained snow, provided that more detailed microstructure information can be obtained (i.e., the three-point correlation function). The general case of anisotropic media is explicitly treated in TK21, which is needed to explain some experimental results on snow scattering at low frequencies (Leinss et al., 2016). Finally, we suggest that further work should assess the accuracy of the different long-range theories, which will require more precise in situ active or passive microwave (backscatter or brightness temperature) and snow measurements (density, grain size, temperature) from snowpack with intermediate densities (450–500 kg m−3) than are available at present.
The SMRT model code is available from https://github.com/smrt-model/smrt and https://doi.org/10.5281/zenodo.7086080 (Picard et al., 2022b). The code to produce the figures is available from https://github.com/smrt-model/strong_expansion_theory_paper/ (https://doi.org/10.5281/zenodo.7086089, Picard, 2022). The DMRT-QMS model is available from https://web.eecs.umich.edu/~leutsang/Computer Codes and Simulations.html (Tan and Tsang, 2022).
GP conducted the study, implemented the SCE in SMRT and ran the simulations. HL and CM contributed to the analysis and the results. All the authors contributed to the manuscript.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This research has been supported by the European Space Agency (grant no. 4000112698/14/NL/LvH).
This paper was edited by Mark Flanner and reviewed by two anonymous referees.
Dierking, W., Linow, S., and Rack, W.: Toward a robust retrieval of snow accumulation over the Antarctic ice sheet using satellite radar, J. Geophys. Res., 117, D09110, https://doi.org/10.1029/2011JD017227, 2012. a
Gallet, J.-C., Domine, F., Zender, C. S., and Picard, G.: Measurement of the specific surface area of snow using infrared reflectance in an integrating sphere at 1310 and 1550 nm, The Cryosphere, 3, 167–182, https://doi.org/10.5194/tc-3-167-2009, 2009. a
Jin, Y. Q.: Electromagnetic scattering modelling for quantitative remote sensing, World Scientific, https://doi.org/10.1142/2253, 1994. a
Kim, J. and Torquato, S.: Multifunctional composites for elastic and electromagnetic wave propagation, P. Natl. Acad. Sci. USA, 117, 8764–8774, https://doi.org/10.1073/pnas.1914086117, 2020. a, b
Leinss, S., Löwe, H., Proksch, M., Lemmetyinen, J., Wiesmann, A., and Hajnsek, I.: Anisotropy of seasonal snow measured by polarimetric phase differences in radar time series, The Cryosphere, 10, 1771–1797, https://doi.org/10.5194/tc-10-1771-2016, 2016. a
Liang, D., Tse, K., Tan, Y., Tsang, L., and Ding, K. H.: Scattering and Emission in Snow Based on QCA/DMRT and Numerical Maxwell Model of 3Dimentional Simulations (NMM3D), IEEE MicroRad, In Proceedings of the IEEE 9th Specialist Meeting on Microwave Radiometry and Remote Sensing of the Environment (MicroRad 2006), 28 February–3 March 2006, San Juan, Puerto Rico, 197–202, https://doi.org/10.1109/MICRAD.2006.1677088, 2006. a
Löwe, H. and Picard, G.: Microwave scattering coefficient of snow in MEMLS and DMRT-ML revisited: the relevance of sticky hard spheres and tomography-based estimates of stickiness, The Cryosphere, 9, 2101–2117, https://doi.org/10.5194/tc-9-2101-2015, 2015. a, b
Mätzler, C.: Microwave permittivity of dry snow, IEEE T. Geosci. Remote, 34, 573–581, 1996. a, b
Mätzler, C.: Improved Born approximation for scattering of radiation in a granular medium, J. Appl. Phys., 83, 6111–6117, 1998. a, b, c
Mätzler, C.: Relation between grain-size and correlation length of snow, J. Glaciol., 48, 461–466, https://doi.org/10.3189/172756502781831287, 2002. a
Olmi, R., Bittelli, M., Picard, G., Arnaud, L., Mialon, A., and Priori, S.: Investigating the influence of the grain size and distribution on the macroscopic dielectric properties of Antarctic firn, Cold Reg. Sci. Technol., 185, 103254, https://doi.org/10.1016/j.coldregions.2021.103254, 2021. a
Picard, G.: smrt-model/strong_expansion_theory_paper: v1.0 (v1.0), Zenodo [code], https://doi.org/10.5281/zenodo.7086089, 2022. a
Picard, G., Sandells, M., and Löwe, H.: SMRT: an active–passive microwave radiative transfer model for snow with multiple microstructure and scattering formulations (v1.0), Geosci. Model Dev., 11, 2763–2788, https://doi.org/10.5194/gmd-11-2763-2018, 2018. a, b
Picard, G., Löwe, H., Domine, F., Arnaud, L., Larue, F., Favier, V., Le Meur, E., Lefebvre, E., Savarino, J., and Royer, A.: The microwave snow grain size: a new concept to predict Satellite observations over snow-covered regions, AGU Advances, 3, e2021AV000630, https://doi.org/10.1029/2021AV000630, 2022a. a, b
Picard, G., Sandells, M., and Löwe, H.: smrt-model/smrt: v1.1.0 (v1.1.0), Zenodo [code], https://doi.org/10.5281/zenodo.7086080, 2022b. a
Polder, D. and van Santen, J. H.: The effective permeability of mixtures of solids, Physica, 12, 257–271, 1946. a
Pulliainen, J. T., Grandell, J., and Hallikainen, M. T.: HUT snow emission model and its applicability to snow water equivalent retrieval, IEEE Geosci. Remote, 37, 1378–1390, https://doi.org/10.1109/36.763302, 1999. a
Rechtsman, M. C. and Torquato, S.: Effective dielectric tensor for electromagnetic wave propagation in random media, J. Appl. Phys., 103, 084901, https://doi.org/10.1063/1.2906135, 2008. a, b
Royer, A., Roy, A., Montpetit, B., Saint-Jean-Rondeau, O., Picard, G., Brucker, L., and Langlois, A.: Comparison of commonly-used microwave radiative transfer models for snow remote sensing, Remote Sens. Environ., 190, 247–259, https://doi.org/10.1016/j.rse.2016.12.020, 2017. a
Sandells, M., Lowe, H., Picard, G., Dumont, M., Essery, R., Floury, N., Kontu, A., Lemmetyinen, J., Maslanka, W., Morin, S., Wiesmann, A., and Matzler, C.: X-Ray Tomography-Based Microstructure Representation in the Snow Microwave Radiative Transfer Model, IEEE T. Geosci. Remote, 60, 4301115, https://doi.org/10.1109/tgrs.2021.3086412, 2021. a, b, c, d
Sihvola, A.: Electromagnetic Mixing Formulas and Applications, Institution Of Engineering & T, http://www.ebook.de/de/product/21470462/a_sihvola_electromagnetic_mixing_formulas_and_applications.html, (last access: 14 September 2022), 1999. a
Tan, S. and Tsang, L.: DMRT QMS model, [software], https://web.eecs.umich.edu/~leutsang/Computer Codes and Simulations.html, last access: 22 September 2022. a
Torquato, S. and Kim, J.: Nonlocal Effective Electromagnetic Wave Characteristics of Composite Media: Beyond the Quasistatic Regime, Phys. Rev. X, 11, https://doi.org/10.1103/physrevx.11.021002, 2021. a, b, c
Tsang, L. and Kong, J. A.: Scattering of electromagnetic waves, vol. 3: Advanced Topics, Wiley Interscience, New York, https://doi.org/10.1002/0471224278, 2001. a, b, c, d
Tsang, L., Kong, J. A., and Shin, R. T.: Theory of Microwave Remote Sensing, Wiley-Interscience, New York, ISBN 10 0471888605, ISBN 13 9780471888604, 1985. a, b
Tsang, L., Kong, J. A., Ding, K. H., and Ao, C.: Scattering of electromagnetic waves, vol. 2: numerical solutions, Wiley Interscience, New York, https://doi.org/10.1002/0471224308, 2000. a
Tsang, L., Pan, J., Liang, D., Li, Z., Cline, D. W., and Tan, Y.: Modeling Active Microwave Remote Sensing of Snow Using Dense Media Radiative Transfer (DMRT) Theory With Multiple-Scattering Effects, IEEE T. Geosci. Remote, 45, 990–1004, https://doi.org/10.1109/tgrs.2006.888854, 2007. a