the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Long-period variability in ice-dammed glacier outburst floods due to evolving catchment geometry
Amy Jenson
Jason M. Amundson
Jonathan Kingslake
Eran Hood
We combine a glacier outburst flood model with a glacier flow model to investigate decadal to centennial variations in outburst floods originating from ice-dammed marginal basins. Marginal basins can form due to the retreat and detachment of tributary glaciers, a process that often results in remnant ice being left behind. The remnant ice, which can act like an ice shelf or break apart into a pack of icebergs, limits a basin's water storage capacity but also exerts pressure on the underlying water and promotes drainage. We find that during glacier retreat there is a strong, nearly linear relationship between flood water volume and peak discharge for individual basins, despite large changes in glacier and remnant ice volumes that are expected to impact flood hydrographs. Consequently, peak discharge increases over time as long as there is remnant ice remaining in a basin, and peak discharge begins to decrease once a basin becomes ice-free. Thus, similar size outburst floods can occur at very different stages of glacier retreat. We also find that the temporal variability in outburst flood magnitude depends on how the floods initiate. Basins that connect to the subglacial hydrological system only after reaching flotation depth yield greater long-term variability in outburst floods than basins that are continuously connected to the subglacial hydrological system (and therefore release floods that initiate before reaching flotation depth). Our results highlight the importance of improving our understanding of both changes in basin geometry and outburst flood initiation mechanisms in order to better assess outburst flood hazards and their impacts on landscape and ecosystem evolution.
- Article
(8310 KB) - Full-text XML
- BibTeX
- EndNote
Glacier outburst floods (also referred to as jökulhlaups) are sudden releases of water from ice-dammed or moraine-dammed lakes. There has been a recent increase in the size and number of glacial lakes due to deglaciation (e.g., Clague et al., 2012; Shugar et al., 2020; Mölg et al., 2021), raising concerns about the hazards that these lakes pose to downstream communities and infrastructure. More accurate estimates of flood magnitude and timing may help mitigate risk in areas where these hazards exist (e.g., Vincent et al., 2010; Werder et al., 2010). In addition, outburst floods cause semi-regular but short-lived perturbations to downstream ecosystems by rapidly changing sediment and nutrient concentrations and proglacial water temperatures (e.g., Neal, 2007; Kjeldsen et al., 2014; Meerhoff et al., 2019). The largest of these floods create major erosional features during glacial periods (e.g., Larsen and Lamb, 2016; Keisling et al., 2020); smaller, more frequent outburst floods are also important in driving landscape change (e.g., Russell et al., 2006; Cook et al., 2018; Carrivick and Tweed, 2019). Here, motivated by observations from Mendenhall Glacier, Alaska, we focus on glacier outburst floods from ice-dammed marginal basins, which form following the thinning, detachment, and retreat of tributary glaciers and often contain remnant ice left behind during deglaciation (e.g., Capps et al., 2010; Kingslake and Ng, 2013a; Kienholz et al., 2020) (Fig. 1).

Figure 1Repeat photos of Mendenhall Glacier, Alaska, taken in (a) 1893 (Ogilvie, 1893) and (b) 2018 (courtesy of Christian Kienholz). Suicide Basin formed in the early 2000s when Suicide Glacier detached from Mendenhall Glacier. Annual outburst floods now originate from Suicide Basin, which contains remnant ice from Suicide Glacier.
The theory of ice-dammed outburst floods is based on the consideration of mass, momentum, and energy balances of water flowing through the subglacial drainage system (e.g., Rothlisberger, 1972; Nye, 1976; Fowler, 1999; Kingslake, 2013; Kessler and Anderson, 2004; Stubblefield et al., 2019; Schoof, 2020). Many outburst flood models are based on the assumption of a circular or semicircular channel (e.g., Nye, 1976; Fowler, 1999; Kingslake, 2013); others allow for more complex drainage configurations such as multiple lakes in a connected hydrological system (e.g., Stubblefield et al., 2019) or a system of linked cavities (e.g., Kessler and Anderson, 2004; Schoof, 2020), which may be more accurate at modeling outburst events early in the melt season. In these models, once a flood initiates, the water begins to drain through an existing subglacial drainage system. The energy dissipated in the flowing water causes the conduit(s) to grow and the discharge to increase until the peak discharge is reached and the basin has drained. A positive feedback loop between discharge, melt rates, and conduit area results in flood hydrographs that rise quasi-exponentially and then rapidly drop once the basin is empty (or nearly empty) (Nye, 1976). The mechanics of flood initiation are less understood. One proposed mechanism is that a basin begins to drain when the water pressure equals the overburden pressure of the ice dam, which occurs at the lake level referred to as flotation depth (Thorarinsson, 1953). When an outburst flood initiates due to the basin reaching flotation depth, water floats the ice dam and flows beneath the ice (1) forming a channel, (2) enlarging an existing channel, or (3) propagating a subglacial sheet of water toward the terminus (e.g., Flowers et al., 2004). There are also many occurrences of outburst floods initiating prior to a basin reaching flotation depth (e.g., Bjornsson, 1992) or alternatively exceeding flotation depth (e.g., Huss et al., 2007; Kienholz et al., 2020). Several studies have also considered the possibility that marginal basins remain continuously connected to the subglacial and englacial hydrological systems and that drainage onset is dictated by the interplay between the water depth in the basin relative to the ice dam height, the hydraulic gradient in the vicinity of the basin, and the state of the hydrological system (e.g., Kessler and Anderson, 2004; Kingslake, 2015; Bigelow et al., 2020; Schoof, 2020). Due to a poor understanding of drainage onset, the timing and magnitude of outburst floods are difficult to predict (e.g., Ng and Björnsson, 2003; Kingslake and Ng, 2013b).
Outburst flood theory dictates that flood characteristics, such as event timing and peak discharge, depend on glacier and basin geometry, both of which evolve as glaciers advance or retreat. Consequently, outburst floods can be viewed as semi-periodic disturbances to glaciated landscapes that switch on/off and evolve in response to climate change. We are motivated by a desire to understand the evolving hazard of outburst floods as well as the impacts of these extreme events on landscape and ecosystem evolution. Thus, our work complements efforts to understand long-term variations in glacier runoff during glacial recession (e.g., Milner et al., 2017; Huss and Hock, 2018). In situ observations of outburst floods from individual glaciers over multiple years or decades are limited to a few sites. Due to a lack of observations, no previous work has tried to develop a theoretical understanding of the impact that glacier retreat has on outburst flood hydrographs. We address this problem with a one-way coupled glacier-basin-outburst flood model and focus on quantifying the long-period variability in outburst floods that arise due to changes in catchment geometry. Our primary objective is to investigate changes in outburst flood hydrographs as a glacier retreats by exploring different basin geometries and flood onset mechanisms. In addition we account for remnant ice left behind in a basin, which reduces the storage capacity of water in the basin but also acts like a gravity piston that pushes water out of a basin. We do not attempt to address the significant year-to-year variability in outburst flood hydrographs that has been observed at some glaciers (e.g., Huss et al., 2007; Neal, 2007; Kienholz et al., 2020); in this light our modeling efforts should be viewed as an attempt to quantify the potential for a given glacierized catchment to produce outburst floods.
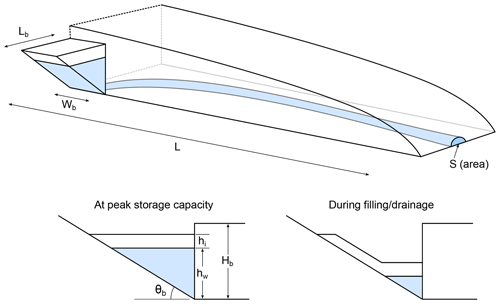
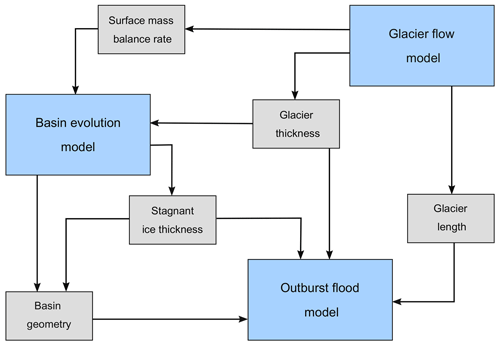
We build on the outburst flood modeling work of Nye (1976), Fowler (1999), and Kingslake (2013) by accounting for changes in glacier and basin geometry (Fig. 2), both of which are expected to affect the magnitude and duration of outburst floods. We first use an idealized glacier flow model to quantify changes in glacier geometry, ice dam thickness, and the amount of remnant, floating ice in a basin as a glacier retreats. For each year of the glacier flow model we extract the glacier geometry and remnant ice volume, which we then feed into the glacier outburst flood model. In the following subsections we describe the outburst flood model, the hypsometry and evolution of the marginal basin, and the glacier flow model. A list of model variables is included in Table 1.
2.1 Outburst flood model
2.1.1 Channel hydrology
The outburst flood model consists of four coupled equations that conserve mass, momentum, and energy as water flows from a marginal basin and through a semi-circular conduit to the glacier terminus, assumed to be open to the atmosphere (Nye, 1976; Fowler, 1999). The ice dam seal is assumed to be located immediately adjacent to the basin. The cross-sectional area of the conduit, S, evolves by melting and creep closure, and consequently discharge Q, effective pressure N (ice-overburden minus water pressure), and melt rate (expressed as mass per unit length per unit time) vary temporally and spatially. We define the densities of ice and water as ρi=917 kg m−3 and ρw=1000 kg m−3, gravitational acceleration as g, and the latent heat of fusion as J kg−1 (Cuffey and Paterson, 2010). Following Fowler (1999), we use the basic hydraulic gradient , where θ is the conduit slope (assumed to equal the bed slope), Pi=ρigH is the ice pressure, H is the glacier thickness, and s is the along-flow coordinate parallel to the bed. The conduit length L, glacier thickness, and glacier thickness gradient evolve as the glacier thins and retreats (Sect. 2.2).
The assumption that the channel walls enlarge by melt and shrink due to creep closure results in an expression for the rate of change of conduit area given by
where (Evatt, 2015) and Pa−3 s−1 and n=3 are the flow law parameter and exponent in Glen's flow law (assuming temperate ice). Assuming pressurized flow, mass conservation dictates that the rate of change of conduit area is also related to the spatial gradient in discharge, the production of meltwater, and additional water input to the conduit, such that
where M represents additional water flux supplied to the conduit per unit length. We prescribe a small value of m2 s−1 to ensure that the conduit always remains open (Fowler, 1999). We use Manning's equation to describe conservation of momentum, yielding an expression relating the discharge and conduit area to the basic hydraulic gradient and effective pressure,
where is a friction factor with m s the hydraulic roughness. Finally, conservation of energy requires that
Two boundary conditions are required to solve this system of equations. We set the effective pressure at the terminus equal to 0. At the basin outlet, the effective pressure is
where Hb and hw are the glacier thickness and water depth at the basin outlet and hi is the thickness of floating ice in the basin. Variations in water level are related to the basin hypsometry and discharge into and out of the basin, as described in Sect. 2.1.2 (see Eq. 10). In addition, the ice dam height and floating ice thickness both vary during glacier recession (Sect. 2.2).
2.1.2 Basin hypsometry and evolution
We assume that the ice-dammed basin has an idealized hypsometry that can be described by
where Ab is the mapview area of the basin at different elevations, zb is the elevation relative to the lowest point in the basin, and a and p are constants that describe the basin shape. For reference, p=1, p=2, and p=3 describe box-, wedge-, and semicircular-cone-shaped basins, respectively. We define Wb, Lb, and θb as the basin width, length, and bed slope (Fig. 2). For a box-shaped basin a=WbLb, for a wedge-shaped basin a=Wbcot θb, and for a semicircular-cone-shaped basin .
The basin is assumed to be completely filled with ice at year 0, at which point the tributary glacier detaches from the trunk glacier and leaves behind remnant ice. Initially the remnant ice may be attached to the trunk glacier and act like a floating ice tongue, but ultimately it breaks into a pack of icebergs. We assume that the remnant ice thins at a rate given by the specific surface mass balance rate. Thus, we neglect replenishment of ice into the basin via glacier flow or iceberg calving. We further assume that the remnant ice is sufficiently mobile and fractured to form a horizontal layer of thickness hi as the basin fills. We therefore assume that drainage proceeds quickly enough that the floating ice thickness does not change during the course of the outburst flood and consequently ice is stranded on the basin walls (see Fig. 2). The floating ice volume at time t is given by
where subscript “,0” refers to initial conditions, is the specific surface mass balance rate (see Sect. 2.2) at the basin's elevation, and we apply the mass balance rate to the surface of the remnant ice.
The volume of water stored in the basin Vw for a given water depth is
Since a and p are constants for a given basin, the water volume in the basin can be expressed as
The volume fluxes of water entering and leaving the basin are Qin and Qb. Thus, we find the rate of change of the water surface elevation by setting the time derivative of Eq. (9) equal to Qin−Qb and rearranging, which yields
We consider two scenarios for evolving the water level. In the first scenario (“flotation scenario”) we assume that the effective pressure is initially zero at the basin outlet and that the basin begins to drain shortly after starting each simulation. In this scenario we set Qin=0 m3 s−1 since the basin is already full and the flood occurs soon after the simulation begins. The initial water level is
and the volume of floating ice is related to its thickness by integrating Eq. (6) and substituting in Eq. (11):
Since the ice volume is known (Eq. 7), hi (and therefore hw,0) can be determined by adjusting its value until Eqs. (7) and (12) are in agreement. In the second scenario (“filling scenario”) we set the initial water level to m and the discharge into the lake to Qin=20 m3 s−1, which allows the basin to fill while draining. In both scenarios, we assume the filling rate Qin remains constant despite the changing climate and year-to-year variability. We tested values of 0–25 m3 s−1, and while different values of Qin impact the flood magnitudes and how quickly a flood is initiated, we found that varying Qin does not qualitatively affect our results, and so we chose to keep Qin constant throughout the filling scenario simulations. Additionally, Qin has little impact on the outburst flood hydrographs once a flood initiates because the flood discharge exceeds Qin by more than 2 orders of magnitude. Note that we only apply the filling scenario to box-shaped basins in order to avoid geometric complexities associated with raising and lowering a fragmented layer of remnant ice along a sloping basin, and therefore we compute the floating ice thickness by simply dividing the ice volume by the basin surface area. We define basin storage capacity, Vs, as the water volume when the basin level is at flotation depth and the peak water volume as the volume of water when the lake in a simulation has reached peak water depth. In the flotation scenario, basin storage capacity and peak water volume are equal; however, in the filling scenario, the peak water volume is less than the basin storage capacity for all simulations.
2.1.3 Numerics
The outburst flood model is nondimensionalized and solved numerically using methods described by Kingslake (2013) and Kingslake and Ng (2013a). We use a constant time step in dimensionless units, resulting in the dimensional time step decreasing from ∼400 to ∼300 s as the glacier thins and retreats. For the grid spacing we set , which equals ∼50 m at year 0 and decreases as the glacier retreats. At each time step, given S, hw, and hi, we solve Eqs. (2) and (3) simultaneously for N and Q, with m defined by Eq. (4), in Eq. (2) provided by Eq. (1), and the boundary condition on N at the lake provided by Eq. (5). Employing an approach referred to as the relaxation method by Kingslake (2013), a fictitious time derivative is introduced to the left of Eq. (2), and, after making an initial guess at the discharge at the lake Q0, the result is solved with Eq. (3) using the forward Euler method in time and an upwind difference in space until the fictitious derivative disappears. This is performed repeatedly within a root-finding algorithm, which tunes Q0, until the N boundary condition (Eq. 5) is met. This results in profiles of N and Q that obey Eqs. (2) and (3) and the boundary conditions. These are used to evolve hw and S forward in time with Eqs. (10) and (1), respectively. Initial values for hw and S are discussed in Sect. 2.3.
2.2 Glacier evolution
We model changes in glacier geometry with a one-dimensional form of the shallow shelf approximation (SSA), which is a depth- and width-integrated flow model (Nick et al., 2009; Enderlin et al., 2013; Carnahan et al., 2019). For our simulations, we use a glacier with a simple bed geometry (a uniformly sloping bed with a slope of 4∘) and assume a simple climate parameterization. After running the model to steady state, we invoke glacier retreat by applying a constant rate of warming. The simulations are run until the glacier terminus retreats past the basin, which is initially located 75 % of the way from the head of the glacier to its terminus. We ran additional simulations with different parameter values for bed slope, climate, and basin location. Although these parameters affect the details of how outburst floods change from year to year, they do not affect the overall pattern of how floods evolve.
The glacier flow model is based on conservation of momentum, which requires that the glaciological driving stress is balanced by gradients in longitudinal stress, lateral drag, and basal drag (van der Veen, 2013), such that
where ν is the depth- and width-averaged viscosity, U is the depth- and width-averaged velocity, W is glacier width, τ is the basal shear stress, and hs is the glacier surface elevation. The viscosity depends on the strain rate according to Glen's flow law:
We assume a simplified ad hoc parameterization of the basal shear stress, in which , with Pa. This parameterization results in shear stresses on the order of 105 Pa, which are typical values for valley glaciers (e.g., Brædstrup et al., 2016), and produces realistic glacier geometries and velocities across a wide range of bed slopes and climates. Importantly, the parameterization ensures that the resistive stresses never exceed the glaciological driving stress. For boundary conditions, we prescribe a velocity of U=0 at the ice divide (x=0) and velocity gradient at the terminus (x=L).
The glacier surface is updated using a depth- and width-integrated mass continuity equation (van der Veen, 2013), in which
where is the width-averaged specific mass balance rate. We prescribe the mass balance rate by using a constant mass balance gradient and imposing a maximum balance rate (as is commonly observed; e.g., Van Beusekom et al., 2010). In other words,
where ELA is the equilibrium line altitude. We use an initial ELA of 1500 m, a balance gradient of a−1, and a maximum balance rate of m a−1. The ELA increases at a rate of 5 m a−1 to approximate expected changes under climate warming scenarios (Huss and Hock, 2015).
The model equations are discretized following the methodology described in Enderlin et al. (2013) using finite differences for the spatial discretization (initial grid spacing of 100 m); a staggered, moving grid; and a forward Euler time step (Δt=0.05 a). At each time step, Eq. (13) is solved for the velocity, and the glacier surface is adjusted according to Eq. (15). The glacier length is updated by allowing the terminus to advance at its flow speed, and any ice thinner than 0.1 m is subsequently removed from the domain.
2.3 Simulations
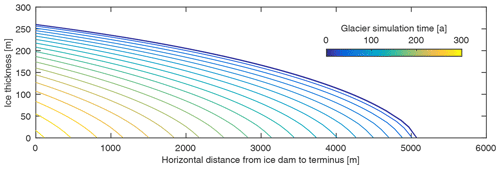
In the glacier flow model it takes about 300 years for the glacier terminus to retreat from its initial position to the location of the marginal basin, a distance of ∼5 km (Fig. 3). For each year of the glacier model output, we extract (i) the distance from the basin to the terminus, which we take to equal the conduit length; (ii) the glacier thickness profile and ice dam thickness; and (iii) the specific mass balance rate of the ice dam. Then (i) and (ii) are fed directly into the outburst flood model, and (iii) is used to calculate the volume of floating ice remaining in the basin (Fig. 4).
To demonstrate how remnant ice affects outburst floods, we first run simulations in which we use the glacier geometry from one time step in the glacier flow model, assume a box-shaped basin, and run the outburst flood model with different starting water volumes. We run the simulations both without ice and with enough ice to force ice dam flotation. Thus, these initial simulations are similar to those that we run in the flotation scenario (next paragraph) except that here the basin is not necessarily at flotation depth unless it contains remnant ice.
We then use the evolving glacier and basin geometries to model long-period variations in outburst floods using the flotation and filling scenarios described in Sect. 2.1.2. In the flotation scenario, we assume that the initial water pressure at the basin outlet equals the overburden pressure of the ice dam. In this scenario, the initial conduit area is 1 m2. Thus, we assume that the basin is not connected to the subglacial drainage system until the onset of the outburst flood. To test the effect of basin geometry and floating ice on outburst flood evolution, we run simulations with (i) box-shaped, wedge-shaped, and semicircular-cone-shaped basins and (ii) both with and without floating ice (Fig. 5). For the box-shaped basin we used a value of m2, for the wedge-shaped basin we used a basin width of 1910 m and a bed slope of 15∘, and for the semicircular-cone-shaped basin we used a bed slope of 10.6∘. These values were chosen so that the basins would initially have the same basin storage capacity Vs.

Figure 5Schematic of the various scenarios that we considered in our simulations, illustrating basin geometry, presence/absence of remnant ice, and whether drainage initiated when the lake reached flotation depth or while the basin was filling. For the flotation scenario, we prescribe Qin=0 m3 s−1, S0=1 m2, and (flotation depth). For the filling scenario simulations, we prescribe the discharge into the basin as Qin=20 m3 s−1, the initial conduit cross-sectional area as S0=0.1 m2, and the initial water level m. The basins all have the same initial volume (year 0 in the ice flow model), but as the ice dam thins the changes in basin volume are nonlinear for the cone- and wedge-shaped basins. The simulations with remnant ice assume the basin is completely filled with ice at year 0.
In the filling scenario we prescribe a small initial water level of 10 m and an initial conduit area of 0.1 m2. The subglacial conduit is connected to the marginal basin as filling occurs, and the conduit therefore evolves prior to the onset of the outburst flood, which occurs naturally once Qb>Qin. The granular nature of the floating ice makes a full treatment of its behavior during filling and drainage nontrivial. The floating ice should gradually expand outward as the basin fills, but then friction should prevent it from flowing back down to the bottom of the basin during rapid drainage. In the filling scenario the basin generally does not fill up completely, greatly complicating the task of tracking the thickness and location of the floating ice except when the basin walls are vertical. For this reason we only apply the filling scenario to box-shaped basins.
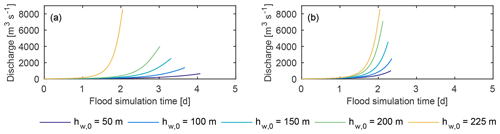
Figure 6Demonstration of the impact of floating ice on outburst flood hydrographs for an ice dam height of 250 m (year 50 in the glacier simulations). The glacier geometry and basin shape (box) are the same in all simulations. In panel (a), the initial water height, hw,0, is varied and there is no floating ice in the basin. The initial water heights are the same in panel (b) except that enough floating ice is added to force ice dam flotation. For m, the water level is equal to flotation depth so there is no remnant ice, and the curves in panels (a) and (b) are the same. Note that the modeled hydrographs do not include the rapidly falling limb of the floods because the outburst flood model is not capable of handling open channel flow, which occurs when the basin water level drops below the conduit roof.
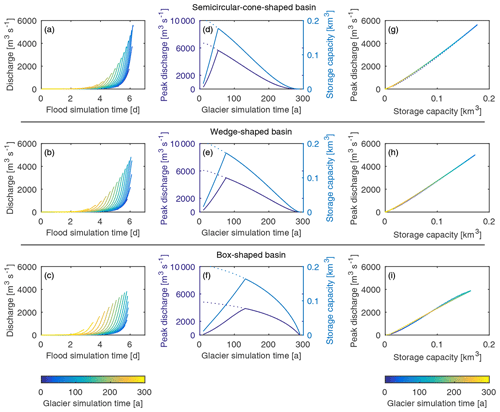
Figure 7Comparison of annual outburst floods for semicircular-cone-, wedge-, and box-shaped basins for the simulations in which the basin is initially at flotation depth. (a–c) Annual outburst flood hydrographs when the basin is initially filled with ice. (d–f) Peak discharge and storage capacity over time. The fork in the early years of the simulations represents ice-filled (solid line) and ice-free (dotted line) scenarios. (g–i) Peak discharge vs. storage capacity for the ice-filled scenario. We refer to the timescale of the glacier flow model as “glacier simulation time” and the timescale of the outburst flood model as “flood simulation time”.
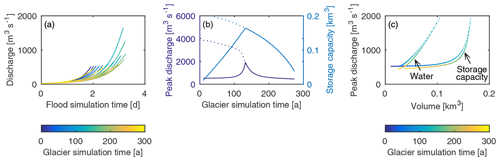
Figure 8Comparison of annual outburst floods for the box-shaped basin in which the basin is connected to the subglacial hydrological system as it fills. (a) Annual outburst flood hydrographs. (b) Peak discharge and basin storage capacity for ice-filled and ice-free basins. The fork in the early years of the simulations represents ice-filled (solid line) and ice-free (dotted line) scenarios. (c) Relationship between peak discharge and peak water volume (“Water”) and basin storage capacity (“Storage capacity”).
For glaciers with a fixed geometry, floating ice in a basin causes outburst floods to have higher peak discharge and shorter duration than might otherwise be expected based solely on the consideration of flood water volume (Fig. 6). Consequently, changes in remnant ice volume impact the evolution of glacier outburst floods over decadal to centennial timescales. In our transient glacier simulations we observed similar trends in flood hydrographs regardless of basin hypsometry and whether the simulations started with the basins filled to flotation depth (Fig. 7) or if the basins were connected to the subglacial hydrological system as they filled (Fig. 8). The floods that occur in the years immediately following the formation of a marginal basin have low peak discharge on account of the basin's small storage capacity. As the climate warms, the remnant ice thins more quickly than the ice dam, which is partially replenished by the delivery of ice from upstream. The largest outburst floods occur when the basin becomes ice-free, after which the peak discharge decreases until the basin is no longer dammed by the trunk glacier.
For the simulations in which the basins were filled to flotation depth before flood onset, we considered three different basin hypsometries (semicircular-cone-, wedge-, and box-shaped) that had identical storage capacities at the time of basin formation (year 0). The cone-shaped basin produced the largest outburst floods in terms of peak discharge, however flood magnitude decreased more rapidly across the simulations for the cone-shaped basin compared to the wedge- and box-shaped basins (Fig. 7a–c). The differences in peak discharge and duration of large magnitude floods arise because, owing to their hypsometry, cone-shaped basins lose their floating ice more rapidly than wedge- or box-shaped basins and because as they drain the floating ice in the basin exerts pressure on the underlying water that helps to drive the water out of the basin. However, ice-dam thinning reduces basin capacity faster in cone-shaped basins than in wedge- or box-shaped basins, and therefore the magnitude of the outburst floods in cone-shaped basins decreases more rapidly. In the early years of the simulations, flood magnitude increases in basins that are initially filled with ice (solid line) until the basin is ice-free, whereas in basins that are initially ice-free (dotted line) the flood magnitude always decreases (Fig. 7d–f). For all three hypsometries we observe a nearly linear relationship between peak discharge and storage capacity (Fig. 7g–i). This relationship holds regardless of whether the basin contains ice or is ice-free.
For the simulations in which the basin is initially drained of water but remains connected to the subglacial hydrological system as the basin fills, the relationship between peak discharge and peak water volume (which is often less than the storage capacity, as defined above) takes a slightly different form. First, the basin often does not reach flotation depth in our simulations because the conduit enlarges at the same time as the basin is filling and consequently the outburst floods tend to be smaller in magnitude (Fig. 8). This behavior is sensitive to the model parameters though, as the basin could be made to reach or even exceed flotation depth by selecting a larger influx Qin. Second, there is a more prominent spike in the peak discharge curve that occurs as the remnant ice is about to melt away completely (Fig. 8b). Similar to the flotation scenario, the relationship between peak discharge and peak water volume is approximately linear; however, in the filling scenario the peak water volume is less than the storage capacity because the basin does not completely fill (Fig. 8c). As a result the relationship between peak discharge and (total) storage capacity is not linear.
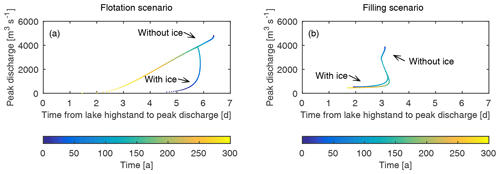
Figures 7 and 8 show that remnant ice can act to produce similar size outburst floods for very different glacier thicknesses. To further illustrate this consequence of remnant ice, we plot peak discharge versus ice dam height for the box-shaped basin in both the filling and flotation scenarios (Fig. 9). In the flotation scenario we observe large variability in outburst floods during glacier recession; for example, a peak discharge of 2000 m3 s−1 occurs when the ice dam height is 240 m and then again when it is 120 m. In contrast, in the filling scenario, the peak discharge is nearly independent of ice dam height except during the years in which the basin becomes ice-free (when the ice dam height was around 210 m). On the other hand, when remnant ice is excluded from the simulations, the peak discharge increases monotonically with ice dam height in both the flotation and filling scenarios. Thus, proper accounting of remnant ice is critical for quantifying the evolution of outburst floods over decadal to centennial timescales.
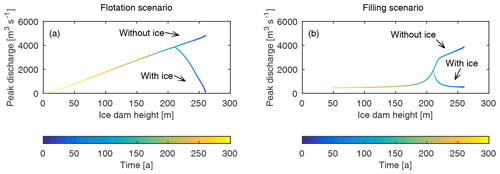
Figure 9Comparison of peak discharge and ice dam height for the box-shaped basin under the (a) flotation scenario and (b) filling scenarios. “With ice” indicates the relationship between peak discharge and ice dam height when remnant ice is accounted for in the model, whereas “Without ice” indicates the relationship when remnant ice is neglected.
4.1 Impact of remnant ice and ice flow on basin storage capacity
During decadal- to centennial-scale glacier retreat, the peak discharge of ice-dammed outburst floods will tend to increase with time as long as there is remnant ice in a basin that is melting away. The peak discharge will begin to decrease only once the remnant ice is gone. This result is independent of basin geometry and the mechanism of drainage onset and is ultimately a consequence of the proportionality between peak discharge and basin storage capacity that occurs for individual basins despite large changes in glacier geometry and remnant ice. In other words, the model exhibits very little hysteresis between peak discharge and basin storage capacity (Figs. 7g–i and 8c). As a result, the time rate change of the basin storage capacity illuminates how peak discharge evolves with time. The storage capacity is found by inserting Eq. (11) into Eq. (8), which gives
Taking the derivative of Eq. (17) with respect to time, we find that storage capacity evolves according to
The term in square brackets in Eq. (18) is always positive, and thus the storage capacity will always increase as long as (i.e., the ice dam is thinning less quickly than the remnant ice). Thinning of the ice dam due to surface melting is partially offset by ice flow from upglacier, and therefore the storage capacity, and by extension the peak discharge of outburst floods, will continue to increase until a basin is ice-free.
However, in our simulations we did not account for ice flow or calving of icebergs into a basin, which would require a significantly more sophisticated ice flow model. Ice flow into a basin shortens the basin and reduces the storage capacity. Calving changes the basin geometry but tends to have little net impact on storage capacity because it has two competing effects: it results in retreat of an ice dam away from a basin, which increases storage capacity, but it also adds to the volume of remnant ice, which reduces storage capacity. For a more detailed discussion on the impacts of ice flow and calving on storage capacity, see Appendix A.
Our analysis here has focused solely on basin storage capacity. The relationship between peak discharge and water volume is likely to become more complicated than presented in Figs. 7 and 8 when changes in basin geometry due to ice flow and calving are accounted for. Moreover, we do not account for lateral variations in glacier thickness that may cause the seal of the ice dam to be located some distance from the basin. Flow redirection toward a marginal basin due to lateral surface gradients will affect the ice dam thinning rates and location of the seal in ways that we are unable to capture in our one-dimensional flowline model. These additional complexities should be considered in more detail in future studies.
4.2 Comparison to the Clague–Mathews relationship
Observations across a range of systems are suggestive of a power-law relationship between the peak discharge and total water volume drained, ΔVw, during outburst floods (Clague and Mathews, 1973; Walder and Costa, 1996):
This relationship is commonly referred to as the Clague–Mathews relationship. Ng and Björnsson (2003) examined the Clague–Mathews relationship by analyzing the equations describing flood evolution. Using a simplified version of the outburst flood model used in this study, they demonstrated that for individual basins that do not drain completely, (i) each flood trajectory has a unique set of initial and final water levels and peak discharge, (ii) peak discharge monotonically increases with water volume, and (iii) there is a power-law relationship between discharge and water volume for floods. They focused on analyzing basins that experience incomplete drainage because some information on flood mechanics is lost if a basin drains completely. Their analysis predicts an exponent in the power-law relationship of about 1–2 for individual basins, depending on basin geometry and ice coverage. When observed flood data from multiple glaciers were scaled and placed into their theoretical framework, they arrived at an exponent close to 1. They hypothesized that the difference between their theoretical exponent and the exponent in the Clague–Mathews relationship is due to confounding factors such as differences in flood initiation, basin geometry, and complete drainage.
Our simulations extend the work of Ng and Björnsson (2003). We modeled variations in outburst floods over decadal to centennial timescales, from different shaped basins, and with different drainage scenarios (flotation vs. filling). In addition, in our simulations the basins always drained completely. We observe that the relationship between peak discharge and peak water volume reached (equal to volume drained) is nearly linear in the flotation scenario (power-law exponent of ∼1; Fig. 7g–i) and superlinear in the filling scenario (power-law exponent >1; Fig. 8c). These trends occur regardless of whether the basins contain remnant ice, in which case peak discharge and storage capacity increase with time, or are ice-free. We also find that the slopes of the discharge-volume curves depend on basin geometry, where basins that contain less volume near their outlets produce a steeper slope. This is likely a result of cone- and wedge-shaped basins being able to maintain high water pressures as they drain, thus favoring more rapid conduit growth.
The explanation for the lower, exponent in the Clague–Mathews relationship remains elusive. Ng and Björnsson (2003) suggest that the lower exponent is due to differences in flood initiation across different basins (implying that flood initiation may depend on basin hypsometry). Flood initiation could also depend on some time-varying property such as ice dam thickness or the size of a previous year's flood, both of which could influence the state of the subglacial hydrological system at the onset of a flood (see also Kingslake, 2015). For example, some flood events involving large volumes of water (i.e., when the basin storage capacity is large) have a persistent impact on the subglacial system, so that when a basin refills it does so while slowly draining, whereas floods involving small volumes of water may have a less persistent impact, and as a result subsequent floods will only initiate after the basin reaches flotation depth.
4.3 Hazard assessment confounded by poor understanding of drainage onset
Mitigating risks due to outburst floods requires accurate predictions of flood initiation, peak discharge, and flood duration. As our results show, these properties depend on basin hypsometry and the amount of remnant ice in a basin, which may be unknown in many situations, making it difficult to assess current and future outburst flood hazards. In contrast, changes in ice dam thickness are much easier to observe, making it tempting to try to relate ice dam thickness to potential flood magnitudes. However, our simulations (Figs. 7 and 8) suggest that similar size outburst floods may occur for very different ice dam thicknesses if a basin contains remnant, floating ice. This nonlinearity occurs both for basins that do not connect to the hydrological system until drainage onset (flotation scenario) and for basins that remain connected to the subglacial hydrological system during filling (filling scenario) (Fig. 9).
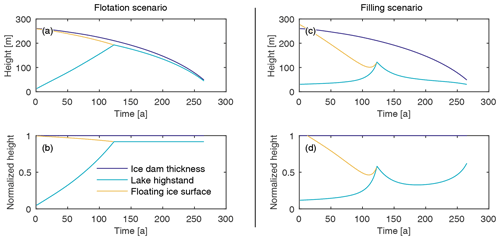
Figure 10Time series of the ice dam elevation, lake highstand (peak water surface), and floating ice surface elevation at lake highstand for the (a) flotation and (b) filling scenarios. In panels (c) and (d), the values for height are normalized using the ice dam thickness as a measure of scale.
Remnant, floating ice affects outburst floods in multiple ways that also affect hazard assessment. First, the presence of floating ice reduces the storage capacity of a basin (Figs. 7d–f and 8b). Shortly after a basin forms, the presence of remnant ice limits the storage capacity and causes the peak discharge to be small. As the ice melts over time the storage capacity and peak discharge increase until the basin is ice-free. The relationship is more clearly seen in the flotation scenario than in the filling scenario (Fig. 10). Floods tend to be more uniform from year to year in the filling scenario because when floating ice is present, the additional pressure causes the outlet conduit to open relatively quickly, and the basin drains before filling to flotation depth. Further, once the floating ice has melted and the ice dam is thinner, the ice-overburden pressure is less and the creep closure is slowed down by the increasing water pressure as the basin is filling. As a result, melt opening overcomes creep closure, which acts to initiate a flood more quickly, and again the basin only fills partially (Fig. 10c–d).
A second consequence of floating ice is that it affects the duration of outburst floods (Fig. 11). The role of floating ice is again most clear in the flotation scenario. Early in the simulations, when the storage capacity is small, outburst floods that have higher peak discharge than might be expected can occur because the pressure from the floating ice helps to drive water out of the basin. However, the small amounts of water (relative to the size of the basin) in these events are not able to melt the conduit walls as rapidly as later floods, and the overburden pressure from the ice dam, which favors creep closure, is high. Consequently, the floods tend to be slower building and the basins may take about a week to drain. Later, when the floating ice is gone and the ice dam is also thinner, drainage can proceed more quickly. This creates challenges for flood risk mitigation because floods with similar peak discharges may occur over timescales of a few days (e.g., Anderson et al., 2003) to a week (e.g., Huss et al., 2007) depending on basin conditions (Fig. 11a). For basins that fill while connected to the subglacial hydrological system, there tends to be less variability in the duration of outburst floods (Fig. 11b).
Our simulations predict differences in how outburst floods will evolve with time, depending on whether a basin begins to drain once it has filled or if the basin remains connected to the subglacial hydrological system and begins to drain as it is filling. Furthermore, our model does not address the large year-to-year variability in peak discharge and total water volume of outburst floods, which may vary by a factor of 2 or more in subsequent years (e.g., Huss et al., 2007; Neal, 2007; Kienholz et al., 2020) and is also likely related to the onset mechanism. A deeper understanding of the onset of outburst floods is therefore critical to improving our ability to assess both the short- and long-term risk associated with outburst floods.
We modeled the effect of changes in glacier and basin geometries on the magnitude and duration of ice-dammed glacier outburst floods. In our simulations we accounted for remnant, floating ice that is left behind in marginal basins during the retreat of tributary glaciers. The remnant ice exerts pressure on the underlying water and thus helps to increase discharge by enlarging the subglacial conduit. Because the remnant ice is not replenished by ice flow from upglacier, it thins more quickly than the adjacent ice dam. As a result the basin storage capacity increases with time as long as the basin contains remnant ice, regardless of basin hypsometry. Despite complex relationships between glacier and basin hypsometry, remnant ice thickness, and discharge, we find nearly linear relationships between peak outburst flood discharge and total water volume for individual basins. This is regardless of whether the basin drains once it reaches flotation depth or if it remains connected to the subglacial hydrological system while filling. However, differences in modeled outburst floods for the two different drainage scenarios that we considered highlight the importance of improving our understanding of drainage onset. Basins that are continuously connected to the subglacial drainage system tend to produce similar outburst floods from one year to the next, except during the years immediately before and after the loss of remnant ice, whereas basins that do not begin to drain until full produce much larger variability in the magnitude and timing of outburst floods.
In our simulations we made a number of simplifying assumptions in order to garner a fundamental understanding of the long-period variability of outburst floods in an evolving catchment. In particular, we (1) assumed that the seal of the ice dam was immediately adjacent to the basin and did not account for changes in the hydraulic potential gradient that could drive water from the glacier into the basin as it is filling; (2) treated remnant ice as a fluid that spreads out as a basin fills, instead of accounting for the granular nature of the icebergs; (3) did not consider the state of the glacier's hydrological system at the time of drainage, which may impact flood evolution, or changes in ice flow due to the evolving subglacial hydrology; (4) did not allow for ice flow into the basin from the trunk glacier; and (5) did not account for interannual variability in climate and its effects on glacier geometry and basin filling rates. Year-to-year variability in the timing, duration, and magnitude of outburst floods (e.g., Huss et al., 2007; Neal, 2007; Kienholz et al., 2020) may mask the longer period changes in outburst floods due to changes in glacier and basin geometry that we modeled here. Additional and more sophisticated modeling studies will be needed to elucidate the impact of these processes on the decadal and centennial evolution of outburst floods and to connect outburst floods to landscape and ecosystem evolution.
For a box-shaped basin, the basin storage capacity is given by
Since we are now allowing for ice flow and calving, the basin length is no longer treated as a constant and the remnant ice thickness varies in response to the addition of new icebergs and compaction/extension due to changes in the location of the ice dam. The rate of change of the storage capacity is
The thickness of the remnant ice changes at a rate that is given by
where Uc is the calving rate. The three terms on the right-hand side of Eq. (A3) describe the changes in ice thickness due to the surface mass balance, the influx of freshly calved ice, and changes in the ice dam location. The rate of change of the basin length is simply , where Ub is the rate at which ice is flowing toward the basin. By inserting these expressions for and into Eq. (A2) and rearranging, we find that
which indicates that the storage capacity will increase as long as . For a box-shaped basin the effects of calving cancel out completely, and changes in storage capacity are only due to thinning of the ice dam, the surface mass balance rate, and the ice flux toward the basin. The effect of ice flow is to reduce the maximum storage capacity that occurs in a basin and to increase the time that it takes for the maximum storage capacity to be reached since contraction of the remnant ice reduces the surface area that is susceptible to melting.
Equation (A4) illustrates that ice flow toward a basin may have important consequences for basin storage capacity. For example, the remnant ice in Suicide Basin, the source of recent outburst floods at Mendenhall Glacier, has a surface mass balance flux () of about m3 a−1, and the ice flux toward the basin (UbHbWb) is roughly 3.5–7.0×105 m3 a−1 (both expressed as ice equivalent) (Kienholz et al., 2020); thus, ice flow is currently offsetting the growth in storage capacity due to melting by about 25 %.
MATLAB script files for the full model are available at https://doi.org/10.5281/zenodo.5488047 (Jenson, 2021).
No data sets were used in this article.
JMA and EH conceived the study, AJ ran the simulations with assistance from JMA and JK, and AJ and JMA prepared the manuscript with contributions from JK and EH.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
This project was supported by funding from the Alaska Climate Adaptation Science Center and the US National Science Foundation (OIA-1757348 and OPP-1743310). We thank Christian Kienholz for fruitful discussions that led to this study.
This research has been supported by the Alaska Climate Adaptation Science Center, University of Alaska Fairbanks (Alaska NSF EPSCoR, grant no. OIA-1208927), and the National Science Foundation (grant no. OPP-1743310).
This paper was edited by Johannes J. Fürst and reviewed by two anonymous referees.
Anderson, S. P., Walder, J., Anderson, R., Kraal, E., Cunico, M., Fountain, A., and Trabant, D.: Integrated hydrologic and hydrochemical observations of Hidden Creek Lake jökulhlaups, Kennicott Glacier, Alaska, J. Geophys. Res., 108, 6003, https://doi.org/10.1029/2002JF000004, 2003. a
Bigelow, D. G., Flowers, G. E., Schoof, C. G., Mingo, L. D. B., Young, E. M., and Connal, B. G.: The role of englacial hydrology in the filling and draining of an ice-dammed lake, Kaskawulsh Glacier, Yukon, Canada, J. Geophys. Res.-Earth Surf., 125, e2019JF005110, https://doi.org/10.1029/2019JF005110, 2020. a
Bjornsson, H.: Jokulhlaups in Iceland: prediction, characteristics and simulation, Ann. Glaciol., 16, 95–106, https://doi.org/10.3189/1992AoG16-1-95-106, 1992. a
Brædstrup, C. F., Egholm, D. L., Ugelvig, S. V., and Pedersen, V. K.: Basal shear stress under alpine glaciers: insights from experiments using the iSOSIA and Elmer/Ice models, Earth Surf. Dynam., 4, 159–174, https://doi.org/10.5194/esurf-4-159-2016, 2016. a
Capps, D. M., Rabus, B., Clague, J. J., and Shugar, D. H.: Identification and characterization of alpine subglacial lakes using interferometric synthetic aperture radar (InSAR): Brady Glacier, Alaska, USA, J. Glaciol., 56, 861–870, 2010. a
Carnahan, E., Amundson, J. M., and Hood, E.: Impact of glacier loss and vegetation succession on annual basin runoff, Hydrol. Earth Syst. Sci., 23, 1667–1681, https://doi.org/10.5194/hess-23-1667-2019, 2019. a
Carrivick, J. L. and Tweed, F. S.: A review of glacier outburst floods in Iceland and Greenland with a megafloods perspective, Earth Sci. Rev., 196, 102876, https://doi.org/10.1016/j.earscirev.2019.102876, 2019. a
Clague, J. J. and Mathews, W. H.: The Magnitude of jökulhlaups, J. Glaciol., 12, 501–504, 1973. a
Clague, J. J., Huggel, C., Korup, O., and Mcguire, B.: Climate Change and Hazardous Processes in High Mountains, Revista de la Asociacion Geologica Argentina, 69, 328–338, https://doi.org/10.5167/uzh-77920, 2012. a
Cook, K. L., Andermann, C., Gimbert, F., Adhikari, B. R., and Hovius, N.: Glacial lake outburst floods as drivers of fluvial erosion in the Himalaya, Science, 362, 53–57, https://doi.org/10.1126/science.aat4981, 2018. a
Cuffey, K. M. and Paterson, W. S. B.: The physics of glaciers, Elsevier, Amsterdam, 4 edn., 2010. a
Enderlin, E. M., Howat, I. M., and Vieli, A.: High sensitivity of tidewater outlet glacier dynamics to shape, The Cryosphere, 7, 1007–1015, https://doi.org/10.5194/tc-7-1007-2013, 2013. a, b
Evatt, G. W.: Röthlisberger channels with finite ice depth and open channel flow, J. Glaciol., 56, 45–50, https://doi.org/10.3189/2015AoG70A992, 2015. a
Flowers, G., Bjornsson, H., Palsson, F., and Clarke, G.: A coupled sheet-conduit mechanism for jokulhlaup propagation, Geophys. Res. Lett., 31, L05401, https://doi.org/10.1029/2003GL019088, 2004. a
Fowler, A. C.: Breaking the seal at Grimsvötn, Iceland, J. Glaciol., 45, 506–516, https://doi.org/10.3189/S0022143000001362, 1999. a, b, c, d, e, f
Huss, M. and Hock, R.: A new model for global glacier change and sea-level rise, Front. Earth Sci., 3, 54, https://doi.org/10.3389/feart.2015.00054, 2015. a
Huss, M. and Hock, R.: Global-scale hydrological response to future glacier mass loss, Nat. Clim. Change, 8, 135–140, https://doi.org/10.1038/s41558-017-0049-x, 2018. a
Huss, M., Bauder, A., Werder, M., Funk, M., and Hock, R.: Glacier-dammed lake outburst events of Gornersee, Switzerland, J. Glaciol., 53, 189–200, https://doi.org/10.3189/172756507782202784, 2007. a, b, c, d, e
Jenson, A. J.: amyjenson/glacier-basin-outburst-flood-model: glacier-basin-outburst flood model (subglacial_hydrology), Zenodo [code], https://doi.org/10.5281/zenodo.5488047, 2021. a
Keisling, B. A., Nielsen, L. T., Hvidberg, C. S., Nuterman, R., and DeConto, R. M.: Pliocene–Pleistocene megafloods as a mechanism for Greenlandic megacanyon formation, Geology, 48, 737–741, https://doi.org/10.1130/G47253.1, 2020. a
Kessler, M. A. and Anderson, R. S.: Testing a numerical glacial hydrological model using spring speed-up events and outburst floods, J. Geophys. Res., 31, L18503, https://doi.org/10.1029/2004GL020622, 2004. a, b, c
Kienholz, C., Pierce, J., Hood, E., Amundson, J., Wolken, G., Jacobs, A., Hart, S., Jones, K. W., Abdel-Fattah, D., Johnson, C., and Conaway, J.: Deglacierization of a marginal basin and implications for outburst floods, Mendenhall Glacier, Alaska, Front. Earth Sci., 8, 137, https://doi.org/10.3389/feart.2020.00137, 2020. a, b, c, d, e, f
Kingslake, J.: Modelling ice-dammed lake drainage, PhD thesis, University of Sheffield, 2013. a, b, c, d, e
Kingslake, J.: Chaotic dynamics of a glaciohydraulic model, J. Glaciol., 61, 493–502, https://doi.org/10.3189/2015JoG14J208, 2015. a, b
Kingslake, J. and Ng, F.: Modelling the coupling of flood discharge with glacier flow during jökulhlaups, Ann. Glaciol., 54, 25–31, https://doi.org/10.3189/2013AoG63A331, 2013a. a, b
Kingslake, J. and Ng, F.: Quantifying the predictability of the timing of jökulhlaups from Merzbacher Lake, Kyrgyzstan, J. Glaciol., 59, 805–818, https://doi.org/10.3189/2013JoG12J156, 2013b. a
Kjeldsen, K. K., Mortensen, J., Bendtsen, J., Petersen, D., Lennert, K., and Rysgaard, S.: Ice-dammed lake drainage cools and raises surface salinities in a tidewater outlet glacier fjord, west Greenland, J. Geophys. Res.-Earth Surf., 119, 1310–1321, https://doi.org/10.1002/2013JF003034, 2014. a
Larsen, I. and Lamb, M.: Progressive incision of the Channeled Scablands by outburst floods, Nature, 538, 229–232, https://doi.org/10.1038/nature19817, 2016. a
Meerhoff, E., Castro, L. R., Tapia, F. J., and Pérez-Santos, I.: Hydrographic and biological impacts of a glacial lake outburst flood (GLOF) in a Patagonian fjord, Estuar. Coast., 42, 132–143, https://doi.org/10.1007/s12237-018-0449-9, 2019. a
Milner, A. M., Khamis, K., Battin, T. J., Brittain, J. E., Barrand, N. E., Füreder, L., Cauvy-Fraunié, S., Gíslason, G. M., Jacobsen, D., Hannah, D. M., Hodson, A. J., Hood, E., Lencioni, V., Ólafsson, J. S., Robinson, C. T., Tranter, M., and Brown, L. E.: Glacier shrinkage driving global changes in downstream systems, P. Natl. Acad. Sci. USA, 114, 9770–9778, https://doi.org/10.1073/pnas.1619807114, 2017. a
Mölg, N., Huggel, C., Herold, T., Storck, F., Allen, S., Wilfried, H., Schaub, Y., and Odermatt, D.: Inventory and evolution of glacial lakes since the Little Ice Age: Lessons from the case of Switzerland, Earth Surf. Process. Landf., 46, 2551–2564, https://doi.org/10.1002/esp.5193, 2021. a
Neal, E.: Hydrology and Glacier-Lake Outburst Floods (1987–2004) and Water Quality (1998–2003) of the Taku River near Juneau, Alaska, USGS Scientific Investigations Report 2007-5027, 27 pp., 2007. a, b, c, d
Ng, F. and Björnsson, H.: On the Clague-Mathews relation for jökulhlaups, J. Glaciol., 49, 161–172, https://doi.org/10.3189/172756503781830836, 2003. a, b, c, d
Nick, F. M., Vieli, A., Howat, I. M., and Joughin, I.: Large-scale changes in Greenland outlet glacier dynamics triggered at the terminus, Nat. Geosci., 2, 110–114, https://doi.org/10.1038/ngeo394, 2009. a
Nye, J.: Water flow in glaciers: Jökulhlaups, tunnels and veins, J. Glaciol., 17, 181–207, https://doi.org/10.3189/S002214300001354X, 1976. a, b, c, d, e
Ogilvie, W.: Mendenhall Glacier: From the Glacier Photograph Collection, National Snow and Ice Data Center, digital media, available at: https://nsidc.org/data/glacier_photo/search/image_info/mendenhall1893000002?order=true (last access: 2 December 2020), 1893. a
Rothlisberger, H.: Water Pressure in Intra- and Subglacial Channels, J. Glaciol., 11, 177–203, https://doi.org/10.1017/S0022143000022188, 1972. a
Russell, A. J., Roberts, M. J., Fay, H., Marren, P. M., Cassidy, N. J., Tweed, F. S., and Harris, T.: Icelandic jökulhlaup impacts: Implications for ice-sheet hydrology, sediment transfer and geomorphology, Geomorph., 75, 33–64, https://doi.org/10.1016/j.geomorph.2005.05.018, 2006. a
Schoof, C.: An analysis of instabilities and limit cycles in glacier-dammed reservoirs, The Cryosphere, 14, 3175–3194, https://doi.org/10.5194/tc-14-3175-2020, 2020. a, b, c
Shugar, D. H., Burr, A., Haritashya, U. K., Kargel, J. S., Watson, C. S., Kennedy, M. C., Bevington, A. R., Betts, R. A., and Strattman, S. H.: Rapid worldwide growth of glacial lakes since 1990, Nat. Clim. Change, https://doi.org/10.1038/s41558-020-0855-4, 2020. a
Stubblefield, A., Creyts, T., Kingslake, J., and Spiegelman, M.: Modeling oscillations in connected glacial lakes, J. Glaciol., 65, 745–758, 2019. a, b
Thorarinsson, S.: Some new aspects of the Grimsvötn problem, J. Glaciol., 2, 267–275, 1953. a
Van Beusekom, A. E., O'Neel, S. R., March, R. S., Sass, L. C., and Cox, L. H.: Re-analysis of Alaska benchmark glacier mass-balance data using the index method, USGS Scientific Investigations, Report 2010-5247, 2010. a
van der Veen, C. J.: Fundamentals of glacier dynamics, CRC Press, Boca Raton, FL, 2 edn., 2013. a, b
Vincent, C., Auclair, S., and Le Meur, E.: Outburst flood hazard for glacier-dammed Lac de Rochemelon, France, J. Glaciol., 56, 91–100, https://doi.org/10.3189/002214310791190857, 2010. a
Walder, J. and Costa, J.: Outburst floods from glacier-dammed lakes: The effect of mode of lake drainage on flood magnitude, Earth Surf. Process. Landf., 21, 701–723, https://doi.org/10.1002/(SICI)1096-9837(199608)21:8<701::AID-ESP615>3.0.CO;2-2, 1996. a
Werder, M. A., Bauder, A., Funk, M., and Keusen, H.-R.: Hazard assessment investigations in connection with the formation of a lake on the tongue of Unterer Grindelwaldgletscher, Bernese Alps, Switzerland, Nat. Hazards Earth Syst. Sci., 10, 227–237, https://doi.org/10.5194/nhess-10-227-2010, 2010. a
- Abstract
- Introduction
- Model description
- Results
- Discussion
- Conclusions
- Appendix A: Effect of ice flow and calving on basin storage capacity of a box-shaped basin
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Model description
- Results
- Discussion
- Conclusions
- Appendix A: Effect of ice flow and calving on basin storage capacity of a box-shaped basin
- Code availability
- Data availability
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References