Two-dimensional liquid water flow through snow at the plot scale in continental snowpacks: simulations and field data comparisons

Modeling the multidimensional flow of liquid water through snow has been limited in spatial and temporal scales to date. Here, we present simulations using the inverse TOUGH2 (iTOUGH2) model informed by the model SNOWPACK, referred to as SnowTOUGH. We use SnowTOUGH to simulate snow metamorphism, melt/freeze processes, and liquid water movement in two-dimensional snowpacks at the plot scale (20 m) on a sloping ground surface during multi-day observation periods at three field sites in northern Colorado, USA. Model results compare well with sites below the treeline and above the treeline but not at a site near the treeline. Results show the importance of longitudinal intra-snowpack flow paths (i.e., parallel to ground surface in the downslope direction and sometimes referred to as lateral flow), particularly during times when the snow surface (i.e., snow–atmosphere interface) is not actively melting. At our above-treeline site, simulations show that longitudinal flow can occur at rates orders of magnitude greater than vertically downward percolating water flow at a mean ratio of 75:1 as a result of hydraulic barriers that divert flow. Our near-treeline site simulations resulted in slightly less longitudinal flow than vertically percolating water, and the below-treeline site resulted in negligible longitudinal flow of liquid water. These results show the increasing influence of longitudinal intra-snowpack flow paths with elevation, similar to field observations. Results of this study suggest that intra-snowpack longitudinal flow may be an important process for consideration in hydrologic modeling for higher-elevation headwater catchments.

1 Introduction

The presence, storage, and movement of liquid water within a snowpack has direct implications for land surface albedo (Dietz et al., 2012), wet-snow avalanches (Mitterer et al., 2011), streamflow generation (Hirashima et al., 2010; Wever et al., 2014), and rain-on-snow runoff generation (Würzer et al., 2016). During snowmelt and rain-on-snow events, the movement of liquid water through snow is a major factor in controlling the timing and magnitude of runoff (Brauchli et al., 2017; Colbeck, 1972; Musselman et al., 2018; Würzer et al., 2016). Although liquid water flow is typically thought of as acting primarily in the vertical direction, previous work has shown that intra-snowpack longitudinal flow can affect the timing, volume, and spatial patterning of runoff. We define intra-snowpack longitudinal flow as flow parallel to the ground surface in the downslope direction (sometimes referred to as lateral flow). Such intra-snowpack longitudinal flow has been shown to deposit runoff directly into streams, bypassing soil interactions (Eiriksson et al., 2013; Liu et al., 2004), and to create focused soil infiltration capable of altering runoff processes (i.e. produce infiltration excess; Webb et al., 2018d). Field observations have shown intra-snowpack flow paths to range in scale from centimeters up to tens of meters (Avanzi et al., 2017; Kattelmann, 1985; Schneebeli, 1995; Webb et al., 2018a; Williams et al., 2010). However, modeling of this spatiotemporally complex process has been limited to one-dimensional (i.e., vertical) or centimeter-scale simulations (e.g., Wever et al., 2014; Würzer et al., 2017).

Multidimensional numerical models simulating preferential flow (vertical and/or longitudinal) through snow have only been recently developed (Hirashima et al., 2019 2017, 2014; Leroux and Pomeroy, 2017). These models apply long-understood soil physics using the laboratory parameterization of snow properties (Calonne et al., 2012; Yamaguchi et al., 2010). As a result, these processes have been simulated primarily in centimeter-scale studies (e.g., Hirashima et al., 2019). However, there remains a need to understand these processes at the plot scale (multiple meters) to further understand the hydrological impacts, namely the amount of liquid water transported in the horizontal relative to the vertical direction. Processes to consider during liquid water flow through snow include snow metamorphism, the melting of snow, and the refreezing of liquid water. These processes create temporally dynamic media properties, specifically snow grain size and porosity, creating a more complex environment relative to soil (Webb et al., 2018b). The layered characteristics of a snowpack and rapid metamorphism that occurs during melt (McGurk and Marsh, 1995; Marsh, 1987; Marsh and Woo, 1985) create temporary hydraulic barriers (Webb et al., 2018b) and thus temporally dynamic flow paths. Understanding and modeling these dynamic flow paths at the plot scale remain an outstanding challenge in snow science.

The goal of this study is to advance the understanding of the spatiotemporal scales of longitudinal intra-snowpack flow paths by simulating liquid water flow through a layered snowpack at the plot scale. The research objectives are (1) to use the model SNOWPACK (Bartelt and Lehning, 2002) to simulate snow metamorphism, melting, and refreezing processes, (2) to utilize enhancements to the TOUGH2 (Pruess et al., 2012) non-isothermal multiphase flow and transport model, as implemented in the inverse TOUGH2 (iTOUGH2) simulation-optimization framework (Finsterle, 2020; Finsterle et al., 2017), to simulate water flow through a two-dimensional, temporally dynamic, and layered snowpack at the plot scale, and (3) to compare results to field observations under varying snowpack conditions.

2 Methods

We simulated liquid water flow through snow at three experimental plots, modeled as 20 m long, two-dimensional domains with a hillslope angle of 10^∘ (Fig. 1). Within this domain, the iTOUGH2 numerical model simulated the flow of liquid water with time-varying snow layer properties provided by the SNOWPACK model. It is important to note that the models were not fully coupled. For each iTOUGH2 time step, material properties were updated using output from SNOWPACK at that time step. For the remainder of this paper, this soft coupling of SNOWPACK and iTOUGH2 will be referred to as SnowTOUGH. For SnowTOUGH testing, we limited the time domain of simulations to match field observations. We initiated the simulations during the first snow pit observations and ended them approximately 3 d later at the completion of experiments at each study plot.

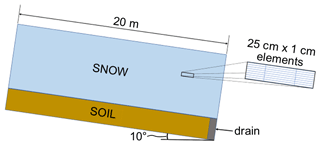
Figure 1 Conceptual diagram of the model domain showing the snowpack above soil, the location of the drain in the soil, and element discretization. Figure not to scale.

2.1 SNOWPACK

The time-dependent material properties of the SnowTOUGH simulations were informed using the physically based SNOWPACK model (Bartelt and Lehning, 2002; Lundy et al., 2001). SNOWPACK discretizes the snow profile into layers, adding layers during accumulation events and consolidating them during compaction and melt. SNOWPACK closes the mass and energy balances at each time step and includes physically based routines for internal snowpack processes, including energy exchange, snow grain metamorphism, and liquid water transport. SNOWPACK has been extensively validated in multiple environments and snow conditions (e.g., Jennings et al., 2018; Lundy et al., 2001; Meromy et al., 2015; Wever et al., 2016).

Simulations were run at hourly time steps with quality-controlled meteorological observations. Air temperature, relative humidity, wind speed, incoming shortwave radiation, incoming longwave radiation, and snow depth data were used as forcing data for the SNOWPACK simulations. The SNOWPACK canopy module was activated for the below-treeline (BT) study plot (described below) using physically representative values of leaf area index (4.0 m² m⁻²), canopy height (7.0 m), and direct throughfall fraction (0.2, dimensionless). Liquid water transport was simulated using the default bucket scheme for full water year simulations and the Richards equation option (Wever et al., 2014) for simulating the intensive observation period (IOP) at each study plot. Full water year simulations were used to offer context to the timing of each IOP relative to peak snow water equivalent (SWE) and snowmelt processes (Fig. 2). For the IOP simulations, initial conditions were provided through manual snow pit observations (Webb et al., 2020, 2018c) so that we could focus our analysis on the intra-snowpack flow of liquid water and comparisons to field observations rather than the accuracy of the SNOWPACK-simulated stratigraphy and the potential implications for our results. We revised input files for these simulations to be as consistent as possible with SNOWPACK's representation of measured and non-measured parameters. For example, we set liquid water fraction values based on snow pit observations (very wet/slush = 0.07, wet = 0.05, little water = 0.03, sticky = 0.01; Bradford et al., 2009; Techel and Pielmeier, 2011; Webb et al., 2018c). We also defined sphericity to be 1 and dendricity to be 0 as most of the snow had metamorphosed by the time of observation, and we set grain types based on Lehning et al. (2002). We estimated bond radius as 30 % of the measured grain radius. For more information on SNOWPACK simulations, see Webb et al. (2020, 2018c).

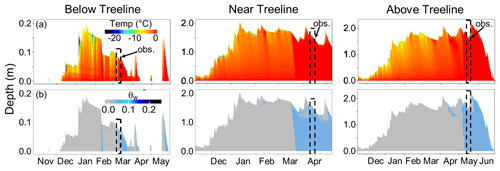
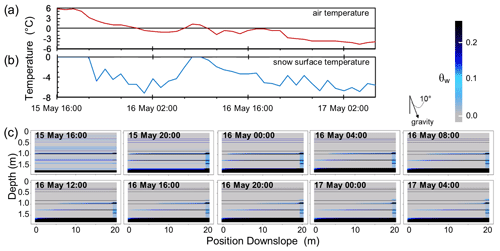
Figure 2 Results of SNOWPACK simulations of the entire water year for below-treeline (BT), near-treeline (NT), and above-treeline (AT) study sites. Results shown are (a) snow temperature and (b) volumetric liquid water content (θ_w) with the observation (obs.) and SnowTOUGH simulation period highlighted in the dashed box. Note that the axes have different scales for each site and that these are not used as input for the SnowTOUGH simulations but used for context in the timing of observations to seasonal processes.

Snow layer variables were calculated by SNOWPACK at hourly intervals, specifically snow grain diameter (d), bulk snow density (ρ_s), volumetric liquid water content (θ_w), and volumetric ice content (θ_i). The dry density of each snow layer (ρ_ds) was calculated by multiplying θ_i by the density of ice (917 kg m⁻³). The melt/freeze rate of each layer was determined by changes in θ_i. Van Genuchten parameters (Van Genuchten, 1980) of unsaturated flow and water retention (i.e., α and n) were determined from SNOWPACK output using equations developed by Yamaguchi et al. (2012):

$$\begin{array}{}\text{(1)}& {\displaystyle }\mathit{\alpha }=\mathrm{4.4}\left({\mathrm{10}}^{\mathrm{6}}\right){\left({\displaystyle \frac{{\mathit{\rho }}_{\mathrm{ds}}}{d}}\right)}^{-\mathrm{0.98}},\text{(2)}& {\displaystyle }n=\mathrm{1}+\mathrm{2.7}\left({\mathrm{10}}^{-\mathrm{3}}\right){\left({\displaystyle \frac{{\mathit{\rho }}_{\mathrm{ds}}}{d}}\right)}^{\mathrm{0.61}}.\end{array}$$

The intrinsic permeability (K) of each snow layer was defined using SNOWPACK output and the equation developed by Calonne et al. (2012):

$$\begin{array}{}\text{(3)}& K=\mathrm{3.0}{r}_{\mathrm{es}}^{\mathrm{2}}\exp \left(-\mathrm{0.013}{\mathit{\theta }}_{\mathrm{i}}{\mathit{\rho }}_{\mathrm{i}}\right),\end{array}$$

where r_es is the equivalent sphere radius and ρ_i is the density of ice.

2.2 iTOUGH2

iTOUGH2 is a simulation-optimization framework for the TOUGH suite of numerical models that have been utilized and validated for a range of processes in porous media (e.g., Fujimaki et al., 2008; Hannon and Finsterle, 2018; Ho and Webb, 1998; Kechavarzi et al., 2008; Lippmann and Bodavarsson, 1983). For this study, we used the equation of state module 9 (EOS9), applying the Richards equation (Richards, 1931) for the transport of liquid water only which does not consider energy transport (Pruess et al., 2012). We used new enhancements to the iTOUGH2 code (Finsterle, 2020) that allow for time-dependent material properties and time-dependent material-related source/sink terms to simulate the snow metamorphism and melt/freeze processes in a layered snowpack. The layered snowpack was modeled above a 10–30 cm deep soil, increasing in depth under deeper snow. Deeper soil was modeled under deeper snow to increase pore storage volume available for any infiltrating water released from the snowpack. The boundary conditions of the upslope and downslope ends of the domain were simulated as no-flow conditions, and a drain was modeled at the downslope end to remove excess liquid water that may build up on the no-flow boundary (Fig. 1). Soil types for each site are known as silty loam, and retention parameters common to this soil type were used. These parameters were a van Genuchten m value of 0.29, a porosity of 0.67, and a van Genuchten α value of 0.02 cm⁻¹. The slightly high porosity was chosen to allow for additional soil moisture storage, if necessary. Saturated hydraulic conductivity estimates of the soils were taken as the mean of more than 15 mini-disk infiltrometer observations distributed evenly across a 10 m × 20 m plot at each site. These saturated hydraulic conductivity values for the below-treeline (BT), near-treeline (NT), and above-treeline (AT) sites were 1.36 × 10⁻³, 6.93 × 10⁻⁴, and 8.46 × 10⁻⁴ cm s⁻¹, respectively. The model was discretized into elements 25 cm in length and 1 cm in height (Fig. 1). Similar to SNOWPACK simulations used for the IOP, initial conditions were provided through manual snow pit observations (Webb et al., 2020, 2018c).

The material properties that we defined to vary through time were permeability, the van Genuchten m term ($m=\mathrm{1}-\mathrm{1}/n$), and the van Genuchten α term. The time-dependent source/sink terms were used to simulate the melt/freeze processes. The melt rate of snow and refreezing of liquid water, determined from SNOWPACK, were used to quantify time-dependent source terms for liquid water introduction via snowmelt and as corresponding sink terms for the refreezing of water. The movement of liquid water simulated by SnowTOUGH was then compared to field observations at the three study plots.

Flow rates for each simulation were calculated for a 1 m × 1 m footprint of hillslope. Thus, longitudinal flow is for a 1 m wide section of hillslope summed over the entire depth of the snowpack, and vertical flow is for a 1 m² area on the ground surface summed over the entire depth of the snowpack. These calculations were conducted at a location 15 m downslope and as an average per snow profile for 10 m upslope from this location. Bulk θ_w values were also calculated for all snow profiles for this same area between 5 and 15 m downslope for SnowTOUGH simulations to compare to field observations. SnowTOUGH results were analyzed for this 10 m length of hillslope to eliminate boundary effects of the upslope and downslope boundary conditions in analyses.

3 Field sites

Field observations of snowpack θ_w, stratigraphy, and longitudinal flow paths were conducted at three locations in the Colorado Rocky Mountains using a combination of dye tracer experiments and ground-based remote sensing. These sites ranged in elevation from a north-facing BT site at 2700 m a.s.l. (above sea level) in a lodgepole pine forest, a south-facing NT site at 3350 m a.s.l. in a large forest clearing, and a southeast-facing AT site at 3500 m a.s.l. Each site had continuous observations of snow depth and air temperature with additional meteorological stations at the AT and BT sites. All sites had a ground surface slope of ∼ 10^∘. For more information on site descriptions and meteorological data, see Webb et al. (2020, 2018c).

During the IOPs, which we timed to occur near peak SWE in spring 2017, a dye tracer (Rhodamine WT) was applied at each of the study plots immediately prior to the first snow pit observation. This was the time of initiation for SnowTOUGH simulations. The dye tracer was subsequently allowed to move into and through the snow undisturbed for at least 2 full days prior to a second set of snow pits being dug downslope of application. These snow pits allowed us to observe locations of longitudinal flow paths that transported the dye tracer. For further information concerning the dye tracer experiments, see Webb et al. (2020). Additionally, ground-based remote sensing techniques were used to estimate the plot-scale distribution of bulk θ_w multiple times throughout each IOP for the NT and AT sites. Snow depths derived from terrestrial lidar scanning were collected in combination with ground penetrating radar surveys to obtain spatially distributed dielectric properties of the snowpack that were used to estimate the spatial distribution of bulk snowpack θ_w. For further details of these ground-based remote sensing methods, see Webb et al. (2018c).

4 Results

4.1 SNOWPACK

SNOWPACK output shows the progression of liquid water development, snow layer metamorphism, and melt/freeze processes at our three sites on both the seasonal timescale (Fig. 2) and during the IOP (Fig. 3). The timing of our observations was such that we captured a period early in the melt season for each plot. Spring snowmelt, defined to begin on the first simulated day of persistent liquid water in the snowpack in the full season simulations, began on 3 March, 18 March, and 4 May for the BT, NT, and AT study plots, respectively (Fig. 2). The first day of the IOP for each plot was 5 March, 12 April, and 15 May for the BT, NT, and AT study plots, respectively. The BT plot was the only site that was not actively melting and releasing liquid water immediately prior to our IOP, while the NT site was melting for the longest time prior to our observations (Fig. 2a). The IOP at the AT site captured the onset of a storm and refreezing of the snow surface (Fig. 3c). Thus, these three sites and IOPs captured varying stratigraphy and conditions that occur within any given melt season in mountainous environments.

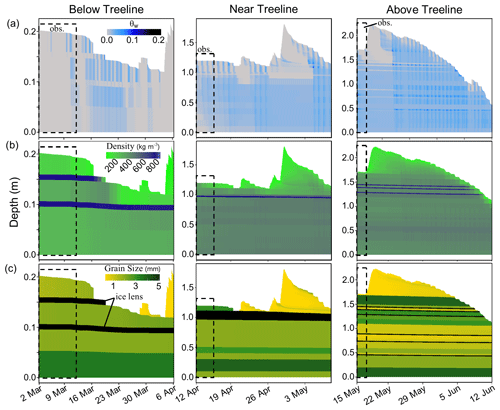
Figure 3 Results of SNOWPACK simulations of the intensive observation periods (IOPs) for below-treeline (BT), near-treeline (NT), and above-treeline (AT) study sites. Results shown are (a) volumetric liquid water content (θ_w), (b) snow density, and (c) grain size with the observation (obs.) and SnowTOUGH simulation period highlighted in the dashed box. Note that the axes have different scales for each site.

During the IOP simulations, SNOWPACK results show little metamorphism with the majority of the grain size changes occurring near the snow–atmosphere interface as a result of surface melt (Fig. 3). All three site simulations expressed diurnal melt cycles, including the retention of liquid water overnight. The BT simulations resulted in diurnal melt cycles that ranged from 0 to 1.1 mm h⁻¹. The NT simulations resulted in melt rates ranging from 0 to 3.9 mm h⁻¹, and the AT simulations resulted in melt rates ranging from 0 to 2.7 mm h⁻¹. Additionally, the NT and AT SNOWPACK simulations display the occurrence of hydraulic barriers that persist throughout the entire melt season (Fig. 3). These results also highlight the increased stratigraphy and formation of ice lenses that occur at higher elevations and impact liquid water flow processes (e.g., Webb et al., 2018b). Thus, the IOP SNOWPACK simulations resulted in three different snowpack conditions that varied in melt–freeze cycles, metamorphism, and snow accumulation/disappearance throughout the profiles.

4.2 SnowTOUGH

SnowTOUGH incorporated the melt/freeze processes and temporally dynamic snow layer variables into a two-dimensional plot-scale model. At the AT and NT sites, SnowTOUGH simulated the presence of multiple hydraulic barriers, holding vertically percolating water and transporting it longitudinally downslope (Fig. 4). Conversely, the BT simulations simulated minimal longitudinal liquid water flow (mean < 0.1 mL s⁻¹), though increased water retention of vertical flow in specific layers did occur as a result of the layer water retention properties. During the IOP, the mean vertical flux of water at the BT site was 1.5 mL s⁻¹ (Fig. 5). This dominance of vertical flow contrasts with the simulations of the two higher-elevation snowpacks which display the higher occurrence of hydraulic barriers as a result of the more complex stratigraphy (Figs. 3 and 4). Furthermore, soil infiltration was minimal at all three sites during the IOPs (Fig. 5), indicating that the majority of vertically moving liquid water was either held within the pore space of a snow layer or transported longitudinally. For all study sites, the vertical flow of liquid water displayed negligible differences between locations at 5 and 15 m downslope. Conversely, longitudinally diverted flow accumulated along flow paths for the entire length of the hillslope (Fig. 5).

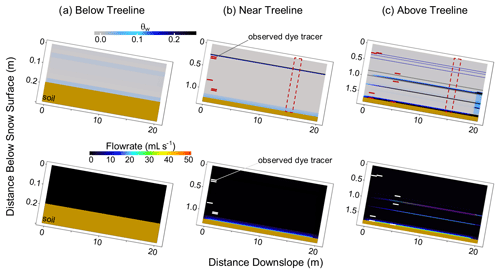
Figure 4 Results of SnowTOUGH simulations for the study sites: (a) below the treeline (BT) on 3 March at 06:00, (b) near the treeline (NT) on 14 April at 04:00, and (c) above treeline (AT) on 15 May at 23:00. Results shown are (top) volumetric liquid water content (θ_w) distribution and (bottom) liquid water flow rates in the longitudinal (i.e., parallel to ground surface) direction. The soil elements within the model domain are shown in solid brown to focus results on intra-snowpack distributions. Dashed red boxes in the θ_w plots indicate the profile of model elements used for flow rate calculations at 15 m downslope.

For the NT site, peak longitudinal flow rates occurred just prior to 12:00 each day local time (Fig. 5b; all times refer to mountain time zone of North America). The vertical flow of water was more variable than longitudinal flow at the NT site with a mean of 9.1 mL s⁻¹ and a standard deviation of 8.5 mL s⁻¹. The longitudinal flow remained relatively steady at the 15 m downslope profile with a mean rate of 6.6 mL s⁻¹ and a standard deviation of 1.4 mL s⁻¹. Infiltration into the soil at the NT site showed a mean value of 0.7 mL s⁻¹ with a standard deviation of 0.5 mL s⁻¹. Longitudinal flow at the NT site occurred within a single longitudinal intra-snowpack flow path near the snow–soil interface.

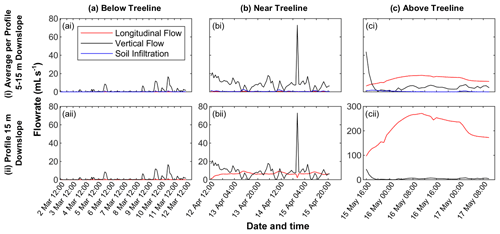
Figure 5 Results of SnowTOUGH simulations over the entire intensive observations periods (IOPs) for the study sites (a) below the treeline (BT), (b) near the treeline (NT), and (c) above the treeline (AT). Results shown are (i) the average longitudinal flow, vertical flow, and infiltration across the snow–soil interface per square meter area of hillslope from 5 to 15 m downslope in simulated plots and (ii) the longitudinal flow and vertical flow rates at 15 m downslope for a 1 m² area of hillslope.

The AT site had unique meteorological conditions during the IOP relative to the other sites. An incoming storm resulted in all surface melt halting during the afternoon of 15 May (Fig. 6). The snow surface temperature later warmed back to 0 ^∘C for a 2 h period with minimal surface melt simulated to occur during this brief time (1.2 mm). Though surface melt stopped, liquid water continued to flow for the entirety of the simulation, predominantly in the longitudinal direction (Figs. 5c and 6). The vertical flow of water at the AT site decreased rapidly as the storm moved in. For the entire IOP simulation, the AT site resulted in a mean vertical flow rate of 5.8 mL s⁻¹ with a standard deviation of 6.6 mL s⁻¹. At the 15 m downslope profile, the AT simulations resulted in a mean longitudinal flow rate of 212 mL s⁻¹ with a standard deviation of 47 mL s⁻¹. Soil infiltration for the AT site showed a mean value of 0.5 mL s⁻¹ with a standard deviation of 0.3 mL s⁻¹. SnowTOUGH simulations of the AT site resulted in three longitudinal intra-snowpack flow paths. The simulated number of intra-snowpack longitudinal flow paths for the AT and BT sites was equal to field observations, whereas the NT site simulations did not match well with field-observed locations of the dye tracer during experiments described in Webb et al. (2020).

Figure 6 Time series results of SnowTOUGH simulations for the above-treeline (AT) site showing (a) measured air temperature, (b) simulated snow surface temperature, and (c) volumetric liquid water content (θ_w) distribution at 4 h intervals.

4.3 Comparison to field data

Comparisons of SnowTOUGH to field observations indicated varying results based on site and parameter of interest. The simulated bulk θ_w showed little temporal variability for both the NT and AT sites, while field observations showed greater variability (Fig. 7). Simulated bulk θ_w remained near 3 % for both the NT and AT sites throughout the IOPs. The average of all field observations was generally greater than simulated values, though simulated values were always within 1 standard deviation of field observations. The mean of all field observations for the NT and AT sites was 4.2 % and 3.5 %, respectively. The large standard deviations of field observations were largely driven by converging intra-snowpack flow paths creating areas of bulk θ_w as high as 20 % (Webb et al., 2020). Though different, the comparison of θ_w between SnowTOUGH simulations and field observations are within the estimated error of the field methods (∼ 2 %).

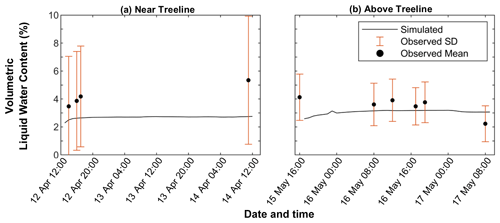
Figure 7 Comparison of SnowTOUGH-simulated volumetric liquid water content (θ_w) and field observations using ground-based remote sensing for the (a) near-treeline and (b) above-treeline sites.

Dye tracer experiments compared well at the AT and BT sites but not the NT site (Fig. 4). The number of intra-snowpack flow paths shown in the SnowTOUGH simulations were similar to those shown from dye tracer experiments at the AT (three longitudinal flow paths) and BT (no longitudinal flow paths) sites presented in Webb et al. (2020), though the depths of these flow paths beneath the snow surface differed slightly. The field-observed dye tracer locations that were not simulated as longitudinal flow paths for some instances still display increased liquid water retention or ice lens formation (Fig. 6). Additionally, simulation results suggest increasing longitudinal fluxes in liquid water with elevation, which was similarly observed at these sites (Webb et al., 2020). The largest discrepancy between simulations and field observations occurred at the NT site where only one intra-snowpack flow path was simulated using SnowTOUGH and three were observed in the field at different depths beneath the snow surface (Fig. 4).

Comparing simulated longitudinal flow rates to field observations is difficult because no flow rates were directly measured in the field. However, locations of converging intra-snowpack flow paths were used in Webb et al. (2020) to estimate effective upslope contributing areas (EUCAs), defined as the minimum upslope contributing area required to produce observed changes in liquid water content from melt rate estimates if all meltwater was diverted longitudinally and collected in a single observation location. Therefore, these observations are not directly comparable to SnowTOUGH simulations, but insights can still be gained from comparisons. These field observations resulted in peak EUCA of 6 and 17 m² for the NT and AT sites, respectively. For the NT site, this occurred over a 2 h time period with a total of ∼ 5 mm of melt. At this same time in the NT SnowTOUGH simulations, the location 15 m downslope resulted in an accumulation of longitudinal flow of 28.7 mm of water (Fig. 5bii; 12 April at 12:00, mean longitudinal flow of ∼ 4 mL s⁻¹ for 2 h) or roughly 5.7 times greater than the simulated melt. For the AT site, the simulated melt was ∼ 7.5 mm with a total accumulation of simulated longitudinal flow at the 15 m downslope location of 386 mm (Fig. 5cii; 16 May at 12:00, mean of 268 mL s⁻¹ for 2 h) or roughly 51 times greater than the estimated contributing melt. Therefore, relative to the calculations from Webb et al. (2020), SnowTOUGH-simulated longitudinal fluxes are similar to observations at the NT site and greater by a factor of 3 at the AT site.

5 Discussion

This is the first study, to our knowledge, that has simulated the two-dimensional flow of liquid water through a snowpack at the experimental plot scale. Our simulations show the presence of hydraulic barriers that divert liquid water longitudinally via preferential flow paths at the two upper-elevation sites (AT and NT) that were also present in field observations.

SnowTOUGH simulations produced the greatest rates of longitudinal flow at the highest-elevation site, the AT plot, similar to field observations using dye tracer experiments and ground-based remote sensing techniques (Webb et al., 2020). The number of longitudinal flow paths observed in the field at this site was equal to simulations. The depths of these flow paths beneath the snow surface, however, differed slightly between field observations and simulations. This is likely a result of SnowTOUGH simulations not accounting for snow depth variability across the plot and natural snowpack layer heterogeneity (Leroux and Pomeroy, 2017; Marsh and Woo, 1985; Molotch et al., 2016). At the NT plot, some of the field-observed dyed flow paths were noted as dyed ice lenses (Webb et al., 2020) where SnowTOUGH-simulated liquid water storage increased and ice lenses formed with no longitudinal flow. This may result in a longitudinal flow path during later melt events, though further experiments with longer IOPs are necessary. The natural heterogeneity of snowpack stratigraphy would be difficult to characterize at this scale without disturbing the snow at the location of the dye tracer experiment. Maintaining undisturbed conditions is essential to study the natural transport of the dye. Additional studies are necessary to characterize the horizontal heterogeneity of stratigraphy in varying snowpack conditions. Previous snow studies have suggested that the discontinuity of layers (such as ice lenses) can be a major factor in flow path continuity (Eiriksson et al., 2013; Kattelmann and Dozier, 1999; McGurk and Marsh, 1995; Schneebeli, 1995; Yamaguchi et al., 2018). However, previous studies of capillary barriers at the interface between soil layers have shown that homogenous layer assumptions, as those made in the present SnowTOUGH simulations, capture the average of randomized heterogeneous simulations (Ho and Webb, 1998). The validity of this assumption for snow should be further studied. In general, it is likely that the natural heterogeneity of both permeability and capillary barriers will decrease the amount of longitudinal flow simulated in this study. Thus, SnowTOUGH simulations are likely overestimating the amount of longitudinal flow for specific flow paths.

Relative to estimates of EUCA, the AT site simulations overestimated longitudinal flow. However, it is important to note that the field methods used to estimate the EUCA likely underestimate the value because it assumes all diverted liquid water remains in the snowpack at the point of calculation. Additionally, the low melt rates as a result of the incoming storm add uncertainty to the appropriateness of these calculations using snowmelt rates. Therefore, it is likely that the true value of EUCA is between 17 and 51 m² for the AT site. Conversely, the NT site simulations resulted in a similar amount of longitudinal flow within the plot-scale simulations as field-observed EUCA suggests. Considering the underestimation of the number of flow paths simulated at this site and the underestimation of EUCA from field methods, as previously mentioned, the true EUCA is likely larger than the SnowTOUGH-simulated longitudinal flow. Additionally, the longitudinal flux for the single flow path is likely overestimated. We recommend the use of snow lysimeters similar to those implemented in Eiriksson et al. (2013) in future studies to further quantify intra-snowpack longitudinal flow for comparison with the SnowTOUGH model.

The continued flow of liquid water after surface melt ceased at the AT site provides insights into the movement of liquid water during the melt season. The flow paths continued to direct liquid water longitudinally downslope 40 h after surface melt ceased (Fig. 4) and was confirmed during dye tracer collection and ground-based remote sensing observations. The dyed flow paths still contained liquid water at the time of field observations, implying that further longitudinal flow would have likely occurred for an uncertain time and distance. Furthermore, multiple layers retained liquid water that will be more readily available for transport during later melt events (Fig. 6). During this time of no surface melt, little vertical movement of water towards the ground surface occurred in the SnowTOUGH simulations and the dominant flow direction was longitudinal as a result of hydraulic barriers. The simulated longitudinal movement of water through the snowpack was orders of magnitude greater than vertical downward movement of meltwater with mean values of 212 and 5.8 mL s⁻¹, respectively (mean ratio of 75:1; Fig. 5cii). Though this ratio is likely overestimated, as previously mentioned, we estimate that the order of magnitude is correct. This suggests that during regular diurnal melt cycles in the spring snowmelt season, meltwater may continue flowing downslope overnight or during cold periods, accumulating at downslope convergent locations. For the AT plot, this location is where the ground surface and snow surface slope gradients decrease; this location was observed to accumulate liquid water in the ground-based remote sensing observations (Webb et al., 2020, 2018c) which produced large variability in snowmelt lysimeter discharge in previous years (Rikkers et al., 1996). This process also has implications for SWE distribution during midwinter melt events. Midwinter melt events may initiate flow paths that divert liquid water along longitudinal flow paths with no infiltration across the snow–soil interface. This meltwater may flow downslope for many hours due to the relatively slow refreezing process, accumulating flow at convergent locations prior to refreezing. As a result, the distribution of SWE may be such that increased bulk density occurs at downslope locations of convergent flow paths with no obvious increase in depth and potentially a decrease in depth. For example, Webb et al. (2018a) observed a 170 % increase in SWE with a decrease in snow depth as a result of increased liquid water content from upslope locations.

The SnowTOUGH simulations bring new modeling capabilities of two-dimensional liquid water flow through snow. To date, multidimensional modeling has been limited to the centimeter scale (e.g. Hirashima et al., 2017; Leroux and Pomeroy, 2017). For simulations at the scale of meters to tens of meters as presented in the current study, variable parameterization remains a challenge. Current hydraulic variables for snow layers have been developed at the centimeter scale in controlled laboratory environments (Calonne et al., 2012; Yamaguchi et al., 2010) and shown improvement for one-dimensional (vertical) models on flat terrain (e.g., Wever et al., 2016, 2014). However, difficulties arise with layer heterogeneity, as previously mentioned, for sloping terrain, as presented in this study, and if snow grain types vary (Yamaguchi et al., 2012). While these variable parameterizations worked well for the BT and AT study plots to identify longitudinal flow paths, the NT site simulations did not match field observations well, indicating the variables do not work as well when hydraulic barriers of lesser strength are present (i.e., smaller differences in layer properties across interfaces). Future studies at the plot scale may improve effective parameterization of specific layer variables through the application of snowmelt lysimeters and inverse modeling techniques. The improved parameterization of snow variables for modeling liquid water flow through snow would likely improve the modeling accuracy for hydraulic barriers that dominate liquid water transport during times of little or no surface melt (Fig. 4). These hydraulic barriers cause longitudinal flow paths at the plot scale and control the storage and release of liquid water. A logical next step for future studies aiming to model this process is to develop a fully coupled two-dimensional model and build upon parameterization of variables to determine effective properties at the plot to hillslope scales and the implications for hydrological modeling.

Current hydrological models do not account for longitudinal intra-snowpack flow paths. Snowmelt is assumed to vertically percolate through the snow and infiltrate the soil at the same location at which it originated as melt. However, the present study indicates that longitudinal intra-snowpack flow (i.e., lateral flow in hydrologic modeling terms) can be a dominant process at the plot scale. Given the higher hydraulic conductivities of snow relative to common soils (Calonne et al., 2012), the flow paths identified in our study may have important implications for headwater catchment dynamics during the snowmelt period. These processes may be of particular interest if models are to be used in a predictive manner for future meteorological scenarios (i.e., climate warming).

6 Conclusions

Through the soft coupling of SNOWPACK and iTOUGH2, we successfully simulated the two-dimensional movement of liquid water through a layered snowpack, including snow metamorphism and melt/freeze processes, at spatial scales previously unstudied. The simulations compared well with field data at two of the three field sites. Results show the importance of longitudinal intra-snowpack flow paths, particularly during times when the snow surface refreezes. We show the importance of longitudinal flow paths at the multiple-meter scale and for temporal scales beyond regular diurnal fluctuations. At the above-treeline study site, the longitudinal flow was orders of magnitude greater than vertically downward percolating water with a mean ratio of 75:1. At the near-treeline site, longitudinal flow was simulated as slightly less than vertically downward percolating water. The below-treeline simulations resulted in negligible longitudinal flow. This study shows the increasing influence of longitudinal intra-snowpack flow paths at higher elevations where a snowpack develops a more complex and persistent stratigraphy. Results of this study suggest that intra-snowpack longitudinal flow may be an important process for the consideration of streamflow timing in snowmelt-dominated hydrographs for hydrologic modeling purposes.