the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Sensitivity of inverse glacial isostatic adjustment estimates over Antarctica
Matthias O. Willen
Martin Horwath
Ludwig Schröder
Andreas Groh
Stefan R. M. Ligtenberg
Peter Kuipers Munneke
Michiel R. van den Broeke
Glacial isostatic adjustment (GIA) is a major source of uncertainty for ice and ocean mass balance estimates derived from satellite gravimetry. In Antarctica the gravimetric effect of cryospheric mass change and GIA are of the same order of magnitude. Inverse estimates from geodetic observations hold some promise for mass signal separation. Here, we investigate the combination of satellite gravimetry and altimetry and demonstrate that the choice of input data sets and processing methods will influence the resultant GIA inverse estimate. This includes the combination that spans the full GRACE record (April 2002–August 2016). Additionally, we show the variations that arise from combining the actual time series of the differing data sets. Using the inferred trends, we assess the spread of GIA solutions owing to (1) the choice of different degree-1 and C20 products, (2) viable candidate surface-elevation-change products derived from different altimetry missions corresponding to different time intervals, and (3) the uncertainties associated with firn process models. Decomposing the total-mass signal into the ice mass and the GIA components is strongly dependent on properly correcting for an apparent bias in regions of small signal. Here our ab initio solutions force the mean GIA and GRACE trend over the low precipitation zone of East Antarctica to be zero. Without applying this bias correction, the overall spread of total-mass change and GIA-related mass change using differing degree-1 and C20 products is 68 and 72 Gt a−1, respectively, for the same time period (March 2003–October 2009). The bias correction method collapses this spread to 6 and 5 Gt a−1, respectively. We characterize the firn process model uncertainty empirically by analysing differences between two alternative surface mass balance products. The differences propagate to a 10 Gt a−1 spread in debiased GIA-related mass change estimates. The choice of the altimetry product poses the largest uncertainty on debiased mass change estimates. The spread of debiased GIA-related mass change amounts to 15 Gt a−1 for the period from March 2003 to October 2009. We found a spread of 49 Gt a−1 comparing results for the periods April 2002–August 2016 and July 2010–August 2016. Our findings point out limitations associated with data quality, data processing, and correction for apparent biases.
- Article
(2429 KB) - Full-text XML
-
Supplement
(6064 KB) - BibTeX
- EndNote
The quantification of recent and current sea level changes plays a crucial role for local, regional, and global projections. Mass changes of the Greenland and Antarctic ice sheets are responsible for approximately 20 % of the global mean sea level rise between 1991 and 2010 (Church et al., 2013). Space gravimetry observes temporal gravity changes which result from mass redistribution on and in Earth. An ice mass trend estimation can be determined using time-variable gravity fields from the Gravity Recovery And Climate Experiment (GRACE) mission (e.g. Groh et al., 2014; Forsberg et al., 2017), which is continued by its follow-on mission GRACE-FO.
Large uncertainty in the ice mass change estimates derived from space gravimetry is related to viscoelastic deformation of the solid Earth by glacial isostatic adjustment (GIA). This is the deformation of the solid Earth due to loading variations through sequences of past glacial advance and retreat over many millennia. The manifestation of ice sheet and GIA mass change signals is superimposed and is of the same order of magnitude over Antarctica (Sasgen et al., 2017). This requires GIA to be carefully considered when determining ice mass change. Moreover, quantified GIA provides insights into the glacial history of ice sheets or changing tectonic stress (Johnston et al., 1998).
One approach to determine the GIA signal is forward modelling (e.g. Ivins and James, 2005). GIA forward models are obtained using assumptions about the ice load history and the solid-Earth rheology, which are both subject to large uncertainties (Whitehouse, 2018; Whitehouse et al., 2019). GIA-induced vertical bedrock elevation change (BEC) derived from the Global Navigation Satellite System (GNSS) observations have been used to constrain forward models (e.g. King et al., 2010; Ivins et al., 2013; Whitehouse et al., 2012) or, more recently, to test probabilistic information of a suite of globally consistent forward models (Caron et al., 2018). Caron and Ivins (2020) used this method to investigate the regional GIA signal over Antarctica and to separate the contributions from oceanic and far-field regions.
In an alternative approach, satellite gravimetry and altimetry are combined to separate the GIA and ice-related mass signals (Wahr et al., 2000). Both spaceborne techniques observe a superposition of GIA and ice sheet change signals. For example, satellite altimetry observes surface elevation changes (SECs), some of which are caused by GIA-induced BEC. The combination requires assumptions about the relation between surface geometry changes and gravity field changes induced by GIA and likewise between the respective changes induced by ice sheet processes. These relations may be expressed in terms of effective densities. This combination approach was first implemented by Riva et al. (2009) and later refined by Groh et al. (2012) and Gunter et al. (2014). Hereinafter they are called the inverse (Whitehouse, 2018) because they use present-day observations to determine the GIA signal (in contrast to forward models). Results from Riva et al. (2009) fit better with GNSS-derived GIA rates than forward models (Thomas et al., 2011).
Recent studies separate the individual processes of the ice sheet and the underlying bedrock with statistical modelling (Zammit-Mangion et al., 2015; Martín-Español et al., 2016a). They use spatial and temporal a priori information (from numerical simulations), additional GNSS observations, and altimetry data of several satellite missions. Furthermore, a joint inversion has been presented that takes into account the rheological parameters of the solid Earth (Sasgen et al., 2017). Engels et al. (2018) use a regularized parameter estimation approach (dynamic patch) to resolve the superimposed mass trends in Antarctica. Martín-Español et al. (2016b) compared available GIA solutions from forward modelling and inverse estimation and have shown that differences are larger than indicated uncertainties.
We analyse the sensitivity of inverse GIA estimation on the choice of data input and methodology, thereby identifying both the possible causes of discrepancies and the uncertainty. Our inverse GIA estimation is based on the approach of Gunter et al. (2014) but uses both contrasting and updated data sets. Special attention is paid to surface processes, namely changes of mass and volume of the firn layer. By the term firn, we assume both snow and firn. In inverse GIA estimation, changes in the firn layer need to be separated from those in the ice layer below. For that purpose, the surface mass balance (SMB) as well as the volume change from the firn layer are needed. These are usually provided by regional climate models like RACMO2 (van Wessem et al., 2018) and firn densification models (FDMs) forced with climate models, like IMAU FDM (Ligtenberg et al., 2011). Uncertainties of these model products are poorly known. Here, we characterize the uncertainty by comparing the RACMO2.3p2 SMB products with those of the MAR model (Agosta et al., 2019).
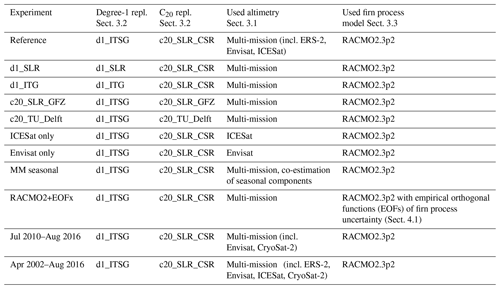
Another focus of this research is on the use of ice altimetry data. Different altimeter missions such as Envisat, ICESat, or CryoSat-2 use different observation techniques and differ in their spatial and temporal coverage. The multi-mission (MM) altimetry data set delivered by Schröder et al. (2019a) is well suited for a GIA inversion over nearly the full GRACE observation period (April 2002–August 2016). The effect of using different gravity field solutions from the GRACE processing centres and different filtering options is shown by Gunter et al. (2014). We use different degree-1 and C20 products to quantify their effect on inverse GIA estimation. We contrast estimates derived by combining linear trends of input data to estimates derived by combining monthly-sampled time series of input data.
Section 2 derives and describes in detail the combination approach, bias corrections using the low-precipitation zone (LPZ) of East Antarctica, estimation of the mass balance, and filtering. Afterwards, we explain how the errors for the firn process models are characterized and how the sensitivity analysis is performed. Furthermore, the approach is adapted to extract a more nuanced and self-consistent combination of input-data time series. Section 3 describes the products employed, processing steps, and additional assumptions. Section 4 presents results of derived uncertainties of the firn process models, the sensitivity analysis, and the time-series-based combination. Finally, the results are discussed and the most important findings are summarized in the conclusions.
2.1 Combination approach
Wahr et al. (2000) were the first to suggest the combination of satellite geodetic methods – gravimetry and altimetry – to estimate GIA. We use the analytical approach from Wahr et al. (1998) to explain gravity changes by mass changes projected into a spherical layer (with radius a) – termed area density changes (ADCs) or surface density changes. Note that a change of mass is with respect to a reference mass distribution. Based on GRACE solutions given in the spherical harmonic domain, the conversion of changes in Stokes coefficients with degree n and order m (Δcnm) into spherical harmonic coefficients of ADC (Δκnm) is
where ME is the total mass of the Earth, a the equatorial radius of the reference ellipsoid, and the second-load Love number to account for the deformation potential of the solid Earth induced by the mass redistribution. The linear ADC is synthesized into spatial domain , which is the superposition of the ADC through GIA, and processes in the ice (ID) and firn layer:
While GIA is not a process of ADC, is defined as the apparent ADC that would induce a gravity field effect equal to the GIA-induced gravity field effect. We refer to (as well as spatial integrals of ) as GIA-related mass change. ID summarizes all processes which are weighted with ice density, e.g. ice-dynamic flow or basal melt. We summarize the ice-induced, or cryospheric, area density trend as .
Analogously, the overall linear SEC derived from altimetry is the sum of the linear SEC through ID, firn, GIA, and elastic BEC:
Note that GIA refers to the viscoelastic deformation of the solid Earth. The elastic BEC () triggered by present-day ice mass changes needs to be subtracted from the overall SEC observed by altimetry prior to the combination. We define . Doing this, the SEC signals in are consistent with ADC signals in .
The process-related elevation and area density changes are linked with effective density assumptions (ρGIA, ρID):
Rearranging Eq. (3) to
and substituting it together with Eqs. (4) and (5) into Eq. (2) leads to
which can be solved for
In Gunter et al. (2014), Eq. (8) is modified with a criterion to include assumptions about the difference using a priori uncertainties. ρID is replaced by ρα to permit the following case distinction:
where
with
The case distinction accounts for uncertainties in altimetry and in the firn densification model (FDM) as well as a priori knowledge on ice sheet processes. The GIA-induced BEC is in the millimetre per year range, whereas and can be in the centimetre to metre per year range. If altimetry and FDM are perfect, would leave essentially (apart from a very small ). The following case distinctions are made.
-
Case I. If differences between and are significantly negative, an ice-dynamic-induced SEC is assumed (glacial thinning). Gunter et al. (2014) argue that only one region in Antarctica is known to show glacial thickening: the area of the Kamb Ice Stream (Retzlaff and Bentley, 1993; Wingham et al., 2006). This region is therefore treated separately by a mask which sets ρα to ρID. The mask is generated from positive SEC from altimetry in this area.
-
Case II. If differences between and are significantly positive, it is assumed that the FDM underestimates SEC due to firn processes and the remaining part therefore must not be weighted with ice density but with firn density.
-
Case III. If differences between and are not significant (with an absolute value smaller than 2σh), those differences are ignored by setting ρα=0, which means . That is, no mass change in the ice layer is considered and a mass trend of the ice sheet only arises by the trend of cumulated surface mass balance anomalies.
Making this case distinction for ρα has the advantage of solving for GIA without a predefined spatial mask to distinguish between firn and ice processes (e.g. density mask in Riva et al., 2009) except for the Kamb Ice Stream. An underestimated σh leads to differences between and being included in the mass balance, although they are within their true uncertainty bounds and vice versa if σh is overestimated.
2.2 Bias corrections and estimation of the mass balance
The following steps are performed in sequence.
-
Step 1. Estimation of biased using the data combination approach (Eq. 9).
-
Step 2. Removing the bias from , leading to the debiased .
-
Step 3. Removing the bias from , leading to the debiased .
-
Step 4. Estimation of the debiased ice mass trend from debiased GIA-related mass trend (Step 2) and debiased total-mass trend (Step 3).
The bias corrections are necessary to consider offsets introduced by systematic errors in degree-1 and C20. The estimation of the bias is done using the same strategy as Gunter et al. (2014). They argue that the effect of such offsets is significantly larger than potential mass signals in a low-precipitation zone (LPZ) of the East Antarctic Ice Sheet.
In Step 2, the LPZ-based GIA bias correction is applied. It is assumed that the GIA-induced BEC should be negligibly small in this area. The GIA estimate from Step 1, averaged over the LPZ, , is interpreted as a bias due to the input data sets. It is subtracted from . The debiased GIA-induced BEC is
From this we derive the debiased GIA-related mass trend
This means that input-data-set biases are jointly removed. Removing a small GIA-induced BEC introduces an error in the final result. GIA models predict approximately −3 to +1 mm a−1 in the area of the LPZ (Whitehouse et al., 2019). Gunter et al. (2014) argue that the error introduced by the LPZ bias correction is smaller than other bias contributors.
In Step 3, the LPZ-based GRACE bias correction is applied. ADCs from gravimetry are calibrated to the LPZ by removing the mean ADC in this area, . The debiased gravimetric ADC is
In Step 4, the debiased ice mass trend is calculated as
Note that the gravimetric bias correction is not applied to used in Step 1, the initial combination (Eq. 9).
2.3 Filtering
For the necessary noise suppression we use GRACE data with a de-striping filter applied () in addition to the filtering implied by the spherical harmonic truncation. Ideally, the data and models involved in the combination should have consistent spatial resolution; that is, they should be filtered consistently. This is not strictly possible for the quotient in Eq. (9) because no unfiltered is available that could be divided by (ρGIA−ρα) before filtering. Pragmatically, components with a similar spatial resolution are combined before they are filtered with a Gaussian filter ℱ. Hence, we obtain a filtered GIA-induced BEC:
For integrating mass trends in space, the signal redistribution (leakage) is taken into account by a buffer zone equal to the half-response width of the Gaussian filter appended to the grounding line of the ice sheet (Sect. 4.2). We do not correct for leakage through ocean mass signal separately as it amounts to only 4.5 Gt a−1 (Gunter et al., 2014). This ocean mass leakage is the same in every experiment, because we do not test the sensitivity to filters.
2.4 Uncertainty characterization of firn process models
In Eqs. (9) and (10), assumptions on uncertainties of the FDM and altimetry are crucial. Gunter et al. (2014) take from the formal uncertainty of the least-squares estimation. can be derived in the same way from the estimated trend of FDM SEC for the observation period. Note that both uncertainties are derived from stochastic information of the least-squares estimation rather than from an uncertainty characterization of the measurements and the model. Gunter et al. (2014) have also performed an uncertainty analysis of the combination result. For this purpose, they define the SMB-related uncertainty as 10 % of the estimated trend value, referring to Rignot et al. (2008). Note that the uncertainty assessment by Rignot et al. (2008), which amounts to 10 %–30 % of the signal, is applied to a different physical quantity than : namely to the snow accumulation in a drainage basin.
Because there is no comprehensive regional climate model ensemble, we quantify the error of firn process models by statistics on differences between two models. We use differences of trends of cumulated surface mass balance anomalies (cSMBAs) and of firn thickness trends. We assume those differences are due to modelling errors. This characterization comprises only a part of the full uncertainty, because it is based on two alternative climate model products.
2.5 Time-series-based combination
Previous studies combining gravimetry and altimetry are based on linear seasonal deterministic models over certain periods (Riva et al., 2009; Gunter et al., 2014; Martín-Español et al., 2016a; Sasgen et al., 2017; Engels et al., 2018). However, signals in the firn and ice layer over the Antarctic Ice Sheet (AIS) show inter-annual changes (Horwath et al., 2012; Ligtenberg et al., 2012; Mémin et al., 2015). In theory, combining observations on a time series level will lead to a linear GIA signal. For T months the vector
contains the differences in mass at month with respect to a reference mass distribution. The combination of all time series is
This requires that all data are available as monthly gridded products. To simplify, we assume that effective densities do not change over time. To be consistent with the combination of trends, ρID is replaced with ρα from the trend-based approach.
The data and models of every month are filtered in the same way as for the trend-based approach to make the resolution consistent (Sect. 2.3). Afterwards they are combined according to Eq. (18), which results in a GIA time series for each grid cell.
By assumption the GIA signal in the resulting time series hGIA is linear over decades of satellite observations (e.g. Huybrechts and Le Meur, 1999). A fitted trend to hGIA is . We are aware that for regions with a low-viscosity asthenosphere, e.g. Pine Island Bay, the viscoelastic deformation associated with GIA may be non-linear even for decadal periods (Barletta et al., 2018). In this case, the assumption of a linear GIA-induced BEC introduces an error.
2.6 Sensitivity analysis
The sensitivity of inverse GIA estimates to different data, models, and assumptions is quantified. Starting from a reference experiment, certain parameters are changed. Every experiment is performed with and without the two LPZ-based bias corrections to demonstrate their effect. It is examined how different altimetry data (Sect. 3.1), degree-1 and C20 products (Sect. 3.2), and the empirically determined errors of the firn process models (Sect. 4.1) affect the GIA solution. Analogous to Riva et al. (2009) and Gunter et al. (2014), a Gaussian filter (half-response width = 400 km) is applied to all data sets. For the integration of mass trends over the AIS, the West Antarctic Ice Sheet (WAIS), and the East Antarctic Ice Sheet (EAIS), we use a buffer zone of 400 km grounding-line distance to mitigate leakage. The Antarctic Peninsula (AP) is not considered separately here.
For each inverse GIA solution, the integrated mass change is calculated. In addition, a root-mean-square (rms) difference with respect to the reference experiment is determined, hereinafter referred to as the rms difference from reference experiment (RMSRE),
Here, N is the number of grid cells of a Cartesian grid in the polar stereographic projection of the AIS area (EPSG: 3031) including the buffer zone. refers to the GIA solution which is compared to the reference experiment (). The RMSRE values are sensitive to regional differences, which may be hidden in the comparison of integrated mass trends.
The sensitivity to the choice of firn process models is investigated as follows: based on the comparison of two firn process models, empirical samples of error patterns are generated. They are added to and and propagated to the empirical GIA estimates. Additionally, all identified trend differences of cSMBAs are added to and .
Furthermore, the dependency on differing time periods is investigated. Under the assumption that GIA is linear in time, the used time interval should have negligible influence. While the time interval for the reference experiment is March 2003–October 2009 (according to Gunter et al., 2014), alternative periods are the main GRACE observation period (April 2002–August 2016) and the overlap period between GRACE and CryoSat-2 (July 2010–August 2016).
This section specifies the data sets and processing steps used in the sensitivity experiments which are summarized in Table 1. Furthermore, models and assumptions are explained. Reference system parameters are chosen according to the IERS Conventions (Petit and Luzum, 2010).
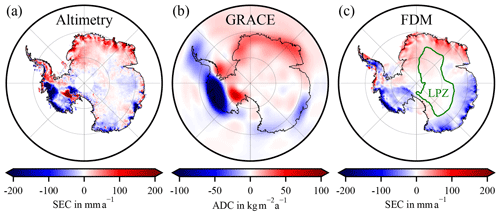
Figure 1(a) Surface elevation change (SEC) from the multi-mission altimetry product (Schröder et al., 2019a), (b) GRACE-derived area density changes (ADC), and (c) FDM-derived SEC (time period: April 2002–August 2016). A Gaussian filter was applied to the GRACE result (half-response 250 km). Low-precipitation zone (LPZ) (green, c).
3.1 Altimetry
The SECs from Schröder et al. (2019a) are based on a repeat-altimetry analysis in a multi-mission altimetry (MM altimetry) framework. Data from the Seasat, Geosat, ERS-1, ERS-2, Envisat, ICESat, and CryoSat-2 missions are combined, resulting in a monthly sampled time series on a 10 km grid. The reader is referred to Schröder et al. (2019a) for details on processing and background information. In order to combine the altimetry time series with GRACE, we use the monthly results from April 2002 at the earliest to August 2016 at the latest. This period involves observations of ERS-2, Envisat, ICESat, and CryoSat-2 missions (Fig. 1a). The altimetry missions have a different spatial and temporal sampling, e.g. ICESat's campaign-style temporal sampling. Further, the data quality varies over mission lifetime. For this reason every month of the combined time series differs in spatial coverage. We obtain a linear rate over the respective intervals by adjusting an offset and a linear trend to the MM time series for each cell of the 10 km grid. For the reference experiment no annual periodic signal is co-estimated in order to be consistent with Gunter et al. (2014). We apply weights according to the uncertainty estimates of each epoch of the MM time series. We took the criterion that the trend would only be estimated for a grid cell if more than 5 months with observations are available and at least 80 % of the selected total time span is covered. This criterion should avoid outlier trends through insufficient sampling. The uncertainty used in Eq. (11) is the a posteriori standard deviation derived from the least-squares adjustment of the MM time series.
To investigate how the choice of altimetry products affects the GIA estimation, single-mission time series are calculated for Envisat and ICESat. They consistently use the same processing steps as the MM altimetry from Schröder et al. (2019a), with the exception that the final step of weighted spatio-temporal smoothing is applied to single-mission data rather than multi-mission data. In total three different altimetry time series are used for testing the gravimetry–altimetry combination approach. To assess the sensitivity of results to the co-estimation of seasonal signals, an additional version of the MM altimetry trends is calculated by co-estimating the annual sinusoidal signal (MM seasonal in Table 1). This is consistent with the treatment of GRACE and the firn process models.
Part of the altimetry-derived SEC is caused by the elastic BEC of the solid Earth due to present-day ice mass change (), which needs to be subtracted from the altimetry observations () prior to the combination (Eq. 9). We estimate to be −1.5 % of (Riva et al., 2009). Hence, the elastic-corrected altimetry-derived SEC is
The approximative nature of this elastic correction leaves an error, but its influence on the GIA estimate is negligible (Gunter et al., 2014).
3.2 Gravimetry
GRACE-derived monthly mass variations are calculated from the ITSG-Grace2016 monthly gravity field solutions up to a degree and order of 90 (Mayer-Gürr et al., 2016) using Eq. (1). Monthly solutions from other processing centres are not considered because ITSG-Grace2016 is identified through internal comparison as the gravity field solution series with a high signal-to-noise ratio. This is supported by Jean et al. (2018), who found that the precursor ITSG-Grace2014 show a lower noise level compared to solutions from other processing centres. The influence of the different GRACE monthly solutions on the inverse GIA result was shown and discussed in Gunter et al. (2014). We do not use solutions after August 2016. Those solutions show a much higher noise level due to accelerometer issues.
GRACE monthly solutions need to be complemented by the degree-1 term of the spherical harmonic coefficients, as this is not observed by GRACE. Three different products to replace the degree-1 coefficients are evaluated. (1) A product is determined following Swenson et al. (2008) using ITSG-Grace2016 monthly solutions (d1_ITSG). (2) A satellite laser ranging (SLR) product by Cheng et al. (2013b) (d1_SLR) and (3) degree-1 coefficients by Rietbroek et al. (2016) are used (d1_ITG).
Furthermore, the influence of the flattening term C20 is investigated. Because C20 is poorly determined by GRACE (Cheng and Ries, 2017), external products are compared. (1) SLR-based time series are used from the Center for Space Research at the University of Texas, USA (c20_SLR_CSR; Cheng et al., 2013a). (2) SLR-based time series from the German Research Centre for Geosciences, Potsdam, Germany are used (c20_SLR_GFZ; König et al., 2019). (3) A time series from the Delft University of Technology, Delft, Netherlands (c20_TU_Delft), which is derived from GRACE observations themselves and an ocean model is used (Sun et al., 2015).
A critical point is filtering because the monthly solutions are noisy and have a correlated error pattern (Horwath and Dietrich, 2009). A de-striping filter is applied in the spherical harmonic domain (Swenson and Wahr, 2006).
A linear seasonal model is adjusted to fit the filtered Stokes coefficients (offset, linear, annual periodic, and 161 d periodic). The trend is synthesized from the spherical harmonic into the spatial domain on the altimetry grid with 50 km resolution. In this way for each grid cell a linear area density trend in kilogrammes per square metre per year is determined (Fig. 1b).
3.3 Firn process models
Information on variations in the firn layer is required in the combination approach (Eq. 10). SMB is the sum of precipitation, snow drift, sublimation, and meltwater runoff. The SMB components are numerically simulated with the RACMO2.3p2 model, which contains a multilayer snow model developed by the Royal Netherlands Meteorological Institute (KNMI) and the Institute for Marine and Atmospheric Research, Utrecht, Netherlands (IMAU) (van Wessem et al., 2018). These results are compared to the MAR model of the Laboratory of Climatology, Liège, Belgium (Agosta et al., 2019). The regional climate models are forced at their lateral boundaries with the ERA-40 and ERA-Interim reanalyses. Mass fluxes (snowfall, snow drift, sublimation, erosion–deposition, and surface melt) as well as surface temperature are then used to force an offline firn densification model that includes firn compaction, vertical meltwater transport and refreezing, and thermodynamics of the firn layer.
The RACMO2 and MAR SMB products are appropriate for comparison as both are similar in terms of temporal (monthly) and spatial resolution (RACMO2: 27 km; MAR: 35 km). Moreover, both variants considered here use the same forcing. There is no independent knowledge (in a spatial resolution similar to that of SMB models) about the ice flow contribution to ice mass balance and hence about the degree of balance or imbalance between SMB and ice flow. Therefore, the modelled SMB is only used to derive SMB-induced mass variations with respect to any background signal of mass change. The unknown background signal of mass change is the possible imbalance between the mean SMB over a multi-year reference period and the mean effect of ice flow over the same reference period. The considered SMB-induced mass variations hence arise from the temporal cumulation of SMB anomalies with respect to the mean SMB over the reference period. Here, we define the reference period to be the entire model period for RACMO2.3p2 and MAR (January 1979–December 2016). For the satellite observation periods (e.g. April 2002–August 2016) the surface mass trend (), or literally the trend of cumulated surface mass balance anomalies (cSMBAs), is estimated (co-estimated with bias and annual periodic signal).
The used firn model IMAU FDM (Ligtenberg et al., 2011) is forced at the upper boundary by SMB components from RACMO2. The firn layer is initialized by forcing the FDM repeatedly with the 1979–2016 surface mass fluxes and temperature, until an equilibrium firn layer is established. This implies that present-day conditions represent a state of equilibrium and that there is no net firn thickness change over the model period January 1979–December 2016. One result of the actual model run is the firn-elevation-change time series. A linear seasonal model (bias, trend, annual periodic signal) of firn-process-induced SEC is adjusted to fit the FDM time series for the observation periods under investigation (Fig. 1c).
The LPZ (Fig. 1c) is defined based on the ECMWF ERA-Interim reanalysis precipitation product. We use 20 mm a−1 annual precipitation as a threshold for low precipitation (Riva et al., 2009), rather than 21.9 mm a−1 used by Gunter et al. (2014).
The trend differences between RACMO2.3p2 and MAR SMB products are used for uncertainty characterization of firn process models. In order to gain statistical information on possible trend differences over a 7-year interval, we calculate trend differences over 32 intervals of 7 years (January 1979–December 1965; January 1980–December 1966;...; January 2010–December 2016) covered by RACMO2.3p2 and MAR. The 7-year length is the approximate length of the observation period of our reference experiment (March 2003–October 2009) defined by the ICESat observation period. A FDM forced with MAR SMB does not exist. However, the RACMO2.3p2 SMB and the derived FDM are directly linked to each other. For this reason we assume that derived conclusions on errors of SMB are transferable to the FDM as a lower bound. Pseudo FDM trend differences are estimated out of the cSMBA trends by
is the jth trend difference between cSMBA from RACMO2 and cSMBA from MAR. ρMAR is calculated from MAR density fields by taking their average over the near-surface layers (0–1 m) and over the whole model period. This does not consider the evolution of the firn layer, as an independent FDM driven by MAR outputs would consider it. Furthermore, uncertainties associated with equilibrium assumptions are not considered.
Prior to the combination, cSMBA and FDM trends are linearly interpolated to the polar stereographic grid. The high-resolution products (altimetry and firn process models) are modified as follows. NaN-Grid cells on the grounded part of the ice sheet (missing data) are treated as case III in Eq. (10).
3.4 Density assumptions
The ratio between volume changes and area density changes is defined by the effective densities ρGIA, ρfirn, and ρID for GIA-related, firn-related, and ice-related processes, respectively. We use a ρID of 917 kg m−3. The firn density is variable in space and time. The location-dependent estimation for ρfirn is calculated using the empirical Eq. (2) in Ligtenberg et al. (2011).
The density mask for ρGIA is generated as follows: The ratio between the GIA-induced BEC and the GIA-induced ADC is about 3700 kg m−3 (Wahr et al., 2000). We use 4000 kg m−3 over the Antarctic continent and 3400 kg m−3 under the ice shelves and the ocean with a smooth transition (according to Riva et al., 2009; Gunter et al., 2014). These numbers account for the redistribution of ocean mass through GIA and are derived from forward-model results. This density is not a density in a material-science sense. It is an effective value which sets GIA-induced BEC and the ADC in relation. The term rock used in the literature might be misleading.
Table 1Overview of all performed experiments of the sensitivity analysis (Sects. 2.6 and 4.2, Table 2). All experiments use ITSG-Grace2016 monthly solutions (Mayer-Gürr et al., 2016) over the March 2003–October 2009 time period, except for the last two experiments which use the quoted time period.
4.1 SMB uncertainty
There are considerable differences between the time series of cSMBA from the RACMO2 and MAR SMB products for each cell. Figure 2 shows the integrated values for the AIS. Note that a ∼400 Gt cSMBA difference in 1987 (8 years after model start) represents a 50 Gt a−1 difference in SMB, which is ∼2 % of the total grounded ice sheet SMB. The integrated SMB from RACMO2.3p2 is 2229 Gt a−1 with an interannual variability of 109 Gt a−1 (van Wessem et al., 2018). We use the 32 trend differences from the moving 7-year intervals to quantify discrepancies of derived cSMBA trends between both models. Figure 3 shows (1) the rms of all trend differences and compares it with (2) the formal uncertainty we derive from the least-squares estimation and with (3) the 10 % uncertainty assumption (Sect. 2.4). The last two are derived from the estimated cSMBA trends of the RACMO2.3p2 SMB product over the ICESat observation period (March 2003–October 2009). The formal uncertainty and the 10 % assumption are similar in spatial pattern and magnitude. The rms of trend differences is similar in spatial pattern, too, but approximately 3 times larger in magnitude.
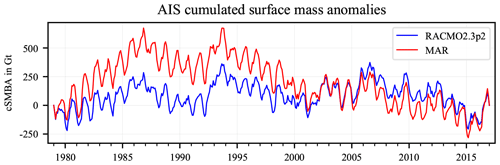
Figure 2Cumulated surface mass balance anomalies (cSMBAs) of the regional climate models RACMO2.3p2 (blue; van Wessem et al., 2018) and MAR (red; Agosta et al., 2019), integrated over the grounded AIS.
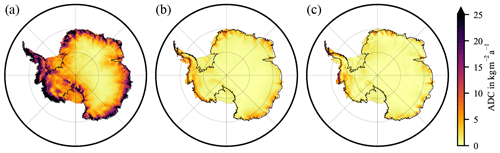
Figure 3Three uncertainty assessments for the area density change (ADC) trend induced by cumulated surface mass balance anomalies (cSMBA). (a) The rms of cSMBA trend differences between RACMO2.3p2 and MAR for all 7-year intervals (Sect. 3.3), (b) the formal uncertainty from least-squares estimation for March 2003–October 2009, and (c) the 10 % uncertainty assumption.
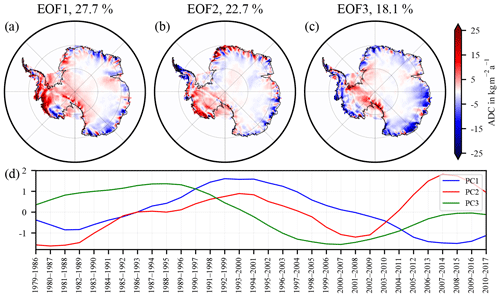
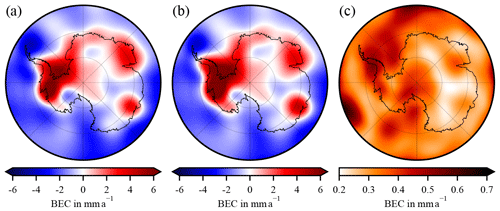
Figure 4(a)–(c) Area density change (ADC) of the first three EOFs of the trend differences between RACMO2.3p2 and MAR cumulated surface mass balance anomalies (cSMBA). (d) The respective principal components (PCs).
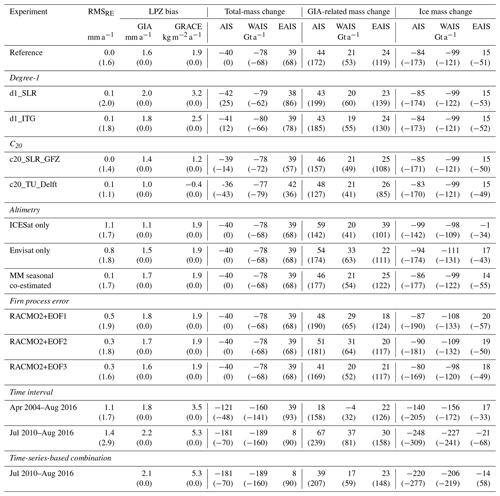
Table 2Results from the sensitivity experiments. This table is structured like Table 2 in Gunter et al. (2014). Each line reports results from one experiment, where line one reports the reference experiment. The time period is March 2003–October 2009 except where it is quoted by experiment name. Column 1: experiment name, according to Table 1. Column 2: rms difference of the GIA-induced bedrock elevation change (BEC) estimate (RMSRE) to the reference experiment. Columns 3 and 4: applied LPZ-based bias correction (see Sect. 2.2) for GIA-induced BEC and GRACE area density change, respectively. Columns 5, 6, and 7: spatial integral of total-mass change (Eq. 14) over the Antarctic Ice Sheet (AIS), the West Antarctic Ice Sheet (AIS), and the East Antarctic Ice Sheet (EAIS), including a 400 km buffer zone. Columns 8–10 and 11–13: same as columns 5–7, but for the GIA-related mass change (Eq. 13) and for the ice mass change (Eq. 15), respectively. Numbers in brackets give results of experiments with no bias corrections.
To extract the dominant error patterns, a spectral decomposition of the 32 7-year trend differences (see Sect. 3.3) is carried out using principal-component analysis (using singular value decomposition). Hence, the dominant empirical orthogonal functions (EOFs) and accompanying principal components are computed. From this analysis we obtain the dominant error patterns that are uncorrelated to each other and capture characteristic features of uncertainty. The first three EOFs of the trend differences explain ∼68 % of the total variance (Fig. 4a–c). The normalized EOF is scaled with the square root of the particular eigenvalue. Figure 4d shows the principle components indicating the scaling of the corresponding EOF. For instance, EOF-1 is dominated by variations in the WAIS. EOF-2 shows more variations on smaller scales. Without an attempt to further interpret the patterns of trend differences between the two models, the explored trend differences are used here to investigate the sensitivity of the inverse GIA estimates to these differences characterizing firn process uncertainty. For this purpose, (1) we add the EOFs to the firn process trends (, ), which we use as input for the data combination. Because a FDM forced with MAR products does not exist, we transfer the cSMBA-derived EOFs to FDM EOFs by calculating pseudo EOFs using MAR density fields (see Sect. 3.3, Eq. 21). The pseudo EOFs account for a lower bound of uncertainties of the firn thickness trends. True firn thickness trend differences are presumably higher as they would contain the potential mis-modelling of firn densification. From the added EOFs we get three GIA estimates to be compared with our reference solution. (2) Moreover, we add each trend difference separately to the cSMBA trend and each pseudo trend difference separately to the firn thickness trend. The pseudo firn thickness trend differences are likewise calculated using MAR density. This results in another 32 GIA estimates.
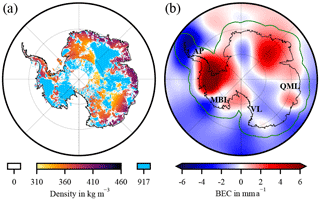
Figure 5(a) Estimated ρα density (Eq. 10) of the reference experiment. (b) GIA-induced bedrock elevation change (BEC) of the reference experiment (rms: 2.2 mm a−1); 400 km buffer zone (green line); geographical regions indicated: Antarctic Peninsula (AP), Marie Byrd Land (MBL), Victoria Land (VL), and Queen Mary Land (QML). For results from the other simulation experiments see Figs. S4 and S5.
4.2 Sensitivity analysis
Inverse GIA estimates are calculated using different choices of (1) degree-1 solutions, (2) C20 substitutions, (3) altimetry products, (4) empirical orthogonal functions (EOFs) of firn process errors, and (5) time intervals (Table 1). The reference experiment refers to the time period March 2003–October 2009 and uses the MM-altimetry-derived SEC, ITSG-Grace2016 monthly solution (degree-1: d1_ITSG, C20: SLR_CSR) and the firn process trends from RACMO2.3p2 over this period. The rms of the reference GIA-induced BEC estimate is 2.2 mm a−1. The estimated ρα (Eq. 10) is shown in Fig. 5a. Apart from the gridded GIA-induced BEC (Figs. 5b, S5 in the Supplement), we compare the integrated trends , , and corresponding to total-mass change (from GRACE), GIA-related mass change, and ice mass change, respectively. The results are summarized in Table 2. Furthermore, the RMSRE (Eq. 19) quantifies the discrepancy to the reference experiment GIA estimate. Figure 6 shows the mass balance estimates for March 2003–October 2009.
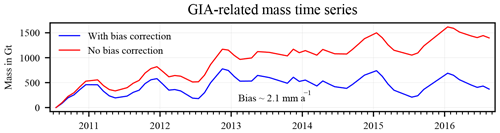
Biased total-mass changes for different C20 and degree-1 products vary between −43 Gt a−1 (c20_TU_Delft) and +25 Gt a−1 (d1_SLR), a range of 68 Gt a−1. Debiased total-mass change (Eq. 14) only differ by 6 Gt a−1 for the same time period (Table 2). Figure 6 illustrates biased and debiased total-mass changes of the entire AIS. Note that the biased total-mass change of 0 Gt a−1 in Table 2 arises coincidentally.
The biased GIA-related mass change of the AIS with MM altimetry (reference experiment) is very close to the Envisat-only estimate (174 vs. 172 Gt a−1). The biased ICESat-only result differs from the reference experiment by about 30 Gt a−1 (142 vs. 172 Gt a−1). Debiased estimates that use Envisat-only or ICESat-only results differ from the estimate of the reference experiment by 10 and 15 Gt a−1, respectively. The differences due to the co-estimation of seasonal components are marginal (∼2 Gt a−1).
Applying the approach to different time intervals April 2002–August 2016 and July 2010–August 2016 leads to debiased total-mass changes of −121 and −181 Gt a−1, respectively (biased estimates: −48 and −70 Gt a−1).
The addition of the EOFs (Sect. 4.1) propagates to differences in the GIA solution of up to 7 Gt a−1 for the debiased GIA-related mass change and up to 18 Gt a−1 for the biased GIA-related mass change. Additionally, Fig. S6 shows the standard deviation of the 32 GIA estimates resulting from propagating the 32 trend differences between RACMO2 and MAR.
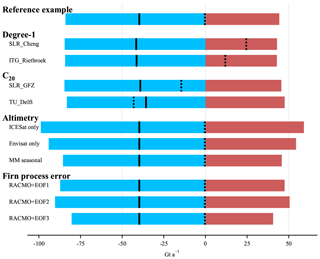
Figure 6Mass change results for the entire AIS over the interval March 2003–October 2009 from experiments with different data products and methodological choices. The LPZ-based bias correction was applied. Debiased total-mass change (solid black lines) is separated into debiased GIA-related mass (red) and ice mass change (blue). Dotted lines show the total-mass changes that arise when no bias corrections are applied. The case of no bias correction is further illustrated in Fig. S7.
4.3 Time-series-based combination
Our time-series-based combination takes advantage of the fact that gravimetry, altimetry, SMB, and FDM are available as monthly gridded products with sufficient spatial coverage from July 2010 to August 2016, owing to the availability of GRACE, CryoSat-2, and RACMO2.3p2. Riva et al. (2009) and Gunter et al. (2014) only use ICESat altimetry data, which does not allow a monthly sampling, as it has only 2–3 months of observation per year.
We used the values of ρα estimated from the trend-based combination during the same time interval (Fig. S4I) to be consistent for comparison. Figure 7 shows the GIA-related mass change time series for the AIS (with 400 km buffer-zone). For applying the LPZ-based GIA bias correction, the linear GIA trend in the LPZ is estimated (offset and trend only). Figure 8A shows the debiased GIA-induced BEC based on the time series combination. Figure 8c shows its formal uncertainty from least-squares estimation, which should be considered as a lower bound. For comparison, Fig. 8B shows the GIA-induced BEC following the trend-based combination approach. The GIA-related mass changes from the time-series-based and trend-based combinations are 39 and 67 Gt a−1 for the AIS, 17 and 37 Gt a−1 for the WAIS, and 23 and 30 Gt a−1 for the EAIS, respectively (Table 2). The ice mass changes are −220 and −248 Gt a−1 for the AIS, −206 and −227 Gt a−1 for the WAIS, and −14 and −21 Gt a−1 for the EAIS, respectively. The integrated formal uncertainty of the GIA-related mass change for the AIS with a 400 km buffer zone is 25 Gt a−1 (Fig. 8c).
Since the aim of this study is to examine the sensitivity of the inverse approach to several data input and methodological choices, differences from the reference experiment are discussed on the basis of the selected processing parameters.
5.1 Assessment of the results
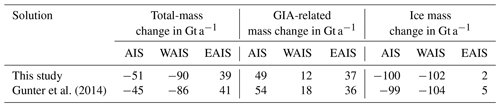
To test our data processing we performed a run with similar input data as used in Gunter et al. (2014). We used GFZ RL05 GRACE solutions, ICESat Altimetry, the RACMO2.1 SMB product, and the corresponding IMAU FDM. Table 3 shows the comparison of both results. AIS total-mass, GIA-related mass, and ice mass change estimates reproduce results by Gunter et al. (2014) to within 6, 5, and 1 Gt a−1, respectively. Those differences might be attributed to a slightly different LPZ, altimetry processing, and the missing ocean mass leakage correction. Gunter et al. (2014) indicate that the uncertainty for the GIA-related mass change and ice mass change from various GRACE solutions and filtering variants is 40 and 44 Gt a−1, respectively.
In general our GIA estimate (Fig. 5b) shows a similar spatial pattern compared to estimates by Gunter et al. (2014). Nonetheless, notable differences appear in the AP, Marie Byrd Land (MBL), Victoria Land (VL), and Queen Mary Land (QML).
In the AP, altimetry-derived SECs are available for a part of the area only (Fig. S1). As a result of missing altimetry data, GRACE-derived area density changes are attributed mainly to GIA-related mass change. The result is a negative GIA-induced BEC. Although negative GIA-induced BECs are predicted by forward models for other regions (e.g. Whitehouse et al., 2019), we consider it unphysical for this particular region because we cannot find any further indications to substantiate it. Furthermore, the missing altimetry leads to unconsidered elastic deformation. The negative signal in MBL is of a similar order of magnitude as in Riva et al. (2009) and Sasgen et al. (2017). A negative GIA signal in QML can be found in Martín-Español et al. (2016a). The uncertainty of the GIA signal is sometimes so large that even its sign cannot be determined.
For example, propagating trend differences between RACMO2.3p2 and MAR cSMBA products to GIA estimates (Fig. S6) leads to a high standard deviation of the GIA signal in MBL and Victoria Land (VL). This issue cannot be resolved by considering the results of forward models because they also show large variations and sign differences in the predicted spatial pattern of the GIA-induced BEC (Martín-Español et al., 2016b; Whitehouse et al., 2019).
Gunter et al. (2014)Table 3The comparison of integrated mass changes calculated in this study and those published in Gunter et al. (2014). For this we used GFZ RL05 GRACE solutions, ICESat-only altimetry, and RACMO2.1 products during March 2003–October 2009.
5.2 Sensitivity to degree-1 and C20 products and the effect of bias estimation
The use of several degree-1 and C20 products for the GRACE processing leads to a differing total-mass trend for the AIS (Barletta et al., 2013). The Gunter et al. (2014) Supplement showed the influence of two different degree-1 products. Here we show how the bias corrections eliminate those differences in total-mass and GIA-related mass change (Sect. 4.2, Table 2). The RMSRE of all debiased GIA estimates amounts to only 0.1 mm a−1 (Table 2). As discussed in Sect. 2.2, any GIA signal over the LPZ would be removed erroneously in the method of Gunter et al. (2014), but the uncertainty in low-degree harmonics is assumed to be much higher than a potential GIA signal within the LPZ. The bias correction regionalizes the GIA estimate; i.e. derived mass changes are always given relative to the mean LPZ mass change. The bias correction defines how the total-mass change is decomposed into mass signals and is made to ensure that the combination approach produces robust mass estimates. The large uncertainty introduced by degree-1 and C20 is suppressed at the cost of global consistency.
Several objections can be made to the assumption that over the LPZ the mean GIA-induced BEC, the mean total-mass change, and hence the mean ice mass change are zero. (1) The precipitation of the last 40 years is not directly linked to GIA. (2) Areas are included which show quite relevant GIA-induced BEC in forward models, e.g. close to the Ross Ice Shelf (Martín-Español et al., 2016b). (3) The threshold for low precipitation is arbitrary and cannot be based on physical reasons in relation to GIA. For a given threshold, the definition of the LPZ still depends on the precipitation product used. (4) The LPZ is a large area in which even a low GIA effect can cause several gigatonnes per year of mass changes. (5) The LPZ bias correction does not allow for a simple transfer of the approach to Greenland or to a global framework. Nevertheless, the calibration over the LPZ is at least one possibility to consider the presumably existing biases.
Shepherd et al. (2012, Fig. 3) show large differences in the EAIS mass change estimates derived from satellite gravimetry and altimetry. In principle, the question of quantifying GIA in the EAIS arises. For this discussion, the reader is referred to Whitehouse (2018) and Whitehouse et al. (2019), for example.
5.3 Sensitivity to altimetry product
The choice of the altimetry product has a major effect on the GIA estimate. Using ICESat-only and Envisat-only products leads to a RMSRE of 1.1 and 0.8 mm a−1, respectively (Table 2). Both missions use different observation methods and have different spatial coverage. The radar altimetry time series of Envisat is sampled monthly but only to a latitude of 81.5∘ south. ICESat uses laser altimetry and its polar gap is smaller (south of 86∘). These differences affect the results across Kamb Ice Stream where a dominant ice-dynamic signal is expected (Retzlaff and Bentley, 1993). ICESat's campaign-style temporal sampling may affect the trend estimation significantly. For the time period March 2003–October 2009 the MM altimetry product uses mainly observations from ICESat and Envisat. The trend derived from the MM altimetry product shows a spatial discontinuity at the 81.5∘ latitude limit of Envisat coverage (Figs. S1A, 5a). We attribute this to the sparse time sampling of the ICESat mission. The spread of debiased GIA-related mass change estimates of the AIS using various altimetry products is 15 Gt a−1 (Table 2). Furthermore, differences in the spatial GIA pattern are remarkable in MBL and VL (Fig. S5f, g). The co-estimation of an annual seasonal signal in altimetry only leads to small changes in the overall result (Sect. 4.2, RMSRE: 0.1 mm a−1) but is more consistent with processing of other data and models.
5.4 Firn process assumptions and uncertainties
A crucial point in the combination approach is the case distinction for ρα (Eq. 9). As mentioned in Sect. 2.1, it accounts for the uncertainty of altimetry and the FDM but does not account for the uncertainty of GRACE and the cSMBA trends. The resulting map of ρα (Figs. 5a, S4) does not agree with predefined, physically reasonable density maps. For example, ρα is set to ice density in large areas of the EAIS where dynamically induced ice mass losses are not plausible. The values of ρα largely depend on used data sets (Fig. S4b, c). An alternative to the ρα approach could be the formal approach shown in Eq. (8). Technically this would be correct. However, it results in an ice density weight for the whole AIS. We are aware that this is not correct either because presumable processes in the firn layer are not completely considered by input data and models. Another strategy may use a predefined density mask similar to Riva et al. (2009), but with a predefined significance criterion for all input data sets. This would need further investigation.
The ρα approach (Eq. 10) to assign height changes to either ice dynamics or firn processes may be a source of bias. For example, if a negative SEC is firn-related, but erroneously attributed to the density of ice by Eq. (10), this will lead to a higher ice mass decrease assigned to altimetry. GRACE would sense the true smaller ice mass decrease. Through combination of both, this discrepancy in ice mass change would be assigned to a positive GIA signal. We suppose this is qualitatively visible for ice-density-weighted regions in the EAIS (Fig. 5a, b), e.g. the sector between a longitude of 30 and 100∘ (Dome F). We presume this erroneously introduced positive GIA signal explains a part of the GIA bias.
The propagation of the empirically determined error patterns (EOFs 1–3) of the firn process models (Sect. 4.1) shows small effects on the spatial pattern of inverse GIA estimates (Fig. S5i–k). The RMSRE for the EOF 1, EOF 2, and EOF 3 experiments is 0.5, 0.3, and 0.3 mm a−1, respectively (Table 2). Note that this deviation arises solely from differences in similar climate models that use the same forcing data.
Uncertainties assumed in Gunter et al. (2014) for are very small compared to our results (Sect. 4.1, Fig. 3). In addition, any long-term trend in firn mass and firn thickness is ignored by the equilibrium assumption made by the firn modelling. SEC from Altimetry and the IMAU FDM show major differences even with a different sign for some areas, such as the AP and QML (Fig. 1a, c). These differences may indicate that the equilibrium assumption of the FDM (Sect. 3.3) is not fulfilled for those areas of the AIS, i.e. that net firn thickness changes occur over the modelling period.
5.5 Sensitivity to time interval
We also investigate a GIA solution derived from data sets over almost the entire GRACE period (April 2002–August 2016) and the approximately 6-year period of CryoSat-2 overlapping with GRACE (July 2010–August 2016). The variability of these estimates cannot be attributed to a single processing choice. On the one hand, different data sets are used (depending on assembled altimetry missions). On the other hand, cSMBA trends and FDM-derived SEC differ largely depending on the selected time interval (Sect. 3.3, Fig. S3). Ice mass change estimates are very high for the time interval July 2010–August 2016 (Table 2). The quality of input data varies over time, e.g. due to the changing availability of data. Therefore the GIA estimates show large discrepancies among different time intervals, which is incompatible with the assumption of a constant linear rate of GIA-induced BEC. However, regions (e.g. Pine Island Bay) are known where a non-linear deformation through GIA is plausible during decadal periods (Barletta et al., 2018).
5.6 The role of time-series-based combination
The combination of time series leads to similar results compared to the trend-based approach for the same July 2010–August 2016 interval (Sect. 4.3). We combined time series only for this time period, where CryoSat-2 and GRACE data are available with monthly sampling and sufficient spatial coverage. A closer examination of the time series approach is the aim of ongoing research. It needs to account for monthly uncertainties in all input data sets. Similar to the trend-based combination, challenges include (1) the consideration of uncertainties of all data sets, (2) differences in spatio-temporal sampling of both sensors, and (3) dealing with the resolution discrepancies including the consideration of signal leakage in GRACE observations. For further discussion of the challenges associated with combining geodetic time series, the reader is referred to King et al. (2006), for example. It should be noted that state-space approaches in geodetic Earth system research show promising results dealing with time-variable geophysical signals in observational time series (Didova et al., 2016; Frederikse et al., 2016).
We investigated a combination method to isolate the GIA signal from satellite gravimetry and altimetry data. Our analysis is an extension of ideas presented by Gunter et al. (2014) for the inverse estimation of GIA-induced BEC. We investigated the sensitivity of this approach (Eq. 9) to the variation in input parameters (Table 1): (1) degree-1 and C20 products in satellite gravimetry, (2) different satellite altimetry products, (3) empirically determined errors of firn process models (SMB and FDM), and (4) the use of different time epochs including diverse data.
The comparison between the data sets used in this study shows impressive similarities in terms of the spatial pattern of determined trends (Fig. 1), given that the results of altimetry, gravimetry, and the FDM are independent. The separation of GIA and ice mass signals following Gunter et al. (2014) depends strongly on the input parameters and processing steps (Table 2).
Following Gunter et al. (2014), gravimetry data are treated differently for (1) estimating the GIA signal and (2) determining the mass balance (Sect. 2.2). (1) A Gaussian filter and a de-striping filter are applied to gravimetry observations. This predetermines the smoothness of the GIA solution. The GIA-induced BEC is calibrated over the LPZ. It is converted to mass change by an effective density mask. (2) GRACE-derived area density change is calibrated over the LPZ, too. The mass balance is the difference between the debiased total-mass change and the debiased GIA-related mass change. The estimated biases and the Gaussian filtering are an implementation of a priori information which regionally constrains the GIA solution and the ice mass balance. We conclude that the LPZ-based bias correction facilitates regional but robust mass change estimates (Figs. 6, S7, Tables 2, S1).
The definition of ρα according to Eq. (10) does not lead to a readily decipherable density pattern that can account for processes in the firn and ice layer (Figs. 5a, S4). Furthermore, it is highly sensitive to input data sets.
A critical feature of the combination approach is the observational constraints that are imposed on the inversions by the limitations of the actual geodetic satellite sensors. On the one hand, altimetry enables the derivation of SEC with a high resolution. However, observations are missing in some areas, especially in areas of high topographic relief, such as valleys and mountainous coastal regions. In many of these regions lateral ice mobility may have a more complex relationship to ice heights that are extracted from altimetry as SEC. On the other hand, GRACE records all mass changes, albeit with lower resolution and signal-to-noise ratio. Because of the availability of the MM altimetry from Schröder et al. (2019a), the used GRACE observations limit the time period to 14 years from April 2002 to August 2016. This may be extended with GRACE-FO (and bridging solutions). We note that Sasgen et al. (2019) have presented a new combination approach in the spherical harmonic domain with the potential to take advantage of both sensors.
For the integrated mass changes over the AIS area, results of our sensitivity analysis are as follows. (1) The use of different degree-1 and C20 products in GRACE processing leads to biased total-mass changes from −43 to 25 Gt a−1. The LPZ-based bias correction almost completely eliminates the effect on the GIA estimate (RMSRE≤0.1 mm a−1) and on derived mass change estimates. (2) Using different altimetry products generates a spread of GIA-related mass change of 15 Gt a−1 if the GIA bias correction is applied. The spread is 35 Gt a−1 without correcting for a bias. (3) The uncertainty patterns empirically estimated from the firn process models generate a spread of debiased and biased GIA-related mass estimates of 7 and 21 Gt a−1, respectively. (4) The spread of GIA-related mass change estimated between the time periods April 2002–August 2016 and July 2010–August 2016 is 49 (debiased) and 81 Gt a−1 (biased). (5) The debiased GIA-related mass change derived by the time-series-based combination is 28 Gt a−1 smaller than the corresponding trend-based estimate.
Our results do not fully address the uncertainty introduced by input parameters. Especially important may be the assumption of an equilibrium state assumed in the firn model. In future work, improvement is needed for the correction of apparent biases and for the separation of processes in the firn and the ice layer. This might improve the self-consistency of GIA inverse estimates from satellite observations and generate a more appropriate time-series-based estimate.
GRACE monthly solutions: https://doi.org/10.5880/icgem.2016.007 (Mayer-Gürr et al., 2016). Altimetry time series: https://doi.org/10.1594/PANGAEA.897390 (Schröder et al., 2019b). Sensitivity results: this study. Contact: matthias.willen@tu-dresden.de.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-14-349-2020-supplement.
MOW and MH conceptualized the study. MOW performed the investigation, computation, and visualization tasks and wrote the manuscript. LS provided the ice altimetry time series. AG supported the GRACE data processing and the development of the data combination approach. SRML, PKM, and MRvdB provided the SMB output from RACMO2.3p2, the FDM, and assistance in their uncertainty characterization. All co-authors discussed and improved the manuscript.
Michiel R. van den Broeke is a member of the editorial board of the journal. The authors declare that they have no conflict of interest.
We thank Cécile Agosta (Université de Liège, Belgium) for providing the SMB output and density fields of the MAR model, Erik Ivins (JPL, Caltech, Pasadena, USA) for improving the manuscript, and Olga Engels (Universität Bonn, Germany) for discussion on details of data combination strategies. We thank the editor Pippa Whitehouse and the two anonymous referees for their constructive reviews which helped to improve the manuscript. We acknowledge the German Space Operations Center (GSOC) of the German Aerospace Center (DLR) for providing continuously and nearly 100 % of the raw telemetry data of the twin GRACE satellites. Further, we thank the developers of Matplotlib (Hunter, 2007) and the Matplotlib Basemap Toolkit which we used to create the figures.
This work was supported in part through grant no. HO 4232/4-1 “Reconciling ocean mass change and GIA from satellite gravity and altimetry (OMCG)” from the Deutsche Forschungsgemeinschaft (DFG) as part of the Special Priority Program (SPP)-1889 “Regional Sea Level Change and Society” (SeaLevel).
This paper was edited by Pippa Whitehouse and reviewed by two anonymous referees.
Agosta, C., Amory, C., Kittel, C., Orsi, A., Favier, V., Gallée, H., van den Broeke, M. R., Lenaerts, J. T. M., van Wessem, J. M., van de Berg, W. J., and Fettweis, X.: Estimation of the Antarctic surface mass balance using the regional climate model MAR (1979–2015) and identification of dominant processes, The Cryosphere, 13, 281–296, https://doi.org/10.5194/tc-13-281-2019, 2019. a, b, c
Barletta, V. R., Sørensen, L. S., and Forsberg, R.: Scatter of mass changes estimates at basin scale for Greenland and Antarctica, The Cryosphere, 7, 1411–1432, https://doi.org/10.5194/tc-7-1411-2013, 2013. a
Barletta, V. R., Bevis, M., Smith, B. E., Wilson, T., Brown, A., Bordoni, A., Willis, M., Khan, S. A., Rovira-Navarro, M., Dalziel, I., Smalley Jr., R., Kendrick, E., Konfal, S., Caccamise II, D. J., Aster, R. C., Nyblade, A., and Wiens, D. A.: Observed rapid bedrock uplift in Amundsen Sea Embayment promotes ice-sheet stability, Science, 360, 1335–1339, https://doi.org/10.1126/science.aao1447, 2018. a, b
Caron, L. and Ivins, E. R.: A baseline Antarctic GIA correction for space gravimetry, Earth Planet. Sc. Lett., 531, 115957, https://doi.org/10.1016/j.epsl.2019.115957, 2020. a
Caron, L., Ivins, E. R., Larour, E., Adhikari, S., Nilsson, J., and Blewitt, G.: GIA Model Statistics for GRACE Hydrology, Cryosphere, and Ocean Science, Geophys. Res. Lett., 45, 2203–2212, https://doi.org/10.1002/2017GL076644, 2018. a
Cheng, M. and Ries, J.: Decadal variation in Earth's oblateness (J2) from satellite laser ranging data, Geophys. J. Int., 212, 1218–1224, https://doi.org/10.1093/gji/ggx483, 2017. a
Cheng, M., Tapley, B. D., and Ries, J. C.: Deceleration in the Earth's oblateness, J. Geophys. Res.-Solid Earth, 118, 740–747, https://doi.org/10.1002/jgrb.50058, 2013a. a
Cheng, M. K., Ries, J. C., and Tapley, B. D.: Reference Frames for Applications in Geosciences, Vol. 138 of International Association of Geodesy Symposia, chap. Geocenter Variations from Analysis of SLR Data, 19–25, Springer Berlin Heidelberg, https://doi.org/10.1007/978-3-642-32998-2_4, 2013b. a
Church, J. A., Clark, P. U., Cazenave, A., Gregory, J. M., Jevrejeva, S., Levermann, A., Merrifield, M. A., Milne, G. A., Nerem, R. S., Nunn, P. D., Payne, A. J., Pfeffer, W. T., Stammer, D., and Unnikrishnan, A. S.: Climate Change 2013: The Physical Science Basis. Contribution of Working Group I to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, chap. Sea Level, Cambridge University Press, Cambridge, United Kingdom and New York, NY, USA, 2013. a
Didova, O., Gunter, B., Riva, R. E. M., Klees, R., and Roese-Koerner, L.: An approach for estimating time-variable rates from geodetic time series, J. Geod., 90, 1207–1221, https://doi.org/10.1007/s00190-016-0918-5, 2016. a
Engels, O., Gunter, B., Riva, R. E. M., and Klees, R.: Separating Geophysical Signals Using GRACE and High-Resolution Data: A Case Study in Antarctica, Geophys. Res. Lett., 45, 12340–12349, https://doi.org/10.1029/2018GL079670, 2018. a, b
Forsberg, R., Sørensen, L., and Simonsen, S.: Greenland and Antarctica Ice Sheet Mass Changes and Effects on Global Sea Level, Surv. Geophys., 38, 89–104, https://doi.org/10.1007/s10712-016-9398-7, 2017. a
Frederikse, T., Riva, R. E. M., Slobbe, C., Broerse, T., and Verlaan, M.: Estimating decadal variability in sea level from tide gauge records: An application to the North Sea, J. Geophys. Res.-Oceans, 121, 1529–1545, https://doi.org/10.1002/2015JC011174, 2016. a
Groh, A., Ewert, H., Scheinert, M., Fritsche, M., Rülke, A., Richter, A., Rosenau, R., and Dietrich, R.: An Investigation of Glacial Isostatic Adjustment over the Amundsen Sea sector, West Antarctica, Global Planet. Change, 98–99, 45–53, https://doi.org/10.1016/j.gloplacha.2012.08.001, 2012. a
Groh, A., Ewert, H., Rosenau, R., Fagiolini, E., Gruber, C., Floricioiu, D., Abdel Jaber, W., Linow, S., Flechtner, F., Eineder, M., Dierking, W., and Dietrich, R.: Mass, volume and velocity of the Antarctic Ice Sheet: present-day changes and error effects, Surv. Geophys., 35, 1481–1505, https://doi.org/10.1007/s10712-014-9286-y, 2014. a
Gunter, B. C., Didova, O., Riva, R. E. M., Ligtenberg, S. R. M., Lenaerts, J. T. M., King, M. A., van den Broeke, M. R., and Urban, T.: Empirical estimation of present-day Antarctic glacial isostatic adjustment and ice mass change, The Cryosphere, 8, 743–760, https://doi.org/10.5194/tc-8-743-2014, 2014. a, b, c, d, e, f, g, h, i, j, k, l, m, n, o, p, q, r, s, t, u, v, w, x, y, z, aa, ab, ac, ad, ae, af
Horwath, M. and Dietrich, R.: Signal and error in mass change inferences from GRACE: the case of Antarctica, Geophys. J. Int., 177, 849–864, https://doi.org/10.1111/j.1365-246X.2009.04139.x, 2009. a
Horwath, M., Legrésy, B., Rémy, F., Blarel, F., and Lemoine, J.-M.: Consistent patterns of Antarctic ice sheet interannual variations from ENVISAT radar altimetry and GRACE satellite gravimetry, Geophys. J. Int., 189, 863–876, https://doi.org/10.1111/j.1365-246X.2012.05401.x, 2012. a
Hunter, J.: Matplotlib: A 2D Graphics Environment, Comput. Sci. Eng., 9, 90–95, https://doi.org/10.1109/MCSE.2007.55, 2007. a
Huybrechts, P. and Le Meur, E.: Predicted present-day evolution patterns of ice thickness and bedrock elevation over Greenland and Antarctica, Polar Res., 18, 299–306, https://doi.org/10.3402/polar.v18i2.6588, 1999. a
Ivins, E. R. and James, T. S.: Antarctic glacial isostatic adjustment: a new assessment, Ant. Sci., 14, 541–553, https://doi.org/10.1017/S0954102005002968, 2005. a
Ivins, E. R., James, T. S., Wahr, J., O. Schrama, E. J., Landerer, F. W., and Simon, K. M.: Antarctic contribution to sea level rise observed by GRACE with improved GIA correction, J. Geophys. Res.-Solid Earth, 118, 3126–3141, https://doi.org/10.1002/jgrb.50208, 2013. a
Jean, Y., Meyer, U., and Jäggi, A.: Combination of GRACE monthly gravity field solutions from different processing strategies, J. Geod., 92, 1313–1328, https://doi.org/10.1007/s00190-018-1123-5, 2018. a
Johnston, P., Wu, P., and Lambeck, K.: Dependence of horizontal stress magnitude on load dimension in glacial rebound models: Glacial rebound models, Geophys. J. Int., 132, 41–60, https://doi.org/10.1046/j.1365-246x.1998.00387.x, 1998. a
King, M., Moore, P., Clarke, P., and Lavallée, D.: Choice of optimal averaging radii for temporal GRACE gravity solutions, a comparison with GPS and satellite altimetry, Geophys. J. Int., 166, 1–11, https://doi.org/10.1111/j.1365-246X.2006.03017.x, 2006. a
King, M. A., Altamimi, Z., Boehm, J., Bos, M., Dach, R., Elosegui, P., Fund, F., Hernández-Pajares, M., Lavallee, D., Mendes Cerveira, P. J., Penna, N., Riva, R. E. M., Steigenberger, P., Dam, T., Vittuari, L., Williams, S., and Willis, P.: Improved Constraints on Models of Glacial Isostatic Adjustment: A Review of the Contribution of Ground-Based Geodetic Observations, Surv. Geophys., 31, 465–507, https://doi.org/10.1007/s10712-010-9100-4, 2010. a
König, R., Schreiner, P., and Dahle, C.: Monthly estimates of C(2,0) generated by GFZ from SLR satellites based on GFZ GRACE/GRACE-FO RL06 background models. V. 1.0., GFZ Data Services, https://doi.org/10.5880/GFZ.GRAVIS_06_C20_SLR, 2019. a
Ligtenberg, S. R. M., Helsen, M. M., and van den Broeke, M. R.: An improved semi-empirical model for the densification of Antarctic firn, The Cryosphere, 5, 809–819, https://doi.org/10.5194/tc-5-809-2011, 2011. a, b, c
Ligtenberg, S. R. M., Horwath, M., van den Broeke, M. R., and Legrésy, B.: Quantifying the seasonal “breathing” of the Antarctic ice sheet, Geophys. Res. Lett., 39, L23501, https://doi.org/10.1029/2012GL053628, 2012. a
Martín-Español, A., King, M. A., Zammit-Mangion, A., Andrews, S. B., Moore, P., and Bamber, J. L.: An assessment of forward and inverse GIA solutions for Antarctica, J. Geophys. Res.-Solid Earth, 121, 6947–6965, 2016a. a, b, c
Martín-Español, A., Zammit-Mangion, A., Clarke, P. J., Flament, T., Helm, V., King, M. A., Luthcke, S. B., Petrie, E., Rémy, F., Schön, N., Wouters, B., and Bamber, J. L.: Spatial and temporal Antarctic Ice Sheet mass trends, glacio-isostatic adjustment and surface processes from a joint inversion of satellite altimeter, gravity and GPS data, J. Geophys. Res.-Earth Surf., 121, 182–200, https://doi.org/10.1002/2015JF003550, 2016b. a, b, c
Mayer-Gürr, T., Behzadpour, S., Ellmer, M., Klinger, B., Kvas, A., and Zehentner, N.: ITSG-Grace2016 – Monthly and Daily Gravity Field Solutions from GRACE, GFZ Data Services, https://doi.org/10.5880/icgem.2016.007, 2016. a, b, c
Mémin, A., Flament, T., Alizier, B., Watson, C., and Rémy, F.: Interannual variation of the Antarctic Ice Sheet from a combined analysis of satellite gravimetry and altimetry data, Earth Planet. Sci. Lett., 422, 150–156, https://doi.org/10.1016/j.epsl.2015.03.045, 2015. a
Petit, G. and Luzum, B.: IERS Conventions. IERS Technical Note No. 36, p. 179, Verlag des Bundesamts für Kartographie und Geodäsie, Frankfurt am Main, Germany, ISBN 3-89888-989-6, 2010. a
Retzlaff, R. and Bentley, C.: Timing of stagnation of Ice Stream C, West Antarctica, from short-pulse radar studies of buried surface crevasses, J. Glac., 39, 553–561, 1993. a, b
Rietbroek, R., Brunnabend, S.-E., Kusche, J., Schröter, J., and Dahle, C.: Revisiting the contemporary sea-level budget on global and regional scales, P Natl. Acad. Sci. USA, 113, 1504–1509, https://doi.org/10.1073/pnas.1519132113, 2016. a
Rignot, E., Bamber, J., van den Broeke, M. R., Davis, C., Li, Y., van de Berg, W. J., and van Meijgaard, E.: Recent Antarctic ice mass loss from radar interferometry and regional climate modelling, Nat. Geosci., 1, 106–110, https://doi.org/10.1038/ngeo102, 2008. a, b
Riva, R. E. M., Gunter, B. C., Urban, T. J., Vermeersen, B. L. A., Lindenbergh, R. C., Helsen, M. M., Bamber, J. L., van de Wal, R. S. W., van den Broeke, M. R., and Schutz, B. E.: Glacial Isostatic Adjustment over Antarctica from combined ICESat and GRACE satellite data, Earth Planet. Sci. Lett., 288, 516–523, https://doi.org/10.1016/j.epsl.2009.10.013, 2009. a, b, c, d, e, f, g, h, i, j, k
Sasgen, I., Martín-Español, A., Horvath, A., Klemann, V., Petrie, E. J., Wouters, B., Horwath, M., Pail, R., Bamber, J. L., Clarke, P. J., Konrad, H., and Drinkwater, M. R.: Joint inversion estimate of regional glacial isostatic adjustment in Antarctica considering a lateral varying Earth structure (ESA STSE Project REGINA), Geophys. J. Int., 211, 1534–1553, https://doi.org/10.1093/gji/ggx368, 2017. a, b, c, d
Sasgen, I., Konrad, H., Helm, V., and Grosfeld, K.: High-Resolution Mass Trends of the Antarctic Ice Sheet through a Spectral Combination of Satellite Gravimetry and Radar Altimetry Observations, Remote Sens., 11, 144, https://doi.org/10.3390/rs11020144, 2019. a
Schröder, L., Horwath, M., Dietrich, R., Helm, V., van den Broeke, M. R., and Ligtenberg, S. R. M.: Four decades of Antarctic surface elevation changes from multi-mission satellite altimetry, The Cryosphere, 13, 427–449, https://doi.org/10.5194/tc-13-427-2019, 2019a. a, b, c, d, e, f
Schröder, L., Horwath, M., Dietrich, R., Helm, V., van den Broeke, M. R., and Ligtenberg, S. R. M.: Gridded surface elevation changes from multi-mission satellite altimetry 1978–2017, PANGAEA, https://doi.org/10.1594/PANGAEA.897390, 2019b. a
Shepherd, A., Ivins, E. R., A, G., Barletta, V. R., Bentley, M. J., Bettadpur, S., Briggs, K. H., Bromwich, D. H., Forsberg, R., Galin, N., Horwath, M., Jacobs, S., Joughin, I., King, M. A., Lenaerts, J. T. M., Li, J., Ligtenberg, S. R. M., Luckman, A., Luthcke, S. B., McMillan, M., Meister, R., Milne, G., Mouginot, J., Muir, A., Nicolas, J. P., Paden, J., Payne, A. J., Pritchard, H., Rignot, E., Rott, H., Sorensen, L. S., Scambos, T. A., Scheuchl, B., Schrama, E. J. O., Smith, B., Sundal, A. V., van Angelen, J. H., van de Berg, W. J., van den Broeke, M. R., Vaughan, D. G., Velicogna, I., Wahr, J., Whitehouse, P. L., Wingham, D. J., Yi, D., Young, D., and Zwally, H. J.: A Reconciled Estimate of Ice-Sheet Mass Balance, Science, 338, 1183–1189, https://doi.org/10.1126/science.1228102, 2012. a
Sun, Y., Ditmar, P., and Riva, R. E. M.: Observed changes in the Earth's dynamic oblateness from GRACE data and geophysical models, J. Geod., 90, 81–89, https://doi.org/10.1007/s00190-015-0852-y, 2015. a
Swenson, S. and Wahr, J.: Post-processing removal of correlated errors in GRACE data, Geophys. Res. Lett., 33, L08402, https://doi.org/10.1029/2005GL025285, 2006. a
Swenson, S., Chambers, D., and Wahr, J.: Estimating geocenter variations from a combination of GRACE and ocean model output, J. Geophys. Res., B113, B08410, https://doi.org/10.1029/2007JB005338, 2008. a
Thomas, I., King, M., Bentley, M., Whitehouse, P., Penna, N., Williams, S., Riva, R., Lavallee, D., Clarke, P., King, E., Hindmarsh, R., and Koivula, H.: Widespread low rates of Antarctic glacial isostatic adjustment revealed by GPS observations, Geophys. Res. Lett., 38, L22302, https://doi.org/10.1029/2011GL049277, 2011. a
van Wessem, J. M., van de Berg, W. J., Noël, B. P. Y., van Meijgaard, E., Amory, C., Birnbaum, G., Jakobs, C. L., Krüger, K., Lenaerts, J. T. M., Lhermitte, S., Ligtenberg, S. R. M., Medley, B., Reijmer, C. H., van Tricht, K., Trusel, L. D., van Ulft, L. H., Wouters, B., Wuite, J., and van den Broeke, M. R.: Modelling the climate and surface mass balance of polar ice sheets using RACMO2 – Part 2: Antarctica (1979–2016), The Cryosphere, 12, 1479–1498, https://doi.org/10.5194/tc-12-1479-2018, 2018. a, b, c, d
Wahr, J., Molenaar, M., and Bryan, F.: Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE, J. Geophys. Res., 103, 30205–30229, https://doi.org/10.1029/98JB02844, 1998. a
Wahr, J., Wingham, D., and Bentley, C.: A method of combining ICESat and GRACE satellite data to constrain Antarctic mass balance, J. Geophys. Res., 105, 16279–16294, https://doi.org/10.1029/2000JB900113, 2000. a, b, c
Whitehouse, P., Gomez, N., King, M., and Wiens, D.: Solid Earth change and the evolution of the Antarctic Ice Sheet, Nat. Commun., 10, 503, https://doi.org/10.1038/s41467-018-08068-y, 2019. a, b, c, d, e
Whitehouse, P. L.: Glacial isostatic adjustment modelling: historical perspectives, recent advances, and future directions, Earth Surf. Dynam., 6, 401–429, https://doi.org/10.5194/esurf-6-401-2018, 2018. a, b, c
Whitehouse, P. L., Bentley, M. J., Milne, G. A., King, M. A., and Thomas, I. D.: A new glacial isostatic adjustment model for Antarctica: calibrated and tested using observations of relative sea-level change and present-day uplift rates, Geophys. J. Int., 190, 1464–1482, https://doi.org/10.1111/j.1365-246X.2012.05557.x, 2012. a
Wingham, D., Shepherd, A., Muir, A., and Marshall, G.: Mass balance of the Antarctic ice sheet, Phil. Trans. R. Soc. Lond. A, 364, 1627–1635, 2006. a
Zammit-Mangion, A., Rougier, J., Schön, N., Lindgren, F., and Bamber, J.: Multivariate spatio-temporal modelling for assessing Antarctica's present-day contribution to sea-level rise, Environmetrics, 26, 159–177, https://doi.org/10.1002/env.2323, 2015. a