the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
IcePAC – a probabilistic tool to study sea ice spatio-temporal dynamics: application to the Hudson Bay area
Charles Gignac
Monique Bernier
Karem Chokmani
A reliable knowledge and assessment of the sea ice conditions and their evolution in time is a priority for numerous decision makers in the domains of coastal and offshore management and engineering as well as in commercial navigation. As of today, countless research projects aimed at both modelling and mapping past, actual and future sea ice conditions were completed using sea ice numerical models, statistical models, educated guesses or remote sensing imagery. From this research, reliable information helping to understand sea ice evolution in space and in time is available to stakeholders. However, no research has, until present, assessed the evolution of sea ice cover with a frequency modelling approach, by identifying the underlying theoretical distribution describing the sea ice behaviour at a given point in space and time. This project suggests the development of a probabilistic tool, named IcePAC, based on frequency modelling of historical 1978–2015 passive microwave sea ice concentrations maps from the EUMETSAT OSI-409 product, to study the sea ice spatio-temporal behaviour in the waters of the Hudson Bay system in northeast Canada. Grid-cell-scale models are based on the generalized beta distribution and generated at a weekly temporal resolution. Results showed coherence with the Canadian Ice Service 1981–2010 Sea Ice Climatic Atlas average freeze-up and melt-out dates for numerous coastal communities in the study area and showed that it is possible to evaluate a range of plausible events, such as the shortest and longest probable ice-free season duration, for any given location in the simulation domain. Results obtained in this project pave the way towards various analyses on sea ice concentration spatio-temporal distribution patterns that would gain in terms of information content and value by relying on the kind of probabilistic information and simulation data available from the IcePAC tool.
- Article
(7632 KB) - Full-text XML
- BibTeX
- EndNote
Numerous scientific projects have recognized the link between climate change and changes in the spatio-temporal sea ice distribution (Andrews et al., 2017; Cavalieri and Parkinson, 2012; Comiso, 2011, 2002; Comiso et al., 2008; Gloersen et al., 1999; Johannessen et al., 2004; Rothrock et al., 1999; Stocker, 2014; Stroeve et al., 2007; Stroeve et al., 2014; Stroeve et al., 2012; Wang and Overland, 2009). The climate change in the Arctic (60–90∘ N) is expected to be, on average, 1.9 times greater than the global mean warming (Winton, 2006), and this “Arctic amplification” is expected to strengthen in coming decades (Serreze and Barry, 2011).
In this changing environment, an adequate and efficient monitoring of sea ice is of key importance in better understanding the climate and its impacts on marine and coastal areas (Barnhart et al., 2014; Bintanja and Selten, 2014; Davies et al., 2014; Holland et al., 2006; Kowal et al., 2017; Manabe and Stouffer, 1995; Overeem et al., 2011; Peterson et al., 2002; Rahmstorf, 1995; Rahmstorf and Ganopolski, 1999; Vermaire et al., 2013), on the security of economical and logistical activities in northern communities (Aksenov et al., 2017; Andrews et al., 2017; Ho, 2010; Lasserre and Pelletier, 2011; Liu and Kronbak, 2010), on arctic marine fauna protection (Bhatt et al., 2010; Castro de la Guardia et al., 2013; Darnis et al., 2012; Laidre et al., 2015; Post et al., 2013; Wassmann et al., 2011), and on the traditional way of life of Inuit communities (Durkalec et al., 2015; Laidler et al., 2010).
To understand and appreciate the role of sea ice cover regarding climate, marine and coastal environment management, fauna protection, and the cultural traditions of northern communities, access to informative and reliable sea ice spatio-temporal distribution information is fundamental. Engineers, stakeholders, Inuit and northern populations, navigators, and scientists must be able to quantify hazards related to the sea ice cover in order to efficiently evaluate, anticipate, and minimize the risks of usage, building, and exploitation in marine and coastal areas. Given the increase in activity like tourist cruises, shipping, and mining observed in the Arctic and the north (Dawson et al., 2018; Lasserre and Pelletier, 2011; Pizzolato et al., 2016), one can expect the demand in information to also increase. For example, engineers could make use of probabilistic data to assess the potential duration of sea ice presence for an infrastructure they are planning to build; mariners could use the data to estimate the best departure date from their home port to reach their final destination according to a certain sea ice concentration probability threshold; fauna specialists could use the data to estimate the risk encountered by species dependent on sea ice cover for their fitness, such as polar bears and seals; and finally, Inuit communities could use the tool to evaluate if their planned travel routes are risky for a given period of the year given the known history of the sea ice spatio-temporal behaviour.
Despite a large number of Earth observation datasets on sea ice cover, only a few provide both high temporal and spatial resolution. National ice services, such as the Canadian Ice Service (CIS), provide users with sea ice conditions' climatology that is a reliable source of descriptive statistics on the sea ice spatio-temporal behaviour, such as the average freeze-up or maximum extent date. The CIS also provides daily and weekly regional ice condition maps that inform users of the observed concentrations and the ice development stage reached by sea ice, as well as detailed sea ice condition reports, for all regions of the Canadian Arctic. These maps and reports are created by experienced and skilled professional sea ice analysts who make use of diverse sources of sea ice information such as radar, optical microwave imagery, and passive microwave imagery in combination with in situ observations to prepare their analyses (Iacozza, 2000). However, even if the CIS data and other national ice service products do provide probabilistic information, these datasets do not carry information on the nature of the underlying statistical distributions of sea ice parameters, such as sea ice concentration (SIC %), at any given point.
To build a probabilistic model of sea ice concentrations, historical information is needed and must meet specific needs such as long-term availability, reliability, large spatial coverage and high temporal frequency. As visible imagery is largely affected by cloud coverage, especially prominent in the Arctic, it is not a reliable source of information with which we can build our model. In spite of its independence of atmospheric conditions, synthetic aperture radar (SAR) imagery does not provide sufficient spatial coverage for our purpose. Therefore, passive microwave observation turned out to be a compromise as this dataset, even if its resolution is coarse, provides daily data for the entire Arctic and historical data are available for it from 1978 onwards.
By exploring an innovative probabilistic sea ice concentration modelling avenue, this study proposes a tool, named IcePAC, to characterize the underlying statistical distributions of the SIC % at any point in the Hudson Bay system (Saucier et al., 2004) based on historical passive microwave remote sensing data from 1978 to 2015. These data are than used to analyze the spatio-temporal behaviour of SIC % in the Hudson Bay area, with a probabilistic perspective and compared to the CIS climatology.
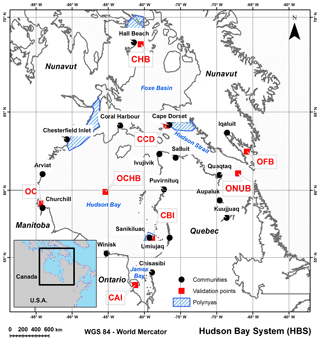
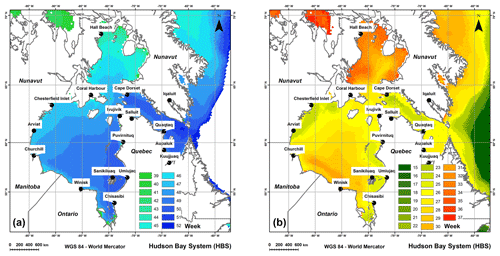
The study area is the Hudson Bay system (HBS), consisting of the Hudson Bay, Hudson Strait, James Bay, and Foxe Basin (Fig. 1). The HBS is surrounded by the three Canadian provinces of Quebec, Ontario, and Manitoba and the territory of Nunavut. It is the largest inland sea on Earth, with a total area of 1 300 000 km2 (Etkin, 1991; Gagnon and Gough, 2005a; Martini, 1986), and is located in both subarctic and Arctic regions. An estimated 20 % of the flux of freshwaters to the Arctic Ocean are thought to come from rivers flowing into the HBS, which represents 900 km3 yr−1 (Déry and Wood, 2005, 2004). It is connected to the Labrador Sea via the Hudson Strait while waters from the Arctic Ocean flow through the Fury and Hecla Strait to the Foxe Basin (Prinsenberg, 1986), and it is characterized by shallow depths of less than 100 m in the Foxe Basin, of a maximum of 125 m in the Hudson Bay, and of more than 200 m in the Hudson Strait (Jones and Anderson, 1994). It has cyclonic currents generated mostly by winds, with a maximum intensity in November (Saucier et al., 2004).
A large amount of research has been done to document the average sea ice behaviour in the HBS (CIS, 2013; Gagnon and Gough, 2005a, b; Hochheim and Barber, 2010, 2014; Kowal et al., 2017; Maxwell, 1986), which goes through a complete freeze–thaw cycle every year. The sea ice cover in the HBS is primarily constituted of first-year ice, with the exception of traces of multi-year ice drifting in the Foxe Basin (CIS, 2013; Etkin and Ramseier, 1993). The sea ice cover initially forms in the northwestern part of the HBS near Southampton Island in late November and progresses towards the southeastern part of the HBS (Hochheim and Barber, 2014; Maxwell, 1986) to finally cover most of the HBS in late December. Sea ice maximum extent in the HBS is usually achieved in April (Gagnon and Gough, 2005b), after which the melt begins in May along the northwestern shoreline of the HBS. The melt progresses from the shores toward the centre of the Hudson Bay, which usually results in an agglomerate of sea ice in the south central part of the Hudson Bay in late July (CIS, 2013). In summary, the HBS is, on average, frozen in late December and free of ice in mid-August (Mysak et al., 1996; Wang et al., 1994).
Many authors have studied the trends in sea ice cover extent for the Hudson Bay area (Galbraith and Larouche, 2011; Hochheim and Barber, 2014; Tivy et al., 2011). Among them, Tivy et al. (2011) arrived at the conclusion that the Hudson Bay area was affected by some of the strongest downward trends regarding the ice season duration in the entire circumpolar Arctic. Confirming the results of Tivy et al. (2011), Hochheim and Barber (2014) measured trends of the open water season duration comparing a 1996–2010 climatology with a 1980–1995 climatology based on a modified Comiso SIC % dataset. Their results showed lengthening of ice-free seasons in Foxe Basin, Hudson Strait, and Hudson Bay, of 3.5, 4.9, and 3.1 weeks respectively. It is worth noting that, since the HBS is mostly covered by first-year ice, the natural variability of the sea ice conditions is considerable since it is mostly driven by warming temperatures, but also by changes in atmospheric circulation (Mudryk et al., 2018).
Ice thickness during winter in the HBS ranges from 1 to >2.5 m according to numerical modelling studies, though, as reported by Landy et al. (2017), these studies do not agree on the spatial distribution of sea ice. Gough et al. (2004) identified an east–west asymmetry in long-term trends of sea ice thicknesses in the HBS using drill-hole measurements acquired between 1960 and 2000. These trends show a tendency of thickening on the western side (+0.1 to 1.5 cm yr−1) of the Hudson Bay, while the eastern side shows, conversely, a trend towards a thinning ice pack (−0.5 to 0.8 cm yr−1).
Polynyas are also present in the HBS, such as the northwestern Hudson Bay polynya between the western coast of the Hudson Bay and Southampton Island that forms occasionally throughout the winter and spring (Gough et al., 2004), the Fury and Hecla Strait and Hall Beach polynyas (Barber and Massom, 2007), located in northwestern parts of the Foxe Basin, and the Cape Dorset polynya, which is a shore lead polynya (Stirling, 1980).
Sea ice extent has displayed an important decline in the last decades (Cavalieri and Parkinson, 2012), as it can be observed with remote sensing data, such as passive microwave data, which have been acquired since 1978. Another important source of information on sea ice cover is model predictions which come from deterministic models (Hunke et al., 2017; Rousset et al., 2015; Weaver et al., 2001), based on dynamical and thermodynamic equations evolving in synergy inside a modelling framework, or from statistical models, based on statistical tools such as simple and multiple regression analysis (Ahn et al., 2014; Drobot, 2007; Pavlova et al., 2014) to explain an expected sea ice parameter value (e.g. sea ice extent, sea ice area, sea ice concentration, sea ice thickness).
Another statistical approach, focusing on the estimation of the probabilities of occurrence of specific sea-ice-related events, has been used in recent research (Dirkson, 2017; Rajak et al., 2015). It is achieved either by using the simple count method (e.g. an event occurred four times in the last 10 years, which corresponds to a 40 % probability of occurrence) or by using the frequency modelling method, which consists of adjusting a theoretical distribution to a series of observations, consequently defining the plausible sea ice events for the entire range of probabilities (i.e. p=0 to 100 %). In this research, the frequency modelling method is used for a series of passive microwave historical SIC % remote sensing data to adjust distributions to a total of 20 738 grid cells or sites within the HBS (i.e. the spatial dimension) for each of the 52 weeks of the year (i.e. the temporal dimension), resulting in a total of 1 078 376 distribution fits.
The datasets used and protocols followed in the IcePAC tool to model SIC % distributions at every grid cell in the HBS are described in the following sections.
3.1 Sea ice concentration dataset
Sea ice concentration is defined as the proportion of sea ice covering a predefined area, expressed as a percentage. In remote sensing, this predefined area is represented by a grid cell. The choice of a SIC dataset for frequency modelling in our study is highly influenced by the extent of the HBS (1 300 000 km2) and has been made to ensure uniformity and continuity of the series used for analysis.
Multiple SIC datasets are generated using either visible, thermal, SAR, or passive microwave remote sensing. As the objective of the IcePAC tool is to provide the capacity to evaluate the spatio-temporal evolution of the SIC, the source of data needed to ensure a complete coverage of the HBS (i.e. the spatial dimension) and to ensure continuity in the series (i.e. the temporal dimension). A passive microwave dataset was chosen as it meets these two needs.
The global reprocessed sea ice concentration dataset, OSI-409 (Eastwood et al., 2015; Tonboe et al., 2016), was selected as it enables the reconstitution of SIC series for more than 30 years with a 12.5 km grid size and is processed with a unique hybrid SIC algorithm. The hybrid algorithm only uses the information taken from the “Bootstrap” algorithm (Comiso, 1995) when SIC <70 %, linearly weights the SIC estimated by the Bootstrap and Bristol (Smith, 1996) algorithms when 70 % < SIC > 90 %, and only uses the information from the Bristol algorithm when SIC > 90 %. Another passive-microwave-based SIC % dataset is used in this study as a comparison dataset, the OSI-430, and its only difference from OSI-409 is that it uses SSM/I data obtained from NOAA instead of recalibrated SSM/I data from RSS (Remote Sensing Systems). The difference in the resulting SIC % product is, according to Eastwood et al. (2015), expected to be minimal.
In OSI-409, the passive microwave channels used for ice concentration mapping have footprint sizes ranging from 56 km for the 19 GHz channels to 33 km for the 37 GHz channels. As SIC % values are represented on 12.5 km grid cells in the OSI-409 and 430 products, inputs of different resolutions are combined using a gridding procedure that loads all passive microwave observations within the period of a day for a 12.5 km grid cell (centred on 12:00 UTC) and averages them using a weighting value (dependent on the distance between the observation and the centre of the grid cell) and an influence radius (dependent on the passive microwave channel resolution). A detailed explanation of the method is provided in Eastwood et al. (2015).
It is important to note that passive microwave SIC % datasets are known to be affected by diverse error factors such as a land spill-over effect along coasts that triggers false higher SIC % estimation if not taken into account. To mitigate the errors caused by this phenomenon, a coastal correction is applied to the data with a method inspired from Cavalieri et al. (1999). This method first calculates monthly average SIC % for all months and finds the minimum ice concentration from these averages. This minimum is then used to correct the ice concentration values in the coastal zone if adjacent non-coastal grid points are ice-free. Also, climatological maximum extent masking is done to mask out erroneous ice outside areas where sea ice is ever likely to occur using a sea ice extent monthly climatology from the NSIDC (National Snow and Ice Data Center) (NSIDC, 2013).
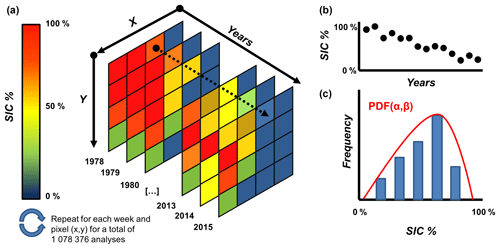
Figure 2The process of frequency modelling from series building to model fit. (a) The SIC % data stacking and series building for every pixel in the simulation domain. (b) An example of a unique site complete series plotted. (c) An example of model fit (beta) to the density distribution of the SIC % values in the series with the α and β model parameters.
Another error factor with passive microwave data is data gaps which can occur either in the form of missing scan lines, missing orbits, or polar observation holes. As reported by Eastwood et al. (2015), these gaps, when small, can be corrected through simple interpolation. However, when facing large gaps, a blurring effect appears in the interpolated area. To correct this effect, an interpolation approach using the information from the past and following days is used in the OSI products. And last but not least, the effect of ponds appearing during the melt is that the resulting maps tend to underestimate SIC % during summer since there is confusion between open water areas and melt ponds on top of sea ice. Finally, another underestimation of the SIC % results from thinner ice types which do not act as a radiometric insulator for the passive microwave frequencies around 19 and 37 GHz that are the base of the OSI-409 and OSI-430 datasets (Eastwood et al., 2015).
These different error sources in the process of estimating SIC % using passive microwave imagery are known to have an impact on the reliability of the data, especially during the freeze-up and the melt periods, as brought forward by Agnew and Howell (2003), who noticed that the underestimation of ice extent in the Hudson Bay during summer, when compared to CIS maps, could go up to 43.5±27.9 % (while considering the CIS data as ground truth). Since the HBS is an area where new ice forms every year, this systematic underestimation when using passive microwave data must be kept in mind.
The data have been clipped to the HBS extent using the Natural Earth (NaturalEarth, 2014) vector dataset with an estimated spatial resolution of 500 m (Wessel and Smith, 1996), well beyond the resolution of the OSI-409 and OSI-430 datasets. As the coasts of the HBS are highly dynamic, other datasets could have been used such as the CanVec product from Natural Resources Canada, which is updated regularly. However, considering the 12.5 km grid size, the Natural Earth product was chosen.
3.2 Frequency modelling
The IcePAC tool uses frequency modelling to describe the underlying SIC % probability distribution at a given site with a simplified model fitted on historical SIC data. The first step in this approach is to build the time series of historical data, then to ensure their quality using preliminary tests, and finally to identify and fit the model on the data (Fig. 2).
3.2.1 Building the sea ice concentration (SIC) series
The SIC series are built to represent the SIC state for a specific week, for all years between 1978 and 2015. It is for these series that we adjust a theoretical distribution to estimate the probabilities of SIC-related events. First, the daily OSI-409 data have to be averaged every 7 days to create weekly datasets. This operation is made following a 365-day “no-leap” calendar convention (i.e. every year has 365 days), separated in 52 weeks (31 December is included in week 52). Second, the data for each week number are stacked in chronological order, from 1978 to 2015.
3.2.2 Preliminary tests
Series have to go through a set of preliminary tests to assess their stationarity, homogeneity, and independence, assuring they are suitable for frequency modelling. The tests used in IcePAC are the Mann–Kendall test for stationarity (Mann, 1945), the Wald–Wolfowitz test for independence (Wald and Wolfowitz, 1940), and the Wilcoxon test for homogeneity (Wilcoxon, 1945).
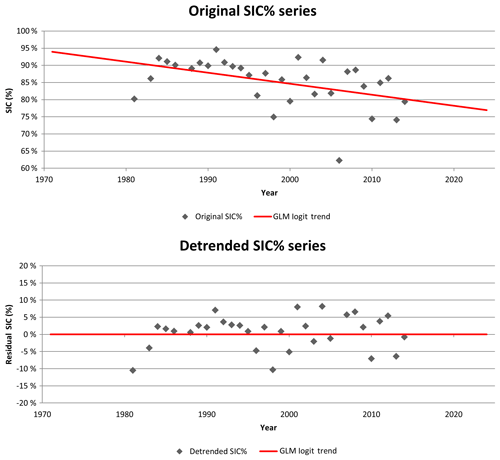
Series are considered independent if the subsequent unique SIC observations have no dependence on one another, they are considered homogeneous if they are reputed to be from the same distribution, and they are stationary if they are not affected by a trend. In the case of a detected non-stationarity, the trend is modelled and subtracted from the series (Cave and Pearson, 1914).
All the time series, either original or detrended in regard to the Mann–Kendall test, satisfied the preliminary tests for a significance level of α=0.05.
3.2.3 Trend estimation and removal
The estimation of a trend on a percentage data series has the particularity that the trend must, in order to be coherent with the physics of the studied phenomenon, be bounded in a [0,1] domain (Baum, 2008). In other words, we must ensure we do not measure a trend that generates SIC values larger than 100 % or smaller than 0 %. To guarantee the respect of this criterion, a generalized linear model with a logit link function has been used to estimate the trend. The logit link function linearizes the SIC values using the logit transformation (Eq. 1) and it is with these transformed values that a linear regression of the form is measured.
where SIC is defined ]0,1[.
For the trend to be removed from the series, an inverse transformation (Eq. 2) must be applied to the estimated trend to turn its logit values into SIC values.
The removal of the trend in the time series ensures that we model the natural variability of the sea ice concentration phenomenon, without any influence from the trend (Fig. 3). In IcePAC, the trend is modelled using the aforementioned method (GLM with logit link), then it is removed from the original SIC % data, and finally the residuals are used to adjust the distribution model.
Once adjusted, the distribution models are used for queries, in conjunction with the trend that is taken into account to generate the final result. For example, one could ask for the probability of a specific SIC %. In such a case, the trend for the prediction year is first removed from the SIC %, and the probability of the residual is then estimated from the distribution model. Inversely, one could ask for the SIC % for a given probability. In such a case, the probability is first used to get the corresponding residual value (representing the natural variability of sea ice) and the trend is reinjected afterward to obtain a realistic SIC % value. In both cases, the trend is taken into account when generating the final results.
It is important to note that frequency analysis is not a projective approach but a predictive approach. In other words, IcePAC is not to be used to get an outlook of long-range future SIC % conditions (projection) but to assess what is expected for the short-term conditions (prediction). As the trend will change in time with the addition of new SIC % data, the further we try to temporally expand our prediction, the more erroneous our probability estimates may be.
3.2.4 Distribution selection and fit
The selection of adequate candidate distributions to fit on the series is largely limited by the bounded nature of the data. The selected distribution has to be bounded to [0,1] and be available in a generalized form in order to adapt to detrended series which are bounded to [−1,1]. Their generalized forms are to be used with the position parameter a fixed at −1 and the scale parameter b fixed at 2, in coherence with the phenomenon. It must also present enough flexibility in shape to adapt to the different type of SIC series in the HBS domain. Two different distributions, the generalized beta distribution and Johnson's SB (system-bounded) distribution (Johnson, 1949), both bounded and displaying flexibility in shape, have been fitted on the series using the maximum likelihood estimator (MLE; NIST, 2013) and compared by measuring the root mean square error (RMSE) between observations and adjusted curves as well as the Akaike information criterion (Akaike, 1998) and the Bayesian information criterion (Schwarz, 1978).
The generalized beta distribution (Eq. 3) has four parameters which are the p (p>0) and q (q>0) shape parameters, the position parameter , and the scale parameter b=2. In Eq. (3), B is the beta function. This distribution has been used before in climatology (Dirkson, 2017; Falls, 1974; Henderson-Sellers, 1978; Sulaiman et al., 1999), in seismology (Lallemant and Kiremidjian, 2015), to study air pollution (Nadarajah, 2008) and in hydrology (Chen and Singh, 2017; Yao, 1974).
where ; .
Johnson's SB (Eq. 4) is, under its generalized form, a four-parameter distribution, for which the γ and δ (δ>0) are the shape parameters, the parameter is the position, and the parameter b=2 is the scale. This distribution has been used before in meteorology (Cugerone and Michele, 2015; Wakazuki, 2013), in forestry (Rennolls and Wang, 2005), and in hydrology (D'Adderio et al., 2016).
where .
Two approaches were tested for distribution selection. The first approach considered fitting the distributions to the series according to their Mann–Kendall test results (i.e. managing detected trends only). The second approach considered fitting the distributions to systematically detrended series (i.e. removing the trend from every time series in the simulation domain) in order to ensure spatial coherency in the IcePAC outputs.
The use of a systematic trend removal approach is justifiable by the fact that natural phenomena are considered by nature non-stationary (Lins, 2012; Rao et al., 2012) and by the relative shortness of the series which can have an effect on the conclusions of the Mann–Kendall test (Hirsch et al., 1982). Also, it is important to state that the frequency analysis approach is rarely used to generate spatialized results like it is in the IcePAC approach in which every time series (linked to a specific location or grid cell) is processed as an individual station.
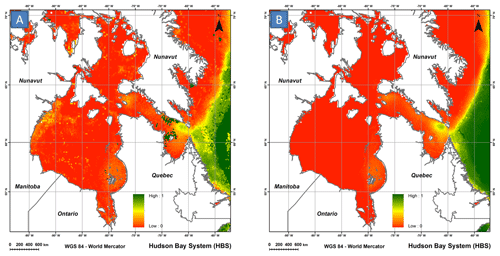
The two trend removal approaches, tested on 958 randomly chosen series, yielded similar conclusions. In 71.4 % of cases, the beta distribution outperformed Johnson's SB distribution. For the remaining 28.6 % adjustments for which Johnson's SB distribution did perform better, both the information criterion and the RMSE showed a non-significant difference with the beta distribution. In light of these results and to preserve parsimony in IcePAC, it was decided to use only the beta distribution for all series, for which a systematic trend removal was applied.
As expected, using an approach which systematically corrects for trends in time series before the distribution fit improved the spatial coherency of the resulting probability maps generated by IcePAC (Fig. 4).
3.2.5 Model queries
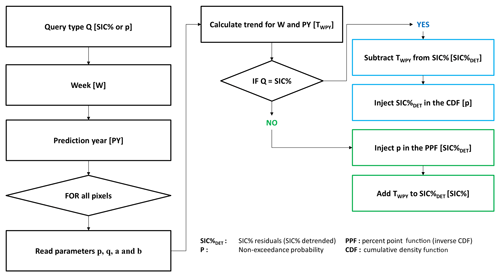
Queries with the IcePAC tool are possible via three important functions resulting from the distribution fit, the probability density function (PDF), the cumulative distribution function (CDF), and the percent point function (PPF). These functions are obtained using the fitted parameters from the beta distribution independently for each of the 20 738 grid cells in the IcePAC simulation domain.
The PDF is obtained by fitting a theoretical distribution on the frequency histogram of the SIC % observations. The selected distribution in IcePAC is the beta distribution for which the parameters of Eq. (3) were estimated using the MLE. The PDF shows how probability is distributed between SIC % values and how it evolves.
Derived from the PDF, the CDF (Eq. 5) gives the probability for a given range of SIC % values. It corresponds to the area under the PDF curve for a specific range of SIC values, usually from 0 % to SIC %max. As an example of the CDF, one could query the probability of non-exceedance (p) for a sea ice concentration of 25 % (SICmax) for week number 1 for the year to come.
The inverse function of the CDF, the PPF (Eq. 6), estimates the SIC % value for a given probability of non-exceedance. As an example of PPF, one could query the SIC %max for a probability of non-exceedance of 55 % for week 1 for the year to come.
Since the IcePAC fits are made on detrended series (e.g. residuals), the trend has to be taken into account when processing queries, meaning that it has to be either removed from the SIC %max value if the CDF is used or added to the result of the PPF query in order to render a physically valid result. The query flow chart is presented in Fig. (5).
3.2.6 IcePAC versus observations in 2016
The assessment of the validity of IcePAC predictions was done by comparing IcePAC weekly output time series for the entire year with the OSI-430 product, a data source not used in IcePAC development but based on the same SIC % retrieval algorithm (Tonboe et al., 2016). The comparison was made between the 2015–2016 sea ice season SIC % values (not included in the input data for IcePAC) and the IcePAC SIC % for a non-exceedance probability of 90 % (P=0.9)
Eight different comparison sites were selected to represent different sea ice spatio-temporal behaviours (see Fig. 1). Four coastal sites, Akismi Island (CAI), Cape Dorset (CCD), Belcher Islands (CBI), and Hall Beach (CHB), were sampled to assess the behaviour of IcePAC predictions along the coastline at different latitudes. Also, four offshore sites, Frobisher Bay (OFB), Central Hudson Bay (OCHB), Churchill (OC), and Northern Ungava Bay (ONUB) were sampled to assess the behaviour of IcePAC predictions offshore at different latitudes and at critical navigation passage points.
Figure 6 displays SIC % prediction outputs from IcePAC, for a probability of non-exceedance of 90%. Each comparison site shows a modelled dynamic which is coherent with reality and with the OSI-430 2015–2016 observation data. As it could be expected, for all sites, it is during the freeze-up and melt periods that we can observe the largest differences between the 2015–2016 OSI-430 SIC % observations and the model outputs, compared to stable cover periods during which the range of probable SIC % values is narrowed down (i.e. the mean and the P=90 % lines are almost overlaid), and therefore the observations tend to rejoin with the model output. Some anomalies of various intensities can be detected in the series such as early 2015 melt-out events at Hall Beach and Churchill (▵ in Fig. 6), late 2016 freeze-up events at points Akismi Island and Churchill (∘ in Fig. 6), and early 2016 melt-out event at Hall Beach (◊ in Fig. 6), which all are in agreement with the anomaly maps (Fetterer et al., 2017) of the NSIDC's Arctic Sea Ice News and Analysis (https://nsidc.org/arcticseaicenews/, last access: 18 May 2018). The fact that the Cape Dorset site displays a SIC % for a probability of non-exceedance of 90 % of about 80 % at most is coherent with its shore lead polynya status. Similar conclusions can be made for the Hall Beach point for which the polynya tends to appear by late May, which in our case was earlier in 2015 and 2016, as confirmed by NSIDC. In Fig. 6, daily model outputs (green lines) are presented as a comparison with the weekly outputs (black dots) in order to justify why the IcePAC model outputs were generated at a weekly interval, to filter the effects of the daily variability of SIC % estimations in OSI-409, especially visible at coastal sites.
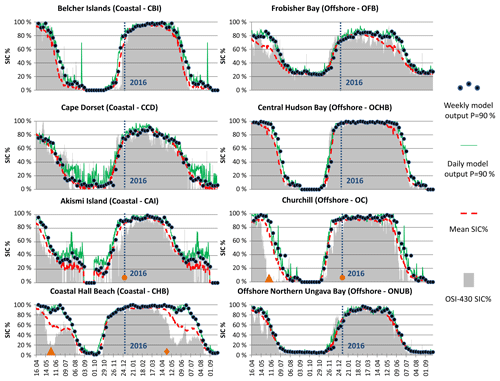
Figure 6IcePAC weekly and daily P=90 % outputs (i.e. it represents a value of SIC % for which there is a 90 % probability that it is equal to or lower than the given SIC % level) versus OSI-430 SIC % observations for the 2015–2016 sea ice season. Some anomalies of various intensities can be detected in the series such as early 2015 melt-out events at Hall Beach and Churchill (▵), late 2016 freeze-up events at Akismi Island and Churchill (∘), and an early 2016 melt-out event at Hall Beach (◊).
The OFB site, near Iqaluit, has a behaviour that indicates an underlying error. In fact, neither the predictions nor the observations reach a SIC % value of 0 %, which is improbable in our study area. The reason behind these discrepancies with the validation data is that the OSI-409 product does not adequately estimate the SIC in this area, as can be seen in Fig. (7). The Frobisher Bay is usually ice-free around mid-July, which is never the case in the OSI-409 dataset. The source of this error is the land spill-over effect (i.e. land contamination) on estimated SIC combined with an inadequate sea ice presence estimation in the NSIDC sea ice monthly maximum extent climatology used as a mask for restricting areas where sea ice is likely to occur. Given the fact that the climatology mask states that there is possibly ice in the Frobisher Bay on that date, the algorithm attempts to measure it, with erroneous results. It has been found that this condition does occur in the Frobisher Bay and also west of Southampton Island, in Roes Welcome Sound.
Such errors make it important to emphasize that the results obtained from the model are to be used with care and ideally in combination with other sources of information such as local knowledge, other remote sensing imagery, and historical sea ice maps from national sea ice services.
The major asset of the IcePAC tool is that its output data give a probabilistic perspective on relevant sea ice event in comparison to the usual static descriptive statistics. Therefore, IcePAC gives not only the capacity to determine the mean event, but also to estimate the range of plausible events for a given site and date.
Here, the IcePAC outputs are used to assess the sea ice spatio-temporal dynamics, given different probability scenarios and in terms of three cover indicators, which are the length of the ice-free season (or its corollary, the ice-covered season), the probable complete melt-out week, and the probable complete freeze-up week.
4.1 Analysis with the IcePAC tool
Before presenting any results, the ice indicators analyzed in the next paragraphs must be clearly defined. First, the probable complete melt week corresponds to, for varying probability scenarios, the first week for which the SIC % is below 15 % in a given grid cell (starting its research from week 36 – 1 September – onwards). Second, the probable complete freeze-up week corresponds to, for varying probability scenarios, the first week for which the SIC % is above 15 % in a given grid cell (starting its research from week 14 – 1 April – onwards). To be considered valid, these events must be sustained for at least 3 consecutive weeks. Finally, the probable duration of the ice-free season corresponds to the gap, in weeks, between the different probable melt-out and freeze-up weeks.
The use of the 15 % limit to define the presence or absence of sea ice is a convention used by many authors (Andersen et al., 2006; Cavalieri et al., 1997, 1999; Divine and Dick, 2006; Gloersen et al., 1993; Pang et al., 2018) for SIC derived with passive microwave data and was therefore used in this analysis.
To estimate the aforementioned ice indicators, the probable SIC value for a given non-exceedance probability (p) was extracted from IcePAC for every location and week. For this analysis, a range of non-exceedance probabilities going from 5 % to 95 % was evaluated, with a step of 5 % between each analysis. Time series of the results were compiled and it is for these series that the complete freeze-up and melt-out events were identified. Figure 8 shows the estimated freeze-up and melt-out event weeks for p=50 %.
This detection process was repeated for each of the 20 738 grid cells of the simulation domain and for each probability step. It is worth noting that while the melt is described as a non-exceedance event (SIC < 15 %), directly deduced from p, the freeze-up is actually defined as an exceedance event (SIC > 15 %), deduced from 1−p.
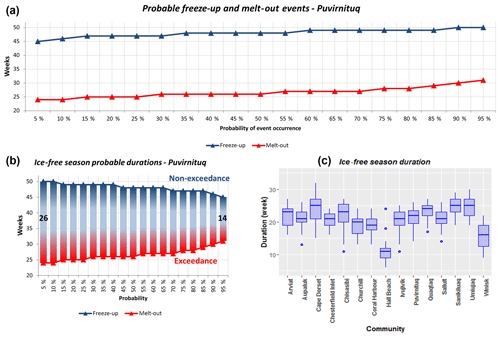
Figure 9Probable freeze-up and melt-out events for the coastal community of Puvirnituq (a), the range of probable ice-free season duration for the same community (b), and probable ice-free season lengths for all coastal communities of the HBS (c).
Figure 9a presents the probable freeze-up and melt-out events for the coastal community of Puvirnituq, located in the northeastern part of the Hudson Bay. In this figure we notice that melt has a 25 % probability to be completed by week 25 (18–24 June), only has a 10 % probability of being completed for week 24 (11–17 June), and is certain to be completed by week 31 (30 July–5 August). According to the two curves plotted in Fig. 9a, we can state that a complete freeze-up and complete melt at Puvirnituq can be expected, with a very high probability of occurrence (p>95 %) on weeks 50 (10–16 December) and 31 (30 July–5 August). Figure 9b shows an assessment of the range of probable ice-free season duration made for the same coastal community. Here, the freeze-up curve is inversed (1−P) as the shortest possible ice-free season duration is a combination of the latest possible melt (high exceedance probability) and the earliest possible freeze-up (high non-exceedance probability). By comparing the space between the two curves for the 5 % to 95 % probability range, we observe that the shortest possible ice-free season at Puvirnituq is 14 weeks and that the longest is 26 weeks. Figure 9c shows the ice-free season duration estimated for numerous coastal communities located in the study area using the method described for Fig. 9b. Particularly remarkable cases can be noticed, such as Cape Dorset, which displays a large variability in possible ice-free season duration given the shore lead polynya located in front of the community, Hall Beach in Foxe Basin with generally shorter ice-free seasons, with outliers corresponding to the occasional enlargement of the Hall Beach polynya, and finally Winisk, located in the south central part of the Hudson Bay, where ice tends to form early and melt late, which explains the shorter ice-free seasons when compared to other communities.
4.2 Comparison with the Canadian Ice Service atlas
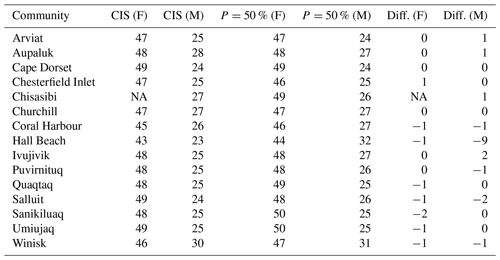
The HBS has been analyzed since 1972 (i.e. first regional Hudson Bay map) by the Canadian Ice Service (CIS) and they have gathered numerous sea ice condition maps in the area from which they built a 30-year sea ice climatological atlas (CIS, 2013), portraying the average sea ice conditions and freeze-up and melt-out dates. As the information provided by the CIS atlas is given based on median SIC % values, a comparison with the p=50 % IcePAC output gives an outlook on the coherency of the model when compared with another source of data, built around a different methodology.
The “Dates of freeze-up and break-up” charts of the CIS 1981–2010 atlas depict the extent of ice on a biweekly basis during the freeze-up and break-up periods (CIS, 2013). They provide a pictorial representation of the evolution of the ice extent during those two periods. The freeze-up and break-up dates are estimated using median values for 1981–2010 computed from CIS regional ice charts, a collection of over 40 years of data which were digitized in the late 1990s as a raster with a 1 km grid size. These charts were prepared by trained sea ice analysts who used high-resolution RADARSAT images as inputs to their analyses, since its acquisitions started in 1996, in combination with AVHRR, NOAA, SSM/I, and ERS-1 data. However, all maps produced prior to 1996 were made without RADARSAT and therefore could be apprehended as less accurate than maps produced post-1996. The CIS also started using RADARSAT-2 in 2008. Another important information is that SIC % is estimated in tenths in CIS datasets in respect to the formalism of the egg code, meaning that SIC % marked as 1∕10 in an egg code could be in reality any value between 10 % and 19.99 %. Considering this, ice presence is defined as SIC for CIS data (CIS, 2013), while we stated that it was an SIC % % for OSI-409.
Compared to the CIS data, IcePAC is based on algorithmically generated weekly averaged ice maps and calculated from adjusted frequency models. Also, there is a difference in spatial resolution between the two products; CIS uses 1 km digitized historical ice charts, while IcePAC uses passive-microwave-estimated SIC % resampled at a 12.5 km grid size. Finally, there is a time frame difference as the CIS atlas is built with data from 1981 to 2010 (30 years), while IcePAC is built with data from 1978 to 2015 (37 years).
The comparison, as displayed in Table 1, confirms that the freeze-up and melting dates identified by IcePAC are realistic when compared to the CIS historical data. Small differences in weeks are present and may be linked to a multitude of factors, the most important being the different methodologies used to generate the data.
The melt of the Hall Beach point does however come out as a relevant difference between the CIS and IcePAC melt week estimate. Since we find the freeze-up week adequately at the Hall Beach point and we use the same model distribution to derive both the freeze-up and melt information, it would be incorrect to simply flag this point as erroneous.
The overestimation of the ice-free season at Hall Beach by a 9-week gap compared to CIS could be explained by considering
-
the land spill-over effect that would make the OSI-409 overestimate SIC %;
-
the fact that the selected point (Hall Beach) is located on the edge of the polynya area;
-
that the melt week statistics are not measured exactly for the same time period (1981–2010 versus 1978–2015);
-
that we compare median values taken from CIS maps (values given in tenths of SIC %) with IcePAC outputs based on OSI-409 SIC % averages and that the definition of melt is not the same for both products (CIS is , while IcePAC is <15 %).
By comparing the IcePAC P=50 % and P=15 % melt week output (Fig. 10) with the CIS melt dates, we can easily note that the CIS melt dates are quite variable in the polynya area and that by selecting a point a little further offshore, the results would have been comparable, towards advocation of the land spill-over effect as a coherent explanation. However, as we also compared the CIS melt weeks with a lower probability scenario (P=15 %), it turns out that the Hall Beach polynya does appear close to the community, as expected. This specific situation is certainly linked to the fact that IcePAC uses average SIC % values compared to the CIS median values. As the SIC % in this specific area tends to be either very low (open polynya) or very high (consolidated sea ice cover), it is credible to think that the average and median values do differ considerably. In a case of frequent low concentration like the Hall Beach polynya, the median tends toward a low SIC %, while the few higher SIC % events do bring the average SIC % up, increasing the gap between the median and the average values, enough so that with an average value we cannot detect the melt-out, therefore giving a plausible explanation for the 9-week difference noticed here.
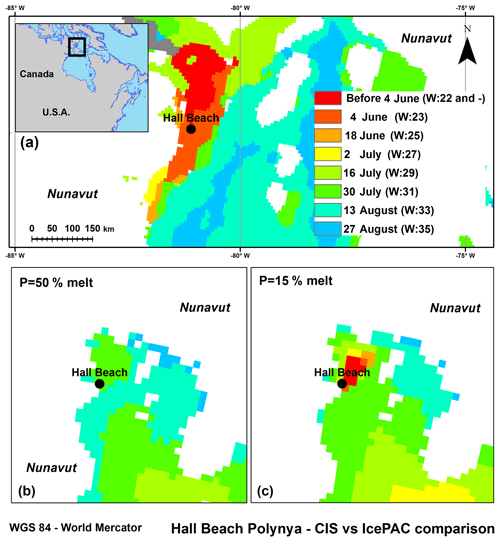
Figure 10Comparison of probable melt weeks for the coastal community of Hall Beach in Foxe Basin with the CIS melt weeks (a) and two IcePAC melt week scenarios for 50 % (b) and 15 % (c) probabilities. No data appear north of the IcePAC outputs since Hall Beach is located at the upper limit of the IcePAC model test domain.
4.3 Applicability of the IcePAC approach to other locations and data sources
The IcePAC modelling approach is replicable to any site for which SIC % data are available. Evidently, to ensure relevance for the resulting probability maps, the length of the time series used as inputs to adjust the beta models must be sufficient (∼30 years). Logically, the simulation domain grid cells will fall into one of the three following categories: (1) ice-covered grid cells with constant high SIC %, during the stable cover period; (2) marginal zone grid cells, in which SIC % will oscillate from high to low for the different years, during the freeze-up and melt periods; and (3) open water grid cells with constant low SIC %, during the ice-free season. As these are the ice regimes one could expect anywhere in the Arctic, including the HBS, there are no limitations on this side for using the IcePAC approach in other locations.
Other data sources could also be used with the IcePAC approach such as climate model outputs or different sea ice concentration maps. As climate model outputs provide future projections of SIC %, an evaluation of the range of probable SIC % patterns for a future year could be achieved (i.e. 2050 or 2080). However, one downside of these datasets is their coarse spatial resolutions.
The IcePAC tool permits an assessment of plausible sea-ice-related events for the entire range of probabilities for 20 738 sites (grid cells) in the Hudson Bay system, for all 52 weeks of the year. It is based on local (grid-cell) models that use the generalized beta distribution to describe the sea ice behaviour with four parameters at each site (with position and scale being fixed), based on historical 1978–2015 information from passive microwave imagery (OSI-409). From these parameters, IcePAC generates spatialized sea ice probabilistic information that can be used in any geographic information system or a web-based map interface for further analyses.
An analysis has been made to define, for each grid cell in the simulation domain, the plausible scenarios for each probability. A subsequent comparison with the 1981–2010 Canadian Ice Service sea ice climatology atlas (CIS, 2013) showed that the information generated with the IcePAC tool, for the p=50 % case, renders coherent probabilities for freeze-up and melt events over the HBS. A noticeable difference in the melt weeks was detected for the community of Hall Beach, suggesting that using median values instead of average SIC % could be of interest in order to be able to adequately detect specific events like polynyas. Another analysis, focused on the community of Puvirnituq, showed that it is possible to evaluate the range of plausible scenarios in terms of ice-free season length locally.
The model outputs generated with the IcePAC tool provide a novel probabilistic perspective regarding important events related to sea ice dynamics that was not available before. With its capacity to be utilized in other areas (with respect to the grid size of the passive microwave product), and the fact that it could easily be updated using new data, the IcePAC tool has the potential to provide valuable information on probable freeze-up and melt weeks as well as on ice presence and ice-free season lengths.
This relevant information will help decision makers such as engineers wanting to build a new marine coastal or offshore infrastructure to estimate ice hazards, fauna specialists trying to understand the vulnerability of a given species living dependent on the ice cover, or mariners wanting to estimate the feasibility of navigating a certain route. Turning the raw probabilistic information gathered from IcePAC into valuable thematic information will give stakeholders a capital gain in apprehending the possible spatio-temporal sea ice concentration patterns and in preparing for an effective mitigation of climate change impacts in coastal and offshore environments.
IcePAC data are available on a web interface at http://icepac.ete.inrs.ca (last access: 26 August 2018, Gignac, 2017).
CG defined the objectives of this research project, processed the data, coded the IcePAC tool, analyzed the results, and wrote and reviewed this research paper. MB and KC participated in defining the objectives, guiding the development of the tool, and writing this paper.
The authors declare that they have no conflict of interest.
The authors would like to acknowledge the Adaptation Platform of Natural
Resources Canada (NRCAN) for the funding of this research (AP060). They would
also like to recognize and thank Salah El Adlouni (U. Moncton), Fateh Chebana
(INRS-ETE), Luke Copland (U. Ottawa) and Simon Bélanger (UQAR) for their
suggestions and comments on this work. The authors would also like to thank
EUMETSAT OSI-SAF (http://osisaf.met.no/p/ice/, last access: 26 August
2018) for the access to their OSI-409 and OSI-430 datasets. Finally, we would
like to extend our thanks to the five anonymous reviewers who provided
numerous relevant comments which helped improve our
manuscript.
Edited by: John Yackel
Reviewed by: five anonymous referees
Agnew, T. and Howell, S.: The use of operational ice charts for evaluating passive microwave ice concentration data, Atmos. Ocean, 41, 317–331, 2003.
Ahn, J., Hong, S., Cho, J., Lee, Y.-W., and Lee, H.: Statistical Modeling of Sea Ice Concentration Using Satellite Imagery and Climate Reanalysis Data in the Barents and Kara Seas, 1979–2012, Remote Sens., 6, 5520–5540, 2014.
Akaike, H.: Information theory and an extension of the maximum likelihood principle, in: Selected Papers of Hirotugu Akaike, Springer, 1998.
Aksenov, Y., Popova, E. E., Yool, A., Nurser, A. J. G., Williams, T. D., Bertino, L., and Bergh, J.: On the future navigability of Arctic sea routes: High-resolution projections of the Arctic Ocean and sea ice, Mar. Policy, 75, 300–317, 2017.
Andersen, S., Tonboe, R., Kern, S., and Schyberg, H.: Improved retrieval of sea ice total concentration from spaceborne passive microwave observations using numerical weather prediction model fields: An intercomparison of nine algorithms, Remote Sens. Environ., 104, 374–392, 2006.
Andrews, J., Babb, D., and Barber, D. G.: Climate change and sea ice: Shipping accessibility on the marine transportation corridor through Hudson Bay and Hudson Strait (1980–2014), Elem. Sci. Anth., 5, p. 15, https://doi.org/10.1525/elementa.130, 2017.
Barber, D. G. and Massom, R. A.: The Role of Sea Ice in Arctic and Antarctic Polynyas, chap. 1, in: Elsevier Oceanography Series, edited by: Smith, W. O. and Barber, D. G., Elsevier, 2007.
Barnhart, K. R., Overeem, I., and Anderson, R. S.: The effect of changing sea ice on the physical vulnerability of Arctic coasts, The Cryosphere, 8, 1777–1799, https://doi.org/10.5194/tc-8-1777-2014, 2014.
Baum, C. F.: Stata tip 63: Modeling proportions, Stata J., 8, 299–303, 2008.
Bhatt, U. S., Walker, D. A., Raynolds, M. K., Comiso, J. C., Epstein, H. E., Jia, G., Gens, R., Pinzon, J. E., Tucker, C. J., Tweedie, C. E., and Webber, P. J.: Circumpolar Arctic Tundra Vegetation Change Is Linked to Sea Ice Decline, Earth Interact., 14, 1–20, 2010.
Bintanja, R. and Selten, F. M.: Future increases in Arctic precipitation linked to local evaporation and sea-ice retreat, Nature, 509, 479–482, 2014.
Castro de la Guardia, L., Derocher, A. E., Myers, P. G., Terwisscha van Scheltinga, A. D., and Lunn, N. J.: Future sea ice conditions in Western Hudson Bay and consequences for polar bears in the 21st century, Glob. Change Biol., 19, 2675–2687, 2013.
Cavalieri, D. J., Gloersen, P., Parkinson, C. L., Comiso, J. C., and Zwally, H. J.: Observed Hemispheric Asymmetry in Global Sea Ice Changes, Science, 278, 1104–1106, 1997.
Cavalieri, D. J. and Parkinson, C. L.: Arctic sea ice variability and trends, 1979–2010, The Cryosphere, 6, 881–889, https://doi.org/10.5194/tc-6-881-2012, 2012.
Cavalieri, D. J., Parkinson, C. L., Gloersen, P., Comiso, J. C., and Zwally, H. J.: Deriving long-term time series of sea ice cover from satellite passive-microwave multisensor data sets, J. Geophys. Res.-Oceans, 104, 15803–15814, 1999.
Cave, B. M. and Pearson, K.: Numerical illustrations of the variate difference correlation method, Biometrika, 10, 340–355, 1914.
Chen, L. and Singh, V. P.: Generalized beta distribution of the second kind for flood frequency analysis, Entropy, 19, 254–271, 2017.
CIS: Sea Ice Climatic Atlas for the Northern Canadian Waters 1981–2010, Canadian Ice Service (CIS), Ottawa, 2013.
Comiso, J. C.: Large Decadal Decline of the Arctic Multiyear Ice Cover, J. Climate, 25, 1176–1193, 2011.
Comiso, J. C.: SSM/I sea ice concentrations using the bootstrap algorithm, National Aeronautics and Space Administration, Goddard Space Flight Center, 1995.
Comiso, J. C.: A rapidly declining perennial sea ice cover in the Arctic, Geophys. Res. Lett., 29, 1956, https://doi.org/10.1029/2002GL015650, 2002.
Comiso, J. C., Parkinson, C. L., Gersten, R., and Stock, L.: Accelerated decline in the Arctic sea ice cover, Geophys. Res. Lett., 35, L01703, doi10.1029/2007GL031972, 2008.
Cugerone, K. and Michele, C. D.: Johnson SB as general functional form for raindrop size distribution, Water Resour. Res., 51, 6276–6289, 2015.
D'Adderio, L. P., Cugerone, K., Porcù, F., De Michele, C., and Tokay, A.: Capabilities of the Johnson SB distribution in estimating rain variables, Adv. Water Resour., 97, 241–250, 2016.
Darnis, G., Robert, D., Pomerleau, C., Link, H., Archambault, P., Nelson, R. J., Geoffroy, M., Tremblay, J.-É., Lovejoy, C., Ferguson, S. H., Hunt, B. P. V., and Fortier, L.: Current state and trends in Canadian Arctic marine ecosystems: II. Heterotrophic food web, pelagic-benthic coupling, and biodiversity, Clim. Change, 115, 179–205, 2012.
Davies, F. J., Renssen, H., and Goosse, H.: The Arctic freshwater cycle during a naturally and an anthropogenically induced warm climate, Climate Dynam., 42, 2099–2112, 2014.
Dawson, J., Pizzolato, L., Howell, S. E. L., Copland, L., and Johnston, M. E.: Temporal and Spatial Patterns of Ship Traffic in the Canadian Arctic from 1990 to 2015, Arctic, 71, 15–26, 2018.
Déry, S. J. and Wood, E. F.: Decreasing river discharge in northern Canada, Geophys. Res. Lett., 32, L10401, https://doi.org/10.1029/2005GL022845, 2005.
Déry, S. J. and Wood, E. F.: Teleconnection between the Arctic Oscillation and Hudson Bay river discharge, Geophys. Res. Lett., 31, L18205, https://doi.org/10.1029/2004GL020729, 2004.
Dirkson, A.: Initializing sea ice thickness and quantifying uncertainty in seasonal forecasts of Arctic sea ice, PhD thesis, University of Victoria, available at: https://bit.ly/2WxBhFF (last access: 1 February 2019), 2017.
Divine, D. V. and Dick, C.: Historical variability of sea ice edge position in the Nordic Seas, J. Geophys. Res.-Oceans, 111, C01001, https://doi.org/10.1029/2004JC002851, 2006.
Drobot, S. D.: Using remote sensing data to develop seasonal outlooks for Arctic regional sea-ice minimum extent, Remote Sens. Environ., 111, 136–147, 2007.
Durkalec, A., Furgal, C., Skinner, M. W., and Sheldon, T.: Climate change influences on environment as a determinant of Indigenous health: Relationships to place, sea ice, and health in an Inuit community, Soc. Sci. Med., 136–137, 17–26, 2015.
Eastwood, S., Jenssen, M., Lavergne, T., Sorensen, A., and Tonboe, R.: Global Sea Ice Concentration Reprocessing – Product User Manual, EUMETSAT–OSISAF, User guide, 29 pp., 2015.
Etkin, D. A.: Break-up in Hudson Bay: its sensitivity to air temperatures and implications for climate warming, Climatol. Bull., 25, 21–34, 1991.
Etkin, D. A. and Ramseier, R. O.: A comparison of conventional and passive microwave sea-ice datasets for Hudson Bay, Atmos. Ocean, 31, 359–378, 1993.
Falls, L. W.: The beta distribution: a statistical model for world cloud cover, J. Geophys. Res., 79, 1261–1264, 1974.
Fetterer, F., Knowles, K., Meier, W., Savoie, M., and Windnagel, A.: Sea Ice Index, Version 3, National Snow and Ice Data Center (updated daily), NSIDC, Boulder, CO, available at: https://nsidc.org/arcticseaicenews/ (last access: 18 May 2018), 2017.
Gagnon, A. S. and Gough, W. A.: Climate Change Scenarios for the Hudson Bay Region: An Intermodel Comparison, Clim. Change, 69, 269–297, 2005a.
Gagnon, A. S. and Gough, W. A.: Trends in the dates of ice freeze-up and breakup over Hudson Bay, Canada, Arctic, 58, 370–382, 2005b.
Galbraith, P. S. and Larouche, P.: Reprint of “Sea-surface temperature in Hudson Bay and Hudson Strait in relation to air temperature and ice cover breakup, 1985–2009”, J. Marine Syst., 88, 463–475, 2011.
Gignac, C.: Ice Pac Interface – Version 1.5 Beta, available at: http://icepac.ete.inrs.ca (last access: 26 August 2018), 2017.
Gloersen, P., Campbell, W. J., Cavalieri, D. J., Comiso, J. C., Parkinson, C. L., and Zwally, H. J.: Satellite passive microwave observations and analysis of Arctic and Antarctic sea ice, 1978–1987, Ann. Glaciol., 17, 149–154, 1993.
Gloersen, P., Parkinson, C. L., Cavalieri, D. J., Cosmiso, J. C., and Zwally, H. J.: Spatial Distribution of Trends and Seasonality in the Hemispheric Sea Ice Covers, J. Geophys. Res., 104, 20827–20835, 1999.
Gough, W. A., Gagnon, A. S., and Lau, H. P.: Interannual Variability of Hudson Bay Ice Thickness, Polar Geography, 28, 222–238, 2004.
Henderson-Sellers, A.: Surface type and its effect upon cloud cover: A climatological investigation, J. Geophys. Res.-Oceans, 83, 5057–5062, 1978.
Hirsch, R. M., Slack, J. R., and Smith, R. A.: Techniques of trend analysis for monthly water quality data, Water Resour. Res., 18, 107–121, 1982.
Ho, J.: The implications of Arctic sea ice decline on shipping, Mar. Policy, 34, 713–715, 2010.
Hochheim, K. and Barber, D.: Atmospheric forcing of sea ice in Hudson Bay during the fall period, 1980–2005, J. Geophys. Res.-Oceans, 115, C05009, https://doi.org/10.1029/2009JC005334, 2010.
Hochheim, K. P. and Barber, D. G.: An update on the ice climatology of the Hudson Bay system, Arct. Antarct. Alp. Res., 46, 66–83, 2014.
Holland, M. M., Finnis, J., and Serreze, M. C.: Simulated Arctic Ocean Freshwater Budgets in the Twentieth and Twenty-First Centuries, J. Climate, 19, 6221–6242, 2006.
Hunke, E., Lipscomb, W., Jones, P., Turner, A., Jeffery, N., and Elliott, S.: CICE, The Los Alamos Sea Ice Model, Los Alamos National Laboratory (LANL), Los Alamos, NM, 2017.
Iacozza, J.: Assessment of ice monitoring in Canada, Report to the Department of Fisheries and Oceans Canada, 51 pp., available at: http://www.dfo-mpo.gc.ca/Library/243202.pdf (last access: 1 February 2019), 2000.
Johannessen, O. M., Bengtsson, L., Miles, M. W., Kuzmina, S. I., Semenov, V. A., Alekseev, G. V., Nagurnyi, A. P., Zakharov, V. F., Bobylev, L. P., and Pettersson, L. H.: Arctic climate change: Observed and modelled temperature and sea-ice variability, Tellus A, 56, 328–341, 2004.
Johnson, N. L.: Systems of frequency curves generated by methods of translation, Biometrika, 36, 149–176, 1949.
Jones, E. P. and Anderson, L. G.: Northern Hudson Bay and Foxe Basin: water masses, circulation and productivity, Atmos.Ocean, 32, 361–374, 1994.
Kowal, S., Gough, W. A., and Butler, K.: Temporal evolution of Hudson Bay Sea Ice (1971–2011), Theor. Appl. Climatol., 127, 753–760, 2017.
Laidler, G. J., Elee, P., Ikummaq, T., Joamie, E., and Aporta, C.: Mapping Inuit Sea Ice Knowledge, Use, and Change in Nunavut, Canada (Cape Dorset, Igloolik, Pangnirtung), in: SIKU: Knowing Our Ice: Documenting Inuit Sea Ice Knowledge and Use, edited by: Krupnik, I., Aporta, C., Gearheard, S., Laidler, G. J., and Kielsen Holm, L., Springer Netherlands, Dordrecht, 2010.
Laidre, K. L., Stern, H., Kovacs, K. M., Lowry, L., Moore, S. E., Regehr, E. V., Ferguson, S. H., Wiig, Ø., Boveng, P., and Angliss, R. P.: Arctic marine mammal population status, sea ice habitat loss, and conservation recommendations for the 21st century, Conserv. Biol., 29, 724–737, 2015.
Lallemant, D. and Kiremidjian, A.: A Beta Distribution Model for Characterizing Earthquake Damage State Distribution, Earthq. Spectra, 31, 1337–1352, 2015.
Landy, J. C., Ehn, J. K., Babb, D. G., Thériault, N., and Barber, D. G.: Sea ice thickness in the Eastern Canadian Arctic: Hudson Bay Complex & Baffin Bay, Remote Sens. Environ., 200, 281–294, 2017.
Lasserre, F. and Pelletier, S.: Polar super seaways? Maritime transport in the Arctic: an analysis of shipowners' intentions, J. Transp. Geogr., 19, 1465–1473, 2011.
Lins, H. F.: A note on stationarity and nonstationarity, World Meteorological Organization, Commission for Hydrology, Advisory Working Group, available at: http://www.wmo.int/pages/prog/hwrp/chy/chy14/documents/ms/Stationarity_and_Nonstationarity.pdf (last access: 1 February 2019), 2012.
Liu, M. and Kronbak, J.: The potential economic viability of using the Northern Sea Route (NSR) as an alternative route between Asia and Europe, Tourism and Climate Change, J. Transp. Geogr., 18, 434–444, 2010.
Manabe, S. and Stouffer, R. J.: Simulation of abrupt climate change induced by freshwater input to the North Atlantic Ocean, Nature, 378, 165–167, 1995.
Mann, H. B.: Nonparametric Tests Against Trend, Econometrica, 13, 245–259, 1945.
Martini, I. P.: Coastal features of Canadian inland seas, in: Elsevier oceanography series, Elsevier, 1986.
Maxwell, J. B.: A climate overview of the Canadian inland seas, in: Elsevier oceanography series, Elsevier, 1986.
Mudryk, L. R., Derksen, C., Howell, S., Laliberté, F., Thackeray, C., Sospedra-Alfonso, R., Vionnet, V., Kushner, P. J., and Brown, R.: Canadian snow and sea ice: historical trends and projections, The Cryosphere, 12, 1157–1176, https://doi.org/10.5194/tc-12-1157-2018, 2018.
Mysak, L. A., Ingram, R. G., Wang, J., and Van Der Baaren, A.: The anomalous sea-ice extent in Hudson Bay, Baffin Bay and the Labrador Sea during three simultaneous NAO and ENSO episodes, Atmos. Ocean, 34, 313–343, 1996.
Nadarajah, S.: A truncated inverted beta distribution with application to air pollution data, Stoch. Env. Res. Risk A., 22, 285–289, 2008.
NaturalEarth: Coastline, NaturalEarth, Coastline, available at: http://www.naturalearthdata.com/downloads/110m-physicalvectors/110m-coastline/ (last access: 26 August 2018), 2014.
NIST: e-Handbook of Statistical Methods, available at: https://www.itl.nist.gov/div898/handbook/index.htm (last access: 26 August 2018), 2013.
NSIDC: Monthly Ocean Masks and Maximum Extent Masks, available at: https://nsidc.org/data/pm/ocean-masks (last access: 1 February 2019), 2013.
Overeem, I., Anderson, R. S., Wobus, C. W., Clow, G. D., Urban, F. E., and Matell, N.: Sea ice loss enhances wave action at the Arctic coast, Geophys. Res. Lett., 38, L17503, https://doi.org/10.1029/2011GL048681, 2011.
Pang, X., Pu, J., Zhao, X., Ji, Q., Qu, M., and Cheng, Z.: Comparison between AMSR2 Sea Ice Concentration Products and Pseudo-Ship Observations of the Arctic and Antarctic Sea Ice Edge on Cloud-Free Days, Remote Sens., 10, 317, https://doi.org/10.3390/rs10020317, 2018.
Pavlova, O., Pavlov, V., and Gerland, S.: The impact of winds and sea surface temperatures on the Barents Sea ice extent, a statistical approach, J. Marine Syst., 130, 248–255, 2014.
Peterson, B. J., Holmes, R. M., McClelland, J. W., Vörösmarty, C. J., Lammers, R. B., Shiklomanov, A. I., Shiklomanov, I. A., and Rahmstorf, S.: Increasing river discharge to the Arctic Ocean, Science, 298, 2171–2173, 2002.
Pizzolato, L., Howell, S. E. L., Dawson, J., Laliberté, F., and Copland, L.: The influence of declining sea ice on shipping activity in the Canadian Arctic, Geophys. Res. Lett., 43, 12146–12154, 2016.
Post, E., Bhatt, U. S., Bitz, C. M., Brodie, J. F., Fulton, T. L., Hebblewhite, M., Kerby, J., Kutz, S. J., Stirling, I., and Walker, D. A.: Ecological Consequences of Sea-Ice Decline, Science, 341, 519–524, 2013.
Prinsenberg, S. J.: On the physical oceanography of Foxe Basin, in: Elsevier oceanography series, Elsevier, 1986.
Rahmstorf, S.: Bifurcations of the Atlantic thermohaline circulation in response to changes in the hydrological cycle, Nature, 378, 145–149, 1995.
Rahmstorf, S. and Ganopolski, A.: Long-term global warming scenarios computed with an efficient coupled climate model, Clim. Change, 43, 353–367, 1999.
Rajak, D., Singh, R. K., Jayaprasad, P., Oza, S. R., Sharma, R., and Kumar, R.: Sea ice occurrence probability data and its applications over the Antarctic, J. Geomatics, 9, 193–197, 2015.
Rao, A. R., Hamed, K. H., and Chen, H.-L.: Nonstationarities in hydrologic and environmental time series, Springer Science & Business Media, 2012.
Rennolls, K. and Wang, M.: A new parameterization of Johnson's SB distribution with application to fitting forest tree diameter data, Can J. Forest Res., 35, 575–579, 2005.
Rothrock, D. A., Yu, Y., and Maykut, G. A.: Thinning of the Arctic sea-ice cover, Geophys. Res. Lett., 26, 3469–3472, 1999.
Rousset, C., Vancoppenolle, M., Madec, G., Fichefet, T., Flavoni, S., Barthélemy, A., Benshila, R., Chanut, J., Levy, C., Masson, S., and Vivier, F.: The Louvain-La-Neuve sea ice model LIM3.6: global and regional capabilities, Geosci. Model Dev., 8, 2991–3005, https://doi.org/10.5194/gmd-8-2991-2015, 2015.
Saucier, F., Senneville, S., Prinsenberg, S., Roy, F., Smith, G., Gachon, P., Caya, D., and Laprise, R.: Modelling the sea ice-ocean seasonal cycle in Hudson Bay, Foxe Basin and Hudson Strait, Canada, Climate Dynam., 23, 303–326, 2004.
Schwarz, G.: Estimating the dimension of a model, Ann. Stat., 6, 461–464, 1978.
Serreze, M. C. and Barry, R. G.: Processes and impacts of Arctic amplification: A research synthesis, Global Planet. Change, 77, 85–96, 2011.
Smith, D.: Extraction of winter total sea-ice concentration in the Greenland and Barents Seas from SSM/I data, Remote Sens., 17, 2625–2646, 1996.
Stirling, I.: The Biological Importance of Polynyas in the Canadian Arctic, Arctic, 33, 303–315, 1980.
Stocker, T.: Climate change 2013: the physical science basis: Working Group I contribution to the Fifth assessment report of the Intergovernmental Panel on Climate Change, Cambridge University Press, 2014.
Stroeve, J., Holland, M. M., Meier, W., Scambos, T., and Serreze, M.: Arctic sea ice decline: Faster than forecast, Geophys. Res. Lett., 34, L09501, https://doi.org/10.1029/2007GL029703, 2007.
Stroeve, J., Markus, T., Boisvert, L., Miller, J., and Barrett, A.: Changes in Arctic melt season and implications for sea ice loss, Geophys. Res. Lett., 41, 1216–1225, 2014.
Stroeve, J. C., Kattsov, V., Barrett, A., Serreze, M., Pavlova, T., Holland, M., and Meier, W. N.: Trends in Arctic sea ice extent from CMIP5, CMIP3 and observations, Geophys. Res. Lett., 39, L16502, https://doi.org/10.1029/2012GL052676 , 2012.
Sulaiman, M. Y., Oo, W. H., Wahab, M. A., and Zakaria, A.: Application of beta distribution model to Malaysian sunshine data, Renew. Energ., 18, 573–579, 1999.
Tivy, A., Howell, S. E. L., Alt, B., McCourt, S., Chagnon, R., Crocker, G., Carrieres, T., and Yackel, J. J.: Trends and variability in summer sea ice cover in the Canadian Arctic based on the Canadian Ice Service Digital Archive, 1960–2008 and 1968–2008, J. Geophys. Res.-Oceans, 116, C03007, https://doi.org/10.1029/2009JC005855, 2011.
Tonboe, R. T., Eastwood, S., Lavergne, T., Sørensen, A. M., Rathmann, N., Dybkjær, G., Pedersen, L. T., Høyer, J. L., and Kern, S.: The EUMETSAT sea ice concentration climate data record, The Cryosphere, 10, 2275–2290, https://doi.org/10.5194/tc-10-2275-2016, 2016.
Vermaire, J. C., Pisaric, M. F., Thienpont, J. R., Courtney Mustaphi, C. J., Kokelj, S. V., and Smol, J. P.: Arctic climate warming and sea ice declines lead to increased storm surge activity, Geophys. Res. Lett., 40, 1386–1390, 2013.
Vermote, E. F.: MOD09A1 MODIS/Terra Surface Reflectance 8-Day L3 Global 500 m SIN Grid V006, DAAC, NASA EOSDIS LP DAAC, available at: https://lpdaac.usgs.gov/dataset_discovery/modis/modis_products_table/mod09a1_v006 (last access: 18 May 2018), 2017.
Wakazuki, Y.: Modified Relative Humidity Based on the Johnson's SB Distribution Function, SOLA, 9, 111–114, 2013.
Wald, A. and Wolfowitz, J.: On a Test Whether Two Samples are from the Same Population, Ann. Math. Statist., 11, 147–162, https://doi.org/10.1214/aoms/1177731909, 1940.
Wang, J., Mysak, L. A., and Ingram, R. G.: Interannual variability of sea-ice cover in Hudson Bay, Baffin Bay and the Labrador Sea, Atmos. Ocean, 32, 421–447, 1994.
Wang, M. and Overland, J. E.: A sea ice free summer Arctic within 30 years?, Geophys. Res. Lett., 36, L07502, https://doi.org/10.1029/2009GL037820, 2009.
Wassmann, P., Duarte, C. M., Agusti, S., and Sejr, M. K.: Footprints of climate change in the Arctic marine ecosystem, Glob. Change Biol., 17, 1235–1249, 2011.
Weaver, A. J., Eby, M., Wiebe, E. C., Bitz, C. M., Duffy, P. B., Ewen, T. L., Fanning, A. F., Holland, M. M., MacFadyen, A., Matthews, H. D., Meissner, K. J., Saenko, O., Schmittner, A., Wang, H., and Yoshimori, M.: The UVic earth system climate model: Model description, climatology, and applications to past, present and future climates, Atmos. Ocean, 39, 361–428, 2001.
Wessel, P. and Smith, W. H. F.: A global, self-consistent, hierarchical, high-resolution shoreline database, J. Geophys. Res.-Sol. Ea., 101, 8741–8743, 1996.
Wilcoxon, F.: Individual Comparisons by Ranking Methods, Biomet. Bull., 1, 80–83, 1945.
Winton, M.: Amplified Arctic climate change: What does surface albedo feedback have to do with it?, Geophys. Res. Lett., 33, L03701, https://doi.org/10.1029/2005GL025244, 2006.
Yao, A. Y. M.: A Statistical Model for the Surface Relative Humidity, J. Appl. Meteorol., 13, 17–21, 1974.