Simulated retreat of Jakobshavn Isbræ during the 21st century

The early 21st century retreat of Jakobshavn Isbræ into its overdeepened bedrock trough was accompanied by acceleration to unprecedented ice stream speeds. Such dramatic changes suggested the possibility of substantial mass loss over the rest of this century. Here we use a three-dimensional ice sheet model with parameterizations to represent the effects of ice mélange buttressing, crevasse-depth-based calving and submarine melting to adequately reproduce its recent evolution. We are the first study on Jakobshavn Isbræ that solves for three-dimensional ice flow coupled with representations of hydro-fracturing-induced calving and mélange buttressing. Additionally, the model can accurately replicate interannual variations in grounding line and terminus position, including seasonal fluctuations that emerged after arriving at the overdeepened basin and the disappearance of its floating ice shelf. Our simulated ice viscosity variability due to shear margin evolution is particularly important in reproducing the large observed interannual changes in terminus velocity. We use this model to project Jakobshavn's evolution over this century, forced by ocean temperatures from seven Earth system models and surface runoff derived from RACMO, all under the IPCC RCP4.5 climate scenario. In our simulations, Jakobshavn's grounding line continues to retreat ∼18.5 km by the end of this century, leading to a total mass loss of ∼2068 Gt (5.7 mm sea level rise equivalent). Despite the relative success of the model in simulating the recent behavior of the glacier, the model does not simulate winter calving events that have become relatively more important.

1 Introduction

Jakobshavn Isbræ (Fig. 1) is Greenland's largest and fastest outlet glacier, with transient speeds of up to 17 km a⁻¹ (Joughin et al., 2014). Jakobshavn Isbræ drains ∼6.5 % of the Greenland ice sheet (Krabill et al., 2000), and it alone contributed ∼1 mm to global sea level rise between 2000 and 2011 (Howat et al., 2011). Since 1997, measurements indicate that the water entering Ilulissat Fjord, where Jakobshavn Isbræ terminates, is about 1.1 ^∘C warmer than it was during 1987–1991 (Holland et al., 2008). This rise in water temperature coincided with the onset of dramatic thinning, speedup and retreat of Jakobshavn Isbræ. By 2003 its velocity near the grounding line had reached ∼12.6 km a⁻¹, more than double that of 1992, and the ice shelf in the fjord had disintegrated (Joughin et al., 2004). From 2005 to 2007, as it retreated inland, seasonal fluctuations in velocity 4 km inland from the calving front amounted to ±1 km a⁻¹. The winter slowdowns and summer accelerations occurred in tandem with the calving front winter advance and summer retreat. By 2012 the seasonal velocity fluctuations 4 km upstream from the calving front were nearly ±8 km a⁻¹ and the grounding line of Jakobshavn Isbræ had reached the bottom of a subglacial bedrock trough after years of downslope migration (Joughin et al., 2014).

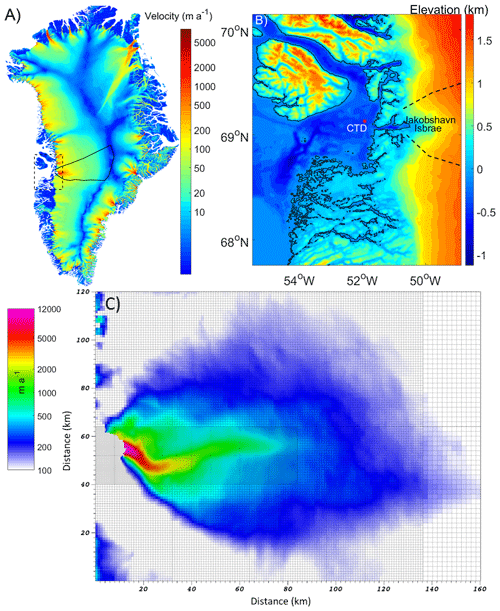
Figure 1 (a) Greenland ice sheet flow speeds from Joughin et al. (2018), with the Jakobshavn drainage basin outlined by the solid black line and the area shown in (b) by the dashed box. (b) Ilulissat Fjord and Disko Bay bathymetry from Jakobsson et al. (2012), with the CTD (conductivity temperature depth) site used for ocean temperature marked by the red star. (c) Example of the mesh used with finest resolution of 500 m with modeled velocities at the beginning of 2004.

Before 1997, Jakobshavn had a ∼15 km long ice shelf in front of its grounding line and experienced submarine melting on its ice–ocean interface (Amundson et al., 2010). After 1998 the terminus became more crevassed, coinciding with acceleration of the glacier, implying that weakened buttressing had triggered its dramatic speed-up. A thinning rate of 230±50 m a⁻¹ between the summers of 1984 and 1985 was deduced from photogrammetric surveys, with 98 % contributed by submarine melting (Motyka et al., 2011). The ice shelf thickened during the mid-1990s, followed by progressive thinning after 1997 (Motyka et al., 2011). From 1997 to 2008, the average ocean temperature was 1.1 ^∘C higher than during the period 1980–1991, which raised its thinning rate substantially, affecting the whole ice shelf that eventually collapsed in 2003. Many lines of evidence suggest that warm water was responsible for the submarine melting beneath the ice mélange and ice shelf, brought by a buoyancy-driven, overturning circulation in Ilulissat Fjord (Gladish et al., 2015).

Jakobshavn, in common with most outlet glaciers in Greenland, flows through a narrow, deeply incised bedrock trough at a much faster rate than the ice surrounding it (Joughin et al., 2010). Gravity surveys suggest a deep layer of soft till underlies much of the Jakobshavn trough (Block and Bell, 2011). This soft bed provides almost no resistance to ice flow, and basal shear stress maps show that most of the gravitational driving force on the glacier is balanced by lateral drag (Shapero et al., 2016).

Basal drag decreased from 1995 to 2006 (Habermann et al., 2013), possibly due to fast thinning that reduced the effective pressure, i.e., the ice overburden minus water pressure, at the bed. The effective pressure distribution under the glacier is important to basal drag and approaches zero at the grounding line as the ice begins to float. Several sliding parameterizations (also termed sliding relations or sliding laws) have been used in the literature that assume basal drag depends on sliding speed (so-called Weertman sliding; Weertman, 1957) or on effective pressure (Schoof and Hindmarsh, 2010; Gagliardini et al., 2014). Tsai et al. (2015) introduced a combined Weertman and Coulomb sliding law based on effective pressures with a boundary layer at the grounding line; this has a higher scaling of ice flux with grounding line thickness compared with the Weertman sliding. However, in the Jakobshavn case, both Weertman and Coulomb sliding produce very similar fluxes because the basal shear stresses along the main trough are typically only 2 % of the driving force (Shapero et al., 2016).

Simulations using a flow band model with a crevasse-depth-based calving parameterization (Vieli and Nick, 2011) demonstrated that loss of buttressing from the weakening mélange or enhanced submarine melting could have triggered the dramatic changes seen in Jakobshavn Isbræ at the end of the 20th century. Later work (Muresan et al., 2016) using a simple calving model with dependence on the strain field at the terminus was able to reproduce the interannual retreat of Jakobshavn Isbræ until 2009, when the terminus arrived at the beginning of the reverse sloping bed. But retreat after 2010 was not captured by their model and neither were the seasonal fluctuations in terminus position. Bondzio et al. (2018) applied a similar calving model that removes any ice where tensile stress exceeds a threshold, as simulated with a SSA (shallow shelf approximation) model, regardless of ice thickness. To represent seasonal fluctuation of front position, their stress threshold is a stepwise constant function in time with low values in summer. After calibration, their model can closely reproduce the observed behavior from 1985 to 2018 when forced only with ocean temperatures.

In this paper we use a three-dimensional ice flow model with a treatment of calving that successfully tracks the seasonal terminus position and its retreat into the overdeepened basin. We use historic observations of ocean temperature as forcing and ice shelf melting rate to scale submarine melting rates for our model and thence make future projections. Our aim is to track the evolution of Jakobshavn Isbræ through the 21st century under a specific climate forcing scenario. In Sect. 2 we describe the approach and calibration of our model, Sect. 3 shows the simulations for the period to 2100 under the IPCC RCP4.5 scenario (Moss et al., 2010), Sect. 4 is a discussion of our results with reference to other studies and suggestions for improvements, and we conclude in Sect. 5.

2 Methods and data

2.1 Ice sheet model

We model Jakobshavn Isbræ using the BISICLES ice sheet dynamics model that is based on the vertically integrated stress balance formulation of Schoof and Hindmarsh (2010), which treats longitudinal and lateral stresses as depth independent, but allows for vertical shear in the nonlinear rheology (Cornford et al., 2013). BISICLES is particularly useful for Jakobshavn Isbræ as it uses block-structured finite volume discretization with adaptive mesh refinement (Cornford et al., 2013) allowing for high-resolution modeling of critical sections of the glacier. Jakobshavn Isbræ is fed by a ∼400 km long extensive drainage basin (Fig. 1), but the fast flow area is only around 10 km in width. Our highest mesh resolution of 500 m is used to cover the whole fast flow area including the shear margin (Fig. 1c), while the rest of the glacier is modeled at 1000 m resolution.

We assume the floating part of Jakobshavn Isbræ to be in hydrostatic equilibrium, thus the upper surface elevation s is

$$\begin{array}{}\text{(1)}& s=max\left[h+b,\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}}{{\mathit{\rho }}_{\mathrm{w}}}}\right)h\right],\end{array}$$

where ρ_i and ρ_w are the densities of ice (917 kg m⁻¹) and ocean water (1027 kg m⁻¹), h is ice thickness, and b is bedrock elevation relative to sea level. The ice thickness evolves in time as

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{\partial h}{\partial t}}+\mathrm{\nabla }\cdot \left[\mathit{u}h\right]=M_{\mathrm{s}}-M_{\mathrm{b}},\end{array}$$

where M_s, M_b are surface mass balance (SMB) and submarine melt rate, respectively, and u is the depth-independent horizontal velocity. No basal melting over the grounded area is allowed. The velocity u satisfies an approximate stress balance equation (Schoof and Hindmarsh, 2010)

$$\begin{array}{}\text{(3)}& \mathrm{\nabla }\cdot \left[\mathit{\varphi }h\stackrel{\mathrm{‾}}{\mathit{\mu }}\left(\mathrm{2}\dot{\mathit{ϵ}}+\mathrm{2}tr\left(\dot{\mathit{ϵ}}\right)\mathbf{I}\right)\right]-{\mathit{\tau }}^{\mathrm{b}}={\mathit{\rho }}_{i}gh\mathrm{\nabla }s,\end{array}$$

where I is the identity tensor, s is the ice surface elevation, g is the acceleration due to gravity, $\dot{\mathit{ϵ}}$ is the horizontal strain-rate tensor defined by

$$\begin{array}{}\text{(4)}& \dot{\mathit{ϵ}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}\left[\mathrm{\nabla }\mathit{u}+{\left(\mathrm{\nabla }\mathit{u}\right)}^{\mathrm{T}}\right],\end{array}$$

and τ^b is the basal shear stress. The vertically integrated effective viscosity $h\stackrel{\mathrm{‾}}{\mathit{\mu }}$ is given by

$$\begin{array}{}\text{(5)}& h\stackrel{\mathrm{‾}}{\mathit{\mu }}\left(x,y\right)=\underset{s-h}{\overset{s}{\int }}\mathit{\mu }\left(x,y,z\right)\mathrm{d}z,\end{array}$$

where the vertically varying effective viscosity μ includes a contribution from vertical shear and satisfies

$$\begin{array}{}\text{(6)}& \mathrm{2}\mathit{\mu }A\left(T\right)(\mathrm{4}{\mathit{\mu }}^{\mathrm{2}}{\dot{\mathit{ϵ}}}^{\mathrm{2}}+{\left|{\mathit{\rho }}_{i}g\left(s-z\right)\mathrm{\nabla }s\right|}^{\mathrm{2}}{)}^{(n-\mathrm{1})/\mathrm{2}}=\mathrm{1},\end{array}$$

where n is the flow rate exponent, set to 3 in the current study, and A(T) is the rate factor, dependent on the ice temperature T through an Arrhenius law (Hooke, 1981). ϕ is a stiffening factor estimated by solving an inverse problem (Cornford et al., 2015) using measured surface velocities.

We use a viscous Weertman sliding relation to define the basal friction:

$$\begin{array}{}\text{(7)}& {\mathit{\tau }}^{\mathrm{b}}=\left\{\begin{array}{l}-C{\left|\mathit{u}\right|}^{m-\mathrm{1}}\mathit{u}\mathrm{if}\frac{{\mathit{\rho }}_{\mathrm{i}}}{{\mathit{\rho }}_{\mathrm{w}}}h>-b\\ \mathrm{0}\mathrm{otherwise}\end{array},\right.\end{array}$$

and here we assume a linear relation taking m=1. The basal traction coefficient C(x,y) is estimated simultaneously with the stiffening factor ϕ by solving the inverse problem (Cornford et al., 2015). C and ϕ are adjusted iteratively to reduce the misfit with a set of 2010 surface velocity observations (Joughin et al., 2010). We hold the fields C and ϕ constant over time throughout our simulations, although they must actually change as the glacier retreats. We also do not thermomechanically couple the model but use a constant ice temperature of −10^∘.

Reflection boundary conditions were applied at the edge of the domain:

$$\begin{array}{}\text{(8)}& \mathit{u}\mathbf{\cdot }\mathit{n}=\mathrm{0},\mathit{t}\cdot \mathrm{\nabla }\mathit{u}\mathbf{\cdot }\mathit{n}=\mathrm{0},\mathrm{\nabla }h\cdot \mathit{n}=\mathrm{0},\end{array}$$

where n is normal to a boundary and t is parallel to it. Normal stress across the calving front is equal to the hydrostatic water pressure:

$$\begin{array}{}\text{(9)}& \mathit{n}\cdot \left[\mathit{\varphi }h\stackrel{\mathrm{‾}}{\mathit{\mu }}\left(\mathrm{2}\dot{\mathit{ϵ}}+\mathrm{2}\mathrm{tr}\left(\dot{\mathit{ϵ}}\right)\mathbf{I}\right)\right]-{\mathit{\tau }}^{\mathrm{b}}={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}{\mathit{\rho }}_{\mathrm{i}}\mathrm{g}\left(\mathrm{1}-{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{i}}}{{\mathit{\rho }}_{\mathrm{w}}}}\right)h^{\mathrm{2}}\mathit{n}.\end{array}$$

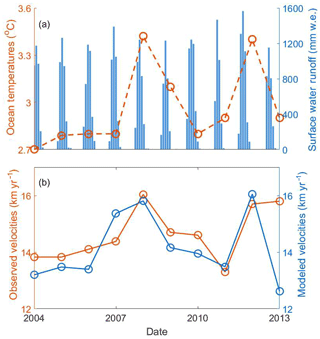
Figure 2 (a) Time series of observed ∼300 m deep ocean temperature (red) from near the mouth of Ilulissat Fjord (see Fig. 1 for location). Blue bars are simulated monthly surface water runoff from the MAR regional surface mass and energy balance model (Alexander and Luthcke, 2016). (b) Measured ice front annual mean ice flow speeds (red) from Joughin et al. (2010), compared with our modeled speeds (blue).

2.2 Forcing

Local ocean circulation in Ilulissat Fjord driven by buoyancy plume brings deep water from outside to the grounding line of Jakobshavn and renews the fjord waters within 90 d in summer (Gladish et al., 2015). Generally, Jakobshavn's fjord is ∼800 m deep but with a sill of only ∼200 m depth at its entrance. The deepest water outside the sill can flow over the sill and reach the grounding line of Jakobshavn (Gladish et al., 2015). We use 300 m depth ocean temperatures collected from a conductivity temperature depth (CTD) site close to the mouth of Ilulissat Fjord (Fig. 1) as an approximation of ocean temperatures near the glacier grounding line (Gladish et al., 2015). A positive correlation (r=0.74, p<0.05) exists between deep ocean temperatures and flow speed near the terminus of Jakobshavn Isbræ (Fig. 2) from 2004 onwards. There is no significant correlation prior to 2004, the ice shelf period. As a working hypothesis we assume that the correlation since 2004 reflects the effects of the sea ice and iceberg mélange in the fjord on the flow speed near the terminus: a warmer ocean reduces mélange and sea ice thickness and therefore buttressing. There appears to be no lag between the glacier acceleration and change in deep ocean temperature, suggesting mélange response times are faster than 1 year. When the ice shelf was present, lags in the system were likely longer, accounting for the lack of correlation between ocean temperatures and glacier flow speed prior to 2004. It is also possible that ocean temperatures reflect changes in surface runoff and basal lubrication for sliding, but we consider that the runoff more strongly affects calving mechanisms, as discussed later. We therefore modify the driving force (Eq. 3) on the grid cells next to the calving front by multiplying by a factor α that is linearly related to ocean temperature (T) as a means of representing the buttressing effects of the ice mélange in the fjord.

$$\begin{array}{}\text{(10)}& \mathrm{\nabla }\cdot \left[\mathit{\varphi }h\stackrel{\mathrm{‾}}{\mathit{\mu }}\left(\mathrm{2}\dot{\mathit{ϵ}}+\mathrm{2}\mathrm{tr}\left(\dot{\mathit{ϵ}}\right)\mathbf{I}\right)\right]+{\mathit{\tau }}^{\mathrm{b}}=\mathit{\alpha }\cdot {\mathit{\rho }}_{i}gh\mathrm{\nabla }s\end{array}$$

$$\begin{array}{}\text{(11)}& \mathit{\alpha }={\mathit{\alpha }}_{\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}\cdot T\end{array}$$

The coefficients α₁ and α₂ are tunable with limits based on observations, as discussed later in Sect. 2.4. This approach is similar to Nick et al. (2013), which also alters the stress balance at the calving front. Our buttressing parameterization gives a longitudinal resistance that is 18 % of the driving force at the calving front (Eq. 10) for the instance of 2004.

We use a crevasse-based calving parameterization (Benn et al., 2007; Nick et al., 2013) that calves ice where the crevasse penetration depth (D_s) is greater than upper surface elevation. D_s is defined as

$$\begin{array}{}\text{(12)}& D_{\mathrm{s}}={\displaystyle \frac{S}{g\cdot {\mathit{\rho }}_i}}+{\displaystyle \frac{{\mathit{\rho }}_{\mathrm{w}}}{{\mathit{\rho }}_{\mathrm{i}}}}\cdot R\cdot \mathit{\beta },\end{array}$$

where S is the magnitude of extensional stress, R is surface water runoff and β is a tuning scalar. We estimate runoff from the 25 km resolution regional climate model, MAR, (Alexander et al., 2016), driven by the ERA-Interim reanalysis (Dee et al., 2011).

We characterize submarine melting as a linear function of ocean forcing

$$\begin{array}{}\text{(13)}& M_{\mathrm{b}}=\mathit{\gamma }{T}_{\mathrm{f}},\end{array}$$

where T_f is the far-field ocean forcing temperature, taken in Disko Bay (CTD in Fig. 1), relative to pressure melting temperature under the ice shelf. Thus, T and T_f are related simply by ice depth and salinity. We derive γ (Sect. 2.3) from the 1985 observed submarine melt rate of 1±0.2 m d⁻¹ beneath the ice shelf of Jakobshavn Isbræ, when Disko Bay ocean temperatures were 4.2 ^∘C warmer than the pressure melting point at the bottom of the floating ice shelf (Motyka et al., 2011). We test the sensitivity of the modeled glacier to uncertainty in submarine melt rate in Sect. 2.4.

We force Jakobshavn Isbræ in the 21st century using SMB and runoff from the 11 km resolution RACMO model (Van Angelen et al., 2013) driven by the RCP4.5 scenario (Moss et al., 2010). The runoff values are averaged over the nine grid points nearest to the terminus of Jakobshavn (69.1^∘ N, 50.0^∘ W). In general we use RACMO products to drive the model; however, they only span the period of 2006–2099. For the period 2004–2014, SMB and surface water runoff forcing come from MAR model outputs. We use the common overlap period (2006–2014) to correct the bias between two models outputs. The RACMO simulation was forced by the HadGEM2-ES Earth system model (Collins et al., 2011), as this climate model was found to be the most realistic for present-day simulations of the Greenland ice sheet (Van Angelen et al., 2013). Ocean forcing in Eqs. (10) and (13) should relate to temperatures off the continental shelf close to the fjord mouth. Cowton et al. (2018) achieved success in simulating the terminus position and yearly variability of 10 glaciers along the eastern coast of Greenland using mean 200–400 m depth temperatures from reanalysis data. For consistency with the RACMO results, we use deep ocean temperatures at ∼300 m depth from the 0.83^∘ × 1^∘ resolution HadGEM2-ES driven by the RCP 4.5 climate scenario from 2005 to 2100 at the three closest grid points to Disko Bay. We also compare this with results from seven other climate model simulations of RCP4.5: HadGEM2-ES (Collin et al., 2011), BNU-ESM (Ji et al., 2014), MIROC-ESM (Watanabe et al., 2011), IPSL-CM5A-LR (Dufresne et al., 2013), CSIRO-Mk3L-1-2 (Phipps et al., 2011), NorESM1-M (Bentsen et al., 2013) and MPI-ESM-LR (Giorgetta et al., 2013).

2.3 Initialization procedure

As we are interested in high-resolution simulations and validating our model parameterizations with observations over the last decade, we take care to initialize the model as accurately as possible. Detailed bedrock topography and ice thickness data in the year 2009 come from Gogineni (2012); we chose this product because it has 500 m resolution and so matches the highest resolution of our mesh. Jakobsson et al. (2012) provide ocean bathymetry data (Fig. 1). In 2004 the floating ice shelf disintegrated, making it a convenient starting point for simulations since we might expect the system to respond differently to forcing when there was a floating ice shelf compared with the situation of ocean forcing along a near-vertical ice cliff. This is consistent with the observed good correlation between ocean temperature and flow speed after, but not before, 2004. The aim of this initialization is to provide a state rather similar to 2004, i.e., barely retreating on interannual scales (Joughin et al., 2010), and small changes of annual mean velocity in the following 3 years. This was performed as follows.

1. We solved the inverse problem for basal conditions (Eq. 7) and stiffening factor using 2010 velocities (Joughin et al., 2010) and 2009 geometry (Gogineni, 2012), following Cornford et al. (2015). Our friction coefficient and stiffening factor fields are shown in Fig. 3. Figure S1 in the Supplement shows the discrepancy between observed velocity field (Joughin et al., 2010) and the velocity derived from the inversion.

2. Starting from the inversion of step 1, we let the model glacier evolve freely without calving and with zero SMB and sub-shelf melting (γ=0.0238) forced by repeating the observed 2004 ocean temperature for 11 years until its surface elevation profile reached a state shown in Fig. S2.

3. We carried out several 10-year simulations, each with different β values. These simulations were forced by repeatedly applying the 2004 seasonal climate forcing so that the glacier approaches a steady state. From these, we selected the β that provided a calving front position closest to that observed in 2004. The best β here is 0.034, and this is our best guess for the 2004 state. The annual minimum extent of Jakobshavn retreats ∼2 km from 2004 to 2005 following the loss of ice shelf buttressing but then stabilizes until 2007 (Joughin et al., 2010). Annual maximum extents are stable over the 2004–2007 period. Front velocity increases slowly from 2004 to 2007 (∼5.9 % a⁻¹ Joughin et al., 2010), and the model-simulated velocities increase by about 3 % a⁻¹. This period of relative stability also makes 2004 a good time from which to start transient simulations.

Basal friction coefficient values downstream of the 2010 grounding line were set equal to that in the nearest 2010 grounded location. This was necessary because steps 2 and 3 involved grounding line advance beyond the region for which basal friction coefficients had been inferred. The geometry after this spin up procedure, and the friction coefficient and stiffening factor distribution from the inversion in step 1 were used as the initial condition for model calibration.

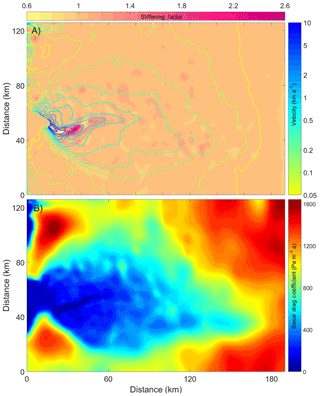
Figure 3 (a) Stiffening factor Φ (Eq. 3) and (b) basal traction coefficient C (Eq. 7) over the computational domain from solving the inverse problem. Contour lines in (a) show the modeled velocity (logarithmic scale).

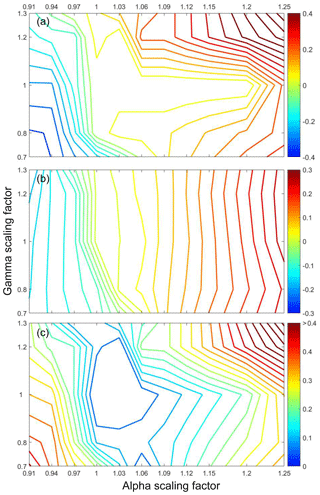
Figure 4 Relative mismatches defined as (model observed)/observed for (a) total calving front retreat, (b) average of annual mean front velocity during 2004–2013, and (c) the vector sum of mismatches in (a) and (b) $\sqrt{(A^{\mathrm{2}}+B^{\mathrm{2}})}$ in our 2-D parameter space. The x and y axes are multipliers of α and γ.

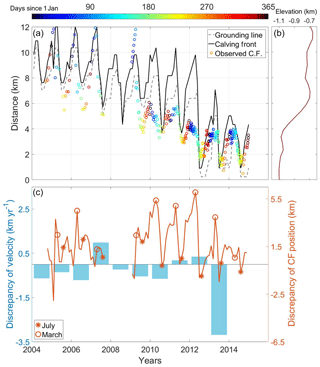
Figure 5 (a) Modeled retreat of the calving front (solid black line), grounding line (dashed gray line) and observed calving front positions (color-coded circles and scale bar) from Joughin et al. (2014). (b) Bedrock elevations. (c) Residuals (modeled minus observed) of annual mean front velocity (blue bars, left axis) and of calving front position (red lines, right axis) with typical timings of annual maximum (March) and minimum (July) extent marked. The modeled front velocities and calving positions explain about 49 % and 76 % of the variance in corresponding observations.

2.4 Model calibration

The parameters in the model, α,  β and γ, representing mélange buttressing, crevasse depth sensitivity to surface runoff and shelf melt sensitivity to ocean temperatures, need to be estimated. The measured relationship between ocean temperatures and sub-shelf melt rate (Motyka et al., 2011) gives the value of γ as 0.238. We manually tune parameters in Eqs. (11) and (12): α over the range 0.7–1.2 for α₁ and 0.09–0.12 for α₂ and using β (0.04–0.075) to best reproduce Jakobshavn Isbræ's calving front position and surface velocity evolution for the 10-year period 2004–2013. Reproducing the total retreat distance and the temporary stable state after 2012 were secondary desirable features to match. The best set of parameters are α₁=0.82, α₂=0.111 and β=0.0638. Since these values come from a manual search we do not claim them to be the best in all parameter spaces. We assess model sensitivity to the parameter values next.

We explore the glacier's sensitivity to two types of boundary perturbations. They are ice mélange buttressing effect (defined by α) and submarine melting (defined by γ). We scaled submarine melt rates by multiplying it by values from 0.8 to 1.2, based on the range of the observation uncertainty in melt of ∼20 % (Motyka et al., 2011). Also we varied α by multiplying by factors from 0.91 to 1.25 to represent different buttressing strengths (Eq. 10). These multiplication factors were varied systematically with typical intervals of 0.1 and 0.03, respectively, for the γ and α factors. We calculated the following relative mismatches, defined as (model observations)/observations for each simulation (Fig. 4), as follows:

1. total calving front retreat from 2004 to 2013 measured by the difference between 2004 and 2013's annual maximum extent,

2. annual mean front velocities,

3. vector sum of (1) and (2).

We used β (Eq. 12) from our optimal set of parameters. Our optimal value for α is such that a 20 % rise of its value does not affect modeled retreat when β and γ are kept to be their optimal values (Fig. 4a).

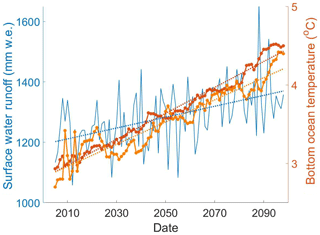
Figure 6 Climate forcing for future projection under the RCP4.5 scenario taken as 300 m depth ocean temperatures from HadGEM2-ES (orange) compared with the ensemble mean (red) of seven Earth system models (HadGEM2-ES, BNU-ESM, MIROC-ESM, IPSL-CM5A-LR, CSIRO-Mk3L-1-2, NorESM1-M and MPI-ESM-LR) (right axis), with their linear trends. Annual maximum monthly surface water runoff near Jakobshavn Isbræ's terminus from RACMO (forced by outputs from HadGEM2-ES) is shown in blue.

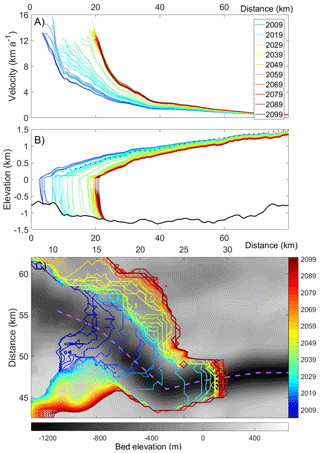
Figure 7 Modeled profiles of (a) January velocity and (b) January surface elevation along the center flow line (dashed purple line in c) of Jakobshavn Isbræ from 2004 to 2099 for the RCP4.5 scenario. Bedrock elevation is shown in black. The dotted black line is the surface elevation profile extracted from radar data measured around 2010 (Gogineni et al., 2012). Profiles are shown at intervals of 1 year. Profiles are color coded in the legend and range from blue to green and red. (c) Modeled July front positions (color bar) over its bedrock (grayscale bar) at intervals of 2 years.

The two biggest mismatches occur with the 2007 and especially 2013 velocities (Fig. 5). Of all the years since 2004, 2013 has the lowest simulated surface water runoff (Fig. 2). The Benn calving model we use is sensitive to runoff, with reduced runoff leading to lower crevasse penetration depth and reduced terminus fracturing, thus increasing its buttressing force. Furthermore, 2013 had relatively cool ocean temperatures, which were lower than the average of 2004–2013. The cool ocean temperatures also increased buttressing, leading to low simulated annual mean velocities. Jakobshavn Isbræ did not in fact slow down very much in 2013 because there were calving events (Cassotto et al., 2015) that are unrepresented in our model. The relevant mechanisms are discussed later. In 2007 high runoff caused more simulated calving and retreat than in reality. These retreat phases reduced the buttressing and lateral drag due to shear margin weakening, all of which lead to excessive speedup near the terminus.

Modeled calving front retreat is ∼7 km in total from 2004–2014 (Fig. 5), which is consistent with observations (Joughin et al., 2014). In 2009 a dramatic retreat brought the grounding line to the bottom of the bedrock slope, and since then it has gradually retreated with smaller seasonal fluctuations. The runoff forcing we applied triggered major retreats in the summers of 2007 and 2012, due to large summer peak runoff (Fig. 2), demonstrating the sensitivity of our calving parameterization to runoff forcing. Modeled timings of maximum extent and minimum extent each year are in good agreement with observations, also demonstrating that summer, in particular, May to July, runoff determines much of the behavior of Jakobshavn Isbræ.

The modeled range of seasonal fluctuation in front position is ∼5 km, which is similar to observations in the period before 2008. From January 2009 to December 2011, there was an abrupt decrease in seasonal front fluctuation, with many winter calving events occurring, in contrast with previous years (Cassotto et al., 2015). These winter calving events may explain the small observed seasonal fluctuations because they limit the winter advance. Our model is unable to stimulate these winter calving events because there is no winter runoff, and as extension stresses are never enough to cause winter calving, calving is then zero. The largest discrepancy of front position occurs during these winter calving periods (Fig. 5). Observations also showed that from 2013 to 2017 Jakobshavn Isbræ barely retreated (Joughin et al., 2010). The decline of runoff (Fig. 2) in 2014 suggests the reason. But since no RACMO runoff simulations are yet available for 2015 and later, our parameterizations cannot be tested against this lack of retreat.

3 Future evolution

Under the RCP4.5 scenario (Fig. 6) surface runoff slowly rises over the 21st century, with RACMO simulating slightly greater runoff during the second half than for the first 50 years. Runoff increases by 14 % over the century. Ocean temperature at 300 m depth in the grid cell closest to Jakobshavn increases by 52 % and, as may be expected, has less variability than runoff.

Under this forcing, Jakobshavn Isbræ continues its retreat (Fig. 7) for 18 years after 2013, producing a total grounding line retreat of ∼18 km upstream. As calving produces a steepening surface profile, terminus velocities increase, to reach a 21st century peak of ∼19 km a⁻¹ in 2031 summer. Eventually the front height (relative to sea level) becomes larger than the crevasse penetration depth in the calving parameterization. This leads to a stable period with little interannual retreat, which lasts until the end of this century. During this period, nearly all of the seasonal retreats are offset by the following winter readvances. Mass transport continually flattens and thins the ice geometry, leading to reduced flow speeds that eventually become half those of 2031, the 21st century peak.

The surprisingly high runoff anomaly in 2088 (Fig. 6) does not affect the stable state indicating runoff fluctuation alone cannot break this retreat pattern immediately. Once the interannual retreats cease in 2031, the dynamic thinning rate is greatly reduced because calving front height stops increasing.

Table 1 Estimates of glacier mass loss and grounding line retreat from different sources.

Table 1 shows estimates of glacier mass loss and retreat. Under RCP4.5, total cumulative mass change of Jakobshavn Isbræ is 2068 Gt by 2100, using the best set of α, β and γ with ocean temperature inputs from ensemble mean of seven Earth system models (Fig. 6). To estimate an upper bound for mass loss over this century, we scale the α parameter by 1.2, giving 2723 Gt for the same forcing (Fig. 8a). Using the HadGEM2-ES forcing, which is the same model used to force RACMO with α and γ set to their best estimates (Fig. 4) gives 2044 Gt. We suggest that this may be the lower reasonable bound of mass loss since the HadGEM-ES ocean temperatures rise notably slower than the ensemble mean (Fig. 6). Note that all three simulations of front position (Figs. 7c, 8) show a relatively stable position around 18 km upstream from its 2013 location. Examination of the change in velocities during the simulation (Fig. 9) suggests that the explanation for this stability is strong flow convergence near the future glacier front that largely offsets dynamic thinning. Notice that the south side of the fast flow area in 20th century was quite close to ice-free land, while in later half of this century convergent flow in the south is fed by a substantial area of ice stream.

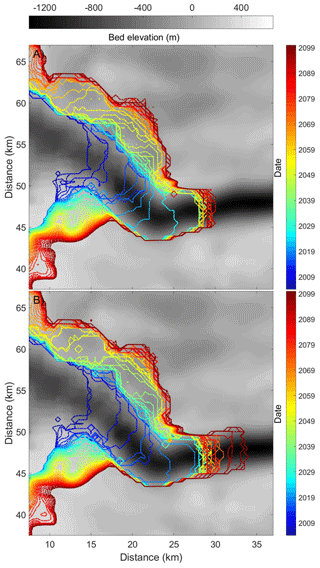
Figure 8 Upper and lower estimates of July front positions within this century with colors indicating the date (color bar) for (a) lower bound with scalings of (1,0.8) and the HadGEM-ES forcing (b) upper bound of mass loss projection with (α, γ) parameter scalings of (1.2,1) and the seven-model-ensemble climate forcing.

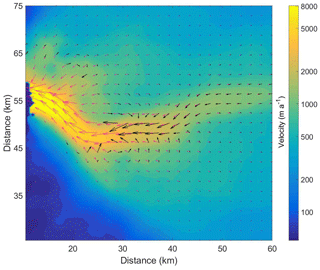
Figure 9 Simulated velocity vectors in 2004 (pink vectors) with their magnitudes (right color bar) and velocity difference between 2004 and 2099 (2099's minus 2004's, black vectors), for clarity vector lengths are clipped at 5 km a⁻¹.

Exploring the (α, γ) scaling parameter space we notice that values of (1.0, 0.8) produce a mass loss over this century of 2083 Gt with the HadGEM-ES ocean forcing, almost the same value as for the best set of parameters. This implies that less submarine melting (determined by γ) leads to larger ice loss by dynamic processes. The reason is that lesser submarine melt allows a larger ice thickness at the grounding line with stronger dynamic thinning in the advancing season. Notice that in our stress balance equation (Eq. 3) thickness contributes to driving force term, thus ice flux across the grounding line is highly nonlinear in ice thickness. This highly nonlinear relationship is also shown in our sensitivity tests (Fig. 4). Over the mismatch field measured by front velocity (Fig. 4b), the velocity is partly dominated by low values of γ scaling around the scaling line for α=1.06, while α is almost the only control on velocity over the region where scaled α<1.09. Within our sample space, the nonlinear and non-monotonic relationship between submarine melting and retreats is clear (Fig. 4a). Around the point of scalings (α=1.12, γ=1.0), total retreat will increase no matter if γ is decreasing or increasing within the scaling range 0.8 < γ < 1.2. The area where scaled α > 1.0 in sample space is the very likely future condition for Jakobshavn Isbræ because increasing terminal ice cliff height caused by retreating into deep water will act as an amplifier to frontal driving force.

4 Discussion

4.1 Parameterization of buttressing effect

The sudden 1.1^∘ rise in temperature of water entering Ilulissat Fjord in 1997 (Holland et al., 2008) initiated rapid melting and disintegration of the ice shelf in 2003. This disintegration coincided with a near doubling of ice velocities. Modeling (Vieli and Nick, 2011) suggested that this was due to the reduction in buttressing from the ice mélange. We can realistically reproduce the velocity variation at Jakobshavn Isbræ on seasonal and interannual scales using our parameterization of the buttressing effect from the ice mélange in the fjord.

Gladish et al. (2015) analyzed glacial flow speeds from 1998 to 2014, finding no correlation with Ilulissat Fjord temperatures. This is because at the beginning of 2004, Jakobshavn's evolution entered a new phase with the disintegration of the ice shelf. We find good correlations between Disko Bay temperatures and ice velocities from 2004 to 2014. The improvement in correlation with temperatures may be explained by a faster response between the grounded glacier and the fjord water temperatures after loss of the floating ice shelf.

Buttressing would affect the calving process by altering the longitudinal resistive stress in the glacier. Temperatures in Ilulissat Fjord will be warmer during the 21st century under essentially all climate scenarios, even those with modest emissions, due to the thermal inertia of the oceans. Thus, a new floating ice shelf is unlikely to form. Prior to 2004, there were large changes in Jakobshavn: loss of the ∼15 km long ice shelf and the sudden rise in fjord temperatures in 1998. There are fewer mechanisms to effect such dramatic changes in the future now that almost the entirety of the glacier is grounded. We therefore propose that our representation of the mélange buttressing mechanism, tuned for 2004–2013, is likely to maintain its validity during the 21st century.

4.2 Horizontal shearing and viscosity

Van Der Veen et al. (2011) estimated a maximum horizontal shear stress of ∼800 kPa across the shear margin of Jakobshavn Isbræ where the horizontal velocity shear reaches the peak, while the bed stress is only 10–40 kPa in fast-flowing regions (Shapero et al., 2016). Given that the width of the Jakobshavn Isbræ fast flow region is typically under 5 km and its thickness is typically between 1 and 2 km, these numbers indicate that the shear margins provide at least an order of magnitude greater total resistance than the bed. Thus, the shear margin, rather than the bed of Jakobshavn Isbræ provides most of the resistance balancing the driving force. The main trunk of Jakobshavn Isbræ exhibits considerable seasonal velocity changes, while the slow-moving ice outside the shear margin has little or no seasonal cycle. This flow structure implies speed gradients perpendicular to the flow direction with large seasonal variation. These velocity shears would in turn generate large seasonal variations in effective ice viscosity (Eq. 6). This mechanism is due to the nonlinear rheology of the ice in the fast flow region: increases in the speed of fast-flowing ice cause increases in horizontal shear stress across the margins, reduced viscosity and further increased horizontal velocity shear, allowing further increase to speeds in the fast flow region. Observations show that, as the terminus retreated into deeper water, seasonal fluctuations in terminus velocity increased (Joughin et al., 2008). By 2012, the summertime peak terminus velocity was ∼17 km a⁻¹, more than twice the wintertime minimum velocity (Joughin et al., 2014). This amplified seasonal velocity cycle was likely enhanced by the shear margin weakening mechanism.

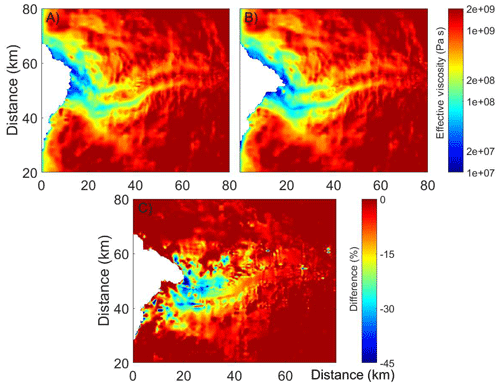
Figure 10 Modeled annual mean of vertically averaged effective viscosity Φ⋅μ (Eq. 5) in 2004 (a) and 2013 (b) and the percentage decreases from 2004 to 2013 (c).

Our modeled shear margin weakening on decadal scales is consistent with other estimates from a thermomechanical ice flow model of Jakobshavn Isbræ forced by calving front positions (Bondzio et al., 2017). Their modeled viscosity drops between 2003 to 2015 reach ∼40 %, which is close to our maximum viscosity decrease of ∼45 % between 2004 to 2013 (Fig. 10). The extreme calving season we simulated in summer 2012 was accompanied by ∼12 km a⁻¹ variations in speed at the calving front, which were facilitated by the accompanying shear-margin-induced ice viscosity reductions of 60 % at the time of maximum terminus advance. Simpler models of Jakobshavn Isbræ, using a flow band model (Nick et al., 2013) or simple calving parameterizations with no seasonal cycle (Muresan et al., 2016) cannot produce these seasonal variations in shearing. However, our model accommodates both the seasonal forcing from calving and the three-dimensional seasonal velocity shear impacts on effective viscosity. Without this physical process, speedups during intense calving events would be underestimated, and this would lead to underestimated mass transportation during the retreat. Bondzio et al. (2017) used a thermomechanical ice flow model to evolve the ice viscosity, which depends on a damage parameter that softens the ice in the shear margins. But their damage parameter also stays constant in time. Thus, both the models of Bondzio et al. (2017) and ours only consider the contribution from strain rate weakening in time to evolving viscosity. Thermodynamics could play some role in changing viscosity, presumably if the ice temperatures increased over time, but our temperatures are fixed at −10 ^∘C.

Several processes absent from our model could affect ice viscosity. Crevasses saturated by surface meltwater within the shear margins of Jakobshavn are visible on satellite images (Lampkin et al., 2013). This meltwater can transfer heat throughout the ice column through discharge within crevasses and moulins thus softening the ice (Phillips et al., 2010). Incorporating a continuum damage model in BISICLES would further exaggerate the shear margin weakening, as it raises the nonlinear dependence of strain rates on stress fields (Sun et al., 2017).

4.3 Comparison with previous estimates

The cumulative mass change of Jakobshavn Isbræ estimated from airborne and satellite laser altimetry for 1997–2014 was tabulated Muresan et al. (2016). The mass loss over the 10-year period 2004–2013 modeled by Muresan et al. (2016) is closer to observations than ours (Table 1). This is partly due to different tuning targets: matching observed mass change was a stated target in their study, whereas our study targets ice front position and velocity. Their close match to observed mass loss may be partly due to canceling errors: (1) their modeled calving front barely moves after 2006, which leads to underestimation of mass change, and (2) the modeled fast flow widths are larger than observations, which amplifies the mass flux across the calving front. These two biases will not always offset each other perfectly in the future.

Muresan et al. (2016) failed to simulate the retreat of Jakobshavn Isbræ after 2010. This may be due to the thickness threshold employed in their calving parameterization. Once Jakobshavn Isbræ terminus has retreated into the deeper part of the bedrock trough, the terminus height might never drop below their calving threshold of 375 m. In this case their calving rate will be solely due to the eigenparameterization of strain rates. Moreover, absence of seasonality in their calving front leads to underestimated dynamic thinning, which is a key prerequisite for further calving. In contrast, our crevasse depth calving model depends on stresses and surface water runoff with strong seasonal variation. As the terminus retreats and the surface slope steepens, the enhanced surface stretching enhances the opening of crevasses in both calving parameterizations.

Nick et al. (2013) used a flow band model to estimate a mass loss of 2280 Gt for Jakobshavn Isbræ by 2100 under the A1B climate scenario (Table 1). In our model we use RCP4.5 climate forcing, which has lower temperature rises than A1B, especially after 2050. Nick et al. (2013) prescribed a flow band that has a near uniform width of 5 km near the terminus. Later modeling work using a similar model suggested that stability of the glacier is fundamentally controlled by geometry, and in reality the width varies along the ice stream (Steiger et al., 2018). Nick et al. (2013) chose sets of parameters that produced small interannual retreats of Jakobshavn from 2000–2010, which may limit mass loss and retreat. The absence of the shear margin weakening feedback in their model also likely causes underestimation of mass loss. This could account for the comparable projected mass loss to our results and less terminus retreat (Table 1), even though their climate forcing scenario was warmer.

Another SSA model (Bondzio et al., 2018) projects larger retreats than ours and uses a calving parameterization that predicts the location of calving depending on tensile stress distribution, regardless of ice thickness. In contrast our calving parameterization uses mélange buttressing effects and calving driven by seasonal filling of crevasses with surface water runoff, while Bondzio et al. (2018) drive their calving seasonality by a seasonal varying stress threshold. However, in the real world Jakobshavn, calving does not have to be of the full-thickness type and can involve vertical motions (Xie et al., 2016) or the MICI (Marine Ice Cliff Instability) mechanism (Pollard et al., 2015), all of which are difficult to resolve by an SSA model. These calving types are probably becoming more and more important as it retreats into deep water. Therefore, we cannot confidently claim our crevasse-depth-based calving parameterization is better than the calving criterion that only depends on tensile stress (Bondzio et al., 2018) for the future. In the next section we discuss how the model might be improved.

4.4 Model improvements

We overestimate mass loss relative to observations over Jakobshavn Isbræ drainage basin for 2004–2013 (Table 1). One reason for the discrepancy may be errors in initial ice thickness and real geometry in 2004. Excessive dynamic thinning was simulated over the lowest ∼20 km of the main trunk due to overestimated summer speed. For example, modeled front velocity soared to a peak of ∼20 km a⁻¹ in summer 2012, while the observed maximum speed is only 18 km a⁻¹ (Joughin et al., 2014). In this summer, we simulated a series of full-thickness calving events that eventually left an unprecedentedly tall ice cliff. In reality, calving events do not always occur to full thickness, thus the glacier tends to form a shorter ice cliff that caters for lower velocity and less dynamic thinning.

Since the grounding line of Jakobshavn retreated to the bottom of a reverse bed slope in 2009, the height of the calving front has generally increased, causing larger mass flux downstream across the calving front. Instead of enhancing the seasonal fluctuation of calving front position, substantial winter calving events have occurred instead. Given the fact that these calving events have reduced the typical winter advance from ∼6 to ∼3 km since 2010, winter calving is now likely as important as summer runoff-driven calving. During this period of low-magnitude seasonal fluctuations, a series of retreats gradually moved the calving front position on interannual scale. In contrast, the interannual retreats before 2009 were mostly driven by single calving seasons, e.g., May to July 2009. Our model using the Benn calving model is better able to simulate this earlier retreat pattern, which is largely determined by each year's peak surface water runoff.

The grounding line of Jakobshavn Isbræ is unlikely to return to shallow water in the remainder of the 21st century because bedrock elevations $<-\mathrm{1000}$ m beneath the main trunk further extend ∼60 km inland. Accordingly, the latest retreat pattern, including winter calving, is likely closer to the pattern of future evolution of Jakobshavn Isbræ. A short floating part due to winter calving is always accompanied by weaker lateral drag and steeper surface slope near the grounding line, all of which are conducive for faster ice flow. So, winter calving would enhance the downstream mass transportation, a missing process in our model.

The process of winter calving must take place without any surface water. That calving must be generated by processes affecting ice front stability and this is likely due to changes at the base rather than the surface. Evidence of calving by opening of basal crevasses and splitting comes from terrestrial radar showing the terminus lifting several days prior to a large calving (Xie et al., 2016; James et al., 2014). These observations suggest that the glacier is not in hydrostatic equilibrium during calving. Our simulation specifies the glacier is in hydrostatic equilibrium on timescales of the simulation. Our model cannot simulate the process of uplifting. Instead we assume the upper and lower surface would instantly lift to the state of floating (Eq. 1). However, there is some evidence that Jakobshavn must behave super-buoyantly in winter. We observe that the simulated grounding line of Jakobshavn retreats even after cessation of calving front retreat (Fig. 3). These retreats can be explained by rapid dynamic thinning near the grounding line leading to its buoyancy exceeding gravity and, consequently, floating. Winter calving can occur in later winter (Cassotto et al., 2015) when calving front height is at its annual minimum and presumably at its least vulnerable to structural failure. Hence, MICI cannot explain this type of calving (Pollard et al., 2015). The existence of winter calving has greatly reduced the range of seasonal fluctuations in front position, which inhibited the growing of a temporary ice shelf that would buttress the grounded ice. Thus, lack of winter calving would cause underestimation of dynamic thinning as the glacier grows in winter.

A combination of discrete element model and continuum ice-dynamic model (solving the three-dimensional full Stokes equation) is able to reliably replicate observed calving styles in the case of a super-buoyant terminus (Benn et al., 2017). The discrete element model allows investigation of calving processes in unprecedented detail by analyzing the stress pattern dominated by glacier geometry and boundary conditions. However, these calving processes are beyond the capability of a calving parameterization based on surface crevasse depth, assuming depth-independent flow. Better understanding of this buoyancy-driven calving and further model development to represent more details such as fracture propagation are needed to accurately simulate glacier's future evolution.

Ice thickness and basal topography with a resolution of 150 m became available for main outlet glaciers of Greenland (Morlighem et al., 2017) recently (Fig. S3). This eases the finer mesh resolution to be used for modeling, which then might reveal more details of ice stream behavior especially perpendicular-to-flow direction, including more precise shear margin weakening and calving near side walls. Our assumption of simple Weertman basal drag (Eq. 7) may be improved by implementing a physics-based basal sliding law (Schoof and Hindmarsh, 2010; Gagliardini et al., 2014; Tsai et al., 2015), although basal drag accounts for only about 2% of present-day buttressing (Shapero et al., 2016). An improved sliding relation would likely produce more speedup and retreat in model results as dynamic thinning can reduce the effective pressure, leading to lower basal shear stress.

5 Conclusions

We use a three-dimensional dynamic ice sheet model with a physics-based calving parameterization to model the evolution of Jakobshavn Isbræ. After tuning the parameters, our model can accurately reproduce Jakobshavn Isbræ's retreats and velocity changes from 2004 to 2013 on both seasonal and interannual scales. We project Jakobshavn Isbræ's future dynamic changes with climate forcing data from RACMO (2014–2099) and an ensemble mean of seven Earth system models for the RCP4.5 scenario.

We successfully model two-dimensional ice velocity and viscosity structures and their seasonal variations for Jakobshavn Isbræ, which are missing from several previous modeling studies. Moreover, capturing these two-dimensional structures allows us to handle the influence of horizontal velocity shear on effective ice viscosity, which impacts on speedup processes of Jakobshavn Isbræ.

We predict that Jakobshavn Isbræ's grounding line will retreat along the deep parts of a basal trough where bedrock elevation is significantly lower than at the present grounding line until about 2070. Retreat slows as the front reaches the deepest parts of the trough, but by the end of the century acceleration is possible as the front passes that position. Using the current generation of calving parameterizations, which are essentially thickness threshold models, is challenging because of the increasing height of the calving front as Jakobshavn Isbræ retreats, meaning that crevasse penetration depths become too small to initiate calving. Our model successfully reproduced Jakobshavn Isbræ's retreat down a reverse bed slope with an elevation drop of ∼400 m and the subsequent temporarily stable calving front position in 2013 and 2014.

Our results suggest that rapid dynamic thinning and calving caused by deep crevasse penetration are responsible for most of its recent mass loss and will be decisive processes in future mass loss. Further exploration of the physics of calving and basal sliding of Greenland outlet glaciers are required to improve future projections.