Detecting dynamics of cave floor ice with selective cloud-to-cloud approach

Ice caves can be considered an indicator of the long-term changes in the landscape. Ice volume is dynamic in the caves throughout the year, but the inter-seasonal comparison of ice dynamics might indicate change in the hydrological–climatic regime of the landscape. However, evaluating cave ice volume changes is a challenging task that requires continuous monitoring based on detailed mapping. Today, laser scanning technology is used for cryomorphology mapping to record the status of the ice with ultra-high resolution. Point clouds from individual scanning campaigns need to be localised in a unified coordinate system as a time series to evaluate the dynamics of cave ice. Here we present a selective cloud-to-cloud approach that addresses the issue of registration of single-scan missions into the unified coordinate system. We present the results of monitoring ice dynamics in the Silická ľadnica cave situated in Slovak Karst, which started in summer of 2016. The results show that the change of ice volume during the year is continuous and we can observe repeated processes of degradation and ice formation in the cave. The presented analysis of the inter-seasonal dynamics of the ice volume demonstrates that there has been a significant decrement of ice in the monitored period. However, further long-term observations are necessary to clarify the mechanisms behind this change.

1 Introduction

Ice caves are considered the most dynamic types of caves in terms of morphology and speleoclimate changes, which results from numerous processes acting inside the cave but also in its immediate exterior surroundings (Perşoiu and Lauritzen, 2018). Cave ice originates and accumulates mainly as a result of water freezing (congelation) and to a lesser extent as a result of snow densification and diagenesis (Perşoiu, 2018). Mavlyudov (2018) articulates that cave glaciation at above-freezing temperatures in the bedrock is potentially possible only at certain winter temperatures where the external air cools the cave walls to temperatures below the point of the water freezing. In addition, the quantity of ice formed depends on the quantity of water inflow. The morphology of ice is more dynamic than carbonate speleothems due to higher plasticity and sensitivity to cave microclimate. Ice in the caves acts as an important archive of past atmospheric and environmental conditions in places where no icebergs or glaciers exist anymore or ever existed. The proportion of different radioactive markers in the ice can be used for calculating the absolute age of the ice formation (Kern, 2018; Kern et al., 2018). The proportion of gases trapped inside the ice indicates the composition of the atmosphere at the time of freezing (Bender et al., 1997). Biological remains such as pollen, fragments of leaves, and microbial life preserved in the ice provide proxies for reconstructing the palaeoenvironment. Furthermore, ice caves react differently to climate change, perhaps not as rapidly as the mountain glaciers. Therefore, monitoring the change of ice morphology and ice volume in such caves can improve our understating of past climate and the concurrent climate changes.

Snow and ice formations in caves are classified by many authors based on different criteria (place of formation, state of water, process of formation, salinity, composition) at the time when the formation was initiated and by the age of the formations (Mavlyudov, 2018). Several types of ice formations originate in caves, such as icings, ice of lakes, ice in rocks, snowfields, glaciers, ice breccia, and hoarfrost. These types of cave ice can be classified based on their age as (i) ephemeral (short-term), (ii) seasonal, and (iii) perennial (long-term), i.e. existing more than 1 year (Mavlyudov, 2018). In this paper, we evaluate the change of large perennial ice formations, revealing more about the cave environment than the short-term living formations, which tend to degrade after smaller fluctuations in cave temperature. In addition to the change of ice formations over time, ice movement can be observed in places where it is possible to detect the most active areas of ice flow, melting, subsiding, or collapsing. Therefore, we focused on detecting possible movement of ice formations by monitoring objects trapped in the cave ice.

The dynamics of the cave ice formations were studied by combining various sources of data and methods. Assessment of photographic material has been the most widely used method for monitoring the extent of the ice and its change (Fuhrmann, 2007). The other methods comprise markers distributed and attached on the ice floor and/or cave walls (Pflitsch et al., 2016), geodetic surveying (Gašinec et al., 2014), absolute dating (Luetscher et al., 2007), and drilling (May et al., 2011). Comprehensive monitoring programmes of detecting dynamics of the cave ice accumulations are rare, but some examples can be listed, e.g. Perşoiu and Pazdur (2011), Kern and Perşoiu (2013), and Kern and Thomas (2014).

Quantifying the changes of ice formations over a certain period in high spatial resolution can improve understanding of the cave ice formation including factors affecting the accumulation or loss of ice. The challenge is in defining the method by which cryomorphological topography could be recorded quickly, repeatedly, and reliably. In the last decade, terrestrial laser scanning (TLS) has provided the opportunity to map the challenging environment of the caves in an unprecedented level of detail (Gallay et al., 2015). TLS is an active remote sensing technique allowing for contactless sampling of the 3-D point positions on the surface of the scene surrounding the scanner with a millimetre accuracy and precision (Vosselman and Maas, 2010). The cave surface can be modelled from the point cloud as a 3-D polygonal mesh or a 2.5-D raster surface, which was demonstrated in Gallay et al. (2016). Applications of TLS in non-glaciated caves are diverse, comprising the field of geomorphology (Cosso et al., 2014; Silvestre et al., 2014; Idrees and Pradhan, 2016; Fabbri et al., 2017; De Waele et al., 2018), studies on light conditions (Hoffmeister et al., 2014), archaeology (Gonzalez-Aguilera et al., 2009; Rüther et al., 2009; Lerma et al., 2010), and projects aiming to increase awareness and tourism (Buchroithner et al., 2011, 2012). However, the use of TLS in ice caves is possible but more challenging than in non-ice or exterior environments due to the slippery surface, harsh climate, and physical properties of ice, which absorbs a considerable portion of the shortwave infrared energy typically used by the laser scanner (Kamintzis et al., 2018). Gómez-Lende and Sánchez-Fernández (2018) demonstrate the potential of TLS technology in the mapping of ice accumulations in the caves. Repeated use of TLS allows us to generate time series of cryomorphological topographies easily. The suitability of using the TLS method for mapping ice is supported by many works related to monitoring of glaciers and ice (Bauer et al., 2003; Avian and Bauer, 2006; Gašinec et al., 2012; Gabbud et al., 2015; Fischer et al., 2016; Xu et al., 2019). A plethora of research papers evaluated snow-depth change with various strategies in mutual spatial registration of time series with reference points (Jörg et al., 2006; Kaasalainen et al., 2008; Prokop, 2008; Deems et al., 2013). Avian et al. (2018) also addressed the issue of generation of time series with TLS in the glacier monitoring. Registration of single-scan missions was based on one scan position and six reference points leading to generation of a time series database. The registration of single-scan missions without reference points remains open in case of cave cryomorphological mapping.

Assessment of changes of the ice accumulations based on TLS point clouds requires the adjustment and relocation of measurements of individual missions (point clouds) into a uniform coordinate system in which the differences between the missions could be compared. For such a purpose, Barnhart and Crosby (2013) used a global coordinate system for TLS point clouds based on the ground control points (GCPs) acquired via Global Navigation Satellite System (GNSS). This approach has a disadvantage in the need of scanning the parts of the cave exterior where GNSS signal is strong enough to obtain the GCPs. Traditionally, a system of stabilised GCPs located in a cave and acquired based on geodetic methods such as tachymetry is used (Gašinec et al., 2014). The placement of the GCPs on the cave floor is not possible in many caves due to the changing ice accumulations. On other hand, placing of the GCPs on the wall of cave at a sufficient height poses a risk of injury to the surveyor or damage to speleothems. In relation to a long-term monitoring programme, the position of the GCPs over a longer time period can become uncertain due to the frost, water, and erosion, which can move the GCPs to another location. For detailed mapping of the cave ice morphology, i.e. with the density over one point per square metre, the use of standard tachymetric methods becomes more tedious and challenging than TLS, which is capable of sampling the ice surface in a contactless fashion.

The presented paper builds on the published works and further develops the methodology of detecting changes in ice accumulations using the TLS. We described an original framework of registration procedure based on selective cloud-to-cloud approach and generating a time series database. The novel aspect in the presented method is in using the non-iced (i.e. rocky, exposed) cave ceiling as the stable component of the scanned scene to register the time series. The scientific contribution is also in the procedure of deriving a complex 3-D cave surface from point clouds as a 3-D mesh surface model. By this means, we identified and quantified cave floor ice changes in ultra-high resolution and we assessed the dynamics of cryomorphology based on vertical profiles, change of the ice area, and volume.

The applied approach was demonstrated in the case study of the Silická ľadnica ice cave situated in the south margin of the Western Carpathians in Slovakia, central Europe. The cave is unique in the world for its permanent ice accumulations formed at the lowest altitude in the moderate climate zone.

2 Area of interest

The Silická ľadnica cave is one of the oldest well-explored ice caves in Slovakia (Bella and Zelinka, 2018). The cave (Fig. 1) is located in eastern Slovakia, in the southwest part where several karst plateaux formed in the Slovak Karst. The cave evolved in the Silická planina plateau near the state border with Hungary.

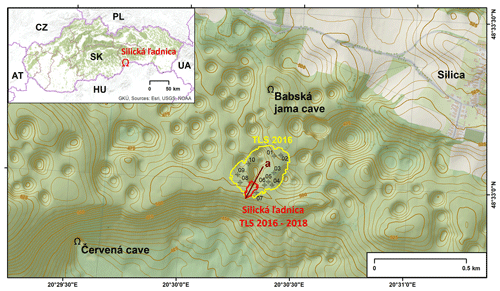
Figure 1 Location of the Silická ľadnica cave. The polygons represent the territory mapped by the TLS method – yellow outline delineates the area of scan mission 1 in 2016, and the red outline represents the area of other scan missions used to build a time series of TLS data. Contours and shaded relief improve the perception of numerous sinkholes on the plateau of Silická planina, which tend to have a regular funnel shape. The dark brown line denoted with “a” marks the vertical profile shown in Fig. 7. Numbered black crosshairs in a circle locate the ground control points used for registration into the common global coordinate system. Base maps: ©2019 GKÚ and ©2019 Esri.

The cave has a descending shape and can be freely accessible only from the north because the other sides form vertical cliffs. The cave entrance is situated in the southern part of a doline and the altitude of the cave cliff edge is 503 m above sea level (Bella and Zelinka, 2018). The cave is located in a warm and moderate humid subregion with cold winters in January (mean temperature $\le -\mathrm{3}$ ^∘C) and mean total annual precipitation of 600–700 mm (Lapin et al., 2002; Faško and Šťastný, 2002). The ice accumulates in an open pit cave formed by the fall of the cave ceiling in light-coloured Wetterstein limestone sediment between Anisian and Ladinian. The limestone bedding is inclined at 30 ^∘ with eastern orientation (Droppa, 1962). Silická ľadnica is classified as a static cave with congelation ice and firn (Luetscher and Jeannin, 2004). Bella (2018) describes the cave as a cave with downward sloping or cascading glacier-like ice block in the entrance or upper descending parts of the cave. Roda et al. (1974) reported the ice area being from 710 to 970 m² and the ice volume being from 213 to 340 m³ based on ice drilling and considering the precipitation and air temperature during the period before their measurement. Archaeological findings by Kunský, Roth, and Bohm, as reported by Droppa (1962) were used to estimate ice to be 2000 years old.

Over the last decades, there was a significant decrease in the ice, which is particularly evident in Fig. 2. Ondrej (2014) measured the ice surface in 2014 with a total station and generated a map of ice distribution in the cave (Fig. 3). The sampling density was sparse (a point per square metre) and surveying on the icefall was dangerous. Therefore, we designed a new approach using terrestrial laser scanning to capture the cave cryomorphology in ultra-high resolution and to assess change of ice surface and volume over time. We have tested the method in the cave since 2016 until present.

Figure 2 Photographic evidence of cave floor ice in the Silická ľadnica cave over the last 80 years. All three photos are captured from approximately the same position (shown in Fig. 3 as a red point A) from inside the cave outward and show different states of cave floor ice. Identical points are marked in yellow. As a scale, objects marked in red can be used – (a) is the figure of a speleologist and (b) is a wooden stick 30 cm high. Based on the photographs we can conclude that there is a gradual loss of ice. The photographs were taken in different years but also at different periods within the year.

The bottom of the glaciated part of the Silická ľadnica cave can be accessed from the eastern side of a debris cone (prolluvial fan) formed by a mixture of fine-grain sediment and limestone scree. Seasonal ice accumulations cover the western part of the cave floor. The cave ceiling is formed by the exposed limestone rock with seasonal occurrence of ice stalactites (Fig. 4). In the lower part of the cave bottom, the ice continues further down by a sharp edge into an icefall with an average slope of 70^∘ (Fig. 3). There is a short, 20 m long passage formed by a palaeo-stream near the lower part of the icefall. The open pit cave closes in the south end of the iced area. No permanent or temporary watercourses flow through the described part of the Silická ľadnica cave. The infiltrated atmospheric precipitation is the only source of water reaching the cave through cracks of the limestone massif, creating cave ice formations whose locations are shown in Fig. 3. The ice accumulations in the Silická ľadnica cave have a different degree of degradation of vertical ice formations or their remains within the year. For optimal ice formation, the conditions of the slow spring warming are most appropriate. Infiltration of snowmelt water or rain freezes in the cave. During the spring season, the floor ice thickness tends to increase from a few centimetres to decimetres. The thickness and area of the ice vary over the year and a large portion of the floor ice is buried under layers of clay, gravel, and stones permanently (Stankovič and Horváth, 2004). The icefall (Fig. 4a) ends at 79 m of the cave depth (424 m above mean sea level) and it is not accessible for ordinary visitors. We hypothesise that the steep slope of the icefall formed by warm air flowing upwards from the lower non-glaciated parts of the cave. Only a few vertical ice formations are visible from a concrete lookout terrace freely accessible to visitors (Fig. 4b).

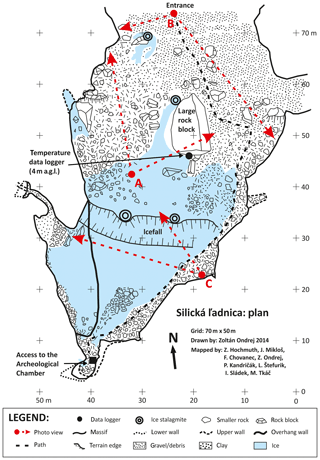
Figure 3 Map of the Silická ľadnica cave floor. The cave is an open pit cave with the entrance being approximately 30 m wide and 20 m tall. It is freely accessible to the public from the north by a concrete staircase. Gravel and debris cover the floor mainly in the upper part of the cave near the entrance. There is a large limestone boulder labelled as a large rock block in the central part. The cave floor ice starts to occur from the boulder to the bottom part of the cave in the south. There are smaller blocks of rock in the ice and around the icefall. The deepest part of the Silická ľadnica cave is in the south. There is an artificial entrance to the Archaeological Chamber, which is closed by a hatch and covered with rock blocks. The red points and arrows mark the field of view in the photographs in Figs. 2 and 4.

The largest stalactite situated in the central part of the cave grows up to several metres during the spring season. There are three large stalactites, two over the icefall and one in the west side of the cave near the cave entrance. The Silická ľadnica cave contains other ice formations such as hoarfrost located mainly in the upper parts and ice coatings on the walls of the cave, which usually appear in the lowermost parts in contact with the non-glaciated parts of the cave.

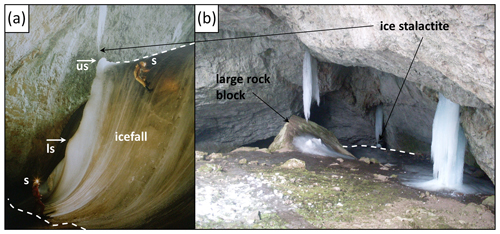
Figure 4 The Silická ľadnica cave contains different types of ice objects. The permanent ice is represented by (a) an icefall (Stankovič and Horváth, 2004) located in the bottom part of the cave. Ice speleothems (b) such as stalactites and stalagmites situated in the upper part of the cave (Ondrej, 2014) are the most dynamic objects with significant seasonal and interannual changes. Approximate size of the icefall can be judged based in the spelunker(s). The icefall is outlined with a white dashed line. The identical location of the ice stalactite in both photographs is marked for better orientation. White arrows indicate stalagmites (us – upper stalagmite; ls – lower stalagmite), which tend to accumulate in dry and wet seasons or years based on the size of the stalactite marked with a black arrow.

One of the negative influences associated with melting of the cave ice is correlated with the discovery of Ján Majko in 1931. He found a way through the collapse and he entered into the further continuation of the cave (Stankovič and Horváth, 2004). Many prehistoric archaeological artefacts and remains of fire places were found in the deposits on the bottom of the gallery, which is why it is called the Archeological Chamber. The brook of Čierny Potok flows into the Archeological Chamber from the south-east and it is hydrologically connected with the Gombasecká jaskyňa cave (Bella and Zelinka, 2018). Gravitational shifting of the debris cone led to the closure of the natural entrance to the Archaeological Chamber, blocking prehistoric people from inhabiting the chamber, but providing suitable conditions for ice formation in the cave further up towards its current open pit entrance. Today, the passage between these parts of the cave is kept closed with a hatch and covered by rock blocks to prevent ventilation of the cold air and degradation of the ice. Sealed closing of the entrance into the chamber facilitates preservation of the static thermodynamic model of the cave (cold trap). Long-term monitoring revealed that the extent of the ice in the Silická ľadnica cave varies over short periods (Stankovič and Horváth, 2004). The seasonal ice formations, which are the main source of water for new layers of floor ice, fill the cave in winter and grow until late spring, when they start degrading and re-icing at the lower, colder parts of the cave as floor ice. Permanent ice in the cave is kept only in the area of the icefall, which is replenished with new layers of ice during the summer, when it reaches its peak volume. The ice degrades during winter by sublimation and transfer of warm air from non-glaciated parts of the cave (Rajman et al., 1987).

3 Data and methods

The ice cave was surveyed by a terrestrial laser scanner VZ-1000 by Riegl to acquire 3-D representation of its surface in ultra-high resolution. The scanner operates with a laser beam in the near-infrared wavelength (1550 nm) with nominal precision of ±8 mm at a distance of 100 m and maximum scanning range up to 1400 m. It uses online processing of the full waveform enabling multi-target scanning and it improves reliability of surveying in fog, dust, and precipitation (Pfennigbauer et al., 2014). The minimum scanning distance of the scanner is 1.5 m. The device dimensions are 0.3 m × 0.2 m × 0.2 m and the weight including batteries is 10 kg (Riegl, 2015).

Figure 5 The workflow for generating a time series database and framework of data processing.

The scanner rotates along its vertical axis establishing a full 360^∘ in the horizontal field of view. The vertical scanning angle is limited to 100^∘. This means that from a single scanner position, it is not possible to capture a portion of the view under the scanner in the nadir direction and a part of the ceiling above the scanner in the zenith direction. The data shadows were eliminated by defining a proper configuration of positions during the scanning in which overlapping point clouds are generated.

The data collection by TLS in Silická ľadnica commenced in June 2016. The first campaign focused on testing the capability of the technology to capture the cave ice surface. There were six scanning missions accomplished by October 2018. The formation of ice and its melting was recorded even in this relatively short period. The ice dynamics were observed by spelunkers over decades but the advancement of TLS opened capabilities for measuring the change of ice morphology in an unprecedented level of detail. After 2 years of monitoring, it became clear when the conditions for mapping are the most appropriate as described in Sect. 4.1. On the other hand, we have no doubts about the methodology of data collection and processing. The number of scan positions differed for each scan mission. Therefore, the number of scan positions was determined mainly by the extent of the floor ice at the time of scanning and achieving sufficient overlaps to eliminate shadows in the final point clouds (Fig. 6).

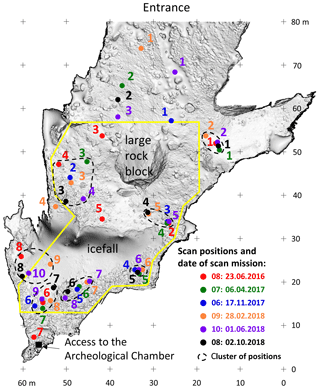
Figure 6 Distribution of scan positions of individual scan missions presented in the plan of the cave derived from TLS mapping. The yellow polygon shows a defined area of interest (AoI) for computation of changes in ice accumulation.

There were 32 individual scan positions used in the first mapping mission. The GCPs were placed in the close exterior of the cave; therefore several scan positions were also located in this area (Fig. 5 phase 1). The scan mission 1 used 10 GCPs for registration in global coordinate systems (Fig. 5 phase 4). Data from all scanning missions were registered in the national coordinate system S-JTSK (Systém jednotnej trigonometrickej siete katastrálnej), EPSG code 5514. The GCPs were measured by the global navigation satellite system (GNSS) using the Topcon HiPER II receiver with a reference connection to the Slovak real-time positioning service – SKPOS. Point measurements were performed for 30 s using the real-time kinematic (RTK) positioning via weighted averaging with overall accuracy of the fixed solution between 1 and 2 cm. The coordinates of the points were calculated with Topcon Link software. The standard deviation error of transformation of scan mission 1 in the global coordinate system based on the GCPs was 5.3 cm.

The setting of scan parameters is reported differently by individual scanner manufacturers. We worked with 0.04 and 0.06^∘ of angular increment in horizontal and vertical rotation, respectively. These modes are termed Panorama 40 and Panorama 60 in the Riegl VZ-1000 scanner. The increment defines the level of spatial detail captured by the scanner. The smaller the increment, the shorter the spacing between the recorded laser pulse echoes at the same range from the scanner. Table 1 summarises the generated datasets in terms of the amount of data and accuracy based on the scanning parameters.

Table 1 Characteristics of the time series database.

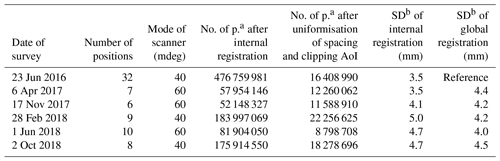
^a No. of p. – number of points. ^b SD – standard deviation.

Precision of scan mission also depends on the number of scan positions. The largest point cloud was recorded within the first scan mission, where we scanned the surroundings of the cave. Subsequent scan missions were focused on acquiring data in the cave in places within the ice formation. Therefore, the number of scan positions and the number of points is lower in comparison with the first scan mission. Scanning at one position with scanner settings of range of 450 m, frequency of 300 kHz, and mode of Panorama 60 took almost 4 min while the duration of scanning was 5 min and 20 s with Panorama 40. The total scanning time of the first scan mission was approximately 12 h due to the challenging terrain and the surrounding forest. Using selective a cloud-to-cloud (sC2C) approach enabled us to perform following scan missions only inside the cave; thus scanning time did not exceed 3 h. Shorter time and fewer data are acceptable for repeating scanning to capture the ice accumulation dynamics and generation of the time series database for long-term monitoring of cave cryomorphology. In the initial phase of the cave floor ice monitoring, we tested various parameters of the scanner settings. The aim was to find if a higher scanning detail influences the precision of the mapping of cryomorphological topography. We found that critical points such as ice have the same point density even with higher scan detail. In addition, there are demands for processing and storing data because of their amount. During the 2-year mapping period, we also identified and optimised the scan positions, which we refer to as the scan position clusters (Fig. 6). Based on this testing, we learned that in our case a minimum of seven positions with Panorama 60 mode are sufficient to scan the cave floor ice.

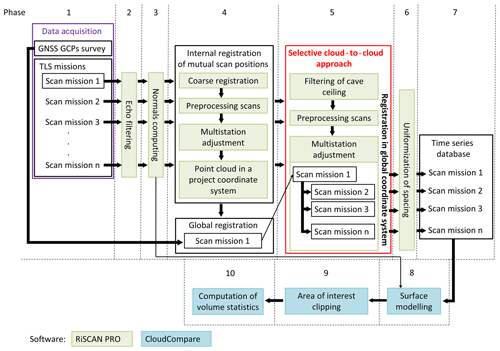
3.1 A framework of registration procedure using TLS data

Data processing consisted of several steps. We used the RiSCAN Pro software for primary data processing. After importing the individual scan positions into the project, we removed the noise points from each single scan position. The noise points occur during scanning in many situations. Some of them are the impact of a laser beam on water level, or in the cases of false reflections in places where the laser beam traces the objects' interface. By removing the noise from point clouds of single scan positions in this phase, we improved the registration result based on the automatic cloud-to-cloud approach. As noted in Gómez-Lende and Sánchez-Fernández (2018), the noise can be removed manually or automatically. In our approach, we suggest automatic noise filtration using parameters of the order of reflection and deformation of the shape of the laser pulse trace. The scanner emits a laser pulse and distributes it to the ambient environment. A laser pulse has a certain shape when it hits the surface. The scanner Riegl VZ-1000 is capable of recording the pulse deformation owing to the online waveform processing of the pulse. This parameter is termed deviation. It is a dimensionless number with values from 0 to 65 535. The value 0 indicates that the track has a circular (ideal) shape, and the value 65 535 represents the shape of the elongated ellipse of the pulse track. We kept only points with a deviation value between 0 and 20 as recommended by the scanner producer. Thus, we filtered out less accurate measurements caused by the deformed shape of the scanner pulse track. In addition, we used only points that represent the first and unique echoes. In this phase, we removed about 35 %–40 % of the points from the point clouds of single scan positions.

The next step was to calculate the normals for points (Fig. 5, phase 3). We recommend performing this step before internal registration of mutual scan positions. The reason is that the direction of normals could be erroneously determined for the cave after internal registration because of the complexity of cave geometry. Derivation of normals is required for the generation of a 3-D model of the cave surface (Fig. 5, phase 8). The direction of the normals was calculated to the scanner position. In the case of irregular distribution of points it is more appropriate to calculate normal vectors with respect to the centre of each scan position than using algorithms based on neighbourhood analysis.

After filtering the points and calculating the normals, mutual orientation of the scan positions followed (Fig. 5, phase 4). It is termed the internal registration and it has two steps. First, the scans acquired within a single mission were coarsely registered via identical points identified in the area of the scans' overlap. We chose edges of rocks on the ceiling and recognisable sharp objects, e.g. fault edges. The second step involved iterative closest point (ICP) adjustment, which is implemented in the RiSCAN Pro software as the Multi-Station Adjustment (MSA) module. The procedure uses the cloud-to-cloud approach to find the closest match of two or more scans (Ullrich et al., 2003). This approach automatically searches and extract groups of points based on certain parameters. We used the method based on filtering planar patches. The minimum number of points to define a planar patch was set to five and the minimum search cube size was 0.128 m. Only the patches from which the points deviated by less than 0.02 m were used for registration of overlapping scans. Subsequently, centroids of the planes and the normals derived for them were determined. The registration of two scan positions is based on the assumption that the same areas with the same or characteristics of normals very similar to the planar patches will be identified as identical within scenes being registered. The tolerance of the normals' deviation is defined by the parameter of maximum tilt angle, which was set to 1^∘. Search radius was set to 0.5 m. Planar patches from two scans are considered identical if their centroids are within 0.5 m of each other (after coarse registration in the first step) and difference of the direction of their normal at centroids does not exceed 1^∘. Such a procedure was used to join all scans from a particular mission into a single point cloud located in a local coordinate system.

3.2 Selective cloud-to-cloud approach

The final point clouds from different missions required transformation into a common coordinate system to allow for the assessment of morphologic changes in ice accumulations. For this purpose, we designed an innovative sC2C approach to register scan missions into a unified coordinate system (Fig. 5, phase 4).

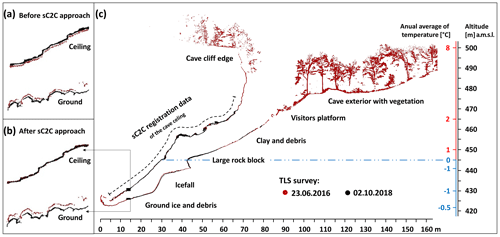
Figure 7 Demonstration of the improved registration accuracy by the sC2C method. Red dots represent the reference point cloud surveyed on 23 June 2016. The point cloud surveyed on 2 October 2018 marked with black dots was used to demonstrate the registration result using the proposed sC2C approach. The results of registering the two scan missions in the detailed views show the performance of (a) the standard C2C approach and (b) after applying the sC2C approach in which stable points of the cave ceiling (c) on the bare rock were used. The size of the cave can be estimated from the vertical and horizontal axes, which are in metres. The left side of the vertical axis shows mean annual air temperature inside the cave based on our temperature data loggers. The mean temperature is the lowest in the area of the icefall. The mean annual temperature of 0 ^∘C is just above the icefall, indicating the approximate maximal vertical range of the cave floor ice.

The key feature of the approach is in using surfaces with unchanged geometry over the monitoring period, which were identified in the first step. In the Silická ľadnica cave, the ceiling of the cave was considered the morphologically stable part of the cave where no change of the mass is expected (Fig. 7c). Certain stable surface features were extracted and they were used to transform the final point clouds for the individual scan missions into a common coordinate system by using the MSA tool. Through a selection of the points representing the cave ceiling, we derived the planes and normals of the plane centroids, which were determined according to the same parameters as in phase 4. We argue that for generating a time series of point clouds, this kind of sC2C approach (Fig. 7b) based on cave ceiling performs better in the automatic registration of individual scan missions than a C2C approach in which the entire scan is used for registration with another member of the time series (Fig. 7a). The point cloud of the reference scan mission was locked, and the propagation of errors of identical planes was distributed only at locations that we considered to be morphologically stable parts of the cave. By this means, in the registration of time series, we avoided the use of moving objects which did not change their geometry but changed their position or orientation, such as stones floating on the ice surface (Fig. 7a and b). Thus, the residuals of normals were not dispersed into places that could have been considered similar in shape but not identical in the position. Such an approach facilitates surface change detection. Finally, all final point clouds of individual missions were placed in the S-JTSK global coordinate system to enable comparison with other older geodetic measurements.

Laser scanning point clouds typically have heterogeneous spatial distribution of points. The first reason is in the very principle of data acquisition for which the point spacing increases with growing distance from the scanner; i.e. the point density per unit area decreases. Another reason is in the need of spatial overlap to perform the mutual registration of scans. The point density increases in the area of overlap, causing data redundancy in places that were in the scanner field of view from multiple positions. The marked variability in spatial distribution of the points within point clouds complicates interpolation of digital surface models and modelling derived surface parameters (Gallay et al., 2016). This complication can be solved by making the distances between points more uniform (Fig. 5 phase 6). We used 0.005 m of spacing to decimate original point clouds, which reduced 60 % of points without a marked decrease in spatial detail captured in the final surface model. Homogenisation of the point distribution was performed using the Octree tool implemented in the RiSCAN Pro software. By removing redundant points, we obtained a spatially homogenised input point cloud for the calculation of cave surface models.

The generated time series from point clouds representing the ice cave is another important outcome of the presented research (Fig. 5, phase 7) resulting from data collection and data processing (Fig. 5, phase 1 until phase 6).

3.3 Deriving complex 3-D cave model from point clouds using a mesh model

Comparison of the cave floor ice over time requires a time series of surface models derived from point clouds representing the floor of the cave. The cave has a very complex geometric structure with floor, ceiling, and perpendicular walls, and therefore some classical bivariate functions hit their limits and cannot be fully applied for modelling of the cave morphology. Commonly used classical bivariate functions in GIS designed for modelling terrain, whose general formulation is $z=f(x,y)$, work only in 2-D space, when only one z coordinate for repeating pairs of coordinates (x,y) can be computed. On the other side, for surface modelling it is only possible to use bivariate functions, but with a local search radius in 3-D space (Gallay et al., 2016), which allows us to generate complex 3-D surface models. Space of input data is temporarily voxelised and bivariate functions are used to find a suitable surface. The result of the proposed modelling approach is still a 2-D surface (plate) which is located in 3-D space. Thus, the bivariate functions with the general form $z=f(x,y)$ are not applied to the whole dataset in 2-D space. Instead, the 3-D space is fragmented locally into, for example, cubes with defined side lengths. This allows us to avoid conflicts in the computation of z coordinates. Therefore, we used a vector-based mesh modelling approach to create the surface of the cave floor, which makes it possible to model such complex shapes. One of the key inputs for calculation of mesh is vector normals of the points that have been derived in phase 3 for each scan position individually. We used the Poisson surface reconstruction (PSR) interpolation method (Kazhdan and Hoppe, 2013) implemented in the open-source software CloudCompare (Girardeau-Montaut, 2018). This global method using a B-spline was chosen because it combines the advantages of global and local surface reconstruction methods without creating jagged polygons in phase of segments joining. Using the coordinates of input points in the form of control vector fields and normal vectors, PSR defines an indicator function to solve the Poisson equation at multiple octree levels resulting in derivation of iso-surfaces for individual fixed depths. Their values are used in the last step to reconstruct the resulting 3-D watertight surface. The generated cave surface model by PSR is dependent on several parameters. Spatial resolution of the 3-D cave surface model is controlled by the octree parameter. It is a dimensionless number used for fragmenting the space defined by the range of input data. Octree 1 means that the space of input data range is fragmented into eight cubes, which are identical to the bounding box cube of input data. Octree 2 means that each cube from the previous step is divided into eight smaller cubes. Thus, 64 smaller cubes are generated. In general, the resulting number n of divisions of the input point cloud is calculated as n=8^d, where d is the octree parameter (i.e. the octree depth). In our case, we used the value of Octree 13, whereby the whole space of input data range was fragmented to 8¹³ (549, 755, 813, 888) cubes, which represents a spatial resolution of 0.0054 m. The used octree value respected point spacing resolution of generated point clouds (Fig. 5, phase 6) without additional generalisation of the 3-D cave model. We used a high resolution of the octree parameter because other parameters such as samples per node and point weight did not have a significant effect on the quality of the final 3-D cave models. For the so-called “full depth” parameter, we set the value of 8, which represents a cube with an edge size of 0.1714 m. By this parameter, the spatial resolution of triangles for parts of the 3-D cave model in places with a lower density of point distribution is set. The lower density of point distribution is located in the icefall, where the highest point-to-point distances reach 0.15 m. Thus, the parameter of the full depth helps us to regulate and limit creation of longitudinal triangles.

After the 3-D cave model was created, it was necessary to cut the area of interest (AoI) (Fig. 5, phase 9). As the area of interest we considered places on the floor of the cave, where we expect the occurrence of visible and buried floor ice. Seasonal ice coating on the walls and hanging from the ceiling was not included in the computation. We argue that all seasonal ice coating in the cave degraded and replenished cave floor ice. For better visualisation and understanding of ice dynamics, we have extended the polygon to the nearest surroundings. The AoI polygon projected orthogonally onto a plane defined by x and y axes is 1200 m². This step is necessary after 3-D cave modelling (Fig. 5, phase 8) because due to the interpolation function there is deformation in the model at the border of the AoI (border effect). We used a segment tool implemented in the CloudCompare software to cut the models based on the AoI polygon.

The resulting truncated 3-D floor cave models were subtracted from each other for calculating volumetric changes (Fig. 5, phase 10). To calculate volumetric changes, we used the M3C2 tool (Lague et al., 2013) implemented in the CloudCompare software. This tool uses normal vectors for computing the 3-D distances between two datasets. Differences between 3-D floor cave models within the time series database were expressed by cross sections and arrows representing movement of objects (Fig. 8), seasonal and annual changes via surfaces derived from the differences of distances (DoDs) approach (Fig. 10), and numerically (Table 2).

4 Results and discussion

In this paper we introduce a new approach to generate time series by using TLS missions and the sC2C approach. This approach is characterised by the fact that no targets, markers, or stabilised points are needed in the research area to place individual scan missions in a single coordinate system. As detailed in the methodology of this article, those parts of the cave that are stable are used to place the individual scan missions in a common coordinate system. In our case it is the ceiling of the cave. We decided to then analyse, using two methods such as overlapping cross sections (Fig. 8) and calculation of volumetric changes based on DoDs using 3-D floor cave models (Fig. 10) with interpretation, due to precipitation and temperatures during the monitored period (Fig. 9).

4.1 Detection of floor ice dynamics and analysis of its movements

One of the easiest options for detecting floor cave ice dynamics is to overlay the cave floor cross sections as shown in Fig. 8. This approach for analysing the change in ice cave requires the location of individual measurements in a common coordinate system. We evaluated the quality of the placement of individual scan missions in a common coordinate system based on (1) the calculation of the standard registration error and (2) the visual check on the overlapped vertical cross sections that represent point clouds from each scan mission.

The calculation of the standard deviation error of registration was presented in Table 1. The internal registration of scan positions within individual scan missions ranged from 3.5 to 5.0 mm. To compare the quality of internal registration, we used the same parameters in the plane patch filter for all scan missions. We reached the lowest standard deviation error of internal registration in the summer of 2016. This was because up to 24 positions were located in external parts around the cave, where the reflectivity of objects was higher, thus achieving better scanning quality. Although the number of scan positions was higher, the internal registration error was lower because the higher errors achieved in the cave at ice locations are masked by the lower errors achieved in the exterior parts of the cave; thus the overall standard deviation error is lower. This consideration can also be supported by the measurement on 6 April 2017, where there was a significant loss of ice. Thus, the reflectivity of the objects was higher, which resulted in a lower internal registration error. On the other hand, the highest internal registration error was achieved in the measurement in which new ice increments were recorded. It was a measurement from 20 February 2018. However, during all measurements, we achieved satisfactory results with internal registration. Using the sC2C approach, we have achieved an acceptable standard deviation of global registration, which ranges from 4.0 to 4.5 mm (Table 1).

The floor ice dynamics in the cave using the TLS method are captured with a degree of uncertainty, which is determined by the device error (E_instrument) and the error of registering individual scan positions (E_registration). One of advantages of the proposed sC2C method is that there is no accumulation of errors due to errors in other measurements, such as GNSS (E_GNSS) measurements and global coordinate system registration error (E_GCS). The total error (E_Total) of the proposed method can be calculated using a modified Eq. (1) by Collins et al. (2012):

$$\begin{array}{}\text{(1)}& E_{\mathrm{Total}}=\sqrt{E_{\mathrm{instrument}}^{\mathrm{2}}+E_{\mathrm{registration}}^{\mathrm{2}}}.\end{array}$$

In our case, we used the Riegl VZ-1000 for mapping, whose E_instrument is defined by the manufacturer and is 0.008 m. The highest standard deviation error of global registration has been reached for the measurement on 2 October 2018 and has a value of 0.0045 m. The total error E_Total is ±0.0092 m, which is a threshold for recognising the changes between measurements. Thus, changes in point clouds of less than 0.0092 m cannot be interpreted as a change in the cave ice, as this may be an error propagation of the device and registration.

We also evaluated the quality of registration of the scan missions in the common coordinate system by visual inspection. The best way to evaluate registration quality is through visual inspection on profiles where the cloud points from each scan missions are rendered by a unique colour. During the check we observe the course of point clouds and whether double surfaces of identical objects arise. In Fig. 7b it can be seen that the registration of scan missions by applying the sC2C approach achieves excellent ceiling performance, but there are larger variations on the floor of the cave. Based on a more detailed view of the cave floor presented in Fig. 8b, we conclude that the use of the sC2C approach is equally successful on the cave floor, except that the cave floor has changed in some places due to ice loss or accumulation. Ice dynamics is not the same in all locations. The biggest ice dynamics can be seen in the middle of the profile, which is related to the shape of the icefall.

The convergence of profile lines (areas where the lines become closer together) is not as observable as in the foot of the icefall (Fig. 8a) because there is a mechanically conditional movement of the material by spelunkers. In Fig. 8c, it is possible to observe a random arrangement of the cross sections above a flat stone with a converging character. We argue that based on profile line analysis it is possible to detect area of ice occurrences in the cave. The locations of cross-section divergence (areas where the lines are farther apart) can be considered to be the occurrences of cave floor ice, which may be covered by the sediment of a clastic unsorted material. This indicates the occurrences of buried ice.

A virtual tour of the cave as well as a visual inspection of the quality of registration of individual scan missions can also be performed through a Potree-based web application (Schuetz, 2016), which enables interactive work with scan point clouds of scan missions, for example creating vertical profiles in the optional direction, measurement of distances, or changing number of rendered points. This web application contains a time series database, which will be continuously updated by newer scan missions aiming to document the cryomorphologic changes of the cave floor in the long-term perspective. The web-based interactive application is available at https://geografia.science.upjs.sk/webshared/Laspublish/Ladnica/Silicka_ladnica_All.html (last access: 4 November 2019). For demonstration, we selected cross sections passing through identical cave sites and across the cave floor. The line crosses different types of morphological structures such as stone debris, icefall, subsurface floor ice, and stable elements such as large rocks attached to the subsoil structure (Fig. 8a).

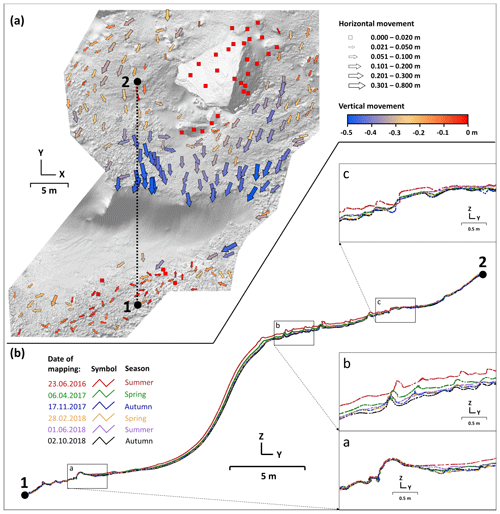
Figure 8 (a) Top view of the AoI-portraying cave floor model with the dotted line indicates the place of the vertical cross section. The arrows indicate the direction of ice movement. The size of the arrow reflects the length of movement in the horizontal direction and the colour expresses the length of movement in the vertical direction. Squares represent the places with no detected movement. (b) The overlaid cross sections represent the cave floor coloured by date of TLS mappings. Changes of the iced part of the cave floor are visualised in selected details. The details represent (a) the foot of the icefall, (b) the place of the most visible changes of the cave floor ice, and (c) the highest occurrence of floor ice in the cave in contact with stone debris.

Point clouds from different scan missions enable identification of rocks that float on the ice surface. To analyse the movement of such an object, we investigated the point clouds from the first and last scan missions (Fig. 8a). There were 250 tie objects manually identified in the point clouds (mostly stones partially drowned in ice), whose shape did not change during the monitored period, only their position. We consider these objects to be identical based on if it is possible to determine the vectors of movement. The selected objects were homogeneously distributed within the grid. No objects were found that could be considered identical to the icefall because the stones that reach the edge of the icefall either fall under the icefall or new ice accumulations bury them. If we look at the movement of ice in the horizontal plane, we can say that the floor ice seems to flow around a large stone block. However, a number of factors need to be considered when interpreting the movement of objects drowned in ice. The general tendency of the objects' movement is in the direction of the lower parts of the cave. This suggests that one of the factors of movement is gravity. Objects from higher glaciated parts of the cave gradually move down. Furthermore, it is clear that the highest objects' movement is near the icefall, where there is a significant horizontal and vertical movement. However, this movement is not the result of the movement of the iceblock itself, but the result of the loss of ice. This indicates that the ice is sublimating and melting at certain times of the year. This leads to a decrease in the volume of ice (Fig. 10) and thus the position of the objects changes as the volume of ice changes. Near the edge of the icefall there is the greatest thickness of ice, where during the monitored period the greatest losses of ice also occurred. In these places the movement of objects is the greatest. On the other hand, in places where the ice was able to recover, in the western part of the cave (to the left of the large rock block) or where regular accumulations of ice occur by destruction of ceiling stalactites, there is less movement. In these places, the ice can recover. Another factor causing movement of objects is mechanical movement caused by spelunkers. This can be observed in particularly in the places where the path is (Fig. 3) and is reflected along the eastern edge (to the right of the large rock block) of the cave (Fig. 8). Analysis of movement of objects also suggests that the large rock block and the rocks below it are associated with the bedrock since they have changed by less than 2 cm during the reported period, which corresponds to the overall global registration error propagation.

4.2 Ice formation and ice dynamics

The results of the repeated terrestrial laser scanning based on the sC2C approach revealed changes of the ice surface and defined areal and volumetric changes. When evaluating and interpreting ice formation and dynamics of ice accumulations, it is necessary to support results with meteorological measurements of temperature and precipitation (Fig. 9). The meteorological data were recorded by the official meteorological station in the Silica village located about 5 km east of the cave. The data on air temperature from the interior of the cave are from an automated data logger, which is located in Fig. 3.

The mean daily air temperature from the Silica weather station ranged from −15 to +28 ^∘C throughout the monitored period. The highest temperatures were in summer, when the daily mean temperature did not drop below 12 ^∘C. The lowest mean air temperatures occurred in winter, when their values oscillated around 0 ^∘C and only sporadically rose above 5 ^∘C. The monitored period was above the long-term average in comparison with the mean daily temperatures of the previous 30 years. Below-average daily temperatures occurred in two instances: autumn 2016 and the subsequent winter 2017 and winter 2018 during the winter–spring transition.

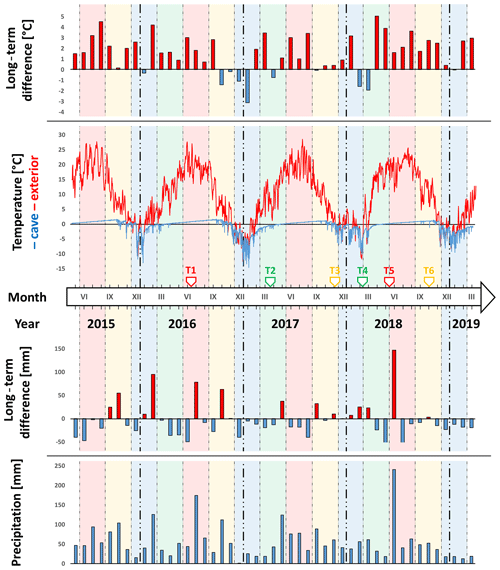
Figure 9 Long-term daily and monthly mean temperature (above the timeline) and precipitation (below the timeline) and their deviations from the long-term average. The timeline shows the dates on which TLS mapping was performed. The background colours of the graph show the season (red – summer, yellow – autumn, blue – winter, green – spring). The bold dashed lines separate the years. Source: data supplied by SHMÚ (2019) and our own measurements.

Based on the analysis of mean daily temperatures inside the cave, we can identify the three phases described by Rajman et al. (1987) following the annual cycle of ice formation in Silická ľadnica: winter, transitional, and summer phases. The winter phase occurs at a time when the ambient air temperature drops below 0 ^∘C and the temperature in the cave decreases until it reaches a warm minimum. In the case of the Silická ľadnica cave, the first cold air enters the cave from mid-autumn, when the first ground frosts occur. Although negative temperatures do not appear on daily averages, short-term fluctuations are evident in the cave. However, due to the temperature of the rock, this cold air is not maintained for a long time. In the later autumn period, the ambient air temperature already approaches 0 ^∘C, which is also reflected in the gradual lowering of the temperature in the cave because cold air inlets of daily temperature lows are more frequent. In the winter months the cave cools and freezes. Since the water is in a solid state during this period, the ice in the cave is not renewed but the sublimation of the ice occurs. At the end of winter with the onset of spring, there is a transitional phase in which the greatest amount of ice is formed. The temperature of the cave is low after winter, but water in the surrounding environment is in a liquid state and flows into the cave where it freezes. The onset of the summer phase of the cave occurs in the second half of spring, when the internal temperature of the cave gradually rises above 0 ^∘C, mainly due to higher temperatures of the external environment and due to the penetration of warm water from precipitation into the cave. Thus, the formation and ablation of cave ice is influenced by precipitation, which is a source of water (Perşoiu and Pazdur, 2011). The graph of monthly cumulative precipitation (Fig. 9) indicates that the precipitation was mostly below average during the whole monitoring period. Precipitation in June 2018 seems to be significantly above average. However, there were only two precipitation events with short-term but intensive precipitation (summer storms). The situation was similar in July 2016.

For the formation of ice in the cave, the inflow of water into the cave during the transition phase (the end of winter and the first half of spring) is important. The rock and ice in the cave are cooled enough below 0 ^∘C during this period. If the inflow of water is sufficient, it has a significant effect on the increase in the amount of cave ice. Most of the ice mass in Silická ľadnica is found on the icefall. However, the recovery of ice on the icefall is gradual. The first stage involves formation of vertical ice stalactites (Fig. 4b). After melting, degradation, or collapse, the stalactites become the source of water for the formation of ice accumulations on the icefall. The equilibrium between the ice accumulation rate during different climate conditions is controlled by a complex interplay between the climatic factors that control the mass balance of ice, i.e. wet vs. dry summers and/or winters and cold vs. warm summers and/or winters (Perşoiu and Pazdur, 2011). Ice increments in the Silická ľadnica occur mainly during the transition phase. During the summer and winter phases, there is a loss of ice. In the summer phase, the melting of ice is due to the higher temperature of the ambient air and warm water penetrating into the cave. Ice degradation in winter is mainly caused by ice sublimation. It is precisely this principle of ice formation and ablation in the Silická ľadnica that can be better described based on the time series of the TLS scan missions using DoD (Fig. 10 and Table 2). Seasonal comparison of surface dynamics (Fig. 10, seasonal) demonstrates that there is a constant change in ice volume (Table 2). Thus, the ice in the cave is constantly increasing or decreasing between time periods.

The biggest ice volume was recorded at the beginning of the monitoring in June 2016, as much water entered the cave due to above-average precipitation from the end of winter and early spring of 2016 (Fig. 9). Interestingly, the temperature in the cave at the turn of winter and spring 2016 was higher compared to the same period in spring 2017, but there was less ice in the cave (Figs. 9 and 10). A similar meteorological situation was repeated at the turn of winter and spring 2018, although the amount of precipitation in this period was less than in spring 2016. Between summer 2016 and spring 2017 (Fig. 10, T1–T2) on icefall, while ice increment can be seen on a large stone block in the middle of the cave, where water dripping from vertical ice hanging from the ceiling formed ice accumulations (Fig. 4b). This phenomenon always occurs in the spring when the water from the melting snow and spring rains passes through the cracks into the frozen part of the cave.

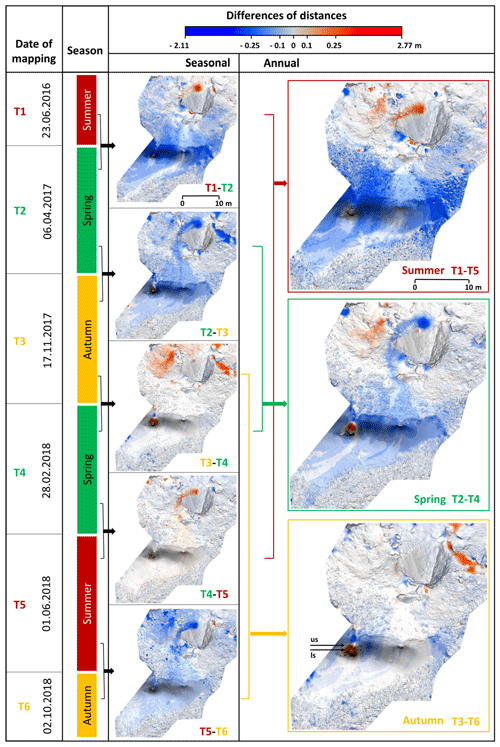
Figure 10 Differences of distances (DoD) between the individual cave floor surface models. Blue represents the decrease and red indicates the increase in the surface elevation. Arrows mark the position of the upper stalagmite (us) and lower stalagmite (ls).

A similar phenomenon can be seen in Fig. 10 (T4–T5). Another phenomenon is the collapse of the glacial stalactites that we caught before the autumn (Fig. 10, T3–T4). Thus this phenomenon is not in the true sense of increments of cave ice volume, but the destruction of the original ice drops hanging from the ceiling. The ice degrades during the summer and autumn. In winter, a seasonal minimum in the volume of cave ice can be observed (Fig. 10, T2–T3 and T5–T6).

There is an interesting formation of a stalagmite on the icefall (Fig. 4a), which is related with a crevice in the rock ceiling filled with an ice stalactite (Fig. 4). We empirically observed over the last decade that in dry years the stalactite above the stalagmite melts and its shape reduces. In the case of a dry spring the stalactite does not grow to a significant enough size to contribute with meltwater to the growth of the stalagmite right below it. When the stalactite is smaller, the dripping meltwater flows further down along the ceiling to another location and a new stalagmite accumulates just below the original one (Fig. 4a, white arrows). The change of volume of the ice stalagmites was recorded by monitoring with TLS. The lower stalagmite grew while the upper stalagmite generally decreased during the whole surveying period (Fig. 10).

However, based on the presented analysis, we can conclude that the assessment of floor cave ice dynamics in terms of overall trends is only possible to observe through a season-to-season comparison between the same periods, e.g. between summer or spring seasons over a longer time period (Fig. 10, seasonal).

A considerable loss of ice formation volume has been seen in Fig. 10 (T1–T5), which demonstrates the rapid decrement of ice between summer 2016 and summer 2018. DoD was calculated with respect to the z axis, so there is a considerable drop in surface, even more than 2 m. However, it should be interpreted that if the ice on a steep icefall with a slope of more than 70^∘ falls 0.2 m in a direction perpendicular to the slope of the profile, the difference in z axis (height) for a place with the same x and y coordinates can reach 2 m, which is visible from the comparison of individual cross sections (Fig. 8b and Table 2, max. decrease).

Red shows the increment in two places, which are demonstrated in Fig. 4. The increment in the massive rock in the middle of the cave was caused by the destruction of the glacial stalactite. The second distinctive height increment is located on the icefall in the form of a stalagmite, which is formed from dripping water from the shrinking stalactite hanging from the crevice in the cave ceiling, as described above. Another inter-seasonal comparison between spring 2017 and spring 2018 (Fig. 10, T2–T4) indicates a year-to-year loss of ice. In the case of DoD between autumn 2017 and autumn 2018 (Fig. 10, T3–T6), there is no considerable decrement or increment of ice accumulations. We can conclude that the ice volume is comparable between these periods; so, it is relatively stable.

The biggest benefit of the created time series database of the complex 3-D surface model is also in the quantification of the volume changes of the cave floor ice and its expression through summary numerical statistics (Table 2).

Given the total error of E_Total 0.0092 m and the area of observation of 1200 m², it should be emphasised that a volume of up to 11.04 m³ may be the result of a measurement error. The highest difference in ice volume was observed at the beginning of the monitored period between summer 2016 and spring 2017 (Fig. 10, T1–T2) and spring 2017 and autumn 2017 (Fig. 10, T2–T3), when a total ice loss was approximately 70 m³ in both cases (Table 2).

Table 2 Summary statistics of volumetric and vertical changes of the selected cave floor extent during the monitored period.

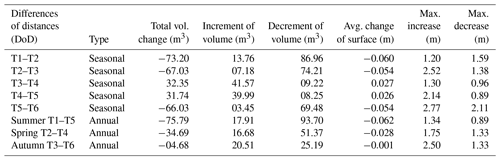
Considerable loss of ice in these periods can also be identified from the average change of surface, which in this period reaches a loss of about 0.06 m. The highest increase was recorded between autumn 2017 and spring 2018, when new ice from spring rains is usually formed in the cave. The increase in ice should culminate in summer, but in 2018 there was little rainfall and it was relatively warm. The loss of ice between summer and autumn 2018 is already a natural phenomenon. The inter-seasonal comparison suggests that there is a considerable loss of ice due to the lack of water flowing into the cave during the monitored period, as evidenced by the comparison between summer 2016 and summer 2018, when about 75 m³ of ice was lost in the cave.

5 Conclusions

Ice caves can be considered an indicator of the long-term changes in the landscape. Hydrological and climatic dynamics of the landscape are manifested in the ice caves, and it is recognisable because the caves are evidently linked with the immediate surroundings. The interpretation of the dynamics in the ice cave accumulations is a challenging task that should be based on long-term and regular monitoring. In this paper we presented the analysis of the floor ice dynamics in the Silická ľadnica cave.

Our research was inspired by the observations made from the middle of the 20th century, which reported ice formation and ablation in the Silická ľadnica cave (Roda et al., 1974; Rajman et al., 1987; Stankovič and Horváth, 2004). The described thermodynamic regime and process of ice formations in Silická ľadnica are similar to the caves of Grotta del Gelo (Maggi et al., 2018), Ledenica u Čudinoj uvali (Buzjak et al., 2018), or Stojkova Ledenica (Nešić and Ćalić, 2018), but most of these caves contain only seasonal ice formations. We also presented new results in the methodology of TLS data collection and processing, generation of a database of 3-D surface time series, floor ice dynamics evaluation using object movement analysis, and quantification of ice mass dynamics based on complex 3-D cave models.

Terrestrial laser scanning was used to record the dynamics of cave sediments containing ice accumulations. In order to evaluate the changes in the cave ice accumulations, it was necessary to register the individual mappings into a uniform coordinate system. For this purpose, we proposed an innovative method based on automatic registration of the individual scan positions using stable objects of the cave such as the ceiling of the cave. The presented sC2C approach reduces the overall registration error of the data time series into a unified coordinate system by avoiding the repeated positioning of GCPs by GNSS. We argue that the presented methodological framework of the sC2C approach has the potential to be used in other applications where it is necessary to identify landscape dynamics, such as mountain glacier assessment and sediment accumulation dynamics analysis.

Finally, the developed methodological framework of data processing enables us to generate a 3-D time series database of the interior cave surface at ultra-high resolution. We also presented a procedure for the modelling of complex 3-D surfaces from the point clouds. The presented data and methods provided means for evaluating the dynamics of the cave floor ice. We detected the dynamics of the ice based on a cross-section method and via differences of 3-D distances analysis. Complex 3-D models of the cave floor were used to quantify the volumetric changes.

Results of the quantitative assessment of cryomorphological changes showed that there was a considerable loss of ice in the cave during the monitored period. The 3-D mapping over the 2-year period was coupled with continuous monitoring of air temperature inside and outside the cave and monitoring of rainfall. Linking the findings on the dynamics of the cryomorphology and the meteorological monitoring shows the well-known fact that a cold but dry winter will lead to less ice accumulation compared to a warmer but wetter one, while a warm but dry summer will lead to less melting than a cold but wet one. Naturally, the question arises of whether there is irreversible year-to-year loss of ice mass or only a longer cycle of perennial ice accumulation replenishment. To be able to answer this question, it is necessary to continue monitoring cave ice and to analyse other factors such as temperature of precipitation, air circulation, evapotranspiration, tectonics and geological structure of the massif, morphology of the cave and immediate surroundings, and connection with other parts of the cave system.