Kinematic response of ice-rise divides to changes in ocean and atmosphere forcing

The majority of Antarctic ice shelves are bounded by grounded ice rises. These ice rises exhibit local flow fields that partially oppose the flow of the surrounding ice shelves. Formation of ice rises is accompanied by a characteristic upward-arching internal stratigraphy (“Raymond arches”), whose geometry can be analysed to infer information about past ice-sheet changes in areas where other archives such as rock outcrops are missing. Here we present an improved modelling framework to study ice-rise evolution using a satellite-velocity calibrated, isothermal, and isotropic 3-D full-Stokes model including grounding-line dynamics at the required mesh resolution (<500 m). This overcomes limitations of previous studies where ice-rise modelling has been restricted to 2-D and excluded the coupling between the ice shelf and ice rise. We apply the model to the Ekström Ice Shelf, Antarctica, containing two ice rises. Our simulations investigate the effect of surface mass balance and ocean perturbations onto ice-rise divide position and interpret possible resulting unique Raymond arch geometries. Our results show that changes in the surface mass balance result in immediate and sustained divide migration (>2.0 m yr⁻¹) of up to 3.5 km. In contrast, instantaneous ice-shelf disintegration causes a short-lived and delayed (by 60–100 years) response of smaller magnitude (<0.75 m yr⁻¹). The model tracks migration of a triple junction and synchronous ice-divide migration in both ice rises with similar magnitude but differing rates. The model is suitable for glacial/interglacial simulations on the catchment scale, providing the next step forward to unravel the ice-dynamic history stored in ice rises all around Antarctica.

1 Introduction

Ice rises are parabolically shaped surface expressions along the margin of the Antarctic ice sheet, and they form where the otherwise floating ice locally regrounds. They are characterised by their local ice-flow centre – henceforth referred to as ice-rise divide – that is independent of the main ice sheet and the surrounding ice shelves, resulting in divergence of the main ice flow around the obstacle. These obstacles act as a decelerating force that restricts ice flow which is commonly referred to as “ice-shelf buttressing”. More than 700 ice rises (Matsuoka et al., 2015) are distributed along the Antarctic perimeter (Fig. 1a), providing additional buttressing to the ice upstream. Ice rises archive their flow history in their characteristic internal stratigraphy (e.g. Conway et al., 1999; Nereson and Waddington, 2002; Drews et al., 2015), making them potentially suitable sites for ice-core drilling such as for the International Partnerships in Ice Core Sciences (IPICS) 2K and 40K Array (Brook et al., 2006).

Figure 1 (a) Location map of ice rises along the margin of the Antarctic ice sheet (Matsuoka et al., 2015). The base map combines ice velocity of the ice sheet (Rignot et al., 2011) and the bathymetry of the adjacent ocean regions (Arndt et al., 2013). The blue rectangle shows zoomed-in area of (b). (b) RADARSAT image (Jezek and 5 RAMP-Product-Team:, 2002) of the study area with locations mentioned in the main text. Dashed lines (A-A', B-B') show the extent of the cross section shown in Fig. 12. Please note that (b) is rotated by 180^∘ with respect to (a).

Due to very low deviatoric stresses near the bed of the divide region and the power law rheology of ice, the effective viscosity (e.g. the stiffness of ice) is significantly higher towards the ice sheet bottom under the divide than in the surrounding areas. The stiff ice impedes downward flow under the divide in comparison to the flank regions (Kingslake et al., 2016) such that ice of the same age is found at shallower depths in the ice column under the divide compared to the flank regions (Raymond, 1983). This results in the formation of upward arches in the isochronal ice stratigraphy commonly referred to as “Raymond arches”.

Previous studies have made much progress in interpreting the Raymond arches as ice-dynamic archives. The arch amplitude and the tilt of multiple Raymond arches – commonly referred to as Raymond stack – have been used to infer migration of ice divides (e.g. Nereson et al., 1998), onset of local divide flow (e.g. Conway et al., 1999; Martín et al., 2006, 2014), and ice-rise residence time (e.g. Drews et al., 2013, 2015; Goel et al., 2017). Common to all these studies is the comparison of the observed isochrones derived from radar data, with the predicted age fields from models with varying input scenarios. The full stress solution of the Stokes equations is necessary because both longitudinal and bridging stress gradients are important near ice divides (e.g. Martín et al., 2009b; Gillet-Chaulet and Hindmarsh, 2011).

Fast migration of ice divides results in abandoned Raymond stacks in the flanks, and a new Raymond stack starts to develop at the new divide position (Jacobson and Waddington, 2005; Martín et al., 2009b, Fig. 2d–f). Slow migration of ice divides results in tilted Raymond stacks (Nereson et al., 1998; Nereson and Waddington, 2002; Jacobson and Waddington, 2005; Martín et al., 2009b). For a new Raymond stack to form, a sudden displacement of 1–2 ice thickness is required (Martín et al., 2009b), but thus far a clear threshold between both endmember scenarios remains elusive. Even though divide migration has been an active focus in ice-rise research, most studies have focussed on the ramifications of divide migration (Hindmarsh, 1996; Nereson et al., 1998; Jacobson and Waddington, 2005; Conway and Rasmussen, 2009) rather than what causes the divide to migrate. Additionally, modelling thus far has been restricted to 2-D and has not included interactions between ice rises and the surrounding ice shelves (Martín et al., 2009a, b; Gillet-Chaulet and Hindmarsh, 2011; Drews et al., 2015). This means that the underlying processes resulting in different Raymond arch geometries from radar observations are still incomplete and poorly constrained.

Another poorly understood phenomenon for ice-rise evolution is triple junctions (Gillet-Chaulet and Hindmarsh, 2011). Triple junctions are points where three ice-divide ridges meet. They often coincide with the summits of ice domes. It has been proposed that changes in triple junction position (e.g. merging of two divide ridges) might explain observed relic arches in ice-divide flanks, which cannot be explained with ice-divide migration in a 2-D setting (Drews et al., 2015).

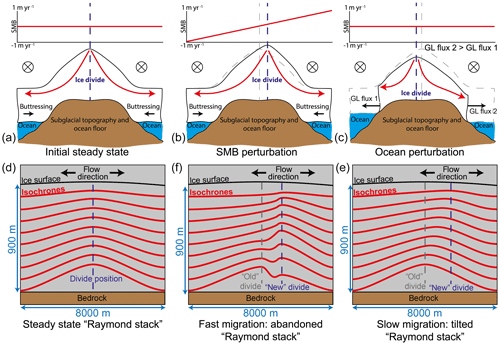
Figure 2 Upper panel (a–c) shows schematic (a) steady state, (b) divide migration induced by asymmetric surface mass balance forcing, and (c) divide migration induced by ocean perturbation forcing. Buttressing in (c) is asymmetric. Solid red arrows indicate approximate ice-flow path from the ice-rise divide to ice shelf. Grey dashed lines in (b) and (c) display the steady-state geometry and divide position of (a). GL is the grounding line. Lower panel (d–f) shows schematic of expected internal stratigraphy for steady state (d), fast migration (e), and slow migration (f). (e) and (f) are not necessarily the result of forcing in (b) and (c), respectively.

Here, we use the full-Stokes (FS) ice-sheet model Elmer/Ice in 3-D (Gagliardini et al., 2013) and extend the model domain in contrast to previous studies to include grounding-line dynamics and ice-shelf flow to study potential causes for ice-rise divide migration. We apply the model to the Ekström Ice Shelf catchment bounded by two large (15th and 16th largest in Antarctica, Matsuoka et al., 2015) ice rises. The model is calibrated by tuning basal friction and ice viscosity so that modelled surface velocities match today's flow field. Perturbations to the surface mass balance (SMB) and ice-shelf thickness are applied in forward simulations to investigate the coupled transient response of the two ice rises. The experiments are tailored to help improve our understanding of what processes cause ice-divide migration. Specifically, we address the following questions. Is the amplitude of divide migration controlled by the SMB, ice-shelf buttressing, and/or is the divide position determined by the subglacial topography? Do ice rises in close proximity of each other show a similar response? Can we differentiate between the different trigger mechanisms? Furthermore, we investigate if the triple junction at one of the ice rises in the catchment – the Halvfarryggen Ice Rise – also migrates in synchronicity with the main divide ridge.

2 Study area: Ekström Ice Shelf catchment

The Ekström Ice Shelf is located in the Atlantic sector of the East Antarctic ice sheet and is a medium-sized ice shelf. The embayment is characterised by two prominent ice rises: the Söråsen Ice Rise in the west and the Halvfarryggen Ice Rise, an ice promontory sandwiched between the Ekström Ice Shelf and Jelbart Ice Shelf in the east (Fig. 1b). While the Söråsen Ice Rise is made up of a single ridge divide, Halvfarryggen consists of three main ridges that meet to form a triple junction close to the summit (Hofstede et al., 2013). Both ice rises belong to the larger ice rises in Antarctica with areas of about 5700 and 5500 km² for Halvfarryggen and Söråsen, respectively (Matsuoka et al., 2015). The Söråsen Ice Rise is additionally buttressed in the west by the Quar Ice Shelf (Fig. 1b). SMB across both divide ridges is strongly asymmetric with the western downwind side of the divide receiving much less accumulation (<0.6 m yr⁻¹ ice equivalent) than the eastern side (up to 2.9 m yr⁻¹ ice equivalent) (Drews et al., 2013; Lenaerts et al., 2014). The catchment is a suitable test site to study the dynamics of ice rises because the boundary input datasets such as subglacial topography, ice thickness, and ice surface elevation are well constrained (with many flight lines across the region due to the vicinity of the Neumayer III station). In addition, the confined geometry of both ice rises suggests that significant lateral buttressing is provided by the Ekström and Jelbart ice shelves. This means that the buttressing the Ekström and Jelbart ice shelves provide also restricts ice flow across the grounding line from both ice rises, making the divide position potentially sensitive to ocean forcing.

3 Methods

3.1 Model description

3.1.1 Governing equations

Ice flow is dominated by viscous forces (e.g. low Reynolds number) permitting the dropping of the inertia and acceleration terms in the momentum equations. Using these simplifications, a complete description of ice flow is the full-Stokes (FS) flow model. The Stokes equations for linear momentum are

$$\begin{array}{}\text{(1)}& \mathrm{div}\mathit{\sigma }=-{\mathit{\rho }}_{\mathrm{i}}\mathit{g},\end{array}$$

where $\mathit{\sigma }=\mathit{\tau }-p\mathbf{I}$ is the Cauchy stress tensor, τ is the deviatoric stress tensor, $p=-\mathrm{tr}\left(\mathit{\sigma }\right)/\mathrm{3}$ is the isotropic pressure, I the identity matrix, ρ_i the ice density, and g is the gravitational vector. Ice flow is assumed to be incompressible, which simplifies mass conservation to

$$\begin{array}{}\text{(2)}& \mathrm{div}\mathit{u}=\mathrm{0},\end{array}$$

with u being the ice velocity vector. Here we model ice as an isotropic material. Its rheology is given by Glen's flow law, which relates deviatoric stress τ with the strain rate $\dot{\mathit{ϵ}}$:

$$\begin{array}{}\text{(3)}& \mathit{\tau }=\mathrm{2}\mathit{\eta }\dot{\mathit{ϵ}},\end{array}$$

where the effective viscosity η can be expressed as

$$\begin{array}{}\text{(4)}& \mathit{\eta }={\displaystyle \frac{\mathrm{1}}{\mathrm{2}}}EB{{\dot{\mathit{ϵ}}}_{\mathrm{e}}}^{\frac{(\mathrm{1}-n)}{n}}.\end{array}$$

In this equation E is the enhancement factor, B is a viscosity parameter computed through an Arrhenius law, n is Glen's flow law parameter (n=3), and the effective strain rate is defined as ${\dot{\mathit{ϵ}}}_{\mathrm{e}}^{\mathrm{2}}=\mathrm{tr}\left({\dot{\mathit{ϵ}}}^{\mathrm{2}}\right)/\mathrm{2}$. Although there is evidence that the Glen flow parameter is >3 (Bons et al., 2018), particularly near ice rises (Gillet-Chaulet et al., 2011), we stick to the current modelling standard of n=3, because we focus on divide migration rather than Raymond arch amplitudes here. The same holds for the enhancement factor, which is often used to account for anisotropic effects but is set to 1 (isotropic conditions) in all simulations. In future applications of this model, these assumptions should be revisited.

Table 1 Standard physical and numerical parameters used for the simulations.

3.1.2 Boundary conditions

A kinematic boundary condition determines the evolution of the upper and lower surfaces z_j:

$$\begin{array}{}\text{(5)}& {\displaystyle \frac{\partial z_j}{\partial t}}+u_x{\displaystyle \frac{\partial z_j}{\partial x}}+u_y{\displaystyle \frac{\partial z_j}{\partial y}}=u_z+{\dot{a}}_j,\end{array}$$

where ${\dot{a}}_j$ is the accumulation/ablation term and $j=(b,s)$, with s being the upper surface and b being the lower surface (base) of the ice sheet. The ice-shelf basal mass balance (${\dot{a}}_{\mathrm{b}}$) parameterisation follows Favier et al. (2016):

$$\begin{array}{}\text{(6)}& {\dot{a}}_{\mathrm{b}}=H^{\mathit{\alpha }}({\mathit{\rho }}_{f}G+(\mathrm{1}-{\mathit{\rho }}_f\left)A\right),\end{array}$$

where H is the ice thickness; G and A are tuning parameters to constrain melt rates at the grounding line and away from the grounding line, respectively; and α is a local tuning parameter (Table 1). The parameter ρ_f(x,y) decreases exponentially with distance from the grounding line, varying from ${\mathit{\rho }}_f(x,y)=\mathrm{1}$ at the grounding line to ${\mathit{\rho }}_f(x,y)=\mathrm{0}$ some distance (∼40 km) away from it. This ensures that the highest melt rates are always specified at the grounding line and decrease exponentially with distance away from it. The tuning parameters are chosen such that basal melt rates roughly agree with melt rates derived from satellite observations and mass conservation (Neckel et al., 2012). Melt rates under the shelf are generally low, ranging from −0.2 to 1.1 m yr⁻¹ near the grounding line (Neckel et al., 2012). No basal melting is applied to the grounded ice sheet.

Where the ice is in contact with the bedrock a linear Weertman-type basal sliding law is employed:

$$\begin{array}{}\text{(7)}& {\mathit{\tau }}_{\mathrm{b}}=C|{\mathit{u}}_{\mathrm{b}}{|}^{m-\mathrm{1}}{\mathit{u}}_{\mathrm{b}},\end{array}$$

where τ_b is the basal traction, m is the basal friction component – set to 1 in all simulations, and C is the basal friction coefficient inferred by solving an inverse problem (see Sect. 3.3, Model initialisation). Underneath the floating part (ice shelves) of the domain basal traction is zero (τ_b=0), but hydrostatic sea pressure is prescribed.

For the ice-shelf-front boundary, the true vertical distribution of the hydrostatic water pressure is applied and the calving front is held fixed throughout the simulations. We assume the ice is isothermal with a constant temperature of −10 ^∘C. We specify depth-independent horizontal ice velocities taken from the MEaSUREs dataset (Rignot et al., 2011) at all lateral boundaries other than the ice-shelf front. To solve the presented system of equations with the appropriate boundary conditions, we use the open-source finite element code Elmer/Ice (Gagliardini et al., 2013).

3.2 Initial geometry and input data

To initialise the model geometry, subglacial topography was taken from the BEDMAP2 dataset (Fretwell et al., 2013). Our surface elevation is a merged product of CryoSat-2 and, where available, higher-resolution TanDEM-X digital elevation models (Veit Helm, personal communication, 2018). SMB (${\dot{a}}_{\mathrm{s}}$, Eq. 5) in our simulations was taken from regional climate model simulations with RACMO2.3 (Lenaerts et al., 2014). This model reproduces the commonly observed asymmetric SMB across ice rises (Callens et al., 2016). Velocity observations to match modelled ice velocities in the inversion procedure were taken from the MEaSUREs dataset (Rignot et al., 2011).

3.3 Model initialisation

We perform the model initialisation in two steps using two different mechanical models: the shallow shelf approximation (SSA; Morland, 1987) and the FS model. The SSA ice-sheet model is initialised by solving an optimisation problem to simultaneously infer the basal traction coefficient C and the viscosity parameter B. This type of snapshot initialisation is well known and widely employed in ice-sheet modelling and aims to match modelled velocities with observed velocities (e.g. MacAyeal, 1993; Gillet-Chaulet et al., 2012; Cornford et al., 2015). In a more formal way, we seek a minimum of the objective function

$$\begin{array}{}\text{(8)}& J=J_{\mathrm{m}}+J_{\mathrm{p}},\end{array}$$

where J_m is the misfit between observed and modelled velocities and J_p is a Tikhonov penalty function described by

$$\begin{array}{}\text{(9)}& J_{\mathrm{p}}={\mathit{\lambda }}_C{J}_C^{\mathrm{reg}}+{\mathit{\lambda }}_B{J}_B^{\mathrm{reg}},\end{array}$$

where λ_C and λ_B are the Tikhonov parameters and $J_C^{\mathrm{reg}}$ and $J_B^{\mathrm{reg}}$ represent the smoothness constraints of basal drag and viscosity (e.g. Gillet-Chaulet et al., 2012; Cornford et al., 2015). The smoothness constraints penalise the square of the first derivatives. An L-curve analysis was performed to pick the Tikhonov parameters and avoid overfitting or overregularisation (Fürst et al., 2015). The selected values are λ_C=10⁷ and λ_B=10⁶ (Fig. 3). Velocity misfits obtained with these parameters are of similar magnitude to previous studies (e.g. Cornford et al., 2015; Schannwell et al., 2018).

However, when the inferred basal traction coefficient and viscosity fields from the SSA inversion were used in forward simulations, unrealistically high surface lowering rates (200 m/century) in the vicinity of the divide were observed. To circumvent this problem, the output fields from the SSA inversion were used as input for a second inversion using the FS model, but only adjusting the basal friction coefficient, while keeping the viscosity of the first inversion fixed. The Tikhonov parameter from the SSA inversion was used for the FS inversion as well. For both inversions a horizontal grid resolution of ∼1 km was used. Following initialisation, as is commonly done in ice-sheet modelling, we performed a short 10-year relaxation simulation to smooth out data inconsistencies such as differences introduced by differing acquisition dates of ice surface elevation and surface velocity. This simulation length for the relaxation lies in the range of what other studies have done previously (e.g. Cornford et al., 2015; Schannwell et al., 2018).

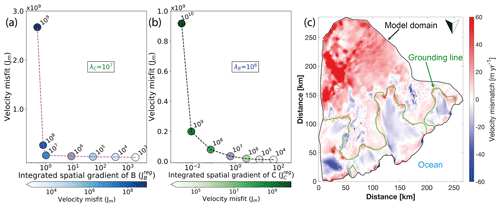
Figure 3 L-curve analysis to select Tikhonov parameters λ_B and λ_C: (a) 2-D cross section for variable λ_B and λ_C fixed at 10⁷ Pa⁻² m⁶ a⁻⁴. (b) Reverse case with constant λ_B at 10⁶ m⁴ a⁻² and varying λ_C. J_m (m⁴ a⁻²) and $J_C^{\mathrm{reg}}$ (Pa² m⁻² a²) are colour-coded. $J_B^{\mathrm{reg}}$ is unitless. (c) shows mismatch between modelled and observed velocities (Rignot et al., 2011) after FS inversion for the modelling domain (Fig. 1b, blue outline).

3.4 Experimental design

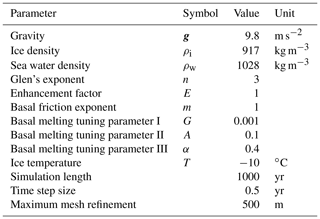
The forward simulations focus on two types of perturbation simulations: (1) perturbations to the SMB and (2) ocean perturbations resulting in changing ice-shelf thickness and hence ice-shelf buttressing. For the SMB, we use modelled values from RACMO2.3 (Lenaerts et al., 2014). The spatial pattern of the SMB is such that low accumulation rates are applied on the western (downwind) side (<0.5 m yr⁻¹) of the ice rises and high accumulation rates (>1 m yr⁻¹) are applied on the eastern (upwind) sides. This asymmetric SMB pattern is consistent with observations (Drews et al., 2013) but does not capture the correct magnitudes. Therefore, we adjust the SMB using the computed model drift following the relaxation simulation. This means that for the reference simulation the SMB forcing consists of the RACMO2.3 field plus the computed spatial thickening/thinning rate (model drift) at the end of the relaxation simulation. This approach ensures that the model drift is eliminated and the divides stay at their initial positions. Since without this model drift correction there is a change in divide position, we treat the unadjusted SMB as a simulation with a perturbed SMB. In the second type of experiments, we perturb the reference run by thinning ice shelves through an increase in ocean-induced melting. The extreme scenario, where all ice shelves are removed, is simulated by cutting the numerical mesh ∼1 km downstream of the present grounding-line position. This ensures that the same frontal boundary conditions still apply to this geometry. To test more ice-shelf buttressing reduction scenarios, we performed additional model simulations with intermediate shelf thinning scenarios, where shelf thickness was reduced by 10 % and 50 % at the start of the perturbation simulation. For both simulations the shelf geometry is kept constant for the remainder of the simulation by applying a synthetic steady-state ocean forcing. To permit a more direct comparison between ocean forcing and SMB forcing, an additional SMB perturbation simulation is performed, where the SMB is unadjusted and the initial grounding-line flux perturbation from the shelf removal simulation on either side of Halvfarryggen is added to the SMB term (Table 2, Run 6). This is done such that the spatial pattern of the SMB remains unchanged, but the magnitude is different by about a factor of 2 in comparison to the unadjusted SMB. In all perturbation simulations the grounding line is permitted to freely evolve. All perturbation simulations are run forward for 1000 years, which is about the characteristic time T (T = ice thickness/accumulation) for the Halvfarryggen and Söråsen ice rises (Drews et al., 2013). After one characteristic time, the formation of synclines in the internal stratigraphy can usually be observed (Martín et al., 2014). Most of the simulations are performed with two different mesh resolutions (Fig. 4). The first isotropic mesh uses a horizontal resolution of ∼2 km throughout the domain (henceforth regular mesh), whereas for the second mesh (henceforth refined mesh), we initially use the same footprint as for the regular mesh but use the meshing software MMG (http://www.mmgtools.org/, last access: 2 October 2019) to refine the mesh along the grounding line and all ice-divide ridges to a resolution of ∼500 m. Mesh resolution then decreases with distance away from the regions of interest to the lowest resolution of ∼10 km (Fig. 4). A second refined mesh, where we refine down to ∼350 m at the divides and grounding line, was used for two simulations. All meshes are held fixed over time and no dynamic remeshing is performed. A summary of all perturbation experiments is provided in Table 2.

Table 2 List of all perturbation experiments including forcings and mesh resolution.

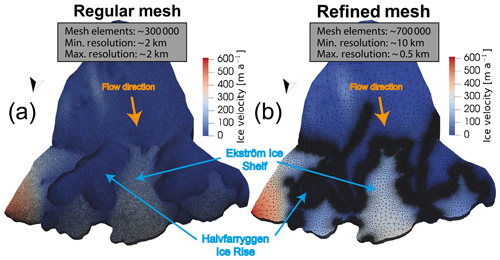
Figure 4 The 3-D plot of the model domain showing the two main mesh resolutions employed in this study. (a) shows uniform mesh of 2 km resolution and (b) shows refined mesh in areas of interest such as the grounding line and the ice-rise divides. In these areas the mesh resolution is ∼500 m and away from these regions the mesh resolution increases to 10 km.

4 Results

4.1 Effect of mechanical model in initialisation on transient simulations

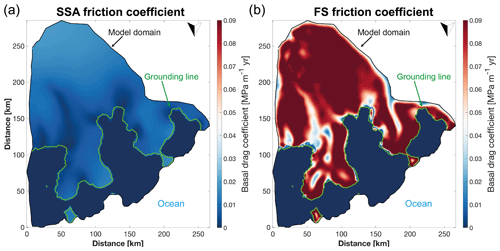
We observed an order-of-magnitude difference in the basal drag coefficients found by solving an inverse problem, depending on whether we use the SSA or the FS approximation as a forward model (Fig. 5). This means that sliding is more restricted in the FS case in comparison to the SSA case. Most notably, in comparison to the SSA inversion, the slippery regions in the FS inversion do not extend as far upstream. For example, between the ice divide of Halvfarryggen and the grounding line on either side, there are areas of stickier bedrock conditions that are missing in the drag field of the SSA inversion (Fig. 5). Spuriously high ice surface lowering rates (200 m/century) near the divide were simulated when basal drag and viscosity fields were used from the inversion using the SSA. Thinning rates were much smaller (≤50 m/century) when using the FS forward model.

Figure 5 Inferred basal traction fields C using (a) the SSA model and (b) the FS model.

4.2 Reference simulation (runs 1–2)

The reference simulation serves the purpose of ensuring that the applied synthetic SMB does indeed result in a steady-state geometry in which divide positions do not migrate and surface topography changes are minimal. It then also functions as a baseline against which the perturbation simulations can be compared. The thinning/thickening rates in this type of simulation for both meshes are highest at the start of the simulation but never exceed 0.05 m yr⁻¹ near the divide region. These low thinning/thickening rates result in a steady-state geometry of the model domain that is also characterised by stable positions of the ice-rise divides. For both ice rises total divide-migration amplitudes are <60 m throughout the forward simulation of 1000 years. Divide positions are computed at every time step along two swath profiles (∼8 and ∼23 km for Halvfarryggen and Söråsen, respectively; e.g. Fig. 7). The shorter swath profile for Halvfarryggen was chosen to permit a simple flux balance analysis. The initial start point of the divide is the location of highest surface elevation. From this point, the divide is tracked along the swath profile by following the minimum direction of the aspect gradient until the end of the swath. Computed mean divide-migration amplitudes are then averaged along the swath profiles (e.g. Fig. 6).

4.3 Surface-mass-balance-induced divide migration (runs 3–6)

4.3.1 Halvfarryggen Ice Rise

In simulations 3–5 (Table 2), the SMB perturbation results in immediate divide migration for both meshes (Fig. 6a). For Halvfarryggen, we focus our analysis on the main (eastern) divide ridge (Fig. 1b). Owing to the more positive SMB on the eastern side of both divides, the divide migrates towards this region (Fig. 7a). Almost all of the divide migration occurs over the first 200 years of the simulation before a new steady-state position is reached (Fig. 6a). During the first 200 years, the entire divide migrates at an average rate of 16–20 m yr⁻¹ to the east for the Halvfarryggen Ice Rise. This range shows there is a clear mesh dependence on the magnitude of divide migration over this timeframe (3.2–3.8 km, Fig. 6a), whereas this difference is less pronounced in the steady-state divide positions at the end of the simulation (2.5–2.8 km). For the two refined meshes (runs 4 and 5; Table 2), mesh dependence is still present, even if reduced, and first-order convergence between the simulations is absent. This indicates that a very fine mesh resolution is required to capture divide migration, but, in the light of the high computational costs to run all simulations at such a resolution, we restrict ourselves to a maximum resolution of 500 m. While the averaged absolute magnitude along the swath profile is offset by about 300 m between the refined grid simulations (runs 3 and 4; Table 2), the temporal pattern of divide migration is identical (Fig. 6a). This is in contrast to the regular mesh, where divide migration reaches its maximum (most eastern position) after ∼200 years and remains almost stable for the remaining simulation period. In comparison, the refined mesh simulations reach their maximum divide migration at a similar time (∼200 years) but start to slowly migrate back towards its initial position until a steady state is reached after 700 years (Fig. 6a). The SMB grounding-line flux perturbation simulation (Run 6, Table 2) has almost an identical steady state to the unadjusted SMB simulation (Fig. 6a), despite the SMB flux difference between east and west of the divide being twice as high. While this does not affect the steady-state divide position, it does result in faster migration with a larger maximum amplitude of divide migration (∼3.9 km vs. ∼3.4 km).

4.3.2 Söråsen Ice Rise

The Söråsen Ice Rise shows a very similar response – both in absolute magnitude of divide migration as well as temporal evolution of divide migration – to the applied SMB perturbation (Fig. 6b) The most pronounced differences of ∼ 4 m yr⁻¹ are in the divide-migration rates (11–15 m yr⁻¹) in the first 200 years of the simulation, when most of the divide migration takes place. The mesh dependence on divide-migration amplitudes is also present for Söråsen, even though it is slightly reduced in comparison to Halvfarryggen (2.9–3.3 km, Fig. 6b). Unlike Halvfarryggen, simulations with the refined mesh do not show any backward migration of the Söråsen divide (Fig. 7c) but reach a new steady-state position after ∼300–400 years with little migration beyond this point in all simulations (Fig. 6b).

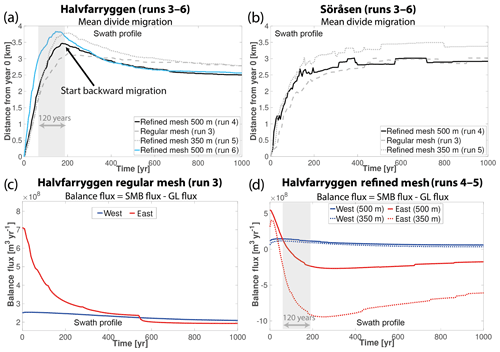
Figure 6 Ice-rise divide migration for (a) the Halvfarryggen Ice Rise and (b) the Söråsen Ice Rise induced by surface mass balance perturbation for different mesh resolutions. Positive numbers indicate migration to the east. Panels (c) and (d) show balance fluxes for the eastern and western side of the divide to the grounding line for the Halvfarryggen Ice Rise. Grey shaded areas in (a) and (d) highlight the time lag between the balance flux east being smaller than the corresponding flux west and the start of backward migration. “Swath profile” indicates that computed divide migration is averaged over cross sections shown in Fig. 7. For the grounding line (GL) flux, this means that the flux is summed along the current grounding-line position over the swath length. The surface mass balance (SMB) flux is area averaged from the current divide position to the respective grounding-line position in the east and west of the divide over the swath length. Note different y-axis scales in (c) and (d).

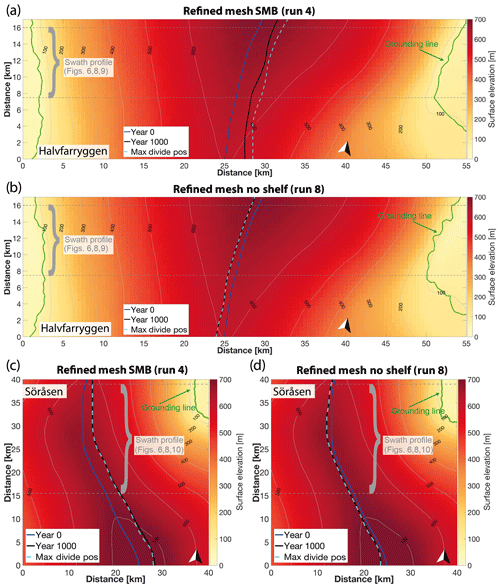
Figure 7 Ice-rise divide positions using the refined mesh for the Halvfarryggen Ice Rise induced by (a) surface mass balance perturbation and (b) shelf removal perturbation. Panels (c) and (d) show the same simulations for the Söråsen Ice Rise. Divide positions are plotted at the start of the simulation, at the end of the simulation, and at the time of maximum divide-migration amplitude for each simulation.

4.4 Ocean-perturbation-induced divide migration (runs 7–11)

Ocean perturbation causes the adjacent ice shelves to thin and reduce their ability to buttress the ice upstream. If buttressing of ice shelves on either side of the ice rise is asymmetric, this should lead to an asymmetric increase in grounding-line flux, which in turn should result in an asymmetric thinning perturbation. This asymmetric thinning perturbation should then push the divide in the direction of the smaller thinning perturbation (Fig. 2c). In our model simulations, we test this hypothesis using the real-world example of the Ekström Ice Shelf embayment.

4.4.1 Halvfarryggen Ice Rise

All ocean perturbation experiments result in an instantaneous divide migration. For the extreme case of ice-shelf removal (runs 7–9, Table 2) the maximum mean ice-divide migration along the swath is −0.4 and −0.7 km with local maximum amplitudes of −1.7 and −2.3 km, occurring after 700 and 1000 years for the regular and refined mesh, respectively (Fig. 8a). Negative numbers indicate westward migration (Fig. 7b, d). For the intermediate thinning scenarios (runs 10–11, Table 2), there is no divide migration for the 10 % thinning scenario and −0.2 km divide migration for the 50 % thinning scenario. So even though half of the shelf's thickness is removed, the magnitude of the divide migration is reduced by 77 %, indicating that the response to ice-shelf thinning is non-linear and requires a strong perturbation for a significant response. Most of the divide migration takes place in the centuries following the perturbation. A stable divide position is reached after ∼690 years for the regular mesh simulation and after ∼480 years for the refined mesh simulation in the shelf removal scenario (Fig. 8a). In the 50 % shelf thinning scenario, a stable divide position is reached after ∼600 years. As was the case for the SMB, the shelf removal simulations exhibit mesh dependence with mesh convergence present for the two refined meshes (Fig. 8a).

To shed light on why divide-migration amplitudes differ for the different shelf thinning scenario, grounding-line fluxes for the eastern and western side were computed for Halvfarryggen (Figs. 8c, d and 9c). In all simulations, an initial sharp increase in grounding-line flux is computed, which then quickly decays and is even lower for the eastern side of the divide than in the reference simulation (Fig. 8c, d). The initial flux perturbation is largest for the shelf removal scenario and is non-linear, where halving of the ice-shelf thickness results in a flux reduction of 60 %.

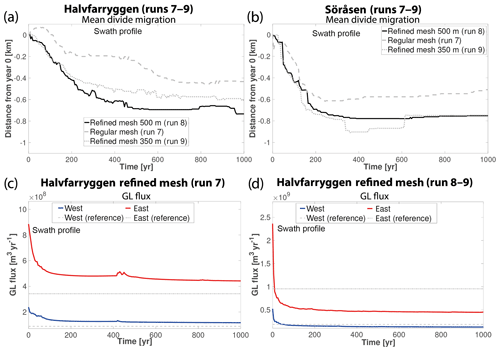
Figure 8 Ice-rise divide migration for (a) the Halvfarryggen Ice Rise and (b) the Söråsen Ice Rise induced by ocean perturbation (shelf removal) for different mesh resolutions. Negative numbers indicate migration to the west. Panels (c) and (d) show grounding-line (GL) fluxes for the eastern and western side of the divide to the grounding line for the Halvfarryggen Ice Rise. “Swath profile” indicates that computed divide migration is averaged over cross sections shown in Fig. 7. For the GL flux, this means that the flux is summed along the current grounding-line position over the swath length. Note different y-axis scales in (c) and (d).

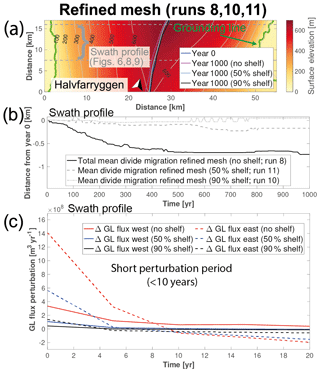
Figure 9 (a–c) Ice-rise divide migration for the Halvfarryggen Ice Rise induced by different ocean perturbations (shelf removal, 50 % ice-shelf thickness, and 90 % ice-shelf thickness) for the refined mesh. (a) shows divide position at the end of the simulation period. Grey dashed lines show the approximate area used for flux calculations in (c). (b) shows mean divide migration for the different perturbations. Negative numbers indicate migration to the west. (c) displays ice flux perturbation across the grounding line for the eastern and western side of the divide for the first two decades. Perturbation fluxes smaller than 0 indicate that ice flux across the grounding line is reduced in comparison to the reference simulation. (b, c) “Swath profile” indicates that computed divide migration is averaged over cross sections as shown in (a). For the ΔGL flux, this means that the flux is summed along the current grounding-line position over the swath length.

4.4.2 Söråsen Ice Rise

For the extreme case of ice-shelf removal (runs 7–9, Table 2) the maximum ice-divide migration is −0.5 and −0.7 km with local maximum rates of −1.0 and −1.5 km for the regular and refined mesh, respectively (Fig. 8b). Almost all of the divide migration happens in the first half of the simulation period before a new steady-state position is reached after 300 years for the regular mesh and after ∼400 years for the refined mesh (Fig. 8b). This behaviour closely follows Halvfarryggen both in terms of migration amplitudes and direction (Fig. 8b). This is not the case for the intermediate thinning scenarios (runs 10–11, Table 2), where no divide migration (<60 m) occurs in any of them.

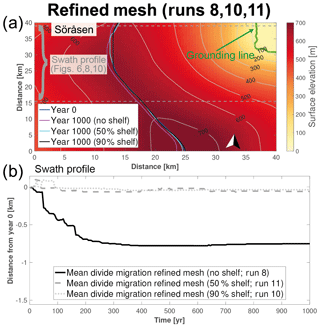
Figure 10 (a, b) Ice-rise divide migration for the Söråsen Ice Rise induced by different ocean perturbations (shelf removal, 50 % ice-shelf thickness, and 90 % ice-shelf thickness) for the refined mesh. (a) shows divide positions at the end of the simulation period. (b) shows mean divide migration for the different perturbations. Negative numbers indicate migration to the west.

4.5 Triple junction migration for the Halvfarryggen Ice Rise

In both experiments (runs 4 and 8), the triple junction immediately migrates in response to the perturbations. The triple junction evolution closely follows the temporal evolution of the main divide. The maximum migration amplitude is 3.3 and −1.2 km for the SMB and shelf removal simulations, respectively. Most of the triple junction migration takes place over the first ∼400 years, before a new steady-state position is reached (Fig. 11). The temporal evolution of the triple junction migration also shows a tendency to migrate back to its initial position in the latter part of the SMB simulation (Fig. 11c). Because the SMB is most positive to the east of the main divide arm, the eastward migration of the divide leads to an increased angle between these two ridges of 3.5^∘, translating into a widening of 5 %. In addition to the widening, the minor ridge appears less distinct at the end of the simulation period (Fig. 11b). This feature is absent in the shelf removal simulation. In contrast to the SMB simulation, the westward migration of the divide leads to a narrowing of the angle between the two ridges, albeit only by 1.1^∘, corresponding to a narrowing of 1.4 %. The main component of the migration is east–west, but in both simulations the triple junction also migrates south.

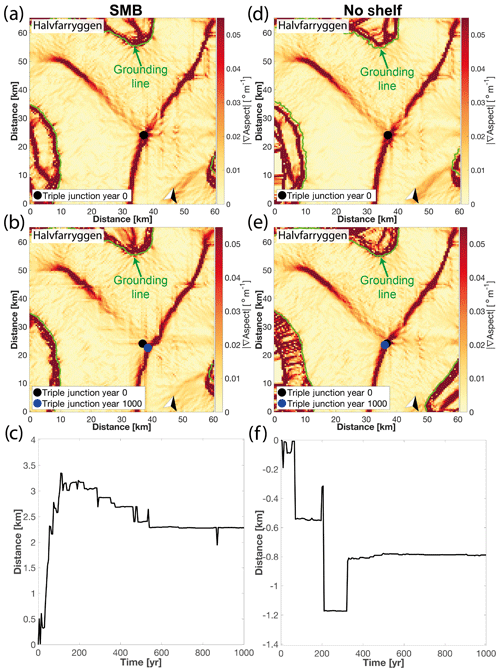
Figure 11 Triple junction migration for the Halvfarryggen Ice Rise induced by (a–c) surface mass balance perturbation for the refined mesh and (d–f) ocean perturbation (shelf removal) for the refined mesh. Upper and middle panels (a, b, d, e) were regridded onto a 500 m Cartesian mesh and show the triple junction position at the start and end of the simulation period, respectively. Lower panel (c, f) shows mean divide migration for the respective perturbation simulations. Negative numbers indicate migration to the west. Note different y-axis scales in (c) and (f).

5 Discussion

5.1 Effect of mechanical model in initialisation on transient simulations

Transient simulations using basal drag coefficient and ice viscosity fields from the SSA inversion result in unrealistically large ice mass loss rates in the decades following model initialisation. Knowing that the Ekström catchment is likely close to a steady state (Drews et al., 2013), we attribute these differences in the transient simulations to the difference in force balance approximation used in the inversion and transient simulation. This shows that for the presented ice-rise modelling a FS inversion is necessary for plausible transient simulations.

5.2 Surface-mass-balance-induced divide migration

The computed mean divide-migration rates of 2.5–3.5 m yr⁻¹ for both ice rises are higher than what has previously been inferred from the geometric analysis of Raymond stacks (0.5 m yr⁻¹, Siple Dome; Nereson et al., 1998). This means a realistic SMB perturbation, which could have occurred at the Last Glacial Maximum (LGM), leads to fast divide migration – even more so because these migration rates are even higher (11–20 m yr⁻¹) if only the first 200 years are considered. Such a perturbation would likely lead to an abandoning of the Raymond stack and the formation of a new Raymond stack at the new steady-state divide position (Fig. 2e), as the divide migrates >3 ice thicknesses away from its initial position. Because the Raymond stack at Halvfarryggen and Söråsen are well developed and it takes ∼10T (T = characteristic time, T=900 years, Drews et al., 2013) to form such a stack, we conclude that both ice rises have not experienced a perturbation of such magnitude over the last ∼9000 years, indicating stable ice-flow conditions in this embayment for at least the Holocene time period.

For both ice rises, divide migration shows a clear dependence on mesh resolution. As the regular mesh simulations are most likely under-resolved, we will mainly focus here on the refined mesh simulations. In the latter half of the simulation period (Fig. 6a), the refined mesh simulations show a subtle backward migration trend. We attribute this backward migration pattern to be a direct result of an imbalance in balance fluxes for the eastern and western side of the divide (Fig. 6c, d). The more positive SMB on the eastern side of the divide results in an initial increase in balance flux, which quickly decays over time because the grounding-line flux compensates for the increased ice thickness by discharging more ice into the shelf. After ∼80 years the balance flux on the eastern side is lower than the corresponding flux on the western side. However, the balance flux continues to decrease because of the continuing increase in grounding-line flux up to ∼250 years, before it recovers slightly. The negative balance flux in the east leads to the computed subtle back migration trend from ∼185 years to ∼700 years. However, the timing of when the balance flux in the east starts to be lower than the balance flux in the west is 120 years prior to this (Fig. 6a, d). This means that there is a time lag of 120 years before the divide reacts to changes in the balance fluxes. The time lag may be a little smaller since the balance flux in the east is also lower than the balance flux in the west for the regular mesh simulation, but it does not result in backward migration of the divide. This indicates that there must be a certain magnitude in the imbalance of the balance fluxes on either side of the divide before the divide responds to this. The difference in the balance flux analysis between the regular and refined mesh (Fig. 6c, d) also highlights the importance for fine mesh resolution to resolve these processes, corroborating that mesh resolutions finer than 500 m are required. A flux analysis could not be performed for Söråsen because the selected model domain does not completely cover the ice rise.

5.3 Ocean-perturbation-induced divide migration

Since divide-migration amplitude is ≤1 ice thickness away from the initial divide position and the mean migration rates are <0.75 m yr⁻¹, we interpret this as shelf thickness perturbations resulting in slow divide migration. Especially in the context of complete shelf removal as a rather extreme perturbation, the intermediate thinning scenarios might provide a more realistic experiment for the recent past of the Ekström catchment. The simulated small migration amplitudes for the intermediate shelf thinning scenarios (<300 m) indicate that, due to the wedged-in geometrical setting of the Ekström Ice Shelf, a large portion of the shelf thickness needs to be removed before any flux increase across the grounding line becomes apparent and leads to migration of the divide. This means that shelf thickness perturbations in our experiment would most likely result in a left-tilted Raymond stack rather than lead to the abandoning of the initial Raymond stack (Fig. 2f). The low migration amplitudes also show that the employed mesh resolution (∼500 m) may be insufficient for the intermediate scenarios, but owing to computational restrictions this is the highest resolution possible.

As all mean migration amplitudes are <1 km, we will restrict our discussion to the refined mesh simulations (runs 8–9, Table 2). Based on our asymmetric buttressing hypothesis, a simple interpretation of our results would be that the Jelbart Ice Shelf for Halvfarryggen and the Ekström Ice Shelf for Söråsen provide more buttressing than their respective counterparts in the west, as the divides of both ice rises migrate to the east. However, when using Schoof's flux formula (Schoof, 2007) together with the computed initial fluxes to estimate buttressing (Θ) for Halvfarryggen, the derived values for Θ are similar for both shelves (Table 3). Despite the similar stress reduction through thinning or removal of the ice shelf, the increase in absolute flux across the grounding line differs. This asymmetry is not induced by asymmetric buttressing but is caused by the difference in initial flux across the grounding line, which is almost an order of magnitude higher in the east than the counterpart in the west. If now the stress is reduced by the same percentage, the flux imbalance between east and west will widen (Table 3), resulting in the divide migrating to the west. We infer from our model simulations that while buttressing induces divide migration, it is by no means necessary to have asymmetric buttressing for the divide to migrate. The more important determining factor as to how far the divide is going to migrate is the absolute flux imbalance between the two sides of the divide. If we use the flux imbalance from the three different shelf thinning/removal simulations (runs 8 and 10–11, Table 2), the relationship is almost linear between flux imbalance and the resulting divide migration. If this linear fit equation and the modelled flux imbalances are used to predict divide migration for the same three simulations, migration amplitudes of −718, −277, and −16 m are predicted. This compares reasonably well with the computed divide-migration amplitudes after 100 years of −734, −235, and −43 m, respectively. This does not mean that this relationship must be linear but underlines the fact that flux imbalance is much more important than the buttressing provided by the ice shelf for divide migration.

Table 3 Flux calculations, derived buttressing factors, and stress reduction calculations for both sides of the divide for the Halvfarryggen Ice Rise from runs 8 and 10–11 (Table 2). GL flux reduction in relation to the shelf thickness perturbation simulations (column 2) is computed by dividing ΔGL flux (column 3) by GL flux (column 2), and the buttressing factor and stress reduction are calculated from Schoof (2007) (Eq. 29).

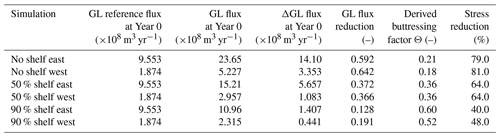
5.4 Comparison of SMB- and ocean-induced divide migration

Despite the fact that the SMB perturbation represents the more physically realistic perturbation rather than the most extreme shelf thickness perturbation (shelf removal), the SMB perturbation results in fast divide migration and the shelf thickness perturbation leads to slow divide migration. This leads us to a different interpretation for the resulting geometry of the Raymond stack, with SMB perturbations leading likely to a Raymond stack abandoning and ocean perturbations resulting in a left-tilted Raymond stack (Fig. 2e, f).

The response of the divide position to ocean perturbations is primarily controlled by the subglacial topography with lateral buttressing only being a controlling factor of secondary order. The modelled short-lived response of the increased grounding-line flux to all ocean perturbations is typical of drainage basins located on prograde sloping bedrock (Fig. 12), where the instantaneous removal of all buttressing leads to a sudden but short-lived response. Similar results have been obtained from the modelling of ice-shelf collapse in the Antarctic Peninsula region (Schannwell et al., 2018).

As both ice rises in the model domain, and to the authors' knowledge most other ice rises around Antarctica as well, are located on subglacial topography plateaus, the potential for grounding-line retreat is limited. Because ice flux across the grounding line is primarily a function of ice thickness at the grounding line (Schoof, 2007), the initial retreat of the grounding line on prograde slopes often leads to thinner ice at the grounding line and in turn leads to a reduction of ice flux across the grounding line that can even be lower than before the perturbation. Similarly, the response of the divide position to SMB perturbations also seems to be primarily controlled by the subglacial topography with the magnitude of the flux imbalance between east and west of the divide being a controlling factor of secondary order. Evidence for this is provided by the unadjusted SMB perturbation (Run 5, Table 2) and the SMB grounding-line flux perturbation (Run 6, Table 2) simulations, which both converge to the same new steady-state divide position, even though the forcing is different by a factor of 2.

As SMB perturbations directly affect surface topography, this type of perturbation leads to quicker response times of ice-divide migration in comparison with shelf thickness perturbation with e-folding times of 95–170 and 30–50 years for shelf thickness and SMB simulations, respectively. This means that not only is the magnitude lower, but also the timing of ice-rise divide migration is delayed in the case of shelf thickness perturbations. Moreover, even though the magnitude of the initial perturbation is lower for the SMB simulations, divide migration is larger by a factor of ∼3.4 and ∼3.9 for Halvfarryggen and Söråsen, respectively. The divide-migration rate and amplitude for SMB perturbations is most likely heavily dependent on the spatial pattern of the perturbation, with SMB perturbations near the divide likely leading to faster and larger divide migration than SMB perturbations that have their maximum farther away from the divide (Hindmarsh, 1996).

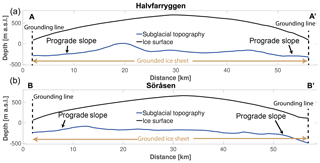
Figure 12 Cross sections of grounded subglacial topography from the BEDMAP2 dataset (Fretwell et al., 2013) for the (a) Halvfarryggen and (b) Söråsen ice rises, underlining the prograde sloping subglacial topography of both ice rises in the vicinity of the current grounding line.

In spite of the lower divide-migration rates computed from shelf thickness perturbations, the magnitude of the migration is still large enough to affect the geometry of Raymond stacks. The computed magnitudes are of similar amplitude to divide-migration rates inferred for Siple Dome (Nereson and Waddington, 2002). Moreover, the Ekström Ice Shelf and Jelbart Ice Shelf belong to the smaller ice shelves around Antarctica, making it likely that ice rises with larger ice flux across the grounding line in combination with larger buttressing provided by the surrounding ice shelves may well have the potential to experience larger divide-migration rates.

The rate of triple junction migration appears to be closely linked to the migration rate of the main divide arm and thus seems to be similarly susceptible to migration as divide ridges. There appears to be a widening/splitting trend of the triple junction in the SMB simulations and a narrowing/merging trend for the shelf thickness simulations. However, the migration amplitudes are insufficient to evaluate if a merging or splitting of a divide triple junction might explain observed radar features such as relic arches in the divide flank (Drews et al., 2015). Migration of the triple junction also bears importance for selecting potential ice-core drilling sites on these types of ice domes, and a tilted Raymond stack may indicate a displacement of the triple junction as well.

5.5 Model limitations

By calibrating our ice-sheet model on the Ekström Ice Shelf catchment, we aim to introduce commonly employed initialisation techniques in large-scale ice-sheet modelling to ice-rise modelling. The advantage of the calibration is that buttressing is simulated in a realistic fashion. Without the calibration, large thinning/thickening rates would result in unrealistic model results. However, the calibration matches observed horizontal velocities with modelled horizontal velocities without any constraints on vertical ice velocities. This leads to the situation that any errors in the horizontal velocities propagate into the vertical velocity through mass conservation. As horizontal velocities in the divide region are close to zero, small errors in horizontal velocities have a large effect on vertical velocities, and therefore we were unable to solve for the age field (Raymond stacks). In addition, due to computational constraints, only 10 equally spaced vertical layers could be employed. For an ice thickness of ∼900 m at the Halvfarryggen Ice Rise, this corresponds to a vertical resolution of ∼90 m. While this vertical resolution is sufficient for our ice-rise divide migration purposes, a much higher vertical resolution (∼30–40 layers) would be necessary to model Raymond arches at the required detail (Drews et al., 2015). Similarly, despite refining the mesh locally down to 350 m, this may still not suffice for some of the shelf removal simulations, where finer meshes than presented here (<350 m) may result in larger divide-migration amplitudes.

In spite of the advanced ice-sheet model employed, compromises in the complexity of the experimental setup had to be made to make these simulations computationally feasible. These simplifications or approximations were done with the goal of focussing on ice-rise divide migration at the expense of accurately simulating Raymond arch formation. In the following, we will list these simplifications and regard each of them as future avenues to improve on the simulations presented here. As suggested by many previous ice-rise divide studies, the commonly used exponent of the ice rheology law (n=3) is not able to reproduce the Raymond arch amplitudes from observations, but often a higher exponent (n≈4.5) is chosen that better matches the arch amplitudes from observations (Martín et al., 2014; Drews et al., 2015; Bons et al., 2018). Moreover, Martín et al. (2009a) showed that the commonly employed approximation of ice being an isotropic material in large-scale ice-sheet models is not valid at ice divides, where a preferential orientation of the ice crystals leads to enhanced ice deformation. Changes in ice deformation can also be caused by changes in ice temperature, where warmer ice leads to enhanced ice deformation and cold ice reduces ice deformation. While the effect of temperature and enhanced/decreased ice deformation could introduce differences in divide position, to the author's knowledge no one has comprehensively shown this. However, previous studies have found that thermomechanically coupled models exhibit warmer ice at the base under the divide (Martín and Gudmundsson, 2012), which could potentially indicate that divide migration may occur faster. As our model is not thermomechanically coupled, these effects are ignored in the simulations. Even though ice temperature and anisotropy have been identified as important parameters to be able to reproduce the internal structure of ice divides, it is still uncertain as to how much they affect divide migration.

We performed our simulations with only one type of sliding law (linear Weertman), without testing alternative implementations. Even though other modelling studies have shown that this type of sliding law generally results in smaller grounding-line retreat than other sliding laws (e.g. pressure-limited sliding law; e.g. Schannwell et al., 2018), it remains difficult to assess the importance of the sliding law for divide migration. On the one hand, reduced basal drag may lead to enhanced grounding-line retreat (Price et al., 2008; Gillet-Chaulet et al., 2016), but on the other hand ice near the divide region might be frozen to the bed and sliding can be neglected in these areas. Therefore, we believe that the choice of the sliding law is likely to have a limited impact on our results. Given that many previous ice-divide modelling studies assume no basal sliding at all (e.g. Martín et al., 2006), the largest impact of this simplification will be on the grounding-line position in the ocean perturbation simulations. But even there, owing to the prograde sloping subglacial topography, the effect of different sliding laws should not be a major concern for the computed divide-migration rates.

6 Conclusions

We used a calibrated 3-D ice-sheet model including grounding-line dynamics and shelf flow for the Ekström catchment to investigate the coupled transient response of ice-rise divides and triple junctions to perturbations in the SMB and ice-shelf thickness. Our perturbation simulations for the Ekström catchment reveal that SMB perturbations result in fast divide migration (up to 3.5 m yr⁻¹), while shelf thickness perturbations only trigger slow divide migration (< 0.75 m yr⁻¹). The amplitude of divide migration is predominately controlled by the subglacial topography and SMB, with ice-shelf buttressing being of secondary importance.

We find in our simulations that asymmetric buttressing is not a required condition for ice-rise divide migration, but rather how much the divide will migrate is determined by the flux imbalance between either side of the divide. Both ice rises show a closely coupled response to the perturbations with divide migration being similar in timing and magnitude. Based on our simulations, the geometry of the Raymond stack could provide clues about the forcing mechanism behind the divide migration, with an abandoned Raymond stack being more likely linked to SMB perturbations. For tilted Raymond stacks the interpretation of the internal structure remains difficult with either a smaller SMB perturbation than prescribed here or shelf thickness perturbations equally likely. It is important to further unravel (e.g. through synthetic experiments) the different trigger mechanisms for different types of Raymond arch geometries in order to fully unlock the potential of ice rises as ice-dynamic archives, potential ice-core drilling site, and to better constrain palaeo-ice-sheet models.

We find that a high mesh resolution (<500 m) is required in the vicinity of the dome and the grounding-line to capture ice-rise divide migration at the desired detail, as mean maximum migration amplitude is <4 km in our perturbation experiments. To avoid unrealistic ice mass loss in transient simulations around the divide region, where longitudinal and bridging stresses are important, the same force balance approximation (e.g. FS for ice divides) should be used in the initialisation and forward simulation of the ice-sheet model.

Finally, migration of the triple junction closely follows the migration pattern of the main ridge, which may prove useful in the future selection of ice-core drilling sites. However, more targeted simulations are required to determine whether a merging or splitting of the triple junction can explain relic Raymond stacks in the flanks of ice rises. The model setup is suitable for glacial/interglacial simulations on the catchment scale, providing the next step forward to unravel the ice-dynamic history stored in ice rises all around Antarctica.