the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Snow-driven uncertainty in CryoSat-2-derived Antarctic sea ice thickness – insights from McMurdo Sound
Daniel Price
Iman Soltanzadeh
Wolfgang Rack
Ethan Dale
Knowledge of the snow depth distribution on Antarctic sea ice is poor but is critical to obtaining sea ice thickness from satellite altimetry measurements of the freeboard. We examine the usefulness of various snow products to provide snow depth information over Antarctic fast ice in McMurdo Sound with a focus on a novel approach using a high-resolution numerical snow accumulation model (SnowModel). We compare this model to results from ECMWF ERA-Interim precipitation, EOS Aqua AMSR-E passive microwave snow depths and in situ measurements at the end of the sea ice growth season in 2011. The fast ice was segmented into three areas by fastening date and the onset of snow accumulation was calibrated to these dates. SnowModel captures the spatial snow distribution gradient in McMurdo Sound and falls within 2 cm snow water equivalent (s.w.e) of in situ measurements across the entire study area. However, it exhibits deviations of 5 cm s.w.e. from these measurements in the east where the effect of local topographic features has caused an overestimate of snow depth in the model. AMSR-E provides s.w.e. values half that of SnowModel for the majority of the sea ice growth season. The coarser-resolution ERA-Interim produces a very high mean s.w.e. value 20 cm higher than the in situ measurements. These various snow datasets and in situ information are used to infer sea ice thickness in combination with CryoSat-2 (CS-2) freeboard data. CS-2 is capable of capturing the seasonal trend of sea ice freeboard growth but thickness results are highly dependent on what interface the retracked CS-2 height is assumed to represent. Because of this ambiguity we vary the proportion of ice and snow that represents the freeboard – a mathematical alteration of the radar penetration into the snow cover – and assess this uncertainty in McMurdo Sound. The ranges in sea ice thickness uncertainty within these bounds, as means of the entire growth season, are 1.08, 4.94 and 1.03 m for SnowModel, ERA-Interim and AMSR-E respectively. Using an interpolated in situ snow dataset we find the best agreement between CS-2-derived and in situ thickness when this interface is assumed to be 0.07 m below the snow surface.
- Article
(3445 KB) - Full-text XML
- BibTeX
- EndNote
The knowledge of Antarctic sea ice extent, area, drift and roughness have been greatly improved over the last 40 years, principally supported by satellite remote sensing. Nevertheless, many knowledge gaps remain which restrict our ability to better understand the Antarctic sea ice system. A foremost concern is inadequate data for the snow depth distribution on Antarctic sea ice (Pope et al., 2016) as the presence of snow has many important implications for the sea ice cover (Massom et al., 2001; Wu et al., 1999; Fichefet and Maqueda, 1999). The thermal conductivity of snow is almost an order of magnitude less than sea ice (Maykut and Untersteiner, 1971) and as snow accumulates, it reduces the conductive heat flux from the ocean to the atmosphere, slowing growth rates, but also leads to thickening of the ice cover through snow–ice formation (Maksym and Markus, 2008). Snow significantly increases the albedo of the sea ice cover and in the austral spring and summer snowmelt is responsible for freshwater input to the Southern Ocean (Massom et al., 2001). Perhaps most crucially from a satellite observation perspective is our inability to accurately monitor its depth and distribution causes large uncertainty when estimating sea ice thickness. Sea ice thickness measurements as inferred via satellite freeboard estimates (Schwegmann et al., 2016; Kurtz and Markus, 2012; Giles et al., 2008) currently present the best opportunity to establish yet unpublished datasets on decadal trends in Antarctic sea ice volume. Without improved snow depth measurements, it is impossible to discern meaningful trends in Antarctic sea ice thickness. Errors are introduced to thickness estimates via the snow cover for two principal reasons:
-
Snow depth information is inaccurate or not available and therefore the ratio of ice and snow above the waterline is poorly quantified or unknown.
-
Uncertainty about what surface the retracking point on the radar waveform actually represents between the ice freeboard and snow freeboard. This initial measurement is commonly referred to as radar freeboard.
The uncertainty associated with these two factors has not been directly investigated using satellite altimeter information over Antarctic sea ice. This work provides insights from a case study region, McMurdo Sound in Antarctica. Snow on Arctic sea ice has been investigated in more detail and over a longer period than the Antarctic so climatologies can be produced (Warren et al., 1999). These datasets, in combination with satellite altimetry, and suitable airborne investigations have permitted the completion of pan-Arctic thickness assessments (Kurtz et al., 2014; Laxon et al., 2013; Kwok and Cunningham, 2008). The research community lacks snow climatology information in the Southern Ocean, though dedicated basin-scale snow depth assessments are available via passive microwave sensors (Markus and Cavalieri, 2006). Continual improvements in our monitoring ability are key to supporting the current ESA satellite altimeter missions, CryoSat-2 (CS-2) and Sentinel-3, and NASA's laser altimeter mission ICESat-2. To date only AMSR-E passive microwave data have been used in combination with altimetry to estimate sea ice thickness. The AMSR-E algorithm's accuracy is decreased by rough sea ice and deep and complex snow (Kern and Ozsoy-Çiçek, 2016; Kern et al., 2011; Worby et al., 2008b; Stroeve et al., 2006), both typical characteristics of the Antarctic sea ice cover. Using laser altimetry, some investigators have assumed a zero-ice freeboard (Kurtz and Markus, 2012); that is, the snow loading forces the ice surface to the waterline, negating the need for snow depth data. Thickness estimates using this approach are likely biased low and although this simplification provides valuable insights, it does not provide sea ice thickness at the desired accuracy. This work is motivated by the necessity for a comprehensive understanding of the usefulness of snow products in the Southern Ocean, and the need to investigate new avenues for producing snow depth products over Antarctic sea ice. Here we make use of a detailed in situ dataset to assess modelling and satellite approaches to construct snow depth over the 2011 sea ice growth season. In a first attempt over Antarctic fast ice, using a high-resolution snow accumulation model called SnowModel (Liston and Elder, 2006a) and synthetic aperture radar imagery, we are able to establish when the sea ice fastens and accumulate snow from those dates for three areas of fast ice in McMurdo Sound in the south-western Ross Sea. The high-resolution model results are compared to snow products from two other independent datasets, the first being ERA-Interim (ERA-I) precipitation and the second being satellite passive microwave snow depth from AMSR-E. With these different snow depth datasets we infer sea ice thickness via freeboard measurements from CS-2. The interaction of radar energy with the snow pack is highly complex and here we take a simplified approach given the surface height has already been established by the ESA retracking procedure. Given the uncertainty of the position of the retracking point with reference to the height above sea level, we assume different penetration depths into the snowpack by varying the proportion of ice and snow that represents the freeboard. We compare the inferred CS-2 thicknesses with in situ information.
2.1 McMurdo Sound and field data
A detailed in situ sea ice measurement campaign was carried out in November 2011 on the fast ice in McMurdo Sound (Fig. 1). This involved sea ice thickness, freeboard, snow depth and snow density measurements at 39 sites. The freeboard was measured 5 times in a cross-profile at each site, once at the centre of the cross and once at the terminus of each line, as was thickness. Mean snow depths for each in situ site represent 60 individual snow depth measurements over that same cross-profile at 50 cm intervals. Snow density was measured at 18 sites, well distributed across the area, and the mean of these sites is used for this analysis unless stated otherwise. A full overview of the measurement procedure is provided in Price et al. (2014). Additional in situ measurements of sea ice thickness are included in the analysis: two measurements taken at one location in McMurdo Sound in July and November. Assuming a constant growth rate between these measurements they are used in Sect. 5 as a comparison to CS-2 inferred sea ice growth rates. More detail on how the in situ thickness measurements are used and how they should be interpreted is provided in Sect. 5.
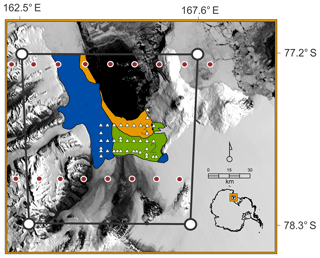
Figure 1McMurdo Sound study area with each fastening area as identified by Envisat radar imagery: area 1 – 1 April 2011 (blue), area 2 – 29 April 2011 (green), area 3 – 1 June 2011 (orange). The SnowModel domain bounded by the black box. Fastening areas are superimposed on a MODIS image acquired on 15 November at the time of maximum fast ice extent in 2011. The locations of 39 measurement sites used to produce the in situ snow and sea ice statistics are shown as white triangles. The centre points of each ERA-I grid cell in the vicinity of the study area are displayed as red circles.
2.2 Envisat
The sea ice freeze-up provides a point from which snow can begin to accumulate on the sea ice surface. Freeze-up could be identified using passive microwave information, but these data do not provide the spatial resolution to segment the sea ice area appropriately for SnowModel's 200 m resolution. In McMurdo Sound during the freeze-up period, pack ice is generally advected north out of the study area unless it fastens. In addition to floe movement, before fastening occurs, snowfall is subject to uncertainty from flooding events and snow loss to leads, influences on the eventual snow depth that we have no way of accurately monitoring. With the resolution restriction in mind and these uncertainties, we have selected the sea ice fastening date to begin snow accumulation. To identify the dates and the pattern in which the sea ice fastens across the study area, we use a string of C-band Advanced Synthetic Aperture Radar (ASAR) images from Envisat acquired in Wide Swath mode. We process these files using GAMMA Software to produce ASAR imagery with a spatial resolution of 150 m × 150 m. By comparing motion and patterns between sequential images we are able to identify three areas that fastened independently of one another. The first area of fast ice was established by 1 April (area 1 – Fig. 1). By the end of April, a second area of fast ice had formed along the southern extremity of the Sound (area 2 – Fig. 1), and by the beginning of June, a third area had fastened (area 3 – Fig. 1). The largest gap in the Envisat image string is 8 d but no large gaps are found around key fastening dates. The typical spacing is 1–2 d so we have confidence we have reduced our error in the fastening date to less than 2 d. These three areas persisted for the winter and, when combined, made up the fast ice area present in late November when in situ measurements were made.
2.3 AMSR-E
The EOS Aqua Advanced Microwave Scanning Radiometer (AMSR-E) provided data between 18 June 2002 and 4 October 2011. The snow depth product provided by NSIDC (https://nsidc.org/data/ae_si12, last access: April 2018) is provided at a 12.5 km × 12.5 km polar stereographic projection and reported as a 5 d running mean, that mean inclusive of that day and the prior 4 d. We remove data where ice concentrations are lower than 20 %. Gridded snow depth values are calculated using the spectral gradient ratio of the 18.7 and 36.5 GHz vertical polarization channels. For snow-free sea ice the emissivity is similar for both frequencies. Snow depth increases attenuation from scattering but is more pronounced at 36.5 GHz than at 18.7 GHz, resulting in higher brightness temperatures at 18.7 GHz (Comiso et al., 2003; Markus and Cavalieri, 1998). Using coefficients derived from a linear regression of in situ snow depth measurements on microwave data, and a 36.5–18.7 GHz ratio corrected for sea ice concentration, snow depth can be estimated (Comiso et al., 2003). Snow depth retrievals are restricted to dry snow only and to a depth of less than 50 cm. Variable snow properties including snow grain size, snow density and liquid water content influence microwave emissivity from the sea ice surface and the algorithm is reported to have a precision of 5 cm (Comiso et al., 2003). Given the extreme southern latitude of the study area, snow conditions throughout this study were very dry, supported by snow pit analysis on the sea ice in November with no wet snow or lensing observed. AMSR-E cells are included in the analysis if over 50 % of the cell lies within the fast ice mask and segmented into each fastening area by that same criteria. A total of 22 AMSR-E cells are used and, due to the instrument failure in early October 2011, data for the last 2 months of this investigation do not exist.
2.4 CryoSat-2
CS-2 was launched in 2010 and houses a Ku-band radar altimeter (centre frequency 13.6 GHz). The altimeter has an approximate footprint size of 380 m × 1560 m and takes samples along the satellite ground track at 300 m intervals. The instrument has three modes and over the coastal Antarctic operates its interferometric (SIN) mode. This mode uses both of the satellite's antennas to identify the location of off-nadir returns accurately. This is not the dedicated sea ice mode, but it is still suitable for sea ice freeboard retrieval (Price et al., 2015; Armitage and Davidson, 2014). In Sect. 5, to assess the usefulness of the evaluated snow products, we infer sea ice thickness from CS-2 freeboard measurements.
The ESA L2 baseline C SIN mode (SIR_SIN_L2 – available at http://science-pds.cryosat.esa.int/, last access: April 2018) dataset provides a retracked height for the surface over sea ice and this initial measurement is termed the radar freeboard. The processing closely follows that described in Price et al. (2015), but to reduce noise, two modifications are made to achieve more detailed scrutiny of the CS-2 height retrievals. The first is a more stringent exclusion of off-nadir elevation retrievals, and the threshold is halved from ±750 to ±375 m; data located at greater distances from nadir are discarded. The second is the rejection of freeboard measurements of less than −0.24 m and greater than 0.74 m. Following Schwegmann et al. (2016) the ±0.24 m accounts for speckled range noise in the CS-2 data and the +0.5 m threshold additionally incorporates an expected maximum sea ice freeboard of 0.5 m for fast ice in McMurdo Sound (as measured in situ in 2011). Each CS-2 radar freeboard measurement is cross-referenced to fastening areas 1, 2 and 3 and assigned a snow depth (Ts) value from the described snow products. From the ESA retracked product there is currently no consensus on what surface the radar freeboard represents over sea ice, the air–snow interface, the snow–ice interface or an undefined interface between the two. Laboratory experiments (Beaven et al., 1995) and comparisons of other radar altimeter systems with in situ measurements (Laxon et al., 2003) suggest the snow–ice interface is detected. It is clear that the presence of snow influences the CS-2 height retrieval, but precisely how is dependent on the surface roughness (Kurtz et al., 2014; Hendricks et al., 2010; Drinkwater, 1991), its depth (Kwok, 2014) and its dielectric properties (Hallikainen et al., 1986). The mean depth of the dominant backscattering surface measured using a surface-based Ku-band radar over snow covered Antarctic sea ice was around 50 % of the mean measured snow depth, and the snow–ice interface only dominated when morphological features or flooding were absent (Willatt et al., 2010). Wingham et al. (2006) indicate the snow–ice interface is represented by the ESA retracked height. No other information is available about the assumptions made here, only that for diffuse echoes in SAR processing, for baseline C, a new retracker was implemented (Bouffard, 2015). It is unclear what the original retracking assumptions are for any retrieval mode and if any changes were made to the SIN mode for baseline C. A prior study of CS-2 waveform behaviour over the same study area found the ESA L2 freeboard to be located between the air–snow and snow–ice interfaces (Price et al., 2015). Given this uncertainty we apply a simple methodology to discover the range of thicknesses as inferred via these CS-2 data. We explore this possible range by changing the amount of snow and ice assumed to represent the freeboard measurement in the thickness equation. There is no physical change to the actual radar penetration; the inferred thickness is simply altered mathematically using a varying penetration depth (Pd) into the snow pack. Equation (1) assumes that the snow surface is detected, Eq. (2) that the sea ice surface is detected and Eq. (3) that an arbitrary surface at varying Pd values into the snow pack (0.02, 0.05, 0.10, 0.15, 0.30 and 0.50 m – or to the snow–ice interface, whichever criterion is met first) represents the retracking point. The radar freeboard is corrected when snow is present and penetration is assumed (i.e. Pd>0) for the reduction of the speed of the radar wave through the snow pack following the procedure described in Kurtz et al. (2014). We derive sea ice thickness (Ti) using the newly corrected freeboard (Fb) and the described equations:
where ρw (1027 kg m−3), ρi (925 kg m−3) and ρs (385 kg m−3) are the densities of water, sea ice and snow respectively. ρw is informed by an unpublished time series of surface salinity measurements taken from October 2008 to October 2009 along the front of the McMurdo Ice Shelf. The range in pw during this period is less than 1 kg m−3. The ρi value used here is in the middle of the measured range in McMurdo Sound, the use of which is discussed in Price et al. (2014). ρs is the mean value taken from 18 of the 39 in situ sites where snow density was measured.
3.1 High-resolution model
SnowModel is a numerical modelling system with four main components: (1) MicroMet, a quasi-physically based, high-resolution meteorological distribution model (Liston and Elder, 2006b); (2) Enbal, a surface energy balance and snowmelt model (Liston et al., 1999); (3) SnowTran-3D, a wind-driven snow redistribution routine (Liston et al., 2007; Liston and Sturm, 1998); and (4) SnowPack, a multilayer snow depth and water-equivalent model (Liston and Sturm, 1998). The main objective of MicroMet is to provide seamless atmospheric forcing data, both temporally and spatially, to the other SnowModel components. MicroMet is capable of downscaling the fundamental atmospheric forcing such as air temperature, relative humidity, wind speed, wind direction, incoming solar radiation, incoming longwave radiation, surface pressure and precipitation. Other SnowModel sub-models simulate the surface energy balance and moisture exchanges including snowmelt, snow redistribution and sublimation. SnowModel also incorporates multilayer heat and mass-transfer processes within the snow (e.g. snow density evolution).
SnowModel is capable of initializing with both in situ and gridded model data and has been evaluated in many geographical locations including Greenland and Antarctica (Liston and Hiemstra, 2011, 2008; Liston and Winther, 2005; Mernild et al., 2006). To the authors' knowledge, and at the time of writing, this is only the second application of SnowModel in a sea ice environment. Liston et al. (2018) applied SnowModel with an additional component that accounted for snowdrifts and snow dunes, at very high spatial resolution over Arctic sea ice with positive results.
SnowModel requires topography, land cover and various atmospheric forcing. The minimum meteorological requirements of the model are near-surface air temperature, precipitation, relative humidity, wind speed and direction data from automatic weather stations and/or gridded numerical models. Determining the influence of wind and other atmospheric forcing on snow distribution in a complex terrain requires the use of numerical atmospheric models. Many studies have demonstrated that high-resolution models are vital for simulating topographic and land-use impacts on wind, hydraulic jump and associated turbulence (Olafsson and Agustsson, 2009; Agustsson and Olafsson, 2007). For this research, hourly atmospheric forcing data were generated by version 3.5 of the polar-optimized version of the Advanced Research Weather Research and Forecasting Model (WRF-ARW; Skamarock et al., 2008) known as Polar WRF (Bromwich et al., 2009) or PWRF (http://polarmet.osu.edu/PWRF, last access: April 2018) at 3 km horizontal resolution.
The WRF-ARW (hereafter, WRF) is a state-of-the-art model that is equipped with a fully compressible, Eulerian and nonhydrostatic dynamic core. This model uses Arakawa C-grid staggering in the horizontal and utilizes a mass terrain-following coordinate vertically. Several physical parameterization schemes are available in WRF, and some of those used for this work are described below. The WRF single-moment six-class microphysics scheme (WSM6; Hong and Lim, 2006) is a cloud microphysics scheme, which includes various water phases including graupel. This likely improves precipitation- and cloud-related predictions at higher spatial resolution. For radiation, the rapid radiative transfer model (RRTM; Mlawer et al., 1997) and the empirically based Dudhia shortwave radiation scheme (Dudhia, 1989) are used as the long- and shortwave radiation schemes, respectively. The Mellor–Yamada–Nakanishi–Niino (MYNN; Nakanishi and Niino, 2006, 2004; Nakanishi, 2001) level-2.5 scheme is used to take into account subgrid-scale turbulent fluxes.
The Noah LSM (Chen and Dudhia, 2001) with four soil layers, which is able to handle sea ice and polar conditions through modifications described below was chosen as the land surface model. Generally, mesoscale numerical models including WRF have simple representations for sea ice thickness and snow depth on sea ice. This shortcoming leads to an outstanding error in the simulation of the snow and mass balance in the polar regions. To address this issue, PWRF improved the representation of heat fluxes through snow and ice in the Noah LSM. Further, this version of PWRF modified sea ice and snow albedos and made it accessible to define spatially varying sea ice thickness and snow depth on sea ice (for further detailed information about PWRF see Hines et al., 2015).
The models, PWRF and SnowModel, are coupled in an off-line manner. This means that the PWRF model ran for the entire study period first, then SnowModel initiated based on the PWRF simulated atmospheric forcing and there is no feedback from SnowModel to the atmospheric model. In order to increase the spatial resolution of the PWRF outputs, before the atmospheric forcing is input to the SnowModel, PWRF gridded data are interpolated to a new grid, and then corrected physically according to topography using the MicroMet sub-model. The spatial resolution of SnowModel is 200 m and its output is segmented into sea ice fastening areas as indicated by the Envisat imagery (Fig. 1). Model outputs are reported as hourly means beginning at 00:00 UTC on 1 April 2011 and ending at 00:00 UTC on 1 December 2011. SnowModel outputs snow depth and s.w.e.. The model has a varying density over time. The s.w.e. output is important as it allows comparison of the model to the other snow products which have different density assumptions.
3.2 Low-resolution model
ERA-I is a global atmospheric reanalysis product on a grid available from 1 January 1989 (Dee et al., 2011). Precipitation data (millimetre water equivalent) are available at 3-hourly intervals and are converted to snow depth when required using the average snow density of 385 kg m−3 measured in situ in 2011. Using splines we interpolate the coarse-resolution ERA-I grid and provide a 10×10 grid over the study area with a cell resolution of 12 km. The reanalysis does not account for snow transport but with the interpolated grid we are able to segment the model for sea ice fastening dates and begin snow accumulation at the correct time. We average the 3-hourly outputs, and the reported ERA-I data are daily averages for each fastening area.
When the three snow products are compared to one another, or to in situ measurements, all snow depths are reduced to snow water equivalent (s.w.e.) via their respective densities to remove any bias associated with varying density between snow datasets. SnowModel provides a s.w.e. output via a time-varying snow density during the model run, AMSR-E snow depths are reduced to s.w.e. using average in situ measured snow density in November, and ERA-I precipitation is provided as s.w.e. in its original format. The SnowModel evaluation is split into three parts. Firstly, an accumulation time series is presented for each snow product segmented by each fastening area, and this time series is the mean snow depth for each product within each area (Fig. 2). Secondly, selected SnowModel grid cells are directly compared to spatially coincident in situ measurement sites in November (Fig. 3), and thirdly, the SnowModel and ERA-I distributions are plotted as maps at the end of the model run for spatial comparison (Fig. 4). The model s.w.e. values used for direct comparison to in situ measurements in Figs. 3 and 4 are the mean at each site between 25 November and 1 December, the period over which in situ measurements were made.
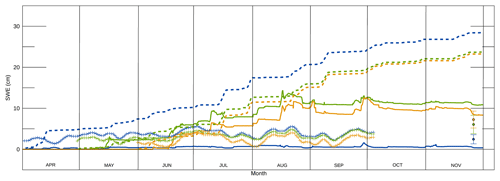
Figure 2SnowModel hourly (solid lines) and ERA-I daily (hashed lines) snow water equivalent (s.w.e.) accumulation and AMSR-E daily snow depth (crosses) converted to s.w.e. for fastening areas 1 (blue), 2 (green) and 3 (orange). The mean in situ s.w.e. and standard deviations for each area are displayed as circles at the end of November and colour coded to their respective fastening areas.
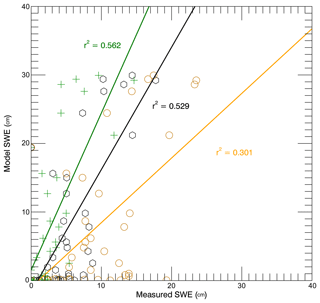
Figure 3Mean (black), maximum (green) and minimum (orange) in situ measured snow water equivalent (s.w.e.) for each site against mean SnowModel s.w.e. at each coincident model cell for the in situ measurement period.
The SnowModel mean s.w.e. for all areas at the end of the simulation is 2 cm higher than the in situ s.w.e. mean. However, SnowModel clearly presents two very different snow accumulation patterns, one in the west covering area 1 and one in the east covering areas 2 and 3. Mean s.w.e. values in area 1 reach a maximum of 2 cm during the 8-month study period while in areas 2 and 3 they are in excess of 10 cm. This broad spatial distribution produced by SnowModel compares well with in situ measurements and general observations in November 2011, which recorded an increasing gradient in snow depth from west to east (Fig. 4). However, when each fastening area is directly compared to in situ means for those areas, s.w.e. is underestimated in area 1 (2 cm > in situ), slightly overestimated in area 3 (1 cm > in situ) and substantially overestimated in area 2 (5 cm > in situ) (Fig. 2). Only modelled s.w.e. in area 3 falls within the standard deviation of the in situ mean. In the east, snow depth increases are noted in mid-May, mid-June, early July, early and mid-August, and late September. The snow depth evolution in the west of the sound over area 1 follows a separate pattern with negligible increases in mid- to late April, mid-May, mid-July, late September and early November. When coincident pixels are directly compared to in situ data with coincident pixels SnowModel overestimates s.w.e. in the study area and therefore the model has better agreement with in situ maximum values (r2=0.56) than with the mean (r2=0.53) or minimum (r2=0.30) values (Fig. 3). It is important to note the importance of redistribution by wind which is provided by SnowModel. The consequences of neglecting this influence on snow accumulation in the study region are clearly demonstrated in Fig. 4. Figure 4a displays the accumulated precipitation from MicroMet, while this is built on in Fig. 4b with the inclusion of the other SnowModel components. Over eastern areas of the study region, the MicroMet precipitation output as a standalone product provides s.w.e. values double that of the highest s.w.e. measured in situ. Although vastly improved, the general overestimation of s.w.e. by SnowModel is clearly visible in Fig. 4b. Values in the eastern-most section of the sea ice cover in McMurdo Sound, adjacent to Ross Island, are of the order of 20 to 35 cm s.w.e. These values are all larger than the highest in situ measured s.w.e. of 17.7 cm and, for large areas, they still remain over double the measured value. In the central area of the sound, modelled s.w.e. decreases in agreement with measured s.w.e., with 5 in situ sites agreeing within ±0.5 cm of SnowModel s.w.e. (Figs. 3 and 4b). The western region of sea ice in fastening area 1 has far less measured snow. The model produces this well but values are too low. The extremes, where there is a lot of snow and where there is very little snow, both seem to be exaggerated by the model.
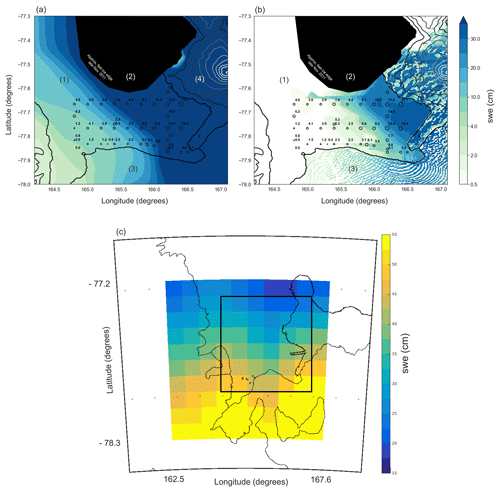
Figure 4(a) MicroMet s.w.e. distribution and (b) SnowModel s.w.e. distribution in McMurdo Sound, with (1) fast ice, (2) open water/pack ice, (3) McMurdo Ice Shelf and (4) Ross Island identified. The model s.w.e. distribution is the mean of the simulation over the in situ measurement period (25 November–1 December). The in situ measurements were converted to s.w.e. via the density measured at each site; if no measurement was taken (21 sites) the average in situ snow density was used (385 kg m−3). In situ measurement locations are shown as black circles and are the mean of the 60 snow measurements taken at each site. The circle sizes are weighted for s.w.e. to allow visualization of the decreasing s.w.e. distribution from east to west. Elevation contours are spaced at 400 m intervals; Mt Erebus (3794 m) is the dominant topographic feature on Ross Island to the east of the fast ice. (c) The interpolated 10×10 ERA-I grid with 1 December accumulation total; the boundary of the SnowModel inset from (a) is shown as the black box. The ERA-I centre points of the original grid are displayed as red dots.
Unlike SnowModel or the in situ distribution in late November AMSR-E s.w.e. follows a similar pattern over time in all fastening areas. For areas 2 and 3, May through June, AMSR-E, and SnowModel produce similar s.w.e. values, agreeing within 1.5 cm in areas 2 and 3. In area 1 AMSR-E s.w.e. fluctuates but is typically about 2.5–3 cm higher than SnowModel. As the growth season progresses AMSR-E remains significantly lower than SnowModel s.w.e. in areas 2 and 3, by up to 10 cm. s.w.e. values are higher in area 2 than area 3 in agreement with SnowModel. However, in area 1 s.w.e. values are 4 times larger than SnowModel. Most importantly, the longitudinal s.w.e. gradient indicated by SnowModel and supported by in situ data is opposite when measured using AMSR-E (i.e. s.w.e. is higher in the west than in the east for the duration of the times series). As the AMSR-E instrument failed in early October, we are unable to validate it with in situ measurements. ERA-I also produces a different snow distribution to SnowModel and in situ data (Fig. 4c) with an area of lower s.w.e. values in the central area of the fast ice and higher s.w.e. values over the western and eastern areas. The mean deviation over the entire study area from in situ measurements is 20 cm s.w.e. ERA-I s.w.e. values are over double that of SnowModel for areas 2 and 3 and an order of magnitude higher for area 1 (Fig. 2). The ERA-I temporal snowfall pattern is the same between all areas and is similar to that produced by SnowModel in areas 2 and 3.
In this section, we review the usefulness of the snow products by using them as inputs to Eqs. (1)–(3) and infer sea ice thickness in McMurdo Sound through the growth season. Snow information, coincident in space and time for each CS-2 measurement, is retrieved from the SnowModel and AMSR-E products as snow depth, while ERA-I s.w.e. is converted to snow depth using the mean in situ measured density.
Sea ice thickness inferred from altimetry in McMurdo Sound will be influenced by the buoyant sub-ice platelet layer (Price et al., 2014). The Fb measurement used to infer thickness is representative of the solid sea ice and the layer of sub-ice platelets attached below. Therefore, comparisons to in situ thickness referenced in this work actually refer to the “mass-equivalent thickness”, that is, the resultant thickness taking account of both the solid sea ice and the sub-ice platelet layer (sub-ice platelet layer multiplied by the solid fraction). The only exception to this is the red line in Fig. 5 which is a linear fit between two measurements of consolidated sea ice thickness in July and November 2011, used here to show the sea ice thickness growth rate for comparison to CS-2 thickness trends.
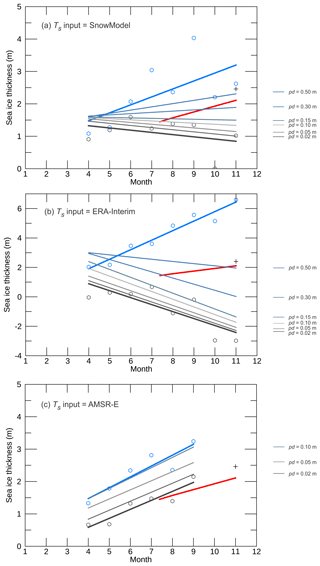
Figure 5Sea ice thickness trends derived by CS-2 freeboard measurements with snow data provided by (a) SnowModel, (b) ERA-I and (c) AMSR-E. Grey dots and bold linear fit are sea ice thickness calculated using Eq. (1). Blue dots and bold linear fit show the trends using Eq. (2) and the thin lines between them show Eq. (3) with varying penetration factors (Pd). The red line shows sea ice thickness from in situ measurements of consolidated sea ice thickness with a tape measure taken in July and November in one location in the south of McMurdo Sound, joined assuming a constant growth rate. The black plus sign is the mean “mass-equivalent thickness” from all in situ measurements in November. This is slightly thicker than the end-of-season thickness indicated by the red line given that it takes account of the influence of the sub-ice platelet layer. This black plus sign is what CS-2 thickness should be compared to (see text).
From Eqs. (1)–(3), sea ice thickness is highly sensitive to the snow–ice ratio for the measured freeboard. This results in a large range in sea ice thickness for all snow products through the growth season (Fig. 5). This range in inferred thickness is driven by the amount of snow produced by the models as Eqs. (1) and (2) subtract and add the product of this value in their second terms respectively. As the snow depth increases, in some cases to higher values than the measured freeboard, the Pd simply provides a correcting factor for this discrepancy. The AMSR-E-derived thickness trend is not comparable to the model output trends as the last 2 months are missing. However, it is useful to highlight the importance of the snow–ice freeboard ratio. AMSR-E snow depths remain relatively stable for the duration of the study. Because of this, the ratio of ice to snow above the waterline remains very similar. In the case of the models, snow depths gradually increase and snow makes up an ever-increasing proportion of mass above the waterline. If the air–snow interface (Eq. 1) is taken to represent Fb then the trend in sea ice thickness through the growth season is negative for SnowModel- and ERA-I-derived thicknesses and if the snow–ice interface (Eq. 2) is assumed the trend is too positive. The trends are more extreme for the ERA-I estimates simply because the snow loading is greater. The ranges in sea ice thickness estimated with SnowModel as the snow depth input are substantially smaller than ERA-I (Fig. 5), but still have a larger range than the mean discrepancy from in situ measurements might suggest (Fig. 2). This is driven by CS-2 retrievals over the eastern areas of fastening areas 2 and 3 where s.w.e. values are high, especially towards the end of the growth season (Fig. 4b). The range in uncertainty between Eqs. (1) and (2) derived thickness as means of available data for the entire growth season are 1.08, 4.94 and 1.03 m for SnowModel, ERA-I and AMSR-E respectively. The mean CS-2-derived thickness values for November using Eqs. (1) and (2) are 1.02 m (−2.98 m) for SnowModel (ERA-I) and 2.62 m (6.59 m) for SnowModel (ERA-I) respectively compared to an in situ thickness of 2.4 m. The trends that result in a November thickness supported by the in situ measurements are those that assume penetration into the snow cover, analogous with the retracked surface representing a surface between the air–snow and snow–ice interfaces. For thicknesses derived using the models to match in situ thickness, large Pd values of 0.5 m are required given the higher snow depth values. These values are lower for AMSR-E as the snow loading is less.
The differences in the snow depths from each model result make it difficult to constrain what Pd value provides CS-2 thicknesses that agree best with measured thickness. To assess the penetration uncertainty further we use interpolated in situ measurements for snow depth as input to the sea ice thickness calculation. We reduce the CS-2 measurements used in this comparison to the same area bounded by in situ measurements. The total range in estimated sea ice thickness using interpolated in situ snow depth between equations 1 and 2 is 1.7 m. For Pd values 0.02 m through 0.20 m the best agreement between in situ thickness and CS-2-derived thickness is found between 0.05 and 0.10 m (Fig. 6 – third column, “In situ”). The CS-2 thickness is only 0.02 m thicker than in situ thickness for this particular dataset when Pd=0.07 m. The range in SnowModel-derived thickness between Eqs. (1) and (2) is nearly 4 m while the range when using the ERA-I dataset is very large at 5.7 m (Fig. 6). Again this large range in thickness reflects the higher average snow depth produced by ERA-I. The deeper snow creates a larger range of snow-to-ice ratios for the freeboard.
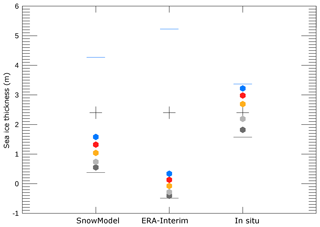
Figure 6The range in CS-2-derived sea ice thickness in November using snow inputs from SnowModel and ERA-I compared to snow input from in situ interpolated snow depths. Thickness derived from Eqs. (1) and (2) are shown with the grey and blue lines respectively and for Eq. (3) the dots are colour coded for different penetration depths (Pd): dark grey is 0.02 m, light grey is 0.05 m, orange is 0.10 m, red is 0.15 m and blue is 0.20 m. Black plus signs show in situ “mass-equivalent thickness”. This comparison is produced from all CS-2 data height retrievals available over the in situ measurement area in November (n=279).
In this section, the performance of the snow depth retrieval methods and CS-2 thickness uncertainty is evaluated. We briefly discuss their future applicability to larger Antarctic sea ice areas.
Any method attempting to accumulate snow on sea ice requires the establishment of a starting date from which a sea ice surface is present. This approach used Envisat ASAR imagery and motion between scenes to identify when the sea ice fastened. Freezing may have started prior to the fastening date but the authors are unaware of any other method to monitor sea ice formation at the required spatial resolution for SnowModel. Sea ice could have begun to form slightly before this date, which, assuming a net gain in snow, would result in an improvement in SnowModel's performance in area 1, but increased separation between in situ validation and SnowModel in areas 2 and 3. ERA-I performance would be worse in all cases, and AMSR-E would not be impacted as it is a real-time snow depth measurement. In larger open-water areas, passive microwave sea ice concentration information could be used to establish the formation date. Detail would be lost via this method given the high (200 m) resolution of SnowModel against the coarser-resolution passive microwave data. Early snowfall on more dynamic pack ice will also be subject to flooding, sea spray (both likely to result in snow–ice formation) and loss to leads. These uncertainties must all be considered in future work.
Modelled snow depths have been evaluated in previous work over Antarctic sea ice (Maksym and Markus, 2008), but the study produced precipitation data while this assessment takes the next step by using a model that accounts for surface transportation, a significant redistribution mechanism in the Antarctic. Without this model component included the precipitation provided by MicroMet (downscaled PWRF) provides very poor estimates of snow depth on sea. Leonard and Maksym (2011) report that over half of precipitation over the Southern Ocean could be lost to leads and the application of any model to construct snow depth on sea ice in open sea areas will need to account for this. In coastal regions, local topography will also play a key role, such as is the case in McMurdo Sound where Ross Island acts to encourage snow accumulation on the eastern portion of the sea ice cover. This was well replicated in SnowModel although the overestimation of snow was driven by unrealistic values in this area, the model likely accumulating too much snow due to this topographic barrier. Smaller-scale snow features such as snow drifts and snow dunes should also be accounted for in future work, as applied in a recent study by Liston et al. (2018). These metre-scale features will be important to capture, especially to support compatibility with smaller satellite altimeter footprints, particularly ICESat-2 (Markus et al., 2017). This work used fast ice to reduce the uncertainty associated with pack ice and used available in situ data to validate the snow products. To build on this approach, and make its application valuable in the Southern Ocean, sea ice motion within the SnowModel domain must be incorporated.
We find the ERA-I mean s.w.e. to be 20 cm higher than mean in situ s.w.e. in McMurdo Sound. In area 1 ERA-I s.w.e. is an order of magnitude higher than in situ s.w.e., while in areas 2 and 3 it is over double the value. These create very high, unrealistic snow depths, which causes a large range in CS-2-derived thickness using Eqs. (1)–(3). This is a very poor result and the product is inadequate to infer sea ice thickness when combined with altimetry data. Of further interest is that the clear longitudinal gradient in snow depth as indicated by SnowModel and measured in situ (November only) is not produced by ERA-I, and s.w.e. values are lower in the central fast ice area and higher in the western and eastern areas. The performance of ECMWF reanalysis products over the satellite period has been reported as good when compared to Antarctic coastal stations (Bromwich and Fogt, 2004), but there are limited data available to assess the accuracy of these data over Antarctic sea ice. ERA-I ranked best among five assessed models for its depiction of interannual variability and overall change in precipitation, evaporation and total precipitable water over the Southern Ocean (Nicolas and Bromwich, 2011). Maksym and Markus (2008) used ERA-40 reanalysis for a snow assessment of the Antarctic sea ice pack but had difficulties in evaluating its accuracy. A first step to improve reanalysis results will be to incorporate snow redistribution (including snow loss to leads), and parameterizations for this could be built from wind vectors provided by the same reanalysis data.
In general, when compared to SnowModel, AMSR-E underestimates snow depth in areas 2 and 3 (eastern Sound) and overestimates snow depth in area 1 (western Sound). The snow distribution gradient from east to west is reversed in the AMSR-E dataset. Worby et al. (2008b) report that AMSR-E snow depths were significantly lower than in situ measurements on sea ice in the East Antarctic and that sea ice roughness is a major source of error using passive microwave retrieval techniques. However, they also conclude that, when compared to basin-wide observations from ASPECT, large differences of up to +20 cm in the Weddell Sea and +5–10 cm in the Ross Sea were noted in the AMSR-E snow depths. Vessels are restricted in their ability to sample in heavily deformed and thicker sea ice areas where the snow is typically higher. Because of this, it is postulated that shipborne observations of in situ snow thickness were biased low in comparison to AMSR-E snow depth. More work is required to validate passive microwave snow depth estimates over Antarctic sea ice. No detailed sea ice surface condition survey was completed for this investigation; however, from visual observations sea ice had clearly been subjected to dynamics in the west, whereas ice was very level in the east. It is possible that snow depth was underrepresented here by in situ measurements and that rougher sea ice in the west affected the AMSR-E retrieval algorithm. Because of the failure of the instrument, we are unable to compare AMSR-E snow depth directly to in situ measurements.
CS-2 has difficulty estimating the freeboard over thin ice areas (Price et al., 2015; Ricker et al., 2014; Wingham et al., 2006). Here, at the beginning of the growth season CS-2 generally overestimates sea ice thickness with mean April values inferred using snow data from SnowModel and ERA-I of around 1 m (with the exception of AMSR-E assuming the air–snow interface is measured Ti=0.66 m). Other investigations indicate that sea ice thickness in McMurdo Sound in April is between 0.5 and 0.8 m (Frazer et al., 2018; Gough et al., 2012; Purdie et al., 2006). This represents a large obstacle to overcome for the application of CS-2 in the Southern Ocean as the mean thickness of Antarctic sea ice is only 0.87 m as reported from ship-based observations (Worby et al., 2008a). This supports the need for multisensor analysis, perhaps using methods already employed in the Arctic (Ricker et al., 2017; Kaleschke et al., 2012; Kwok et al., 1995). As discussed in Sect. 2.4 assumptions must be made about what surface the freeboard measurement represents. In general, using the two modelled snow products (because trends from AMSR-E are incomplete), the thicknesses derived assuming the air–snow interface is the freeboard are too thin and those assuming the snow–ice interface is the freeboard are too thick, a simple consequence of the density-dependent hydrostatic equilibrium assumption. By using the interpolated in situ measured snow depth as the snow thickness input to the thickness calculation, the error is minimized. With this, we find CS-2 thickness to correlate best with in situ thickness if Pd values are between 0.05 and 0.10 m. This is supported by other work in the study area (Price et al., 2015) which estimated the ESA elevation to be between the air–snow and snow–ice interfaces when sea surface height error was ruled out via a manual sea surface classification. Also, recent work in the Arctic suggests that the height that represents the radar freeboard provided by the ESA Level 2 product is closer to the air–snow interface than the snow–ice interface (King et al., 2018).
Having confidence in the results assumes that the sea surface height has been accurately identified for each CS-2 track. Freeboard errors from automated sea surface height identification were of the order of 0.05 m when compared to supervised procedures in the study area (Price et al., 2015). To eliminate this uncertainty throughout the study period the sea surface would need to be manually identified for each individual CS-2 track. This is not practical for basin-scale assessments and confidence needs to be built in the sea surface height identification algorithm. The modification of the sea surface height will apply a systematic increase or decrease in the freeboard, making each thickness from each assumption thicker or thinner. The freeboard measurements exhibit an unexpected decrease in October and November and it is impossible to discern whether this is forced by a sea surface height that is too high or a change in the sea ice surface conditions that causes a decrease in the freeboard measurement, an additional uncertainty. More detailed in situ investigations, with surface roughness and snow characteristic statistics at the scale of the altimeter footprint, are required before a seasonally varying Pd can be applied with any confidence. As this analysis was focused on the combination of independent snow products and CS-2 altimeter data, the range in sea ice density has not been taken into account. We have confidence in the middle ground ρi value used from previous work in McMurdo Sound (Price et al., 2014) but this is another source of uncertainty for regional- and basin-scale assessments.
This work has evaluated the ability of three independent techniques to provide snow depth on fast ice in the coastal Antarctic. SnowModel accurately captures the in situ measured snow distribution in November 2011 and produces a s.w.e. mean value that is 0.02 m above the mean of in situ validation, but when sea ice is segmented by fastening date large deviations of up to 5 cm are present in the east where the model has overestimated snow depth. This accurately captures the mechanism of snowfall and transport driven by the topography of Ross Island, but the rates are higher than in reality. ERA-I s.w.e. is 20 cm higher than in situ measurements and the gradient of the snow distribution produced by the analysis does not match that measured in situ. A positive bias in accumulation should be expected from ERA-I as no snow redistribution mechanism is included. Any future work making use of precipitation reanalysis over Antarctic sea ice must include snow redistribution by wind, shown here by SnowModel to dramatically improve results. AMSR-E snow depth information suffers from problems already documented in the literature, and we find that its performance may have again been influenced by rough sea ice. The snow distribution produced by AMSR-E was opposite to that provided by SnowModel and measured in situ at the end of the growth season. We were unable to validate the instrument due to its failure 2 months before the in situ data were collected. The uncertainty in the snow depth estimates manifest themselves in the sea ice thickness estimates from CS-2. The range in sea ice thickness uncertainty from the assumption that the snow surface or ice surface represents the freeboard, as means of the entire growth season are 1.08, 4.94 and 1.03 m for SnowModel, ERA-Interim and AMSR-E respectively. Using interpolated in situ snow information, we find CS-2 freeboard measurements provided by the ESA retracker agree best with in situ measured thickness if a dominant scattering horizon 0.07 m beneath the air–snow interface is assumed, in agreement with the recent literature. It is impossible to confidently constrain this number without reducing uncertainty in the established sea surface height from which the freeboard is estimated. This work demonstrates the need to reduce the uncertainty associated with the ambiguity of the altimeter radar freeboard measurement over Antarctic sea ice. Sea ice in McMurdo Sound is atypical of Antarctic pack ice, so improved understanding of the CS-2 freeboard measurement over varying snow and sea ice conditions in open water areas will be critical to accurately provide sea ice thickness estimates for the Southern Ocean.
Here, we show that modelled snow information has the potential to produce a time series of snow depth on Antarctic sea ice. However, major developments in modelling capability are required before their snow products can provide useful information for use in combination with altimetry data to provide Antarctic sea ice thickness. With improvements to redistribution mechanisms and adequate representation of the effect of topographic features, atmospheric models could be used as an alternative to contemporary passive microwave algorithms. Future work should begin to assess the usefulness of SnowModel products over the larger pack ice areas and critically develop a method to (1) incorporate sea ice drift through the atmospheric model domains and (2) account for snow loss to leads. If these two influences can be adequately incorporated, SnowModel could provide a valuable resource for snow and sea ice thickness investigations over the wider Antarctic sea ice area, especially where snow depth is high and passive microwave techniques are non-informative.
All satellite data sets and coarse-resolution model precipitation outputs are publicly available at the URLs noted in the text. SnowModel data and in situ information will not be available at the time of publication; however, plans are in place to make available all Ross Sea sea ice data collected by the involved institutions.
DP carried out all satellite data analysis, combined the satellite outputs with precipitation model outputs, undertook in situ validation and wrote the manuscript. IS produced the SnowModel output and provided detailed input on the modelling aspects of the study. WR undertook in situ validation and provided input to satellite assessments. ED worked with ERA-Interim data and assisted with its analysis and interpretation in the paper.
The authors declare that they have no conflict of interest.
Gratitude is shown for the support of Antarctica New Zealand and Scott Base staff during the 2011–2012 Antarctic field season permitting the collection of in situ snow and sea ice measurements, and the members of field team K053. We thank Glen E. Liston for providing the code for SnowModel. Further thanks are given to Oliver Marsh and Christian Wild for productive discussions about the topic. This work was partially supported by NIWA subcontract C01X1226 (Ross Sea Climate and Ecosystem) and the Marsden Fund Council from Government funding, managed by Royal Society Te Apārangi. We are grateful to Victoria Landgraf, Troy Beaumont, and Grant Cottle from Antarctica New Zealand's Scott Base 2011 over-winter team for making the July sea ice thickness measurements as part of the winter support of a University of Otago Research Grant funded project (PI: Pat Langhorne, AI: Inga Smith). We thank Peter Green and Inga Smith for their insights into the 2011 sea ice growth rates, which were supported by the fieldwork and analytical efforts of Greg Leonard, Alex Gough, Tim Haskell, Pat Langhorne and Jonothan Everts; the technical advice of Joe Trodahl and Daniel Pringle; and the technical support of Myles Thayer, Peter Stroud and Richard Sparrow. Final thanks are given to Eamon Frazer and Pat Langhorne for the time given to discussions about and analysis of seawater density in the study region. This research was completed at Gateway Antarctica, University of Canterbury, Christchurch, New Zealand.
This paper was edited by Ted Maksym and reviewed by two anonymous referees.
Agustsson, H. and Olafsson, H.: Simulating a severe windstorm in complex terrain, Meteorol. Atmos. Phys., 103, 173–185, https://doi.org/10.1007/s00703-008-0347-y, 2007.
Armitage, T. W. K. and Davidson, M. W. J.: Using the Interferometric Capabilities of the ESA CryoSat-2 Mission to Improve the Accuracy of Sea Ice Freeboard Retrievals, IEEE T. Geosci. Remote, 529–536, https://doi.org/10.1109/TGRS.2013.2242082, 2014.
Beaven, S. G., Lockhart, G. L., Gogineni, S. P., Hossetnmostafa, A. R., Jezek, K., Gow, A. J., Perovich, D. K., Fung, A. K., and Tjuatja, S.: Laboratory measurements of radar backscatter from bare and snow-covered saline ice sheets, Int. J. Remote Sens., 16, 851–876, 1995.
Bouffard, J.: CryoSat-2 Level 2 product evolutions and quality improvements in Baseline C, available at: https://earth.esa.int/documents/10174/1773005/C2-Evolution-BaselineC-Level2-V3 (last access: January 2018), 2015.
Bromwich, D. H. and Fogt, R. L.: Strong Trends in the Skill of the ERA-40 and NCEP–NCAR Reanalyses in the High and Midlatitudes of the Southern Hemisphere, 1958–2001, J. Climate, 17, 4603–4619, https://doi.org/10.1175/3241.1, 2004.
Bromwich, D. H., Hines K. M., and Bai, L. S.: Development and testing of Polar WRF: 2. Arctic Ocean, J. Geophys. Res., 114, D08122, https://doi.org/10.1029/2008JD010300, 2009.
Chen, F. and Dudhia, J.: Coupling an Advanced Land Surface–Hydrology Model with the Penn State–NCAR MM5 Modeling System. Part I: Model Implementation and Sensitivity, Mon. Weather Rev., 129, 569–585, https://doi.org/10.1175/1520-0493(2001)129<0569:CAALSH>2.0.CO;2, 2001.
Comiso, C., Cavalieri, J., and Markus, T.: Sea Ice Concentration, Ice Temperature, and Snow Depth Using AMSR-E Data, IEEE T. Geosci. Remote, 41, 243–252, https://doi.org/10.1109/TGRS.2002.808317, 2003.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., Mcnally, A. P., Monge-Sanz, B. M., Morcrette, J. J., Park, B. K., Peubey, C., De Rosnay, P., Tavolato, C., Thépaut, J. N., and Vitart, F.: The ERA-I reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Drinkwater, M.: Ku-band airborne radar altimeter observations of marginal sea ice during the 1984 Marginal Ice Zone Experiment, J. Geophys. Res., 96, 4555–4572, https://doi.org/10.1029/90JC01954, 1991.
Dudhia, J.: Numerical study of convection observed during the winter monsoon experiment using a mesoscale two-dimensional model, J. Atmos. Sci., 46, 3077–3107, https://doi.org/10.1175/1520-0469(1989)046<3077:NSOCOD>2.0.CO;2, 1989.
Fichefet, T. and Maqueda, M. A. M.: Modelling the influence of snow accumulation and snow-ice formation on the seasonal cycle of the Antarctic sea-ice cover, Clim. Dynam., 15, 251–268, https://doi.org/10.1007/s003820050280, 1999.
Frazer, E. K., Langhorne, P. J., Williams, M. J. M., Goetz, K. T., and Costa, D. P.: A method for correcting seal-borne oceanographic data and application to the estimation of regional sea ice thickness, J. Marine Syst., 187, 250–259,m https://doi.org/10.1016/j.jmarsys.2018.08.002, 2018.
Giles, K. A., Laxon, S. W., and Worby, A. P.: Antarctic sea ice elevation from satellite radar altimetry, Geophys. Res. Lett., 35, L03503, https://doi.org/10.1029/2007GL031572, 2008.
Gough, A. J., Mahoney, A. R., Langhorne, P. J., Williams, M. J. M., and Haskell, T. G.: Sea ice salinity and structure: A winter time series of salinity and its distribution, J. Geophys. Res.-Oceans., 117, C03008, https://doi.org/10.1029/2011JC007527, 2012.
Hallikainen, M., Ulaby, F., and Abdelrazik, M.: Dielectric properties of snow in the 3 to 37 GHz range, IEEE T. Antenn. Propag., 34, 1329–1340, 1986.
Hendricks, S., Stenseng, L., Helm, V., and Haas, C.: Effects of surface roughness on sea ice freeboard retrieval with an Airborne Ku-Band SAR radar altimeter, in: International Geoscience and Remote Sensing Symposium (IGARSS 2010), 25–30 July 2010, Proceedings, Institute of Electrical and Electronics Engineers, Piscataway, NJ, 3126–3129, https://doi.org/10.1109/IGARSS.2010.5654350, 2010.
Hines, K. M., Bromwich, D. H., Bai, L., Bitz, C. M., Powers, J. G., and Manning, K. W.: Sea Ice Enhancements to Polar WRF, Mon. Weather Rev., 143, 2363–2385, https://doi.org/10.1175/MWR-D-14-00344.1, 2015.
Hong, S.-Y. and Lim, J.-O. J.: The WRF Single-Moment 6-Class Microphysics Scheme (WSM6), J. Korean Meteor. Soc., 42, 129–151, 2006.
Kaleschke, L., Tian-kunze, X., Maaß, N., Mäkynen, M., and Drusch, M.: Sea ice thickness retrieval from SMOS brightness temperatures during the Arctic freeze-up period, Geophys. Res. Lett., 39, L05501, https://doi.org/10.1029/2012GL050916, 2012.
Kern, S. and Ozsoy-Çiçek, B.: Satellite Remote Sensing of Snow Depth on Antarctic Sea Ice: An Inter-Comparison of Two Empirical Approaches, Remote Sensing, 8, 450, https://doi.org/10.3390/rs8060450, 2016.
Kern, S., Ozsoy-Çiçek, B., Willmes, S., Nicolaus, M., Haas, C., and Ackley, S.: An intercomparison between AMSR-E snow-depth and satellite C- and Ku-band radar backscatter data for Antarctic sea ice, Ann. Glaciol., 52, 279–290, https://doi.org/10.3189/172756411795931750, 2011.
King, J., Skourup, H., Hvidegaard, S. M., Rosel, A., Gerland, S., Spreen, G., Polashenski, C., Helm, V., and Liston, G. E.: Comparison of freeboard retrieval and ice thickness calculation from ALS, ASIRAS, and CryoSat-2 in the Norwegian Arctic to field measurements made during the N-ICE2015 expedition, J. Geophys. Res.-Oceans, 123, 1123–1141, https://doi.org/10.1002/2017JC013233, 2018.
Kurtz, N. T. and Markus, T.: Satellite observations of Antarctic sea ice thickness and volume, J. Geophys. Res.-Oceans, 117, C08025, https://doi.org/10.1029/2012JC008141, 2012.
Kurtz, N. T., Galin, N., and Studinger, M.: An improved CryoSat-2 sea ice freeboard retrieval algorithm through the use of waveform fitting, The Cryosphere, 8, 1217–1237, https://doi.org/10.5194/tc-8-1217-2014, 2014.
Kwok, R.: Simulated effects of a snow layer on retrieval of CryoSat-2 sea ice freeboard, Geophys. Res. Lett., 41, 5014–5020, https://doi.org/10.1002/2014GL060993, 2014.
Kwok, R. and Cunningham, G. F.: ICESat over Arctic sea ice: Estimation of snow depth and ice thickness, J. Geophys. Res.-Oceans, 113, C08010, https://doi.org/10.1029/2008JC004753, 2008.
Kwok, R., Nghiem, S. V., Yueh, S. H., and Huynh, D. D.: Retrieval of thin ice thickness from multifrequency polarimetric SAR data, Remote Sens. Environ., 51, 361–374, https://doi.org/10.1016/0034-4257(94)00017-H, 1995.
Laxon, S., Peacock, N., and Smith, D.: High interannual variability of sea ice thickness in the Arctic region, Nature, 425, 947–950, https://doi.org/10.1038/nature02050, 2003.
Laxon, S. W., Giles, K. A., Ridout, A. L., Wingham, D. J., Willatt, R., Cullen, R., Kwok, R., Schweiger, A., Zhang, J., Haas, C., Hendricks, S., Krishfield, R., Kurtz, N., Farrell, S., and Davidson, M.: CryoSat-2 estimates of Arctic sea ice thickness and volume, Geophys. Res. Lett., 40, 732–737, https://doi.org/10.1002/grl.50193, 2013.
Leonard, K. C. and Maksym, T.: The importance of wind-blown snow redistribution to snow accumulation on Bellingshausen Sea ice, Ann. Glaciol., 52, 271–278, https://doi.org/10.3189/172756411795931651, 2011.
Liston, G. E. and Elder, K.: A Distributed Snow-Evolution Modeling System (SnowModel), J. Hydrometeorol., 7, 1259–1276, https://doi.org/10.1175/JHM548.1, 2006a.
Liston, G. E. and Elder, K.: A Meteorological Distribution System for High-Resolution Terrestrial Modeling (MicroMet), J. Hydrometeorol., 7, 217–234, https://doi.org/10.1175/JHM486.1, 2006b.
Liston, G. E. and Hiemstra, C. A.: A Simple Data Assimilation System for Complex Snow Distributions (SnowAssim), J. Hydrometeorol., 9, 989–1004, https://doi.org/10.1175/2008JHM871.1, 2008.
Liston, G. E. and Hiemstra, C. A.: Representing Grass- and Shrub-Snow-Atmosphere Interactions in Climate System Models, J. Climate, 24, 2061–2079, https://doi.org/10.1175/2010JCLI4028.1, 2011.
Liston, G. E. and Sturm, M.: A snow-transport model for complex terrain, J. Glaciol., 44, 498–516, https://doi.org/10.3189/S0022143000002021, 1998.
Liston, G. E. and Winther, J.-G.: Antarctic Surface and Subsurface Snow and Ice Melt Fluxes, J. Climate, 18, 1469–1481, https://doi.org/10.1175/JCLI3344.1, 2005.
Liston, G. E., Pielke, R. A., and Greene, E. M.: Improving first-order snow-related deficiencies in a regional climate model, J. Geophys. Res.-Atmos., 104, 19559–19567, https://doi.org/10.1029/1999JD900055, 1999.
Liston, G. E., Haehnel, R. B., Sturm, M., Hiemstra, C. A., Berezovskaya, S., and Tabler, R. D. Instruments and Methods Simulating complex snow distributions in windy environments using SnowTran-3D, J. Glaciol., 53, 241–256, https://doi.org/10.3189/172756507782202865, 2007.
Liston, G. E., Polashenski, C., Rösel, A., Itkin, P., King, J., Merkouriadi, I., and Haapala, J.: A Distributed Snow Evolution Model for Sea Ice Applications (SnowModel), J. Geophys. Res.-Oceans, 123, 3786–3810, https://doi.org/10.1002/2017JC013706, 2018.
Maksym, T. and Markus, T.: Antarctic sea ice thickness and snow-to-ice conversion from atmospheric reanalysis and passive microwave snow depth, J. Geophys. Res.-Oceans, 113, C02S12, https://doi.org/10.1029/2006JC004085, 2008.
Markus, T. and Cavalieri, D. J.: Snow Depth Distribution Over Sea Ice in the Southern Ocean from Satellite Passive Microwave Data, Antarctic Sea Ice: Physical Processes, Interactions and Variability, American Geophysical Union, edited by: Jeffries, M. O., https://doi.org/10.1029/AR074p0019, 1998.
Markus, T. and Cavalieri, D. J.: Interannual and regional variability of Southern Ocean snow on sea ice, Ann. Glaciol., 44, 53–57, https://doi.org/10.3189/172756406781811475, 2006.
Markus, T., Neumann, T., Martino, A., Abdalati, W., Brunt, K., Csatho, B., Farrell, S., Fricker, H., Gardner, A., Harding, D., Jasinski, M., Kwok, R., Magruder, L., Lubin, D., Luthcke, S., Morison, J., Nelson, R., Neuenschwander, A., Palm, S., Popescu, S., Shum, C. K., Schutz, B. E. Smith, B., Yang, Y., and Zwally, J.: The Ice, Cloud, and land Elevation Satellite-2 (ICESat-2): Science requirements, concept, and implementation, Remote Sens. Environ., 190, 260–273, https://doi.org/10.1016/j.rse.2016.12.029, 2017.
Massom, R. A., Eicken, H., Hass, C., Jeffries, M. O., Drinkwater, M. R., Sturm, M., Worby, A. P., Wu, X., Lytle, V. I., Ushio, S., Morris, K., Reid, P. A., Warren, S. G., and Allison, I.: Snow on Antarctic sea ice, Rev. Geophys., 39, 413–445, https://doi.org/10.1029/2000RG000085, 2001.
Maykut, G. and Untersteiner, N.: Some results from a time dependent thermodynamic model of sea ice, J. Geophys. Res., 76, 1550–1575, 1971.
Mernild, S. H., Liston, G. E., Hasholt, B., and Knudsen, N. T.: Snow distribution and melt modeling for Mittivakkat Glacier, Ammassalik Island, southeast Greenland, J. Hydrometeorol., 7, 808–824, https://doi.org/10.1175/JHM522.1, 2006.
Mlawer, E. J., Taubman, S. J., Brown, P. D., Iacono, M. J., and Clough, S. A.: Radiative transfer for inhomogeneous atmospheres: RRTM, a validated correlated-k model for the longwave, J. Geophys. Res.-Atmos., 102, 16663–16682, 1997.
Nakanishi, M.: Improvement of the Mellor-Yamada turbulence closure model based on large-eddy simulation data, Bound.-Lay. Meteorol., 99, 349–378, https://doi.org/10.1023/A:1018915827400, 2001.
Nakanishi, M. and Niino, H.: An Improved Mellor–Yamada Level-3 Model with Condensation Physics: Its Design and Verification, Bound.-Lay. Meteorol., 112, 1–31, https://doi.org/10.1023/B:BOUN.0000020164.04146.98, 2004.
Nakanishi, M. and Niino, H.: An Improved Mellor–Yamada Level-3 Model: Its Numerical Stability and Application to a Regional Prediction of Advection Fog, Bound.-Lay. Meteorol., 119, 397–407, https://doi.org/10.1007/s10546-005-9030-8, 2006.
Nicolas, J. P. and Bromwich, D. H.: Precipitation Changes in High Southern Latitudes from Global Reanalyses: A Cautionary Tale, Surv. Geophys., 32, 475–494, https://doi.org/10.1007/s10712-011-9114-6, 2011.
Olafsson, H. and Agustsson H.: Gravity wave breaking in easterly flow over Greenland and associated low level barrier-and reverse tip-jets, Meteorol. Atmos. Phys., 104, 191–197, https://doi.org/10.1007/s00703-009-0024-9, 2009.
Pope, A., Wagner, P., Johnson, R., Shutler, J. D., Baeseman, J., and Newman, L.: Community review of Southern Ocean satellite data needs, Antarctic Sci., 29, 97–138, https://doi.org/10.1017/S0954102016000390, 2016.
Price, D., Rack, W., Langhorne, P. J., Haas, C., Leonard, G., and Barnsdale, K.: The sub-ice platelet layer and its influence on freeboard to thickness conversion of Antarctic sea ice, The Cryosphere, 8, 1031–1039, https://doi.org/10.5194/tc-8-1031-2014, 2014.
Price, D., Beckers, J., Ricker, R., Kurtz, N., Rack, W., Haas, C., Helm, V., Hendricks, S., Leonard, G., and Langhorne, P. J.: Evaluation of CryoSat-2 derived sea-ice freeboard over fast ice in McMurdo Sound, Antarctica, J. Glaciol., 61, 285–300, https://doi.org/10.3189/2015JoG14J157, 2015.
Purdie, C. R., Langhorne, P. J., Leonard, G. H., and Haskell, T. G.: Growth of first-year landfast Antarctic sea ice determined from winter temperature measurements, Ann. Glaciol., 44, 170–176, https://doi.org/10.3189/172756406781811853, 2006.
Ricker, R., Hendricks, S., Helm, V., Skourup, H., and Davidson, M.: Sensitivity of CryoSat-2 Arctic sea-ice freeboard and thickness on radar-waveform interpretation, The Cryosphere, 8, 1607–1622, https://doi.org/10.5194/tc-8-1607-2014, 2014.
Ricker, R., Hendricks, S., Kaleschke, L., Tian-Kunze, X., King, J., and Haas, C.: A weekly Arctic sea-ice thickness data record from merged CryoSat-2 and SMOS satellite data, The Cryosphere, 11, 1607–1623, https://doi.org/10.5194/tc-11-1607-2017, 2017.
Schwegmann, S., Rinne, E., Ricker, R., Hendricks, S., and Helm, V.: About the consistency between Envisat and CryoSat-2 radar freeboard retrieval over Antarctic sea ice, The Cryosphere, 10, 1415–1425, https://doi.org/10.5194/tc-10-1415-2016, 2016.
Skamarock, W. C., Klemp, J. B., Dudhia, J., Gill, D. O., Barker, D. M., Duda, M. G., Huang, X.-Y., Wang, W., and Powers, J. G.: A Description of the Advanced Research WRF Version 3, NCAR Technical Note, 2008.
Stroeve, J. C., Markus, T., Maslanik, J. A., Cavalieri, D. J., Gasiewski, A. J., Heinrichs, J. F., Holmgren, J., Perovich, D. K., and Sturm, M.: Impact of Surface Roughness on AMSR-E Sea Ice Products, IEEE T. Geosci. Remote, 44, 3103–3117, https://doi.org/10.1109/TGRS.2006.880619, 2006.
Warren, S. G., Rigor, I. G., Untersteiner, N., Radionov, V. F., Bryazgin, N. N., Aleksandrov, Y. I., and Colony, R.: Snow Depth on Arctic Sea Ice, J. Climate, 12, 1814–1829, https://doi.org/10.1175/1520-0442(1999)012<1814:SDOASI>2.0.CO;2, 1999.
Willatt, R. C., Giles, K. A., Laxon, S. W., Stone-Drake, L., and Worby, A. P.: Field Investigations of Ku-Band Radar Penetration Into Snow Cover on Antarctic Sea Ice, IEEE T. Geosci. Remote, 48, 365–372, https://doi.org/10.1109/TGRS.2009.2028237, 2010.
Wingham, D. J., Francis, C. R., Baker, S., Bouzinac, C., Brockley, D., Cullen, R., De Chateau-Thierry, P., Laxon, S. W., Mallow, U., Mavrocordatos, C., Phalippou, L., Ratier, G., Rey, L., Rostan, F., Viau, P., and Wallis, D. W.: CryoSat: A mission to determine the fluctuations in Earth's land and marine ice fields, Adv. Space Res., 37, 841–871, https://doi.org/10.1016/j.asr.2005.07.027, 2006.
Worby, A. P., Geiger, C. A., Paget, M. J., Woert, M. L. V., Ackley, S. F., and DeLiberty, T. L.: Thickness distribution of Antarctic sea ice, J. Geophys. Res.-Oceans, 113, C05S92, https://doi.org/10.1029/2007JC004254, 2008a.
Worby, A. P., Markus, T., Steer, A. D., Lytle, V. I., and Massom, R. A.: Evaluation of AMSR-E snow depth product over East Antarctic sea ice using in situ measurements and aerial photography, J. Geophys. Res.-Oceans, 113, C05S94, https://doi.org/10.1029/2007JC004181, 2008b.
Wu, X., Budd, W. F., Lytle, V. I., and Massom, R. A.: The effect of snow on Antarctic sea ice simulations in a coupled atmosphere-sea ice model, Clim. Dynam., 15, 127–143, https://doi.org/10.1007/s003820050272, 1999.





