Simulated dynamic regrounding during marine ice sheet retreat

Marine-terminating ice sheets are of interest due to their potential instability, making them vulnerable to rapid retreat. Modelling the evolution of glaciers and ice streams in such regions is key to understanding their possible contribution to sea level rise. The friction caused by the sliding of ice over bedrock and the resultant shear stress are important factors in determining the velocity of sliding ice. Many models use simple power-law expressions for the relationship between the basal shear stress and ice velocity or introduce an effective-pressure dependence into the sliding relation in an ad hoc manner. Sliding relations based on water-filled subglacial cavities are more physically motivated, with the overburden pressure of the ice included. Here we show that using a cavitation-based sliding relation allows for the temporary regrounding of an ice shelf at a point downstream of the main grounding line of a marine ice sheet undergoing retreat across a retrograde bedrock slope. This suggests that the choice of sliding relation is especially important when modelling grounding line behaviour of regions where potential ice rises and pinning points are present and regrounding could occur.

1 Introduction

Marine ice sheets, which are grounded below sea level, have been identified as having the potential to contribute significantly to future sea level rise through the rapid loss of ice under changing climate conditions. It has been suggested (Mercer, 1978; Weertman, 1974) that, when they are grounded on a retrograde-sloping bedrock (i.e. sloping downwards towards the interior of the continent), the positive relationship between ice thickness and ice flux leads to a positive feedback in which rapid retreat of the grounding line may occur, termed “marine ice sheet instability” (MISI). MISI theory predicts that the grounding line of a glacier cannot stabilise on a retrograde bedrock slope. Thus, if a glacier retreats onto a region with such a bedrock geometry, it will continue retreating rapidly at least until reaching a prograde slope, potentially discharging large amounts of previously grounded ice into the ocean. Large regions of the Antarctic Ice Sheet, particularly in West Antarctica, are grounded below sea level with retrograde-sloping bedrock (Fretwell et al., 2013) and thus may be susceptible to MISI. Marine ice sheets have been investigated widely, with Pattyn et al. (2017) providing a recent review of development in modelling their dynamics. They have been the subject of recent model intercomparison projects looking at idealised systems, such as the Marine Ice Sheet Model Intercomparison Project (MISMIP) (Pattyn et al., 2012), MISMIP3d (Pattyn et al., 2013) and MISMIP+ (Asay-Davis et al., 2016). Retreating glaciers showing a geometry making them susceptible to MISI, such as Pine Island Glacier, have also been a particular focus (Favier et al., 2014; Gladstone et al., 2012; Joughin et al., 2010). More recent analysis has shown that stable grounding line configurations may be possible on retrograde-sloping bedrock when the buttressing of floating ice shelves and 3-D geometry of the system are included (Gudmundsson, 2013; Gudmundsson et al., 2012; Katz and Worster, 2010) or in some configurations where the basal friction coefficient is tuned spatially (Brondex et al., 2017).

Many ice sheet models use a power-law relationship between the basal shear stress and sliding velocity, such as that of Weertman (1957). These models require very fine mesh resolution due to the sharp change in shear stress across the grounding line (Cornford et al., 2013; Gladstone et al., 2010, 2017; Leguy et al., 2014; Vieli and Payne, 2005). Other relations have been investigated which take into account the effective pressure of the ice at its base, determined either empirically, such as that of Budd et al. (1984), or by including in the presence of water-filled cavities (Schoof, 2005). Sliding relations in ice sheet models which include an effective-pressure dependence – such as those of Schoof and Budd, which are implemented in Elmer/Ice (Brondex et al., 2017; Gagliardini et al., 2007; Gladstone et al., 2017) – provide a theoretically based treatment of basal friction; do not cause such strong mesh resolution dependency; and, in the case of Schoof (2005), satisfy Iken's bound (Iken, 1981). Recently Tsai et al. (2015) explored the effect of using a modification to the power-law basal sliding with Coulomb friction used close to the grounding line on the stability and profiles of marine ice sheets.

The underlying geometry of the bedrock is an important control in the stability of marine ice sheets. The role of ice rises and pinning points (Favier and Pattyn, 2015; Favier et al., 2012; Fürst et al., 2016) in affecting buttressing forces and stabilisation of the grounding line has been investigated in numerical modelling efforts, as has the role of glacial isostatic adjustment (Gomez et al., 2012). Recent ensemble simulations of Antarctic Ice Sheet deglaciation since the Last Glacial Maximum (Kingslake et al., 2017) have demonstrated that regrounding of pinning points in large ice shelves due to glacial uplift after a period of retreat can cause a stabilisation and re-advance of the grounding line. Thus regrounding can be important to large-scale marine ice sheet dynamics, even leading to a partial recovery from MISI, with the grounding line advancing again after a period of retreat.

In this study, we further investigate the impact of the sliding law on glacier trajectory in an idealised 2-D flow line model, showing that dynamic regrounding on a retrograde bedrock slope can occur when a sliding relation with a dependency on the effective pressure at the base of the ice is used.

2 Methods

2.1 Model description

In this study we use a finite-element model Elmer/Ice (Gagliardini et al., 2013) to solve the full-Stokes equations for a viscous fluid. A rheology following Glen's law is used, with the temperature held constant through the whole of the ice sheet at −15 ^∘C. We use a two-dimensional flow line geometry with the bedrock shape the same as that used in a recent model intercomparison project (Pattyn et al., 2012), featuring a section of retrograde slope, described by

$$\begin{array}{ll}{\displaystyle }B\left(x\right)& {\displaystyle }=\mathrm{729}-\mathrm{2184.8}{\left({\displaystyle \frac{x}{\mathrm{750}\mathrm{km}}}\right)}^{\mathrm{2}}+\mathrm{1031.72}{\left({\displaystyle \frac{x}{\mathrm{750}\mathrm{km}}}\right)}^{\mathrm{4}}\\ \text{(1)}& {\displaystyle }& {\displaystyle }-\mathrm{151.72}{\left({\displaystyle \frac{x}{\mathrm{750}\mathrm{km}}}\right)}^{\mathrm{6}},\end{array}$$

where x is distance from the inland boundary and B is bedrock elevation relative to sea level.

The grounding line position is solved in the model through a contact problem, taking into account the geometry of the lower surface with respect to the bedrock, the effective pressure at the base of the grounded ice and the buoyancy of the ice in contact with the ocean.

We use a basal sliding relation that is based on the theory of sliding with cavitation (Schoof, 2005) and has been implemented in Elmer/Ice (Gagliardini et al., 2007). The basal friction is related to the sliding velocity by

$$\begin{array}{}\text{(2)}& {\displaystyle \frac{{\mathit{\tau }}_{\mathrm{b}}}{N}}=C_{max}{\left({\displaystyle \frac{\mathit{\chi }}{\mathrm{1}+\mathit{\alpha }{\mathit{\chi }}^q}}\right)}^{\mathrm{1}/n},\end{array}$$

where τ_b is the basal shear stress; u_b is the basal ice sliding velocity, with

$$\begin{array}{}\text{(3)}& \mathit{\chi }={\displaystyle \frac{u_{\mathrm{b}}}{C_{max}^n{N}^n{A}_{\mathrm{S}}}}\end{array}$$

and

$$\begin{array}{}\text{(4)}& \mathit{\alpha }={\displaystyle \frac{{\left(q-\mathrm{1}\right)}^{q-\mathrm{1}}}{q^q}}.\end{array}$$

A_S is the sliding parameter in the absence of cavitation; n=3 is the Glen's law exponent; $C_{max}=\mathrm{0.1}$ is the maximal value of τ_b∕N, bounded by the maximum slope of the bedrock; and q=1 is the exponent controlling the post-peak decrease. The effective pressure N is calculated based on the assumption of full connectivity between the subglacial hydrologic system and the ocean. This sliding relation is henceforth referred to as the “cavitation sliding relation”.

The other sliding relation used in this study is a non-linear, Weertman type friction law of the form

$$\begin{array}{}\text{(5)}& {\mathit{\tau }}_{\mathrm{b}}=C_{\mathrm{W}}{u_{\mathrm{b}}}^m,\end{array}$$

where $m=\mathrm{1}/n$, τ_b and u_b the basal shear stress and ice velocity respectively, and C_W is a constant friction coefficient. This sliding relation is henceforth referred to as the “Weertman sliding relation”.

A buttressing-like force due to friction along glacier side walls is included by adding a body force into the force balance using a parameterisation relating lateral resistance to the rheological parameters of the ice and an ice shelf embayment width described by Gagliardini et al. (2010). The body force is given by

$$\begin{array}{}\text{(6)}& \mathit{f}=-K|\mathit{u}{|}^{m_{\mathrm{lr}}-\mathrm{1}}\mathit{u},\end{array}$$

where $m_{\mathrm{lr}}=\mathrm{1}/n$ is the lateral resistance exponent, with n as the usual Glen's law parameter. The resistance parameter K is given by

$$\begin{array}{}\text{(7)}& K={\displaystyle \frac{(n+\mathrm{1}{)}^{\mathrm{1}/n}}{W^{\frac{n+\mathrm{1}}{n}}(\mathrm{2}A{)}^{\mathrm{1}/n}}},\end{array}$$

with A being the fluidity parameter of the ice. W is a parameter corresponding to a channel half-width which we use to modify the lateral drag during the experiment from being initially high (i.e. low W) and then decreased by changing to a high value of W as a means of forcing the glacier to retreat.

The experiments presented here used a horizontally uniform mesh resolution with a 500 m element size for simulations using the cavitation sliding relation and 250 m element size for simulations using the Weertman sliding relation. Tests were carried out at coarser resolutions to test for resolution dependence (see Appendix A for details and Appendix B for a table of model parameter values). The mesh is extruded in the vertical direction to 20 equally spaced layers in all simulations.

2.2 Experimental description

The retreat experiments examine the behaviour of an ice sheet retreating across a section of retrograde slope when using the cavitation sliding relation, which incorporates a dependency of basal shear stress on effective pressure at the base of the ice. We begin with a 2-D ice sheet grown from a uniform initial thickness of 100 m. During the initial 5000 years of spin-up the parameterised buttressing is set to zero. The buttressing is then linearly increased from zero to an effective channel half-width of 100 km over the next 5000 years, resulting in a high buttressing force. The model is then continued until the grounding line position rests on the seaward side of the bedrock overdeepening (at approximately 1400 km from the ice divide). During this initial spin-up period the top surface accumulation rate is set to 1 m yr⁻¹, to reduce the total run time for the spin-up. After 10 000 years the accumulation rate is then decreased to 0.3 m yr⁻¹ and held at this value while the ice sheet stabilises, and it remains at this value throughout the retreat experiments. We determine that the spin-up has finished and the ice sheet has reached a steady state when there has been no change in the grounding line position and the mesh velocity, determining the change in the top and bottom free surfaces, remains less than 0.001 m yr⁻¹ over 10 000 years, resulting in a total spin-up time of 25 000 years.

We run a series of experiments where we trigger retreat of the glacier through a reduction in the buttressing force by linearly increasing the channel half-width parameter over 10 years to reduce the buttressing force, using values of W equal to 250, 300, 350, 375, 400 and 450 km. An infinitely wide channel corresponds to the case of no lateral drag, and the values of W used in the experiments should be considered as simply providing a range of values for buttressing. Simulations are then run for 2500 years, with 0.1-year time steps with no further forcing change applied after the initial buttressing adjustment.

We carry out a similar retreat experiment using the Weertman sliding relation (Eq. 5). In this experiment we again spin up the ice sheet, initially for 5000 years with no buttressing and accumulation of 1 m yr⁻¹, increasing the buttressing with W=100 km linearly over 5000 years. The accumulation rate is then reduced to 0.3 m yr⁻¹, and the model is left to evolve for a further 10 000 years until the top and bottom free surfaces show minimal change, resulting in a total spin-up time of 20 000 years.

Recently, Brondex et al. (2017) showed that far from the grounding line (i.e. for large values of height above flotation) the Weertman and cavitation sliding relations give an approximately equivalent relationship between basal velocity u_b and basal sheer stress τ_b. For this study the Weertman friction coefficient used corresponds to a similar value of τ_b given by the cavitation sliding relation in the high effective-pressure limit (inland), while also resulting in the initial position of the grounding line being within a few kilometres for both sets of experiments.

To trigger a retreat of the grounding line, we again reduce the buttressing by increasing W from 100 km to values equal to 350, 400 and 500 km linearly over a period of 10 years and then continuing to let the simulation run without further forcing. A time step of 0.5 years was used throughout the experiment.

3 Results

3.1 Cavitation sliding

The position of the grounding line is tracked over time during the channel half-width increase and through the continuation of the model run (Fig. 1a). In most simulations using the cavitation sliding relation, the grounding line has retreated across the retrograde slope within the first 1000 years, and by 2500 years grounding lines and surface slopes are stabilising. The simulations with higher buttressing (i.e. a smaller forcing perturbation relative to the pre-retreat state) take longer to retreat and stabilise.

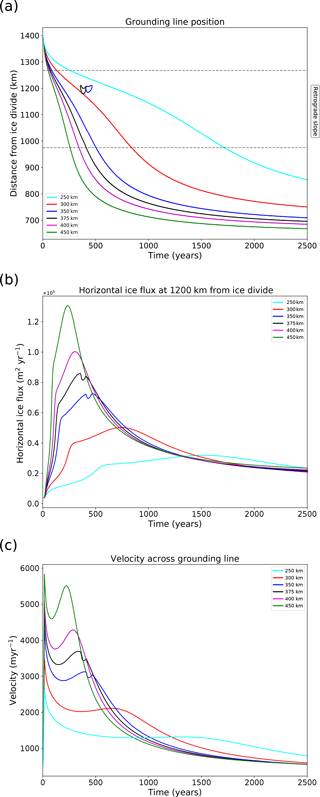
Figure 1 Retreat experiments using the cavitation sliding relation. (a) Evolution of grounding line position over time for a range of parameterised channel half-widths. Dashed lines indicate the extent of the retrograde bedrock. (b) Total flux of ice in the horizontal direction across a line 1200 km from the ice divide. (c) Sliding speed across the grounding line.

The simulations with W=350 and 375 km feature a temporary regrounding of the ice shelf during retreat on the retrograde bedrock. The temporary regrounding occurs approximately 200 km downstream of the original (henceforth “upstream”) grounding line. The upstream grounding line continues to retreat during regrounding of the shelf.

This regrounding is likely caused by the downstream advection of thicker interior ice, which is mobilised by the buttressing reduction. In general, dynamic thinning of the ice shelf due to reduced buttressing competes with thickening due to downstream advection of thicker interior ice to give either a net thinning or thickening in the shelf. For simulations with parameterised channel half-width W ≥ 400 km the peak ice discharge comes early (approximately 300 years; see also Fig. 1b), and dynamic thinning is sufficient to prevent regrounding. For simulations with W ≤ 300 km a sharp peak in discharge is not seen (Fig. 1b), and downstream advection of thicker ice is slow, too slow to overcome dynamic thinning in the shelf. Thus the simulations with W=350 and 375 km represent a key region of input space in which regrounding may occur. We refer to this as “dynamic regrounding” to distinguish it from regrounding due to bedrock uplift (described in Sect. 1).

The position of the flux gate in Fig. 1b (1200 km from the ice divide) is chosen as it is located where the regrounding occurs. The flux reaches a maximum as the grounding line approaches the inland end of the retrograde-bedrock region and decreases as the grounding line migrates up the prograde slope. Similarly, we see a reduction in the sliding speed of the ice across the grounding line as shown in Fig. 1c. For the cases where dynamic regrounding occurs we see a temporary reduction in the flux and sliding speed, but this reduction is not sufficient to stabilise retreat.

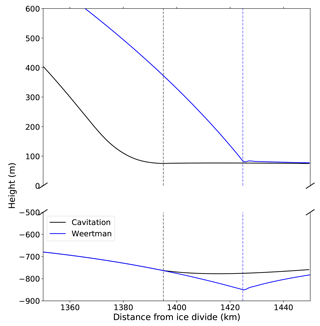
Figure 2 presents a more detailed analysis of retreat and dynamic regrounding for W=350 km. It can be seen that the slope of the lower surface of the ice shelf is similar to the retrograde bedrock slope, and this corresponds to a very shallow water column under the shelf. The implication is that only a very small amount of thickening is needed to cause regrounding. The shallow water column is common to all retreat simulations with the cavitation sliding relation (not shown).

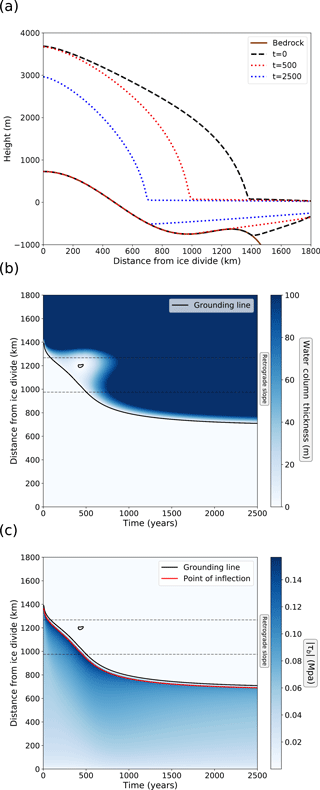
Figure 2 Retreat experiment details with the cavitation sliding relation and W=350 km. (a) Ice sheet profiles during retreat. Bedrock profile is also shown. (b) Evolution of the water column thickness during retreat. (c) Evolution of the basal shear stress.

Figure 2c shows basal shear stress, the point of inflection and the grounding line. The point of inflection is with respect to the upper surface height of the ice sheet and indicates the switch from a convex ice sheet surface (inland, which includes most of the grounded ice) to concave. It is identified here through calculation of the maximum gradient of the upper surface. Figure 2c shows that the point of inflection corresponds to the maximum in basal shear stress. Downstream of this line basal shear stress drops rapidly to zero, due to the dependence on effective pressure at the bed, N, in the cavitation sliding relation (Eq. 2). The grounding line is persistently a few tens of kilometres downstream of the point of inflection. The implications of the point of inflection and basal shear stress pattern for transition zones and ice sheet profiles with different sliding relations will be discussed further in Sect. 4. Basal shear stress is also very low under the regrounding region, again due to the dependence on N.

3.2 Weertman sliding

In experiments where the Weertman sliding law is used we see no temporary regrounding of the ice sheet. The ice shelf develops a thinner profile than with the cavitation sliding relation and a markedly different shape, as shown in Fig. 4a. A strongly concave shape is evident immediately downstream of the grounding line, in contrast to the more linear ice shelf profile when using the cavitation sliding relation. As a result of this difference, water column thickness is much larger during retreat than for the cavitation sliding relation.

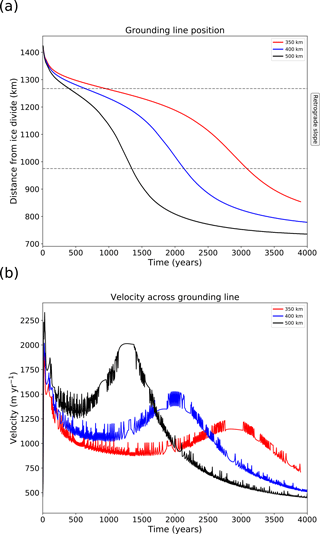
Figure 3 Evolution of (a) grounding line position and (b) cross-grounding-line sliding speed for a range of parameterised channel half-widths using the Weertman sliding relation.

In Fig. 3b we see high-frequency changes in velocity, with each jump in velocity likely to correspond to grounding line movement between neighbouring mesh elements. Ungrounding of an element significantly reduces the basal friction, allowing speedup. This does not happen with the cavitation sliding law (Fig. 1c) because the dependence on effective pressure means that the basal shear stress is in any case close to zero for elements that are newly ungrounded.

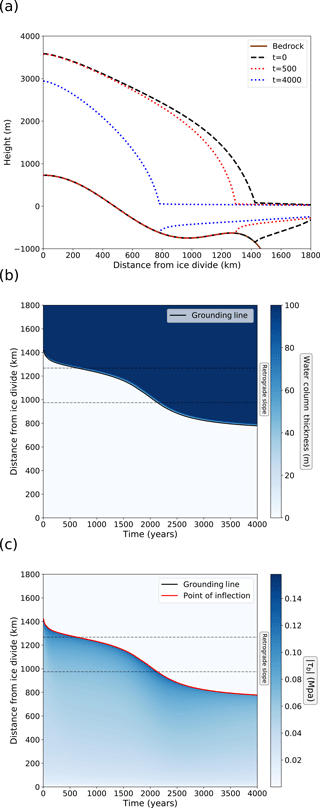
Figure 4 Retreat experiment details with the Weertman sliding relation and W=400 km. (a) Ice sheet profiles during retreat. Bedrock profile is also shown. (b) Evolution of the water column thickness during retreat. (c) Evolution of the basal shear stress. Note that the point of inflection and grounding line position are co-located.

Figure 5 Detail of ice sheet profiles at t=0 for both cavitation sliding and Weertman sliding. Dashed vertical lines indicate the position of the grounding line.

4 Discussion

Retreat simulations in the current study have demonstrated that regrounding of an ice shelf, associated with a small drop in ice flow velocities, may occur under certain conditions during the rapid, unstable retreat of a marine ice sheet. Whether or not this kind of dynamic regrounding could occur on larger spatial or temporal scales, or even stabilise a marine ice sheet, cannot be inferred from the current study. The regrounding occurs as thick, previously grounded ice is advected downstream toward a bedrock rise in response to reduced buttressing.

While a thorough investigation into conditions for regrounding to occur is beyond the scope of the current study, it does provide insight into possible conditions when regrounding may occur. The geometry of the ice sheet is clearly important, as advection of thicker ice is required to cause regrounding. This may be more complicated in three dimensions – flow convergence may itself provide thickening in response to grounded ice speed-up. Bedrock geometry is also important – the retrograde slope is a key feature of the current set-up, and it is unlikely that regrounding could occur without an overdeepening. We suggest that a higher (closer to sea level) bedrock maximum and steeper retrograde slope are both likely conducive to regrounding. Choice of sliding relation and the parameters used is also important. The strongly concave lower surface of the ice shelf just downstream from the grounding line in the case of Weertman sliding increases the water column depth under the ice shelf and reduces the likelihood of regrounding. High sub-shelf melt rates may also cause a concave lower surface profile, reducing the likelihood of regrounding.

Impact of sliding law merits further consideration. The stress state in the ice sheet changes from the grounded region to the floating ice shelf over what is typically termed a “transition zone” (Pattyn et al., 2006; Schoof, 2007a). Grounded ice typically features high gravitational driving stress and high basal shear stress, especially for the high surface gradients and high velocities as the transition zone is approached. The floating ice shelf features smaller magnitude forces, with the parameterised buttressing approximately balancing longitudinal stress and driving stress being close to zero. In the absence of buttressing the ice shelf thickness would be almost constant through most of its length (Schoof, 2007b). For the case of Weertman sliding, the basal shear stress drops from its maximum value to zero as the grounding line is crossed (Fig. 3). The high basal shear stress right up to the grounding line is balanced by a correspondingly high driving stress, with maximum surface slope occurring at the grounding line. Thus instead of a transition zone upstream of the grounding line, a geometrically concave region with very high spatial gradients in driving stress and flow speed extends downstream into the ice shelf (typically around 20 km in our experiments) before a more typical shelf regime is attained. For the cavitation sliding relation, the rapid decay of basal shear stress to zero in the vicinity of the point of inflection in surface slope (Fig. 2) leads to a grounded transition zone with the concave ice thickness occurring upstream of the grounding line, resulting in a thicker, more linear ice shelf. Figure 5 shows example ice sheet/shelf geometries over the transition zone for both sliding relations. This difference in ice shelf profile is a direct result of dependence on effective pressure at the bed and is likely to be present also for other sliding relations featuring such a dependence, as has been shown in, for example, Tsai et al. (2015), Gladstone et al. (2017) and Brondex et al. (2017). The length of the grounded transition zone in the cavitation sliding law is a function of parameter choices, especially C_max. For higher values of C_max the transition zone would be smaller, and the ice sheet geometry closer to that obtained with Weertman sliding. Thus the occurrence of dynamic regrounding may depend not only on choice of sliding relation but also on parameter choices for the chosen sliding relation.

The plots of sliding velocity across the grounding line in Figs. 1c and 3b also point to differences resulting from the choice of sliding relation. After the initial adjustment period in response to the change in buttressing, the peak in grounding line ice velocity corresponds to the time when the position of the grounding line crosses from being situated on a retrograde to a prograde bedrock slope. In the cavitation sliding case we also see a small drop in velocity occurring at the same time as the regrounding. Farther from inland and towards the grounding line, the value of basal friction changes markedly depending on the sliding relation used. In the Weertman case the basal friction must increase towards the grounding line position (because the ice velocity has increased), while in the cavitation sliding case the friction must decrease due to the effective-pressure dependence. This results in the Weertman sliding case showing higher basal friction and slower velocities compared to the cavitation sliding case.

The contrasting ice shelf profiles for the two sliding relations in the current study could indicate a means for validation of the choice of sliding relation through comparison against observed ice shelf profiles. Ideally, observed profiles for simulations with low ice shelf basal melting and low buttressing would be used, as both of these factors could impact the ice shelf geometry.

The dynamic regrounding in the current study has some similarity to the regrounding that occurs following the overshoot mechanism presented by Kingslake et al. (2017), in which regrounding of an ice shelf after grounding line retreat may occur through bedrock uplift after ice unloading. Both regrounding mechanisms impose a reduction in ice discharge, though the overshoot regrounding is lasting and the dynamic regrounding in the current simulations is transient. The suggested timescale for overshoot regrounding is an order of magnitude greater than the timescale for dynamic regrounding in the current study, but these timescales are also controlled by the size of the system, the ice flow speeds, and potentially ice and bedrock geometry. In the case of overshoot regrounding the timescale is also strongly dependent on mantle viscosity. It may be possible that for some bedrock configurations, and in the case of low mantle viscosity, dynamic regrounding could sufficiently retard ice sheet retreat to prevent overshoot and allow a post-retreat steady state to be reached more quickly.

5 Conclusions

Flow line ice sheet simulations carried out in the current study demonstrate that regrounding on a retrograde bedrock slope can occur during marine ice sheet retreat. It is not yet clear under what conditions this regrounding, combined with isostatic rebound, could counter retreat and stabilise the ice sheet.

The current study also demonstrates that use of a sliding relation in which basal shear stress is dependent on effective pressure at the bed impacts transition zone location and ice shelf thickness profiles immediately downstream of the grounding line. This dependence implies that regrounding is less likely to occur when a Weertman sliding relation is used and could provide a means for validating choice of sliding relation through comparison with observed ice shelf profiles.

Appendix A: Mesh resolution dependence

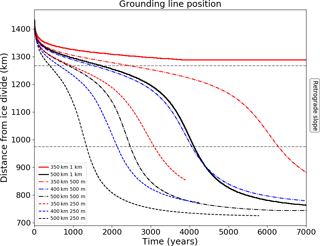
A number of experiments were run at different mesh resolutions demonstrating convergent behaviour. Identical retreat experiments were performed using the cavitation sliding relation on uniform meshes with 2 km, 1 km and 500 m grid spacing. Runtime is considerably longer for the finest mesh resolution. The results, shown in Fig. A1, demonstrate that the regrounding behaviour is present and almost identical in both the 1 km and 500 m mesh spacing cases. For values of W=300, 350 and 400 km, the final position of the grounding line is the same for all mesh resolutions. We conclude that the effects shown here are not dependent on the mesh resolution and that a finer resolution is not required to get convergent behaviour of the grounding line.

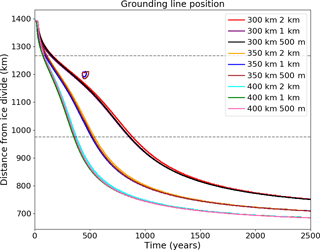
Figure A1 Grounding line retreat for the mesh resolution dependence experiments using the cavitation sliding relation. Buttressing parameters of 300, 350 and 400 km are used with 2 km, 1 km and 500 m uniform element size in the horizontal.

Similar experiments were performed using the Weertman sliding relation on uniform meshes with 1 km, 500 m and 250 m grid spacing. In this case, while the end position of the grounding line appears to converge, the finer mesh results in faster retreat of the grounding line across the retrograde slope. The concave geometry of the lower surface of the ice shelf, however, is consistent across the mesh resolution experiments. Previous studies into the mesh resolution dependence of the grounding line position and evolution using Weertman sliding, e.g. Durand et al. (2009), have shown that consistency in the final grounding line positions can be obtained with horizontal mesh elements of below 5 km.

Figure A2 Grounding line retreat for the mesh resolution dependence experiments using the Weertman sliding relation. Buttressing parameters of 350, 400 and 500 km are used with 1 km, 500 m and 250 m uniform element size in the horizontal.

Appendix B: Model parameters

Table B1 Values of model parameters used.