the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Greenland Ice Mapping Project: ice flow velocity variation at sub-monthly to decadal timescales
Ian Joughin
Ben E. Smith
Ian Howat
We describe several new ice velocity maps produced by the Greenland Ice Mapping Project (GIMP) using Landsat 8 and Copernicus Sentinel 1A/B data. We then focus on several sites where we analyse these data in conjunction with earlier data from this project, which extend back to the year 2000. At Jakobshavn Isbræ and Køge Bugt, we find good agreement when comparing results from different sensors. In a change from recent behaviour, Jakobshavn Isbræ began slowing substantially in 2017, with a midsummer peak that was even slower than some previous winter minima. Over the last decade, we identify two major slowdown events at Køge Bugt that coincide with short-term advances of the terminus. We also examined populations of glaciers in north-west and south-west Greenland to produce a record of speed-up since 2000. Collectively these glaciers continue to speed up, but there are regional differences in the timing of periods of peak speed-up. In addition, we computed trends in winter flow speed for much of the south-west margin of the ice sheet and find little in the way of statistically significant changes over the period covered by our data. Finally, although the consistency of the data is generally good over time and across sensors, our analysis indicates that substantial differences can arise in regions with high strain rates (e.g. shear margins) where sensor resolution can become a factor. For applications such as constraining model inversions, users should factor in the impact that the data's resolution has on their results.
- Article
(10332 KB) - Full-text XML
-
Supplement
(4901 KB) - BibTeX
- EndNote
As recently as the 1990s (Paterson, 1994), it was assumed that the Greenland Ice Sheet and its outlet glaciers would respond slowly to climate change. Since the satellite record began, largely since the 1990s, it has proved these early assumptions false. In particular, many glaciers in Greenland have sped up substantially over the last two decades (e.g. Joughin et al., 2010; Moon et al., 2012; Rignot and Kanagaratnam, 2006), including several of Greenland's largest glaciers (Howat et al., 2005; Joughin et al., 2004; Luckman et al., 2006). In addition to the ice sheet's outlet glaciers, slow-flowing areas near its margin speed up and slow down seasonally (e.g. Joughin et al., 2008a; van de Wal et al., 2008; Zwally et al., 2002) in response to surface meltwater making its way to the bed through moulins, which can penetrate ice more than 1 km thick (Das et al., 2008).
Several groups have produced estimates of velocity for Greenland using synthetic aperture radar (SAR) and optical images (Mouginot et al., 2017; Nagler et al., 2015; Rosenau et al., 2015). As part of the work described here, several maps from 2000 onwards have been produced by the Greenland Ice Mapping Project (GIMP) (Joughin et al., 2010, 2017; Moon et al., 2012). The GIMP maps have made extensive use of SAR data from the European Space Agency's (ESA) ERS 1&2, the Canadian Space Agency's (CSA) RADARSAT 1, the Japanese Space Agency's (JAXA) ALOS-PALSAR, and the German Space Agency's (DLR) TerraSAR-X and TanDEM-X missions.
In late 2014 the European Union's Copernicus programme began providing Sentinel 1A SAR data at 12-day intervals suitable for ice-sheet mapping (Mouginot et al., 2017; Nagler et al., 2015). With the addition of Sentinel 1B to the Copernicus constellation in late 2016, ESA began processing and distributing regular 6-day coverage of Greenland's coastal regions. These coastal data are complemented by several cycles of coverage over the interior each winter to provide annual coverage of the entire ice sheet. These data are routinely ingested into the NASA MEaSUREs programme's GIMP velocity products, which are freely distributed through the National Snow and Ice Data Center (NSIDC, 2018). In addition to radar data, the maps from 2014 onwards also include Landsat 8 data.
Here we describe the production of new GIMP velocity maps that incorporate the Sentinel 1A/B and Landsat 8 data along with data from other sources. Although we emphasize the new products, we examine these products in the context of the entire GIMP 17-year time series to estimate seasonal- to decadal-scale variability in Greenland. We analyse the continuity of the data set and evaluate the magnitudes of any systematic differences between data sets produced using different sensors. Finally, we examine changes in ice flow at several locations in Greenland to demonstrate the utility of the time series for understanding processes related to ice-sheet and outlet glacier dynamics.
The GIMP velocity products are derived using speckle-tracking/feature-tracking cross-correlation algorithms applied to pairs of SAR or Landsat 8 images. In cases where the interferometric phase is available, it is also included in the solution since it improves the resolution and provides greater accuracy for the component of motion directed in the satellite look direction (Joughin et al., 2010). The GIMP velocity products described here are processed using the same core set of algorithms, which have been described extensively elsewhere (Joughin, 2002; Joughin et al., 2010, 2017). As a result, here we focus only on the details of the processing relevant to Sentinel 1A/B data.
Unlike traditional stripmap SAR data used in earlier GIMP products, which are distributed as spatially continuous images, the data from the Interferometric Wide (IW) swath mode of the Sentinel 1 Terrain Observation with Progressive Scans SAR (TOPSAR) are distributed as series of overlapping ∼ 82 by 20 km discrete bursts, acquired along three adjacent sub-swaths. Since the bursts are small relative to the scale of the ice sheet, the first step in our processing is to use the GAMMA Interferometric SAR (ISP) package to assemble each set of bursts into a continuous single-look complex (SLC) image with a width of ∼ 250 km and a length of several hundred kilometres. Once the SLCs are assembled, we process them in the same way that we would normal stripmap (i.e. non-bursted) SAR images, using our in-house speckle-tracking algorithms. Although some data acquisitions traverse the full length of Greenland, we typically break these data acquisitions up in to individual pieces of more manageable size (< ∼ 1200 km).
For many early SAR missions, the accuracy of the orbital state vectors was not sufficient to determine the geometric baseline (difference in position) between the satellite(s) on successive passes. As a result, ground control points of known elevation and speed often are used to solve for the geometric baseline parameters to produce calibrated velocity measurements (Joughin et al., 1996). In principal, the Sentinel 1A/B orbital state vectors are sufficiently accurate to calculate the baseline and other geometric parameters with little or no ground control (Nagler et al., 2015). Since our workflow is adapted to use ground control points, however, we use these points with Sentinel 1 data to maintain consistency with earlier GIMP products. For the regular 6- and 12-day Sentinel coastal acquisitions, our baseline solutions are largely constrained by bedrock points, where we know that the velocity should be zero. For the winter campaigns, however, some swaths are positioned well away from the coasts. In these cases, we use our existing control-point database, which includes balance velocities and GPS measurements from areas where little change in flow speed is expected (Joughin et al., 2017). We augment these control points by extracting SAR-derived point velocity estimates from areas where there is overlap with well-constrained coastal data takes acquired at similar times.
An advantage of using control points is that they offer the potential to improve the baseline solution, although this improvement has declined over time as orbit reconstructions improve with each new sensor. A second advantage is that the control-points may, at least partially, mitigate other, non-positional, sources of error. For example, the baseline solution can partially compensate for ionospheric path delays, particularly at L-band for which such delays are larger. The potential downside to using control points is that velocity errors at the control points can bias the solution. Our baseline solutions, however, use 100s to 1000s of points to solve for at most six parameters, providing a relatively robust solution. Furthermore, we have carefully culled the control points to avoid introducing biases (Joughin et al., 2017).
The Landsat 8 panchromatic (band 8) 15 m data are high-pass filtered and then processed using a cross-correlation-based feature-tracking algorithm similar to that used by others (Fahnestock et al., 2016; Jeong et al., 2017). The images are delivered in UTM format, so we first project them to the polar stereographic projection (EPSG:3413) that we use for all of the GIMP products. Although the Landsat-8 offsets are produced in map-projected coordinates, we use a control-point procedure to fit a simple plane to each velocity component in each image pair to compensate for geolocation errors (Joughin et al., 2017). In the final stage of calculation, corrections are made for the projection-dependent-scale distortion.
Once the SAR and Landsat 8 data have been calibrated using control points, all of the data are combined and mosaicked to the final output grid using our velocity-determination algorithms (Joughin, 2002; Joughin et al., 2010, 2017). At each point in the output, the result represents an inverse-error-weighted (i.e. 1∕σ2) average of all viable estimates. As described below, besides the inverse-error weighting, additional weighting is applied to the data as needed. As part of the velocity estimation procedure, a formal error estimate is produced for each point in the output grid. In general, these errors agree well (within about a factor of 2) with independent estimates of error (Joughin et al., 2017). Although the error estimates are given as 1σ values, the actual distribution likely has a heavier tail than that of a Gaussian distribution but with the same standard deviation. Care should be taken, therefore, in applying standard tests of statistical significance due to the potential for large outliers.
Most prior SAR missions have provided coverage exclusively along ascending or descending orbits. With the Sentinel 1A/B mission, however, the measurements often cover an area from both ascending and descending orbits, particularly during the winter mapping campaigns. In such cases, we apply a surface-parallel flow assumption to determine the velocity solely from ascending and descending range offsets (Joughin et al., 1998). The advantage of this approach is that it avoids using the noisier, along-track azimuth offsets. A disadvantage is that range-offset errors tend to be amplified by about a factor of 3 in the north–south direction. Nonetheless, such solutions are generally far less noisy than pure range-azimuth offset estimates, particularly at times when the ionosphere introduces errors in the azimuth component of the speckle-tracked velocity estimates (Gray et al., 2000). In our final solutions, we include both types of estimates, weighted by their respective inverse-error estimates.
The GIMP project produces two types of velocity products. The first type provides “snapshot” velocities calculated from the displacements in a single image pair. The second type provides aggregated estimates, which represent a single time period but are formed by averaging multiple individual estimates. In the latter case, the individual constituent estimates may not uniformly sample the output interval. In these cases, there are various trade-offs that must be considered to produce accurate results without sacrificing too much temporal resolution or introducing too large deviations from the nominal time stamp (temporal skew).
Through GIMP, we produce annual (12-monthly), winter (up to 9-monthly), quarterly (3-monthly), and monthly aggregate products. As an example of the temporal-resolution issues that arise in producing such data sets, consider the case of monthly sampling, with time intervals corresponding to each calendar month. If our only source data are 12-day Sentinel 1A pairs, then some pairs will straddle the beginning and end of each month. In this case, we weight each pair by its duration of overlap with the month. In the absence of other weighting, this operation is equivalent to linearly interpolating the 12-day time series to each day of the month and then averaging the result. This operation necessarily degrades the temporal resolution of the product, since interpolation can be represented as the convolution of a low-pass filter with the data. In this example, degradation would be relatively small.
Another problem with temporal sampling is what to do with data with coarser temporal resolution than the sampling interval. In areas where data are plentiful, coarsely-sampled data may be discarded. There are cases, however, where these data may be the only available or their inclusion might significantly improve accuracy. As a result, we do include some data with coarser temporal resolution than the nominal sampling interval. In particular, we allow the inclusion of data collected over a time span up to ∼ 60 % greater than the sampling interval. Weighting is applied to these data (e.g. for a 30-day interval; a 48-day Landsat 8 would be weighted by a factor of 30/48) so they mainly contribute to the solution in cases where there is insufficient finer-resolution data. Thus, in some areas the temporal resolution of the GIMP products is coarser than the posted sampling interval, with the degree of resolution degradation depending on the spatially varying mix of data used to compute the velocity.
Both the weighting to accommodate temporal sampling and the inverse-error weighting can skew the nominal centre data for each aggregated product. For example, if a subset of the data is much less noisy, it will contribute more heavily to the average and skew the effective data toward the time covered by the less noisy result. Similarly, missing data can skew the effective time away from the nominal sampling time. To indicate where a large temporal skew may have occurred, we apply the data weights to compute the average of the deviation of the data for each pair from the nominal centre date. Since this scalar variable represents a complicated average of many data, it is best used to diagnose cases where temporal skew could be an issue rather than to serve as a correction. All data plotted here are shown for their nominal time stamp.
While our goal is to produce uniform sampling, some degree of temporal skew and loss of resolution as described above is inevitable. Our approach attempts to optimally balance the level of noise with the size of data gaps for the anticipated common applications of the data set, as illustrated in the examples below. The individual estimates, however, remain available for cases where more precise timing is needed and a higher noise level can be tolerated (e.g. to compare speed-up with terminus retreat events).
Table 1 summarizes only the GIMP velocity products discussed here. For simplicity it excludes the multi-year average product (Joughin et al., 2017) and optical-only (Howat, 2017) GIMP products. Of the products in Table 1, the winter velocities and the individual glacier velocities have been described earlier (Joughin et al., 2010; Moon et al., 2012). Here we describe updates to these products and provide details related to several new products.
3.1 GIMP products
The oldest set of GIMP products presented here is a series of winter velocity maps, which extend back to the winter of 2000–2001 and are derived entirely from SAR data (Joughin, 2017b). For these maps, we define winter to be the period with little or no melt, extending from 1 September to 31 May. Many of these earlier GIMP winter velocity maps use campaign-mode data and are hence derived from acquisitions spanning only a few months. The first winter map to include Sentinel 1A data, available from late 2014, was produced largely from data collected toward the latter half of the 2014–2015 winter. The 2015–2016 and 2016–2017 winter maps include data from the full 9-month period along the coasts, with campaign coverage in the interior.
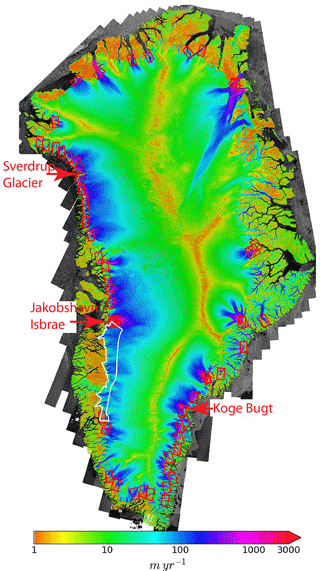
Figure 1Annual velocity map for 2016 plotted over a SAR image mosaic. Arrows indicate glaciers plotted in subsequent figures. The white outline shows the area shown in Fig. 7. Red boxes show the locations of TerraSAR-X and TanDEM-X scenes used in GIMP velocity maps.
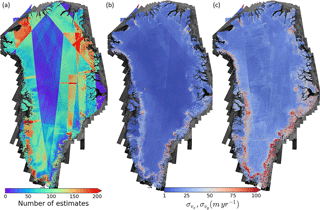
Figure 2(a) Number of valid Sentinel 1A/B estimates made using data collected over the period from January 2015 to September 2017. Standard deviations (b) and (c) of velocity estimates collected over the same period.
Our individual glacier estimates (see red boxes in Fig. 1 for locations) provide 11-, 22-, and 33-day “snapshot” estimates for many of Greenland's fastest outlets, derived using data from DLR's TerraSAR-X and TandDEM-X missions (Joughin et al., 2016a). At present these estimates cover the period from 2009 to 2017, with future coverage dependent on data availability. The high (1–3 m) single-look resolution of these X-band instruments is such that of all of the GIMP products, these products have the best resolution and short-term accuracy.
Regular Sentinel-1A/B and Landsat 8 coverage now allows GIMP to produce annually averaged velocity maps from 2015 onwards (Joughin, 2017a). To temporally align these products with other GIMP products, each year extends from December to November (e.g. the 2015 product extends from 1 December 2014 to 30 November 2015). Figure 1 shows the 2016 annual velocity map. These annual products tend to have the best coverage because Landsat 8 data are often able to fill in those areas, primarily in the high-accumulation areas of the south-east, where SAR methods consistently produce gaps on some glaciers.
The GIMP project also produces a routine set of monthly and quarterly velocity maps as detailed in Table 1. This time series begins in December 2014 and includes Copernicus Sentinel 1A/B, TerraSAR-X/TanDEM-X, and Landsat 8 data. For periods with daylight, the Landsat 8 data contribute heavily to the results. By contrast, in winter some products are entirely radar derived. For the spring and autumn quarterly products in particular, the Landsat 8 data can contribute to the temporal skew because daylight collection is skewed toward the early (autumn) or late (spring) part of the period.
3.2 Sentinel 1 coverage and individual estimates
The Copernicus Sentinel 1A/B satellites now provide routine coastal sampling, with less frequent sampling in the interior during each winter. Together, these satellites have mapped the velocity of many coastal areas more than 100 times since late 2014 (Fig. 2a), exceeding the collective coastal coverage of all prior SAR missions. A further advantage of the Sentinel instruments is the fine (2.3 m) slant-range sampling of the single-look data, which is second only to the TerraSAR-X/TanDEM-X instruments. The azimuth sampling (13.9 m) of the Sentinel IW TOPS mode is ∼ 7 times coarser, however, than that of TerraSAR-X/TanDEM-X and ∼ 2.7 times coarser than that of RADARSAT 1. Resolution has a direct effect on accuracy; hence the error in the azimuth (parallel to the satellite track) component of motion typically is about a factor of 3.5 times worse than that in the range (cross-track) direction (see also Mouginot et al., 2017). In many cases, the azimuth offset accuracy is further degraded by ionospheric effects (Gray et al., 2000).
Successful velocity estimation with speckle-tracking relies on maintaining a strong interferometric correlation between images, which declines with the time between image acquisitions due to processes such as melt and firn compaction. As a consequence, the Sentinel 1A/B 6- and 12-day repeat intervals greatly improve the ability to detect displacement relative to the 24-day repeat period of RADARSAT and the 35-day repeat periods of ENVISAT and ERS-1/2 (when not in tandem or ice modes). This improvement is particularly evident for high-accumulation coastal areas in the south-east (Fig. 2a), where Sentinel 1 provides ∼ 20 or more measurements for regions in which all RADARSAT 1 data, collected over a 13-year period, provided few or no viable estimates (Joughin et al., 2017).
Since displacement data are scaled by the observation interval used to derive velocity, individual Sentinel 1A/B velocities derived using 6- and 12-day image pairs are relatively sensitive to errors that are uncorrelated in time, such as those caused by the ionosphere. These errors, however, are reduced when stacking (averaging) multiple estimates. To help assess the errors of individual Sentinel 1A/B pairs, Fig. 2b and c shows the standard deviations ( of the individual estimates collected from January 2015 and extending to September 2017. For the interior of the ice sheet, where there is little or no melt and speeds do not vary significantly, the means of the individual standard deviations are .2 and .5 m yr−1. The large difference between the x (east-west) and y (north–south) components indicates the dominance of the azimuth errors, which are more closely aligned with the north–south direction. These values provide estimates of uncertainty for the individual velocity estimates under relatively stable conditions, as is evident over the ice-free areas in Fig. 2b. The data in Fig. 2b represent a mix of 6- (∼ 60 %), 12- (37 %) and 24-day (3 %) pairs. As a result, these values should underestimate the uncertainty for 6-day pairs and overestimate it for 12-day or longer pairs.
The causes of the large standard deviations in velocity for coastal areas (reddish areas in Fig. 2b and c) are more complicated because some of the variability indicates actual variations in speed, such as seasonal variability and marine-terminating glacier dynamics. Close inspection of the data, however, reveals that much of the variability, especially on slow-moving coastal areas, is due to noise. In these areas, surface melting and other changes (e.g. high firn compaction rates) lead to weaker intra-pair correlation and, thus, noisier estimates.
Although the results shown in Fig. 2b and c are representative of mean performance, there is substantial variability in data quality, with some estimates being much better than others. For this reason, we expect the temporally aggregated, error-weighted averages described above to yield much lower errors in aggregated velocity maps relative to unweighted averaging. In areas where there is both ascending and descending coverage, we reduce errors further by including offsets derived entirely from crossing range-offset data as described above.
3.3 Resolution and systematic differences
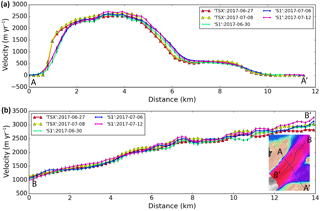
Figure 3Profiles of speed from Sverdrup Glacier (see Fig. 1 for location) along the (a) transverse (A-A′) and (b) longitudinal (B-B′) profiles shown in the inset. The speeds were calculated using individual TerraSAR-X (TSX) and Sentinel 1A/B (S1) pairs collected in early summer 2017.
Figure 3 shows a comparison of individual Sentinel 1A/B and TerraSAR-X velocity estimates for transverse and longitudinal profiles (see inset) from Sverdrup Glacier (see Fig. 1 for location) in north-west Greenland. All of these data were collected over a ∼ 3-week period in the summer of 2017. The transverse-profile data (Fig. 3a) indicate summer speed-up of about 100 to 200 m yr−1 over the period covered by the data. For estimates that are nearly coincident in time, there is agreement between the TerraSAR-X and Sentinel 1A/B data toward the centre of fast flow and in the adjacent, slow-moving areas. Along the shear margins, however, there are systematic differences of up to ∼ 700 m yr−1. For the most part, these differences can largely be attributed to differences in the sensor resolution. With an adequate cross-correlation window size and further smoothing to improve accuracy, the effective azimuth-direction resolution is ∼ 1.5 km for Sentinel 1 A/B and 460 m for TerraSAR-X. As a result, the TerraSAR-X data track the sharp gradients at the shear margins, while Sentinel 1A/B tends to smooth over them.
Figure 3b plots data for a longitudinal profile down Sverdrup Glacier. Over most of the profile, the data agree to within roughly the level of uncertainty indicated by the error bars and any seasonal variation. The error bars represent the random errors for individual estimates, which are uncorrelated from one estimate to the next. Examination of the data, however, indicates that some of the differences between the profiles is sensor-specific rather than random. Some of these differences are attributable to the different resolutions as just described. Other sources of systematic error, however, may be present. For example, the DEM used for the surface parallel flow correction can introduce slope-dependent errors that depend on the imaging geometry (i.e. results from the same sensor with the same viewing geometry have a common error). For past products, we have assumed a worst-case error of about 3 % or ∼ 30 to 90 m yr−1 for the speeds shown in Fig. 3, which is of similar magnitude to the observed differences. For these products, however, we expect improved performance based on the quality of the latest GIMP DEM (Howat, 2017). Because these errors are mixed in with the resolution errors, it is difficult to isolate and quantify each source of error.
We also note that the accuracy of the DEM determines the geolocation accuracy of the final results (∼ 1.25 m horizontal location error for each 1 m of elevation error). For areas similar to the Sverdrup Glacier example, where thinning rates are small, geolocation errors have a negligible impact on the results. In areas of rapid thinning and strong velocity gradients, such as Jakobshavn Isbræ, the surface height at the time of data acquisition may substantially differ from that of the DEM, resulting in significant geolocation errors. Since the tens of metres per year variability of Jakobshavn Isbræ make it an extreme case, we have mitigated the resulting errors in TerraSAR-X products using annually updated DEMs for this glacier.
3.4 Outlet glaciers: Jakobshavn Isbræ and Køge Bugt
As indicated in Table 1, GIMP provides several data sets at a variety of spatial and temporal resolutions generated from multiple sensors, covering overlapping periods. To better understand the temporal consistency of these data sets for outlet glacier studies, here we examine the speeds over a 9-year period, during which there is substantial overlap of the various data sets. In particular, we focus on Jakobshavn Isbræ and Køge Bugt. Although some intercomparison for a more limited set of the Jakobshavn Isbræ data has been presented elsewhere (Joughin et al., 2012; Lemos et al., 2018), we present a more comprehensive intercomparison here. Køge Bugt is estimated to be the glacier with the third greatest imbalance in Greenland for the period 2000 to 2012 (Enderlin et al., 2014), making its record of flow variability of interest for understanding ice loss. Finally, with high strain rates and as two of the fastest glaciers in Greenland, they represent some of the most difficult areas to map, providing a robust demonstration of GIMP's measurement capabilities.
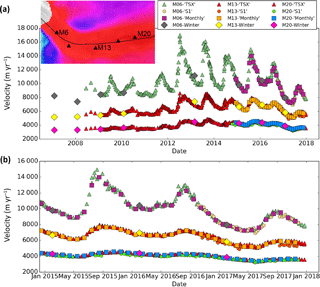
Figure 4Speeds for Jakobshavn Isbræ at the points M6, M13, and M20 shown in the inset over the periods from (a) 2007 to 2017 and (b) January 2015 to December 2017. Results show individual TerraSAR-X/TanDEM-X (triangles) and Sentinel 1A/B estimates (circles). Also shown are the aggregate monthly (squares) and winter (diamonds) products, which take advantage of all available data. For clarity we omitted the annual and quarterly products listed in Table 1. Error bars also are omitted because they are small relative to the plot marker size.
Figure 4a shows the Jakobshavn Isbræ time series for the last decade plotted using many of the GIMP products listed in Table 1. The labels of the points on the main trunk (see M6, M13, and M20 in inset) give their approximate distance in kilometres from the 2004 terminus, which we use for consistency with earlier work (Joughin et al., 2012, 2008b, 2014). As previously noted, there is a strong annual cycle of speed-up, coinciding with summer retreats of the terminus, followed by slowdown during the winter re-advances. A new finding is that the summertime (maximum) speeds have declined since 2012, and the summer 2017 peak is the slowest for the period shown in Fig. 4. Moreover, this peak was actually slower than the winter 2016 minimum and just slightly faster than 2015 winter minimum.
To facilitate a more detailed comparison of the data, Fig. 4b shows the period from January 2015 to December 2017. The good agreement in this figure between the monthly and 11-day TerraSAR-X/TanDEM-X data largely reflects the dominant contribution of the X-band data to the monthly time series. For the two fastest points (M6 and M13), Sentinel 1A provides no valid measurements in the early part of the time series. Once Sentinel 1B acquisitions commenced in October 2016, however, the 6-day sampling began providing estimates for the faster-flowing ice. At all three points, the Sentinel data provide close agreement with the TerraSAR-X/TanDEM-X data consistently with other independent Sentinel 1A/B estimates (Lemos et al., 2018).
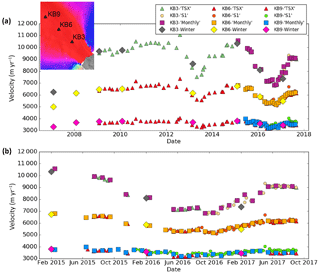
Figure 5Speeds for the glacier discharging ice through to Køge Bugt at the points M6, M13, and M20 shown in the inset over the periods from (a) 2007 to 2017 and (b) January 2015 to December 2017. Results show individual TerraSAR-X/TanDEM-X (triangles) and Sentinel 1A/B estimates (circles). Also shown are the aggregate monthly (squares) and winter (diamonds) products, which take advantage of all available data. For clarity we omitted the annual and quarterly products listed in Table 1. Error bars also are omitted because they are small relative to the plot marker size.
Figure 5a shows the variation in speed at approximately 3, 6, and 9 km (see KB3, KB6, and KB9 in the inset) from the 2017 terminus position of a large unnamed glacier that discharges ice through Køge Bugt (bay). In contrast to Jakobshavn Isbræ, there is no clear seasonal signal, although the speed changes substantially on timescales of a few years. From 2007 to 2009, KB3 sped up from just over 6 to nearly 10 km yr−1. For the next few years the speed at KB3 remained relatively constant before peaking briefly at 11 km yr−1 in 2012, after which it slowed to ∼ 7.4 km yr−1 by May 2013. This decline was followed by another speed-up to > 10 km yr−1 by spring 2015. Speeds then dipped to ∼ 6.8 km yr−1 in autumn 2016 but picked up again soon after. The prominent signal at KB3 is far more muted at points inland, with speeds 6 km upstream at KB9, staying within the range of 3 to 4 km yr−1.
Figure 5b shows the same Køge Bugt data over the period from 2015 to 2017. Relative to Jakobshavn Isbræ, the Køge Bugt glacier was sampled far less frequently with TerraSAR-X, so there are several gaps in this time series, especially during the non-summer months. As with Jakobshavn Isbræ, the 12-day Sentinel 1A sampling prior to October 2016 did not yield valid measurements for the two fastest points (KB3 and KB6). Farther inland at KB9, the 12-day Sentinel data worked well, with almost every possible pair yielding velocity estimates. The missing points in 2015 at KB9 are largely due to the Sentinel 1A acquisition schedule.
In general, the points from the different sensors agree well, although close inspection does indicate that there are some small biases. For example, the summer 2017 speeds at KB9 measured with TerraSAR-X (red triangles) are consistently about 200 m yr−1 slower than those measured with Sentinel 1 (green circles). Although small, this bias is larger than the expected level of error (< ∼ 100 m yr−1). Differences of similar magnitude occur at M13 on Jakobshavn Isbræ. In both cases, these differences likely result from differing sensor resolution, as described above.
3.5 North-west and south-east
Numerous glaciers have sped up in Greenland (Joughin et al., 2010; Moon et al., 2012; Rignot and Kanagaratnam, 2006), which is well documented by the GIMP data set. Many of these speed-ups have been concentrated in north-west and south-east Greenland. To demonstrate the collective behaviour of north-west glaciers, Fig. 6a shows a stack (summed speeds) plot for the 43 glaciers (excluding Jakobshavn Isbræ), for which there is good temporal coverage over the 16-year period. Figure 6b shows a similar plot for 29 glaciers in south-east Greenland. For each glacier, we sampled the centre of the main trunk at a point a few kilometres up stream of its terminus. We did not use a fixed distance because the position of many the termini vary secularly or seasonally by up to several kilometres over the period covered by the data set.
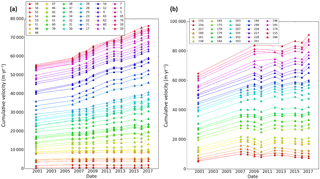
Figure 6Summed speeds for collections of glaciers in (a) north-west and (b) south-east Greenland. For these plots the bottom curve represents the speed of the first glacier (58 for the north-west). The next curve from the bottom is the sum of the first glacier and the second (58+56 for the north-west). Each successive curve is then the sum of the next glacier added to the cumulative sum of the previous glaciers. The legend identifies individual glaciers using the glacier IDs (numbers) used for the GIMP terminus position data set (Moon and Joughin, 2008; Moon et al., 2015). Figure S1 in the Supplement shows the location of each numbered glacier. Because Jakobshavn represents such a large signal (Fig. 3), we did not include it the north-west data. For a few glaciers, data are missing for some of the years plotted. In these cases, the stack is arranged with missing points on top so that data on either side bridge the gap.
As shown in Fig. 6, from 2000–2001 to 2016–2017 these glaciers collectively sped up by 38 and 41 % for north-west and south-east Greenland. (Percentage speed-up is calculated as the change in cumulative speed.) Although the degree of regional speed-up is similar, its timing differs. In north-west Greenland, the speed-up was only 7 % from 2000–2001 to 2005–2006, but there was an increase of 29 % over the next 11 years. By contrast, in south-east Greenland the majority of the speed-up occurred over the first half of the observation interval (by 29 % from 2000–2001 to 2008–2009). Over the last 8 years, glaciers only sped up by a more modest 9 %, mostly due to increases in speed from 2015–2006 to 2016–2017.
3.6 Decadal-scale ice sheet trends in south-west Greenland
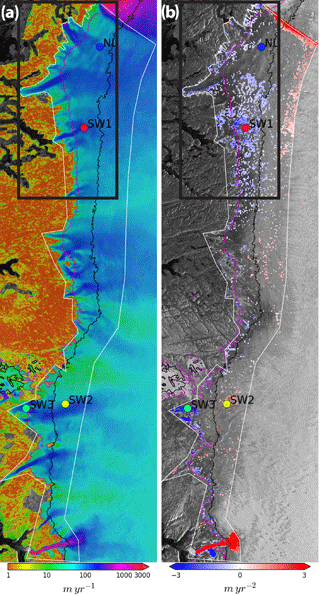
Figure 7(a) Speed along a section of the south-west ice-sheet margin and (b) significant (p < 0.05) trends (colour) for the period from winter 2000–2001 to 2016–2017 calculated for the area enclosed by the white outline. Within the outline, grey indicates no significant trend (p≥0.05). The underlying grey-scale image is a SAR image from RADARSAT (Joughin et al., 2016b). Bright radar returns upstream of the outline generally indicate percolation facies, while darker tones within the outline indicate bare-ice or wet-snow facies (Fahnestock et al., 1993). The circles (SW1-3, and NL) indicate the locations for data plotted in Fig. 8. The black rectangle shows the approximate area examined by Tedstone et al. (2015), which we refer to as T2015 in the text. The 700 (magenta) and 1100 (black) elevation contours are also shown.
Earlier work indicated that an area of the land-terminating margin of the Greenland Ice Sheet is slowing down, possibly as the result of a more efficient basal drainage network that has evolved to accommodate recent increases in melt (Tedstone et al., 2015). The black rectangles in Fig. 7 show the location of this region, which we refer to as T2015. Although the data from that study extend over a much longer interval than the GIMP data, all of the significant change occurred since 2000, which closely matches the period covered by GIMP. Thus, we use the GIMP data to explore the hypothesis that the changes observed by the previous study were representative of the behaviour of the south-west sector as a whole. We use the winter data set for this analysis because it provides the longest time span. As noted above, we employ control points in the interior of the ice sheet where we expect the change to be small, which could bias the results. To help avoid this problem, we restrict our analysis to slow-flowing (Fig. 7a) areas where the elevation is less than 1400 m (see white outline Figs. 1 and 7), which we know to be near the coast and thus well constrained by bedrock control points. As Fig. 7 indicates, this region roughly corresponds to the bare-ice and wet-snow zones (Fahnestock et al., 1993), where substantial melt and lake drainage occur.
Figure 7b shows the spatial distribution (colour) of statistically significant (p≤0.05) trends in our study area. In the southernmost part of the region, there is a strong speed-up trend associated with the large outlet glacier, Narsap Sermia. Similarly, there is a strong positive trend where the top part of the region borders Jakobshavn Isbræ. In the T2015 region (see black rectangle in Fig. 7), we find some indication of slowdown, but the trends are less than those estimated by Tedstone et al. (2015). One land-terminating glacier displays a pronounced slowdown (SW3 in Fig. 7), but the slowing is confined to near the terminus. Any trends for the rest of the region are small and scattered.
The results in Fig. 7 indicate where significant (p≤0.05) trends occur (e.g. those that are unlikely to be false alarms). The results do not answer the question of whether given data with a trend of X m yr−2 can we reliably detect a non-zero trend of magnitude X above the noise (missed detections). As an extreme example, if the trend was 0.01 m yr−2 and the noise was 100 m yr−2, then the confidence test should fail 95 % of the time and we would miss such a weak trend. Thus, in interpreting Fig. 7, it is important to understand how small a trend we can detect given our level of noise and sampling strategy. (We assume that our noise is substantially larger than any natural variability.)
To establish the detection capability of our time series, we ran Monte Carlo simulations in which we added Gaussian noise to specified linear trends, sampled during the same years in which we had data (see Fig. S2). In these simulations, we assume a velocity vector (∼ 100 m yr−1) that is directed along the x axis. We evaluated several cases in which the magnitudes of the errors are equal in both direction (2.5–20 m yr−1). The magnitudes of our errors, however, are direction dependent (mean errors of σx=2.9 and σy=6.1 m yr−1 for the area in Fig. 7). When computing speed, the error is almost entirely dominated by the component of uncertainty directed along flow. In our case, the mean component of error in the direction of flow is 3.7 m yr−1, with 5.6 m yr−1 in the cross-flow direction. Thus, we ran our simulations with a typical flow direction (σx=3.7 and σy=5.6 m yr−1), best-case flow direction (σx=2.9 and σy=6.1 m yr−1), and worst-case flow direction (σx=2.9 and σy=6.1 m yr−1). These simulations (Fig. S2) indicate that if the entire region had a uniform trend of 1.0 m yr−2, then with σx=3.7 m yr−1 we would detect a significant trend 94 % of the time, while with σx=6.1 m yr−1 the detection rate drops to 58 %. For a trend of 1.5 m yr−2, the detection rate is 89 % with σx=6.1, dropping to 50 % for σx=10 m yr−1, which is well above the expected level of error.
While Fig. 7 provides detail about the spatial distribution of trends, it reveals little about the nature of those trends. To provide more detail, Fig. 8 shows the full winter time series for four points (NL, SW1, SW2, SW3) shown in Fig. 7. The first point, NL (North Lake) corresponds to an area on the ice sheet were GPS data have been collected over a multi-year period (Joughin et al., 2008a; Stevens et al., 2016). While only a few months of each winter are measured by GIMP, the GPS data measure flow over the ∼ 9-month period with little or no melt. Despite this difference in sampling, most of the GPS points agree well with the radar-derived speeds. Although the GPS data suggest a weak trend of −1.3 m yr−2 (p=0.06), the longer radar record reveals no significant trend.
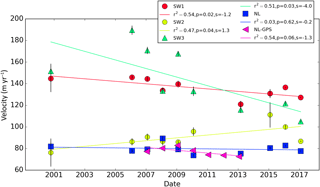
Figure 8Winter velocities and corresponding trends for the points SW1–3 and NL (see Fig. 7 for location) with error bars from the formal error estimates that are distributed with the velocity estimates. Also shown are GPS derived speeds at NL (Stevens et al., 2016).
The point SW1 is located in the T2015 region and it has a trend −1.2 m yr−2 (p=0.02), which explains about half of the variance in the speed (r2=0.54). Farther to the south at SW2, there is a significant acceleration trend (1.3 m yr−2, r2=0.47). Downstream of this point, there is a slowdown trend at SW3 (−4.0 m yr−2) but with a high degree of interannual variability (r2=0.37).
We have presented data at several sites around Greenland. Here we discuss the results in the context of overall data quality as well as the processes that contributed to the behaviour at each site.
4.1 Data quality
Overall the times series shown in Figs. 4–8 indicate a high level of temporal consistency between data sets. Such consistency is important for tracking and understanding changes in glacier speeds on timescales of weeks to decades. Although Jakobshavn Isbræ has some of the most rapidly varying seasonal behaviour, the monthly time series captures this variability nearly as well as the 11- and 12-day individual estimates. To the extent that points in the finer-resolution time series depart from the monthly data at both Jakobshavn and Køge Bugt, it is not always clear whether the data reveal actual short-term behaviour (e.g. response to a calving event) or instead are the result of noise.
Relative to the individual snapshot estimates, the monthly time series provide the advantage of greater accuracy through averaging of multiple estimates. As mentioned above, this accuracy comes at the expense of potential deviation of the actual time stamp from the nominal time stamp. Inspection of the results in Figs. 4 and 5, however, reveals no detectable skew of the monthly data relative to individual estimates. Some of the winter estimates deviate from the more frequently sampled data, but this behaviour is due to averaging of a rapidly varying signal rather than temporal skew in the data. Thus, the data indicate that the trade-off made between accuracy and temporal resolution may often favour the monthly time series for studies on seasonal variation. Exceptions may occur when trying to study and isolate the effect of specific events (e.g. high melt or calving), where the finer temporal resolution becomes important. Nonetheless, in such cases the observed change needs to stand well above the expected level of uncertainty.
Although the results reveal that the multi-sensor data sets work well for studying glacier changes, Fig. 3 reveals some potential pitfalls for process studies. For example, the smoothed velocity estimates across shear margins from the Sentinel 1A/B data could yield unreliable results when using the data to constrain a model to invert for basal shear stress. Without conducting a detailed sensitivity study, it is difficult to assess how much the results would be degraded using Sentinel 1A/B data instead of TerraSAR-X data in any given application. Qualitatively, however, Fig. 3 indicates that if a study needs data that capture high strain rates, then the finer-resolution TerraSAR-X velocities are preferred. This statement applies to a relatively small fraction (∼ 1 % or less) of the ice sheet (i.e. fast outlets). In other areas, the accuracy obtained by averaging large numbers (e.g. Fig. 2a) of estimates may weigh in favour of using the results that include Sentinel 1A/B data.
4.2 Jakobshavn and Køge Bugt
The much slower 2016–2017 winter minimum and 2017 summer maximum seen in Fig. 4a indicate a major recent slowdown at Jakobshavn Isbræ. To help examine the cause of this slowdown, Fig. 9a shows the history of the terminus position plotted relative to the glacier geometry, which is an update to an earlier time series (Joughin et al., 2014). The ice thickness of Jakobshavn Isbræ is exceptionally difficult to measure and several maps have been published with substantial differences in bed topography (An et al., 2017; Morlighem et al., 2017), with those differences being especially large along any particular profile along-flow. Profiles that follow the greatest bed depth for a particular DEM, however, show similar overdeepenings between data sets. Thus, for consistency with past work, we use the Plummer et al. (2008) bed model and caution that the uncertainty in bed topography renders the interpretation somewhat qualitative as would be the case with other bed DEMs for this region.
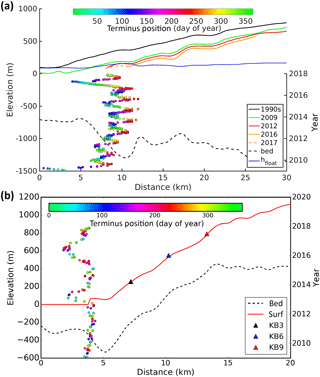
Figure 9(a) Surface and bed elevation, terminus (2009–2017), and flotation height for Jakobshavn Isbræ updated from a similar figure (Joughin et al., 2014). The bed data are from CRESIS (Plummer, 2008) and the surface elevations are from the NASA Airborne Topographic Mapper (ATM) (Krabill et al., 2004) and WorldView DEMs (Noh and Howat, 2015). (b) Surface and bed elevation and terminus position for Køge Bugt. The surface elevations are from the GIMP DEM (Howat, 2017), and the bed elevations are from Bedmap 3 (Morlighem et al., 2017).
Past work has shown that the strong seasonal variations in speed on Jakobshavn Isbræ correspond to the retreat and advance of the often-grounded terminus across a basal overdeepening (Joughin et al., 2012, 2014). This earlier work demonstrated that, as the grounded-terminus height changes, the sensitivity of the speed to the pressure boundary condition at the terminus is sufficient to explain much of the seasonal variation. Over the course of the seasonal cycle, the speed increases as the terminus recedes into deeper water each summer and slows each winter as it advances into shallower water (see Fig. 9a). Peak summer speeds occurred in 2012, when the terminus retreated to the deepest point of the overdeepening. In subsequent summers, the terminus retreated past the overdeepening to shallower water, yielding smaller summer peaks.
In the winter of 2016–2017 the terminus advanced nearly 5 km farther seaward than any time since the 2009–2010 winter, coinciding with speeds that were at least 900 m yr−1 slower than all winter minima since 2008 (Fig. 4). Through much of this advance, the terminus likely was floating (see orange curve Fig. 9a), so the buttressing provided by the longer floating tongue should have contributed to reducing the speeds relative to recent winters. Speeds would also have been reduced if the extended terminus grounded on the shallower areas downstream of the overdeepening in the latter part of the 2016–2017 winter.
In the summer of 2017, the terminus retreated inland by 1–2 km less than it had during the five prior summers. Although the points of maximum terminus retreat were similar for the summers of 2011 and 2017, the maximum speed in 2017 was ∼ 1800 m yr−1 slower than in 2011. This difference may be due to the ungrounding of the area above the terminus from 2011 to 2017. The terminus appears to have been grounded in water ∼ 1250 m deep in 2011, yielding a strong summer peak due to the non-linear relation between speed and ice thickness (Howat et al., 2005; Joughin et al., 2012). By 2017, the grounding line appears to have retreated to the local high above the overdeepening (∼ 975 m depth at ∼ 12.2 km in Fig. 9a), with a floating terminus extending a few kilometres farther downstream. The combination of this thinner ice at the grounding line and the additional buttressing provided by the floating ice tongue should be of sufficient magnitude to explain much of the reduction in peak summer speed from 2011 to 2017. Other factors such as the rapidly evolving ice-sheet geometry and changes in effective pressure at the bed may also have played a role that could either enhance or suppress the effects of changes in grounding-line/terminus thickness (Joughin et al., 2012).
It is unclear whether external forcing, internal dynamics, or some combination of both have contributed to the changes in terminus extent that have produced the recent slowdown. Temperature records from the nearby coastal station at Egedesminde indicate that 2017 was the second coldest year, behind 2015, in the 21st century (GISS, 2018). Colder temperatures should have produced a more rigid iceberg melange or extended the period over which the melange was rigid, which could have suppressed calving, allowing greater terminus advance (Amundson et al., 2010; Joughin et al., 2008b). Cooler temperatures also may have suppressed calving through a reduction in melt-driven hydrofracturing (Sohn et al., 1998). Thus, one plausible hypothesis is that the recent colder temperatures may have contributed to the advance and slowdown, although if there was cooler water at the terminus it could have played a role as well. Whether this slowdown could reduce summer thinning and increase winter thickening sufficiently to stabilize the glacier over scales of years to decades is unclear.
Figure 9b shows the variation in terminus position and surface and bed elevation profiles for the Køge Bugt glacier. Unlike at Jakobshavn Isbræ, the bed of this glacier rises above sea level within several kilometres of the terminus (between KB3 and KB6). In the region upstream of approximately 4 km in Fig. 9b, the bed is determined using mass-conservation methods constrained by ice velocity and radar depth-sounding data (Morlighem et al., 2017). Downstream of the terminus, bed depths are far more uncertain due to limited availability of bathymetric data. The terminus position data show good correspondence with the speed record (Fig. 5), with slow speeds corresponding to times when the terminus advanced. With the uncertain nature of the bed in the region over which this advance occurred, the terminus could have been grounded or floating as it migrated. In some of the images used to digitize the terminus position, large tabular icebergs were present, suggesting that, at least at times, the terminus was at or near flotation. Whether grounded or floating, it likely is that the extra resistance provided by the terminus advance produced the slower periods of flow, similar to the case for Jakobshavn. The response at 6 km inland (KB9) of KB3 is far more muted than the response a similar distance inland on Jakobshavn Isbræ. This difference in behaviour may be due to the much thinner ice at Køge Bugt, since the distance a stress perturbation at the terminus is transmitted upstream should scale with ice thickness (Cuffey and Paterson, 2010).
With the exception of its brief advances, the Køge Bugt terminus maintained a relatively fixed position over nearly a decade, apparently near the top of an overdeepening. Although this glacier appears to have been losing mass rapidly between 2000 and 2012 (Enderlin et al., 2014), it seems unlikely that there could have been strong thinning near the terminus over the period since 2009. Any sustained thinning likely would have caused the terminus to retreat down the reverse slope to the higher ground on the other side of the overdeepening, from which point retreat would have been slowed or stopped by the forward slope and elevations above sea level. The apparent loss measured by Enderlin et al. (2014) was computed as a discharge anomaly relative to 2000, at which time speeds where similar to the minima seen in Fig. 4. Thus, if the minimum in 2000 represents an anomalously slow period when the glacier might even have been gaining mass, then the Køge Bugt glacier may be losing mass far less quickly than previously indicated (Enderlin et al., 2014), which is consistent with the terminus position data in Fig. 9.
It is interesting to compare Køge Bugt and Jakobshavn Isbræ and their relation to their respective topographic settings. If the recent slowdown is not the beginning of a period of stabilization, then the terminus of Jakobshavn Isbræ likely will continue to retreat at least 60 km inland until it recedes from the trough's deeper parts (Joughin et al., 2012). Once this retreat occurs, the terminus would be in a position more like that of Køge Bugt, which has almost completely pulled back out of its trough. Yet the speeds of both glaciers are similar in magnitude. In the case of Køge Bugt, the glacier is able to maintain high slopes and driving stresses to produce the high speed necessary to drain the high accumulation along the south-east coast, despite the fact that much of this flow is over a bed well above sea level. This behaviour indicates that once the terminus of Jakobshavn Isbræ reaches the shallower part of its trough, it too may be able to maintain a similar equilibrium.
If climate conditions similar to the present persisted over long periods (many millennia integrated over multiple glacial cycles), then the Køge Bugt terminus may have stayed near its current position for extended periods as it has over the past decade. This stability likely would occur when sea level was within several metres of its present level (e.g. other interglacials), because its terminus could not retreat past this point and still maintain contact with the ocean, which would be required in order to evacuate the large volume of snowfall (retreat from the ocean would cause thickening and re-advance). As a result of maintaining its terminus at or near this position for extended periods, erosion may have been focused here to produce the abrupt transition from a bed above sea level to a deep submarine trough. Initially the head of the trough may have been located farther seaward than at present, so that trough formation would have occurred as its head migrated inland over time. If so, then abrupt transitions at the heads of many subglacial troughs may be due to a combination of climate and geography causing termini to maintain stable positions at the heads of their respective troughs over extended periods. Thus, such points may represent the “last stands” of these glaciers before a warming climate draws down the ice sheet sufficiently to pull them completely from their troughs.
4.3 Regional outlet glacier changes
Figure 6 indicates collective speed-ups of glaciers in north-west (38 %) and south-east (41 %) Greenland since 2000, but at rates varying with time. In north-west Greenland, the speed-up was greatest over roughly the last 11 years, whereas in the south-east it was highest from 2001 to 2009. Because the glaciers that sped up have also likely thinned substantially and have different widths, these results cannot be directly scaled to estimate increased discharge. The patterns of speed-up, however, are consistent with estimates of discharge in 2012 (Enderlin et al., 2014) and suggest that discharge has increased since then. In particular, speeds in north-west Greenland have increased by nearly 10 % since 2012. Jakobshavn Isbræ was not included in Fig. 6, so its recent slowdown could offset some of the north-west discharge increases.
The data from both regions indicate that, for individual glaciers there is substantial variability, with some glaciers slowing and other glaciers speeding up in any given year as several earlier results have shown (e.g. Moon et al., 2012). For example, many of the south-east glaciers that sped up in 2008 slowed over the period from 2008 to 2010 and then sped up slightly thereafter. The response of an individual glacier depends on its internal dynamics (e.g. geometry, terminus position, bed conditions) and it its recent history. Thus, as noted by many other studies, similar glaciers subjected to similar forcing may exhibit substantially different responses, making it difficult to determine the influence of the forcing. With populations of glaciers such as shown in Fig. 6, however, it should be easier to determine the average response to climate forcing once the records are sufficiently long. Past studies have been hindered by the limited duration of the satellite record, but GIMP and other projects are now producing records of sufficiently long periods to begin multi-decadal analyses.
4.4 South-west Greenland ice sheet trends
For much of south-west Greenland, Fig. 7 indicates little in the way of significant multi-annual trends in speed for the bare-ice and wet-snow zones over the winters from 2000–2001 to 2016–2017. Where statistically significant trends occur, they are generally associated with areas of focused outlet flow at either marine or land-terminating glaciers. An exception is a region (∼ centred on SW1 in Fig. 7) that lies within the T2015 region.
The results of our Monte Carlo simulation indicate that, given the levels of noise in our data (Fig. S2), we would have a difficult time reliably distinguishing a trend of 0.5 m yr−2 from zero using our data. For 1.0 m yr−2, we would detect most (94 %) trends with our typical errors and 58 % with our nominally worst-case example. We expect most errors to fall within this range, so if much (> 50 %) of our study area had a trend of 1.0 m yr−2, while we did not detect the trend at every point, we would expect to see a much higher rate of detections than that shown in Fig. 7. For trends of ≥ 1.5 m yr−2 we should reliably detect most (> ∼ 90 %) trends. Thus, our results indicate that trends of > 1.5 m yr−2 are rare in our study area, and widespread trends of ∼ 1 m yr−2 over a broad area are unlikely, particularly in the areas not covered by the T2015 data.
Tedstone et al. (2015) use annual velocities rather than winter velocities, as we have. Each type of data suffers from sampling problems. Our data do not uniformly sample the winter period as described above. They do, however, sample a period when seasonal variation should be minimal. (In this region, the pre-Sentinel data are all acquired in October–April.) In order to examine the sensitivity to the inconsistent sampling in our data, we compare our data at NL with the GPS data (see Fig. 8), which uniformly sampled the full winter (no-melt) period (Stevens et al., 2016). In the period of overlap, the SAR observations show good agreement with GPS data, suggesting that our results are not unduly biased by seasonal variability. To investigate further, we used these 2006–2007 GPS data to compute partial winter velocities over several 3-month intervals that roughly match the periods covered by the pre-Sentinel SAR campaigns. Relative to the 9-month winter average, the smallest bias was 0.3 m yr−1 (October–December) and the greatest bias was 2.6 m yr−1 (February–April). Overall, these biases are small relative to the noise and should be randomly distributed with time, which would reduce their contribution to the trend. If somehow, they were not randomly distributed, the worst they could skew the trend by is 0.16 m yr−2 (2.6 m yr−1/16 yr). The T2015 data also have issues with sampling because the image pairs they used span a range of values (352 to 400 days) that could introduce similar and potentially larger biases (e.g. a period of longer than a year could sample fast flow in the summer disproportionately). Thus, some, but likely not all, of the observed differences between our results and those of T2015 could be due to sampling issues in one or both of the data sets.
If the processes that contribute to the T2015 slowdown occurred entirely in the summer, then they would not be detected by our winter data, potentially causing the difference between our winter and the T2015 annual velocities. If the entire slowdown occurred from June to August, then a summer slowdown trend of 6 m yr−2 would be required to produce the annually averaged slowdown of 1.5 m yr−2 found in the T2015 data. Over a period of several years, such a trend would yield summer velocities that were lower than winter velocities, which has not been observed thus far. Moreover, when Stevens et al. (2016) examined the NL GPS data, they found significant winter slowdown (−1.13 m yr−2) but no significant trend for the summer. Thus, it is difficult to explain the difference between the winter and annual velocities as being largely the result of changes in speed confined to summer or early autumn periods.
Since the Tedstone et al. (2015) data set ends in 2014, while ours extend to the winter of 2016–2017, differences in observation period may explain some of the differences. Figure 8 indicates that speeds were lower in the winter of 2012–2013 after strong melt in the 2012. Thus, if we only compute trends through to 2013, the area of significant slowdown surrounding SW1 expands (not shown) to include the area around NL.
It is important to note that at the 95 % confidence level (i.e. exceeds 2σ in the Fig. 1 of T2015), the T2015 data only show significant differences at elevations below ∼ 700 m, which represents a relatively small portion of the area (see magenta contour in Fig. 7). Factoring in that we do find some trends in this area, statistically the differences between the two data sets are not all that great, even if the magnitudes and distribution do differ somewhat.
In summary, our data suggest some trends toward slowdown in the T2015 region, though not as strongly as the T2015 results. There is enough uncertainty in both data sets that at this point it is difficult to unambiguously resolve the magnitude of any such trends. As more data become available, the longer time series should produce more certain results. Our results for the 325 km stretch of ice sheet to the south of the T2015 region, however, indicate no slowdown trends with magnitude ∼ > 1 m yr−2 (except on a few small outlets). This lack of change raises the possibility that any change in the T2015 region may not be directly related to melt forcing but instead may be related to the rapid thinning on Jakobshan Isbræ (e.g. water piracy) or some other local rather than regional process.
By analysing results from new and earlier GIMP products, we demonstrate a 17-year growing record of temporally consistent ice-sheet velocity data. The varying mix of sensors through time introduces some differences in spatial resolution, which should be considered in any analysis that could be affected. Early results in the time series were derived from only a few image pairs, and for some years there are no data. Over time as TerraSAR-X, TandDEM-X, Landsat 8, Sentinel 1A/B have come online, temporal sampling and accuracy have improved greatly. Several other SARs are scheduled for launch in the next decade. In particular, the NASA ISRO (Indian Space Agency) SAR (NISAR) is scheduled for launch in 2021. It will sample all areas of the ice sheet at least 66 times per year (33 cycles each from ascending and descending orbits) with 12-day sampling. Its L-band frequency will improve correlation for difficult to map areas, such as south-east Greenland. Collectively the data from the global constellation will allow GIMP and other products to steadily improve with time. The growing duration of these records will also allow more robust analyses of the processes controlling fast flow and how they are affected by climate and other forcings.
The velocity data sets are distributed through the GIMP project page at NSIDC (http://nsidc.org/data/measures/gimp, last access: 4 January 2018); see also Table 1.
The supplement related to this article is available online at: https://doi.org/10.5194/tc-12-2211-2018-supplement.
The authors declare that they have no conflict of interest.
The data described in this paper were produced with support from the NASA
MEaSUREs programme (NASA grants NNX08AL98A and NNX13AI21A), with some basic
algorithm development funded under NISAR (NNX16AK53G). The RADARSAT data
were acquired by the Canadian Space Agency (CSA), and the PALSAR data were
acquired by the Japanese Space Agency (JAXA). The German Space Agency (DLR)
acquired, processed and distributed the TerraSAR-X and TanDEM-X data, and we
gratefully acknowledge the help with these data provided by Dana Floricioiu
at DLR. The Sentinel 1A/B data were acquired through the European
Commission's Copernicus programme and were processed by the European Space
Agency. The RADARSAT data through 2010, the ALOS-PALSAR data, and the
Copernicus Sentinel 1A/B data were archived and delivered by the Alaska
Satellite Facility (ASF). The 2012/13 RADARSAT data were archived and
delivered by CSA. All source data
are available from their respective space agency and/or ASF. The Landsat 8
data were provided by through a joint effort by the United States Geological
Survey (USGS) and NASA and distributed via Google. The NL GPS data were
collected as part of a collaboration with Sarah Das, Mark Behn, and Laura Stevens.
Comments by Mai Maki, Andrew Tedstone, Peter Nienow, Amaury Dehecq,
Noel Gourmelen, and
the two anonymous reviewers helped to improve the
manuscript.
Edited by: Marco Tedesco
Reviewed by: two anonymous referees
Amundson, J. M., Fahnestock, M., Truffer, M., Brown, J., Luethi, M. P., and Motyka, R. J.: Ice melange dynamics and implications for terminus stability, Jakobshavn Isbrae Greenland, J. Geophys. Res.-Earth, 115, F01005, https://doi.org/10.1029/2009JF001405, 2010.
An, L., Rignot, E., Elieff, S., Morlighem, M., Millan, R., Mouginot, J., Holland, D. M., and Paden, J.: Bed elevation of Jakobshavn Isbrae, West Greenland, from high-resolution airborne gravity and other data, Geophys. Res. Lett., 44, 3728–3736, https://doi.org/10.1002/2017GL073245, 2017.
Cuffey, K. M. and Paterson, W.: The Physics of Glaciers, 4th Edn., Amsterdam, 2010.
Das, S. B., Joughin, I., Behn, M. D., Howat, I. M., King, M. A., Lizarralde, D., and Bhatia, M. P.: Fracture Propagation to the Base of the Greenland Ice Sheet During Supraglacial Lake Drainage, Science, 320, 778–781, https://doi.org/10.1126/science.1153360, 2008.
Enderlin, E. M., Howat, I. M., Jeong, S., Noh, M.-J., van Angelen, J. H., and Van Den Broeke, M. R.: An improved mass budget for the Greenland ice sheet, Geophys. Res. Lett., 41, 866–872, https://doi.org/10.1002/2013GL059010, 2014.
Fahnestock, M., Bindschadler, R., Kwok, R., and Jezek, K.: Greenland Ice-Sheet surface-properties and ice dynamics from ERS-1 SAR imagery, Science, 262, 1530–1534, 1993.
Fahnestock, M., Scambos, T., Moon, T., Gardner, A., Haran, T., and Klinger, M.: Rapid large-area mapping of ice flow using Landsat 8, Remote Sens. Environ., 185, 84–94, https://doi.org/10.1016/j.rse.2015.11.023, 2016.
GISS: GISS Surface Temperature Analysis, available at: https://data.giss.nasa.gov/gistemp/stdata, last access: 15 February, 2018.
Gray, A. L., Mattar, K. E., and Sofko, G.: Influence of ionospheric electron density fluctuations on satellite radar interferometry, Geophys. Res. Lett., 27, 1451–1454, https://doi.org/10.1029/2000GL000016, 2000.
Howat, I.: MEaSUREs Greenland Ice Velocity: Selected Glacier Site Velocity Maps from Optical Images, Version 2, https://doi.org/10.5067/VM5DZ20MYF5C, 2017.
Howat, I. M., Joughin, I., Tulaczyk, S., and Gogineni, S.: Rapid retreat and acceleration of Helheim Glacier, east Greenland, Geophys. Res. Lett., 32, L22502, https://doi.org/10.1029/2005GL024737, 2005.
Jeong, S., Howat, I. M., and Ahn, Y.: Improved Multiple Matching Method for Observing Glacier Motion With Repeat Image Feature Tracking, IEEE T. Geosci. Remote, 55, 2431–2441, https://doi.org/10.1109/TGRS.2016.2643699, 2017.
Joughin, I.: Ice-sheet velocity mapping: A combined interferometric and speckle-tracking approach, Ann. Glaciol., 34, 195–201, 2002.
Joughin, I., Smith, B. E., Howat, I. M., Scambos, T., and Moon, T.: Greenland flow variability from ice-sheet-wide velocity mapping, J. Glaciol., 56, 415–430, 2010.
Joughin, I.: MEaSUREs Greenland Annual Ice Sheet Velocity Mosaics from SAR and Landsat, Version 1, https://doi.org/10.5067/OBXCG75U7540, 2017a.
Joughin, I.: MEaSUREs Greenland Ice Sheet Velocity Map from InSAR Data, Version 2, https://doi.org/10.5067/OC7B04ZM9G6Q, 2017b.
Joughin, I., Kwok, R., and Fahnestock, M.: Estimation of ice-sheet motion using satellite radar interferometry: Method and error analysis with application to Humboldt Glacier, Greenland, J. Glaciol., 42, 564–575, 1996.
Joughin, I., Kwok, R., and Fahnestock, M. A.: Interferometric estimation of three-dimensional ice-flow using ascending and descending passes, IEEE T. Geosci. Remote, 36, 25–37, 1998.
Joughin, I., Abdalati, W., and Fahnestock, M.: Large fluctuations in speed on Greenland's Jakobshavn Isbræ glacier, Nature, 432, 608–610, https://doi.org/10.1038/nature03130, 2004.
Joughin, I., Das, S. B., King, M. A., Smith, B. E., Howat, I. M., and Moon, T.: Seasonal speedup along the western flank of the Greenland Ice Sheet, Science, 320, 781–783, https://doi.org/10.1126/science.1153288, 2008a.
Joughin, I., Howat, I. M., Fahnestock, M., Smith, B., Krabill, W., Alley, R. B., Stern, H., and Truffer, M.: Continued evolution of Jakobshavn Isbrae following its rapid speedup, J. Geophys. Res.-Earth, 113, F04006, https://doi.org/10.1029/2008JF001023, 2008b.
Joughin, I., Smith, B. E., Howat, I. M., Floricioiu, D., Alley, R. B., Truffer, M., and Fahnestock, M.: Seasonal to decadal scale variations in the surface velocity of Jakobshavn Isbrae, Greenland: Observation and model-based analysis, J. Geophys. Res., 117, F02030, https://doi.org/10.1029/2011JF002110, 2012.
Joughin, I., Smith, B. E., Shean, D. E., and Floricioiu, D.: Brief Communication: Further summer speedup of Jakobshavn Isbræ, The Cryosphere, 8, 209–214, https://doi.org/10.5194/tc-8-209-2014, 2014.
Joughin, I., Howat, I., Smith, B. S., and Scambos, T.: MEaSUREs Greenland Ice Velocity: Selected Glacier Site Velocity Maps from InSAR, Version 1, https://doi.org/10.5067/MEASURES/CRYOSPHERE/nsidc-0481.001, 2016a.
Joughin, I., Smith, B. E., Howat, I. M., Moon, T., and Scambos, T. A.: A SAR record of early 21st century change in Greenland, J. Glaciol., 62, 62–71, https://doi.org/10.1017/jog.2016.10, 2016b.
Joughin, I., Smith, B. E., and Howat, I. M.: A complete map of Greenland ice velocity derived from satellite data collected over 20 years, J. Glaciol., 56, 1–11, https://doi.org/10.1017/jog.2017.73, 2017.
Krabill, W., Hanna, E., Huybrechts, P., Abdalati, W., Cappelen, J., Csatho, B., Frederick, E., Manizade, S., Martin, C., Sonntag, J., Swift, R., Thomas, R., and Yungel, J.: Greenland Ice Sheet: Increased coastal thinning, Geophys. Res. Lett., 31, L24402, https://doi.org/10.1029/2004GL021533, 2004.
Lemos, A., Shepherd, A., McMillan, M., Hogg, A. E., Hatton, E., and Joughin, I.: Ice velocity of Jakobshavn Isbræ, Petermann Glacier, Nioghalvfjerdsfjorden, and Zachariæ Isstrøm, 2015–2017, from Sentinel 1-a/b SAR imagery, The Cryosphere, 12, 2087–2097, https://doi.org/10.5194/tc-12-2087-2018, 2018.
Luckman, A., Murray, T., de Lange, R., and Hanna, E.: Rapid and synchronous ice-dynamic changes in East Greenland, Geophys. Res. Lett., 33, L03503, https://doi.org/10.1029/2005GL025428, 2006.
Moon, T. and Joughin, I.: Changes in ice front position on Greenland's outlet glaciers from 1992 to 2007, J. Geophys. Res.-Earth, 113, F02022, https://doi.org/10.1029/2007JF000927, 2008.
Moon, T., Joughin, I., Smith, B., and Howat, I.: 21st-Century evolution of Greenland outlet glacier velocities, Science, 336, 576–578, https://doi.org/10.1126/science.1219985, 2012.
Moon, T., Joughin, I., Joughin, J., and Black, T. E.: MEaSUREs Annual Greenland Outlet Glacier Terminus Positions from SAR Mosaics, Version 1, https://doi.org/10.5067/DC0MLBOCL3EL, 2015.
Morlighem, M., Williams, C. N., Rignot, E., An, L., Arndt, J. E., Bamber, J. L., Catania, G., Chauche, N., Dowdeswell, J. A., Dorschel, B., Fenty, I., Hogan, K., Howat, I., Hubbard, A., Jakobsson, M., Jordan, T. M., Kjeldsen, K. K., Millan, R., Mayer, L., Mouginot, J., Noel, B. P. Y., O'Cofaigh, C., Palmer, S., Rysgaard, S., Seroussi, H., Siegert, M. J., Slabon, P., Straneo, F., van den Broeke, M. R., Weinrebe, W., Wood, M., and Zinglersen, K. B.: BedMachine v3: Complete Bed Topography and Ocean Bathymetry Mapping of Greenland From Multibeam Echo Sounding Combined With Mass Conservation, Geophys. Res. Lett., 44, 11051–11061, https://doi.org/10.1002/2017GL074954, 2017.
Mouginot, J., Rignot, E., Scheuchl, B., and Millan, R.: Comprehensive annual ice sheet velocity mapping using Landsat-8, Sentinel-1, and RADARSAT-2 data, Remote Sensing, 9, p. 364, https://doi.org/10.3390/rs9040364, 2017.
Nagler, T., Rott, H., Hetzenecker, M., Wuite, J., and Potin, P.: The Sentinel-1 Mission: New Opportunities for Ice Sheet Observations, Remote Sensing, 9, 9371–9389, https://doi.org/10.3390/rs70709371, 2015.
Noh, M.-J. and Howat, I. M.: Automated stereo-photogrammetric DEM generation at high latitudes: Surface Extraction with TIN-based Search-space Minimization (SETSM) validation and demonstration over glaciated regions, GIScience & Remote Sensing, 52, 198–217, https://doi.org/10.1080/15481603.2015.1008621, 2015.
NSIDC: GIMP Data, available at: http://nsidc.org/data/measures/gimp, last access: 4 January 2018.
Paterson, W.: The Physics of Glaciers, 3rd Edn., Pergammon, Oxford, 1994.
Plummer, J. C.: CRESIS L3 Data Products, available at: ftp://data.cresis.ku.edu/data/grids/old format/2008 Jakobshavn.zip (last access: 2014), 2008.
Rignot, E. and Kanagaratnam, P.: Changes in the velocity structure of the Greenland Ice Sheet, Science, 311, 986–990, https://doi.org/10.1126/science.1121381, 2006.
Rosenau, R., Scheinert, M., and Dietrich, R.: A processing system to monitor Greenland outlet glacier velocity variations at decadal and seasonal time scales utilizing the Landsat imagery, Remote Sens. Environ., 169, 1–19, https://doi.org/10.1016/j.rse.2015.07.012, 2015.
Sohn, H. G., Jezek, K. C., and Van der Veen, C. J.: Jakobshavn Glacier, West Greenland: 30 years of spaceborne observations, Geophys. Res. Lett., 25, 2699–2702, 1998.
Stevens, L. A., Behn, M. D., Das, S. B., Joughin, I., Noel, B. P. Y., Van Den Broeke, M. R., and Herring, T.: Greenland Ice Sheet flow response to runoff variability, Geophys. Res. Lett., 43, 11295–11303, https://doi.org/10.1002/2016GL070414, 2016.
Tedstone, A. J., Nienow, P. W., Gourmelen, N., Dehecq, A., Goldberg, D., and Hanna, E.: Decadal slowdown of a land-terminating sector of the Greenland Ice Sheet despite warming, Nature, 526, 692–695, https://doi.org/10.1038/nature15722, 2015.
van de Wal, R. S. W., Boot, W., van den Broeke, M. R., Smeets, C. J. P. P., Reijmer, C. H., Donker, J. J. A. and Oerlemans, J.: Large and rapid melt-induced velocity changes in the ablation zone of the Greenland Ice Sheet, Science, 321, 111–113, https://doi.org/10.1126/science.1158540, 2008.
Zwally, H., Abdalati, W., Herring, T., Larson, K., Saba, J., and Steffen, K.: Surface melt-induced acceleration of Greenland ice-sheet flow, Science, 297, 218–222, 2002.