Brief communication: Candidate sites of 1.5 Myr old ice 37 km southwest of the Dome C summit, East Antarctica

The search for ice as old as 1.5 Myr requires the identification of places that maximize our chances to retrieve old, well-resolved, undisturbed and datable ice. One of these locations is very likely southwest of the Dome C summit, where elevated bedrock makes the ice thin enough to limit basal melting. A 3-D ice flow simulation is used to calculate five selection criteria, which together delineate the areas with the most appropriate glaciological properties. These selected areas (a few square kilometers) lie on the flanks of a bedrock high, where a balance is found between risks of basal melting, stratigraphic disturbances and sufficient age resolution. Within these areas, several sites of potential 1.5 Myr old ice are proposed, situated on local bedrock summits or ridges. The trajectories of the ice particles towards these locations are short, and the ice flows over a smoothly undulating bedrock. These sites will help to choose where new high-resolution ground radar surveys should be conducted in upcoming field seasons.

1 Introduction

Antarctic ice is an exceptional archive of the Earth's paleoclimates across all the glacial–interglacial periods, and the only one that contains direct samples of ancient atmospheres. The oldest available ice archive goes back 0.8 Myr in time (Jouzel et al., 2007) but is not old enough to study a main climatic transition that occurred between 1.2 and 0.9 Ma, known from the temporal variations of the isotopic composition of benthic sediments (mid-Pleistocene transition, MPT; Lisiecki and Raymo, 2005). The main climatic periodicity and the amplitude of climate cycles seem to radically change during the MPT. There is presently no general agreement on the processes responsible for this transition and its origin; the influence of the trend of atmospheric CO₂, the dynamics of ice sheets in the Northern Hemisphere, the sea ice extent and the dust content of the atmosphere have been proposed. Considering these scientific issues, locating a future 1.5 Myr old ice drill site was identified as one of the main goals of the ice-core community (Jouzel and Masson-Delmotte, 2010).

Thermal and mechanical ice flow simulations have to be carried out to assess the potential of possible drill sites (Fischer et al., 2013). The present study is part of a set of three modeling exercises led by the IGE (Institut des Géosciences de l'Environnement, Grenoble) group and collaborators around Dome C, and more specifically on the bedrock high lying ∼40 km southwest of the Dome C summit, suspected to be a good old-ice candidate (Van Liefferinge and Pattyn, 2013), under the ice ridge linking Dome C to the Vostok region (Young et al., 2017). First, a 1-D thermal model was run over the last 0.8 Myr to determine the present state (temperate or cold) of basal ice, which was compared to the reflectivity map in the region of Dome C (Passalacqua et al., 2017). The value of the local geothermal flux was inferred, and the spatial distribution of interpreted subglacial water was explained. The results of these transient simulations show that the top of this bedrock high is likely to be melt-free on long timescales, or to undergo very limited basal melting. Hence, this subregion is thermally compatible with the archiving process on glacial–interglacial timescales. Second, a kinematic 1-D ice flow model was used to evaluate the age and age resolution of the deepest portion of the ice sheet (Parrenin et al., 2017). The distance between the dated isochrones and the modeled ones was minimized to infer a thinning parameter that characterizes the vertical deformation through the ice column. We showed that the observed isochrones are compatible with high basal age and provide sufficient resolution. However, these two previous studies neglect the horizontal motion of ice, but the trajectories of the ice particles are not only vertical. The travel time of these particles, and consequently their age, is strongly influenced by the shape of the bedrock and the ice surface. These prior studies lacked the description of the local 3-D state of stress of the ice, where the geometry of the terrain and the strain history of the ice particles can be properly taken into account.

To evaluate the quality and position of deep old ice, we here proceed to a steady-state 3-D ice flow simulation, at a regional scale. Whereas these two previous 1-D modeling results alone could not help us determine the best oldest-ice targets, we here intend to provide objective criteria that together delimit kilometer-scale areas of old, well-resolved, undisturbed basal ice. Note that the goal of this study is not to assess the best age estimate but to evaluate which sites show more suitable glaciological characteristics than others. The bottommost ice recovered should be older than the MPT, ideally as old as 1.5 Myr such that several climate cycles pre-MPT can be recorded. The vertical age resolution has to be better than 10 kyr m⁻¹ to detect high-frequency climatic variability in the ice core (Jérôme Chappellaz, personal communication, 2017). Moreover, basal ice will probably be disturbed, similarly to the deepest 60 m of the EPICA Dome C ice core (Jouzel et al., 2007; Tison et al., 2015). We have no better evaluation of the height of disturbed ice in the region, and we will similarly take 60 m as a safety distance for the drilling minimum distance from the bedrock, but we should keep in mind this cutoff height could be an underestimation. One should look for places where the mechanisms responsible for stratigraphy disturbances (cumulated basal shear, bedrock roughness) should be minimal. Convergent flow should be avoided as well, because it tends to thicken basal layers. This is unfavorable to recovering the oldest ice as it will shift older layers downwards and makes the dating process more complex (Tison et al., 2015). Finally, the location of the future drill site should be above the highest subglacial lake detected by the radar survey (Young et al., 2017); otherwise the risk of basal melting could be drastically increased. We will call this threshold the “water limit”, above which there is no evidence of the presence of water in the radargrams.

Another modeling study has been recently led at a continental scale to locate a future >1 Myr old drill site (Van Liefferinge et al., 2018). These authors used a transient thermodynamical model to compute the highest geothermal flux value that would keep basal ice frozen. By comparison with available continental geothermal flux datasets, they locate areas where basal ice has likely remained frozen over 1.5 Myr. The authors also included a further mechanical constraint representing limited impact of bedrock roughness on the preservation of the bottom ice stratigraphy. Our study and the one of Van Liefferinge et al. (2018) differ in the way they account for the heat budget of ice and for the mechanical constraints on the basal ice. We should consider these differences as an interesting source of information for the decision-making process. This will be discussed in Sect. 3.5.

The decision-making process for a future drill site needs both field survey and modeling, the former feeding the latter with geophysical constraints, and the latter reducing the areas of interest for new field surveys, focusing more and more on promising sites. The information brought by the present study should be sufficient for a last high-resolution (few-hundred-meter scale) radar survey to be led on promising sites during the next field seasons. Then the community should be able to make a final decision for a 1.5 Myr old drill site in the Dome C region.

2 Ice flow model

2.1 Model description

The Stokes equations are solved on a 83×114 km domain, approximately centered on Dome C (Fig. 1), using the finite-element model Elmer/Ice. The surface and bed geometries are provided by the Bedmap2 datasets (Fretwell et al., 2013), except on the bedrock high southwest of Dome C, where a dense airborne radar survey has been recently collected (Young et al., 2017). The model works in ice equivalent, and we adjust the surface height by assuming that the density profile of the firn is that of Dome C on the whole domain (Schwander et al., 2001). Horizontal resolution of the corresponding mesh is 1 km. The resolution of the 20 vertical elements of the mesh evolves linearly, so that the deepest one is 25 times finer than the upper one, and to ensure that the velocity field is better resolved near the bottom.

Our domain sits in the center of the Antarctic Plateau, and lateral boundary conditions do not correspond to physical boundaries, but to virtual vertical surfaces. As the domain contains the dome summit, the ice flow is divergent and no input flow should be considered. We impose velocity boundary conditions corresponding to the shallow-ice approximation (Hutter, 1983). The ice surface as observed today may not correspond to the chosen rheology and is relaxed for 50 years such that the present surface slope does not induce an unrealistic velocity field. The ice surface is very flat, and 50 years is enough to accommodate the surface altitude to the ice rheology up to ∼ 1 m, without radically changing the orientation of the ice ridge, on which we have little control. The part of ice motion attributed to basal sliding is not known precisely in the Dome C region and depends on water circulation. We here focus on a region where basal melting is probably not present or limited, and horizontal velocities are very small, so that, for the sake of simplicity, a no-sliding condition is imposed at the bottom of the ice column. Vertical velocities at the base are equal to the basal melt rate output from previous modeling work (Passalacqua et al., 2017).

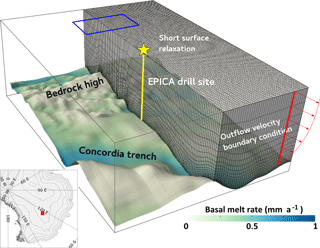
Figure 1 Mesh, bedrock dataset (Fretwell et al., 2013; Young et al., 2017) and basal melt rate (Passalacqua et al., 2017) used for the simulation on a 83×114 km domain. The red patch on the context map (bottom left) shows the domain used for the calculation, and the blue rectangle at the top of the image is the location of Fig. 2.

As we know that the basal ice in the Dome C region is at or near the melting point (Passalacqua et al., 2017; Van Liefferinge and Pattyn, 2013), the temperature profile measured in the EPICA Dome C borehole is a good representation of the thermal structure of the ice in the Dome C vicinity. Hence, we account for ice temperature by using the same normalized temperature profile on all the domain. Solving the coupled thermomechanical equations would require excessive computing resources, without radically changing the ice fluidity – which is mainly controlled by temperature. Similarly, we do not account here for long-term evolutions of the ice sheet surface but are aware that this assumption might considerably affect the trajectories of the ice particles.

As the main interest of this work focuses on the deepest ice, mechanical anisotropy of the ice has to be accounted for. The relation between strain rates and stresses is described by the generalized orthotropic linear flow law Gillet-Chaulet et al. (2005), given a certain vertical profile of ice fabric. By introducing a dependence on the second invariant of the deviatoric stress, this law can be extended to the nonlinear case (Ma et al., 2010). The fabric profile is only known at the dome summit (Durand et al., 2009) and shows that the ice mainly undergoes vertical compression but also undergoes longitudinal extension in the deep layers (Tison et al., 2015). However, there is no reason to use the very same fabric profile everywhere else, where shearing might have more influence and/or the bed shape is different. In this short study we will not discuss the influence of the chosen rheology, but we first made sure that the computed surface velocities correctly simulated the horizontal velocity field measured at the surface by Vittuari et al. (2004) for different n values and fabric profiles. Hence, we decided to use the widely accepted value of 3 for n and a synthetic vertical fabric profile, for which the eigenvalues of the second-order orientation tensor evolve linearly with normalized depth, from isotropy at the surface to a single maximum fabric at the bottom.

2.2 Model outputs

Back trajectories are computed from the 3-D velocity field using a Lagrangian scheme such that the age is known along the forward trajectory of the ice particles, and an age field is generated. The age resolution could be calculated from the vertical derivative of this age field, but we found it more accurate to track the annual layer thickness λ [m a⁻¹] from the ice surface (Whillans, 1979) using

$$\begin{array}{}\text{(1)}& {\displaystyle \frac{\mathrm{d}\mathit{\lambda }}{\mathrm{d}t}}=\mathit{\lambda }{\dot{\mathit{ϵ}}}_{zz},\end{array}$$

where ${\dot{\mathit{ϵ}}}_{zz}$ is the vertical strain rate. This formulation neglects vertical rotation effects that tend to overturn internal layers. This assumption is reasonable if internal layers are mainly horizontal, which is the case over the studied bedrock high. The age resolution is then stated as 1∕λ.

The way ice strains by flowing over a rough bed differs depending on the shape of the bedrock underneath. Similarly, a given bedrock shape can be a convergence or a divergence area, depending on the orientation of horizontal ice flow. Once the velocity field is known, a local coordinate system $(X,Y,Z)$ can be defined at each point, for which the x axis is oriented along flow. The curvature of the bed perpendicular to the flow is then computed everywhere, and convergence areas are identified where the bed curvature is positive.

Beyond the computation of ages and age resolutions, the 3-D simulation is also useful to detect where deep ice is more likely to be folded. Shearing will tend to amplify small wrinkles in the ice layers and so disturb the ice's basal stratigraphy, whereas longitudinal extension will tend to flatten them. Competition between shear and longitudinal stresses can be represented by a dimensionless shear number (Waddington et al., 2001):

$$\begin{array}{}\text{(2)}& \mathcal{S}={\displaystyle \frac{\mathrm{2}{\dot{\mathit{ϵ}}}_{XZ}}{{\dot{\mathit{ϵ}}}_{XX}-{\dot{\mathit{ϵ}}}_{ZZ}}},\end{array}$$

where ${\dot{\mathit{ϵ}}}_{XZ}$ is the shear strain rates along ice flow, and ${\dot{\mathit{ϵ}}}_{XX}$ and ${\dot{\mathit{ϵ}}}_{ZZ}$ are the local longitudinal and vertical strain rates, respectively. Waddington et al. (2001) used this shear number as a criterion to detect if a given wrinkle can be amplified by shear. More simply here, we use it to predict the presence of undisturbed ice, whereby the smallest shear number is best.

2.3 Selection of favorable locations

If the absolute value of the age, age resolution or strain rates can be discussed regarding the choices of the model parameters, we reckon their spatial variabilities are robust since they mainly depend on the shape of the bedrock and of the ice surface. As a consequence, this study focuses on comparing between promising locations rather than on discussing the sensitivity to model parameters.

The five selection criteria (age, age resolution, bed curvature, shear number and bed height) are used to compute five masks, thresholded as follows. For bed curvature, 0 m⁻¹ would have been the natural threshold, but it was too restrictive, and we decided for a slightly higher value ($\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹). The shear number threshold appeared naturally by studying its spatial evolution (see Sect. 3.3). The bed height threshold corresponds to the water limit, at 480 m. Furthermore, our results show that most of the subglacial elevated bed high southwest of Dome C is favorable to the existence of 1.5 Myr old ice, so we adopted more conservative age and age resolution thresholds for the selection of smaller suitable locations (1.8 Myr for the age and 8.5 kyr m⁻¹ for the age resolution, 60 m above the bed). A Boolean combination of the five masks delineates the areas fulfilling all our five selection criteria.

3 Results and interpretation

3.1 Age at 60 m above the bed

The area identified as possibly hosting the oldest ice is elongated along the bedrock high and stands at an intermediate bed elevation (mainly between 400 and 550 m above seal level, Fig. 2a). Neither the very top of the bedrock high nor its lowest foothills appear to be suitable for the archiving process of very old ice. The imposed basal melt rates are zero on the upper part of the bedrock high; therefore infinite age is calculated for the very basal ice. In that case, the age of the ice standing 60 m above the bed is strongly dependent on the ice thickness. On the top of the bedrock high, the ice is at its thinnest, and the old ice is at less than 60 m above the bed. On the foothills of the bedrock high, the ice is thicker, basal melt rates are above zero and the basal ice is therefore continuously being melted from the bottom.

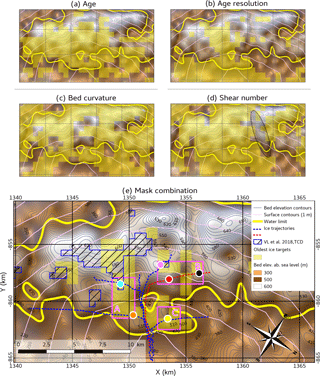
Figure 2 Selection criteria thresholded as follows (yellow areas): (a) age >1.8 Myr, (b) age resolution <8.5 kyr m⁻¹, (c) bed curvature $<\mathrm{2}\times {\mathrm{10}}^{-\mathrm{5}}$ m⁻¹, (d) shear number 𝒮<40, (e) Boolean combination of the selection criteria. The water limit corresponds to a bed height of 480 m and is shown here by a thick yellow contour. In panel (d) the elliptical wavy area corresponds to a region of higher shear. Magenta boxes A, B and C correspond to areas that could be considered as our best oldest-ice targets. Dashed lines show trajectories of ice particles; the red one corresponds to the profile presented in Fig. 3. Colored points locate possible drill sites, discussed in the text. Hatched areas show the best areas of Van Liefferinge et al. (2018). All the panels cover the same area. This figure focuses on the bedrock high designed as such in Fig. 1, located ∼40 km southwest of the Dome C summit. Projection: WGS84/Antarctic Polar Stereographic – EPSG:3031 (kilometers).

Some places may host ice even older than 2 Myr, but they all stand below the water limit of Young et al. (2017; Fig. 2, yellow line). The presence of very old ice in those areas is not impossible, but it may also be the consequence of insufficiently imposed basal melting. The transition between melting and frozen ice should stand somewhere on the flanks of the bedrock high, but it is difficult to pinpoint the precise location of this threshold. Despite the promising thick ice in this region that could allow old ages and sufficient age resolution, the risk of basal melting is real.

3.2 Age resolution at 1.5 Myr

Age resolution in the deepest part of the ice column is influenced by two factors. First and obviously, the thicker the ice, the better the age resolution. As a consequence, the tops of the bedrock high are rarely compatible with a sufficient age resolution of the oldest ice. Bedrock flanks should be preferred, but some of the thickest ice areas on the flanks will be discarded as well because of an increased risk of basal melting. Second, for ice positioned close to the ice divide, age resolution may benefit from a thickening effect of the deeper layers (Raymond, 1983). This results in a band of well-resolved ice, oriented along the ice ridge and perpendicular to the bedrock high. However, no Raymond arch is visible in the radargrams that would indicate a strong Raymond effect here. One explanation is that the shape of the ice surface at these sites is much more rounded than at the Dome C summit, and the produced along-ridge flow tends to dampen the amplitude of the Raymond arches (Martín et al., 2009a). Moreover, the characteristic time for a Raymond arch to form here would be several 100 kyr (Martín et al., 2009b), during which the surface ridge may have moved, smoothing out the developing arches. Unfortunately, the past position and shape of the ridge are unknown, and drilling far from its present position would not guarantee a better resolution.

3.3 Stratigraphic disturbances

At a divide, the shear stress perpendicular to the divide is zero, so that in general the shear number 𝒮 of the deep ice close to the ridge is low (∼ 10). However, a series of subglacial peaks lie immediately west of the ice divide. As a consequence the shear number increases very sharply and reaches much higher values (∼ 100), and this zone of higher shear should be discarded for a future drill site (Fig. 2d, wavy area). All the areas for which the basal ice crossed this zone of higher shear should be discarded as well, so the trajectories of the ice particles need to be evaluated.

3.4 Trajectories for oldest-ice spots

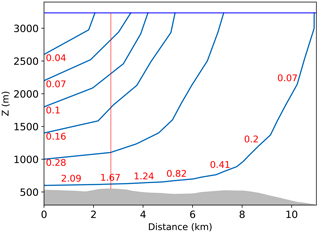
The best combination of age, age resolution, folding, convergence and melting criteria is shown in Fig. 2e, revealing several spots of ice meeting the five criteria. The areas for which the trajectories are shorter should be preferred, highlighted here by three magenta boxes. For boxes A, B and C the ice originates from the divide, guided by the strong lateral divergence resulting from the shape of the ice surface. Locations within boxes C and A are closer to the ice ridge and should be considered first for future oldest-ice drilling because of shorter trajectories and less risk of stratigraphy disturbances. Box B in particular lies on a relatively flat bedrock platform (black point in Fig. 2e), which may ensure stability of ice flow. Figure 3 shows the paths taken by ice from the surface to that site, demonstrating that the horizontal distance traveled does not exceed 10 km from the surface. However, as there is probably no basal melting here, deep ice would closely follow the bed for several kilometers, in a depth range dominated by strong vertical shear, enhanced by an undulating bed underneath. To minimize the bed influence, we could also consider a drill site located 3 km upstream, where the ice age would still exceed 1.5 Myr (red point in Fig. 2e, red dashed line in Fig. 3).

Of course, locating a unique “best” drill site within one of these three boxes is not possible with our 3-D-modeling approach only. However, it allows a restricted area to be defined where a new set of observations will be the most valuable. We should focus on local bedrock summits or crest lines, because local troughs make not only the ice flow but also heat flow converge (Van der Veen et al., 2007), increasing the possibility of insufficient age and positive basal melt. Considering that, only a few set of favorable drill sites remain in boxes A, B and C (blue, orange, pink and yellow points in Fig. 2e). Pink and blue points have less risk of basal melting, while yellow and orange have less risk of stratigraphic disturbances. The best choice between these sites should now be guided by local radar surveys characterizing the internal layering of the ice and the vertical strain rate profile (Nicholls et al., 2015).

Figure 3 Trajectories of the ice particles from the ice surface towards the black point in Fig. 2 (dashed red trajectory). Red numbers indicate the age of the ice, in millions of years. The bed profile is shown in grey. The thin red line corresponds to one possible drill site (red point in Fig. 2).

3.5 Comparison with results based on thermodynamical modeling

Van Liefferinge et al. (2018) identified a 8 km long area covering the SE upper part of the bedrock high, which crosses our box A, but they do not overlap perfectly (Fig. 2e, hatched blue and yellow areas). They also identified a site within our magenta box B, but no site in box C. These comparative results highlight the complementarity of the two approaches. The 1-D thermodynamical model of Van Liefferinge et al. (2018) has a better control over the thermal aspect of the problem than over its mechanical aspect, and it selects sites that are more conservative from a heat budget point of view, i.e., preferentially local bedrock heights. In contrast, our 3-D approach accounts for the horizontal strain of the ice and selects sites that are more conservative from a mechanical point of view. The upper part of box A or the left part of box B validates the constraints of both approaches. In our approach, the bedrock summit in box C is the safest mechanically; however, it was not selected by Van Liefferinge et al. (2018) because of a local bedrock roughness exceeding their threshold of 20 m, despite the fact that their thermal criterion was fulfilled.

4 Conclusions

The three-dimensional ice flow simulation presented here aims at defining and calculating several objective criteria which represent ideal conditions for the retrieval of old, well-resolved, undisturbed ice. The influence of the bedrock high and of the position of the ice ridge allows us to define only few sites compatible with all our selection criteria. The ages calculated at the base by our simulation predict ice older than 1.5 Myr high enough above the bedrock, which gives us confidence that the community's target of 1.5 Myr should be attainable, with the required age resolution. However, the modeling approach implicitly assumes that the ice flow is regular down to the bedrock, but there is no guarantee that it is actually the case. A ground radar survey focusing on several few-hundred-meter-scale areas presented here is essential to explore the structure of the deep layers. Finally, a rapid-access drill (Grilli et al., 2014) is currently planned to be deployed during the 2018/19 season to assess ice quality and age for a chosen target site, before the final site location is decided upon.