Separating snow and ice melt using water stable isotopes and glacio-hydrological modelling: towards improving the application of isotope analyses in highly glacierized catchments

Glacio-hydrological models are widely used for estimating current and future streamflow across spatial scales, utilizing various data sources, notably observed streamflow and snow and/or ice accumulation, as well as ablation observations. However, modelling highly glacierized catchments poses challenges due to data scarcity and complex spatio-temporal meteorological conditions, leading to input data uncertainty and potential misestimation of the contribution of snow and ice melt to streamflow. Some studies propose using water stable isotopes to estimate shares of rain, snow and ice in streamflow, yet the choice of the isotopic composition of these water sources significantly impacts results.

This study presents a combined isotopic and glacio-hydrological model which provides catchment-integrated snow and ice melt isotopic compositions during an entire melting season. These isotopic compositions are then used to estimate the seasonal shares of snow and ice melt in streamflow for the Otemma catchment in the Swiss Alps. The model leverages available meteorological station data (air temperature, precipitation and radiation), ice mass balance data and snow cover maps to model and automatically calibrate the catchment-scale snow and ice mass balances. The isotopic module, building on prior work by Ala-Aho et al. (2017a), estimates seasonal isotopic compositions of precipitation, snow and ice. The runoff generation and transfer module relies on a combined routing and reservoir approach and is calibrated based on measured streamflow and isotopic data.

Results reveal challenges in distinguishing snow and ice melt isotopic values in summer, rendering a reliable separation between the two sources difficult. The modelling of catchment-wide snowmelt isotopic composition proves challenging due to uncertainties in precipitation lapse rate, mass exchanges during rain-on-snow events and snow fractionation. The study delves into these processes and their impact on model results and suggests guidelines for future models. It concludes that water stable isotopes alone cannot reliably separate snow and ice melt shares for temperate alpine glaciers. However, combining isotopes with glacio-hydrological modelling enhances hydrologic parameter identifiability, in particular those related to runoff transfer to the stream, and improves mass balance estimations.

1 Introduction

Highly glacierized catchments are rapidly changing due to climate change and subsequent glacier retreat (Huss and Hock, 2018; Zekollari et al., 2019). Reduced ice melt contribution, combined with more liquid precipitation and earlier snowmelt, will significantly affect water resource availability (Berghuijs et al., 2014; Beniston et al., 2018). These changes will have a serious impact on downstream ecosystems (Milner et al., 2017), water usage for irrigation (Viviroli et al., 2020; Shokory et al., 2023), hydropower (Schaefli et al., 2019) or other domestic water uses (Immerzeel et al., 2020), both in densely populated lowlands (Pritchard, 2019; Biemans et al., 2019) and in small communities at high elevation (Buytaert et al., 2017). Accurate estimates of current and future snow and ice melt amounts are, therefore, vital to mitigating climate change effects.

In this context, glacio-hydrological models have been developed to assess current and future streamflow changes (e.g. Farinotti et al., 2012; Muelchi et al., 2022). The main drivers of annual glacier mass balance variability and glacier evolution are well documented (e.g. Huss et al., 2021). However, complex spatio-temporal processes and the lack of direct, spatially distributed observations below the ground or at the ice surface lead to model simplifications. Streamflow projection corresponds to the statistically best possible representation of the calibration or evaluation datasets, but the underlying physical streamflow generation processes remain simplified (Schaefli et al., 2011). Such processes include the effect of supraglacial debris cover (Jouvet et al., 2011; Ayala et al., 2016), lateral subsurface flow (Carroll et al., 2019), permafrost melt (Rogger et al., 2017), or superficial and deep groundwater recharge and exfiltration (Hood and Hayashi, 2015; Penna et al., 2017). As a result, models may (i) wrongly represent the competing amounts of modelled snow and ice accumulation and melt, (ii) compensate runoff errors in the glacierized and non-glacierized parts of the catchment (van Tiel et al., 2020b), or (iii) overlook or oversimplify processes which may become more dominant in the future such as water storage and delayed water release (Somers and McKenzie, 2020).

Water stable isotopes can provide an alternative approach to estimate the shares of snowmelt, ice melt and rain. In snow-dominated, non-glacierized catchments, stable isotopes of water have been used to build mixing models which estimate the shares of the different water sources in the stream based on the sources of water that compose it (such as snow, rainfall or groundwater; the so-called “end-members”) (Ala-Aho et al., 2017a; Carroll et al., 2018; Beria et al., 2020). Such models can estimate water shares without complex hydrological models and may avoid modelling problems mentioned above. In glacierized catchments, only a few studies have attempted to use water isotopes to provide an estimate of the shares of snow and ice melt at the time of sampling (e.g. Engel et al., 2016; Penna et al., 2017). Despite the emergence of encouraging research, many challenges regarding the use of water isotopes for snow- and ice-dominated catchments remain. Spatial variations in the ice melt and snowmelt isotopic signature may be large, and a limited number of samples may lead to biases (Engel et al., 2016; Schmieder et al., 2018; Zuecco et al., 2019). The temporal evolution of the isotopic signal of snowmelt is difficult to characterize, and the choices of the selected end-member values lead to a significant trade-off between snow and ice melt contributions (Penna et al., 2017).

In addition, a limited number of studies have successfully used water isotopes for glacio-hydrological model evaluation (Hindshaw et al., 2011) or calibration (He et al., 2019; Nan et al., 2022). These studies show promising results, reducing the uncertainties in estimating model parameters and the shares of the water sources when water isotopes are used for calibration.

In this study, we aim to further explore the use of water isotopes in glacierized catchments and, in particular, aim to address the following questions. (i) Can we model the catchment-integrated snow and ice melt isotopic compositions during an entire year using a parsimonious model? (ii) Can we separate snow and ice shares in streamflow at catchment-scale based on water isotope data alone? (iii) What are the benefits of integrating isotopes in glacio-hydrological models, and can it contribute to better separating modelled snow and ice melt shares?

For this purpose, we adapted the parsimonious model proposed by Ala-Aho et al. (2017a) to the case of a heavily glacierized catchment in the Swiss Alps and proposed a new combined isotopic and glacio-hydrological model. The model is composed of three standalone modules, which are calibrated separately: (i) an hourly, spatially distributed mass balance module based on meteorological, glacier mass balance observations and detailed snow cover maps; (ii) for each model cell, an isotopic module which aims to produce a detailed spatio-temporal representation of the isotopic compositions of snow and rain; and (iii) a transfer module which conveys water (snowmelt, ice melt, rain) amounts and isotopic signatures from each model cell to the catchment outlet (via hillslope, snowpack and glacier routing).

The main goal of the model is to simulate the catchment-integrated isotopic compositions of the different water sources at the outlet as precisely as possible. This allows us to characterize the isotopic behaviour of the water sources during a melting season and to highlight better the challenges linked to isotope modelling in glacierized catchments. In particular, our catchment-integrated signals allow us to avoid the typical problems of isotope analyses (e.g. Penna et al., 2017; Schmieder et al., 2018; Zuecco et al., 2019), which rely on strong assumptions regarding the definition of the isotopic composition of the end-members when only a few point field samples are available. Finally, we show how a simple end-member mixing model based on our catchment-integrated isotopic signals can estimate the shares of snow and ice at the river outlet compared with the results from the glacio-hydrological model.

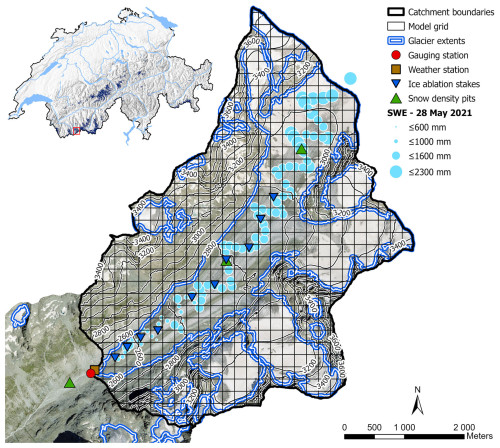
Figure 1 The Otemma glacierized catchment with the locations of (i) the gauging station close to the glacier portal, (ii) the weather station, (iii) 10 ablation stakes used for summer surface ice melt measurements, and (iv) two snow pits for average end-of-winter (28 May 2021) snow density estimation and isotope sampling as well as 92 end-of-winter snow accumulation measurements (28 May 2021, in snow water equivalent (SWE)). The glacier forefield also shows a third snow pit used for isotopic sampling. The black grid represents the perimeter and cell size for mass balance and snow isotopic composition modelling. The small inset indicates the location of the Otemma glacier in Switzerland (red rectangle). Orthoimage provided by swisstopo (2019). Glacier extents adapted from Linsbauer et al. (2016).

2 Study site and experimental methods

2.1 The Otemma glacier

The Otemma glacier is located in the southwestern Swiss Alps (45°57^′00^′′ N, 7°26^′51^′′ E) and is amongst the 15 largest Swiss glaciers (Linsbauer et al., 2021). The glacier is characterized by a long and flat main lobe flowing in a northeast–southwest direction and several steeper tributary glaciers to the southeast (Fig. 1). Due to its limited area at high elevation and its large proportion of the remaining ice volume within the ablation area, Otemma glacier has shown rapid retreat (2500 m or about 40 m per year since the 1970s; GLAMOS , 1881–2020) and comparatively large volume and mass loss (Fischer et al., 2015) in recent decades. Most of the glacier is projected to completely melt already by 2060 under current climate change and to completely disappear by the end of the century (Gabbi et al., 2012). Two medial moraines deliver supra- and englacial sediments to the glacier terminus, especially in its more shaded southern part, where the terminus gradually becomes heavily debris-covered. Except for this area, the glacier mainly consists of relatively clean ice and has a relative debris cover of about 12 % (estimated from Linsbauer et al., 2021).

The catchment boundary was defined about 100 m below the location of the main glacier portal in 2019, where a gauging station was installed (Fig. 1). It has an area of 20.8 km², a mean elevation of 3080 m a.s.l. (2470 to 3730 m a.s.l.) and a glacier coverage of 56 % in 2019 (adapted from Linsbauer et al., 2021). The underlying bedrock consists of orthogneiss and metagranodiorites (Burri et al., 1999), overlain by coarse superficial sediment deposits with limited vegetation development.

2.2 Meteorological observations

In September 2019, a weather station was installed 50 m from the glacier terminus at an elevation of 2450 m a.s.l. (Fig. 1) and continuously recorded meteorological data with a resolution of 5 min until October 2021 with a 5 min resolution. Liquid precipitation was measured with a Davis tipping rain gauge; air temperature, relative humidity and air pressure with a Decagon VP-4; and incoming shortwave radiation with an SP-110-SS from Apogee Instruments. Solid winter precipitation was extrapolated to the analysed catchment from two nearby MeteoSwiss automatic weather stations: from Otemma (∼5 km down-valley, at 2357 m a.s.l.) for the winter 2019/2020 and from Arolla (∼10 km northeast, at 2005 m a.s.l.) for the winter 2020/2021. Wind speed was only available for the MeteoSwiss weather station of Grand St-Bernard (2472 m a.s.l.) about 20 km west of the Otemma glacier. All meteorological data have already been published (Müller, 2022).

2.3 Stream discharge

In July 2020, a stream gauging station was installed 100 m downstream of the glacier portal (Fig. 1) in a bedrock-constrained river section to ensure the collection of all upstream flow. Stream discharge was estimated using a stage–discharge relationship (Müller et al., 2022). The river stage was measured continuously at 10 min intervals with a KELLER DCX-22AA-CTD datalogger. Discharge was estimated by dilution gauging using rhodamine WT 20 % dye. The fluorescent dye concentration was measured with a fluorometer (Albillia GGUN-FL30). Based on 21 gaugings in 2020 and 15 in 2021, the estimated mean discharge uncertainty (95 % confidence) was ±0.55 m³ s⁻¹ but tends to increase for peak discharge with an uncertainty of ±2 m³ s⁻¹ for a river discharge of 13.5 m³ s⁻¹. All stream data have already been published (Müller and Miesen, 2022).

2.4 Mass balance observations and dye tracing

In situ monitoring of the seasonal surface mass balance of the Otemma glacier was started in 2020 by Mauro Fischer using the direct glaciological method (Kurzböck and Huss, 2021). For this study, snow depth measurements were performed manually at 5 locations on 26 June 2020 and 92 locations on 28 May 2021 across the entire main lobe of the glacier (from 2560 to 3020 m a.s.l.; Fig. 1). Snow density was estimated on the same dates by measuring the average density of the whole snowpack with a snow sampler in the centre of the main glacier lobe in 2020 and at two locations in 2021 (Fig. 1). Snow water equivalent (SWE) values were calculated by multiplying the measured snow depths with the average density value from the closest snow pit.

End of June 2020, 10 PVC ablation stakes covering the ablation area of the main glacier lobe from an elevation of 2590 to 2890 m a.s.l. (Fig. 1) were installed using a Kovacs ice drill and 8 m drilling rods. Snow and ice melt were measured at each stake by measuring the decrease in the snow and ice surface. Ablation measurements were performed three times during the summer of 2020 and seven times during the summer of 2021, covering the whole melt season. An ice density of 900 g L⁻¹ was assumed to convert measured ablation values in ice equivalent to water equivalent following Huss et al. (2008).

Between July and August 2020, dye tracing experiments were carried out by injecting sulforhodamine WT into six moulins in the lower part of the glacier at a 370 to 1100 m distance from the glacier portal. The transit time of the dye to the glacier portal was measured to characterize the englacial water drainage velocity.

2.5 Theoretical background on water stable isotopes

The isotopic signature of water is expressed as the ratio of heavy (¹⁸O and ²H) over light (¹⁶O and ¹H) isotopes compared to the Vienna Standard Mean Ocean Water (VSMOW). It usually has a negative value indicating the degree of depletion in heavy isotopes (Beria et al., 2018).

The water isotopic composition of snow appears usually more depleted in heavy isotopes versus light isotopes compared to rainfall. This phenomenon called fractionation occurs because, as air temperature decreases, lower cloud condensation temperature leads to more vapour condensation and a preferential loss of heavy isotopes from the air masses to the liquid phase. This results in an air mass becoming gradually more depleted in heavy isotopes (more negative δ²H) as condensation occurs. The isotopic signature of global precipitation follows a linear relationship called the global meteoric water line (GMWL) with δ²H = 8δ¹⁸O +10. The intercept of the GMWL is called d-excess (d-excess = δ²H − 8δ¹⁸O).

The isotopic composition of the snowpack also tends to evolve over time as mass exchanges between the solid, liquid and vapour phases occur. During the melting season, snow evaporation leads to a preferential loss of light isotopes to the vapour phase, leading to a snowpack more enriched in heavy isotopes. This process is called snow fractionation (Beria et al., 2018).

During non-equilibrium processes such as snow evaporation and sublimation, the snowpack becomes more rapidly enriched in ²H than ¹⁸O, leading to a decrease in the d-excess value compared to its reference value of 10 (see Beria et al., 2018, for a more complete review). D-excess therefore relates to the degree of evaporation that occurs in the snowpack.

2.6 Water sampling for stable isotope measurements

Snow for stable isotope analyses was mainly sampled in spring during two periods: from the glacier snout to the highest ablation stake between 24 and 30 June 2020 and across the main lobe of the glacier on 28 May 2021 (Fig. 1). Snow was sampled systematically at various locations by extracting the first 5 cm of the snowpack, which we define as snow surface, and by sampling snow between 10 and 20 cm below the snow surface, called snow 10 cm. Snow profiles for isotopic analysis were carried out on 28 May 2021 in two snow density pits, where snow was sampled every 50 cm in depth from the surface to the bottom of the snowpack. The snow profile of a third snow pit was sampled for isotopes just below the glacier terminus on 10 June 2021. There, we also sampled snowmelt that formed a thin saturated layer at the base of the snowpack. In summer, the snow surface was sampled on the glacier in mid-July at four locations in 2020 and two locations in 2021. After July, snow only remained on inaccessible parts of the catchment at high elevation.

Ice samples for isotope measurements were collected at various random locations on the glacier surface during two to four sampling campaigns in each summer from 2019 to 2021. Ice cores were extracted using a manual 20 cm ice screw. On 30 June 2021, two ice cores of 5 and 8 m depth were drilled using a Kovacs ice drill at the location of the second and eighth ice ablation stakes from the glacier terminus (Fig. 1). Ice was sampled by taking a bulk sample of the ice core every metre. Ice meltwater from small supraglacial channels was also sampled on the glacier at least 1 km away from the temporal snow line to avoid potential mixing with snow meltwater. All ice and snow samples were completely melted in a sealed plastic bag in situ and then transferred into 12 mL glass vials.

Stream water at the glacier portal was sampled automatically two to three times a day during low and high flows from mid-June to end of September in 2020 and 2021 using an ISCO 6712 full-size portable water sampler with twenty-four 1 L bottles, which were half filled. Water bottles were transferred to 12 mL glass vials every 1 to 2 weeks. The sampler was placed in a protected, shaded location to avoid water evaporation, and the average summer air temperature measured at the nearby weather station was 7 °C between July and September 2021.

From 2019 to 2021, we collected 39 liquid precipitation samples near the weather station at the glacier terminus (Fig. 1). Rainwater was sampled using a simple PVC funnel, which diverted rain into a plastic bag through a 2 mm plastic tube. All samples represent the bulk isotopic composition of single rain events and were usually collected the day after the end of a rain event. We defined rain events as days with rain, separated by at least 1 d without rain. In winter, we also sampled fresh snow directly after a few snow events. Due to air temperatures below 0 °C, we assume that little snow transformation or fractionation occurred and that these samples therefore represent the isotopic composition of solid precipitation events.

All liquid samples were stored in 12 mL amber glass vials in the field, with air-tight screw caps containing a silicone rubber septa. Glass vials were flushed with the sample water prior to sample storage to avoid contamination. All water vials were brought to the laboratory and kept in a cold chamber until analysis. Water stable isotopes were measured using a wavelength-scanned cavity ring-down spectrometer (Picarro 2140i). The median analytical standard deviation of all samples was 0.04 ‰ and 0.25 ‰ (maximum standard deviation of 0.11 ‰ and 0.65 ‰) for δ¹⁸O and δ²H, respectively. All values are expressed relative to the international Vienna Standard Mean Ocean Water (VSMOW) standards (Coplen, 1994). All isotopic data as well as detailed maps of sampling location have been published in Müller (2023a).

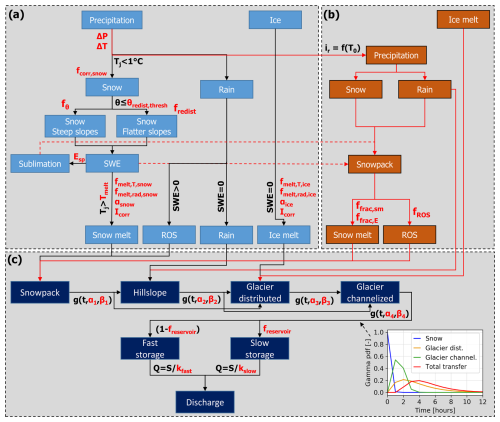
Figure 2 Schematic representation of the main modelling blocks of the combined isotope and glacio-hydrological model, divided into the independently calibrated main modules. Main calibration parameters are highlighted in red. (a) The mass balance module estimates amounts of snowmelt, ice melt, rain on snow (ROS) and rain for each grid cell. (b) The isotopic module uses a calibration curve with air temperature (T₀) to estimate δ²H of precipitation, while δ²H of ice melt is defined based on ice melt samples on the glacier. (c) For each cell, the hydrological transfer module consists of routing the water using a convolution of the water input and gamma distributions ($g(t,\mathit{\alpha },\mathit{\beta })$) which represent the travel time distributions of water through four different land-cover types in the catchment. Water is finally transferred through a “glacial” fast and slow reservoir. The bottom right panel illustrates the gamma distributions for one specific cell.

3 Numerical isotopic and glacio-hydrological modelling

We propose here a framework to model the share of snowmelt, ice melt and rain of water reaching the portal of the Otemma glacier. The model is separated in three main modules, which are calibrated step wise, one after the other (Fig. 2). The first module corresponds to the mass balance model which simulates snow and ice melt. The mass balance model is validated with the measured streamflow at the glacier portal over the observed years. The second module estimates the isotopic composition of each water source based on the mass balance calculations, and the third module implements a hydrological transfer routine that transfers water sources simulated for each model cell of the catchment to the glacier portal. All abbreviations, parameters and variables of the model are summarized in Table A1, including corresponding units.

The model domain, discretized into 200×200 m grid cells (total of 586 grid cells), corresponds to the catchment limits upstream of the glacier portal, where all water drained in the glacierized catchment converges (Fig. 1). For each cell, the mean elevation, slope and aspect were estimated using a 2 m resolution DEM of 2019 from swisstopo (2019).

The following sections provide all model equations and assumptions. Apart from the mass balance model calibration using multi-objective functions (Sect. 3.1.7) and the snow isotopic module (Sect. 3.2), the glacio-hydrological model is not particularly innovative, and we encourage the readers to skip those parts for a faster read.

3.1 Mass balance model

Snow water equivalent (SWE) within the entire catchment was estimated at an hourly time step from October 2019 to October 2021 based on solid precipitation accumulation and an enhanced temperature index snowmelt model. Snow redistribution, snow sublimation or deposition are also accounted for.

3.1.1 Air temperature

For each cell j, air temperature (T_j) is estimated using measured air temperature (T₀) close to the glacier portal (2450 m a.s.l.; Fig. 1) and corrected with the mean cell elevation (z_j) using a calibrated temperature lapse rate (Δ_T) following Eq. (1).

$$\begin{array}{}\text{(1)}& {\displaystyle }{T}_j{\displaystyle }=T_{\mathrm{0}}-{\mathrm{\Delta }}_T{\displaystyle \frac{z_j-\mathrm{2450}}{\mathrm{100}}}\end{array}$$

We allow the temperature lapse rate to change seasonally because in alpine glacierized areas higher lapse rates occur in summer compared to winter (Rolland, 2003; Marshall et al., 2007). It is set to resemble a Gaussian-shaped function depending on the day of the year (DOY) (Eqs. 2 and 3):

$$\begin{array}{}\text{(2)}& {\displaystyle }g\left(\text{DOY}\right)={\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_{{\mathrm{\Delta }}_T}\sqrt{\mathrm{2}\mathit{\pi }}}}{e}^{-\frac{\mathrm{1}}{\mathrm{2}}(\frac{\text{DOY}-{\mathit{\mu }}_{{\mathrm{\Delta }}_T}}{{\mathit{\sigma }}_{{\mathrm{\Delta }}_T}}{)}^{\mathrm{2}}},\text{(3)}& {\displaystyle }{\mathrm{\Delta }}_T\left(\text{DOY}\right)={\displaystyle \frac{g\left(\text{DOY}\right)}{\text{max}\left(g\right(\text{DOY}\left)\right)}}{f}_{{\mathrm{\Delta }}_T\text{,range}}+f_{{\mathrm{\Delta }}_T\text{,inc}}.\end{array}$$

All four parameters of Eqs. (2) and (3) (${\mathit{\mu }}_{{\mathrm{\Delta }}_T}$, ${\mathit{\sigma }}_{{\mathrm{\Delta }}_T}$, $f_{{\mathrm{\Delta }}_T\text{,range}}$,$f_{{\mathrm{\Delta }}_T\text{,inc}}$) are calibrated for each year. An illustration of the calibrated functions is provided in Fig. D1c.

3.1.2 Incoming shortwave radiation

For each model cell, the corrected incoming shortwave radiation (I_corr) is estimated based on the measured incoming shortwave radiation measured at the weather station (I₀) by taking into account the terrain slope (θ in degree) and aspect (γ in degree) (Eq. 4). First, the radiation is increased with a steeper slope by a certain factor (f_rad,slope) until a maximum slope threshold (θ_max,rad) is reached (Eq. 5). Then, a factor (γ_max,rad) is subtracted to account for aspect. It corresponds to 0 when the aspect is 180° (south-facing slopes) and is increased linearly with the terrain aspect facing north until it reaches a maximal calibrated factor (γ_max,rad). This factor is then scaled with slope, so that steep cells are more affected by aspect than flatter cells (Eq. 6). An illustration of the resulting function is provided in Fig. D1d.

$$\begin{array}{}\text{(4)}& {\displaystyle }{I}_{\mathrm{corr}}=I_{\mathrm{0}}(f_{\mathrm{rad},\mathrm{slope},\mathrm{tot}}-f_{\mathrm{rad},\mathrm{aspect},\mathrm{tot}})\text{(5)}& {\displaystyle }{f}_{\mathrm{rad},\mathrm{slope},\mathrm{tot}}=\mathrm{1}+\text{cos}\left({\displaystyle \frac{\mathrm{90}}{{\mathit{\theta }}_{\max ,\mathrm{rad}}}}\right(\mathit{\theta }-{\mathit{\theta }}_{\max ,\mathrm{rad}}\left)\right)f_{\mathrm{rad},\mathrm{slope}}\text{(6)}& {\displaystyle }{f}_{\mathrm{rad},\mathrm{aspect},\mathrm{tot}}={\mathit{\gamma }}_{\max ,\mathrm{rad}}{\displaystyle \frac{|\mathit{\gamma }-\mathrm{180}|}{\mathrm{180}}}\text{sin}\left(\mathit{\theta }\right)\end{array}$$

3.1.3 Liquid and solid precipitation estimation

The temperature thresholds to separate liquid from solid precipitation are set to a lower value of 1 °C (below only snow) and an upper value of 2 °C (above only rain), with a linear fraction in between. For liquid precipitation, we use rain measurements (P₀) from the weather station at the glacier portal (2450 m a.s.l.; Fig. 1). For solid precipitation, snowfall is inferred from the nearest automatic weather stations (P_meteo) located in Otemma for 2019/2020 and Arolla for 2020/2021 (see Sect. 2.2). A fixed snow correction factor (f_corr,snow) for the whole winter is calibrated for each year (Eq. 7). We then correct precipitation (P_j) for each cell j with elevation (z_j) based on a precipitation lapse rate (Δ_P) calibrated for each year.

$$\begin{array}{}\text{(7)}& P_j=\left\{\begin{array}{ll}{P}_{\mathrm{0}}\left(\mathrm{1}+{\mathrm{\Delta }}_P\frac{z_j-\mathrm{2450}}{\mathrm{100}}\right)& \text{if }{T}_{\mathrm{0}}>\mathrm{1}\mathit{°}\mathrm{C}\\ f_{\mathrm{corr},\mathrm{snow}}{P}_{\mathrm{meteo}}\left(\mathrm{1}+{\mathrm{\Delta }}_P\frac{z_j-\mathrm{2450}}{\mathrm{100}}\right)& \text{if }{T}_{\mathrm{0}}\le \mathrm{1}\mathit{°}\mathrm{C}\end{array}\right.\end{array}$$

3.1.4 Snow redistribution

We account for snow redistribution based on terrain slope (θ) by defining a calibrated slope threshold (θ_{redist,thresh}) above which snow redistribution occurs (Eq. 8). Above this threshold, we decrease the amount of solid precipitation (P_j) received by each model cell by a certain factor (f_θ). We then redistribute the corresponding total amount to all other cells by defining a redistribution function which uses an increase factor (f_redist) for solid precipitation (Eq. 8).

$$\begin{array}{}\text{(8)}& P_{\mathrm{sf}}=\left\{\begin{array}{ll}{P}_j(\mathrm{1}-f_{\mathit{\theta }}(\text{tan}(\mathit{\theta }-{\mathit{\theta }}_{\mathrm{redist},\mathrm{thresh}})\left)\right)& \text{if }\mathit{\theta }>{\mathit{\theta }}_{\mathrm{redist},\mathrm{thresh}}\\ P_j{f}_{\mathrm{redist}}& \text{if }\mathit{\theta }\le {\mathit{\theta }}_{\mathrm{redist},\mathrm{thresh}}\end{array}\right.\end{array}$$

The value of f_redist for each cell is calibrated by defining a calibration objective function where the total monthly amount of solid precipitation removed from steep slopes ($\mathit{\theta }>{\mathit{\theta }}_{\mathrm{redist},\mathrm{thresh}}$) equals the monthly total amount redistributed to all other cells based on their elevation. This method conserves the total mass of solid precipitation in a simple way without an estimation of curvature of connected cells and compensates for local anomalies between observed and modelled SWE. An illustration of the resulting functions is provided in Fig. D1a and b.

3.1.5 Snow and ice melt

Snowmelt is estimated using an enhanced temperature index melt model (Gabbi et al., 2014) (Eq. 9). Ice melt at the glacier surface was estimated using the same equation with different parameter values.

$$\begin{array}{}\text{(9)}& {\displaystyle }M=\left\{\begin{array}{ll}{f}_{\mathrm{melt},\mathrm{T}}{T}_j+f_{\mathrm{melt},\mathrm{rad}}(\mathrm{1}-{\mathit{\alpha }}_{\mathrm{snow}})I_{\mathrm{corr}}& \text{if }{T}_j>T_{\mathrm{melt}}\\ \mathrm{0}& \text{if }{T}_j\le T_{\mathrm{melt}}\end{array}\right.\text{(10)}& {\displaystyle }{\mathit{\alpha }}_{\mathrm{snow}}=\mathrm{0.86}-\mathrm{0.155}{\text{log}}_{\mathrm{10}}\left(T_{\mathrm{acc}}\right)\end{array}$$

Here I_corr is the corrected incoming shortwave radiation (see also Eq. 4) and T_j the air temperature for the cell j. Snow albedo (α_snow) was estimated following the work of Gabbi et al. (2014). It is assumed to decrease from a value of 0.86 as a function of the accumulated daily maximum positive air temperature (T_acc) since the last snowfall (Eq. 10). The threshold temperature (T_melt) distinguishing between melt and no melt is a calibration parameter. The temperature melt factor (f_melt,T) and the shortwave radiation factor (f_melt,rad) were calibrated for snow and ice separately. The albedo of ice is set to 0.25 (Gabbi et al., 2014).

3.1.6 Sublimation and deposition

An estimation of the snow sublimation rate was required in this work since it may significantly impact the snowpack isotopic signature due to fractionation (Ala-Aho et al., 2017b). Sublimation is estimated following Todd Walter et al. (2005) based on the difference in vapour density between the snow surface and the air divided by the resistance to vapour exchange, which requires wind speed data and, in particular, an estimation of the snow surface temperature (T_sp). Wind speed is roughly estimated using data from the closest automatic weather station (see Sect. 2.2). Since no snow surface temperature data are available, we propose to estimate T_sp by first defining snow surface temperature similar to air temperature (T_j). Then, we estimate a simplified snow surface energy balance (E_net) based on its two main terms: net shortwave (S_net) and net longwave (L_net) radiation (Stigter et al., 2021). When E_net is positive, usually due to the atmospheric shortwave radiation during clear-sky days, we assume that air and snow temperatures are similar. When E_net is negative, usually during clear-sky nights when outgoing longwave radiation from the snow surface is the major energy flux, T_sp cools more than air. This cooling effect is calibrated by a temperature factor (f_E) following Eqs. (11) to (15). During cloudy nights and days, E_net usually remains close to zero due to limited incoming shortwave radiation (but increased atmospheric longwave radiation), and T_sp is close to T_j. More details on the snow energy balance and snow surface temperature can be found in the work of Stigter et al. (2021).

$$\begin{array}{}\text{(11)}& {\displaystyle }{T}_{\mathrm{sp}}=\text{min}(T_j+E_{\text{net}}{f}_E\text{ ; }\mathrm{0}\mathit{°}C)\text{(12)}& {\displaystyle }{E}_{\text{net}}=\text{min}(S_{\text{net}}+L_{\text{net}}\text{ ; }\mathrm{0}{\text{ J m}}^{-\mathrm{2}})\text{(13)}& {\displaystyle }{S}_{\text{net}}=(\mathrm{1}-{\mathit{\alpha }}_{\mathrm{snow}})I_{\mathrm{corr}}\text{(14)}& {\displaystyle }{L}_{\text{net}}={\mathit{ϵ}}_{\text{air}}\mathit{\sigma }{T}_j^{\mathrm{4}}-{\mathit{ϵ}}_{\text{snow}}\mathit{\sigma }{T}_j^{\mathrm{4}}\text{(15)}& {\displaystyle }{\mathit{ϵ}}_{\text{air}}=(\mathrm{0.72}+\mathrm{0.005}{T}_j)(\mathrm{1}-\mathrm{0.84}{f}_{\text{cloud}})+\mathrm{0.84}{f}_{\text{cloud}}\end{array}$$

Here σ is the Stefan–Boltzmann constant and ϵ_snow=0.97 is the emissivity of the snow surface. The emissivity of air (ϵ_air) is estimated based on the fraction of cloud cover (f_cloud). The fraction of cloud cover was assessed by dividing the measured shortwave radiation (I₀) by the theoretical maximal shortwave radiation. f_cloud was set to 1 when less than 50 % of theoretical maximal shortwave radiation was measured at the weather station and was set to 0 otherwise (Todd Walter et al., 2005).

3.1.7 Calibration

Prior to calibration of the mass balance model, we initialized the model values for SWE and δ²H by first running the model for 1 year with initial SWE =0 for all cells (and uncalibrated model parameter values).

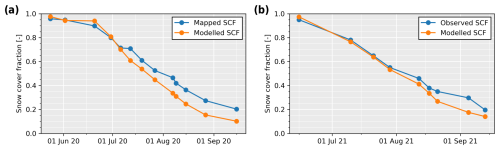
Mass balance model parameter calibration was then performed using PEST-HP. This model-independent algorithm iteratively minimizes the variance of the error between model outputs and corresponding field observations via inverse estimation (Doherty, 2015). We defined three datasets of field observations. The first corresponds to the measured end-of-winter SWE on the main lobe of the glacier. The second dataset corresponds to the annual ice melt measured at the ablation stakes at the end of each summer (Fig. 1). The third dataset of field observations corresponds to maps of the temporal snow cover during the entire ablation periods. We used daily 3 m resolution PlanetScope satellite imagery (PlanetScope Scene; Team Planet, 2017) and manually identified clear-sky days during the summer months of 2020 and 2021. We then automatically identified snow cover using a K-means unsupervised learning algorithm from Google Earth Engine (Arthur and Vassilvitskii, 2007) and created, for approximately every second week during the melting seasons, maps of snow presence/absence for our discretized model domain. We set PEST-HP to minimize the error between modelled and observed snow presence/absence for each grid cell and all available snow maps (maps with dates of calibration are available in Figs.  to E3). This procedure leads to a better determination of the temporal evolution of the snowline and should improve the modelled SWE estimation especially in zones where no direct SWE observations are possible (Barandun et al., 2018).

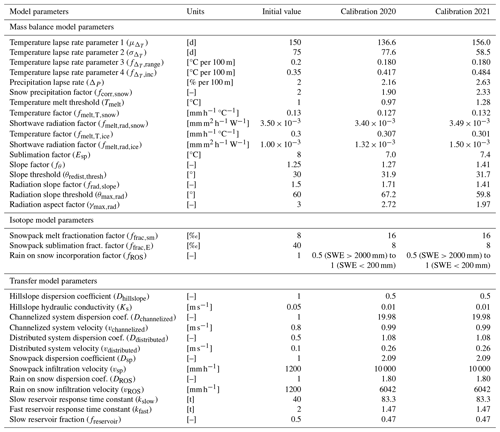
PEST-HP is used to optimize a multi-objective function based on the three field datasets. The weight of the snow cover objective function was set 6 and 3 times higher than the other two objective functions for 2020 and 2021, respectively (see also Sect. 5.1). All 26 calibration parameters of the model were calibrated separately for each hydrological year (starting 1 October), but the calibration procedure was performed by simulating both years at once and calibrating all parameters twice so that SWE and snow cover simulated at the end of the first year are used as initial values for the second simulation year. Model parameters were calibrated for both years in order to model the stream isotopic composition precisely and because both years showed different weather conditions (2020 was drier than 2021). Table A1 summarizes the results of the calibration procedure.

3.2 Snow isotopic module

3.2.1 Basic model formulation

Due to the strong correlation between δ¹⁸O and δ²H, we base the rest of this study on δ²H only.

Using SWE values from the mass balance model, we estimate the mean snowpack isotopic composition (i_sp) for each model cell (Fig. 2). The same approach as proposed by Ala-Aho et al. (2017b) is used to estimate the isotopic composition of the snowpack and snowmelt over time. An amount-weighted approach based on a precipitation input in the form of rain (P_r) or snowfall (P_sf), snow sublimation (E_sp), and snowmelt (M_snow) is applied (Eq. 20). A simple fractionation routine is used for snowmelt (i_sm) and snow sublimation (i_E) using two calibration parameters (f_frac,sm, f_frac,E) and n_melt, the number of days since the beginning of snowmelt (Eqs. 16 and 17).

$$\begin{array}{}\text{(16)}& {\displaystyle }{i}_{\mathrm{sm}}=i_{\mathrm{sp}}-{\displaystyle \frac{f_{\mathrm{frac},\mathrm{sm}}}{n_{\mathrm{melt}}}}\text{(17)}& {\displaystyle }{i}_{\mathrm{E}}=i_{\mathrm{sp}}-f_{\mathrm{frac},\mathrm{E}}\text{(18)}& {\displaystyle }{i}_{\mathrm{r}}=a_r+b_r{T}_{\mathrm{0}}\text{(19)}& {\displaystyle }{i}_{\mathrm{ROS}}=i_{\mathrm{sp}}{f}_{\mathrm{ROS}}+i_{\mathrm{r}}(\mathrm{1}-f_{\mathrm{ROS}})\text{(20)}& {\displaystyle }{i}_{\mathrm{sp}}^t={\displaystyle \frac{i_{\mathrm{sp}}^{t-\mathrm{1}}{h}_{\mathrm{SWE}}^{t-\mathrm{1}}+i_{\mathrm{r}}^t{f}_{\mathrm{ROS}}{P}_{\mathrm{r}}^t+i_{\mathrm{sf}}^t{P}_{\mathrm{sf}}^t-i_{\mathrm{E}}^t{E}_{\mathrm{sp}}^t-i_{\mathrm{sm}}^t{M}_{\mathrm{snow}}^t}{h_{\mathrm{SWE}}^{t-\mathrm{1}}+f_{\mathrm{ROS}}{P}_{\mathrm{r}}^t+P_{\mathrm{sf}}^t-E_{\mathrm{sp}}^t-M_{\mathrm{snow}}^t}}\end{array}$$

The year-round isotopic composition of the precipitation as rain (i_r) or snowfall (i_sf) is determined by computing a linear regression curve between the measured air temperature at the weather station (T₀) and the isotopic composition of sampled precipitation events (Eq. 18; see also Sect. 3.2.2).

3.2.2 Air temperature and precipitation stable isotope relationship

To estimate the snowpack isotopic composition, we relate the isotopic composition of each precipitation event to air temperature. For each precipitation sample, the corresponding temperature of the event is estimated by calculating the average air temperature weighed by the amount of precipitation measured each 10 min during the previous day. No clear trend in δ²H with elevation could be observed from rain samples obtained 8 times during the melt season at both 2450 and 2800 m a.s.l. For this reason, no isotopic lapse rate is used and the isotopic composition of precipitation events was similar for the entire catchment. This choice is discussed in Sect. 5.3.

In order to assess the uncertainty in the relationship between air temperature and precipitation δ²H, we define a normally distributed error for both parameters. We apply a Gaussian distribution with a standard deviation (σ) of 1 °C for air temperature and 5 ‰ for δ²H. We then perform 5000 iterations for which we randomly picked values in their distributions and then calculated a linear fit each time. These 5000 realizations are assumed to represent the uncertainty range of this relationship. This uncertainty margin is used to provide a sensitivity analysis of the impact of the air temperature and precipitation δ²H relationship on the isotopic snowmelt model results.

3.2.3 Rain on snow (ROS)

ROS incorporation in the snowpack and its water release is a complex process, which may have a strong impact on the snowpack isotopic composition depending on whether rainwater leaks through the snowpack, is stored or refreezes in the snowpack (Juras et al., 2017; Beria et al., 2018). The isotopic model from Ala-Aho et al. (2017b) assumes a complete mass exchange (hereafter described as isotopic mixing) between rain and the snowpack so that the snowpack isotopic composition results from the water-equivalent-weighted average of rain and snow. Field-based studies have however highlighted partial isotopic mixing of rain and snowmelt in the snowpack (Juras et al., 2017; Rücker et al., 2019). To account for the latter, we introduce a factor (f_ROS) which defines the fraction of rainwater which is isotopically mixed in the snowpack (Eq. 19). As observed in the work of Juras et al. (2017), we assume that all ROS event water is released from the snowpack with a delay based on a transfer function (see Sect. 3.3.2). However, the isotopic composition of the ROS water (i_ROS) released from the snowpack is a mix of rainwater which did not isotopically mix in the snowpack (equivalent to i_r(1−f_ROS)) and fully mixed water (see Eq. 19). We defined a simple calibration function between SWE and f_ROS, where f_ROS increases with lower SWE. This relationship is based on the assumption that, during the melting season, thicker snowpacks are less ripe (due to less melt). In unripe snowpack, Juras et al. (2017) showed that water infiltration is faster because of more preferential flow paths and that less isotopic mixing occurs. In thinner snowpacks, we assume that snow is ripe, which was shown to lead to more isotopic mixing of the rain within the snowpack (Juras et al., 2017).

3.2.4 Snow isotopic module calibration

The three isotope parameters (f_frac,E, f_frac,sm, f_ROS) were calibrated manually based on the following rules. At the onset of snowmelt, when snow still covers the glacier (in June in this work), snowmelt δ²H should be close to stream δ²H since snowmelt is the major contributor at that time. If snowpack data are available, the modelled snowpack δ²H at a grid cell should also be similar to the measured depth-averaged isotopic composition of the corresponding snow pit (Fig. 1). In our case, snowpack or snowmelt data were limited, and we lacked data for the late summer. For this reason, we first calibrated the hydrological transfer module without isotopes (based on discharge data only; see also Sect. 3.3.6). This allowed us to compare the modelled and measured isotopic composition of the stream (see Fig. 8) and then to adapt the isotope parameters to minimize the error between both curves.

3.3 Hydrological transfer module

A simple hydrological transfer scheme is used to transfer water with its isotopic composition from its input grid cell to the catchment outlet. In this module, we do not consider any interactions between hydrologically connected cells but only use the hydrological path length from each cell to the catchment outlet. We divided the hydrological paths in four different categories: (1) flow through the snowpack, (2) flow through the hillslope sediments (if outside of the glacier), (3) flow through the en-/subglacial distributed system and (4) flow through the en-/subglacial channelized system. The total flow path from each grid cell to the glacier portal was calculated using the “Flow Distance” tool (ArcGIS Pro v2.3) and a 2 m DEM of 2019 (swisstopo, 2019). For each category, we apply a convolution between the water input at time t and a time-dependent gamma distribution probability density function ($g(t,{\mathit{\alpha }}_g,{\mathit{\beta }}_g)$) as described in Eqs. (21) and (22). Here, the gamma function is used to reproduce a realistic transit time distribution (TTD) of the water input (McGuire and McDonnell, 2006). The convolution of the TTD at each time step provides the total TTD of the water from each grid cell to the glacier portal (Fig. 2).

$$\begin{array}{}\text{(21)}& {\displaystyle }{\mathit{\delta }}_{\mathrm{out}}\left(t\right)=\underset{\mathrm{0}}{\overset{\mathrm{\infty }}{\int }}g\left(\mathit{\tau }\right){\mathit{\delta }}_{\mathrm{in}}(t-\mathit{\tau })d_{\mathit{\tau }}=g\left(t\right)\cdot {\mathit{\delta }}_{\mathrm{in}}\left(t\right),\text{(22)}& {\displaystyle }g(t,{\mathit{\alpha }}_g,{\mathit{\beta }}_g)={\displaystyle \frac{{\mathit{\beta }}_g^{{\mathit{\alpha }}_g}{t}^{({\mathit{\alpha }}_g-\mathrm{1})}{e}^{-{\mathit{\beta }}_{g}t}}{\mathrm{\Gamma }\left({\mathit{\alpha }}_g\right)}},\end{array}$$

where δ_in(t) is any given input of water at time t and δ_out(t) is the output water flux.

To estimate the TTD, the parameters of the gamma distribution need to be defined. For each of the four hydrological flow categories, we estimate the mean transit time (t_MTT) of the water based on physical properties of each category and use this travel time to define the mode of the gamma distribution ($t_{\mathrm{MTT}}=\frac{{\mathit{\alpha }}_g-\mathrm{1}}{{\mathit{\beta }}_g}$). The dispersion of the flow for the gamma distribution is defined by a dispersion factor ($D={\mathit{\alpha }}_g-\mathrm{1}$).

3.3.1 Hillslope routing

We assume that the land cover outside glacierized areas is mainly composed of hillslope sediments. Those coarse sediments act as a rapid groundwater reservoir that infiltrates all rain and snowmelt water (Müller et al., 2022). In some steep parts, bedrock is apparent, and therefore the estimated transit time may be somewhat slower than in reality as water flows faster on the bedrock. However, this simplification should not lead to a large bias as sediments still dominate the hillslopes (Müller et al., 2022). For the latter, the average transit time (t_MTT) from each grid cell to the glacier surface was calculated using an estimated groundwater pore velocity (Eq. 23). Pore velocity is defined for kinematic subsurface saturated flow (MacDonald et al., 2012) as a function of slope (θ), aquifer distance (L_a), aquifer porosity (η) and hydraulic conductivity (K_s). We selected a porosity of 0.3 and a hydraulic conductivity for talus slopes of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{2}}$ m s⁻¹ based on previous research (Müller et al., 2022).

$$\begin{array}{}\text{(23)}& t_{\mathrm{MTT}}={\displaystyle \frac{L_{\mathrm{a}}}{v_{\mathrm{p}}}}={\displaystyle \frac{L_{\mathrm{a}}\mathit{\eta }}{K_{\mathrm{s}}\text{sin}\left(\mathit{\theta }\right)}}\end{array}$$

3.3.2 Snowpack routing

For snowmelt or ROS events, a TTD through the snowpack is used. Here, we calibrated an average pore velocity in the snowpack with an initial velocity of 1200 mm h⁻¹ following Juras et al. (2017). As for hillslope, the average transit time (t_MTT) through the snowpack is used to define the mode of the gamma distribution. Since SWE evolves with time, the TTD through the snowpack changes with time and was recalculated for each day.

3.3.3 Glacier routing

Once the flow path reaches the glacier ice surface, we defined two different water flow categories. The en-/subglacial drainage system was considered to be either distributed or channelized. During the winter, less melt and creep closure occurs due to ice dynamics (Flowers, 2015). Subglacial channels tend to close, leading to an inefficiently distributed drainage system characterized by slow water flow. During summer, larger conduit-like subglacial channels tend to develop and extend up-glacier with the recession of the temporal snowline (Nienow et al., 1998). Therefore, based on the temporal snow cover estimated with the mass balance model, we calculated the mean distance between the glacier portal and the first five grid cells on the glacier with snow cover to define the length of the channelized flow. We neglect supraglacial meltwater runoff here. However, the calibration of the glacier routing may compensate for this simplification by artificially increasing the subglacial velocity. The length of the channelized flow and the corresponding TTD for each grid cell changes through time since it is based on the temporal snow cover evolution. The length of the distributed flow is computed as the difference between the total flow length on the glacier and the channelized flow length.

For the snow-covered distributed en-/subglacial system, the mean velocity could not be measured directly. Here, an initial value of 0.1 m s⁻¹ was used following Nienow et al. (1998). For the summer channelized system, the velocity was defined based on 25 dye tracing injections. Measured velocity ranged between 0.29 and 0.83 m s⁻¹, and a velocity of 0.8 m s⁻¹ was selected to represent a fully channelized system.

3.3.4 Total runoff transfer to the outlet

The convolution of the combined gamma distributions (snow, hillslope, distributed subglacial drainage, channelized subglacial drainage) with the different water sources' time series (rainfall (P_r,j), ROS, (P_ROS,j), snowmelt (M_snow,j) and ice melt (M_ice,j)) obtained from the mass balance model for each grid cell j with an area (A_j) provides the estimated discharge contribution at the catchment outlet per water source and per cell. The sum over all grid cells corresponds to the total discharge from each water source. The case for snowmelt is illustrated in Eqs. (24) and (25).

$$\begin{array}{}\text{(24)}& Q_{\mathrm{sm},\mathrm{tot}}=\sum _{\mathrm{cell}=\mathrm{1}}^{\mathrm{cell}=n}\left(g_j\right(t,{\mathit{\alpha }}_g,{\mathit{\beta }}_g)\cdot (M_{\mathrm{snow}}{}_{,j}{A}_j\left)\right),\end{array}$$

where Q_sm,tot is the total discharge from snowmelt at the catchment outlet. The same approach can be applied to estimate the mean isotopic composition of the other water sources by applying the same convolution to the multiplication of the precipitation or melt time series and the isotopic signal (i_sm, i_ROS and i_r). This assumes that the isotopic composition of a water input is transported and redistributed to the catchment outlet following the same TTDs. The sum of each grid cell divided by the total discharge corresponds to the amount-weighted average isotopic composition of the corresponding water source (Eq. 25 for the case of snowmelt).

$$\begin{array}{}\text{(25)}& i_{\mathrm{sm},\mathrm{tot}}={\displaystyle \frac{{\sum }_{j=\mathrm{1}}^{j=n}\left(g_j\right(t,{\mathit{\alpha }}_g,{\mathit{\beta }}_g)\cdot (i_{\mathrm{sm}}{}_{,j}{M}_{\mathrm{snow}}{}_{,j}{A}_j\left)\right)}{Q_{\mathrm{sm},\mathrm{tot}}}}\end{array}$$

3.3.5 Fast and slow glacier storage

It is likely that part of the water is temporally stored in some areas of the en-/subglacial drainage network. To account for this, we ultimately define two reservoirs which represent a fast and slow linear storage. The integrated discharge of all water sources after the convolution with the gamma distributions is then separated between both reservoirs based on a calibrated fraction (f_reservoir) which assigns how much goes into the slow reservoir. The outflow discharge of each reservoir finally depends on a calibrated response time constant (k). For the fast reservoir, this results in Eq. (26):

$$\begin{array}{}\text{(26)}& Q_{\mathrm{fast}}={\displaystyle \frac{S_{\mathrm{fast}}}{k_{\mathrm{fast}}}},\end{array}$$

where S_fast is the filling of the reservoir. The slow reservoir response is computed in analogy to the equation above. The isotopic composition of each reservoir is separated between all water sources and is assumed to be fully mixed at each time step.

3.3.6 Hydrological transfer calibration

The calibration of the entire hydrological transfer module (including hillslope routing, snow routing, routing of distributed subglacial drainage and of channelized subglacial drainage, and transfer via two linear reservoirs) was also performed using the optimization algorithm PEST-HP, as already proposed in other glacio-hydrological studies (e.g. Immerzeel et al., 2012). We set three objective functions. The first function minimizes the error between observed and simulated discharge at the catchment outlet at an hourly time step. The second function optimizes the amplitude of daily stream discharge variations, which is a typical feature of glacier streams and which tends to increase during the summer season (Nienow et al., 1998; Lane and Nienow, 2019). Finally, the last objective function aims to minimize the difference between the observed and modelled δ²H of the stream.

The model was first calibrated based on discharge data only (first two objective functions). In a second phase, the water isotopes' objective function was also included in order to compare the model performance (see Fig. 6). The calibration was performed by only including data for summer 2020 (26 June to 15 September) and 2021 (8 June to 20 June). The first 2 weeks of June 2021 were included as they were not recorded in 2020 and represent the initial significant increase in streamflow after winter (when discharge becomes larger than 1 m³ s⁻¹). The period from 20 June 2021 to 15 September 2021 was then used to evaluate the model performance.

3.4 Mixing model for water sources using water stable isotopes

In order to estimate the contribution from rain, snow and ice melt, a three-component mixing model needs to rely on two independent tracers. Here, since we only rely on water stable isotopes, we propose estimating the shares of rain (ϕ_rain) and rain on snow (ϕ_ROS) using the output discharge of the hydrological transfer module divided by the total modelled discharge at the glacier portal. Then, we only use isotopes to estimate the share of snow (ϕ_snow) and of ice melt (ϕ_ice) following Eq. (27). The isotopic composition of rain (i_r) and snow (i_sm) is estimated using the isotopic model. The isotopic composition of ice melt (i_ice) is defined as constant through the year based on our measurements.

$$\begin{array}{}\text{(27)}& {\displaystyle }{\mathit{\varphi }}_{\mathrm{ice}}={\displaystyle \frac{i_{\mathrm{stream}}-i_{\mathrm{sm}}-(i_{\mathrm{r}}-i_{\mathrm{sm}}){\mathit{\varphi }}_{\mathrm{rain}}-(i_{\mathrm{ROS}}-i_{\mathrm{sm}}){\mathit{\varphi }}_{\mathrm{ROS}}}{i_{\mathrm{ice}}-i_{\mathrm{sm}}}}\text{(28)}& {\displaystyle }{\mathit{\varphi }}_{\mathrm{rain}}={\displaystyle \frac{Q_{\mathrm{rain}}}{Q_{\mathrm{stream}}}}\text{(29)}& {\displaystyle }{\mathit{\varphi }}_{\mathrm{ROS}}={\displaystyle \frac{Q_{\mathrm{ROS}}}{Q_{\mathrm{stream}}}}\end{array}$$

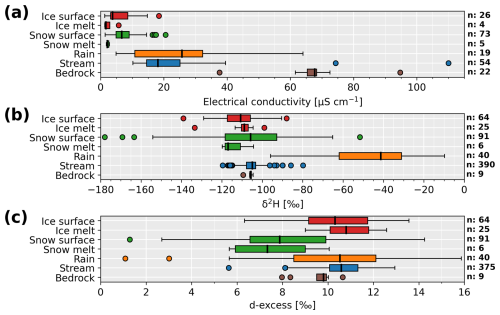
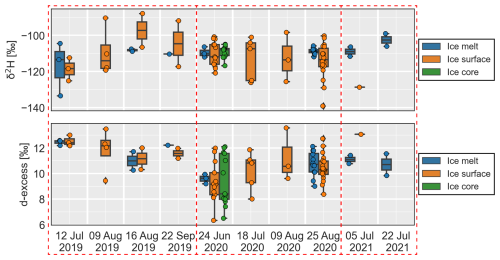
Figure 3 Boxplots of all water sources collected between July 2019 and October 2021 including water exfiltrations from the bedrock sidewalls. (a) Measured water electrical conductivity, (b) δ²H of water stable isotopes and (c) corresponding d-excess. The total number of samples (n) is indicated on the right.

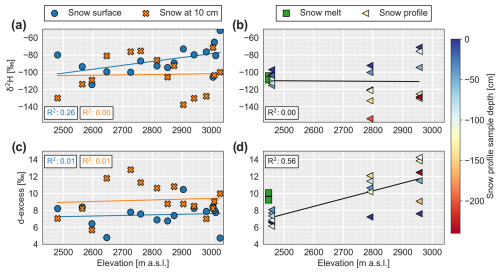
Figure 4 Isotopic composition of snow samples with elevation collected on 28 May 2021 on the main glacier lobe (Fig. 1). (a) Snow samples collected at the surface and at the same location between 10 and 20 cm depth. (b) Snow profiles with sampling depth (0 to −250 cm) indicated by the colour bar. The snowmelt found at the bottom of the lowermost profile is also indicated (green rectangles). (c, d) Corresponding results for d-excess. Linear regression curves for sample class with their coefficient of determination (R²) are also shown.

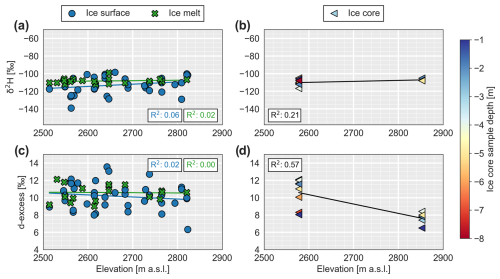
Figure 5 Isotopic composition of ice samples with elevation collected between 2020 and 2021 on the main glacier lobe (Fig. 1). The scale of the y axes is similar to Fig. 4 for comparison. (a) Solid ice samples collected at the glacier surface and ice meltwater samples collected in gullies at the glacier surface. (b) Ice core samples with sampling depth (−1 to −8 m) indicated by the colour bar. (c, d) Corresponding results for d-excess. Linear regression curves for each sample class with their coefficient of determination (R²) are also shown.

4 Results

4.1 Isotopic measurements in the field

Between July 2019 and October 2021, we measured the water δ²H as well as the water electrical conductivity (EC) at different locations within the catchment. We summarize all results in Fig. 3. The rainwater EC has a median value of 26 µS cm⁻¹. Snow and ice samples have lower EC values, usually below 10 µS cm⁻¹. Interestingly, the glacial meltwater stream shows systematically higher EC values than the snow and ice samples, even during the peak snow and ice melt period. Regarding water stable isotopes, only rain has a significantly different composition (Fig. 3). The surface snow and ice samples have similar δ²H ranges and show a large scatter, which completely overlap with the stream δ²H. The composition of the snowmelt samples shows less scatter than the snow surface samples. The snow surface and snowmelt d-excess values appear lower than the other water sources (Fig. 3).

Close to the date of maximum end-of-winter snow accumulation on 28 May 2021, snow surface samples show a large δ²H variability with no clear tendency with elevation (R²=0.26; Fig. 4a). Snow samples at the same locations but at a depth of 10 cm have different values with no clear trend. The snowpack δ²H profiles appear stratified with a tendency towards more isotopically depleted snow with depth, reflecting the colder air temperature of the snowfall in the early winter season, which was conserved in the snowpack.

D-excess at the snow surface shows no particular trend with elevation but appears lower than for samples at 10 cm depth (Fig. 4c). The d-excess of the snow profiles shows a more significant trend with elevation. From all snow samples collected each year, no significant seasonal trend can be observed (Fig. C1).

The δ²H of the surface ice shows a smaller variability than surface snow and no trend with elevation (Fig. 5). Superficial ice melt samples show less scatter than surface ice. Two ice cores reaching 5 and 8 m below the ice surface were also analysed and show limited variations in δ²H with depth, while their average value is close to the ice melt samples. There seems to be a more significant trend in d-excess for the ice cores with elevation, but this trend relies only on two sampling locations.

4.2 Mass balance model calibration results

The mass balance model parameters were calibrated for both years against measured SWE, measured ice melt and mapped seasonal snow cover (Table A1). The calibrated temperature lapse rate shows a maximum around late May to early June, a mean value of 0.42 and 0.48 °C per 100 m for 2020 and 2021, and a maximal seasonal variation of 0.18 °C per 100 m (Fig. D1c). Regarding snow redistribution, both calibration years show a similar slope correction factor, with a slope threshold of 32° above which snow redistribution occurs towards gentler slopes (Fig. D1a). The radiation correction factor varies between 1 for flat slopes and 2.5 for south-facing slopes around 60° (Fig. D1d). Finally, a precipitation lapse rate of 2.2 % and 2.6 % per 100 m for 2020 and 2021 was found (Table A1).

Overall, the model shows good performance for SWE, although the model results show less local variations than the point SWE measurements, which are more spatially variable (Fig. E1). Therefore, the root mean square errors (RMSEs) for SWE are 97.9 and 100.3 mm over the hydrological years (starting 1 October) 2019/2020 and 2020/2021, respectively. Those results are similar to other advanced snow models where RMSE values are in the range of 75 to 150 mm (in water equivalent, hereafter w.e.) for such elevated catchments (Mott et al., 2023). The RMSE values for ice ablation are 237.5 mm w.e. for 2019/2020 and 263.8 mm w.e. for 2020/2021. The mean error in the snow and ice mass balance calculations is close to 0 mm w.e, except for the snow mass balance in 2020, for which the model seems to overestimate SWE with a mean error of 45.7 mm. The mapped temporal snow cover evolution is well represented by the model during the entire melting season, showing similar patterns of melt, with earlier snow disappearance on steep south-facing slopes (Fig.  to E3). In 2020, one summer snow event seems underestimated by the model, leading to a constant bias in the modelled snow cover fraction after July 2020 (Fig. E4). In 2021, the modelled snow cover evolution fits well with the mapped extents during the whole melting season, with a somewhat earlier snow disappearance at high elevation, potentially due to precipitation underestimation in this zone.

Catchment-wide average snowmelt over the hydrological years is 1860 and 1527 mm w.e. for 2019/2020 and 2020/2021 and 1265 and 958 mm w.e. for ice melt. Catchment-wide liquid precipitation amounts to 227 and 320 mm, snow sublimation to 84 and 82 mm w.e., and snow deposition to 34 and 14 mm w.e. for 2019/2020 and 2020/2021.

Finally, the results of the modelled mass balance losses (through rainfall, snowmelt and ice melt) at a daily timescale appear to match well with the measured discharge at the glacier portal (Fig. D2). In particular, the cumulative mass balance follows well the cumulative measured discharge, except for September 2020, when the modelled mass balance is overestimated compared to the measured discharge.

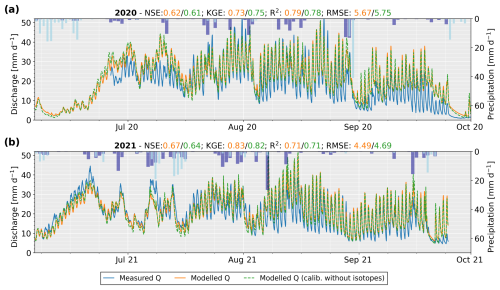
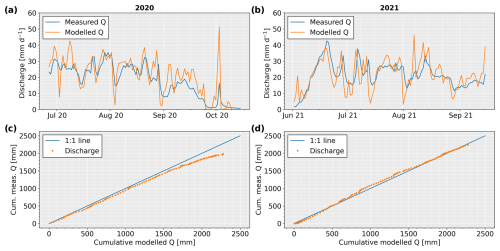
Figure 6 Comparison between hourly measured discharge (Q) at the glacier portal and modelled discharge from the combined mass balance and transfer model for the melting season of 2020 (a) and 2021 (b). Modelled discharge is shown when calibrating the hydrological transfer module with all three objective functions with the stream isotope dataset (orange curve) or without the stream isotopes (dashed green curve). Discharge is expressed in millimetres per day and corresponds to litres per day divided by the catchment area in quare metres. For each year, we show the Nash–Sutcliffe efficiency (NSE) and Kling–Gupta efficiency (KGE), as well as the coefficient of determination (R²) and the root mean square error (RMSE). The colour corresponds to the model discharge with or without isotopes for calibration. Daily solid (light blue) and liquid (dark blue) precipitations are shown as inverted bars.

4.3 Hydrological transfer module results

The calibration of the hydrological transfer parameters was performed in a second separate step following the mass balance model calibration. We tested calibration with and without including stream δ²H as an objective function in PEST-HP. Calibrated parameters are summarized in Table A1 for the calibration with isotopes. Results are shown in Fig. 6.

Over the entire melting season, the calibration of the transfer module led to a satisfying modelled discharge at an hourly time step. In particular, the increase in the magnitude of daily discharge fluctuations during the melt season due to a switch from a distributed to a channelized system (Lane and Nienow, 2019) was well reproduced. This suggests that the modelled evolution of the glacier drainage system based on the distance of the snow line limit was a satisfying proxy for the channelized system. Discharge recessions during short cold spells are also well simulated thanks to the slow reservoir. The hydrological transfer model was only calibrated against data from 2020, but the model performance appears even slightly better for 2021. This behaviour is confirmed by the Nash–Sutcliffe efficiency (NSE) and Kling–Gupta efficiency (KGE) criteria (see Gupta et al., 2009, for references) of 0.62 for NSE and 0.67 for KGE in 2020 and 0.73 and 0.83 in 2021 (Fig. 6).

Compared to other glacio-hydrological models based on enhanced temperature index (ETI) equations, our model efficiency for the NSE of 0.67 is lower, as most models obtained NSE values in the range of 0.7 to 0.9 (e.g. Schaefli et al., 2005; Huss et al., 2008; Magnusson et al., 2011). They are however all calibrated against discharge data, while our mass balance module only relies on snow, ice and weather data. We found only one piece of research by Shakoor et al. (2018), who used an ETI model combined with the distributed snow model Alpine3D. Here, they obtained an NSE value of 0.77 for a similar glacierized catchment but relied on more extensive in situ field weather and snow data for model calibration.

The modelled discharge with (orange curve, Fig. 6) and without (dashed green curve, Fig. 6) including stream isotopes for calibration was very similar, although both NSE and KGE were slightly higher for the calibration with isotopes. While discharge results are similar, notable changes in the model parameters were observed, highlighting the typical problem of equifinality (Acero Triana et al., 2019). In particular, with isotope calibration, the drainage of the hillslope rainwater appears 10 times slower with more dispersion than without isotope calibration. To compensate for this effect on modelled discharge at the glacier portal, it seems that rain infiltration through the snowpack was faster with isotope calibration than without.

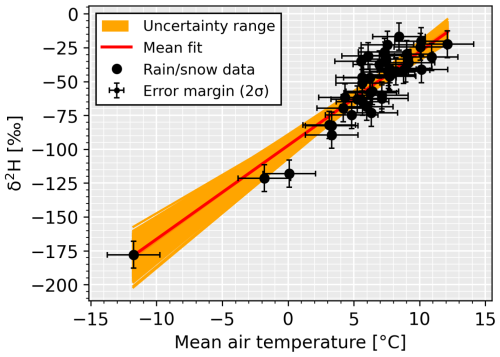
Figure 7 Relationship between air temperature measured at the weather station (Fig. 1) and the isotopic composition of 39 precipitation events between 2019 and 2021. For each point, we defined a normally distributed error margin of 2 standard deviations (2σ). The orange area represents the 5000 linear regressions obtained by randomly picking a set of values in the error margin of all points. The red line corresponds to the mean regression.

4.4 Air temperature and relationship to isotopic composition of precipitation

The relationship between air temperature and precipitation δ²H appears to be linear with a coefficient of determination (R²) of 0.85 for the mean regression (red line in Fig. 7). However, most of our samples cover the summer season; thus the linear trend is strongly influenced by the limited number of winter precipitation samples. We, therefore, also highlight the uncertainty margin which was then used to assess the sensitivity of the modelled snow and stream isotopic behaviour to this relationship (see Sect. 5.3).

4.5 Isotopic model results

Based on the mean δ²H of supraglacial ice melt samples, the ice melt δ²H was set to a fixed value of −109 ‰, which also reflected the minimum stream δ²H in late summer when snow cover is lowest. The snowmelt δ²H was calibrated manually (Sect. 3.2.1).

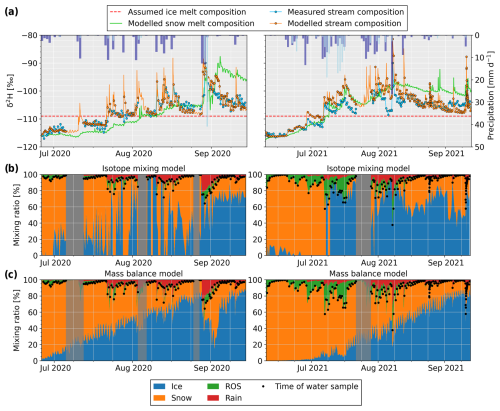
Figure 8 Results of the isotopic model. (a) Measured and modelled stream δ²H at the glacier portal as well as constant δ²H value assumed for the ice melt composition and the modelled evolution of the snowmelt δ²H. Daily solid (light blue) and liquid (dark blue) precipitations are shown as inverted bars. (b) Estimated mixing ratios between ice melt, snowmelt, rain and ROS based on the measured stream δ²H and the modelled δ²H of the water sources. The shares of rain and ROS were estimated using the transfer model. The black dots indicate the dates of each stream water sample used to estimate the mixing ratios. Grey areas represent periods when no samples were available for more than a day. (c) Mixing ratios were estimated from the combined mass balance and transfer model only.

The calibrated modelled snowpack δ²H on 28 May 2021 (−118.4 ‰ and −119.1 ‰) matched well with the δ²H of the two available depth-averaged mean snow pits (−117 ‰ and −125 ‰; see Fig. 4). Over the whole melting season, the modelled stream δ²H also matched well with the measured stream δ²H (Fig. 8a). Parameter f_frac,sm was set to 16 ‰ for δ²H but had little impact on the results, as also shown by Ala-Aho et al. (2017a). The sublimation parameter f_frac,E was set to 8 ‰. f_ROS was manually calibrated to 1 when SWE was below 200 mm w.e. and increased linearly until a SWE value of 2000 mm w.e. was reached; it then remained constant.

The resulting snowmelt δ²H is shown in Fig. 8a. Snowmelt δ²H is similar to the measured stream δ²H in early June and increases during the melting season due to snow evaporative fractionation and the isotopic mixing of the snowpack with rainwater (which has an isotopic composition mainly ranging between −80 ‰ and −20 ‰ in summer; see Fig. 7). This increase is faster in 2021 than in 2020 due to much more precipitation and ROS amounts. In 2020, the modelled stream δ²H appears to fit well with the stream δ²H observations, although the results appear less similar during rain events. In early July 2021, stream δ²H is rapidly overestimated by the model, corresponding to a period of important summer snowfall and ROS events. In the second part of August 2021, when less precipitation occurred, stream δ²H appears better represented. During some important rain/snow events, in particular in mid-July 2021, snowmelt δ²H increases shortly after summer precipitation events. This is due to the short-term deposition and subsequent melt of summer snow at low elevation (where snow was absent) which has a higher δ²H composition than the older remaining winter snowpack at higher elevation. This fresh snow disappears in a few days, after which the snowmelt δ²H gradually returns to the composition of older snow.

4.6 Estimation of mixing ratios

We compare the mixing ratios between the four different water sources (rain, ROS, snowmelt and ice melt), estimated either based on the simulated discharge of each source (using the mass balance and transfer model) or based on the modelled isotopic compositions of the water sources. As detailed in Sect. 3.4, since we only use water isotopes as a tracer, only two components can be separated (snow and ice melt), while we use the results of the mass balance and transfer model to estimate the water fractions of rain and ROS. The results of the mass balance model (Fig. 8c) show a gradual transition from a snow-dominated discharge towards more ice melt in the late melting season. The estimated contributions of rain and ROS remain usually below 20 %, except for large events (>15 mm d⁻¹), during which the peak contribution reaches up to 50 %. The results of the mixing model based on isotopes (Fig. 8b) are more variable. For both years, mixing ratios for the early and late melting seasons are in a similar range to those calculated from the mass balance model. In the middle of the melting seasons, the estimated ratios of snow and ice melt appear much more variable and difficult to interpret.

5 Discussion

5.1 Mass balance model limitations

We created a simple mass balance model relying on readily available point-based data (precipitation, air temperature, incoming solar radiation). Catchment-wide spatio-temporal variations in temperature and precipitation were modelled using seasonal elevation lapse rates, while incoming solar radiation was adapted using a high-resolution DEM to account for slope and aspect. The spatial extrapolation of the meteorological input data relies on an effective calibration procedure that allows the model to be applied to other locations. Some key aspects of the model are discussed hereafter.

The calibrated seasonal temperature lapse rates showed steeper gradients in summer than winter (Fig. D1c), similar to other studies (e.g. Rolland, 2003; Marshall et al., 2007). At high elevations, the colder summer temperatures obtained with a varying lapse rate compared to a constant lapse rate led to less melt, which in turn influenced the calibration of the precipitation lapse rate. Precipitation lapse rate decreased indeed from about 10 % per 100 m with a constant temperature lapse rate to about 2 % with a varying lapse rate, which is closer to observations reported over other glaciers (Schaefli et al., 2011).

The snow loss and redistribution function on steep slopes, combined with the radiation correction function based on slope and aspect, was essential to correctly represent the timing of the presence/absence of snow on the north- and south-facing slopes. Although snow redistribution was only based on slope, it provides a simple and fast way to redistribute snow without accounting for complex wind processes or the topography of connected cells. The calibration of the snow redistribution was relatively similar for both years, confirming the consistency of the method (Fig. D1b). Most redistribution occurred near the glacier terminus and above an elevation of 2800 m a.s.l. A stronger redistribution was calibrated at high elevations in 2021 (3400 to 3600 m a.s.l.), corresponding to a few small, highly elevated hanging glaciers, where snow redistribution from the nearby steep rock walls is likely.

Snow sublimation and deposition were also modelled using a simple method. The amount of snow mass loss due to sublimation remained small compared to snowmelt (<5 %) and is in a similar range to other studies in high-mountain catchments (e.g. Strasser et al., 2008; Stigter et al., 2018). Modelling this process also required additional meteorological data such as wind speed, relative humidity and surface snow temperature. While we proposed a simple procedure to estimate snow surface temperature, wind speed may vary spatially due to katabatic winds in particular (Greuell and Böhm, 1998; Shaw et al., 2024). Snow sublimation remained uncertain and was here required mainly to estimate the isotopic fractionation in the snowpack rather than to improve the mass balance model.

High-resolution daily satellite images from Team Planet (2017) allowed for generating approximately weekly cloud-free snow maps. Including these snow cover maps as a calibration objective function constrained the calibration parameters of our model on steep slopes where no SWE measurements are available, leading to a better representation of the spatial processes (Figs.  to E3). For example, in 2020, with very limited SWE data measured in situ, we put 6 times more weight on the snow cover objective function than on the SWE objective function. Compared to having a similar weight between both objective functions, this led to modelled mass losses closer to measured discharge, even if it increased the error in measured SWE (Fig. E1c). Therefore, snow cover maps may be highly valuable for mass balance model calibration if limited SWE data are available.

5.2 The role of groundwater

In winter, we measured a winter stream discharge at the glacier portal reaching a minimum of about 0.24 mm d⁻¹ (Fig. B1). This residual streamflow is probably due to two main causes. Basal melt in winter could provide such limited flow, creating a thin water film (Flowers and Clarke, 2002), slowly draining through subglacial till or at the contact with bedrock. Alternatively, the groundwater contribution from a deeper aquifer could provide such a baseflow (see Sect. 5.2). To some extent, delayed lateral subsurface flow (Carroll et al., 2019) from elevated snowmelt transmitted through the hillslopes is estimated by the hillslope and snow routing modules, but bedrock exfiltration was not modelled.

Groundwater contributions from the bedrock may not be completely negligible as the discussion of groundwater storage has recently shown for Swiss alpine glaciers (Müller et al., 2022; Oestreicher et al., 2021). For our catchment, it is possible that a part of the early snowmelt contributes to recharge the highly fractured bedrock and is then redistributed towards the late melting season when snow cover is limited. In Otemma, a winter dynamic bedrock storage was estimated to be equivalent to 40 mm of water stored over the entire catchment (Müller et al., 2022). This seasonal storage may increase to about 60 to 100 mm in spring due to snowmelt recharge, as suggested for other glacierized catchments (Hood and Hayashi, 2015; Oestreicher et al., 2021). This recharge is potentially visible in Fig. D2d (cumulative discharge from 0 to 500 mm), as the cumulative modelled discharge in the early melting season is about 50 mm larger than measured, which could be due to some snow meltwater infiltrating into the bedrock and not being routed to the glacier portal. Later in the melting season, groundwater bedrock drainage may then lead to higher modelled discharge than measured (Fig. D2d, cumulative discharge from 1000 to 1500 mm). This amount of storage release lies in the same range as the RMSE of the differences between observed and modelled SWE in 2021 (Fig. E1b) and can therefore not be clearly identified. Stream EC was always higher than ice melt and snowmelt EC (Fig. B1), and it largely increased in winter, which also points to the potential contribution of a groundwater reservoir. However, as highlighted in some studies (e.g. Sharp et al., 1995; Hindshaw et al., 2011), subglacial weathering at the contact with the bedrock or sediments leads to an increase in solutes in the meltwater. Since EC is not a conservative tracer, groundwater estimation via EC measurements may lead to much larger uncertainty than some studies suggest, as subglacial weathering cannot be easily quantified.

In any case, groundwater storage remains very limited, representing only about 2 % of the total snow and ice melt estimated over one melt season. It should also not impact the stream δ²H, as the δ²H of bedrock leakages was found to be close to ice melt δ²H (Fig. 3).

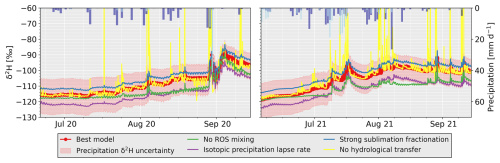
Figure 9 Sensitivity analysis of the modelled catchment-integrated snowmelt δ²H at the glacier portal over the melting seasons 2020 and 2021. The curves shown are best-calibrated model (best model), uncertainty margin from the relationship between precipitation δ²H and air temperature (see Fig. 7), model without ROS δ²H mixing in the snowpack (no ROS mixing, f_ROS=0), model with an isotopic precipitation δ²H lapse rate of −1 ‰ per 100 m, model with a strong isotopic sublimation fractionation ($f_{\mathrm{frac},\mathrm{E}}=\mathrm{80}$ ‰), and model without hydrological transfer (no transfer). Daily solid (light blue) and liquid (dark blue) precipitations are shown as inverted bars.

5.3 Isotopic model sensitivity analysis

5.3.1 Ice melt isotopic composition

In this work, we chose a constant ice melt δ²H composition. Different spatio-temporal studies on ice melt isotopes show conflicting temporal results, with ice becoming either enriched (Penna et al., 2017), depleted (Schmieder et al., 2018) or showing no trends in δ²H (Maurya et al., 2011). For the Swiss Alps, Jenk et al. (2009) analysed an 80 m deep ice core and showed some δ²H variations but no particular trends with depth, except for a shift at the glacier bed. This suggests that older, deeper ice does not have a significantly different isotopic composition. This may also be true for the surface ice melt, as also supported by Fig. 5, where no change in surface ice melt δ²H with elevation can be observed, as also observed in the Italian Alps (Zuecco et al., 2019). In addition, no clear temporal ice melt δ²H trend could be observed (Fig. C2). Therefore, using a constant seasonal ice melt δ²H, equivalent to the mean δ²H of surface ice melt samples, is considered reasonable for alpine temperate glaciers. Alternatively, using the end-of-summer stream δ²H at the glacier portal to approximate the ice melt δ²H composition led to a similar value. However, residual snow cover at high elevations may still contribute to discharge, as illustrated in our case by the 20 % snow contribution in September 2020 before the first snowfall (Fig. 8).

5.3.2 Snowmelt isotopic sensitivity to precipitation δ²H

Several assumptions were made to model the isotopic composition of the snowpack and snowmelt, which in turn strongly influenced the modelled stream δ²H composition. In Fig. 9, we performed a sensitivity analysis by modifying key model parameters to assess their impact on the modelled snowmelt δ²H.

The largest uncertainty in the modelled snowmelt δ²H results from the relationship between air temperature and precipitation δ²H (red area in Fig. 9). Indeed, a change in slope in their linear regression strongly impacts the modelled snowpack δ²H at peak snow accumulation. Moreover, precipitation δ²H may be influenced by other parameters than air temperature. In this study, the limited number of bulk snowpack δ²H samples limits the calibration and evaluation of this approach. Nonetheless, at least one recent study providing a much more in-depth analysis of snowpack δ²H profiles validated the strong relationship between the snowpack δ²H and air temperature (Carroll et al., 2022a).

In addition, precipitation δ²H may also vary with elevation. No isotopic precipitation lapse rate was used in this work, as it could not be observed. This lack of δ²H lapse rate may be due to the complex airflow above a high-elevation terrain, where air parcels may stagnate or flow down-valley (Schäppi, 2013). This modifies vapour condensation and thus invalidates the relationship between elevation and a depletion of heavy isotopes in the water vapour (Galewsky, 2009). Such an absence of δ²H lapse rate trend was also observed from high-elevation precipitation data in Switzerland, especially in winter (Kern et al., 2014). Nonetheless, at least one recent study provided a detailed description of multiple snow profiles with elevation (Carroll et al., 2022a). While they measured a δ²H precipitation lapse rate of −1.28 ‰ per 100 m, they showed no statistically significant differences with elevation in the snowpack bulk isotopic composition at the time of maximum end-of-winter snow accumulation. They attribute this to the persistence of warm, enriched early winter snow at high elevations and different rates of snow accumulation and sublimation in winter. In our model, including a δ²H lapse rate of −1 ‰ per 100 m leads to a more depleted snowpack before the onset of snowmelt (purple curve in Fig. 9). It also reduces the increase in snowmelt δ²H in summer due to ROS events. A winter δ²H lapse rate may lead to a snowpack that is too depleted compared to what is observed (purple curve in Fig. 9). However, a summer δ²H lapse rate may be required to better represent the stream δ²H during wet summers such as 2021, where the effect of ROS (without δ²H lapse rate) led to a modelled snowmelt and stream δ²H that is too rapidly enriched (Fig. 8a).

5.3.3 Snowmelt isotopic sensitivity to ROS

ROS is also influenced by the summer precipitation lapse rate, which was assumed to be similar to winter snowfall (increase of 2 % per 100 m). Similar to the δ²H lapse rate, precipitation lapse rates may become flat or even negative in the Swiss Alps in summer above 2500 m a.s.l. (e.g. Schäppi, 2013). It is therefore likely that precipitation shows a smaller increase with elevation in summer than in winter, resulting in an overestimation of the summer precipitation amounts when using a fixed annual lapse rate. This impacts how much ROS mixes within the snowpack and how it modifies the snowpack δ²H. Both precipitation amounts and δ²H precipitation lapse rates therefore appear challenging to accurately model, which may lead to large uncertainties even for relatively dry years such as 2020.

In addition, how ROS mixes, refreezes or leaks through the snowpack remains a major question. Neglecting ROS δ²H mixing in the snowpack (f_ROS=0) leads to a much slower enrichment of the snowpack in heavy isotopes during the melting season. This process appears to be the main driver of the seasonal increase in the snowmelt δ²H value (green curve in Fig. 9). Only limited experimental work exists on this topic. For instance, for an in situ ROS experiment, Juras et al. (2017) showed that rainwater showed limited isotopic mixing in a 50 cm thick non-ripe cold snowpack and exfiltrated rapidly while retaining its original δ²H composition. They attributed this effect to the formation of preferential flow in colder snowpack and measured an infiltration velocity 10 times higher than in a ripe snowpack. For a ripe snowpack, they showed that less than 50 % of rainwater was directly released from the snowpack, leading to partial isotopic mixing of the rainwater with the snowpack. In another in situ study, Rücker et al. (2019) showed that interactions between rainwater and the snowpack were mainly influenced by the residence time of the rainwater in the snowpack, which mostly depended on snow depth and rainfall amounts.

In this work, we attempted to provide a simple formula for the mixing of ROS in the snowpack based on the SWE amounts (see Sect. 3.2.3), and the best calibration was achieved with a complete incorporation of ROS in the snowpack when the snowpack was thin and likely isothermal (<200 mm w.e.) and a partial mixing of 50 % when the snowpack was thick (>2000 mm w.e.). Such a simple approach can, of course, be questioned. There is indeed no clear evidence that a thicker snowpack is less ripe by assumption. At least in our case, a 2000 mm snowpack was only modelled at high elevations where ripe conditions are unlikely. In our case however the calibration of this function led to satisfying results, and our function had the advantage of being simple, whereas estimating the snow energy state hourly at each grid cell seemed too complex.

5.3.4 Snowmelt isotopic sensitivity to snow fractionation

Based on our calibration, we used a rather low sublimation fractionation factor ($f_{\mathrm{frac},\mathrm{E}}=\mathrm{8}$ ‰) compared to Ala-Aho et al. (2017a), so the differences with no sublimation are limited. Using a 10-times-higher sublimation fractionation factor (blue curve in Fig. 9) leads to a more enriched snowpack before July but does not particularly impact the snowmelt δ²H evolution in summer, which conserves a winter δ²H offset compared to the best model. This is because the modelled sublimation mostly occurs during spring when cold dry air has a lower vapour density than the snow surface. We also estimated a small deposition amount (34 and 14 mm w.e. for 2020 and 2021), but deposition was not included in the isotopic module as the isotopic composition of the water vapour in the air appears very complex, as discussed above for precipitation. Its effect on snow fractionation therefore remains unclear.

Similar to Ala-Aho et al. (2017a), the parameter governing liquid fractionation of the snowpack (f_frac,sm, not shown in Fig. 9) had only limited influence on the modelled summer snowmelt δ²H. Nonetheless, some studies (e.g. Taylor et al., 2001) have reported liquid fractionation during melt as an important driver of isotopic enrichment. For this work however this process defined by Eq. (17) seems to play a minor role due to the rapid increase in the number of melt days (d_melt). While we retained the original equation from Ala-Aho et al. (2017a), its validity could be further explored.

The use of d-excess to constrain sublimation in the modelling framework as proposed by Carroll et al. (2022b) could be explored in future work. Indeed, while the d-excess of surface snow showed no trend with elevation, the d-excess of snow profiles increased with elevation (Fig. 4d), which may suggest more evaporative fractionation at lower elevations and deposition of depleted air vapour at higher elevations, as discussed by Sprenger et al. (2024). The processes of vapour transport and vapour deposition in the snowpack δ²H are however complex (Lambán et al., 2015) and remain challenging to model precisely.

5.3.5 Snowmelt isotopic sensitivity to snowmelt transfer

Finally, we show the isotopic composition of snowmelt if we simply take the average value of all snowmelt grid cells without the transfer module (yellow curve in Fig. 9). In this case, the signal shows more variability and small peaks, mainly due to the effect of summer snowfall or ROS events. The snow transfer to the outlet contributes to smoothing out short-term variations in δ²H, while the signal remains similar when no precipitation occurs.

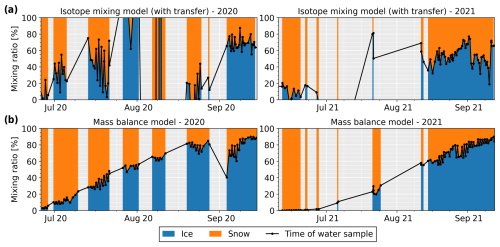
Figure 10 Mixing ratio between snow and ice melt at the catchment outlet when rain contribution to streamflow is less than 5 %. (a) Results based on a mixing model based on measured stream δ²H and where the two end-members are ice melt δ²H (with a fixed value of −109 ‰) and the modelled snowmelt δ²H. (b) Results from the discharge volumes estimated based on the mass balance and transfer modules without using isotopes. Black points show dates when stream δ²H samples were taken.

5.3.6 Snow isotopic module calibration challenges and opportunities

Calibrating the catchment-scale snowmelt δ²H remains challenging. We have shown that relying on surface snow isotopic data is not advisable, as surface snow shows a large scatter (Fig. 4a). This scatter is likely due to (i) different rates of snow fractionation at the surface (as suggested by the lower d-excess at the snow surface; Fig. 4c) or (ii) surface snow originating from different precipitation events due to snowmelt and snow redistribution. Bulk snowpack δ²H data appear more useful, but sampling at high elevations may be compromised by difficult access. In addition, the large spatio-temporal variability in the snow data may strongly influence the results.

In this work, we have shown an alternative method to model snowmelt, which appears promising but still relies on complex modelling and multiple data sources. In the early melting season (when the catchment is fully snow-covered), stream δ²H was similar to snowmelt δ²H, which provides a simple target for calibration. During the mid- and late melting season, we relied on our model to minimize the error between modelled and observed stream δ²H. This involves calibrating a hydrological transfer module against discharge data, which are difficult to acquire for high-elevation and more remote catchments.

However, based on the results of the hydrological transfer module, the delay between snowmelt and its arrival at the catchment outlet was usually less than a day. As a result, the snowmelt δ²H at the catchment outlet modelled using the calibrated transfer scheme was close to the δ²H value calculated using a simple daily amount-weighted mean snowmelt δ²H of all grid cells (Fig. 9). This suggests that the hydrological transfer may not be necessary to estimate the temporal evolution of the catchment-integrated snowmelt δ²H and that it can be obtained solely based on mass balance modelling (with necessary meteorological data) and stream δ²H samples.

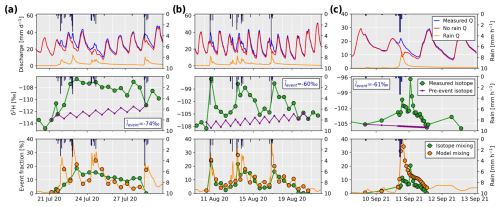
Figure 11 Comparison of the estimated fraction of the total discharge originating from rain events during early 2020 (a), mid-2020 (b) and late 2021 melting season (c). The upper panels show the measured discharge (blue curve) at the glacier portal and the sum of rain and ROS discharge (event discharge) estimated from the model (orange). The red curve shows the measured discharge without the modelled event water. The central subpanels show the measured stream δ²H (green) and an estimation of the pre-event δ²H based on a simple linear interpolation between the pre- and post-event stream compositions. If pre-event stream δ²H showed small daily variations (due to the increase in ice melt during the day), this behaviour was added to the linear interpolation to better represent the baseline δ²H composition. The mean precipitation δ²H of the event (i_event) is indicated in the inserted box. Lower panels show the fraction of event water (rain and ROS) in the streamflow estimated either based on the modelled event discharge (see upper panels) or based on isotopes (see central panels).

5.4 Water isotopes and end-member mixing models in glacierized catchment

In this research, we have proposed a way to better characterize the temporal evolution of the snowmelt δ²H at the outlet of a highly glacierized catchment. This method, especially if validated with more snowpack or snowmelt observations, should contribute to limit snowmelt isotopic uncertainties due to the spatio-temporal variability in the snowpack δ²H. Nonetheless, even with such an approach, answering the question of water sources' mixing ratios at the catchment outlet based on an isotope end-member mixing model appears very challenging. In Fig. 10, we provide an analysis of the ice melt and snowmelt shares when the estimated rainwater fraction was less than 5 %. Even when limited rain drains at the outlet, water shares based on water isotopes (Fig. 10a) appear very variable, especially during the mid-melting season. Indeed, during the mid-melting season, snowmelt δ²H increases and reaches values close to ice melt δ²H so that even a slight error in the estimation of their δ²H values leads to a large uncertainty in their estimated shares using a mixing model approach. Mixing estimations for the early or late melting seasons were more similar to the estimation based on discharge volumes estimated using the mass balance and routing modules.

Mixing results based on a relatively simple combined mass balance and routing model remain more accurate overall (Fig. 10b). This is encouraging since the mass balance model calibration was performed based on weather data and snow observations, without relying on discharge data, which remain the most time and cost-intensive data to acquire in mountainous catchments. Discharge was only used for water routing, and, at least in such a small catchment, water transfer was fast and does not significantly affect results on a daily timescale.

5.5 Water isotopes for hydrological routing in glacierized catchment

In this paper, we focused on modelling the water shares of snow and ice melt either using mass balance modelling or based on isotopes. We showed that the use of isotopes to separate snow and ice melt is not encouraging. However, water isotopes may still provide useful constraints for better calibrating glacio-hydrological models. In Fig. 6, we show that calibration with or without isotopes led to relatively similar results. However, as also suggested in another study by Nan et al. (2022), including isotopes for calibration may improve the model parameters' uncertainty. In our case, although snow and ice melt δ²H compositions were similar, isotopes may improve the parameterization of the water transfer of precipitation event water because precipitation δ²H is usually much higher (more enriched in heavy isotopes) than the meltwater.

In our water transfer equations, we assume that the water transfer is driven by an advective flux but does not depend on previous conditions, such as antecedent wetness or the amount of storage in a compartment (snowpack, groundwater or en-/subglacial system). It was however largely shown in the hydrological literature that older water tends to be rapidly and preferentially released to the stream during rain events, suggesting that “new” water inputs in a catchment tend to activate and push “older” pre-event water out of soils and groundwater reservoirs (e.g. McDonnell, 1990; Kirchner, 2003).

This mechanism can be observed in our results using isotope data. Indeed, during rain events, stream δ²H response is more dampened than the corresponding discharge response. We illustrate this effect in Fig. 11, where we highlighted three periods during the early, mid- and late melting season during which rain events occurred. In the upper plots, discharge response to rain events appears fast (within an hour) during all periods and streamflow seems only briefly influenced by rain events (during about a day). However, when looking at the stream isotopic response (green curve in the second row of plots in Fig. 11), it appears that the stream δ²H seems to be influenced by the rain (with higher δ²H value) during several days before it goes back to its pre-event composition. This is especially visible for the second half of July 2020 (Fig. 11a). This highlights the typical old-water paradox mentioned before, for which hydrograph response is swift but the water is composed of more pre-event water (Kirchner, 2003). Finally, in the lower panel of Fig. 11a, we show how our transfer model estimates the fraction of rain event water. It appears that event water is usually overestimated by our model (orange curve in lower plots of Fig. 11). When involving isotopes for calibration, PEST-HP attempts to reduce the rapid increase in stream δ²H during rain events by adapting the parameters controlling the water drainage from the hillslope. This leads to a slower velocity with more dispersion for the hillslope parameters than without calibration against isotopes (see Sect. 4.3).

Based on this example, involving isotopes for calibration clearly modifies the internal processes within the model, although the effects on stream discharge are negligible. A more robust representation of the model parameters provides better model performance during validation periods and may be useful when models are used to predict the future state of glacierized catchments (He et al., 2019; van Tiel et al., 2020a). The accurate results during the validation of the year 2021 for our data (Fig. 6b) seem to confirm this statement, although we lack a longer time series to provide a more robust statistical analysis.

Finally, although isotopes may contribute to better model parameterization, the prerequisite is that model equations allow for a correct representation of water transfer. In our case, it remains unclear if the hillslope parameters' adaptation improves the model's physical processes or if it simply corrects for a lack of adequate equations to represent the preferential release of older pre-event water.

6 Conclusions

The aim of this research was to (i) provide a framework to model the catchment-integrated snow and ice melt isotopic compositions during a whole year using a parsimonious model, (ii) assess if water stable isotopes alone can be used to estimate the shares of snow and ice melt in the streamflow at the outlet, and (iii) assess the benefits of integrating isotopes in glacio-hydrological models.

Our field data highlighted the large isotopic spatial variability in the surface snow samples, which showed no particular trend with elevation and completely different values than the snowpack at 10 to 20 cm depth. This suggests that only bulk samples of the entire snowpack should be sampled to represent the snowpack. Since isotopic data are difficult to obtain in the field and may change over time and space and since limited data were available for our case study, we proposed to estimate the catchment-wide snowmelt δ²H based on a mass balance approach coupled to a snow isotopic module based on the previous work of Ala-Aho et al. (2017a).

Seasonal measured streamflow volumes agreed well with the melt contribution estimated by the mass balance model, and discharge data were only required to calibrate an hourly water transfer module accounting for hillslope, snow and glacier routing. Modelled streamflow δ²H at the outlet agreed well with observations, suggesting that snowmelt δ²H can be relatively well modelled with our framework.

Modelled snowmelt δ²H could however only be calibrated using our glacio-hydrological model as well as stream discharge and isotopic observations to constrain the isotopic model uncertainties. Indeed, many snowpack processes are difficult to characterize and would require more research with extensive on-site field data which may be site-specific: (i) how vapour transport influences snow sublimation and deposition and how it affects isotopic fractionation and d-excess; (ii) how precipitation lapse rate amounts and δ²H evolve with elevation during different seasons and (iii) how rain on snow isotopically mixes within a ripe or cold snowpack. In addition to those uncertainties, we showed that, for highly glacierized catchments, the gradual snow δ²H enrichment during the melt season leads to a snowmelt δ²H signal close to ice melt δ²H, limiting their use to separate their respective contributions to streamflow.

The key conclusions of the paper are summarized hereafter:

• Snowmelt δ²H can be successfully modelled using our glacio-hydrological model, which relies on parsimonious field-based snow, ice and weather data only if calibration against stream δ²H and discharge can be performed (see Sect. 5.3).

• Due to snowmelt, δ²H modelling uncertainties and a similar composition to ice melt δ²H during the melt season, we do not advise the use of water isotopes in glacierized catchments when the goal is to separate snow and ice melt contributions (see Sect. 5.4).

• Water isotopes may provide useful information to inform glacio-hydrological models to better characterize and constrain water transfer of precipitation events through the catchment, which may provide more robust predictive results for discharge (see Sect. 5.5).

Appendix A: List of glacio-hydrological model parameters

Table A1 Glacio-hydrological model parameters with initial and calibrated values for 2020 and 2021.

Appendix B: Stream data

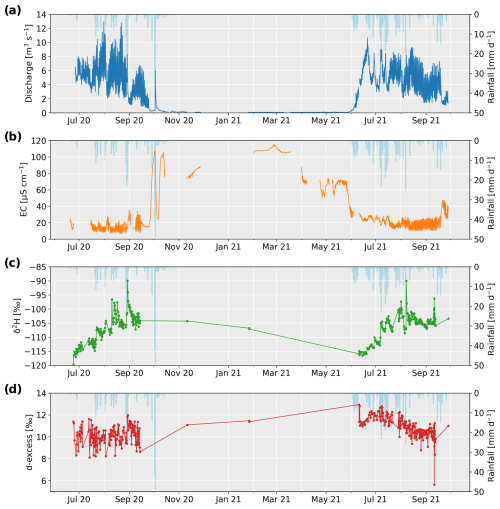
Figure B1 Measurements performed from late June 2020 to mid-September 2021 in the glacial stream directly at the glacier portal. (a) Estimated discharge data based on stream stage and a discharge rating curve. (b) Water electrical conductivity (EC). (c) Water stable isotope (δ²H) measurements with dots representing the date of the sampling (usually twice a day in summer). (d) Corresponding isotopic d-excess. The inverted blue bars show the measured daily rainfall amounts measured at the weather station.

Appendix C: Stable water isotope measurements of snow and ice over time

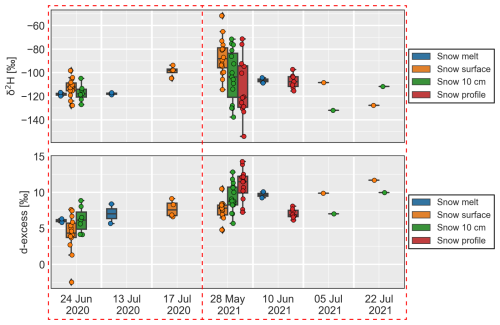
Figure C1 Temporal isotopic (δ²H) and d-excess evolution of snow samples for each sampling date. Dots show the values' distribution. The dashed red squares separate each year of data.

Figure C2 Temporal isotopic (δ²H) and d-excess evolution of ice samples for each sampling date. Dots show the values' distribution. The dashed red squares separate each year of data.

Appendix D: Calibrated snow mass balance functions

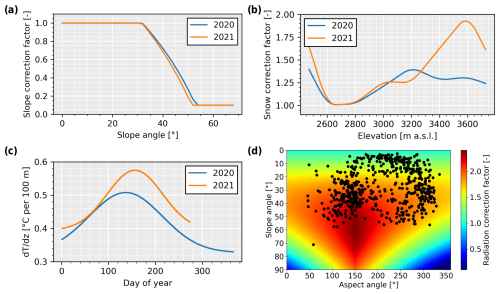
Figure D1 Results of the calibrated mass balance functions for 2020 and 2021 derived using PEST-HP. (a) Slope correction factor showing where snow reduction occurs (if the terrain slope angle is higher than θ_{redist,thresh}, with a reduction rate f_θ). (b) Corresponding snow correction function (f_redist) if slope is smaller than θ_{redist,thresh}. Snow redistribution is estimated based on a simple relationship with terrain elevation. (c) Temperature lapse rate (Δ_T) calibration for both years. (d) Radiation correction factor ($f_{\mathrm{rad},\mathrm{slope},\mathrm{tot}}-f_{\mathrm{rad},\mathrm{aspect},\mathrm{tot}}$) for 2021 based on terrain slope and aspect. Black dots correspond to all grid cells of the model discretization.

Figure D2 Measured and modelled (from rainfall, snowmelt, ice melt) discharge (Q) at the catchment outlet for the melting season in 2020 (a, c) and 2021 (b, d). Panels (c) and (d) show the comparison of the cumulative total modelled discharge versus measured discharge at the glacier portal.

Appendix E: Snow and ice mass balance maps

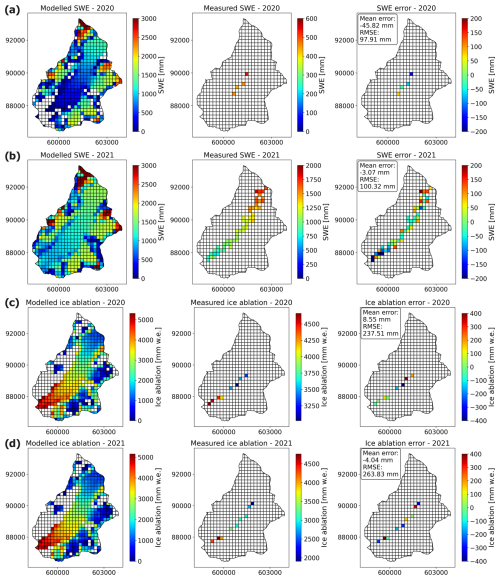
Figure E1 Modelled and measured snow accumulation for 2020 (a) and 2021 (b) and ice ablation for 2020 (c) and 2021 (d). The left subpanels show the modelled snow accumulation (SWE) or ice ablation for the corresponding year. The middle subpanels show the measured point mass balances (a, b: winter mass balance in spring; c, d: annual mass balance in late summer). The right subpanels show the difference between measured and modelled mass balance. The corresponding mean error and root mean square error for each map are also highlighted (all values in w.e.). For the modelled snow accumulation (SWE), 2020 corresponds to the measurement date of 29 June 2020 and 2021 to 28 May 2021. Ice ablation corresponds to the measured annual ablation from 1 October 2019 to 18 September 2020 for 2020 and to the measured annual ablation from 18 September 2020 to 24 September 2021 for 2021.

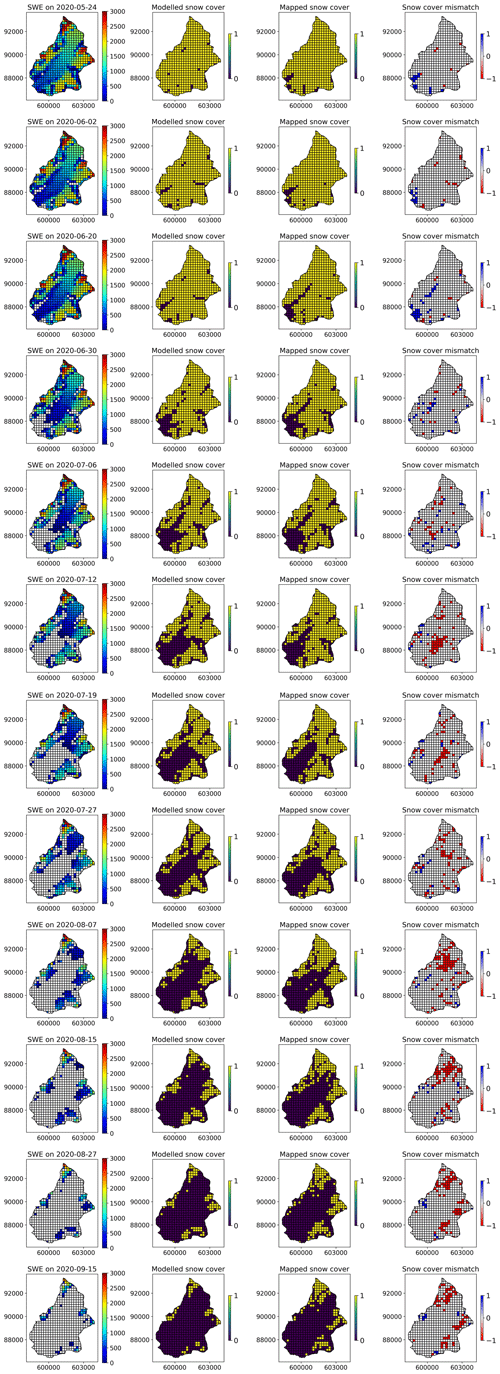
Figure E2 Modelled and mapped snow cover 2020. The left subpanels show the modelled SWE with the corresponding date. The second column shows the modelled snow presence (1) or absence (0). The third column shows the mapped snow presence (1) or absence (0) based on Planet satellite imagery. The last (right) column shows the mismatch between mapped and modelled snow presence and absence (1 for incorrect modelled snow cover presence, −1 for incorrect modelled snow cover absence). The figure lines show different dates as indicated in the left column's map titles.

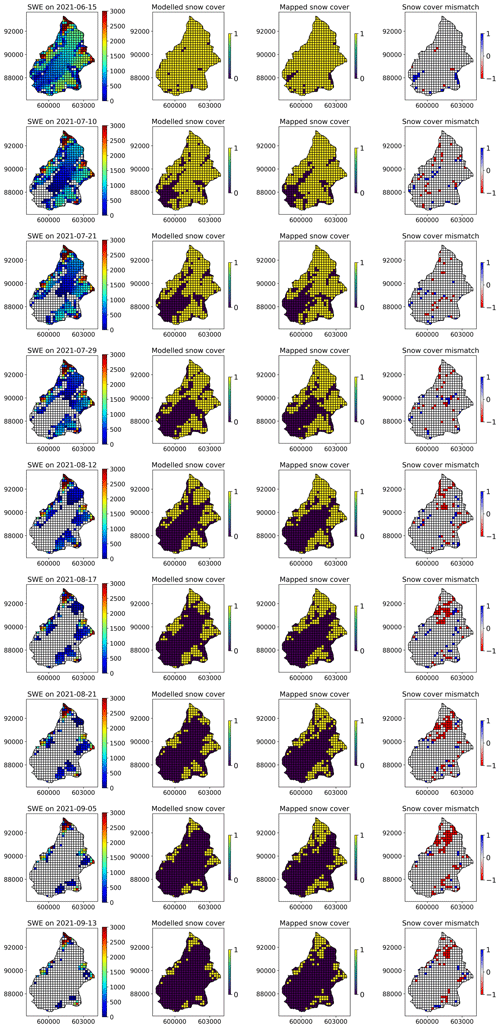
Figure E3 Modelled and mapped snow cover 2021. The left subpanels show the modelled SWE with the corresponding date. The second column shows the modelled snow presence (1) or absence (0). The third column shows the mapped snow presence (1) or absence (0) based on Planet satellite imagery. The last (right) column shows the mismatch between mapped and modelled snow presence and absence (1 for incorrect modelled snow cover presence, −1 for incorrect modelled snow cover absence). The figure lines show different dates as indicated in the left column's map titles.

Figure E4 Modelled and mapped snow cover fraction (SCF) for (a) 2020 and (b) 2021 based on mapped snow cover from Planet satellite imagery and as modelled by the mass balance model.