Bathymetry-constrained warm-mode melt estimates derived from analysing oceanic gateways in Antarctica

Melting underneath the floating ice shelves surrounding the Antarctic continent is a key process for the current and future mass loss of the Antarctic Ice Sheet. Troughs and sills on the continental shelf play a crucial role in modulating sub-shelf melt rates, as they can allow or block the access of relatively warm, modified Circumpolar Deep Water to ice-shelf cavities. Here we identify potential oceanic gateways in at least 7 out of 19 regions subdividing the Antarctic continent that could channel warm water masses to Antarctic grounding lines, based on access depths inferred from high-resolution bathymetry data. We analyse the properties of water masses that are currently present in front of the ice shelf and that might intrude into the respective ice-shelf cavities in the future in case of changes in the ocean circulation. We use the ice-shelf cavity model PICO to estimate an upper bound of melt rate changes in case offshore, intermediate-layer warm water masses gain access to the cavities. Depending on the presence of an oceanic gateway and the current ice-shelf melt conditions, we find up to 42-fold larger basal melt rates. The identification of oceanic gateways is thus valuable for assessing the potential of ice-shelf cavities to switch from a cold to a warm state, which could result in widespread ice loss from Antarctica.

1 Introduction

The current mass loss from the Antarctic Ice Sheet is mainly triggered by thinning of the surrounding ice shelves (Pritchard et al., 2012; Paolo et al., 2015; Gudmundsson et al., 2019). This is caused by ice-shelf basal melting that varies by orders of magnitude depending on the prevailing ocean conditions: a sub-shelf circulation that is initiated by sea-ice formation or tidal pumping and driven by the so-called “ice pump” (mode 1 or 3 melting in  Jacobs et al., 1992, respectively) causes melt rates on the order of centimetres to a few metres per year. For example, area-averaged observed melt rates at Filchner–Ronne Ice Shelf are around 0.3±0.1 m yr⁻¹ (Ronne) and 0.4±0.1 m yr⁻¹ (Filchner) as estimated by Rignot et al. (2013). In these ice shelves, mode 1 melting plays a major role towards the grounding line and mode 3 melting near the ice-shelf front (Silvano et al., 2016). Where melting is driven by Dense Shelf Water (DSW, mode 1) or surface waters (mode 3), generally water masses close to the surface freezing point are present within the cavity and can be hence classified as “cold” – such as for the Filchner–Ronne, Ross, or Amery ice shelves (Joughin et al., 2012; Silvano et al., 2016). DSW, due to the higher density from, for example, brine rejection from sea-ice formation, sinks to the ocean floor and spreads to the grounding line (Silvano et al., 2016). Ice-shelf thinning and upstream mass loss are currently not observed in these cold-cavity regions (Joughin et al., 2012; Paolo et al., 2015; Greene et al., 2022). A different mode of sub-shelf melting is driven by an inflow of water masses from the continental slope (mode 2 melting in Jacobs et al., 1992), bringing water with temperatures well above the pressure melting point into the ice-shelf cavity. Such cavities can be classified as “warm” (Joughin et al., 2012). They experience melt rates up to the order of tens of metres per year (cf. area-average basal melt rates for Pine Island and Thwaites in Rignot et al., 2013).

The exchange of water masses between the continental shelf and the open ocean is strongly influenced by bathymetry (Thoma et al., 2008; Nicholls et al., 2009; Hellmer et al., 2012; Pritchard et al., 2012; Tinto et al., 2019; Sun et al., 2022), but the processes that lead to on-shelf transport of warm water masses, leading to a switch to a warm cavity or mode 2 melting, are highly complex and an active field of research. To what extent the inflow of warm waters from the continental-shelf break into ice-shelf cavities can be related to anthropogenic changes (Holland et al., 2022) or natural variability (Jenkins et al., 2016, 2018) alone remains to be determined. Once, however, warmer water masses enter an ice-shelf cavity, this can lead to a strong increase in sub-shelf melt rates and can subsequently cause the adjacent ice streams to thin, accelerate, and retreat. The highest thinning rates in Antarctica are found for ice shelves in the Amundsen Sea, where relatively warm, modified Circumpolar Deep Water (mCDW) accesses the ice shelves at depth through submarine troughs (Nitsche et al., 2007; Walker et al., 2007; De Rydt et al., 2014; Mouginot et al., 2014; Jenkins et al., 2016; Millan et al., 2017; Naughten et al., 2023). This mCDW comprises relatively warm and salty water masses which reside at mid-depth, on average at around 500 m, in the Southern Ocean in front of the continental shelf (Schmidtko et al., 2014; Holland et al., 2020).

Ocean access to ice-shelf cavities is often modulated by geological structures on the continental shelf that block or channel the distal inflow of deeper and warmer water masses off the continental shelf, i.e. CDW. The abyssal Southern Ocean bathymetry rises towards the continent to form the shallow continental shelf that has a mean depth of about 500 m (Heywood et al., 2014), with the transition zone being called the continental-shelf break (CSB). The width of the continental shelf varies around Antarctica from tens of kilometres in East Antarctica or the West Antarctic Peninsula to hundreds of kilometres in the Ross or Weddell Sea (Heywood et al., 2014). While large data gaps still exist, recent Antarctic bathymetry data incorporate major glacial troughs, ridges, or other features of basal topography crosscutting the continental shelf (Arndt et al., 2013; Morlighem et al., 2020). These bathymetric features were mostly formed by erosion and sedimentation due to dynamic changes of the ice sheet during glacial cycles, e.g. ice streams leaving behind deep troughs when retreating (Bart, 2004; Hein et al., 2011; Morlighem et al., 2020).

The grounding line (or grounding zone; cf. Li et al., 2023) marks the transition between the grounded ice sheet and the floating ice shelves and thus constitutes the triple point of bedrock, ice, and ocean; see Fig. 1. Grounding lines in Antarctica can be found at depths down to 3000 m due to the erosion over long timescales. When considering the general features of sub-shelf melt patterns in each ice shelf, sub-shelf melt rates are generally higher near the grounding line and lower towards the ice shelf's calving front (Lambert et al., 2023) if mode 3 melting is absent (Silvano et al., 2016). This general pattern is modulated by exchanges of water masses within the cavity and through other dynamical processes at play (e.g. the Coriolis effect). Ice-shelf thinning caused by melting close to the grounding line has been found to have the largest impact on the adjacent ice masses, resulting in higher ice fluxes across the grounding line due to a loss in buttressing (Reese et al., 2018b; Goldberg et al., 2019).

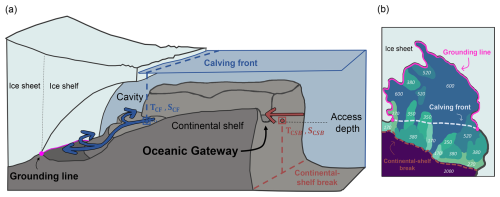
Figure 1 Illustration of used concepts in this study. (a) Schematic of stylised oceanic gateway crosscutting the continental shelf. Beyond the continental-shelf break, relatively warm Circumpolar Deep Water is present at mid-depth. Its access to ice-shelf cavities is modulated by ocean circulation and bathymetry. Ocean temperatures at the bottom topography near the calving front (T_CF) provide information about the water masses that can already access the ice-shelf cavity (in the case of mode 1 melting, blue). If an oceanic gateway is present, water masses with a mean temperature T_CSB from the continental-shelf break (at the gateway's access depth, red arrow) can potentially reach large parts of the grounding line (triple point of bedrock, ice, and ocean; magenta line) of the respective ice shelf. (b) Access depths for each part of the continental shelf are obtained via a connected-component analysis. This yields a 2D field showing at what depths the ocean floor inside the ice-shelf cavity is connected to the open ocean. Analysing the 2D field at the grounding line of the region (magenta line) provides an estimate of the potential impacts when warm water masses are redirected from the continental-shelf break to the grounding lines.

Distinct geological structures, such as troughs, are crucial boundary conditions for modelling ocean dynamics and the interaction of the ocean with the Antarctic Ice Sheet (Thoma et al., 2008; Hellmer et al., 2012). However, previous studies do not systematically investigate the bathymetric access points or pathways to the grounding lines with regards to ice-sheet modelling and focus only on specific regions (see e.g. Herraiz-Borreguero et al., 2015; Tinto et al., 2019). For instance, Hellmer et al. (2012) and Naughten et al. (2021) simulate an inflow of warm water masses through Filchner Trough which subsequently access large parts of the ice-shelf cavity of that region, leading to a drastic change in sub-shelf melt rates, i.e. a switch from a cold to a warm cavity under high-emission scenarios.

Here, we present a simple approach to analyse oceanic gateways (Fig. 1) in all Antarctic regions to the base of the Antarctic Ice Sheet – specifically to the ice sheet's grounding lines. Our study provides a sensitivity experiment, where in the case of a trough-like feature, we assume that offshore ocean water is accessing the cavity (as in the case of Filchner Trough), leading to a drastic change in sub-shelf hydrography. For this, we combine observations of bedrock topography and ocean water masses to assess present-day pre-conditions for enhanced melting in all Antarctic regions. While no dynamic changes in the ocean are taken into account, our analysis serves as a first-order assessment of an upper bound on melt rates that would be caused by an inflow of warm water masses at depth in Antarctica. Our approach of identifying relevant water masses that drive melting in cavities is also useful to improve the input for parameterisations of sub-shelf melt rates: for the ice-shelf cavity model PICO (as used in this study; see methods; Reese et al., 2018a) for instance, ocean temperature and salinity input are averaged over a certain depth to be used as input in the box model. With our analysis, we aim at better estimating this depth, by re-aligning the ocean regions over which input is averaged horizontally to include the relevant depth levels and oceanic gateways.

In this study, we aim to estimate the impact of potential future warm-water inflow on basal melting for all Antarctic regions. In order to do so, we (1) analyse the bathymetry and identify trough-like features that potentially provide access of offshore warm waters into ice-shelf cavities, (2) calculate the increase in thermal forcing resulting from such a regime shift, and (3) compute the respective increase in sub-shelf melting. First we describe our methodology in Sect. 2, which is followed by the presentation of our results in Sect. 3. In Sect. 4 we discuss our approach and findings, with a general conclusion included in Sect. 5.

2 Methodology

The goal of our approach is to quantify an upper bound to melting if cavities switch to a warm mode. To this extent, we use PISM-PICO to compute ice-shelf basal melting for given ocean temperatures and salinities: as a present-day estimate, we take temperatures at the calving front. For the warm mode, we use temperatures at mid-depth at the continental-shelf break (CSB). In order to constrain that latter depth and to estimate the potential impacts of this selection on the melting at the grounding line (accounting for bathymetric constraints), we define oceanic gateways based on access depths found in each region. In the following section, we define the concept of oceanic gateways and access depths (Sect. 2.1), describe the used ocean data (Sect. 2.2), and summarise how we compute sub-shelf melting with PICO (Sect. 2.3).

2.1 Identifying oceanic gateways from bathymetry

Our analysis is based on BedMachine v3 bathymetry (Morlighem et al., 2020; Morlighem, 2022), which is provided on a 500 × 500 m grid spacing and contains ocean bathymetry from IBCSO v2 (Dorschel et al., 2022). From this, we calculate access depths for every location on the Antarctic continental shelf and in the ice-shelf cavities. The access depth, d, for each point on the continental shelf is the deepest vertical level (largest positive depth) for which there is a horizontal connection to the open ocean not obstructed by bathymetry. We obtain these via a connected-component analysis (CCA). More specifically, we use the connected-component approach implemented by Khrulev (2024), with an algorithm similar to He et al. (2010). The algorithm iterates through the vertical column from 0 to 3500 m, spreads out in all horizontal directions, and fills connected cells with the value of the depth at which they are connected until it reaches boundaries or encounters obstacles, i.e. cells with shallower bathymetry (the criterion is whether grid points are horizontally connected to the deep ocean at 3500 m or not). We have included Fig. S1 in the Supplement to help visualise this analysis tool. As a result, our analysis yields circum-Antarctic access depths which are available as a 2D field on a 500 m × 500 m horizontal grid spacing, following the resolution of the BedMachine data (Morlighem et al., 2020; Morlighem, 2022). When newer bathymetry fields become available, this data field can be easily updated with our processing scripts. We define the deepest access depth found along the grounding line of each basin as d_GL,0 and express the fraction of how much the grounding line at that depth is connected to the open ocean with values ranging from 0 % to 100 %. If a comparably large part of the grounding line is reached by only a small increase in vertical access level, an oceanic gateway is present, i.e. a deep trough connecting the (overdeepened) ice-shelf cavity to the open ocean past the continental-shelf break. We thus interpret an oceanic gateway to be the horizontal pathway from the open ocean to the grounding line of the ice sheet along the deepest possible ocean connection between the two. For each region, we ascribe an oceanic gateway as “major” if a global maximum (highest peak) in access depth along the grounding line is found at d_GL,0. On the data grid, we define the grounding line as the contour that delineates the contiguous grounded continental ice sheet (excluding larger islands and ice rises). We analyse oceanic gateways for 19 Antarctic regions based on the drainage basins defined in Zwally et al. (2012) and extended into the ocean, with the Filchner–Ronne and Ross basins congregated as in Reese et al. (2018a); see also Sect. 2.3.

2.2 Deriving changes in ocean forcing

Based on the bathymetric information obtained in the previous step, i.e. identifying the deepest topographic features that connect the deeper open ocean and the ice-shelf cavity (assuming that water follows this pathway), we derive the associated change in oceanic forcing, which results in a hypothetical switch from cold- to warm-cavity conditions.

We analyse the properties of water masses based on the ISMIP6 ocean temperature and salinity climatology (Jourdain et al., 2020). The dataset is available at an 8 km × 8 km horizontal and 60 m vertical resolution. The data points indicate temperatures and salinities averaged over the period 1995–2017. While observational datasets have many data gaps and thus do not provide sufficient horizontal and vertical coverage (especially on the continental shelf), the ISMIP6 approach fills these gaps with a specific extrapolation technique: while accounting for topographic barriers, the temperature and salinity fields from observations are extended, i.e. flooded into the ice-shelf cavities and regions below sea level that are currently covered by grounded ice. Due to this approach and the extended spatial coverage, we consider the ISMIP6 ocean dataset to be very well suited for our study. While the basic concept is the same, the ISMIP6 code is different to our analysis (Asay-Davis et al., 2020): our approach of quantifying the connectedness of the grounded ice to the open ocean aims at identifying pathways through which already existing warm water masses could fuel high melting rather than providing an extrapolated forcing field for projections. We therefore take into account the depth of grounding lines.

We extract ocean properties near the ice shelf's calving front, along the oceanic gateways as well as along the continental-shelf break, based on the local bathymetry and the access depths at the grounding lines for each basin $b=\mathrm{1},\mathrm{2},\mathrm{\dots }\mathrm{19}$. The temperatures in front of the ice shelves (at the calving front) serve as a proxy for ocean water masses that can currently reach the ice shelves' deep grounding lines, similar to the case when mode 1 melting is dominant (cf. Silvano et al., 2016). The calving front (CF) is defined through the native BedMachine mask as the horizontal boundary between floating ice and the ocean. We calculate horizontal averages of temperature and salinity in the bottom layer, just above the bathymetry (topg), along the calving front and define T_CF,mean and S_CF,mean per basin as

$$\begin{array}{}\text{(1)}& \begin{array}{rl}{T}_{\mathrm{CF},\mathrm{mean}}\left(b\right)& =\mathrm{mean}\left\{\left.T(x,y,z)\right|(x,y)\in \mathrm{CF}\left(b\right)\right.\\ & \left.\mathrm{and}z=\mathrm{topg}(x,y)\right\}\end{array}\end{array}$$

and

$$\begin{array}{}\text{(2)}& \begin{array}{rl}{S}_{\mathrm{CF},\mathrm{mean}}\left(b\right)& =\mathrm{mean}\left\{\left.S(x,y,z)\right|(x,y)\in \mathrm{CF}\left(b\right)\right.\\ & \left.\mathrm{and}z=\mathrm{topg}(x,y)\right\}.\end{array}\end{array}$$

For estimating the change in melt rates, when assuming a basin-wide transition into a melt regime where melting becomes dominated by relatively warm CDW (mode 2 in Silvano et al., 2016), we derive properties along the CSB at the deepest grounding line access depth for each basin and compare it to the estimates from the calving front, our proxies for mode 1 melting. We define the CSB to lie in an around 40 km wide perimeter along the horizontal coordinates where the bathymetry is at a depth of 1800 m (i.e. a band of five grid cells along the 1800 m isobath). We assume that once warm water is flowing onto the continent, it will eventually reach the grounding line, as CDW is not only warmer, but also saltier and therefore denser than on-shelf waters. We thus expect it to sink from the shallowest overflow point eventually towards the grounding lines, filling up the cavity basin and replacing the less dense waters at lower depths.

We define the average temperature and salinity along this transect as T_CSB,mean and S_CSB,mean, respectively, as

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{T}_{\mathrm{CSB},\mathrm{mean}}\left(b\right)& =\mathrm{mean}\left\{\left.T(x,y,z)\right|(x,y)\in \mathrm{CSB}\left(b\right)\right.\\ & \left.\mathrm{and}z=d_{\mathrm{GL},\mathrm{0}}\left(b\right)\right\}\end{array}\end{array}$$

and

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{S}_{\mathrm{CSB},\mathrm{mean}}\left(b\right)& =\mathrm{mean}\left\{\left.S(x,y,z)\right|(x,y)\in \mathrm{CSB}\left(b\right)\right.\\ & \left.\mathrm{and}z=d_{\mathrm{GL},\mathrm{0}}\left(b\right)\right\}.\end{array}\end{array}$$

Following the approach, to estimate an upper bound to melt rate changes, we will also use the maximum temperature found along the continental-shelf break to estimate melt rates, which we call T_CSB,max and define as

$$\begin{array}{}\text{(5)}& \begin{array}{rl}{T}_{\mathrm{CSB},\max }\left(b\right)& =\max \left\{\left.T(x,y,z)\right|(x,y)\in \mathrm{CSB}\left(b\right)\right.\\ & \left.\mathrm{and}z=d_{\mathrm{GL},\mathrm{0}}\left(b\right)\right\}.\end{array}\end{array}$$

We will compare these estimates to the mean but also the maximum temperatures found along the calving front T_CF,max,

$$\begin{array}{}\text{(6)}& T_{\mathrm{CF},\max }\left(b\right)=\max \left\{\left.T(x,y,z)\right|(x,y)\in \mathrm{CF}\left(b\right)\mathrm{and}z=\mathrm{topg}(x,y)\right\}.\end{array}$$

To find the highest potential of temperature change, we therefore arrive at three ΔT estimates:

$$\begin{array}{}\text{(7)}& {\displaystyle }\mathrm{\Delta }{T}_{\mathrm{mean}-\mathrm{mean}}\left(b\right)=T_{\mathrm{CSB},\mathrm{mean}}\left(b\right)-T_{\mathrm{CF},\mathrm{mean}}\left(b\right),\text{(8)}& {\displaystyle }\mathrm{\Delta }{T}_{\max -\mathrm{mean}}\left(b\right)=T_{\mathrm{CSB},\max }\left(b\right)-T_{\mathrm{CF},\mathrm{mean}}\left(b\right),\end{array}$$

and

$$\begin{array}{}\text{(9)}& \mathrm{\Delta }{T}_{\max -\max }\left(b\right)=T_{\mathrm{CSB},\max }\left(b\right)-T_{\mathrm{CF},\max }\left(b\right).\end{array}$$

The latter allows us to quantify the change in melting also in those regions, where melting is already driven by relatively warm water masses at depth, i.e. where T_CF is already warm. Using the minimum temperature found along the calving front, T_CF,min(b), and comparing it with the maximum temperature along the continental-shelf break, T_CSB,max(b), would yield the highest temperature difference which would follow our narrative of deriving an upper bound on sub-shelf melting. What is important to note here, however, is that the CF and CSB values are defined differently: CF is averaged over the deepest depth levels along the calving front; i.e. the minimum value will most likely be derived from comparably shallow regions, where waters do not influence melting near the grounding line (Silvano et al., 2016). We therefore do not use T_CF,min in our analysis.

2.3 Upper bounds of sub-shelf melting computed with the ice-shelf cavity model PICO

We compute the change in sub-shelf melt rates with the Potsdam Ice shelf Cavity mOdel (PICO, Reese et al., 2018a). PICO extends the ocean box model by Olbers and Hellmer (2010) to be applicable in 3D ice-sheet models. It mimics the vertical overturning circulation present in ice-shelf cavities and can reproduce the wide range of average observed melt rates for warm and cold cavities. Ocean input is considered in PICO as an average per basin, and once water masses reach the grounding line, they rise along the ice-shelf base towards the calving front, driven by the ice pump (Lewis and Perkin, 1986).

In Reese et al. (2023), PICO model parameters C (in Sv m³ kg⁻¹) that describe the strength of the vertical overturning circulation and the heat-exchange coefficient ${\mathit{\gamma }}_T^{*}$ (given in 10⁻⁵ m s⁻¹) are tuned to capture the sensitivity of melt rates to ocean temperature changes (cf. Reese et al., 2023). Input (T,S) to PICO in Reese et al. (2023) is based on temperature and salinity observations compiled by Schmidtko et al. (2014). In the tuning process, temperatures on the continental shelf were corrected for, similarly to the approach by Jourdain et al. (2020), such that the melt rates calculated by PICO match present-day observations compiled by Adusumilli et al. (2020a). We here calculate melting resulting from a sudden warming of the cavities to the temperatures from the continental-shelf break by applying the differences ΔT_mean−mean, ΔT_max−mean, and ΔT_max−max as anomalies to the temperature fields from Reese et al. (2023).

To capture the parameter uncertainty in our estimates, we use the “best” and “max” parameter combinations from Reese et al. (2023): {C= 2.0 Sv m³ kg${}^{-\mathrm{1}},{\mathit{\gamma }}_T^{*}=\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$m s⁻¹} and {C= 3.0 Sv m³ kg${}^{-\mathrm{1}},{\mathit{\gamma }}_T^{*}=\mathrm{7}\times {\mathrm{10}}^{-\mathrm{5}}$m s⁻¹}, respectively. The maximum number of boxes (N = 5) are used as in Reese et al. (2023). We use the PICO implementation in the Parallel Ice Sheet Model (PISM; https://www.pism.io; Bueler and Brown, 2009; Winkelmann et al., 2011), and as initial conditions we use ice thickness and bed topography from the BedMachine v3 dataset on a 4 km × 4 km grid spacing. We consider this resolution for estimating basal melt rates a good compromise between having a high resolution at the grounding line, on the one hand, and computational feasibility on the other hand.

As our connected-component analysis yields a 2D field of access depths that identifies which parts of the continental shelf are topographically connected to the individual ice-shelf regions (i.e. on the same access depth), we use it to first correct for the existing basin boundaries by which the continental shelf is subdivided in the PICO model. The boundaries on land are based on ice drainage basins from Zwally et al. (2012), were consolidated to 19 regions in Reese et al. (2018a), and for the use for PICO mainly extended along meridians into the ocean. In previous studies (Reese et al., 2018a, 2023; Sutter et al., 2023; Wirths et al., 2024), those basin boundaries in the ocean were used to extract a basin average for temperature and salinity (i.e. average over the region) to feed into the box model. Figure 2 shows the new basin boundaries that we will use throughout this study. We have changed the basin boundaries near the Filchner–Ronne and Amery ice shelves, inside the Amundsen Sea region, and near George VI Ice Shelf in the Bellingshausen Sea based on the region's access depths. For this, we have extended their region's boundaries (by overlaying the access-depth field with the bathymetry) to incorporate the detected pathways through which warm water masses could gain access to the ice-shelf cavities. We have also aligned the basin boundary at the north tip of the Antarctic Peninsula with the local bathymetry of the continental shelf. From here on forward, we use these updated basin boundaries (a first result of our analysis) and encourage other PICO users to do the same. We provide the new basin mask as a NetCDF file as well as the corresponding script to create those boundaries in our data repository.

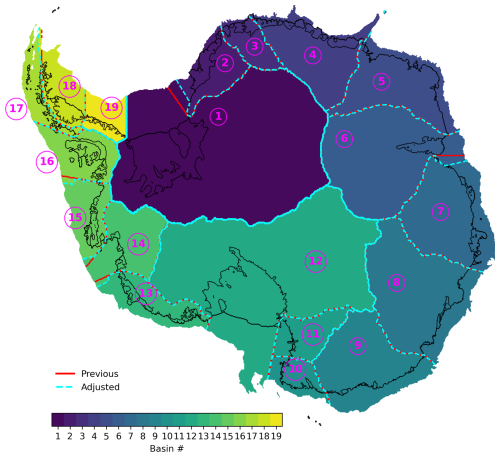
Figure 2 PICO model basin boundaries. The inland boundaries are based on satellite-derived drainage basins from Zwally et al. (2012) and were consolidated to 19 regions in Reese et al. (2018a). For the purpose of PICO, the basin boundaries were mostly extended along meridians into the ocean (red), which we have now partly adjusted (cyan) based on the derived access depths.

3 Results

In the following, we include, firstly, the main results from our access-depth analysis that helps identify oceanic gateways around Antarctica (Sect. 3.1) and, secondly, discuss the warm-mode melt estimates for those regions that we find feature such gateways to the ice sheet's grounding line (Sect. 3.2). We then compare the derived temperature changes and subsequent melt estimates for all Antarctic regions in Sect. 3.3.

3.1 Major oceanic gateways in 7 out of 19 PICO regions

Figure 3 shows the main differences between the computed access-depth field and the bathymetry taken from BedMachine v3 Antarctica (Morlighem et al., 2020). This comparison highlights which parts of the continental shelf (and ice-shelf cavities) are shielded by topographic barriers, potentially blocking the access of warm water masses from the open ocean at depth. The most pronounced differences are found underneath Amery Ice Shelf, where the differences between the two fields can be larger than 1000 m. At Amery, around 91 % of the ice-shelf cavity is shielded by shallower bathymetry; i.e. the access depth is shallower than the topography in 91 % of the cavity area. In contrast, this applies only to about a third of the cavity area for basins 7 or 17. We later see that this can be linked to the absence of any oceanic gateway structure in those regions.

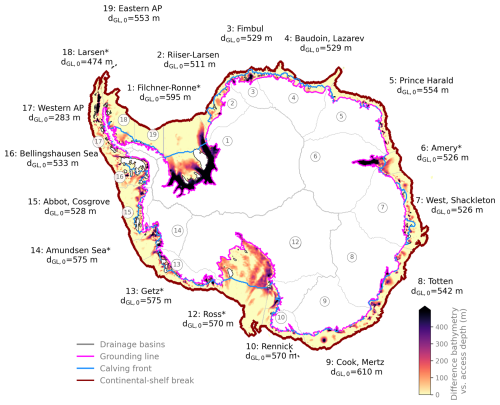
Figure 3 Grounding line access depths and regions of the Antarctic continental shelf shielded by topographic features. Colour shading indicates the difference between the computed access depth over the continental shelf and in the ice-shelf cavities, compared to BedMachine v3 Antarctica bathymetry data (Morlighem et al., 2020). Evaluating the access depths found at each region's grounding line d_GL reveals major oceanic gateways in 7 out of 19 PICO regions, labelled with an asterisk (^*). There, the deepest access depth found at the grounding line, d_GL,0, is most representative of the entire basin, as it represents the largest share of the grounding line. The drainage basins (grey outlines) are based on Zwally et al. (2012), consolidated as in Reese et al. (2018a), and labelled according to prominent ice shelves (with AP being Antarctic Peninsula). Coloured contour lines show the ice sheet's grounding line (magenta), the calving front (blue), and the continental-shelf break (red). For the 2D field of computed access depths, see Fig. S2.

The access depths evaluated at Antarctic grounding lines (d_GL,0) are also included in Fig. 3. The deepest access depth, at which each of the 19 regions is unobstructedly connected to the open ocean, ranges from 283 to 610 m, a similar depth at which warm CDW resides off the continental shelf. We find the deepest ocean access at the Cook and Mertz ice shelves (basin 9) at 610 m, followed by 595 m at Filchner–Ronne (basin 1), and then shallowest ocean access at 283 m at the Western Antarctic Peninsula (basin 17). The 2D field of access depths for all locations on the Antarctic continental shelf and its ice-shelf cavities is provided in Fig. S2.

The distributions of the 2D access-depth field evaluated at the respective grounding lines, d_GL,0, are shown in Fig. 4. We find an oceanic-gateway-like access to the ice sheet's grounding line in 7 out of 19 PICO regions (cf. the first spike in the distribution shown in Fig. 4): Filchner–Ronne (basin 1), Amery (basin 6), Ross (basin 12), the Amundsen Sea region (basin 14), Drygalski (basin 11), Larsen (basin 18), and Getz (basin 13). Our analysis shows that Filchner Trough in basin 1 is the most prominent, or major, oceanic gateway found in the 19 regions. It connects around 81 % of its region's grounding line to the open ocean at an access depth of 595 m. At Amery (basin 6), we find a gateway connecting around 67 % of the region's grounding line to the open ocean at a depth of d_GL,0 = 526 m. At Ross (basin 12) it is around 33 % of the region's grounding line at a depth of 570 m, and in the Amundsen Sea region it is around 31 % at a depth of 575 m. Filchner–Ronne, Ross, and Amery are the regions where not only the grounding lines, but, together with Fimbul (basin 3) and Totten (basin 8), also the cavities are most shielded by shallower bathymetry (Fig. 3). In Sect. 3.2, we give more context and details about which troughs constitute those oceanic gateways in the first four mentioned basins (Filchner-Ronne, Amery, Ross, and the Amundsen Sea region). The access-depths distributions shown in Fig. 4 also highlight those regions, where more than one gateway is present in the region. We find two or more spikes (or local maxima) in the access-depth distribution that can be matched to the access to individual ice shelves comprised in this region: in the Getz region (basin 13), 10 % of the grounding line of the entire PICO region is accessed at Getz Ice Shelf at $d_{\mathrm{GL},\mathrm{0}}=$ 575 m. However, at an access depth of d_GL= 489 m, the cavity of Sulzberger Ice Shelf (in basin 13; for location see e.g.  Davison et al., 2023), which constitutes 8 % of the total region's grounding line, can be, in theory, horizontally accessed by open-ocean water masses. We find multiple gateways also in PICO basin 3 that not only comprise Fimbul Ice Shelf ($d_{\mathrm{GL},\mathrm{0}}=$ 529 m), but also Jelbart Ice Shelf (where 18 % of the grounding line is accessed at d_GL= 427 m) and Ekström Ice Shelf (where 19 % is accessed at an access depth of d_GL= 391 m). We see the same feature in PICO basin 2, comprising the Riiser-Larsen Ice Shelf but also Brunt Stancomb Ice Shelf; in basin 10, which holds Rennick and the smaller Lillie Ice Shelf; and in basin 8, in which the two spikes in the access-depth distribution can be matched to the individual access to the Totten and Moscow ice shelves, respectively. PICO basin 4 also shows a notable difference in access to Roi Boudain Ice Shelf (12 %) compared to Nivi Ice Shelf (11 %). In PICO basins 5 (Prince Harald), 19 (Eastern AP), 9 (Cook, Mertz), 15 (Abbot, Cosgrove), 16 (Bellingshausen Sea), 7 (West, Shackleton), and 17 (Western AP), we do not find a significant spike in the access-depth distribution along the grounding line and hence conclude that no (seen from an Antarctic-wide scale) oceanic gateway is present. This is despite the fact that parts of the respective cavities are shielded by shallower bathymetry (in all regions at least a third of the cavity is shielded). Note that the existence of an oceanic gateway does not influence the melt rates calculated with PICO in Sect. 3.3, as we use d_GL,0 for all regions. However, it allows us to gauge the validity and limitations of our assumptions in each basin.

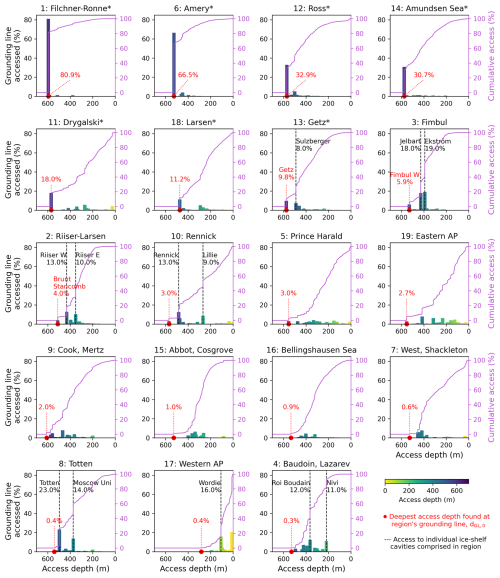
Figure 4 Distribution of access depths at the region's grounding lines. For each depth level, it is shown how much of the region's grounding line is accessed (fraction given in percent, bin width = 30 m). The magenta line shows the cumulative access when adding up all depths levels. The different regions are labelled according to prominent ice shelves (with AP being Antarctic Peninsula) and sorted by d_GL,0, i.e. how much of the region's grounding line is horizontally connected to the open ocean at the deepest access depth found. Where a spike in the distribution can be linked to an individual (smaller) ice shelf comprised in the larger region, the specific access depth is labelled accordingly. The regions follow the drainage basins based on Zwally et al. (2012), consolidated as in Reese et al. (2018a) and adjusted based on our access-depth analysis (but only in the ocean; see above).

3.2 Potential sub-shelf melt changes in oceanic gateways regions

In the following, we further analyse our results for the Filchner–Ronne Ice Shelf, Amery Ice Shelf, and Ross Ice Shelf as well as for the ice shelves in the Amundsen Sea for which we identified major gateways. For the case in which a region comprises two or more ice shelves, we exemplarily present results from the Totten region hereinafter.

3.2.1 Filchner–Ronne Ice Shelf

The Filchner–Ronne basin features an oceanic gateway at d_GL,0 = 595 m, through which 81 % of the grounding line is horizontally connected to the open ocean. The identified oceanic gateway is Filchner Trough, which is a characteristic feature of the submarine topography in the Filchner–Ronne Ice Shelf region; see also Fig. 5. The trough extends from around Foundation Ice Stream to more than 450 km into the Southern Weddell Sea (distance measured from the ice-shelf front and taken from Larter et al., 2012). Its width varies between 125 and 175 km (Larter et al., 2012), and it terminates with a sill on its end towards the Weddell Sea (Hellmer et al., 2012). The sill depth determines the region's access depth in our study. As the mean depth of the basin's grounding lines is around 1000 m, water flowing in at the access depth of 595 m could reach much of the region's grounding zone at once. The deepest grounding lines are found down to around 2000 m in the BedMachine dataset (see Fig. 5b).

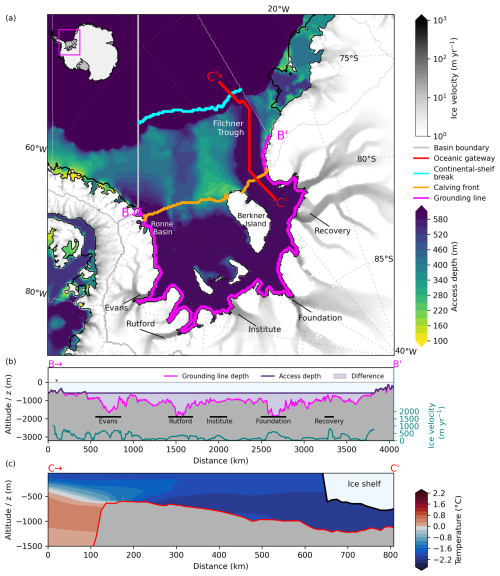
Figure 5 Access depths and temperature profile at Filchner–Ronne Ice Shelf. (a) Access depths within the Weddell Sea indicate a prominent oceanic gateway along Filchner Trough towards Filchner–Ronne Ice Shelf. The transects denote vertical profiles along (b) the grounding line and (c) the oceanic gateway through Filchner Trough showing the potential temperature profile along the transect. Speed of grounded ice shown as grey shading (in panel a) and as a blue-green line (in panel b) indicating the location of major ice streams and taken from Mouginot et al. (2019). The magenta line (in panel b) indicates grounding line depth, while the dark purple line (in panel b) shows the derived access depth (e.g. d_GL,0 = 595 m throughout most of the cavity).

At present, Filchner–Ronne Ice Shelf has a relatively cold cavity, with observed melt rates of around 0.1 to 0.32±0.1 m yr⁻¹ (Adusumilli et al., 2020a; Rignot et al., 2013). It currently contributes 10 % of the total ice-shelf mass loss around Antarctica (Mueller et al., 2018). In our analysis, water masses along the Filchner–Ronne calving front are close to the pressure melting point (with $T_{\mathrm{CF},\mathrm{mean}}=-\mathrm{1.92}$ °C at the ocean floor; cf. Fig. 5c). A slope front in front of the ridge in Filchner Trough (Fig. 5c) currently blocks warmer water masses that are present along the continental-shelf break (0.31 °C in the mean or 0.53 °C at maximum) from entering the cavity. If these were to enter the cavity, Filchner–Ronne would transition from a cold to a warm cavity, as also modelling studies suggest (Hellmer et al., 2012, 2017). At present, high-salinity shelf water (HSSW) is flowing into the ice-shelf cavity from the Ronne basin, while ice-shelf water (ISW) mainly flows outward through Filchner Trough (Nicholls et al., 2009; Naughten et al., 2021; Darelius et al., 2023). In our analysis, we also find colder HSSW residing in front of the sill of Filchner Trough on top of warmer water masses at depth; see Fig. 5c.

The temperatures along the calving front do not have a wide spread, so that the derived temperature differences for a potential warm-mode onset lie close together ($\mathrm{\Delta }{T}_{\mathrm{mean}-\mathrm{mean}}=$ 2.2 °C, $\mathrm{\Delta }{T}_{\max -\max }=$ 2.3 °C, and $\mathrm{\Delta }{T}_{\max -\mathrm{mean}}=$ 2.5 °C). When assuming that warm water masses from the continental-shelf break reach all the way into the cavity, we estimate basal mass fluxes to be 2 orders of magnitude higher and increases from 73.9–78.2 Gt yr⁻¹ (or 0.2 m yr⁻¹; see Reese et al., 2023) to 1466–2050 Gt yr⁻¹ (or 3.8–5.3 m yr⁻¹) using the difference in average temperatures, ΔT_mean−mean, depending on the used PICO parameter combination. The heightened melt rates roughly correspond to the warm melt mode found at present at Getz Ice Shelf (see Fig. S6;  Reese et al., 2018a; Adusumilli et al., 2020a).

Using the difference in maximum temperatures along the calving front and continental-shelf break, ΔT_max−max, and the max PICO parameter combination results in a basal mass flux of 2112 Gt yr⁻¹. The upper-bound estimate using ΔT_max−mean, i.e. the largest difference and the max PICO parameter combination, yields 2367 Gt yr⁻¹, which signifies a 30-fold increase (with melt rates as high as 6.1 m yr⁻¹).

Hellmer et al. (2012) find that a redirection of the slope current through Filchner Trough could occur within the 21st century under high greenhouse gas emissions and find a heightened basal mass flux of around 1600 Gt yr⁻¹ on average, which is on the lower end of our estimate. Naughten et al. (2021) find a two-timescale response of the Filchner–Ronne Ice Shelf under climate change, where warm water begins to intrude into the cavity only at approximately 7 °C warming above pre-industrial levels. In an abrupt 4×CO₂ scenario, due to the inflow of warm water masses, cavity temperatures are 2.7 °C warmer, resulting in melt rates that are 21× higher than the control, > 1400 Gt yr⁻¹. While our temperature differences of 2.2–2.5 °C are slightly lower (we also do not consider a warming scenario here), we conclude that our obtained basal melt estimates are very close to the published literature. As for the drivers for such a regime shift, Haid et al. (2023) find that the density balance between the shelf waters originating from sea-ice production and the warmer water at the continental-shelf break is the most decisive factor for the Filchner–Ronne Ice Shelf cavity to tip into a warm state.

3.2.2 Amery Ice Shelf

Towards Amery Ice Shelf, we identify a gateway through Prydz Channel (see Fig. 6), along which the Amery grounding zone has retreated since the Last Glacial Maximum (Mackintosh et al., 2014). Similar to Filchner Trough, Prydz Channel is an example that shows that gateway-like features can often be linked to glacial erosion. The grounding line of Amery Ice Shelf lies very deep, at a mean depth of around 1100 m in the BedMachine dataset, while the deepest parts of the grounding line are found at 2950 m depth (see Fig. 6b). Once water flows onto the continental shelf at a depth of d_GL,0 = 525 m, it could potentially reach large parts of the basin's grounding line (> 60 % in our analysis).

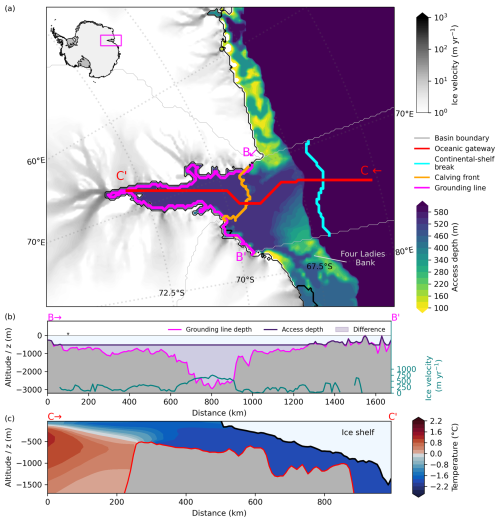
Figure 6 Access depths and temperature profile for Amery Ice Shelf. (a) Computed access depths at Amery Ice Shelf indicate a prominent oceanic gateway along Prydz Channel. The transects denote vertical profiles along (b) the grounding line and (c) the oceanic gateway through Prydz Channel showing the potential temperature profile along the transect. Speed of grounded ice shown as grey shading (in panel a) and as a blue-green line (in panel b) indicating the location of major ice streams and taken from Mouginot et al. (2019). The magenta line (in panel b) indicates grounding line depth, while the dark purple line shows the derived access depth (e.g. d_GL,0 = 525 m throughout most of the cavity).

The temperatures at the ocean floor near the calving front are −1.84 °C on average. At the continental-shelf break, the mean temperature is 0.35 °C, but temperatures are up to 0.60 °C at maximum. When it comes to average melt rates, Rignot et al. (2013) list observed melt rates at Amery Ice Shelf as 0.6±0.4 m yr⁻¹ and Adusumilli et al. (2020a) as around 0.7 m yr⁻¹, which are both similar to 0.6 m yr⁻¹ in Reese et al. (2023). In our study, melt rates would increase to 15.4–21.4 m yr⁻¹ (depending on the PICO parameter combination) when applying the temperature anomaly of 2.2 °C (ΔT_mean−mean). Our upper-bound estimate for Amery Ice Shelf using ΔT_max−mean= 2.4 °C and the max PICO parameter combination yields basal melt rates of 24.9 m yr⁻¹ (or 1339 Gt yr⁻¹), which would result in a 42-fold increase in melting.

Whether warm CDW residing at the continental-shelf break will actually pass through the identified gateway remains uncertain. Williams et al. (2016) find a different pathway of modified Circumpolar Deep Water towards Amery Ice Shelf through Four Ladies Bank more to the east (see Fig. 6a), which is much shallower than Prydz Channel. Here our core assumption that CDW always takes the deepest entry/gateway towards the ice shelf is challenged. Our quantitative estimates, however, fit to a recent preprint, in which Jin et al. (2024), using a regional ocean model, show that melt rates could reach up to 17 m yr⁻¹ given a regime shift in the next century under a high-emission scenario. Amery Ice Shelf is located downstream of Lambert Glacier, which is draining about 16 % of the grounded East Antarctic Ice Sheet (Fricker et al., 2000). Enhanced melting due to warm-water inflow at depth could hence produce an increase in sea-level contribution from large portions of the East Antarctic Ice Sheet.

3.2.3 Ross Ice Shelf

For the majority of the Ross Ice Shelf cavity, we identify the Glomar Challenger Basin (see also Fig. 7) as the topographic feature which provides access at a depth of d_GL,0 = 570 m. The basin is a north-east-trending cross-shelf paleo-trough (Owolana, 2011). We determine its lower-lying western sub-basin as an important gateway that provides access to around 33 % of the basin's grounding line. At d_GL,0 = 570 m, the grounding lines of the Mac Ayeal, Bindschadler, and Mercer/Willans ice streams (western side) are reached as well as the grounding line of Byrd Glacier on the eastern side of Ross Ice Shelf. The mean depth of the basin's grounding lines is rather shallow at around 575 m but can reach around 1000 m in the BedMachine dataset (see Fig. 7b). These deep-lying grounding lines are accessed at d_GL,0, but as visualised in Fig. 3 the cavity is less overdeepened as a whole than those at Amery and Filchner–Ronne.

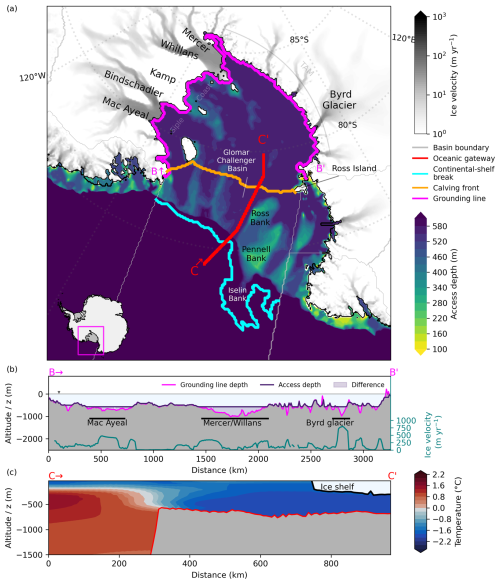
Figure 7 Access depths and temperature profile for Ross Ice Shelf. (a) Computed access depths in the Ross Sea indicate a prominent oceanic gateway through Glomar Challenger Basin towards Ross Ice Shelf. The transects denote vertical profiles along (b) the grounding line and (c) the oceanic gateway through Glomar Challenger Basin showing the potential temperature profile along the transect. Speed of grounded ice shown as grey shading (in panel a) and as a blue-green line (in panel b) indicating the location of major ice streams and taken from Mouginot et al. (2019). The magenta line (in panel b) indicates grounding line depth, while the dark purple line shows the derived access depth. TAM represents the Transantarctic Mountains.

Similar to Filchner–Ronne Ice Shelf, cold water masses are found along the ice-shelf front (Fig. 7c), with warmer water masses beyond the continental slope front. The derived temperatures are in the mean at $T_{\mathrm{CF},\mathrm{mean}}=-\mathrm{1.9}$ °C near the calving front and $T_{\mathrm{CSB},\mathrm{mean}}=\mathrm{1.1}$ °C in the mean at the continental-shelf break, with temperatures of up to $T_{\mathrm{CSB},\max }=$ 1.4 °C. Observed melt rates lie at 0.0±0.1 for the western and at 0.3±0.1 m yr⁻¹ for the eastern part of the ice shelf (Rignot et al., 2013). In Adusumilli et al. (2020a) they are around 0.1 m yr⁻¹. The Ross basin can hence be considered a cold cavity, like Filchner–Ronne Ice Shelf. Present-day melt rates from Reese et al. (2023) lie at 0.3 m yr⁻¹. In our analysis, melt rates would increase to 5.7–7.8 m yr⁻¹, assuming a transition to mode 2 melting by around 3.0 °C warmer water entering the cavity ($\mathrm{\Delta }{T}_{\mathrm{mean}-\mathrm{mean}}=$ 3.0 °C). Using $\mathrm{\Delta }{T}_{\max -\mathrm{mean}}=$ 3.3 °C, i.e. the largest temperature difference we consider for this basin, the heightened bass mass flux corresponds to a roughly 29-fold increase in basal mass flux from around 132 to 3815 Gt yr⁻¹.

Tinto et al. (2019) find that high-salinity shelf water flows under the ice front near Ross Island to the east, then moves southward towards the East Antarctic side of the ice shelf, and eventually exits through Glomar Challenger Trough to the Ross Sea. They highlight that the tectonic boundary between the East and West Antarctic side of Ross Ice Shelf impacts the vulnerability to sub-shelf melting, since the part of the cavity near Siple Coast is rather isolated from the influence of inflowing (warm) water masses. Here we assume, however, an inflow of warm water masses through Glomar Challenger Basin reaching those ice streams, given an access of water masses at d_GL,0 = 570 m. The rest of the cavity near Siple Coast shows generally more shallow access depths in our analysis, which can be linked to the tectonic boundary and the difference in the crustal composition that influences the bathymetry (Tinto et al., 2019).

3.2.4 Ice shelves in the Amundsen Sea

At present, ice shelves in the Amundsen Sea have warm cavities and therefore dominate the current mass loss in Antarctica (see e.g. Pritchard et al., 2012), indicating that this region is already out of balance with the current oceanic forcing. Here, comparably warm water masses have already found their way underneath the ice shelves, in contrast to the three ice-shelf regions detailed before.

When examining the bathymetry in the region, we find the most direct, i.e. horizontally closest, connection from the grounding lines to the open ocean to be Abbot Cosgrove Trough, an around 760 m deep feature that evolved through erosion along a paleo-ice stream across the continental shelf (Hochmuth and Gohl, 2013; Klages et al., 2015). Abbot Cosgrove Trough feeds into Pine Island–Thwaites Trough, close to the “Eastern Trough” as often referred to in the literature (see e.g. Dutrieux et al., 2014). However, the deepest access depth found at the grounding line in this basin is dominated by the access through Dotson–Getz Trough (at 575 m), which enables a potential pathway for water masses from Getz Ice Shelf (accessed via the western Getz/Siple Trough from the open ocean; see Fig. 8) through the Dotson and Crosson ice shelves, eventually reaching Thwaites and Pine Island in our analysis. The mean depth of this basin's grounding line is at around 680 m, but the deepest parts lie at > 1500 m and are reached by the access depth, $d_{\mathrm{GL},\mathrm{0}}=$ 575 m. The ocean dataset we used shows warm water masses along the entire transect from the deep ocean up to the ice-shelf front (Fig. 8c).

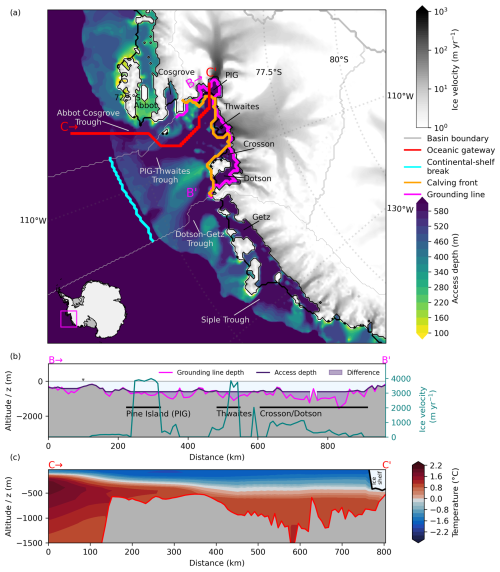
Figure 8 Access depths and temperature profile in the Amundsen Sea region. (a) Computed access depths in the Amundsen Sea indicate a prominent oceanic gateway through Abbot Cosgrove Trough towards Pine Island and Thwaites glaciers. The transects denote vertical profiles along (b) the grounding line and (c) the pathways from the open ocean to the floating extension of Pine Island Glacier showing the potential temperature profile along the transect. Speed of grounded ice shown as grey shading (in panel a) and as a blue-green line (in panel b) indicating the location of major ice streams and taken from Mouginot et al. (2019). The magenta line (in panel b) indicates grounding line depth, while the dark purple line (in panel b) shows the derived access depth (e.g. d_GL,0 = 575 m).

Following the analysis steps similar to the other regions, we derive a mean temperature of $T_{\mathrm{CF},\mathrm{mean}}=-\mathrm{0.23}$ °C near the calving fronts of this region. This is considerably cooler than the near-bottom temperature presented in Dutrieux et al. (2014), namely 1.2 °C in 2012 at the Pine Island Glacier calving front. The latter average is much closer to our workflow-generated T_CSB estimates for that region, T_CSB,mean = 1.42 °C and T_CSB,max = 1.54 °C. In Fig. 10, we show the large spread in temperatures along the calving front in this basin. The highest temperatures along the calving front are found near Pine Island Glacier, with a maximum temperature of $T_{\mathrm{CF},\max }=\mathrm{1.17}$ °C. In contrast, the mean temperature of −0.23 °C is influenced by much colder bottom temperatures found at Crosson Ice Shelf (−1.2 °C; cf. Fig. S7). Considering that warm waters are already present within most of the Amundsen Sea's ice-shelf cavities, T_CF,mean can thus be considered an unrepresentative metric for deriving bathymetry-constrained warm-mode melt estimates in this region. For this region, we thus use the difference of T_CF,max to T_CSB,max, $\mathrm{\Delta }{T}_{\max -\max }=$ 0.4 °C, to derive an upper-bound melt estimate, i.e. assuming an inflow of more, unmodified, CDW to all grounding line parts of the region. See Fig. 10 for the other temperature differences, ΔT_mean−mean and ΔT_max−mean, to compare.

Pine Island Glacier with observed melt rates of 16.2±1.0 m yr⁻¹ and Thwaites Glacier with 17.73±1.90 m yr⁻¹ (Rignot et al., 2013), respectively, have been considered to belong to one basin in our analysis. In Adusumilli et al. (2020a), the melt rates are stated to be around 9.1 m yr⁻¹ for that basin, while melt rates of 14.4–14.5 m yr⁻¹ result from the parameter tuning in Reese et al. (2023). Using ΔT_max−max, sub-shelf melting in the Amundsen Sea could increase to 19.9–21.7m yr⁻¹ or up to 314 Gt yr⁻¹ (1.5-fold increase from around 210 to 314 Gt yr⁻¹ at present). In our study, this change is the second lowest; the neighbouring Getz Ice Shelf region (basin 13) experiences almost no change in melting ($\mathrm{\Delta }{T}_{\max -\max }=$ 0.001 °C). Since the cavities at Amundsen are already in a warm state, it is unsurprising that our analysis shows only a little increase in melting.

How do these findings compare to the published literature? Thoma et al. (2008) simulate an inflow of CDW onto the Amundsen shelf and find that the warm water reaching Pine Island Bay is guided trough a submarine trough from the continental-shelf break, close to where we estimate the continental-shelf break temperatures T_CSB in our study. Haigh et al. (2023) find that the ridge that is indicated in our study as the overflow point (see Fig. 8c) blocks inflow from the Bellingshausen Sea at depth, so water masses rather originate from the Pine Island–Thwaites Trough, similar to Thoma et al. (2008) and Naughten et al. (2022).

3.2.5 The case of multiple gateways as found in the Totten region

For PICO, the Totten region incorporates the Totten and Moscow University ice shelves. Totten Ice Shelf has a direct ocean access at a depth of 496 m through a trough near the Law Dome peninsula that constitutes around 23 % of the total grounding line length; see Fig. 9. Our d_GL,0 estimate for the entire basin is 542 m, however, meaning that there are some deeper grounding line parts that have a deeper horizontal connection to the ocean; see the Totten sub-panel in Fig. 4. These deeper parts constitute less than 1 % (0.4 %) of the region's grounding line. The mean depth of the basin's grounding line is 635 m, but the deepest parts go down to around 2100 m. Moscow University Ice Shelf has a slightly shallower access depth of 384 m (see the second spike in Fig. 4), compared to Totten Ice Shelf.

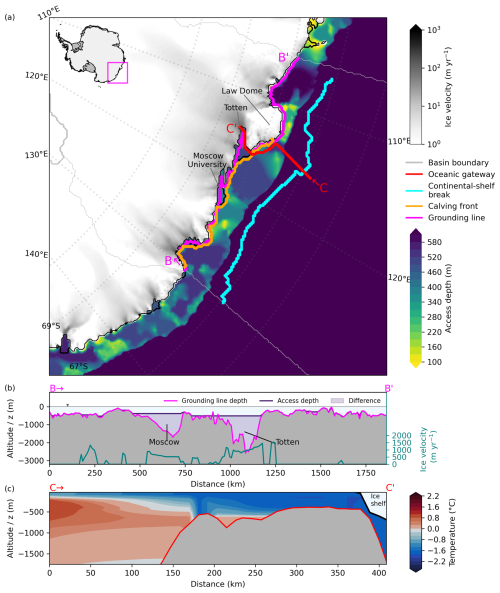
Figure 9 Access depths and temperature profile in the Totten region, East Antarctica. (a) Computed access depths near Totten Glacier indicate a prominent oceanic gateway near the Law Dome peninsula (cf. transect C). The transects denote vertical profiles along (b) the grounding line and (c) the found oceanic gateway showing the potential temperature profile along the transect. Speed of grounded ice shown as grey shading (in panel a) and as a blue-green line (in panel b) indicating the location of major ice streams and taken from Mouginot et al. (2019). The magenta line (in panel b) indicates grounding line depth, while the dark purple line (in panel b) shows the derived access depth at Totten Glacier.

In the ISMIP6 climatology, warm temperatures are not only present along the continental-shelf break but can also be found on the continental shelf in front of Totten Glacier (cf. 190–250 km along the transect in Fig. 9c). Water masses near the calving front have a mean temperature of −1.4 °C but 0.01 °C at maximum. At the continental-shelf break, water masses are 0.67 °C warm, with a maximum of 1.2 °C. The mean temperatures thus differ by 2.1 °C (ΔT_mean−mean). Rignot et al. (2013) find melt rates at Totten Ice Shelf to be 10.47±0.7 m yr⁻¹ (around 7.8 m yr⁻¹ in Adusumilli et al., 2020a). According to our analysis when applying ΔT_mean−mean, melt rates at Totten would see an increase in basal mass flux from around 90 Gt yr⁻¹ in Reese et al. (2023) to 501–664 Gt yr⁻¹ (around 7 to 40–53 m yr⁻¹), depending on the PICO parameter combination. When assuming an inflow from the warmest waters near the continental-shelf break at 496 m, using ΔT_max−mean, the basal mass flux would increase up to 9-fold (to 826 Gt yr⁻¹). Those water masses are 2.6 °C warmer compared to those present at the ocean floor near the calving front.

Totten Ice Shelf is the floating extension of Totten Glacier that drains a catchment containing ice with an equivalent of 3.5 m of global sea-level potential (Greenbaum et al., 2015) and currently experiences the largest thinning rate of all East Antarctic regions (Pritchard et al., 2009; Flament and Rémy, 2012; Greenbaum et al., 2015). Here, elevated sub-shelf melt rates due to warm-water inflow onto the continental shelf could already be the cause for the adjacent glacier to thin. Further ocean-induced melting can therefore have significant consequences for global sea-level rise. Moscow University Ice Shelf is included in the same region as Totten Ice Shelf. From our analysis, we determine the relevant access depth, d_GL,0 to be 373 m, which resembles the second spike in the distribution when evaluating the access depths of the entire region's grounding line(s); see Fig. 4. For more specific regional results for warm-mode melt estimates, the two ice shelves need to be treated as separate basins, which we leave for future research.

3.3 Change in melt rates assuming transitions towards warm-mode melting in all Antarctic regions

After having considered specific aspects of our analysis in individual ice-shelf basins, we now derive generalised insights from our analysis, evaluating all Antarctic regions: average temperatures along the ice-shelf fronts, T_CF,mean, which are derived at the ocean floor in the individual basins, are lower than temperatures found at the relevant access depth at the continental-shelf break, T_CSB,mean; see Fig. 10. This is not surprising as T_CSB incorporates the warm CDW which resides at mid-depth off the Antarctic continent, while T_CF often reflects the cold outflow of ice-shelf meltwater at depth. Figure 10a shows the distribution of temperatures along these two locations for each basin. Mean T_CF estimates range from −1.92 °C at Filchner–Ronne to 0.19 °C in basin 16 (Bellingshausen Sea). Especially in West Antarctica, the spread in T_CF is very large due to warm water masses being present in some troughs along the CF, compared to, for instance, the large ice-shelf regions of Filchner–Ronne, Ross, or Amery, where those water masses are not found. Mean temperatures along the continental-shelf break, T_CSB,mean, range from −0.29 °C in basin 2 (which incorporates the Riiser-Larsen Ice Shelf) to 1.74 °C found in the Bellingshausen Sea region (basin 16). The maximum temperatures near the continental-shelf break, T_CSB,max, are highest in West Antarctica, with the Bellingshausen Sea region reaching 1.86 °C at maximum.

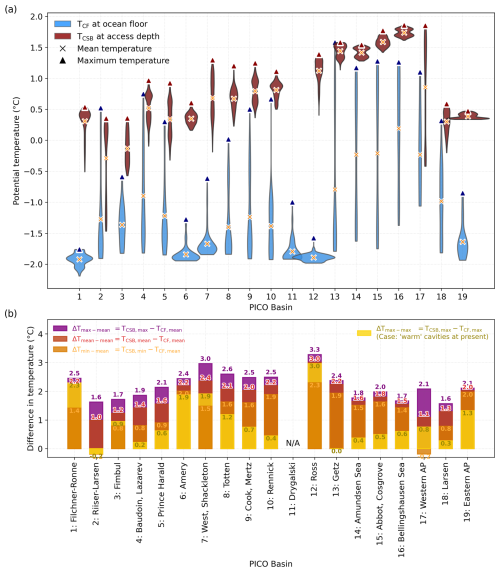
Figure 10 Assessment of extracted temperatures around Antarctica. (a) The distribution of the T_CF (blue) and T_CSB (red) estimates for all 19 PICO regions is shown as kernel density estimates, along with the mean and maximum temperatures. The width of the curves depicts the approximate frequency of data points within the respective temperature range. T_CF incorporates the bottom-most temperatures along the calving front, while T_CSB is evaluated at the relevant access depth (the deepest along the region's grounding line) at the continental-shelf break, a roughly 40 km wide area where the continental shelf transitions to the open ocean (at 1800 m). Corresponding salinity estimates are found in Fig. S5. (b) Differences in temperatures from panel (a) when comparing mean temperatures along the calving front with mean, minimum, and maximum temperatures found along the continental-shelf break (ΔT_min−mean, ΔT_mean−mean, and ΔT_max−mean in orange, red, and purple, respectively). For the case of warm-cavity regions at present, ΔT_max−max is included (yellow). Temperatures relative to the in situ freezing point, i.e. the thermal driving, are provided in Fig. S3. Resulting temperature forcing for PICO is obtained by adding the differences in panel (b) onto the tuned forcing fields from Reese et al. (2023); see Fig. S4.

The temperature differences, shown in Fig. 10b, range from 1.0 to 3.0 °C when comparing mean estimates offshore and along the calving front (ΔT_mean−mean). We find the largest difference in basin 12 that incorporates Ross Ice Shelf ($\mathrm{\Delta }{T}_{\mathrm{mean}-\mathrm{mean}}=$ 3.0 °C); in basin 7 ($\mathrm{\Delta }{T}_{\mathrm{mean}-\mathrm{mean}}=$ 2.4 °C); and in basins 1 (Filchner–Ronne Ice Shelf), 6 (Amery), 10 (Rennick), and 13 (Getz) with $\mathrm{\Delta }{T}_{\max -\max }=\mathrm{2.2}$ °C. Comparably warm temperatures at the calving front ($T_{\mathrm{CF},\max }>$ 0 °C) are found in basins 2, 4, and 5; in basins 8 to 10 in East Antarctica; and in basins 13–18, i.e. in all West Antarctic basins, so the difference to the continental-shelf break temperature is rather small. Especially in West Antarctica, high T_CF,max can be related to warm water already being present in some troughs along the calving fronts. When accounting for this, i.e. using ΔT_max−max, the largest temperatures differences can still be found in the large, at present cold-mode, ice shelves Filchner–Ronne (2.3 °C) and Ross (3.0 °C). In West Antarctica, the difference ranges from almost zero (at Getz) to 0.4 (Amundsen Sea) and 0.6 °C (Bellingshausen Sea). Compared to that, assuming an inflow of the minimum temperatures found along the CSB, T_CSB,min, yields higher temperature differences (0.8–2.3 °C) when excluding basin 2 and 17, where the difference is negative ($T_{\mathrm{CSB},\min }<T_{\mathrm{CF},\mathrm{mean}}$). Since we want to provide an upper-bound estimate for bathymetry-constrained warm-mode melt rates around Antarctica, we employ the anomalies of ΔT_max−mean (i.e. taking the highest continental-shelf break temperature and comparing it to the basin-mean along the calving front). ΔT_max−mean ranges from 1.6 (basin 2 and 18) to up to 3.3 °C (at Ross). It is interesting to note here that for the big ice-shelf regions of Filchner–Ronne, Ross, and Amery, the way we obtain the temperature anomaly in the case of basin-wide transition to warm-mode melting does not matter much: ΔT_mean−mean, ΔT_max−max, and ΔT_max−mean are very similar in these regions, which is due to the narrow temperature distribution along the present-day calving front (Fig. 10a). Since those three regions feature major oceanic gateways, our approach of assuming an inflow from around $\mathrm{\Delta }{T}_{\max -\mathrm{mean}}=$ 3 °C warmer water masses to the respective grounding lines is most valid there. As the Drygalski region (basin 11) shares the continental-shelf break with the Ross region, we do not provide an estimate for T_CSB here. For this region, subsequent melt rates are not estimated either. Temperatures relative to the in situ freezing point, i.e. the thermal driving, are provided in Fig. S3, and the actual PICO forcing temperatures are provided in Fig. S4. In all basins, the water masses from the continental-shelf break are saltier than compared to those near the calving front (S_CSB > S_CF). The difference in the extracted salinity inputs is, however, small, ranging from nearly 0 PSU at Filchner–Ronne (basin 1) to 0.6 PSU at the Bellingshausen Sea region (basin 16). All salinity estimates are shown in Fig. S5.

Melt rates computed with PICO for the anomalous ocean temperatures and salinities are displayed in Fig. 11. Almost all regions show a strong increase in sub-shelf melting when assuming that warm waters from the continental-shelf break can reach the ice-shelf cavities, all the way to the grounding line. Relative to their present-day estimates, melt rates increase most in the big ice-shelf regions of Amery, Filchner–Ronne, and Ross that show a > 20-fold increase in melting (see Fig. 11c), when assuming that warm waters from the continental-shelf break can access the respective ice-shelf cavities. We find the largest increase at Amery Ice Shelf, where melt rates could increase up to 42-fold; cf. Fig. 11c. With our access-depth analysis in these three regions, we have found that, at the access depth used for extracting the temperatures at the CSB, d_GL,0, more than 30 % of the respective grounding lines are accessed. This is why we classified these regions to have major oceanic gateways; see Fig. 4. This gives our results significance, as in those regions our assumptions with PICO are particularly valid; e.g. warm water from the CSB is channelled to the respective grounding lines.

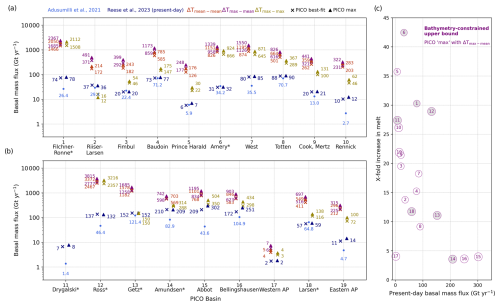
Figure 11 Circum-Antarctic PICO basal mass flux estimates. Estimates for basins 1 to 10 (a) and basins 11 to 19 (b) when assuming an inflow of warm water masses from the continental-shelf break (red/orange: comparing mean temperatures; purple: comparing T_CSB,max and T_CF,mean; and yellow: comparing maximum temperatures) to present-day basal mass flux estimates of Adusumilli et al. (2020a) (light blue) and the tuned forcing fields of Reese et al. (2023) (dark blue) for two different PICO parameter combination (best-fit and max), respectively. Basin-averaged melt rates given in m yr⁻¹ are included in Fig. S6. (c) Upper-bound estimates using the max PICO parameter combination relative to present-day basal mass flux from Reese et al. (2023) using $T_{\mathrm{CSB},\max }-T_{\mathrm{CF},\mathrm{mean}}$. The circle markers indicate the respective basin number. The seven regions we find feature a major oceanic gateway are labelled with an asterisk (^*) in panels (a) and (b); in panel (c) those regions have a grey circle background.

Ice-shelf regions in West Antarctica do feature oceanic gateways as well (e.g. Getz with 9.8 % of its grounding line reached at d_GL,0), but since there is already warm water present at the CF, there is little potential for as drastic changes in the sub-shelf melt rates through bathymetry-constrained inflow as in cold cavities at present. Generally, our analysis highlights the generally strong sensitivity of the large, cold cavities (Filchner–Ronne, Ross, Amery), which stands in contrast to regions with already warm cavities (Getz–Western AP). These cold-cavity regions show major oceanic gateways (Fig. 4) that allow access into a well-shielded cavity (especially true in the case of Filchner–Ronne and Amery; cf. Fig. 3). The Filchner–Ronne, Ross, and Amery regions together hold more than 30 m sea-level equivalent ice volume, with dire consequences in case of a switch to warm mode in any of these regions. Please note that in all cases we assume that the increase in melting is mainly driven by the changes in temperature: the melting effect of the salinity differences of a maximum of 0.6 PSU is around 1 order of magnitude smaller.

4 Discussion

Our data analysis infers potential pathways for warm-water inflow into ice-shelf cavities from access depths for 19 drainage basins in Antarctica and provides estimates for induced changes in sub-shelf melt rates. The results of the analysis need to be evaluated in light of the key assumptions and limitations of our approach: firstly, we assume that ocean waters in front of the ice shelf serve as a valid proxy for water masses that currently drive melting underneath the ice shelf, which is generally valid for cold-mode ice shelves but not for shelves with warm-mode melting (Silvano et al., 2016). Not all ice shelves are considered cold-mode ice shelves at present, most notably the ice shelves in the Amundsen Sea region. We partially considered this special case in our analysis by providing the ΔT_max−max estimates in our analysis. Second, we estimate the continental-shelf break temperatures at the region's deepest grounding line access depth, d_GL,0, assuming that water masses simply follow the bathymetry when flowing onto the shelf and do not follow isopycnals (Drijfhout et al., 2013). Ocean dynamics, which crucially determine sub-shelf circulation patterns and thereby influence the access potential (Nicholls et al., 2009; Williams et al., 2016), are not considered in this study. Our analysis is thus a sole representation of the role of the geometry of the continental shelf including the ice-shelf cavities and connecting features such as the oceanic gateways. Our study could therefore be improved by considering specific ocean circulation patterns informed by high-resolution ocean models, such as in Naughten et al. (2023), which can also assess the boundary conditions for mode 2 onset in all regions. Please note that our results are not directly dependent on the grounding line coverage at the deepest access depth, but it enables us to contextualise the results. Our temperature and melt rate changes would not differ if at d_GL,0 only 1 % instead of a higher percentage were horizontally connected to the open ocean. PICO uses one temperature (and salinity) estimate per basin to compute sub-shelf melt rates. However, the existence of a major oceanic gateway means that a substantial portion of the grounding line is reached at d_GL,0, and the PICO input values are a good representation of potential results. In the case of the Filchner–Ronne basin for instance, d_GL,0 reaches more than three-quarters of the cavity and is thus, in our conclusion, adequately representative of the entire shelf, e.g. for estimating a bathymetry-constrained warm-mode melt estimate. In the other case where no major oceanic gateway exists, PICO input values represent an upper bound on the oceanic properties that would reach the grounding line. Cold and dense shelf waters flowing out of ice-shelf cavities generally shield the ice shelf from warm CDW inflow at depth (Janout et al., 2021). The circulation patterns in an ice-shelf cavity system such as Filchner–Ronne are strongly controlled by dynamical processes, for instance by the Coriolis force or the interplay of sea-ice production and polynya formation, which is in turn linked to anomalies in the large-scale atmospheric circulation around Antarctica (Alley et al., 2015; Janout et al., 2021; Haid et al., 2023). However, our identified gateways could be an entry point to crosscut the density barrier (i.e. the Antarctic Slope Current) in front of the continental shelf (Hirano et al., 2023). Furthermore, changes in the thermocline depth and resulting changes in density could lift up water masses over topographic features (Assmann et al., 2013; Dutrieux et al., 2014; Hattermann, 2018; Daae et al., 2020). Here, again, high-resolution ocean dynamical models could suggest that access is more likely through shallower channels or that even deeper ocean levels than at access depth should be considered.

Typically, if CDW flows onto the continental shelf, it mixes with fresh and colder on-shelf water masses (Wang et al., 2023). This modified Circumpolar Deep Water (mCDW) is generally colder than the temperatures estimated in this study: Williams et al. (2016) define the maximum potential temperature of mCDW to lie between −1.7 and 0 °C, while Ribeiro et al. (2021) use a range from −1.7 to 1.5 °C for mCDW, when classifying water masses near Totten Ice Shelf. Since we neglect the modification of Circumpolar Deep Water when accessing the grounding lines in the ice-shelf cavities, our findings should be understood as upper-bound estimates.

Cavity-resolving ocean models are computational very expensive and therefore limited to simulations on centennial timescales. Millennial timescale studies or large ensembles of simulations thus often rely on parameterisations to infer ocean-driven sub-shelf melting. We here use the PICO model to estimate sub-shelf melt rates based on the temperatures and salinities in front of the ice shelves as well as from the continental-shelf break. Favier et al. (2019) find that a box parameterisation that mimics the vertical overturning in the cavity, such as PICO, provides melt estimates that are comparable to coupled ice–ocean simulations. However, our melt rate estimates could differ when using an alternative melt parameterisation or assuming a higher melt rate sensitivity to thermal forcing, e.g. by using a quadratic melt relationship (Burgard et al., 2022). It should be noted that Burgard et al. (2022) do not find good agreement between PICO and a reference coupled model, but the PICO implementation in that study also uses a completely different PICO parameter tuning. In our study, we assume that once waters can reach the grounding line, it can access all parts, as one temperature and salinity estimate is applied to the whole length of the grounding line in the box model. With a spatially more explicit approach, with which one could provide temperature (and melt) locally to each grid cell, one could apply the extracted temperature offset to only those parts of the grounding lines that are connected to the open ocean at the deepest access depth found at the region's grounding line.

PICO does not include horizontal ocean circulation, modification of water masses on the continental shelf, or blocking of water masses entering the continental shelf or mode 3 melting (where surface waters cause melting near the ice-shelf front). This might bias melt rates in cold cavities at the moment. Furthermore, the melt pattern in PICO is spatially less variable than in ocean circulation models or observations, which means that PICO does not reach the very high melting on the order of 100 m yr⁻¹ reported close to grounding lines (Dutrieux et al., 2014; Paolo et al., 2015). The relevance of this for ice-sheet model studies needs to be further assessed (some first analyses were done in Reese et al., 2018b; Berends et al., 2023). A recent study suggested that bulk melting is more relevant than spatial patterns for the small, constrained Pine Island Glacier ice shelf (Joughin et al., 2021). The question of whether bulk melting or the melt pattern is more relevant is not resolved yet, but our study does not aim to estimate this, and we would hence refer to future work.

Furthermore, we use only two parameter combinations for the overturning and heat-exchange coefficients in PISM-PICO to capture the parameter uncertainty in the melt estimates when assuming a warm-water inflow from the continental-shelf break. We use those parameter sets that were selected to match the sensitivity of melt rates to temperature changes for present-day Antarctica (Reese et al., 2023). However, a full model ensemble would be required to estimate the full uncertainty that arises from the choice of the PICO parameters. Despite these limitations, we want to stress that melt parameterisations such as PICO are essential for large-ensemble studies or long-term studies that cavity-resolving ocean circulation models cannot cover due to computational costs. They will thus serve an important purpose also in future ice-sheet model simulations and projections.

We further assume that the bathymetry is time-invariant, which is not the case when considering longer timescales. Sill depths and grounding line location and thus access depths may change by hundreds of metres in response to erosion, sea-level changes, and glacial isostatic adjustment effects (see Kreuzer et al., 2025a, b.

As we have shown, the analysis of access depths on the continental shelf helps to better inform the basin boundaries in PICO, which could be applied to different melt parameterisations in ice-sheet models as well. However, there are a number of alternative subdivisions of the Antarctic continent, as in van der Linden et al. (2023), following Levermann et al. (2020), in which they differentiate between the Ross, Amundsen, Weddell, Peninsula, and an East Antarctic Ice Sheet ocean sector. In the Ross Sea, however, they separate between the ocean in front of Victoria Land (Drygalski region) and the rest of the Ross Sea. This makes their classification not suitable for our analysis, as we consider the continental-shelf break in front of Ross Sea representative of both regions.

Using the 19 PICO basins in our study, we conclude for basins 1, 6, 12, 14, 11, 18, and 13 (7 out of 19 regions; cf. Fig. 4) that d_GL,0 is representative of the entire basin in the case of an oceanic-gateway-driven switch to warm-mode melt conditions, as d_GL,0 represents the largest grounding line share. In other regions (e.g. in basins 3, 2, 10), however, d_GL,0 and subsequent temperature offsets and melt rates based on that estimate are less representative of the entire basin but constitute an even more upper-bound estimate as d_GL,0 is lower and thus represents warmer CDW. This could be fixed by simulating each individual ice shelf separately. Finer resolutions, i.e. on the individual ice-shelf level, would reveal more individual gateways, but this analysis is out of the scope of this paper.

When it comes to the effects of the potential warm-water inflow, as analysed in our study, the difference in temperatures is small in some regions for physical reasons: this can be the case if the access depth of the basin is shallow and encompasses slightly colder water masses at the CSB, i.e. representing surface waters and not CDW, or if the calving front temperatures are already relatively warm, as in the case of the Amundsen region. In those regions, changes in melting may be more sensitive to gradual offshore changes in continental-shelf break temperatures instead of a qualitative circulation change, i.e. a regime shift of cavity inflow leading to a switch from a cold to a warm cavity, which our method is designed to assess. When considering estimates on CDW-inflow-driven sub-shelf melting, one has to consider, however, that ocean temperatures are projected to become warmer in the future, for instance, by 1.2 °C as found by Gómez-Valdivia et al. (2023), who employ a global climate model on a relatively coarse resolution (1° ocean model).

The temporal evolution of warm water accessing the Antarctic grounding lines at depth depends on the complex interplay of ice, ocean, atmosphere, and solid Earth. Importantly, the timing would mainly depend on the future climate change scenario determining the change in oceanic boundary conditions. We here aim at quantifying the potential effect this might have in the future. Ocean model projections show that warm water access under the Filchner–Ronne Ice Shelf may occur due to ongoing climate change but that it is unlikely to happen within the next decades (Hellmer et al., 2012; Naughten et al., 2021; Haid et al., 2023). Other regions might also be susceptible to a basin-scale transition to mode 2 melting: when assuming that sub-shelf melting becomes intensified by warm water from the continental-shelf break, Jordan et al. (2023) find that the East Antarctic Ice Sheet might lose up to 48 mm of sea-level equivalent ice volume over the next 200 years. However, they artificially alter the ocean forcing to represent a shift to stronger on-shelf CDW transport.

All in all, cavity geometries are highly heterogeneous, and the impact of the onset of mode 2 melting should thus be determined individually in a follow-up study taking into account other measures for the response of the grounding line, e.g. buttressing, as in Naughten et al. (2023). Our analysis follows only an idealised approach; for realistic projections of potential future regime shifts in the Antarctic ice-shelf regions, more sophisticated approaches are needed. These approaches at best have a coupled ice–ocean–atmosphere representation, with interactive ice sheets and ice shelves at high resolution in space and time.

5 Conclusion

In our study, we present a simple approach to calculate the access depths of water masses to Antarctic grounding lines. We combine available bathymetry data with present-day ocean temperature and salinity data. Thereby, we identify major oceanic gateways in 7 out of 19 regions through which warm water masses residing off the continental-shelf break could potentially access large parts of the deep grounding lines in several Antarctic regions. Warm-water inflow to regions with deep-lying grounding lines and subsequent increased sub-shelf melting can have a strong impact on the ice flux across the grounding line and therefore the overall mass balance of the Antarctic Ice Sheet (Reese et al., 2018b; Goldberg et al., 2019).

Perturbing the current state of the Antarctic Ice Sheet with warmer temperatures at the continental-shelf break helps estimate an upper bound on melt rate changes. All regions would experience a strong increase in sub-shelf melting, while basal melt rates would increase up to 42-fold in cavities that are currently in a cold state, are well-shielded by shallower bathymetry, and have a major oceanic gateway that could channel warmer water masses to the grounding lines. We estimate an increase in temperatures at a maximum of 3.3 °C. As our quantitative results match findings from regional modelling studies that exist in some basins, we are cautiously optimistic that our findings can be taken as upper-bound estimates for other regions too. The increase in temperature we estimate here could hence be employed by ice-sheet modellers to calculate an upper-bound estimate of the consequences of a flip of all Antarctic cavities into a warm state for current ocean conditions.

While high-resolution ocean modelling could provide a more detailed estimate on the effect of oceanic gateways on melting, our first-order approach is instead straightforward and easy to run, meaning that only a few analysis scripts are necessary to (re-)produce our results. When new bathymetry or ocean temperature data become available, our study can be repeated in an instant, even on a 500 m × 500 m grid spacing (within < 30 min). The presented approach serves as a refinement on identifying those ocean regions most relevant as input for PICO or other melt parameterisations. We recommend other PICO users take into account the connectedness of the continental bathymetry when preparing the relevant input data. By identifying potential oceanic gateways and analysing the thermal properties of ambient water masses, our study thus contributes to assessing the current and potential future vulnerability of the Antarctic Ice Sheet to changes in its surrounding ocean.