Brief communication: Improving lake ice modeling in ORCHIDEE-FLake model using MODIS albedo data

The FLake lake model embedded in the ORCHIDEE land surface model was recently updated to better represent winter ice cover. MODIS albedo data and the Great Lakes ice cover fraction dataset over the Laurentian Great Lakes were used to calibrate and validate a new parameterization of the lake albedo accounting for a partial ice cover fraction. The developments were validated for the phenology of the ice cover of 200 lakes of various sizes reported in the Global Lake and River Phenology Database. The results are in better agreement with the observations for all lake size categories, with the largest and deepest lakes showing more significant error reductions in the duration of the ice cover period up to 18 d. This study highlights the importance of considering partial ice cover to correctly model lake albedo in cold regions and thus to simulate realistic mass and energy exchanges at the land–atmosphere interface.

1 Introduction

The key role of lakes in the atmosphere–surface water and energy exchanges at local, regional, and global scales (Williamson et al., 2009; Woolway et al., 2020; Huang et al., 2023, to cite but a few) explains the attention given to improving their representation in climate and weather prediction models. Lakes present specific physical properties compared to their surroundings (lower albedo and surface roughness, larger heat capacity, and thermal conductance) that impact the energy exchanges with the atmosphere. Lakes are also a significant source of water, carbon, and methane, whose impact on climate is still not precisely quantified (Johnson et al., 2022; Lauerwald et al., 2023). Moreover, in cold regions, lakes can freeze and store snow, with large impacts on the seasonal evolution of water and energy surface fluxes but also on carbon exchanges as reported by several authors, because of the accumulation of gases under the ice cover that can be released abruptly when the ice melts (Mammarella et al., 2015; Denfeld, et al., 2018). Therefore, the representation of freezing processes is key for modeling the atmosphere thermodynamics and greenhouse gas (carbon and methane) budgets, especially in the present context of climate warming. Indeed, long time series of observations have highlighted the impacts of the combined effects of air temperature increase and volume variations on lake temperature and thermal regime on the loss of winter ice cover (Woolway et al., 2020; Huang et al., 2023). To better understand these connected processes and to better predict future trends, climate models need to develop lake modules able to correctly represent water and energy budgets and the carbon cycle. Such developments have been ongoing in the climate modeling community for several years, with major works demonstrating the benefits of representing lakes at the global scale in numerical weather prediction and climate models (e.g., Balsamo et al., 2012; Le Moigne et al., 2016).

In these large-scale models, the representation of lakes is generally done simplistically, based on 1-D column models that do not represent the spatial variability of the surface exchanges. The same applies to the freezing processes and the fact that ice cover is considered laterally uniform. However, its formation can take several days/weeks and may never be completed for some large and deep lakes. Moreover, because of the spatial variability of the lake properties (bathymetry, for example), the mass and energy transfers can present very heterogeneous features, which is the same for the ice cover and the resulting impacts on surface fluxes, as shown by Lang et al. (2018), for methane emissions from Tibetan lakes.

The modeling of ice conditions is an essential challenge in such large-scale models for several reasons, including the fact that the processes involved are strongly nonlinear because free water and ice show very different characteristics in terms of biogeophysical properties and exhibit high spatial and temporal variability. Scale issues must, therefore, be parameterized to account for these variabilities. Lake temperature results from the energy budget, which strongly depends on the surface albedo, which determines the amount of solar energy absorbed at the surface. In cold conditions, when the surface temperature drops below 0 °C, ice formation may begin to be driven by many variables, including atmospheric conditions, lake size, and depth. In this process, lake bathymetry plays a key role in determining the lake heat capacity and consequently the speed of the ice formation, explaining why lakes freeze from their perimeter to their center and why shallow lakes can freeze quicker than deeper ones in the same atmospheric conditions. In consequence, if one wants to correctly represent the ice cover phenology in 1-D models, an ice cover fraction has to be introduced and used to compute more realistic dynamics of the lake surface albedo.

Several works have shown the impact of the incorrect representation of lake freezing processes in land surface models (LSMs) (e.g., Pietikäinen et al., 2018; Choulga et al., 2019; Garnaud et al., 2022). Based on the FLake lake model, Bernus and Ottlé (2022) also identified shortcomings in modeling lake ice phenology in the ORCHIDEE LSM. Although the model evaluation of lake water surface temperatures showed satisfactory results, with an RMSE of around 2.7 °C at the global scale, systematic errors in the prediction of ice phenology were highlighted, with too early ice onset and late offset, leading to an overestimation of the ice cover period up to 30 d on average (Bernus and Ottlé, 2022). In a previous study, Bernus et al. (2021) studied the surface temperature sensitivity to model parameters and highlighted the key role of snow and ice radiation coefficients (light extinction and albedo) in ice phenology.

Among these two essential radiative variables, surface albedo is the one that has been mapped at the global scale with remote sensing for several years. Various satellite products provide daily albedo time series at a scale of a few hundred meters over the last 30 years, which can be used to evaluate and calibrate LSMs. In ORCHIDEE, such products are commonly used to calibrate model parameterizations. For example, Raoult et al. (2023) calibrated the ORCHIDEE snow model over the Greenland ice sheet using MODIS albedo data and showed improvements in the model fit to the observations and the impacts on the simulated snow states, especially the sublimation processes.

In this paper, we present recent work performed in the ORCHIDEE-FLake model to better represent lake freezing through the account of partial ice cover and the revision of the lake albedo parameterization. The developments are based on the MODIS albedo product used to model ice cover fraction and to calibrate the albedo parameters. The modeled lake ice phenology is evaluated against in situ data. The results and following steps for further parameter optimization are finally discussed.

2 Data, model, and methods

2.1 Datasets used

2.1.1 HydroLAKES database

The HydroLAKES database (Messager et al., 2016) identifies all lakes larger than 0.1 km² at the global scale and provides estimates of their mean depth based on a geostatistical model linking lake bathymetry to surrounding terrain topography. HydroLAKES was used by Bernus and Ottlé (2022) to generate the lake tiles in the ORCHIDEE grid by clustering the lake area according to their mean depth. In this work, HydroLAKES has also been used to mask the studied lakes in the surface albedo time series and extract the data for assessing the ice cover fraction and to analyze its seasonal variations. Data can be downloaded at https://hydrosheds.org/page/hydrolakes (last access: 16 June 2025).

2.1.2 MODIS data products

We used the MCD43A3 albedo product (Schaaf and Wang, 2021) to assess the seasonal evolution of the lake ice cover and to calibrate the model albedo parameters. The data are provided at a daily time step with a 500 m resolution. The bi-hemispherical and directional hemispherical reflectances are given for multiple narrow bands and three broadbands (visible, near-infrared, and entire solar spectrum, corresponding to the surface albedo). The effective surface albedo is a combination of the shortwave bi-hemispherical reflectance, also called white sky albedo (WSA), and the shortwave directional hemispherical reflectance (black sky albedo, BSA) and depends on the cloud coverage. In the absence of such information, and given that our model does not separate direct and diffuse radiation, we assumed that the average of the retrieved WSA and BSA is a better approximation of the surface albedo as modeled in ORCHIDEE. Data are available at https://lpdaac.usgs.gov/products/mcd43a3v006/ (last access: 16 June 2025). Overlying the albedo raster images with the HydroLAKES polygons allowed us to extract the lake's surface albedo and its spatial variability.

2.1.3 Great Lakes Ice Cover (GLIC) database

The GLIC database provides daily gridded ice cover data at a 1.8 km resolution over the Great Lakes from 1973 to the present. The dataset, fully described by Yang et al. (2020), is based on the standardization of the previously existing GLIC multisource dataset developed by the Canadian Ice Service and the U.S. National Ice Center. Using interpolation techniques (nearest neighbor for space and linear for time), combined with new satellite and meteorological information, Yang et al. (2020) created coherent data available at the same standardized spatial and temporal resolutions throughout the entire period. The daily data over the five Great Lakes (Erie, Huron, Michigan, Ontario, and Superior) can be downloaded at https://www.glerl.noaa.gov/data/ice/ (last access: 16 June 2025). These data were used as a reference to calibrate our albedo-based ice cover detection method for 2008–2018.

2.1.4 Lake ice phenology

We used the Global Lake and River Phenology (GLRP) database to evaluate the modeled lake freezing processes (Benson et al., 2000). This dataset provides the onset and offset dates and duration of observed freezing periods for 857 lakes worldwide. Data are available for most lakes back to 1845, even earlier for a few water bodies and up to 2020 for the most recent data. The dataset can be downloaded at https://doi.org/10.7265/N5W66HP8. It should be noted that the reported information is not homogeneous since, for some lakes, the definition of the ice-on date is the date when the lake is entirely ice-covered, while for the other lakes, it is the date when the lake starts to freeze. Moreover, time series are not continuous and may contain long periods without data. We also used the SYKE database from the Finnish Environment Institute, which reports the in situ ice formation and disappearance for 27 lakes located in Finland, as reported by Choulga et al. (2019). The dataset is available at https://www.syke.fi/en/environmental-data/downloadable-spatial-datasets (last access: 16 June 2025).

2.1.5 ERA5 meteorological reanalysis

The ERA5 reanalysis dataset was used to simulate the lake thermal processes with ORCHIDEE. This atmospheric forcing is available globally at an hourly time scale and with a 31 km resolution from 1940 onwards (Soci et al., 2024). It was interpolated at a half-hourly time step and a 0.25° resolution, following the methodology presented by Wei et al. (2014). We used the solar and atmospheric downward radiations, air temperature and humidity, wind speed, precipitation, and atmospheric pressure at the surface to force the model. Data are available at https://cds.climate.copernicus.eu/cdsapp#!/dataset/reanalysis-era5-complete?tab=overview (last access: 16 June 2025).

2.2 ORCHIDEE-FLake model

2.2.1 Current status

ORCHIDEE is the continental component of the Institut Pierre-Simon Laplace (IPSL) Earth System Model, which provides the boundary conditions and the energy, water, and carbon fluxes for the atmospheric general circulation model LMDZ (Cheruy et al., 2020). ORCHIDEE can be run coupled with LMDZ or prescribed atmospheric conditions delivered by in situ measurements or atmospheric forcing datasets. Land surface characteristics are provided by various datasets, such as land cover maps, which can be updated yearly. In ORCHIDEE, vegetation is described with 15 plant functional types (PFTs), whose fractions must be prescribed for each grid point. The model was recently updated with a lake module based on the FLake 1-D lake model (Mironov, 2008), fully described in Bernus and Ottlé (2022). In the present version, lakes are considered as distinct tiles within the grid, on which a separate energy budget is solved independently from the rest of the vegetated grid (no lateral transfers). The lake cover fraction is static and is derived from the HydroLAKES database (Messager et al., 2016), which was used to cluster three categories of lakes according to their average depth. Lake cover fractions for shallow (depth of less than 5 m), deep (depth of over 25 m), and medium (depth ranging between 5 and 25 m) lake types have been derived to generate yearly land cover maps, including lake tile fractions characterized by their surface area and their effective depth and wind fetch (distance that wind blows without obstruction). These three effective lakes were obtained by aggregating the areas of all the lakes falling into each lake category and calculating the median value of their respective depth and fetch approached by the lake surface extent (see Bernus and Ottlé, 2022, for more information). The bulk energy budgets resolved in FLake allow us to predict the evolution of the vertical temperature structure within a mixed layer and an underlying thermocline, given several input parameters, namely the lake mean depth; the light extinction coefficient; the water, snow, and ice albedos; and the wind fetch. In cold conditions, the surface layer can freeze and an ice layer may develop and intercept snow. Because of the 1-D model structure, the whole lake surface freezes when the surface lake temperature falls below 0 °C, and the ice thaws above this temperature threshold, regardless of the lake's size. Water, snow, and ice layer thicknesses and temperatures are prognostic variables calculated at each time step (30 min in ORCHIDEE).

2.2.2 Ice cover fraction

The parameterization proposed by Garnaud et al. (2022) was implemented in ORCHIDEE to represent the lake ice cover, improve the surface albedo, and reduce the cold temperature biases. This model was successfully introduced in the Canadian Small Lake Model (CSLM) and showed improvements in the timing of ice-on/off periods, especially for the Great Lakes. Similar to other parameterizations, such as the one proposed by Choulga et al. (2019) and used in the Integrating Forecasting System of the European Centre for Medium-Range Weather Forecasts (ECMWF), the ice cover fraction is derived from the calculated ice thickness and equals unity above a certain threshold. In Choulga et al. (2019), this threshold is set to 10 cm, which means that above this threshold, the lake tile is completely frozen, and below it, the cover fraction decreases linearly to 0 % until the lake is completely thawed. In Garnaud et al. (2022), the threshold is set to a critical value dependent on the wind fetch, indicating that ice is more likely to break under the action of wind stress until it grows to a critical thickness. This critical ice thickness value H_crit may be written as

$$\begin{array}{}\text{(1)}& H_{\text{crit}}={\displaystyle \frac{{\mathit{\tau }}_a}{P^{\ast }}}\times L,\end{array}$$

where τ_a is the scale of the surface wind stress (set to 0.15 Pa), P^∗ is the compressive strength of ice (set to 27.5 kPa), and L is the lake fetch (in meters). The ice cover fraction of the lake tile, icefrac, is then derived from the modeled ice thickness H_ice using Eq. (2):

$$\begin{array}{}\text{(2)}& \text{Icefrac}={\displaystyle \frac{H_{\text{ice}}}{H_{\text{crit}}}}.\end{array}$$

We have implemented this parameterization in ORCHIDEE-FLake as an input for calculating the lake surface albedo. For each lake tile, the fetch is static and prescribed to the mean of the fetch of all the lakes falling in the tile. It is estimated at the lake level from the surface extent by assuming a circular shape and taking the diameter of this circle. Given that we did not consider lakes smaller than 0.1 km² due to the limitations of the HydroLAKES database, it means that the fetch values range between a few meters and a few hundred kilometers, leading to critical thicknesses ranging between 2 mm for the smallest lakes to 1.1 m for the larger ones.

2.2.3 Albedo revision

In ORCHIDEE-FLake, the lake surface albedo is calculated according to the surface temperature. For free water, the albedo is set to a value of 0.07, which is the standard value used in FLake. In the presence of ice, possibly covered by snow, the lake surface albedo (alb) depends on the temperature, as suggested by Mironov et al. (2012), and varies between two limits corresponding to wet and dry snow (in the presence of snow) and to blue and white ice (without snow), based on the same equation (Eq. 3):

$$\begin{array}{}\text{(3)}& \begin{array}{rl}{\displaystyle }\text{alb}\left(T_{\text{surf}}\right)=& {\displaystyle }{\text{albedo}}_{\text{max}}+({\text{albedo}}_{\text{min}}-{\text{albedo}}_{\text{max}})\\ {\displaystyle }& {\displaystyle }\times \exp \left({\displaystyle \frac{-C_{\text{alb}}\times (\mathrm{273.15}-T_{\text{surf}})}{\mathrm{273.15}}}\right),\end{array}\end{array}$$

where albedo_min and albedo_max are respectively the minima and maxima values for ice or snow; T_surf is the snow or ice surface temperature in kelvin, which is always lower than the water freezing point temperature; and C_alb is a fitted coefficient equal to 95.6 (Mironov et al., 2012). In FLake, the minimum and maximum albedos are equal to 0.1 and 0.6, respectively, for snow and ice. They were revised by Bernus and Ottlé (2022) following Semmler et al. (2012) and Pietikaïnen et al. (2018) and set to 0.3–0.5 and 0.77–0.87 for ice and snow, respectively (see Table S1 in the Supplement). In this work, to account for partial ice coverage, we implemented a supplementary equation, linearly linking the lake albedo to the ice fraction and accounting for the presence of snow, if any. The lake tile surface albedo alb_tile is now given by Eq. (4):

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\displaystyle }{\text{alb}}_{\text{tile}}\left(T_{\text{surf}}\right)=& {\displaystyle }{\text{Icefrac}}_{\text{tile}}\times \text{alb}\left(T_{\text{surf}}\right)\\ {\displaystyle }& {\displaystyle }+(\mathrm{1}-{\text{Icefrac}}_{\text{tile}})\times {\text{alb}}_{\text{water}},\end{array}\end{array}$$

where alb_water is the free water albedo, alb(T_surf) is the snow albedo in snowy conditions and the ice one when there is no snow, both derived from Eq. (3) and dependent on the surface temperature of the lake tile.

2.3 Methods

2.3.1 MODIS albedo processing on Laurentian Great Lakes

The MCD43A3 albedo product was used to analyze the winter seasonal variations of several lakes for which in situ ice cover observations were available. In particular, the Laurentian Great Lakes, well documented in the GLIC database, and the Finnish lakes, included in the SYKE dataset, were studied. We designed a method to estimate ice cover fractions from the albedo observations and used them to evaluate model parameterizations. Moreover, we also used the albedo data to calibrate the free water, snow, and ice albedo parameters.

To estimate lake ice cover fraction from the MODIS albedo data, we first compare the lake-averaged albedo time series over the 2008-2018 period with the in situ ice cover fractions reported in GLIC. This comparison allowed us to determine the lake-averaged albedo time series over the 2008–2018 period with the in situ ice cover fractions reported in GLIC allowed us to determine a lower threshold of the albedo, above which we could assume that the lake started to freeze durably. This threshold appeared to be the same for all five Great Lakes and was found to be 0.15. The maximum value was set to 0.9, since this value was reached for all the lakes that were completely covered at least once during the studied period. Assuming a linear relationship between these two extremes, we derived time series of ice cover fractions for each of the Great Lakes. A comparison of these estimates with in situ measurements over the 11 years studied shows a very good agreement, with RMSE ranging from 4 % for Lake Ontario to 9 % for Lake Erie. The latter showed the largest errors because it is the smallest and shallowest of the five lakes and has the largest ice fractions.

We also checked if our methodology could be applied to smaller lakes and tested it on some of the Finnish lakes present in the SYKE database, for which Choulga et al. (2019) reported the dates when the lake was completely frozen or completely thawed. Therefore, we compared these specific dates estimated from the MODIS albedo time series to those observed in the SYKE database and found that over the period 2010–2015, our method has an average error of 2 d for Lake Nilakka and 5 d for Lake Nasijarvi, the only two lakes that were resolved in our ORCHIDEE lake cover map.

The MODIS albedo time series combined with a literature survey were also used to revise the lake albedo model parameters. For free water, even if some of the larger studied lakes showed lower minimum values, most of the lakes present an average value of 0.07, which is the value used as a standard in FLake. The lower values, such as the ones observed on the Great Lakes (as low as 0.01), could be the result of the larger surface roughness observed over such large lakes, which could increase the multiple reflections and reduce the overall surface reflectances and thus the total albedo. In frozen conditions, the observations confirmed that snow-covered ice could reach values of up to 0.9. Therefore, the maximum values for ice and snow albedos were kept to the prior values set by Bernus and Ottlé (2022), i.e., 0.87 and 0.5 for snow and ice, respectively. Minimum values being more challenging to observe because of the cumulative effect of ice and snow aging and partial coverage, we rely on in situ measurements such as the ones reported by Svacina et al. (2014), showing snow minimum values close to 0.5 or the ones reported by Lang et al. (2018), showing minimum blue ice albedos of around 0.15. The prior and posterior values of the albedo model parameters are summarized in Table S1.

2.3.2 Model experiments

The evaluation of the revised albedo parameterization was done at a global scale. Two ORCHIDEE simulations were performed: a reference one using the standard model (called “prior”) and another one based on the present developments (called “post”), including lake fraction and calibrated albedo parameters. The simulations were performed on the 1979–2019 period, and the results were analyzed over the period 2008–2018 to ensure a 30-year spinup/warmup period necessary to avoid initialization errors. For both simulations, the same atmospheric conditions were prescribed based on the ERA5 reanalysis (Sect. 2.1.5) at the half-hourly model time step and 0.25° spatial resolution. The lake surface temperatures simulated over each lake tile present in the model grid cell were downscaled to extract the lake surface temperatures and ice thicknesses simulated over each lake reported in the GLRP and the SYKE databases. As a result of missing data over our study period (2008–2018), only 200 lakes among the 857 ones reported in the GLRP dataset were used for the model evaluation. These lakes are mainly located in the northeastern part of Canada and the US and in Scandinavia (Fig. S3 in the Supplement), covering a large diversity of boreal and arctic climates. The model performances in the representation of ice cover phenology, surface albedo, and surface temperature are discussed in terms of root mean square errors (RMSEs) and improvement factor (or error reduction, equal to $(\mathrm{1}-{\text{RMSE}}_{\text{post}}/{\text{RMSE}}_{\text{prior}})$), with larger values corresponding to larger improvement. In this comparison, we assumed that the ice-on and ice-off dates correspond to when the lake is completely frozen and ice-free, respectively. Given that deep lakes present partial coverage most of the time and that the observations may not be representative of the whole lake, we decided after various tests to diagnose the ice phenology dates with the simulated surface temperature, as was done in Bernus and Ottlé (2022). Therefore, for the deep lake category, the ice-on period is supposed to start when the modeled surface temperature falls below 0 °C.

3 Results

3.1 Lake albedo evaluation of Great Lakes

Figure 1 presents the lake surface albedo simulated by ORCHIDEE over the five Great Lakes for the “prior” and “post” simulations together with satellite-derived albedo observations (MODIS MCD43A3 data). Here, we present the observed and simulated daily values over the 2008–2018 period. (The mean averaged seasonal cycles over the same period are given in Fig. S1 in the Supplement.) The prior and post RMSE calculated over the whole freezing period and the improvement factors are given in Table S2 in the Supplement.

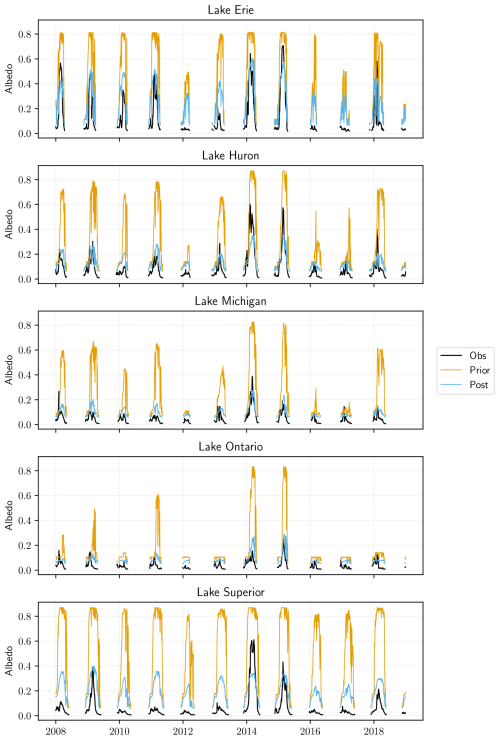
Figure 1 Lake surface albedo calculated by ORCHIDEE over the 2008–2018 period and compared to MODIS albedo observations (Obs) for the five Great Lakes at a daily time step. “prior” refers to the standard model and “post” to the albedo-revised one.

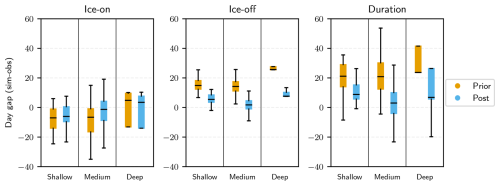
Figure 2 Ice-phenology-modeled errors (in days) obtained on the 200 (139 shallow, 51 medium, and 10 deep) lakes identified in the GLRP database. The boxplots show the median, first, and third quartiles of the time delay (model observations) and the minimum and maximum errors for the ice-on, ice-off, and duration of the ice cover period. “prior” refers to the standard model, “post” to the albedo-revised one, and time errors are expressed in days.

The results highlight the improvements brought by considering partial ice cover and the calibration of the minimum values of ice and snow albedos. The prior simulations presented a systematic overestimation of the albedo resulting from the overestimation of the ice cover (equal to 1 during most of the winter season for the five lakes and all the years except the warmer ones, i.e., 2012, 2016, and 2017). The RMSEs that were ranging between 0.22 (for Lake Ontario) and 0.54 (for Lake Superior) are considerably reduced within the range of 0.05 (for Lake Michigan) to 0.17 (for Lake Erie), with improvement factors larger than 70 % (see Table S2). The error reduction is slightly higher for Lake Michigan, equal to 0.83, and lower for Lake Erie, equal to 0.55. The slightly lower improvement observed for the shallowest lake studied is probably linked to the fact that Lake Erie, contrary to the others, can freeze entirely during the colder winters, thus reducing the benefit of considering the partial ice cover. The albedo time series plotted over the whole studied period (Fig. 1) highlight the overall reduction of the errors with the new parameterizations, especially for the largest and deepest lakes like lakes Superior, Ontario, and Michigan. The errors shown in Fig. S2 in the Supplement reveal the remaining errors during the warmest winters, like in 2016 and 2017, with an overestimation of the ice cover for all categories of lakes and an underestimation during the coldest years (like in 2014 and 2015), especially for the two shallowest lakes (Erie and Huron). It should be noted that the standard deviation of the observations is very large for all these lakes, demonstrating a large spatial variability in the ice coverage among the lakes. We can also see that the free water albedo is lower in the observations compared to the modeled one (prescribed to 0.07), which leads to systematic positive biases in the albedo simulation. Finally, Table S3 in the Supplement demonstrates that the temporal variability of the modeled albedo is in better agreement with the observations of all five Great Lakes. The standard deviation values, which were always overestimated with the prior model, have decreased. The more realistic maximum and minimum albedo values and interquartile range of the distributions show that the ice conditions are better simulated with the revised model.

3.2 Evaluation of lake ice phenology

We compared the key dates of the ice cover phenology predicted by ORCHIDEE to the GLRP observations. Figure 2 presents the errors obtained in the simulation of the ice-on/ice-off dates and the duration of the ice cover period for the 200 observed lakes, clustered into the three depth classes (shallow, medium, and deep lakes).

The results show how the account for partial freezing in the albedo model improved the timing of the lake freezing and the start and the end of the period compared to the prior simulation, with an overall shift in the date of the start of freezing of 1 d for the shallow lakes and 5 d for the medium and deep lakes. The ice-off also happened sooner by about 9 d for the shallow lakes and by about 12 d for the medium lakes, which reduces the overestimation of the ice cover duration by 12 d in the case of the shallow lakes and by nearly 18 d for the medium ones. The improvements are even more significant for the deep lakes, especially for the ice-off date, which has been brought forward by 18 d. The results obtained for the deep lakes show a larger variability in the model errors, especially for the start of freezing, which can be explained both by the lower number of lakes sampled compared to shallow and medium lakes (10 compared to 139 shallow lakes and 51 medium lakes) and by the larger uncertainty in the observations, given the size of these lakes and the larger spatial variability in the ice coverage. All the statistical results are summarized in Table S4 in the Supplement.

Furthermore, the fact that the ice-off date appears to be more impacted by the new parameterization than the ice-on one is explained by the larger sensitivity of the lake energy budget to the surface albedo during the spring months when the ice breaks, compared to the early winter months when the ice-on period starts for most of the lakes observed. This larger sensitivity could be the result of the different amounts of incoming radiation during these two periods – larger in spring compared to winter – as well as the different dynamics of the freezing/melting processes. Our results also show that the deeper the lake, the larger the impact of the ice fraction on the ice phenology. This was expected since the length of the ice-on/ice-off periods increases with lake size and is often positively correlated with depth, explaining the larger time gap between the two ways of parameterizing ice cover fraction and related albedo (prior vs. post).

4 Discussion and conclusion

The representation of lake freezing processes is crucial in LSMs to correctly simulate the water, energy, and carbon exchanges with the atmosphere. This paper presents the contribution of MODIS albedo observations to calibrate a new representation of the freezing processes in the ORCHIDEE lake module. A methodology was set up to estimate the water, snow, and ice albedo range of variations and the ice cover fraction from the MODIS albedo time series. New modeling of the ice fraction, based on Garnaud et al. (2022), was then implemented to better represent the lake surface albedo. Two simulations, with and without accounting for the lake ice fraction, were performed at the global scale to assess the contribution of the new developments on winter lake ice phenology. Our results clearly show the benefits of representing a partial ice coverage on the lake energy budget for the three depth classes modeled in ORCHIDEE. The ice-on, ice-off, and duration of the lake ice cover have been significantly improved, with discrepancies reduced to a few days for the timing of the ice-on and ice-off dates for all categories of lakes (shallow to deep lakes) and a more realistic duration period, with error reductions of up to 18 d.

However, the shallow lakes' ice-on date is still about 6 d in advance, and the ice-off period too is late by about 5 d. This larger residual error for shallow lakes compared to medium ones could be explained by the fact that this category of lakes represents a large proportion of small lakes not explicitly resolved by ORCHIDEE and for which the lake tile mean properties could present larger differences from the real ones compared to the larger medium lakes. Failure to account for this sub-tile variability should have a greater impact on the shallow lake category, for which the depth distribution is the largest. For the deep lakes, we can note a large improvement in the prediction of the ice-off period but still an overestimation of the ice duration by about 7 d.

In this work, we were confronted by the lack of lake ice cover fraction data and, above all, by the lack of homogeneity of these data, with some data documenting the start of the ice period and others the date of complete coverage. In addition, for large lakes, the observations are local and not always representative of the entire lake being modeled. This explains why we chose to diagnose the modeled ice phenology from the overall water temperature and not from the modeled ice fraction as it has been done for the two other lake categories. This approach is empirical and may not be appropriate for all lakes, but it allowed us to get a first picture of the added value of the fractional ice cover parameterization. In any case, we demonstrated here that remote sensing albedo products are extremely useful for supplementing ice cover measurements and for monitoring the seasonality of lake ice cover, especially as the surface albedo is crucial for correctly modeling water, energy, and carbon balances.

Despite the remaining biases and the model limitations due to the crude modeling of the freezing processes in FLake and the effective parameter uncertainties, we think that these developments represent a step forward and pave the way to better simulate the energy and mass exchanges at the atmosphere interface with ORCHIDEE and especially the water and GHG fluxes essential to study the impacts of climate and environmental changes on lakes. New observational datasets will help us to calibrate and evaluate future developments. In particular, the recent satellite-derived products providing global and consistent time series of water levels and extent, ice cover, albedo, and surface temperature, such as the ESA CCI Lakes project (https://climate.esa.int/en/projects/lakes/, last access: 16 June 2025), will be essential for our forthcoming works.