Surface processes and drivers of the snow water stable isotopic composition at Dome C, East Antarctica – a multi-dataset and modelling analysis

Water stable isotope records in polar ice cores have been largely used to reconstruct past local temperatures and other climatic information such as evaporative source region conditions of the precipitation reaching the ice core sites. However, recent studies have identified post-depositional processes taking place at the ice sheet's surface, modifying the original precipitation signal and challenging the traditional interpretation of ice core isotopic records. In this study, we use a combination of existing and new datasets of precipitation, snow surface, and subsurface isotopic compositions (δ¹⁸O and deuterium excess (d-excess)); meteorological parameters; ERA5 reanalyses; outputs from the isotope-enabled climate model ECHAM6-wiso; and a simple modelling approach to investigate the transfer function of water stable isotopes from precipitation to the snow surface and subsurface at Dome C in East Antarctica. We first show that water vapour fluxes at the surface of the ice sheet result in a net annual sublimation of snow, from 3.1 to 3.7 mm w.e. yr⁻¹ (water equivalent) between 2018 and 2020, corresponding to 12 % to 15 % of the annual surface mass balance. We find that the precipitation isotopic signal cannot fully explain the mean, nor the variability in the isotopic composition observed in the snow, from annual to intra-monthly timescales. We observe that the mean effect of post-depositional processes over the study period enriches the snow surface in δ¹⁸O by 3.0 ‰ to 3.3 ‰ and lowers the snow surface d-excess by 3.4 ‰ to 3.5 ‰ compared to the incoming precipitation isotopic signal. We also show that the mean isotopic composition of the snow subsurface is not statistically different from that of the snow surface, indicating the preservation of the mean isotopic composition of the snow surface in the top centimetres of the snowpack. This study confirms previous findings about the complex interpretation of the water stable isotopic signal in the snow and provides the first quantitative estimation of the impact of post-depositional processes on the snow isotopic composition at Dome C, a crucial step for the accurate interpretation of isotopic records from ice cores.

1 Introduction

Polar ice cores have been widely used in paleoclimate studies to reconstruct past atmospheric conditions, up to 800 000 years back in time (EPICA community members, 2004). Within the ice matrix of the core, δ¹⁸O and δD (Craig, 1961) measurements have been commonly used as a proxy for past atmospheric temperatures based on the observed relationships between the local atmospheric temperature and both the isotopic composition of precipitation samples (Dansgaard, 1964) and the snow across spatial transects in Antarctica (Lorius et al., 1969; Masson-Delmotte et al., 2008).

The second-order parameter deuterium excess (d-excess), defined as the deviation from the existing linear relationship between δ¹⁸O and δD (d-excess =δD − 8×δ¹⁸O, Dansgaard, 1964), is driven by physical processes involving non-equilibrium or kinetic fractionation of the different isotopes. The d-excess measured in ice cores has been interpreted as a proxy for moisture origin (Masson-Delmotte et al., 2005) and conditions at the moisture source region, such as sea-surface temperatures and relative humidity above the ocean's surface (Merlivat and Jouzel, 1979; Jouzel et al., 1982; Vimeux et al., 1999; Stenni et al., 2001; Uemura et al., 2008, 2012; Landais et al., 2021; Steen-Larsen et al., 2014b). Further kinetic processes along the distillation path of an air mass have been identified as contributing to the d-excess signal in precipitation, such as condensation in supersaturated conditions (Jouzel and Merlivat, 1984) or mixing of air masses from different origins (Risi et al., 2013).

The reconstruction of the climatic parameters from the water isotopic records in polar ice cores relies on the assumption that the isotopic composition of precipitation is preserved from snowfall to burial and transformation into ice. However, this has been challenged by recent field studies highlighting the significant role of post-depositional processes at the surface of both the Greenland and Antarctic ice sheets modifying the isotopic composition of precipitation after snowfall (Touzeau et al., 2016; Münch et al., 2017; Casado et al., 2018, 2021; Hughes et al., 2021; Wahl et al., 2021, 2022; Zuhr et al., 2023). The post-depositional processes commonly proposed as affecting the water isotopes at the ice sheet's surface include (i) water vapour exchanges between the snow and the lower atmosphere through sublimation and condensation cycles, (ii) wind redistribution, and (iii) diffusion of water vapour within the snowpack.

On the Greenland Ice Sheet, Steen-Larsen et al. (2014a) provided the first evidence of a co-variation in the snow surface and the lower-atmosphere water vapour isotopic compositions during precipitation-free periods in the summertime, suggesting seasonal vapour exchanges between the snow and the atmosphere. Wahl et al. (2021) later measured a depleted sublimation humidity flux compared to the snow surface, showing that fractionation of water isotopes was taking place during sublimation. Including fractionation during sublimation in a simple model also improved the prediction of the day-to-day variability in the snow isotopic composition during summertime (Wahl et al., 2022). Additional laboratory and modelling studies showed that sublimation leads to an enrichment in δ¹⁸O together with a lowering of d-excess in the snow surface and in the firn (Hughes et al., 2021; Dietrich et al., 2023).

In addition, diffusion of water vapour within the snowpack is driven by temperature and isotopic gradients and continuously affects the isotopic composition of the snow and firn (Johnsen et al., 2000; Gkinis et al., 2014). Field studies on both the Greenland and Antarctic ice sheets identified snow metamorphism associated with water vapour diffusion within the top layers of the snow as affecting the snow isotopic composition (δ¹⁸O and d-excess) after snowfall (Casado et al., 2021; Harris Stuart et al., 2023).

Lastly, the wind blowing at the surface of the ice sheet leads to a heterogeneous accumulation by redistributing the snow on the surface (Libois et al., 2014; Picard et al., 2019; Zuhr et al., 2021), which impacts the build-up of the isotopic signal in the snow (Zuhr et al., 2023). Wind is also hypothesized to impact the snowpack isotopic composition through forced pumping and ventilation of the snowpack (Town et al., 2008).

At Dome C, on the East Antarctic Plateau, previous studies have focused on a qualitative description of the impact of post-depositional processes on the snow surface (Casado et al., 2018), monitoring the atmospheric water vapour, snow surface, and precipitation isotopic compositions (Casado et al., 2016; Touzeau et al., 2016; Stenni et al., 2016; Dreossi et al., 2024a) or exploring the isotopic signature of snow metamorphism (Casado et al., 2021). However, a comprehensive understanding of the formation of the isotopic signal in the snow is still missing.

In this study we address the transfer function of stable water isotopes from precipitation to the snow surface and subsurface at Dome C, from intra-monthly to multi-annual timescales. We use a combination of existing and new datasets of the isotopic composition of precipitation, snow surface, and snow subsurface over 5 consecutive years (2017–2021); ERA5 reanalysis products; outputs from the isotope-enabled climate model ECHAM6-wiso; and a simple modelling approach to investigate the contribution of precipitation to the variability observed in the snow surface and subsurface isotopic composition. In addition, we use the meteorological parameters measured continuously on site to estimate the magnitude of sublimation and condensation fluxes between the surface and the lower atmosphere over 3 consecutive years (2018–2020) and qualitatively evaluate their impact on the snow isotopic composition at Dome C.

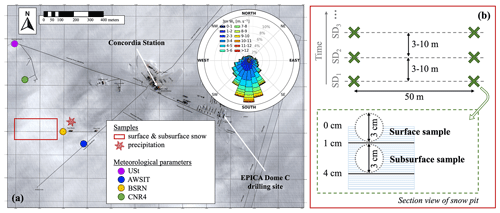
Figure 1 (a) Aerial view of Concordia Station. The coloured circles indicate the location of the meteorological measurements used in this study (Sect. 2.4), and red (rectangle and snowflake) marks the location of the samples presented in this study (Sect. 2.2 and 2.3). The wind rose for the 5-year 2017–2021 period of the wind at 3 m is shown in the upper right corner. Background image from CNES (Centre national d'études spatiales; Pléiades satellite image of Concordia Station, Antarctica, CNES 2016, distribution by Airbus Defence and Space). (b) Snow-sampling scheme taking place in the red rectangle in panel (a) (described in Sect. 2.2). SD stands for sampling day.

2 Data and methods

2.1 Geographical settings

Dome C is located on the East Antarctic Plateau (75.1° S, 123.3° E) at 3233 m above sea level and 1000 km from the coast and is the site where the permanent Concordia Station is installed (see location in Fig. 1a). The site is characterized by a mean annual temperature of about −52 °C (Genthon et al., 2021a) and a low accumulation rate of about 2.5 cm w.e. yr⁻¹ (Genthon et al., 2015). Due to the very small local slope and the location on a dome, the site is not subjected to strong katabatic winds, and the mean annual wind speed close to the surface is about 4 m s⁻¹ (Genthon et al., 2021a).

2.2 Snow surface and subsurface sampling

The regular sampling of the top few centimetres of the snow started in November 2013, and the sampling of a subsurface layer was added in 2017. Since then, the sampling strategy has remained the same. In this study we focus on the 5-year 2017–2021 period, where both surface and subsurface samples are available for analysis (see also Table 1).

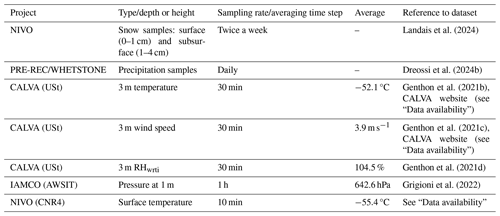
Table 1 Summary of samples and meteorological parameters used in this study and the reference to the data. The average values for temperature and wind speed are calculated over the 2017–2021 period; the relative humidity with respect to ice, the atmospheric pressure, and the surface temperature is calculated over 2018–2020.

The sampling takes place in the clean area about 800 m upwind of the main buildings (see location in Fig. 1a) twice a week and all year round. The samples are taken at two different locations 50 m apart along a straight line 3 to 10 m from the line of the previous sampling day. At each location along the line, a small vertical snow pit is dug (about 20 cm deep). The snow surface and subsurface are collected with two 50 mL Corning tubes, placed horizontally from the snow pit wall, at the surface and just below. The two snow samples correspond to depths of 0 to 1 cm deep for the surface sample and 1 to 4 cm for the subsurface sample, although the exact sampling depths were not recorded and may have slightly varied with the change of operator throughout the years or within 1 year due to for instance hard snow. The sampling scheme is illustrated in Fig. 1b.

Once the snow samples are collected, the tubes are sealed to prevent air exchange with the surrounding atmosphere and stored at temperatures well below freezing. The samples are shipped back once a year to the Laboratoire des Sciences du Climat et de l'Environnement (LSCE) (Centre national de la recherche scientifique, CNRS; Université Paris-Saclay) to measure their isotopic composition with a Picarro L2130-i laser spectrometer in liquid mode. We report the snow isotopic composition with delta notation in per mil (Craig, 1961) with respect to the Vienna Standard Mean Ocean Water (VSMOW) (Gonfiantini, 1978). The associated uncertainty (1 standard deviation including quality control samples, standards, and sample replicates) of these measurements is ±0.2 ‰ for δ¹⁸O and ±0.7 ‰ for δD, which yields an uncertainty of ±0.9 ‰ for d-excess (1 standard deviation).

2.3 Precipitation sampling

Since 2008, precipitation samples have been collected in the vicinity of Concordia Station, as part of different projects operated by the Italian National Research Program in Antarctica (PNRA). Part of this long time series has been published in Stenni et al. (2016) (2008–2010) and Dreossi et al. (2024a) (up to 2017). Here we extend the record of the precipitation isotopic composition to 2021 and use the time series from 2017 to 2021 for our analysis (see also Table 1).

Precipitation samples are collected every day on a wooden platform (bench) 1 m above the ground, covered by a PTFE surface and shielded by an 8 cm rail. The bench is situated about 800 m upwind of the main buildings (see location in Fig. 1a). The samples are collected at 10:00 local time (UTC+8), although the time has varied throughout the years depending on the operator. All the snow laying on the bench is collected, whether it is precipitation (including diamond dust), blown snow, or air hoar from atmospheric condensation. It cannot be ruled out that some of the samples might have undergone sublimation, especially during the summertime, because of exposure to 24 h solar radiation before sample collection (Stenni et al., 2016; Dreossi et al., 2024a). Each precipitation sample collected is weighted, and we use these weights as approximate estimates of the precipitation amounts (details in Sect. 2.5).

After collection, the plastic bag containing the sample is sealed and stored at temperatures well below freezing before annual shipment to the Ca' Foscari University of Venice, Italy, where the isotopic composition of the samples is measured with a Picarro laser spectrometer (L2130-i and L2140-i). We report the snow isotopic composition with delta notation in per mil (Craig, 1961) with respect to the Vienna Standard Mean Ocean Water (VSMOW) (Gonfiantini, 1978). The associated uncertainty (1 standard deviation of quality standard replicates) of these measurements is ±0.1 ‰ for δ¹⁸O and ±0.7 ‰ for δD, which yields an uncertainty of ±0.8 ‰ for d-excess (1 standard deviation).

2.4 Meteorological parameters

2.4.1 Atmospheric monitoring

Atmospheric parameters are measured continuously at Dome C by different weather stations and instruments installed near Concordia Station. For the 2017–2021 period of interest of this study, we used meteorological observations both from an automatic weather station operated by the PNRA (referred to as the AWSIT hereinafter) and from a 42 m meteorological tower (referred to as the USt hereinafter). A summary of the meteorological parameters used in this study is available in Table 1.

The AWSIT is located about 800 m upwind of Concordia Station (see location in Fig. 1a) and has been operating since 2005. Hourly data from the AWSIT are available in Grigioni et al. (2022). In this study, we use the atmospheric pressure measured at 1 m above the surface with a Vaisala PTB100 and a measurements from a 3-month period of the atmospheric temperature measured at 1.5 m by a Vaisala HMP45D. To match the same time step of the observations from the USt described below, we linearly interpolated the data to 30 min.

The USt is part of the CALVA project and located about 1 km from Concordia Station (see location in Fig. 1a). Meteorological instruments are installed at six different levels in the atmosphere and have been measuring continuously for more than 10 years (Genthon et al., 2021a). Due to snow accumulation, the sensors installed on the lowest level of the tower, at 3 m above the surface, were 40 cm closer to the surface in 2021 than in 2017. This height change was not considered here, and the lowest level of the tower is referred to as the 3 m level. All atmospheric parameters are sampled at 30 s intervals; however in this study we use the 30 min averages.

The atmospheric temperature is measured by a Pt100 in a Vaisala HMP155 combined sensor (thermohygrometer) placed in a mechanically aspirated shield (YOUNG 43502), and the wind speed and direction are measured by YOUNG 05103 aerovanes. The quality-controlled (QC) data for temperature and wind speed from 2010 to 2019 are available in Genthon et al. (2021b, c). Here we use this dataset from 2017 to 2019 and extend the record up to 2021 using the data from the same instruments available on the CALVA project website (see Table 1). Since the quality control of this additional period (2019–2021, referred as non-QC) is not guaranteed, we compared the QC and non-QC datasets during an overlapping period (not shown). We found a linear correlation (Pearson correlation coefficient) of 1.0 between the datasets for both temperature and wind speed. Therefore, we use the temperature and wind records from the USt between 2017 and 2021 in our analysis. Note that to fill a 3-month period of missing temperature data from the USt in 2021 (August to October), we use the temperature measured by the AWSIT (described above). The linear correlation (Pearson correlation coefficient) between the two temperature records during overlapping periods is 0.99 (not shown). The mean temperature and wind speed over the 2017–2021 period are summarized in Table 1. The dominant wind direction over the same period is shown in the wind rose in Fig. 1a.

Atmospheric water vapour content (or humidity) is also measured continuously by sensors installed on the meteorological tower. At Dome C, the surface atmosphere is very cold and frequently above saturation (Genthon et al., 2017), and in these conditions the standard humidity sensors fail to accurately measure the true atmospheric humidity content. To cope with this issue, a modified HMP155 was designed and installed on the USt at 3 m above the ground and proved its utility in measuring atmospheric moisture accurately, capturing supersaturation conditions, and expanding the temperature operating range of the humidity sensor (Genthon et al., 2017, 2022). The sensor reports atmospheric humidity with respect to liquid (RH_wrtl) water even at temperatures below 0 °C; we therefore convert RH_wrtl to the relative humidity with respect to ice (RH_wrti), as in Genthon et al. (2017) and Vignon et al. (2022) (see also Sect. S1 in the Supplement). The relative humidity at 3 m in the atmosphere and at 30 min resolution over the 2018–2021 period is available in Genthon et al. (2021d), and an analysis of the dataset is available in Genthon et al. (2022). Vignon et al. (2022) further provide estimations of the uncertainties for RH_wrti associated with the temperature and humidity measurements. In this study, we use this 3-year atmospheric humidity record to estimate water vapour fluxes at the snow surface. The method is described in the following section. The mean RH_wrti between 2018 and 2020 is indicated in Table 1.

2.4.2 Estimation of water vapour flux

During the period of interest of this study, no direct eddy-covariance (EC) flux measurements were available at Dome C. We instead make use of the standard atmospheric parameters measured on site (described in the previous section) to apply the bulk method as described in Genthon et al. (2017) and estimate water vapour fluxes between the surface and the 3 m atmospheric level. We report the 30 min average vapour fluxes during the 3-year 2018–2020 period in millimetres of water equivalent per time step.

The bulk method is based on the Monin–Obukhov (MO) similarity theory (Monin and Obukhov, 1954) and relies on several assumptions, which may not hold over the Antarctic Plateau (Vignon et al., 2016). Nevertheless, this method is still commonly used as the parameterization of surface turbulent fluxes in global and regional climate models (e.g. MAR model, Gallée and Schayes, 1994) and has been compared against eddy-covariance measurements both at Dome C on the East Antarctic Ice Sheet (sensible heat fluxes, Vignon et al., 2016) and at EastGRIP on the Greenland Ice Sheet (water vapour fluxes, Dietrich et al., 2024). It requires the following parameterizations: (1) the choice of roughness length for momentum (z₀), (2) the choice of functions representing the atmospheric stability, and (3) the calculation of the roughness lengths for water vapour (z_0q) and heat (z_0t). In their sensitivity study on the parameterization for sensible heat flux estimations at Dome C, Vignon et al. (2016) recommend the use of the stability functions from Holtslag and De Bruin (1988, referred to hereinafter as H88) for stable cases and the functions from Högström (1996) for unstable cases. They also recommend the use of a constant z₀ of 0.56 mm, which corresponds to the average value observed with an EC system over 1 year at Dome C (Vignon et al., 2016). For the parameterization of z_0q and z_0t, we use the same approach as in Genthon et al. (2017) and King et al. (2001), where $z_{\mathrm{0}}=z_{\mathrm{0}q}=z_{\mathrm{0}t}$. We used this parameterization (H88, $z_{\mathrm{0}}=z_{\mathrm{0}q}=z_{\mathrm{0}t}=\mathrm{0.56}\times {\mathrm{10}}^{-\mathrm{3}}$ m) as the reference parameterization. In addition, similarly to Vignon et al. (2016) and Genthon et al. (2017), we computed the water vapour fluxes using three other stability functions for stable conditions and a range of z₀ values to estimate the sensitivity of the final flux calculations of the parameterization (fluxes computed 16 times; see Table 2 for stability functions and a range of z₀ values). The range of z₀ values tested corresponds to the observed range over 1 year at Dome C (Vignon et al., 2016).

Table 2 Set of roughness lengths for momentum z₀ and stability functions for stable conditions used to compute water vapour fluxes with the bulk method. The reference parameterization is highlighted in bold.

To compute the water vapour fluxes, the bulk method requires temperature, wind speed, specific humidity, and pressure at the chosen atmospheric level (3 m here), as well as the snow surface temperature and the specific humidity at the surface.

For the atmospheric level, we use the temperature, wind, and humidity sensors installed 3 m above the surface on the USt together with the atmospheric pressure measured by the AWSIT (measurements described in Sect. 2.4.1). The formulas from Murphy and Koop (2005) are used to convert RH_wrti into specific humidity. To guarantee that the stationary conditions required to apply the bulk method are met, we removed all 30 min temperature and wind speed data for which the differences in temperature and wind speed with the previous half hour were above 2 °C and 1.1 m s⁻¹, respectively (Vignon et al., 2016). This represents 4 % of the whole dataset.

For the surface level, the snow surface temperature is computed from upward and downward longwave radiative fluxes with the same method as in Vignon et al. (2016) (their Eq. 1), using the same snow emissivity of 0.99 (value given by Brun et al., 2011, used in Vignon et al., 2016, and Genthon et al., 2017). We use the longwave radiative measurements from a CNR4 radiometer installed approximately 500 m away from the USt (see location in Fig. 1a). We average the data over 30 min to match the time resolution of the atmospheric measurements (originally 10 min resolution). Note that to fill a 3-month period of missing data in the CNR4 record at the end 2020, we use the data provided by the Baseline Surface Radiation Network (BSRN) (Lupi et al., 2021). The BSRN data were corrected for the CNR4 data during overlapping periods beforehand, due to a shift identified in the upward longwave flux measured by the BSRN pyrgeometer from December 2019 onwards. The mean surface temperature over the 2018–2021 time period is reported in Table 1. The specific humidity at the snow surface is converted from the surface temperature using the formulas from Murphy and Koop (2005) and assuming saturation.

In total, due to gaps in the different input datasets and the removal of non-stationary data, the missing data in the bulk estimations represent 9 % of the whole dataset.

2.5 Snow Isotopic Signal Generator (SISG)

To evaluate the contribution of precipitation to the isotopic variability observed in the snow surface and subsurface samples collected at Dome C (described in Sect. 2.2), we use a simple modelling approach to create synthetic snow layers based solely on the incoming precipitation. This approach was used in Casado et al. (2018, 2021) for a similar purpose but focused on the top layer of the snowpack. Here we re-implemented the same simple model and added the snow subsurface.

The model (referred to as the Snow Isotopic Signal Generator, SISG) simulates snow layers by stacking precipitation events until the thickness of the stacked precipitation reaches the depths of the snow surface and subsurface layers given as input of the model. The isotopic composition of each snow layer is then calculated as the weighted average (by precipitation amounts) isotopic composition of all precipitation events necessary to build the snow layers. We choose the input snow layers depths to be 0 to 1 cm for the surface layer and 1 to 4 cm for the subsurface layer to match the snow samples collected at Dome C. We run the model at daily resolution over the 5-year 2017–2021 period and retrieve the model results for the same days as the observations. Table 5 summarizes the five model experiments performed with different inputs for the precipitation isotopic composition and precipitation amounts (described in Sect. 2.5.1 and 2.5.2).

2.5.1 Daily precipitation amounts

The first SISG experiment uses a time series with a constant daily precipitation amount, calculated by dividing the mean annual accumulation at Dome C by 365 d. We use a mean annual accumulation of 2.5 cm w.e. yr⁻¹ estimated from stake measurements (Genthon et al., 2015). This corresponds to 8 cm yr⁻¹ using a snow density of 320 kg m⁻³, a typical value for the snow surface at Dome C (Picard et al., 2014; Genthon et al., 2015; Leduc-Leballeur et al., 2017). Hereinafter, we use this same snow density to convert precipitation amounts from snow water equivalent (SWE in mm w.e.) to snow depths (mm of snow) and inversely.

The second experiment uses the precipitation amount time series from the ERA5 reanalysis (Hersbach et al., 2020; dataset available in Hersbach et al., 2023). We use the 24 h average of the hourly snowfall rate data for the grid point nearest Concordia Station as an input to the model.

The third and fourth experiments use the observed precipitation amounts. As in Kopec et al. (2019), we assume that the weight of the daily precipitation samples collected on site for isotopic analysis (Sect. 2.3) is proportional to the amount of precipitation that has fallen over the day.

The fifth experiment uses the precipitation amounts given by the isotope-enabled global circulation model (GCM) ECHAM6-wiso (described in Cauquoin et al., 2019). The simulation was performed at a spatial resolution of 0.9° and nudged to ERA5 reanalyses (Cauquoin and Werner, 2021). The daily precipitation amounts were extracted for the grid point closest to Dome C. As the days with very low precipitation rates are not considered “precipitation days”, any precipitation rate below 0.0016 mm w.e. d⁻¹ is set to 0. Because East Antarctica is a very dry region, this threshold was chosen to be 10 times lower than the one commonly used for rain gauges (0.5 mm w.e. per month, e.g. used for the Global Network of Isotopes in Precipitation data). Note that such a threshold was not applied to the precipitation amounts given by ERA5. The ECHAM6-wiso outputs are available in Cauquoin and Werner (2024).

Because the cumulative sum of the precipitation amounts according to the observations, ERA5, and ECHAM6-wiso was too low (18, 18, and 32 cm of snow after 5 years, respectively) compared to the mean accumulation over 5 years at Dome C (40 cm of snow), we scaled up all daily precipitation amounts in the three time series to match the mean annual accumulation (8 cm yr⁻¹), acknowledging that this value is still underestimated because of net annual sublimation (Sect. 3.1). These scaled time series were used as inputs for the SISG model. The comparison of the three time series is shown in Fig. 5 (Sect. 3.3.1).

2.5.2 Daily precipitation isotopic composition

Due to some gaps in the daily precipitation samples collected at Dome C (described in Sect. 2.3), the time series of isotopic composition cannot be used as a direct input to the SISG model. Instead, we generate three artificial time series based on (1) the atmospheric temperature, (2) the precipitation-weighted mean annual isotope cycle in precipitation, and (3) the arithmetic-mean annual isotope cycle in precipitation. A comparison of these three artificial time series and the daily observations of the precipitation isotopic composition is shown in Fig. S4 (Sect. S4.1).

The first and second SISG experiment use the artificial time series based on the atmospheric temperature. The precipitation isotopic composition is calculated from the atmospheric temperature using the linear relationships between δ¹⁸O and δD of the precipitation samples and the 3 m daily mean temperature (Eqs. 1 and 2 in Sect. 3.3.3). Deuterium excess is then calculated from the theoretical values of δ¹⁸O and δD.

The third SISG experiment uses an artificial time series where all days in each month have the same isotopic composition as the corresponding monthly precipitation-weighted mean isotopic composition calculated over 5 years (results presented in Sect. 3.3.2 and Fig. 6c and f).

The fourth experiment uses an artificial time series where all days in each month have the same isotopic composition as the corresponding monthly arithmetic-mean isotopic composition calculated over 5 years (results presented in Sect. 3.3.2 and Fig. 6b and e).

The fifth experiment uses the daily precipitation isotopic composition modelled by ECHAM6-wiso. To prevent any unrealistic values because of a numerical effect when the precipitation amounts are very low, days with precipitation amounts below 0.0016 mm w.e. (Sect. 2.5.1) were associated with missing values of the precipitation isotopic composition. In addition, all data points outside of the range of the 5-year average ± 3 standard deviations were discarded (6 data points for δ¹⁸O and 20 data points for d-excess over 5 years). A comparison of the observed daily precipitation isotopic composition and ECHAM6-wiso simulations is shown in Fig. 6 (Sect. 3.3.2).

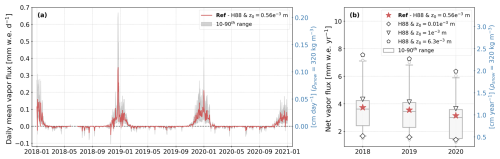
Figure 2 Water vapour flux at Dome C during the 2018–2020 period (positive for sublimation, negative for condensation). Panel (a) displays the 3-year time series of daily mean water vapour flux in millimetres of water equivalent. The red line corresponds to the reference parameterization, and the grey shading corresponds to the 10th–90th-percentile range of all parameterizations (described in Sect. 2.4.2). Panel (b) shows the net annual water vapour flux (sum of sublimation and condensation over 1 year). The red stars indicate the reference parameterization, and the three other black markers indicate the results using the stability function of H88 with a different z₀. The whiskers of the grey boxplots indicate the 10th–90th-percentile range of all parameterizations, and the grey circles indicate the outliers outside of this range. The secondary axis to the right in blue gives water vapour fluxes in centimetres of snow, using a snow density (ρ_snow) of 320 kg m⁻³ to convert SWE to snow height.

3 Results

3.1 Surface water vapour flux

The water vapour flux from the surface to the lower atmosphere for the 2018–2020 period estimated using the meteorological parameters measured at Dome C and the bulk method (described in Sect. 2.4.2) is shown in Fig. 2.

During the 3-year 2018–2020 period, the daily mean water vapour flux calculated with the reference parameterization varied from −0.05 (condensation) to 0.35 mm w.e. d⁻¹ (sublimation) (red line in Fig. 2a). The seasonality of water vapour fluxes over this period is characterized by sublimation during the summer months, while little condensation is observed during the rest of the year. This seasonal pattern is observed independently of the parameterization used in the bulk method, which only affects the magnitude of the fluxes (grey shading in Fig. 2a).

The net annual water vapour flux between 2018 and 2020 is positive, meaning a net annual sublimation of snow, regardless of which parameterization is used (grey boxplots in Fig. 2b). In 2018, 2019, and 2020, water vapour fluxes calculated with the reference parameterization led to a net mass loss of 3.7, 3.6, and 3.1 mm w.e., respectively (red stars in Fig. 2b), which is slightly higher than the net water vapour flux of 2.8 mm w.e. in 2015 (Genthon et al., 2017). These values correspond to 1.2, 1.1, and 1.0 cm of snow, respectively, using a snow density of 320 kg m⁻³ to convert from SWE to snow height. They are doubled when using a roughness length for momentum of $\mathrm{6.3}\times {\mathrm{10}}^{-\mathrm{3}}$ m instead of $\mathrm{0.56}\times {\mathrm{10}}^{-\mathrm{3}}$ m (black pentagons in Fig. 2b) and divided by approximately 2 when using a roughness length for momentum of $\mathrm{0.01}\times {\mathrm{10}}^{-\mathrm{3}}$ m (black triangles in Fig. 2b). The net annual water vapour fluxes are increased by 0.1 mm w.e. using a sensor height of 2 m above the surface instead of 3 m to consider height changes of the sensors (Sect. 2.4.1). During the summer periods only (from November to February, both months included), water vapour fluxes led to a net sublimation of 4.4, 4.1, and 3.8 mm w.e. in 2018, 2019, and 2020, respectively (not shown).

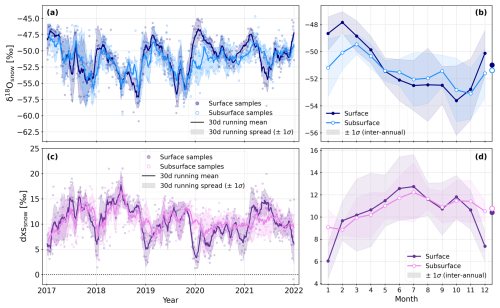
Figure 3 Observations of the snow surface and subsurface isotopic compositions at Dome C. Panels (a) and (c) show the 5-year time series (2017–2021) for δ¹⁸O and d-excess (dxs), respectively. The circles represent the horizontal average between the two samples taken at the two locations 50 m apart on the sampling lines (described in Sect. 2.2), and the solid lines show a 30 d running mean of these horizontal averages. The shaded area represents the 30 d running average of the spatial spread between the two samples taken at the two locations 50 m apart on the sampling lines (1 standard deviation). Panels (b) and (d) show the mean annual cycles (monthly means) of the snow surface and subsurface layers calculated over the 2017–2021 period for δ¹⁸O and d-excess, respectively. The shaded area represents the inter-annual variability around the mean annual cycle (1 standard deviation). The symbols on the right vertical axis indicate the mean isotopic composition of the snow surface and subsurface layers across all years. In all four panels, the darker colours correspond to the surface samples and the lighter colours correspond to the subsurface samples.

3.2 Snow isotopic composition

3.2.1 Temporal variations over 5 years

The 5-year time series of the snow surface and subsurface isotopic composition (δ¹⁸O and d-excess) is displayed in Fig. 3, together with the respective mean annual cycle (monthly means) for each layer over the whole period.

Considering all samples collected during the 5-year period, the δ¹⁸O in the snow has a large amplitude, with values ranging from −60.9 ‰ to −45.1 ‰ in the surface layer and from −59.8 ‰ to −44.7 ‰ in the subsurface layer (circles in Fig. 3a). Both snow layers have a higher δ¹⁸O during the summertime and lower values in the wintertime (lines in Fig. 3a).

This seasonality is further visible in their respective mean annual cycles (Fig. 3b), with the snow surface δ¹⁸O highest in February (−47.8 ‰) and lowest in October (−53.6 ‰, dark blue in Fig. 3b). Compared to the snow surface, the mean annual cycle in the snow subsurface has a smaller amplitude and is shifted in time, with a maximum in March (−49.5 ‰) and a minimum in November (−53.1 ‰, light blue in Fig. 3b).

The temporal variation in the snow surface δ¹⁸O is characterized by sharp increases during the summertime followed by slow decreases through the winter, which is particularly clear for the summers of 2017–2018, 2018–2019, and 2019–2020 (dark blue line in Fig. 3a). This asymmetric seasonal pattern has been previously identified by Casado et al. (2018) for earlier years and is reflected in the mean annual cycle of the snow surface δ¹⁸O (dark blue in Fig. 3b). A similar pattern is visible in the snow subsurface, although with a reduced amplitude (light blue in Fig. 3a and b).

The variations in δ¹⁸O in the snow surface and the subsurface generally follow each other, except for specific periods when the surface and subsurface differ by several per mil, for example at the beginning of 2020 (solid lines and shaded areas in Fig. 3a). This difference between the two snow layers is reflected in their respective mean annual cycles and is the largest during the summer (Fig. 3b).

The overall mean δ¹⁸O of the snow surface and subsurface is $-\mathrm{51.0}\pm \mathrm{0.2}$ ‰ and $-\mathrm{51.4}\pm \mathrm{0.1}$ ‰, respectively (dark- and light-blue dots in Fig. 3b). The uncertainty around these mean values corresponds to the standard error of the mean (SEM), calculated using the effective number of independent samples in the time series (Bretherton et al., 1999; see also Sect. S2 in the Supplement).

As for δ¹⁸O, the snow surface and subsurface show large variations in d-excess over the 5-year period (Fig. 3c). Considering all samples collected over the period, d-excess ranges from −0.9 ‰ to 21.0 ‰ in the snow surface and from 2.8 ‰ to 21.1 ‰ in the snow subsurface (dots in Fig. 3c). In opposition to δ¹⁸O, high d-excess values are encountered in the wintertime and lower d-excess are in the summertime (lines in Fig. 3c).

This seasonality in d-excess is further reflected in the mean annual cycles of both snow layers (Fig. 3d). The snow surface d-excess is the highest in July (12.7 ‰) and the lowest in January (6.0 ‰, dark purple in Fig. 3d). As for δ¹⁸O, the mean annual cycle in the snow subsurface has also a smaller amplitude compared to the surface layer, with a maximum in July (12.2 ‰) and a minimum in February (8.9 ‰, violet in Fig. 3d). However, contrary to δ¹⁸O, the mean annual cycle in the snow subsurface does not show a clear time lag compared to the surface. Instead, the variations in the subsurface follow the ones of the surface, apart from the summer months of January and December where the subsurface has larger d-excess than the surface layer (Fig. 3d). This summertime difference in d-excess between the surface and subsurface layers is also visible in the time series, in particular during the summer of 2019–2020 (Fig. 3c).

Lastly, the variations in d-excess in the snow surface do not have the same pattern as those in δ¹⁸O (sharp increase in summertime and slow decrease in the wintertime). Instead, the d-excess in the snow surface shows a more symmetric seasonal evolution than δ¹⁸O (dark-purple line in Fig. 3c). This symmetry is reflected in the mean annual cycle in d-excess of the snow surface (Fig. 3d).

The overall mean d-excess of the snow surface and subsurface is 10.4±0.2 ‰ and 10.8±0.1 ‰, respectively (dark-purple and violet dots in Fig. 3d). The uncertainty around these mean values corresponds to the SEM, calculated the same way as for δ¹⁸O.

3.2.2 Vertical difference between the snow surface and subsurface

In the previous section, we identified a seasonal pattern in the vertical difference between the snow surface and subsurface isotopic compositions (δ¹⁸O and d-excess). The vertical difference is defined here as the isotopic composition of the surface layer minus the isotopic composition of the subsurface layer.

Considering all samples collected during the 5-year period (displayed as dots in Fig. 3a and c), the minimum difference in δ¹⁸O between the snow surface and the subsurface is −7.5 ‰ (surface depleted in δ¹⁸O compared to subsurface) and the maximum difference is 9.1 ‰ (surface enriched in δ¹⁸O compared to subsurface). The corresponding minimum and maximum values in the vertical difference in d-excess are −10.6 ‰ and 12.3 ‰, respectively.

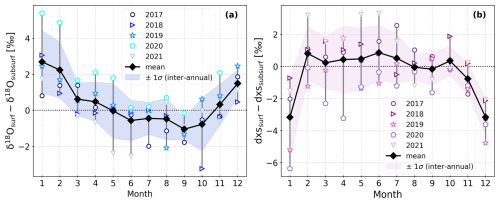
Figure 4 Mean annual cycle (monthly means) of the observed vertical difference between the snow surface and subsurface isotopic composition at Dome C. Panel (a) shows the mean annual cycle of the vertical difference in δ¹⁸O; panel (b) shows the mean annual cycle of the vertical difference in d-excess. In both panels, the black diamonds correspond to the overall monthly means calculated over the 2017–2021 period. The shaded area shows the inter-annual variability in individual years around the overall monthly means (1 standard deviation), and the coloured markers show the monthly means for each individual year.

The mean annual cycles of the vertical difference in δ¹⁸O and d-excess between the two depths show a clear seasonal pattern (Fig. 4a and b). The snow surface is relatively enriched in δ¹⁸O from November to April and relatively depleted from May to October compared to the subsurface (black diamonds in Fig. 4a). The maximum vertical difference is 2.7 ‰ and occurs in January; the minimum difference is −1.0 ‰ and occurs in September. However, compared to the inter-annual variability within the averaging period (coloured markers and shaded area in Fig. 4a), only the months of January, February, September, and December show a substantial vertical difference in δ¹⁸O between the snow layers.

In opposition to δ¹⁸O, the snow surface has a lower d-excess in the summer months of January and December, with a maximum monthly mean difference of −3.2 ‰ in January (black diamonds in Fig. 4b). The minimum difference of 0.9 ‰ is found in June and is, however, negligible compared to the inter-annual variability within the averaging period (coloured markers and shaded area in Fig. 4b).

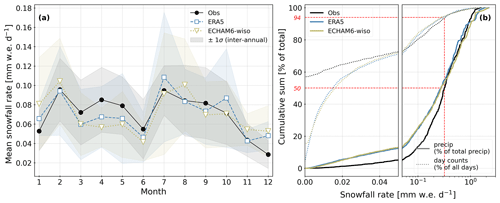
Figure 5 Precipitation amounts at Dome C from observations, ERA5 reanalyses, and ECHAM6-wiso simulation outputs. Panel (a) shows the mean annual cycles (monthly means) of the daily precipitation amounts (in mm w.e. d⁻¹) calculated over the 2017–2021 period. Panel (b) shows the cumulative sum of precipitation over 5 years, reported as a percentage of the total amount of precipitation (black and coloured thick lines), and the cumulative sum of days (black and coloured dotted lines) against the daily snowfall rate in mm w.e. d⁻¹. The dashed red lines guide the reading of the plot to get the snowfall rate and percentage of days responsible for 50 % of the total snowfalls. Note the linear x axis between 0 and 0.05 mm w.e. d⁻¹ and logarithmic scale above.

3.3 Precipitation amounts and isotopic composition in observations, ECHAM6-wiso, and ERA5 reanalyses

3.3.1 Precipitation amounts

To evaluate whether ERA5 reanalysis data and ECHAM6-wiso results correctly capture the precipitation amounts at Dome C, we compare them with the observations in Fig. 5 (all three time series scaled to the observed mean annual accumulation, Sect. 2.5).

Over the whole 5-year period, the precipitation amounts in the observations, ERA5, and ECHAM6-wiso have a comparable seasonal amplitude: from 0.03 to 0.1 mm w.e. d⁻¹ for the observations (black in Fig. 5a), from 0.04 to 0.11 mm w.e. d⁻¹ for ERA5 (blue in Fig. 5a), and from 0.04 to 0.1 mm w.e. d⁻¹ for ECHAM6-wiso (light green in Fig. 5a). The three precipitation time series show a very similar seasonality, with an increase in the snowfall rate at the end of the summertime (from January to February) and in the middle of the winter (from June to July), as well as a decrease from July to December (Fig. 5a).

All three precipitation cumulative sums given by the observations, ERA5, and ECHAM6-wiso show a similar shape with a faster increase with increasing snowfall rates (plain lines in Fig. 5b). The cumulative sums from ERA5 and ECHAM6-wiso are superposed in the whole range of snowfall rates, whereas the precipitation cumulative sum is lower for the observations up to 0.35 mm w.e. d⁻¹, where the three curves meet.

In the observations, 50 % of the total snowfall over 5 years is due to precipitation events with a snowfall rate above 0.32 mm w.e. d⁻¹ (dashed red lines and plain black line in Fig. 5b), which represent only 6 % of all days within the 5-year period (dashed red lines and dotted black line in Fig. 5b). It should be noted that these results are dependent on the precipitation samples collected on site, which have biases (i.e. too little precipitation to collect or blown snow instead of true precipitation, Sect. 2.3). Similarly, in ERA5 precipitation, 50 % of the total snowfall is due to precipitation events with snowfall rates above 0.27 mm w.e. d⁻¹, which corresponds to 7 % of all days (Fig. 5b). In ECHAM6-wiso simulations, 50 % of the total snowfall is due to precipitation events with snowfall rates above 0.28 mm w.e. d⁻¹, which corresponds to 6 % of all days (Fig. 5b).

For all three time series (observations, ERA5, and ECHAM6-wiso), we find that the largest precipitation events described above (contributing to 50 % of the total accumulation) occur alongside temperatures higher than average. In the observations, the mean temperature during all precipitation days within the 5-year period and with snowfall rates above 0.32 mm w.e. d⁻¹ is 2.8 °C warmer than the mean temperature over the whole period (−52.1 °C). For ERA5, the mean temperature (given by ERA5) during the largest precipitation events with snowfall rates above 0.27 mm w.e. d⁻¹ is 8.1 °C above the mean temperature of −49.9 °C. Lastly, for ECHAM6-wiso, the mean temperature (given by the model) during the largest precipitation events with snowfall rates above 0.28 mm w.e. d⁻¹ is 5.7 °C above the mean temperature of −51.1 °C. These results are in agreement with previous studies (Kino et al., 2021; Servettaz et al., 2023).

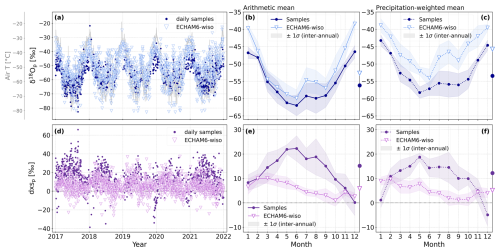
Figure 6 Observed and modelled precipitation isotopic composition at Dome C. Panels (a) and (d) show the 5-year time series (2017–2021) for δ¹⁸O and d-excess (dxs), respectively. The dots represent the daily samples collected in the field (sample description in Sect. 2.3), and the triangles represent the daily precipitation isotopic composition modelled by ECHAM6-wiso (description of simulations in Sect. 2.5). In grey in panel (a) the atmospheric temperature measured at 3 m is displayed (described in Sect. 2.4.1). Panels (b) and (e) show the observed (dots) and ECHAM6-wiso-modelled (triangles) mean annual cycle, calculated over the 2017–2021 period (arithmetic means) for δ¹⁸O and d-excess, respectively. The shaded area represents the inter-annual variability around the mean annual cycle (1 standard deviation). The markers on the right vertical axis indicate the mean observed and simulated precipitation isotopic composition over the whole period. Panels (c) and (f) are the same as (b) and (e) but show the weighted monthly means (by precipitation amounts).

3.3.2 Precipitation isotopic composition

The daily temporal variability in the precipitation isotopic composition (δ¹⁸O and d-excess) from both observations and ECHAM6-wiso simulations is presented in Fig. 6, together with the corresponding mean annual cycles over the same period. In this section, all mean values across the whole period are given with an uncertainty corresponding to the SEM (see Sect. 3.2.1).

The observed precipitation δ¹⁸O shows a large seasonal cycle, ranging from −82.6 ‰ to −21.8 ‰, with higher values in the summertime and lower values in the wintertime (dark-blue dots in Fig. 6a), following the atmospheric temperature (grey line in Fig. 6a). The mean value over the whole period is $-\mathrm{56.2}\pm \mathrm{0.5}$ ‰ (dark-blue dot in Fig. 6b). In comparison, the daily precipitation δ¹⁸O modelled by ECHAM6-wiso shows a seasonality similar to the observations, with higher and lower δ¹⁸O in the summertime and wintertime, respectively, and a comparable amplitude with values ranging from −82.9 ‰ to −22.8 ‰ (blue triangles in Fig. 6a). However, the mean modelled δ¹⁸O in precipitation over the whole period is higher than the observed one ($-\mathrm{52.7}\pm \mathrm{0.5}$ ‰, blue triangle in Fig. 6b). The precipitation-weighted overall means are higher than the arithmetic means, for both observations and ECHAM6-wiso simulations ($-\mathrm{53.4}\pm \mathrm{0.5}$ ‰ and $-\mathrm{45.7}\pm \mathrm{0.5}$ ‰, respectively, dark-blue dot and blue triangle in Fig. 6c).

The observed mean annual cycle (arithmetic monthly means) in the precipitation δ¹⁸O is characterized by the highest δ¹⁸O in December (−46.5 ‰) and the lowest δ¹⁸O in June (−62.0 ‰, dark-blue dots in Fig. 6b). In comparison, the modelled mean annual cycle shows a seasonality similar to but systematically higher than the observed one, ranging from −59.9 ‰ in June to −38.4 ‰ in December (blue triangles in Fig. 6b). The difference between the observations and ECHAM6-wiso results is especially large in the summertime (November to January), with a maximum difference of 8.1 ‰ in December.

The observed and modelled precipitation-weighted δ¹⁸O mean annual cycles also show a similar seasonality (Fig. 6c). However, the bias between ECHAM6-wiso and observations is visible throughout the whole year, with a maximum difference of 10.2 ‰ in October (Fig. 6c). The large difference between the observations and ECHAM6-wiso during the summertime (arithmetic mean, Fig. 6b) decreases when the precipitation δ¹⁸O is weighted by the precipitation amounts (Fig. 6c).

The d-excess in the precipitation samples also shows a large seasonal amplitude, with values ranging from −38.6 ‰ to 65.9 ‰ (dark-purple dots in Fig. 6d); d-excess is in anti-phase to δ¹⁸O, with maximum values found in the wintertime and minimum values found in the summertime, which have been previously identified by Stenni et al. (2016) and Dreossi et al. (2024a). The mean observed precipitation d-excess over the whole period is equal to 15.2±0.5 ‰ (dark-purple dot in Fig. 6e). In comparison, the daily precipitation d-excess modelled by ECHAM6-wiso has a lower amplitude, with values ranging from −26.0 ‰ to 37.2 ‰ (violet triangles in Fig. 6d). The overall mean modelled d-excess is also lower than the observations with a value of 5.8±0.3 ‰ (violet triangle in Fig. 6e). The precipitation-weighted overall means are lower than the arithmetic means, for both observations and ECHAM6-wiso results (12.2±0.5 ‰ and 5.1±0.3 ‰, respectively, dark-purple dot and violet triangle in Fig. 6f).

The observed mean annual cycle (arithmetic monthly means) in the precipitation d-excess is characterized by the lowest value in December (0.1 ‰) and the highest value in June (22.3 ‰, dark-purple dots in Fig. 6e). In comparison, the mean annual cycle in the modelled precipitation d-excess has a lower amplitude than the observed one and a different timing in the minimum and maximum (from 1.0 ‰ in October to 10.1 ‰ in March, violet triangles in Fig. 6e). As opposed to δ¹⁸O, the difference between the observations and ECHAM6-wiso simulations is large in the wintertime (April to October), with a maximum difference of 15.9 ‰ in June.

Compared to the arithmetic-mean annual cycles for d-excess, the bias between the precipitation-weighted monthly means in ECHAM6-wiso and the observations is reduced in the winter but increased in the summer months of January and December (Fig. 6f). The maximum difference is also lowered to 12.6 ‰ and found later in the year (August, Fig. 6f).

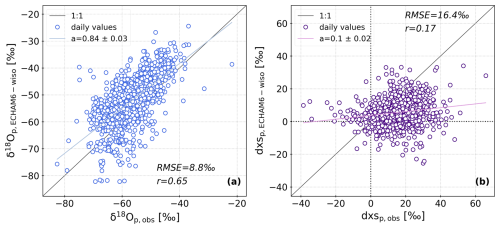
Figure 7 Daily observed precipitation (a) δ¹⁸O and (b) d-excess versus daily modelled precipitation isotopic composition at Dome C. All precipitation samples collected between 2017 and 2021 are shown (described in Sect. 2.3), together with the corresponding daily values from ECHAM6-wiso simulation results (described in Sect. 2.5). Note that due to missing observations and post-processing of ECHAM6-wiso outputs, 886 of 1826 d are shown in panel (a) and 882 of 1826 d are shown in panel (b). The coloured lines correspond to the linear fits between the observations and the model results (slope coefficients given in legends, both linear regression coefficients are significant with a p value <0.001).

We evaluate the performance of ECHAM6-wiso to model the observed daily precipitation isotopic composition in Fig. 7. The daily precipitation δ¹⁸O modelled by ECHAM6-wiso shows good agreement with the observations, with a linear regression slope of 0.84±0.03 (1.0 being the perfect fit), a Pearson correlation coefficient of 0.65, and a root mean square error (RMSE) of 8.8 ‰ (Fig. 7a). The model mostly overestimates the observations with an increase in bias towards more depleted values (Fig. 7a). For d-excess, the ECHAM6-wiso model results only poorly represent the observations, with a linear regression slope of 0.1±0.02, a Pearson correlation coefficient of 0.17, and an RMSE of 16.4 ‰ (Fig. 7b). These results are similar to the comparison of the precipitation samples and ECHAM6-wiso simulation results between 2008 and 2017 (RMSE = 6.1 ‰ for δ¹⁸O and 13.6 ‰ for d-excess, Dreossi et al., 2024a).

3.3.3 Isotope–temperature relationships in precipitation

From the isotopic composition of the daily precipitation samples collected on site and the corresponding daily average temperature measured at 3 m above the surface (described in Sect. 2.4.1), we determine the following linear relationships over the 2017–2021 time period:

$$\begin{array}{}\text{(1)}& {\displaystyle }{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{p}}=\mathrm{0.47}\pm \mathrm{0.01}\times T_{\mathrm{3}\mathrm{m}}-\mathrm{31.2}\pm \mathrm{0.6}\mathrm{‰}\text{(2)}& {\displaystyle }\mathit{\delta }{\mathrm{D}}_{\mathrm{p}}=\mathrm{3.3}\pm \mathrm{0.1}\times T_{\mathrm{3}\mathrm{m}}-\mathrm{262}\pm \mathrm{4}\mathrm{‰}.\end{array}$$

Equation (1) has a coefficient of determination (R²) of 0.62, and Eq. (2) has an R² of 0.63. Both linear regression slopes are significant (p values <0.001, Fig. A1). There are no significant changes in the linear relationships if using the daily mean atmospheric temperature of the day before the sample collection day instead of the daily mean temperature of the sampling day itself (Fig. A1). The slopes in Eqs. (1) and (2) are also comparable to the ones found for the 2008–2010 period (0.49±0.02 for δ¹⁸O, Stenni et al., 2016) and for the 2008–2017 period (0.52±0.01 for δ¹⁸O, 3.52±0.07 for δD, Dreossi et al., 2024a).

In ECHAM6-wiso simulations, the linear relationships between the modelled precipitation isotopic composition and the modelled temperature differ from the observed ones:

$$\begin{array}{}\text{(3)}& {\displaystyle }\begin{array}{rl}{\mathit{\delta }}^{\mathrm{18}}{\mathrm{O}}_{\mathrm{p},\mathrm{ECHAM}\mathrm{6}\mathrm{wiso}}& =\mathrm{0.68}\pm \mathrm{0.02}\times T_{\mathrm{2}\mathrm{m},\mathrm{ECHAM}\mathrm{6}\mathrm{wiso}}\\ & -\mathrm{17.0}\pm \mathrm{0.9}\mathrm{‰}\end{array}\text{(4)}& {\displaystyle }\begin{array}{rl}\mathit{\delta }{\mathrm{D}}_{\mathrm{p},\mathrm{ECHAM}\mathrm{6}\mathrm{wiso}}& =\mathrm{5.3}\pm \mathrm{0.1}\times T_{\mathrm{2}\mathrm{m},\mathrm{ECHAM}\mathrm{6}\mathrm{wiso}}\\ & -\mathrm{134}\pm \mathrm{6}\mathrm{‰}.\end{array}\end{array}$$

These relationships are also established over the period from 2017 to 2021. Equation (3) has an R² of 0.54, and Eq. (4) has an R² of 0.57. Both linear regression slopes are significant (p values <0.001, Fig. A2).

3.4 Contribution of precipitation to the snow isotopic composition

In this section we investigate the contribution of the precipitation isotopic composition to the intra-monthly and seasonal variability in the snow δ¹⁸O and d-excess at Dome C by comparing the observations and the results from the SISG experiments (described in Sect. 2.5).

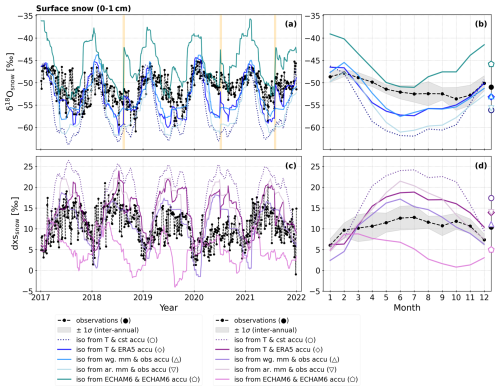
Figure 8 Comparison between observed and simulated snow surface (0 to 1 cm depth) isotopic compositions at Dome C. Panels (a) and (c) show the 5-year time series (2017–2021) of δ¹⁸O and d-excess (dxs), respectively. The black dots represent the horizontal average between the two samples taken at the two locations 50 m apart on the sampling lines (described in Sect. 2.2, also presented in Fig. 3). The coloured lines (dotted and plain) represent the different SISG model experiments (described in Table 3). In panel (a), the vertical orange shadings highlight three specific events (August 2018, July 2020, August 2021). Panels (b) and (d) show the mean annual cycles (monthly means) of δ¹⁸O and d-excess, respectively, calculated over the 2017–2021 period. The black dots and line represent the observations, and the shaded area represents the inter-annual variability around the mean annual cycle (1 standard deviation). The coloured lines (dotted and plain) represent the different SISG experiments (described in Table 3). The markers on the right vertical axis indicate the mean isotopic composition of the observed and simulated snow surface over 5 years (see Table S2 in Sect. S4.2).

Table 3 Experiments performed with the SISG model, with respective inputs for the daily precipitation amounts (described in Sect. 2.5.1) and the daily isotopic composition of precipitation (described in Sect. 2.5.2). Note that the precipitation amounts from the observations, ERA5, and ECHAM6-wiso are scaled to match the mean annual accumulation observed at Dome C.

3.4.1 Snow surface

Some of the features observed in the snow surface δ¹⁸O variability are reproduced by the different experiments performed with the SISG model (Fig. 8a). For example, the observed summer δ¹⁸O values in the snow surface are correctly reproduced in four out of five experiments (“iso from T & cst accu”, “iso from T & ERA5 accu”, “iso from wg. mm & obs accu”, “iso from ar. mm & obs accu”; not correctly reproduced in “iso from ECHAM6 & ECHAM6 accu”). All five experiments correctly reproduce the seasonality in δ¹⁸O observed in the snow surface, with higher values in the summer and lower values in the winter (Fig. 8a and b). In addition, the two model experiments iso from T & ERA5 accu and iso from ECHAM6 & ECHAM6 accu reproduce some of the short-term increases in the snow surface δ¹⁸O during the wintertime, such as the events in August 2018, July 2020, or August 2021 (orange shadings in Fig. 8a). The other three experiments fail to reproduce these events because of the inputs given to the SISG model: either constant daily precipitation that equally weighs the days with high or low δ¹⁸O (iso from T & cst accu) or a daily isotopic composition that does not vary within 1 month and fails to represent the high δ¹⁸O events (iso from wg. mm & obs accu and iso from ar. mm & obs accu, Fig. S4 in Sect. S4.1).

However, regardless of the model experiment, the amplitude of the seasonal cycle in the snow surface δ¹⁸O is systematically overestimated compared to the observations (Fig. 8a and b). All five experiments fail to reproduce the slow decrease in δ¹⁸O during the wintertime observed in the snow surface. This is particularly visible for the winters of 2019 and 2020 where all simulated snow surface has δ¹⁸O values that are too low (Fig. 8a). Most of the short-term variations in the snow δ¹⁸O occurring within the month are also not reproduced by any of the experiments (Fig. 8a). In addition, the experiment iso from ECHAM6 & ECHAM6 accu gives δ¹⁸O values that are too high compared to the observations throughout the whole time period (blue-green lines in Fig. 8a and b), which is consistent with the positive bias between the precipitation-weighted δ¹⁸O modelled by ECHAM6-wiso and the observations, as identified in Sect. 3.3.2 (Fig. 6c).

As for δ¹⁸O, all model experiments fail to reproduce the variability in d-excess observed in the snow surface. Although in some of the experiments (iso from T & cst accu, iso from T & ERA5 accu, iso from wg. mm & obs accu, iso from ar. mm & obs accu), the low summer d-excess in the snow surface is well captured (Fig. 8c), all the simulated mean annual cycles have too large an amplitude (Fig. 8d). The experiment iso from ECHAM6 & ECHAM6 accu provides worse results than the other experiments (pink line in Fig. 8c and d), which can be explained by the poor representation of the observed precipitation-weighted annual cycle in d-excess by ECHAM6-wiso simulations, as identified in Sect. 3.3.2 (Fig. 6f).

To evaluate which SISG experiment best represents the observed snow surface isotopic composition, we perform a linear regression between all modelled and observed monthly means of δ¹⁸O and d-excess in the 5-year period. The linear regression slope (a) and the RMSE of the model results and the observations are summarized in Table 4.

Table 4 Linear regression slope (a) and RMSE of the observed and modelled monthly mean isotopic composition of the surface layer (δ¹⁸O in roman font, d-excess in brackets and italic). The sample size is 60 for all experiments except iso from wg. mm & obs accu and iso from ar. mm & obs accu (n=59). All linear slopes are significant (p value <0.05), except the ones marked with an asterisk (*, p value >0.05).

The best representation of the observed δ¹⁸O in the snow surface is given by the experiment iso from wg. mm & obs accu (a=1.1, RMSE = 3.4 ‰, Table 4). The experiment iso from T & cst accu results in the highest RMSE of all configurations tested (RMSE = 6.9 ‰, Table 4), which is expected due to the intermittent nature of precipitation at Dome C. In addition, the experiment iso from ECHAM6 & ECHAM6 accu gives a high RMSE (6.3 ‰, Table 4).

For d-excess, out of the five model experiments, iso from wg. mm & obs accu gives the lowest RMSE (3.9 ‰, Table 4). As for δ¹⁸O, the experiment iso from T & cst accu results in the highest RMSE (8.8 ‰, Table 4). Lastly, the experiment iso from ECHAM6 & ECHAM6 accu has an RMSE of 7.1 ‰ and a non-significant slope compared to the observations (p value >0.05).

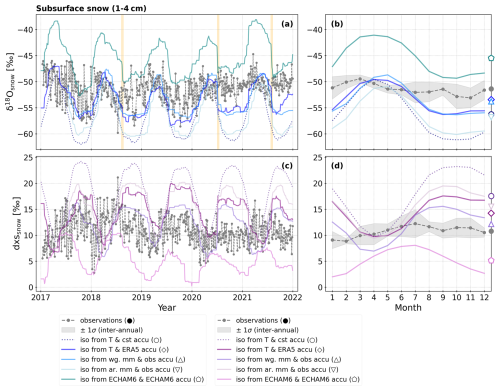
Figure 9 Comparison between observed and simulated snow subsurface (1 to 4 cm depth) isotopic compositions at Dome C. Panels (a) and (c) show the 5-year time series (2017–2021) of δ¹⁸O and d-excess (dxs), respectively. The grey dots represent the horizontal average between the two samples taken at the two locations 50 m apart on the sampling lines (described in Sect. 2.2, also presented in Fig. 3). The coloured lines (dotted and plain) represent the different SISG model experiments (described in Table 3). Panels (b) and (d) show the mean annual cycles (monthly means) of δ¹⁸O and d-excess, respectively, calculated over the 2017–2021 period. The grey dots and line represent the observations, and the shaded area represents the inter-annual variability around the mean annual cycle (1 standard deviation). The coloured lines (dotted and plain) represent the different SISG experiments (described in Table 3). The markers on the right vertical axis indicate the mean isotopic composition of the observed and simulated snow subsurface over 5 years (see Table S2 in Sect. S4.2).

3.4.2 Snow subsurface

For δ¹⁸O in the snow subsurface, we find comparable results as in the surface layer. We find that all five model experiments fail to capture the short-term variations in the snow subsurface, and all experiments result in too large an amplitude in the mean annual cycle over 5 years (Fig. 9a and b). The systematic positive bias given by the model experiment iso from ECHAM6 & ECHAM6 accu is also visible in the simulated subsurface layer (Fig. 9a and b). In addition, all five model experiments provide a mean annual cycle shifted compared to the observed one, with a maximum δ¹⁸O occurring 1 to 2 months later than the observed maximum (Fig. 9b).

For d-excess, we find that four out of five of the model experiments (iso from T & cst accu, iso from T & ERA5 accu, iso from wg. mm & obs accu, iso from ar. mean & obs accu) give d-excess variations that are too high over time, which is reflected in too large an amplitude of the modelled mean annual cycle compared to the observed one (Fig. 9c and d). As for δ¹⁸O, the annual cycle in d-excess modelled in these three experiments is shifted, with the minimum in d-excess found 2 months later than the observed one (Fig. 9d).

On the other hand, although giving a d-excess value that is too low compared to the observations, the experiment iso from ECHAM6 & ECHAM6 accu results in a mean annual cycle similar to that in the observations, with a minimum d-excess in the summertime and maximum d-excess during the wintertime (pink line in Fig. 9d). However, because the precipitation d-excess modelled by ECHAM6-wiso poorly represents the observations (Fig. 6e and f), we argue that the good resemblance (besides the negative bias) between the modelled and observed d-excess in the snow subsurface is due to compensating effects between the precipitation d-excess and precipitation amounts.

As for the snow surface, we perform a linear regression between all modelled and observed monthly means of δ¹⁸O and d-excess. The linear slope (a) and the RMSE of the model results and the observations are summarized in Table 5.

Table 5 Linear regression slope (a) and RMSE of the observed and modelled monthly mean isotopic composition of the subsurface layer (δ¹⁸O in roman font, d-excess in brackets and italic). The sample size is 60 for all experiments except iso from wg. mm & obs accu and iso from ar. mm & obs accu (n=54). All linear slopes are significant (p value <0.05), except the ones marked with an asterisk (*, p value >0.05).

Contrary to the surface layer, the best representation of δ¹⁸O in the subsurface layer is given by the experiment iso from T & ERA5 accu (a=0.8, RMSE = 3.3 ‰, Table 5). The model experiment iso from ECHAM6 & ECHAM6 accu gives the best correlation with observations, although with the highest RMSE (a=1.1, RMSE = 6.7 ‰, Table 5).

For d-excess in the snow subsurface, only the experiment iso from ECHAM6 & ECHAM6 accu gives a significant slope with the observations (a=0.8, RMSE = 6.0 ‰, Table 5), while all other experiments have a non-significant linear slope with the observations (p value >0.05, Table 5). However, as stated above, we argue that this good agreement between the simulated snow subsurface in the experiment iso from ECHAM6 & ECHAM6 accu is due to compensating effects between the precipitation d-excess and precipitation amounts.

4 Discussion

4.1 Limits of the methodological approach

4.1.1 Reliability of the datasets

Our study of the snow water stable isotopic composition is based on snow samples collected regularly all year round at Dome C. In Figs. 3, 8, and 9, we use the average of the two samples collected 50 m apart (Sect. 2.2) to describe the variability in δ¹⁸O and d-excess in the snow surface and subsurface. To ensure that the observed variations reflect a signal of local weather and climate rather than random noise, we analysed the temporal variations of the two samples independently (locations 1 and 2, Fig. S2 in Sect. S3). We see that the variations in δ¹⁸O and d-excess at sampling locations 1 and 2 generally follow each other. Additionally, a wavelet coherence analysis (Grinsted et al., 2004) revealed significant in-phase coherence between both locations for δ¹⁸O and d-excess in the snow surface and subsurface samples, beyond approximately 120 d throughout the 5-year period (Fig. S3 in Sect. S3). Note that this is a bit less evident for d-excess in the subsurface samples. We also see some episodic coherence between the two locations at 30 to 60 d. We argue that this shared signal between both locations indicates that the intra-annual to multi-annual variations in δ¹⁸O and d-excess observed in the snow samples reflect a true temporal climate or weather-driven signal. This brings confidence in using this dataset to investigate the formation of the isotopic signal in the snow. At shorter timescales (intra-monthly), the δ¹⁸O and d-excess variations that are not shared by both locations most likely reflect the spatial heterogeneity of the surface, arising from snow erosion and redistribution leading to an accumulation by patches (Picard et al., 2019). This is one aspect of post-depositional processes that is further discussed in Sect. 4.2.1.

Certain limitations should also be mentioned concerning the precipitation isotopic composition time series presented in Fig. 6. As detailed in Sect. 3.2, all the snow laying on the bench is collected, whether it is precipitation (including diamond dust), blown snow, or hoar formed from atmospheric condensation. In addition, some of the samples might have been affected by ad hoc sublimation, especially during the summertime, due to their exposure to the atmosphere before sample collection. As already pointed out by Dreossi et al. (2024a), the precipitation dataset might also be biased towards higher precipitation events because it was not possible to collect or measure the isotopic composition of the sample when very little snow was present on the table, due to too little precipitation during the day or because the sample was blown away. Lastly, some days with precipitation are missing in the dataset because the sample was simply not collected, due to harsh conditions for example. This also affects the observed precipitation amounts presented in Fig. 5, as they are inferred from the weights of the samples collected on site (Sect. 2.3 and 2.5.1).

Considering the points discussed and to avoid overinterpreting the differences in the isotopic compositions of the individual precipitation and snow samples, we instead use the full datasets presented here to quantify the mean effect of post-depositional processes over 5 years (Sect. 4.2.2).

4.1.2 SISG setup and inputs

In Sect. 3.4.1 and 3.4.2, we showed that none of the five SISG experiments fully represent the variability observed in the snow surface and subsurface isotopic composition (δ¹⁸O and d-excess). However, it should be mentioned that the results of the simple model used in our study come with some limitations.

The model was designed with a fixed depth for both snow samples to best represent the observations, although the depths of the samples collected in the field might have varied over time (Sect. 2.2). Changing the sample depths in the SISG model does not significantly improve the agreement between the model results and the observations (Table S3 in Sect. S4.3); however implementing varying depth for each time step of the model could improve the concordance between the synthetic and observed snow layers.

The inputs of the model might also explain some of the discrepancies between the observed and synthetic snow layers. For example, there are fewer small precipitation events in the observations than given by ERA5 and ECHAM6-wiso (Fig. 5b), which reflects the possible bias of the observations towards higher precipitation events (Sect. 4.1.1). This could lead to an underestimation of the contribution of smaller precipitation events (e.g. diamond dust) to the total accumulation and explain the differences between the experiments iso from wg. mm & obs accu and iso from ar. mm & obs accu and the observations (Figs. 8 and 9). On the other hand, it might be ERA5 and ECHAM6-wiso that overestimate the contribution of smaller precipitation events to the total accumulation, due to for example too frequent precipitation days with low precipitation rates. Some snowfall events in ERA5 and ECHAM6-wiso could also be occurring too early or too late and explain why the short-term increases and decreases in the snow isotopic composition are not reproduced in the experiments using ERA5 and ECHAM6-wiso precipitation amounts (Figs. 8a and c, 9a and c). In addition, we scaled up all three precipitation time series to match the mean annual accumulation of 8 cm yr⁻¹ at Dome C (Sect. 2.5), although this value can vary and estimations over other time periods have given higher mean accumulation rates (e.g. Frezzotti et al., 2005). One way to improve the model results would be to scale the precipitation time series with a different mean annual accumulation rate for each individual year using recent data from the GLACIOCLIM stake network (Genthon et al., 2015; https://glacioclim.osug.fr/, last access: 9 January 2025). Lastly, due to missing data in the observations of the daily precipitation isotopic composition, we used an artificial time series in three out of five experiments (Sect. 2.5), but none of these accurately represent the observations (Fig. S4 in Sect. S4.1). This could also partly explain the differences between the observed and synthetic snow layers.

For the different reasons stated above, we do not quantify the effect of post-depositional processes by directly comparing the model results and the observations but rather use it as a tool to discuss the role of the different surface processes of snow isotopic composition (Sect. 4.2.1).

4.2 Transfer of the isotopic signal between precipitation, the snow surface, and the subsurface

In this section we discuss the potential processes at the surface of the ice sheet responsible for the discrepancies between the precipitation signal and the observed snow surface and subsurface layers and assess the overall impact of these processes on the transfer of the isotopic signal between precipitation to the snow.

4.2.1 Short-term, inter-annual, and seasonal variability in the snow isotopic composition

Several studies have shown that water vapour fluxes between the lower atmosphere and the snow can modify the isotopic composition of the snow surface (Casado et al., 2021; Hughes et al., 2021; Wahl et al., 2021, 2022) and deeper firn cores (Dietrich et al., 2023). Although the impact depends on the isotopic composition of the atmospheric water vapour above, sublimation generally leads to an enrichment in δ¹⁸O of the snow surface and a lowering of its d-excess. In addition, Casado et al. (2018) hypothesized that the inter-annual variability in the summer snow surface isotopic composition is related to the strength of metamorphism and surface vapour fluxes.

We showed that at Dome C, sublimation occurs during the summertime (Fig. 2a) and that there is a net annual sublimation of snow (Fig. 2b), which means that the surface snow isotopic composition must have been affected by these fluxes. We find that in the δ¹⁸O–δD domain, most of the snow surface samples collected in December and January are below the precipitation samples (i.e. with a lower d-excess) collected in the same months (not shown), indicating an effect of sublimation on the snow surface isotopic composition in the summertime. In addition, we observe some inter-annual variability in the vertical difference between the snow surface and subsurface isotopic compositions (Fig. 4). This difference between the layer exposed to the atmosphere and the subsurface could be explained by the inter-annual variability in vapour fluxes (Fig. 2a). For example, the snow surface is most enriched in δ¹⁸O compared to the subsurface in December 2019 and January–February 2020 (Fig. 4). In parallel, we observe strong sublimation occurring in November and December 2019 (Fig. 2a), probably enriching the snow surface in δ¹⁸O and leading to a much more enriched snow surface compared to the subsurface in the samples collected in the following months. Yet, the highest sublimation rate occurring in December 2018 (Fig. 2a) is not necessarily reflected in the vertical difference between the snow surface and subsurface layers (Fig. 4). This could be explained by the length of the sublimation period, critical for the overall impact on the snow surface (Hughes et al., 2021; Wahl et al., 2022).

The mean seasonal cycle in the difference between the surface and subsurface isotopic compositions can, on the other hand, most likely be explained by the depths of the samples that integrate the precipitation events which have fallen during the last couple of months for the surface sample and up to the previous winter for the subsurface sample (assuming no removal or redistribution and no compaction of snow, Fig. S5 in Sect. S4.4). The higher δ¹⁸O and lower d-excess in the summer precipitation compared to the winter precipitation (Fig. 6) explains why the mean summer snow surface is enriched in δ¹⁸O and has a lower d-excess than the snow subsurface (Fig. 4). This integration process can also explain, at first order, why the maximum and minimum monthly mean δ¹⁸O in the precipitation, the snow surface, and the snow subsurface do not occur at the same time (January and May for the precipitation-weighted, Fig. 6c; February and October for the snow surface; and March and November for the snow subsurface, Fig. 3b).

If we would include vapour fluxes in the simple SISG model, the amplitude of the modelled seasonal cycle in the snow surface would be increased (summer months enriched in δ¹⁸O and reduced in d-excess), increasing the discrepancy with the observations (Fig. 8b and d). This shows that an additional process reducing the amplitude of the mean annual cycle in the snow surface takes place. Diffusion is a good candidate.

Indeed, the isotopic composition of the snowpack is affected by diffusion of water molecules along isotopic and temperature gradients (Johnsen et al., 2000; Gkinis et al., 2014). Implementing this process in the model would possibly reduce the amplitude that is too large of the seasonal cycles in the synthetic snow layers to match the observations (Figs. 8b and d, 9b and d). Diffusion might also partly explain the difference observed at the seasonal scale between the precipitation and the snow surface isotopic compositions (Figs. 3b and d, 6c and f), smoothing the incoming high-amplitude seasonal signal of precipitation and leading to a snow surface enriched in δ¹⁸O (and with lower d-excess) in the wintertime compared to precipitation. In addition, some of the short-term variations observed in the snow subsurface that are not explained by the incoming precipitation (Fig. 9a and c) could instead be explained by changes occurring in the snow surface and diffused downwards, as suggested by Casado et al. (2018).

Lastly, although Dome C is not affected by strong katabatic winds, surface winds can still be strong enough to erode and redistribute the snow (Libois et al., 2014). In a study of the process of snow accumulation at Dome C, Picard et al. (2019) showed that the snow surface changes very frequently due to snow erosion and accumulation by small patches (only 10 % of the surface is affected by each precipitation event) and that the snow in a patch can be as old as 1 year at the surface, while another patch was deposited by the last precipitation event. In the snow samples collected at Dome C, we observe higher differences in δ¹⁸O and d-excess between 2 consecutive sampling days of the snow surface and subsurface when the wind speed increases from one sampling day to another (Fig. S6 in Sect. S5), as well as a decrease in δ¹⁸O and d-excess vertical difference between the snow surface and the subsurface (Fig. S7 in Sect. S5). This could indicate that some of the short-term variations observed in the snow surface isotopic composition that cannot be explained by new precipitation falling on the surface (Figs. 3, 8a and c) are caused instead by wind erosion and redistribution.

The wind blowing at the surface of the ice sheet during or adjacent to snowfall could lead to a mixing of new precipitation with already deposited snow. This process was proposed by Casado et al. (2018) to explain the slow decrease in the surface snow δ¹⁸O during the winter, a pattern observed in our study (Fig. 3a and b) that cannot be explained by precipitation only (Fig. 8a and b). A recent laboratory study also suggests that snow metamorphism during wind transport (“airborne snow metamorphism”) has the potential to impact the snow isotopic composition in both δ¹⁸O and d-excess (Wahl et al., 2024). This could be an additional process occurring at Dome C explaining some of the differences between the precipitation and snow isotopic signals, including in the wintertime.

Overall, our results show evidence that the snow isotopic composition is affected by post-depositional processes at different timescales. Disentangling the contribution of the different processes described above regarding the final isotopic signal found in the snow is beyond the scope of this study and requires the use of an isotope-equipped snowpack model that includes post-depositional processes at the surface, such as the one developed recently by Wahl et al. (2022) and Dietrich et al. (2023).

Table 6 Five-year mean isotopic composition of precipitation (weighted by the observed precipitation amounts) and snow samples (δ¹⁸O in roman font, d-excess in brackets and italic). The mean values are given with their respective standard error (see Sect. 3.2.1), and their 95 % confidence interval is in brackets (Student's t test, Sect. S2).

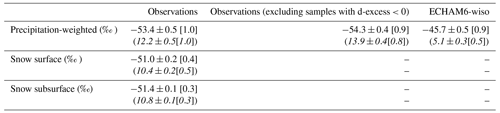
4.2.2 Mean effect of post-depositional processes

The datasets presented in this study permit the quantification of the overall impact of post-depositional processes on the snow isotopic composition. Table 6 summarizes the mean isotopic composition over 5 years of precipitation (weighted average by the observed precipitation amounts; see Sect. 2.5.1), the snow surface, and the snow subsurface. The mean isotopic composition of precipitation excluding all samples with negative d-excess and modelled by ECHAM6-wiso is also provided. All mean values are given with their respective standard error (see Sects. 3.2.1 and S2) and 95 % confidence interval (Student's t test, Sect. S2).

As shown in Sect. 3.3.2, the observed δ¹⁸O precipitation-weighted mean over 5 years is higher than the overall mean (−53.4 ‰ and −56.2 ‰, respectively). This is explained by the lowest δ¹⁸O values in precipitation being associated with smaller precipitation amounts (Fig. S8 in Sect. S6), and therefore they weigh less when computing the precipitation-weighted average. The opposite applies for d-excess: the weighted overall mean is lower than the arithmetic overall mean (12.2 ‰ and 15.2 ‰, respectively) because high d-excess values are associated with lower precipitation amounts (Fig. S8 in Sect. S6).

Now because the snow surface layer represents the amount of snow accumulated over a certain period, its mean isotopic composition should reflect the weighted mean (by precipitation amounts) isotopic composition of precipitation. Therefore, we express the mean effect of post-depositional processes at Dome C as the difference between the observed 5-year weighted mean isotopic composition of precipitation and the observed 5-year mean isotopic composition of the snow surface.

Considering all precipitation and snow samples, the snow surface δ¹⁸O is 2.4 ‰ higher than in precipitation and the snow surface d-excess is 1.8 ‰ lower than in precipitation (Table 6). However, to exclude any imprint of sublimation on the precipitation isotopic composition, we re-compute the mean isotopic composition of precipitation discarding all the samples with a d-excess below 0, as in Steen-Larsen et al. (2011). Although the 0 threshold might be arbitrary, it is supported by laboratory and field studies that showed a decrease in d-excess during snow sublimation and metamorphism (Hughes et al., 2021; Casado et al., 2021; Harris Stuart et al., 2023). In addition, Stenni et al. (2016) and Dreossi et al. (2024a) already stated that some of the samples collected in the summertime at Dome C might have been affected by sublimation, and we observe in the precipitation dataset presented here that the samples with very negative d-excess were collected during the summertime (e.g. December 2019, Fig. 6d) when sublimation occurred (Fig. 2a). We therefore argue that removing all precipitation samples with a d-excess below 0 improves the representation of the true precipitation falling at Dome C. Now considering this new precipitation time series, the δ¹⁸O in the snow surface is 3.3 ‰ higher than in precipitation and the d-excess in the snow surface is 3.5 ‰ lower than in precipitation (Table 6). Both differences are significant on a 95 % confidence level (Table 6).

The weighted mean isotopic composition of precipitation is computed using the observed precipitation amounts, estimated from the weights of the samples collected on site (Sect. 2.3 and 2.5.1). However, as discussed in Sect. 4.1.3, these amounts might not accurately represent the precipitation falling at Dome C. Using the precipitation amounts given by ERA5 instead, the weighted mean δ¹⁸O of precipitation is −54.0 ‰ and 13.8 ‰ for d-excess, which leads to similar differences between the precipitation and the snow surface: δ¹⁸O in the snow surface is 3.0 ‰ higher than in precipitation, and d-excess in the snow surface is 3.4 ‰ lower than in precipitation.

The discrepancies between the precipitation and the snow surface show that the mean isotopic composition of precipitation is not preserved from snowfall to the snow surface. On average over a 5-year period at Dome C, post-depositional processes lead to an enrichment in δ¹⁸O of the snow surface by 3.0 ‰ to 3.3 ‰ (depending on which precipitation amounts are considered) and a lowering of d-excess in the snow surface by 3.4 ‰ to 3.5 ‰ compared to the precipitation signal. The individual contribution of the different post-depositional processes (discussed in Sect. 4.2.1) on the isotopic difference observed between the precipitation and the snow surface is yet to be determined.

In contrast to the isotopic difference between the precipitation and snow surface, there is no significant difference between the mean snow surface and subsurface isotopic compositions, for both δ¹⁸O and d-excess (Table 6). This shows that despite a seasonality in the vertical difference between the two snow layers (discussed in Sect. 4.2.1), the mean isotopic composition of the snow surface layer is preserved in the top few centimetres of the snowpack.

From the sampling of a 2 m snow pit at Dome C, Touzeau et al. (2016) reported mean values (plus and minus the standard error of the mean) of $-\mathrm{51.1}\pm \mathrm{0.2}$ ‰ and 9.1±0.2 ‰ for the δ¹⁸O and d-excess profiles, respectively. As found in our study for the upper layers of the snow, the average isotopic composition of the snow pit is enriched in δ¹⁸O and has a lower d-excess than the mean incoming precipitation isotope signal.

The weighted mean isotopic composition of precipitation modelled by ECHAM6-wiso over the whole period is 7.7 ‰ higher in δ¹⁸O and 7.1 ‰ lower in d-excess than the observed precipitation (Table 6, Fig. 6c and f). These large differences result from the biases identified in the model (Sect. 3.3.2, Figs. 6 and 7), combined with the distribution of the daily isotopic values against precipitation amounts (Fig. S8 in Sect. S6), influencing both the overall mean and the seasonal difference between the observations and the model (Fig. 6 and Sect. S6). This shows the limitations of using ECHAM6-wiso simulations to interpret the isotopic composition of the snow at Dome C. A thorough investigation of the biases in ECHAM6-wiso is beyond the scope of this study, but they might arise from different processes in the model, such as the environmental conditions at the moisture source region, the moisture transport and pathway, the supersaturation parameterization, or the condensation height and temperature at Dome C. The 14-year record of the precipitation isotopic composition (Dreossi et al., 2024a, and this study) gives the opportunity to evaluate isotope-enabled GCMs and can be used to improve the tuning of the empirical parameterization of supersaturation in polar clouds (e.g. Risi et al., 2013).

4.2.3 Seasonal δ¹⁸O–temperature relationships in precipitation and snow

In precipitation, the δ¹⁸O–temperature relationship is determined between the δ¹⁸O in the daily precipitation samples and the corresponding daily atmospheric temperature (Sect. 3.3.3, Eq. 1). For the snow surface and subsurface, we determine the relationships between the δ¹⁸O composition of each snow sample and the weighted-average temperature (by precipitation amounts) over the entire period during which precipitation accumulated and formed the snow sample (Fig. A3). We use the observed precipitation amounts to determine this averaging period (Fig. S5 in Sect. S4.4). Table 7 summarizes the linear regression slopes (a) with their standard errors and the coefficient of determination (R²).

Table 7 Summary of mean seasonal δ¹⁸O–temperature linear relationships in precipitation and snow samples between 2017 and 2021. The slopes (a) are given with their standard error, and all three slopes are significant (p value <0.001).

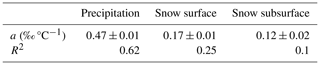
We find a mean seasonal δ¹⁸O–temperature slope in precipitation of 0.47±0.01 ‰ °C⁻¹, in agreement with previous studies for the same location for earlier years (Stenni et al., 2016; Dreossi et al., 2024a). We find a mean seasonal slope of 0.17±0.01 ‰ °C⁻¹ in the snow surface (top 1 cm) and a mean seasonal slope of 0.12±0.02 ‰ °C⁻¹ in the snow subsurface (1 to 4 cm, Table 7). The snow surface slope coincides with the one found for the top 1–2 mm of snow at Dome C (0.14±0.03 ‰ °C⁻¹, Touzeau et al., 2016) but is lower than the ones found by Casado et al. (2018) for similar samples in earlier years (slopes ranging from 0.22 to 0.49 ‰ °C⁻¹). This difference can be due to uncertainties in the precipitation amounts used to determine the averaging period of temperature (i.e. some precipitation days with colder temperatures are not captured), the method used to determine the averaging period of temperature (i.e. assumes that snowfall is not redistributed or removed and does not include snow compaction, Sect. S4.4), or the different method used in Casado et al. (2018) where they compute the slope as the ratio of the maximum amplitude in δ¹⁸O and the maximum amplitude in temperature.

Our results indicate that deriving a temporal slope from seasonal variations in δ¹⁸O in the snow surface to be used for ice core studies is not consistent with other in situ and proxy temperature reconstructions. First, the snow surface δ¹⁸O does not show a symmetric seasonal cycle. Instead, the δ¹⁸O minimum is shifted towards spring (Fig. 3, Sect. 3.2.1), while the minimum temperature occurs in winter. Secondly, our determination of the seasonal relationship between the snow δ¹⁸O and the atmospheric temperature results in a weaker correlation and a lower slope (0.12 ‰ °C⁻¹–0.17 ‰ °C⁻¹, Table 7) than what is found for precipitation (0.47 ‰ °C⁻¹, Table 7). Using the δ¹⁸O–temperature slope found in the upper layers of the snow for temperature reconstructions from ice cores would lead to unrealistic glacial–interglacial temperature change exceeding 30 °C. The change in the seasonal δ¹⁸O–temperature relationship between the precipitation and the upper layers of the snow shows the difficulty of quantitatively interpreting the δ¹⁸O variations in the snow at Dome C in terms of temperature. Instead, it provides an opportunity to document the effects of post-depositional processes at this site and improve the future quantitative interpretation of water isotopic records in ice cores from Dome C for longer timescales (decadal and longer timescales).

4.3 Long-term perspectives for the interpretation of ice core isotope records

The classical paleothermometer approach (Lorius and Merlivat, 1975) to determine past temperature variations from the water isotopic profiles in ice cores uses the present-day spatial slope between the water isotopic composition of the snow surface and the local temperature. However, as illustrated in Casado et al. (2017), this spatial slope differs from the various estimates of the temporal slope between temperature and δ¹⁸O found in the literature and in this study, as determined for different regions and timescales. These discrepancies show the need for calibration of the isotopic paleothermometer. Such calibration has been done using alternative methods at the glacial–interglacial scale (e.g. borehole thermometry and firn properties, Buizert et al., 2021) or using isotope-enabled GCMs to determine the relationship between temperature and water isotopes during past periods (e.g. Werner et al., 2018). However, in these models, the absence of explicit modelling of how the water isotopic signal is archived in the snow and firn limits their use for paleo-reconstructions.

To progress towards an accurate quantitative interpretation of isotopes in ice cores, we recommend developing a proxy system model (Evans et al., 2013) that can be coupled to isotope-enabled GCMs. A first step toward such a model was developed recently by Wahl et al. (2022) and Dietrich et al. (2023) for Greenland and includes mechanical processes leading to the recording of isotopes at the ice sheet's surface and in firn cores. The datasets presented in our study can therefore be useful to calibrate and validate this kind of model at intra-annual, seasonal, and inter-annual timescales at the deep-drilling site of the European Project for Ice Coring in Antarctica (EPICA) Dome C ice core.

5 Conclusions

We have presented a compilation of new and existing datasets of the isotopic composition of precipitation, the snow surface, and the subsurface together with meteorological parameters, reanalysis products, model outputs, and a simple modelling approach to investigate the origin of the stable water isotopic signal in the upper layers of the snowpack at Dome C, East Antarctica.

From in situ meteorological observations, we have quantified the amount of water vapour flux between the snow and the lower atmosphere. Our results show that vapour fluxes contribute to the surface mass balance at Dome C with a net annual mass loss of snow from 3.1 to 3.7 mm w.e. yr⁻¹ between 2018 and 2020, which corresponds to 12 % to 15 % of the annual surface mass balance. Sublimation is relatively strong in the summertime, and there is little condensation in the wintertime.

For the comparison between the snow surface and subsurface isotopic compositions and a simple modelling approach, we show that the precipitation deposited onto the ice sheet cannot explain the variability observed in the snow isotopic composition (δ¹⁸O and d-excess) at seasonal to intra-monthly timescales, highlighting the existence of post-depositional processes affecting the snow isotopic composition.

We quantified the cumulative effect of post-depositional processes on the snow surface over 5 years by comparing the mean isotopic compositions of the precipitation and the snow layers. Our results show that post-depositional processes lead to an enrichment of the snow surface (top 1 cm) in δ¹⁸O by 3.0 ‰ to 3.3 ‰ (depending on the precipitation amounts considered) and a lowering of the snow surface d-excess by 3.4 ‰ to 3.5 ‰. In addition, our results show that the mean isotopic composition of the snow subsurface (1 to 4 cm depth) is not significantly different than the snow surface, which indicates that the mean isotopic composition of the snow surface layer is preserved in the top centimetres of the snowpack and that the processes altering the precipitation isotopic signal mainly take place in the top 1 cm of the snow.

In the observations, ERA5 reanalyses, and ECHAM6-wiso simulation, we showed that 50 % of the accumulation at Dome C over 5 years occurs during large but rare precipitation events associated with temperatures warmer than average, leading to a warm bias in the δ¹⁸O record of precipitation compared to the mean annual temperature. We further find different seasonal relationships between the atmospheric temperature and δ¹⁸O in the precipitation and the snow, showing the difficulty of interpreting the variations in δ¹⁸O in the snow at Dome C.

Overall, our results show that post-depositional processes at the ice sheet's surface have an impact on the isotopic signal (both δ¹⁸O and d-excess) found in the upper layers of the snowpack at Dome C, East Antarctica. The datasets in our study present the possibility of calibrating and validating proxy system models including post-depositional processes that are needed to quantitatively attribute the different mechanisms building up the isotopic signal in the snow surface and to accurately reconstruct the climatic information from the water stable isotope records in ice cores.

Appendix A

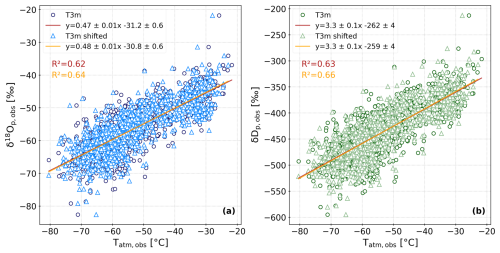
Figure A1 Daily observed precipitation (a) δ¹⁸O and (b) δD versus observed daily mean temperature (T_atm) at Dome C. All precipitation samples collected between 2017 and 2021 are shown against the corresponding daily mean temperature at 3 m (T3m, dark colours) and the daily mean temperature of the day before (T3m shifted, light colours). The linear regressions with the associated coefficients of determination (R²) are shown. Both linear slopes are significant (p values <0.001).

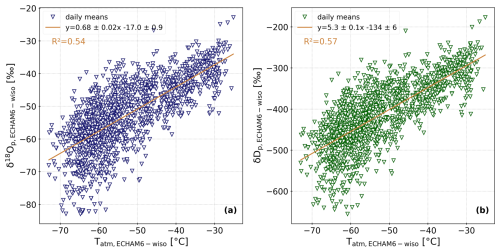
Figure A2 Daily precipitation (a) δ¹⁸O and (b) δD modelled by ECHAM6-wiso versus daily mean temperature (T_atm) modelled by ECHAM6-wiso. The linear regressions with the associated coefficients of determination (R²) are shown. Both linear slopes are significant (p values <0.001).

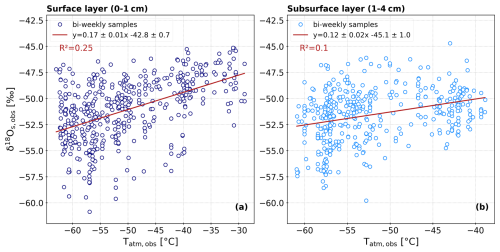
Figure A3 Bi-weekly observed snow (a) surface and (b) subsurface δ¹⁸O versus temperature (T_atm) at Dome C. All snow samples collected between 2017 and 2021 are shown against the weighted-average temperature (by precipitation amounts) over the period corresponding to the accumulation of the snow samples (see Sect. 4.2.3). The linear regressions with the associated coefficients of determination (R²) are shown. Both linear slopes are significant (p values <0.001).