Exploring how Sentinel-1 wet-snow maps can inform fully distributed physically based snowpack models

Distributed energy and mass balance snowpack models at sub-kilometric scale have emerged as a tool for snow-hydrological forecasting over large areas. However, their development and evaluation often rely on a handful of well-observed sites on flat terrain with limited topographic representativeness. Validation of such models over large scales in rugged terrain is therefore necessary. Remote sensing of wet snow has always been motivated by its potential utility in snow hydrology. However, its concrete potential to enhance physically based operational snowpack models in real time remains unproven. Wet-snow maps could potentially help refine the temporal accuracy of simulated snowmelt onset, while the information content of remotely sensed snow cover fraction (SCF) pertains predominantly to the ablation season. In this work, wet-snow maps derived from Sentinel-1 and SCF retrieval from Sentinel-2 are compared against model results from a fully distributed energy balance snow model (FSM2oshd). The comparative analysis spans the winter seasons from 2017 to 2021, focusing on the geographic region of Switzerland. We use the concept of wet-snow line (WSL) to compare Sentinel-1 wet-snow maps with simulations. We show that while the match of the model with flat-field snow depth observation is excellent, the WSL reveals a delayed snowmelt in the southern aspects. Amending the albedo parametrization within FSM2oshd allowed for the achievement of earlier melt in such aspects preferentially, thereby reducing WSL biases. Biases with respect to Sentinel-2 snow-line (SL) observations were also substantially reduced. These results suggest that wet-snow maps contain valuable real-time information for snowpack models, complementing flat-field snow depth observations well, particularly in complex terrain and at higher elevations. The persisting correlation between wet-snow-line and snow-line biases provides insights into refined development, tuning, and data assimilation methodologies for operational snow-hydrological modelling.

1 Introduction

Seasonal snow is crucial for the hydrology of mountains and their tributaries as it stores wintertime precipitation and entails delayed runoff (Barnett et al., 2005). Snowmelt runoff is key for downstream agriculture (Qin et al., 2020) and hydropower production (Gaudard et al., 2014). Intense snowmelt can also lead to dramatic floods (Diffenbaugh et al., 2013). As the inter-annual variability of snow distribution is high, anticipating the amount and timing of melt is therefore essential, especially in a changing climate (Lafaysse et al., 2014).

Snow models have therefore become indispensable in the field of hydrological forecasting (e.g. Griessinger et al., 2019). However, accurately resolving all intricate processes that influence the mass and energy balance of the snowpack across various spatial scales is difficult. The accumulation of snow in a region is contingent upon precipitation patterns, which exhibit substantial variability both regionally (Isotta et al., 2014) and locally (Scipión et al., 2013). Wind and gravitational redistribution contribute to the spatial heterogeneity of snowpacks (Liston and Sturm, 1998; Freudiger et al., 2017; Mott et al., 2018). Meanwhile, the surface energy balance, which governs the amount of snowmelt, is subject to fine-scale variations. These variations are influenced by topographical features and cloud cover, which impact incoming shortwave and longwave radiation (Brauchli et al., 2017; Jonas et al., 2020) as well as air temperature. Wind patterns, too, can exert influence on sensible and latent heat fluxes at small scales (Mott et al., 2011). In summary, the accurate modelling of snowpack ablation necessitates the comprehensive representation of both the variability in snow cover and the multifaceted drivers affecting its energy balance.

Snowmelt is not equivalent to snowmelt runoff. Snowmelt runoff can only commence when meltwater exits the snowpack from its bottom. This journey entails complex processes related to liquid water storage and routing, introducing a substantial temporal lag between the initiation of melt and eventual snowmelt runoff (Lundquist and Dettinger, 2005). Towards the end of the accumulation season, an increase in the surface energy input typically gives rise to more frequent and intense episodes of surface melt, a phase often referred to as the moistening phase (Techel and Pielmeier, 2011; Dingman, 2015; Marin et al., 2020). Concurrently, rainfall events may further augment the liquid water content at the surface. Once the amount of liquid water in the upper layers of the snowpack reaches the maximum holding capacity, the liquid water released or absorbed from the superficial layers gets in contact with the subfreezing snow present underneath and freezes. This releases latent heat that causes the snowpack to warm up, starting the process of snow ripening. This drainage process is influenced by various factors, including refreezing; the presence of preferential flow paths, capillary barriers, and lateral flow (Wever et al., 2014; Würzer et al., 2017); and the occurrence of ice layers (Quéno et al., 2020). Ultimately, snowmelt runoff commences when the liquid water exits the snowpack at its base.

In the context of large-scale and high-spatial-resolution snowmelt applications, compromises are needed to find a good trade-off between model accuracy and computational costs. Often, intermediate-complexity snowpack models provide a good balance (Magnusson et al., 2015). These models solve the energy and mass balance of the snowpack with simplifications to the representation of the internal snowpack structure (Marsh et al., 2020; Essery, 2015). Particularly, they use a limited number of numerical layers (Cristea et al., 2022), resulting in a simplified description of liquid water routing and snow metamorphism. These factors, combined with further uncertainties in meteorological forcings, may result in considerable modelling errors (Raleigh et al., 2015; Krinner et al., 2018), which are often hard to assess because of an intrinsic lack of observational data in mountainous areas.

Satellite observations of the snowpack could help to constrain such model errors, provided that they have adequate spatio-temporal resolution and sufficient accuracy (Largeron et al., 2020). Snow cover fraction (SCF) observations from Sentinel-2, for instance, are available at a resolution of 20 m every 3 to 5 d but only in the absence of clouds. The C-band synthetic aperture radar (SAR) sensor on Sentinel-1, on the other hand, is sensitive to the presence of liquid water in the snowpack irrespective of cloud cover (Veyssière et al., 2019; Marin et al., 2020; Karbou et al., 2021). Binary wet-snow maps (WSMs) can be derived from SAR backscatter at a resolution higher than 100 m, requiring only small amounts of liquid water for snow to be classified as wet (Nagler et al., 2016).

The timing of information is key in real-time operational modelling. Snow cover fraction and wet-snow maps provide information at different times during the season. SCF observations provide information about the first snowfall and during the period of partial snow cover during the ablation season. This information can be used to reconstruct the snow water equivalent (SWE) through data assimilation (e.g. Margulis et al., 2016; Fiddes et al., 2019), but it is not helpful for determining the onset of snowmelt in real time (Andreadis and Lettenmaier, 2006; Buchelt et al., 2022). Wet-snow retrievals, on the other hand, provide qualitative information during the onset of snowmelt, thus having the entire ripening and ablation phase to exploit the information.

Nevertheless, several questions remain as to the potential utility of wet-snow maps in this context. Firstly, the SAR signal may detect superficial short-lived melt events, which are very difficult to capture by intermediate-complexity snowpack models. These models do not represent the intricate microstructure and stratigraphy of the snow, thereby complicating the assimilation process. The duration of the ripening phase, associated with the delay between the SAR signal and the onset of snowmelt runoff, is also arguably very variable, depending on the snowpack thickness, internal properties, and springtime weather conditions (Marin et al., 2020). Finally, due to the sensitivity of radar retrievals to seasonal change in land surface properties (Karbou et al., 2022) and the unavailability of meaningful retrievals in forested areas, reliable observations are confined to elevations above the treeline and away from water bodies and human activities.

In this work, we assess whether information from wet-snow maps can be used to inform a snow-hydrological model used in nationwide operational forecasting in practice. We use two versions of our physically based multi-layer snowpack model FSM2oshd (Mott et al., 2023a), which we run operationally over the entire Switzerland at 250 m spatial resolution. These two versions have different fresh-snow albedo parametrizations. Snow depth data from nearly 450 monitoring stations were assimilated into these simulations to ensure a good model performance free of systematic overall biases to start with. Note that this approach was chosen to reveal the value of information contained in WSM and SCF products beyond the identification and removal of obvious model biases. The study focuses on five ablation seasons (March–July) from 2017 to 2021. The study area, observations, and modelling chain are described in Sect. 2. The results are presented and discussed in Sects. 3 and 4. We finally conclude and open research perspectives in Sect. 5.

2 Material and methods

2.1 Study area

The study area encompasses Switzerland and hydrologically connected areas outside its boundaries (see Fig. 1). The domain size stretches over 272 km in the latitudinal direction and 365 km in the longitudinal direction, totalling 920 884 model grid cells at a resolution of 250 m. We focus our analysis on 16 subcatchments with relatively homogeneous snow conditions (MEZs, as defined by the Swiss Federal Office for Environment), which cover the alpine area of the domain. The average size of the MEZs is about 1600 km², ranging from 721 km² (MEZ 16) to 4470 km² (MEZ 9). All of these units are located within Switzerland, some of them extending to neighbouring countries (Liechtenstein, Austria, Germany, Italy, and France). The MEZs are situated on both sides of the main alpine ridge and encompass diverse hydro-climatic conditions. There are 444 locations with daily in situ snow depth observations measured on a flat surface that are available throughout the domain, indicated by the red dots in Fig. 1. Among these observations, 255 are within the considered MEZs.

Figure 1 Map of the model domain, with the identifier of hydrological units (MEZ) and locations of the snow stations (red points). Switzerland's border is denoted by the thick black line.

2.2 Satellite observations from AlpSnow

AlpSnow is a science activity within the European Space Agency (ESA) Alpine Regional Initiative (https://alpsnow.enveo.at/, last access: 6 December 2024) which provides a 5-year demonstration dataset for novel remote sensing retrievals of snow parameters over the Alps. In this paper, we use a wet-snow-map product, retrieved from Sentinel-1, and snow cover fraction from Sentinel-2.

2.2.1 Wet snow

Wet-snow maps from AlpSnow are processed from Sentinel-1 C-band synthetic aperture radar backscatter time series. C-band backscatter is sensitive to small amounts of liquid water in the snowpack, causing a sharp decrease in backscatter compared to bare ground or dry-snow conditions (Mätzler, 1987). A −2.5 dB threshold with respect to a reference scene is applied to detect wet snow, resulting in binary wet-snow maps (Nagler et al., 2016). As evidenced by Marin et al. (2020), the backscatter signal returns to dry-snow conditions as the snowpack becomes patchy throughout the ablation season, even though at that time the snowpack column is usually entirely saturated with liquid water. Therefore, melting, patchy snow cannot be distinguished from dry snow or bare ground. Furthermore, in snow-free conditions, spurious backscatter drops may be caused by land surface change (e.g. vegetation growth and agriculture), changes in soil wetness, and speckle noise (e.g. Guiot et al., 2023), resulting in false wet-snow classification. For this reason, the wet-snow detection algorithm from AlpSnow includes a snow mask computed from a gap-filled, temporally interpolated remotely sensed snow cover product. Any pixel with 40 % or less snow cover fraction is considered snow-free. Furthermore, due to the slanted angle under which SAR acquisition is performed, geometric distortions (layover and foreshortening) and shadowing result in data gaps in rugged terrain. Therefore, the product can be categorized into the following three classes: wet snow; snow-free, dry snow, or patchy snow; and masked pixels. Satellite acquisition occurs around 05:00 UTC (descending orbit) or 17:00 UTC (ascending orbit) with a revisit time of 3 to 6 d during the study period (see Fig. 2a–b). The AlpSnow wet-snow-map resolution is 0.001° × 0.001° in WGS84 (EPSG:4326), corresponding to approximately 100 m × 100 m in the modelling coordinate system (EPSG:21781).

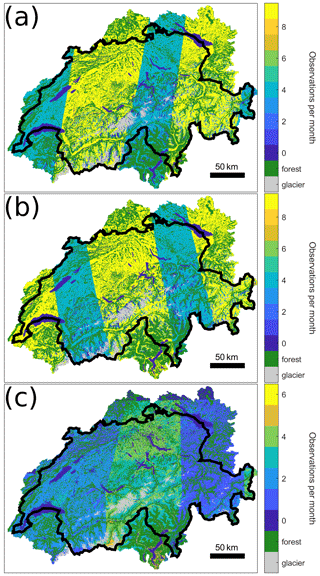
Figure 2 Sentinel-1 at 05:00 UTC (a) and 17:00 UTC (b) and Sentinel-2 (c), with the number of valid observations per month and per pixel over the whole period. Forests and glaciers have been masked out. Switzerland national borders are indicated in black.

Wet-snow maps were aggregated into pixels of 250 m, corresponding to the cells of the model grid. Products were first reprojected and resampled at 50 m into the modelling coordinate system using a nearest-neighbour approach. Then, these products were masked using a 10 m forest mask (Mott et al., 2023a), which is more accurate than the forest mask used in the raw data. Urban areas were also excluded using class 50 of the Copernicus Land Cover Mask (Buchhorn, 2022). For each 250 m pixel, an aggregated binary value was computed from the 25 subpixels of 50 m as follows:

• If more than 90 % of the 50 m subpixels were forest or urban, then the pixel was masked as forest–urban.

• Alternatively, if more than 5 % of the 50 m subpixels were classified as geometric distortions, then the pixel was masked out.

• Otherwise, the 250 m wet-snow binary value was equal to the majority of the valid subpixel values.

Figure 2a and b show that due to overlapping tracks, 5 to 10 Sentinel-1 wet-snow observations were available per month. Some areas (MEZs 6, 14, 17, and 22) are even observed 10 times a month in the morning and evening.

2.2.2 Snow cover fraction

The AlpSnow snow cover fraction is derived by spectral unmixing on Sentinel-2 level 1C radiance at a pixel level (Keuris et al., 2023). The product resolution is 0.0002° × 0.0002° in WGS84 (EPSG:4326) (approximately 20 m × 20 m in EPSG:21781). The satellite acquisition time is around 10:00–11:00 UTC. The following Sentinel tiles were processed: T31TGM, T32TMT, T32TNT, T32TLS, T32TMS, and T32TNS. Based on optical data, these products are inherently affected by the following problems (e.g. Barrou Dumont et al., 2021; Keuris et al., 2023):

• It is difficult to discriminate clouds from snow and to delineate cloud shadows.

• Undetected thin cirrus clouds may cause a decrease in the retrieved snow cover fraction.

• Shaded snow in steep terrain and sparse forests may also be affected by negative biases in SCF, in particular from November to March when shadow extents are larger (and there is snow on the ground).

• There is no discrimination between snow and bare ice, causing snow-free glaciers to be classified as snow.

We mitigate these limitations by focusing on observations available in open terrain in the ablation season from April to June.

SCF images were aggregated following a similar procedure as for the WSM (see Sect. 2.2.1). Products were reprojected and resampled at 10 m. For each 250 m pixel, an aggregated value was computed as follows:

• If more than 90 % of the 10 m subpixels were forest or urban, then the pixel was masked as forest–urban.

• Alternatively, if more than 5 % of the 10 m subpixels were covered by clouds, then the pixel was masked as cloudy.

• Otherwise, the 250 m SCF value was computed as the average value of the valid (non-forested, urban, or cloudy) subpixels.

Figure 2c shows the average value of valid Sentinel-2 SCF observations per pixel during the spring period from April to June (thereby accounting for cloud occurrence). Due to overlapping tracks, the central portion of the domain, covering MEZs 6, 11, 18, 20, and 22, has twice as many Sentinel-2 overpasses as the rest of the domain. On average, two to five cloud-free observations are available per pixel each month.

2.3 FSM2oshd

In this work, we use the physically based multi-layer snowpack model FSM2oshd (Mott et al., 2023a), which we run operationally over the entire Switzerland at 250 m spatial resolution. The snowpack model is run using output from the numerical weather prediction system COSMO-1E operated by MeteoSwiss, which is carefully debiased and downscaled to 250 m using a range of dynamical and statistical methods. In particular, shortwave radiation is provided per inclined surface. FSM2oshd includes an optimal-interpolation-based data assimilation scheme, using in situ snow depth measurements from 444 stations (see Fig. 1) to correct for snowfall input errors (Magnusson et al., 2014). To account for unrepresented preferential deposition, wind transport, and gravitational redistribution of snow, a terrain-dependent correction is applied to solid precipitation based on Vögeli et al. (2016). In its standard configuration, FSM2oshd is a three-layer snowpack model in which liquid water routing through the snowpack is modelled using a bucket approach. A subgrid parametrization is used to derive pixel-level snow cover fraction from seasonal values of SWE and snow depth (Helbig et al., 2021). This model component accounts for the impact of subpixel terrain roughness and slope variability on snow depth distribution at the peak of accumulation. For instance, smooth and flat pixels usually exhibit homogeneous subpixel SWE distribution, leading to a more rapid reduction in snow cover as SWE decreases. Fresh-snow events are assumed to produce abrupt yet transient increases in snow cover fraction. Accounting for this is essential to compare model output with satellite retrievals of snow cover fraction at this scale. FSM2oshd uses a re-calibrated version of the albedo parameterization from Douville et al. (1995) and Essery et al. (2013). In the parameterization, the snowpack albedo decays linearly with time when the snow surface temperature is below 0 °C and decays exponentially when the surface is melting. The minimal albedo value is 0.5. The constant decay timescales are τ_melt=130 h for the melting snowpack surface and τ_cold=3000 h for subfreezing surface temperature, reflecting the fact that wet-snow metamorphism is quicker than dry-snow metamorphism. In the presence of snowfall, the albedo is progressively refreshed to fresh-snow values. In FSM2oshd, the fresh-snow albedo α_fs varies as a function of altitude z as follows:

$$\begin{array}{}\text{(1)}& {\mathit{\alpha }}_{\mathrm{fs}}=\left\{\begin{array}{ll}\mathrm{0.8}& \text{if}z<=\mathrm{1500}\\ {\mathit{\alpha }}_{\mathrm{fs}}^{\max }+\frac{\mathrm{2300}-z}{\mathrm{2300}-\mathrm{1500}}(\mathrm{0.8}-{\mathit{\alpha }}_{\mathrm{fs}}^{\max })& \text{if}\mathrm{1500}<z<=\mathrm{2300}\\ {\mathit{\alpha }}_{\mathrm{fs}}^{\max }& \text{otherwise}.\end{array}\right.\end{array}$$

The snowpack albedo α increases with hourly snowfall Sf (mm):

$$\begin{array}{}\text{(2)}& \mathit{\alpha }=\left\{\begin{array}{ll}{\mathit{\alpha }}_{\mathrm{fs}}& \text{if}{\mathrm{Sf}}_{\mathrm{24}\mathrm{h}}>{\mathrm{Sf}}_{\min }\\ \mathit{\alpha }+({\mathit{\alpha }}_{\mathrm{fs}}-\mathit{\alpha })\frac{\mathrm{Sf}}{{\mathrm{Sf}}_{\min }}& \text{otherwise}.\end{array}\right.\end{array}$$

This rule includes a threshold enforcing an albedo of α_fs for 24 h snowfall above Sf_min=10 mm (Douville et al., 1995). The albedo parameterizations in fsm_preop were tuned through an assessment against snow depletion rates in springtime-measured flat-field sites (Mott et al., 2023a), where ${\mathit{\alpha }}_{\mathrm{fs}}^{\max }$ was set to 0.92. However, a preliminary comparison with Sentinel-1 wet-snow retrievals (see Sect. 3.2) showed that in fsm_preop simulations, melting was initiated too late with a particular focus on the south-exposed slopes. As shown later, this model shortcoming could be mitigated by lowering ${\mathit{\alpha }}_{\mathrm{fs}}^{\max }$ from 0.92 in fsm_preop to 0.86 in the so-called fsm_optim version. Below, we compare both model versions.

2.4 Comparing the model with observations

In order to compare the simulations with observations, model outputs were extracted and masked out when the forest fraction exceeded 80 % of the grid cell. The same mask was applied to the observations to avoid strong geospatial bias in the analysis. The definition of a wet-snow state for the model is required for a direct comparison with the observations. Given the high sensitivity of the observation to small liquid water amounts in the snowpack, we considered modelled snow to be wet as soon as the total liquid water content was strictly above zero at the time of the acquisition (either 05:00 UTC or 17:00 UTC).

2.5 Deriving the wet-snow line

The melting season usually starts with a progressive moistening of the dry snowpack from low to high elevations. The wet-snow line (WSL) is the time-varying elevation of this wetting front (Gupta, 2011), which also depends on topographic factors such as aspect and slope. As shown by Karbou et al. (2021, 2022), wet-snow maps from Sentinel-1 capture this phenomenon well. The WSL is conceptually very similar to the snow line (SL), which can be defined as the elevation where the snow cover fraction equals 50 % (e.g. Parajka et al., 2010).

The WSL was estimated from Sentinel-1 wet-snow maps and wet-snow states from model outputs (Sect. 2.4) using the following algorithm. Using the MEZs as spatial aggregation units, we computed the WSL by aspect sectors each time a Sentinel-1 image was available. Pixels with a slope <8° were considered flat, and pixels above a slope of 30° were excluded from the aggregation. Only data between 1600 and 3200 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ were evaluated to enable a robust estimation of WSL unaffected by forests and high-elevation glacierized areas (see Sect. 2.2.1). All valid pixels in a given aspect were stratified by elevation. We then computed a weighted interpolation of the pixel values using a window width of 300 m elevation, giving us the proportion of wet pixels (wet-snow fraction, WSF) as a function of the elevation, as shown in Fig. 3. Note that towards low elevations, the wet-snow fraction from AlpSnow decreases, probably because of snow roughness and a decreasing snow cover fraction.

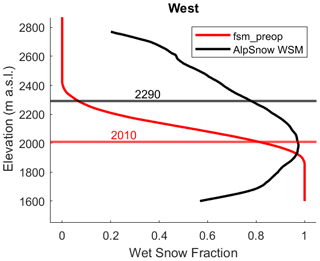
Figure 3 Computation of the wet-snow line, for fsm_preop and AlpSnow data, in this example for westerly aspects (247.5–292.5° N) of MEZ 11 on 1 April 2019 at 17:00 UTC.

For the observations, starting from dry conditions at high elevations, we identify the maximum WSF_max as we go to lower elevations. If WSF_max did not exceed 0.6, then the snowpack was not substantially wet, and no snow line was determined for that aspect class. Otherwise, the WSL was defined as the lowest elevation above that of WSF_max with a $\mathrm{WSF}<=\mathrm{0.8}\times {\mathrm{WSF}}_{\max }$. This value was optimized manually. If it was not reached, the snow cover was assumed to be wet over the entire elevational range considered, and no WSL was determined either.

The snow line (SL) was computed using the same weighted interpolation to arrive at an elevational profile of SCF. The SL was then defined as the highest elevation with SCF<0.5.

3 Results

3.1 Performance of the snow model against flat-field observations

Figure 4 shows the performance of both FSM versions, fsm_preop and fsm_optim, against flat-field observations between 2000 and 2500 $\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ across Switzerland for the 5 considered years. Overall, the match is excellent, in particular during the accumulation period, which is consistent with the fact that these observations were assimilated for correcting errors in the snowfall input (see Sect. 2.3). For a detailed evaluation of FSM2oshd against station data, readers are referred to Winstral et al. (2019), Mott et al. (2023a), and Oberrauch et al. (2024). For both model versions, the most notable differences with respect to the observations arise in the early ablation period, in particular during the spring of 2019 and 2021. As expected, due to a slightly lower fresh-snow albedo, snowmelt is initiated slightly earlier in fsm_optim compared to fsm_preop. Aimed mostly at south-facing slopes, the optimization had only limited influence on simulations at our flat-field monitoring sites. The accelerated melt, however, leads to slightly stronger negative biases, albeit within acceptable limits. This is particularly notable in seasons when fsm_preop already demonstrates a slight negative bias, such as in the winter of 2019 and 2021.

Figure 4 Average of fsm_preop (red), fsm_optim (light blue), and flat-field snow depth observations (black) over the full study domain in the 2000–2500 m a.s.l. elevation range.

3.2 Spatial comparison and topographic aggregation of satellite observations

Satellite data provide much more information on the spatial performance of the model than the station dataset. As an example, Fig. 5 shows the wet-snow map aggregated to the model resolution of 250 m compared with equivalent model simulations with fsm_preop for MEZ 11 on 1 April 2019. Both simulated and observed maps are dry at high elevations and transition into wet conditions at lower elevations. On the south-facing slopes, the observations indicate wet conditions several hundred metres higher than the model simulation. No retrieval is available on some steep slopes of the southwestern aspect due to geometric distortions (shadowing) of the SAR signal.

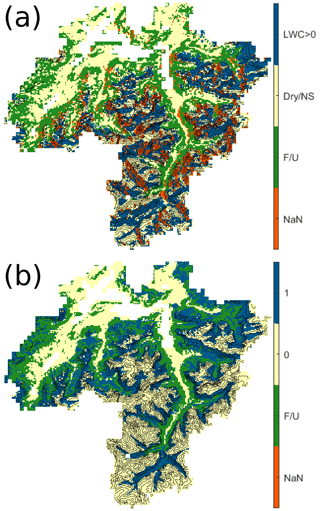
Figure 5 Sentinel-1 250 m wet-snow map (a) and simulated presence of liquid water using fsm_preop (b) for MEZ 11 on 1 April 2019 at 17:00 UTC. Blue denotes wet snow, light yellow denotes dry conditions (or no snow/patchy snow), green denotes forest and urban pixels, and orange denotes missing data due to geometric distortions in the observation. Lakes and pixels outside of MEZ 11 are masked out.

In order to gain quantitative insights into the spatial dynamics of wet snow in both the observations and the model, map products were aggregated by slope classes in Fig. 6, including respective evaluations of the wet-snow line. Observations (Fig. 6a) and fsm_preop (Fig. 6b) show good agreement in the northern sectors and in flat terrain. However, on the southwestern to eastern slopes, the simulated WSL consistently shows notably lower values compared to the observations (as also observed in Fig. 5). This suggests a delayed initiation of simulated snowmelt in sun-exposed terrain. This finding led to testing whether lowering the fresh-snow albedo would mitigate existing model biases by enabling an earlier onset of melt preferentially on sun-exposed slopes, motivating the parameter adaptation applied in fsm_optim. Indeed, simulations of the wetting front with fsm_optim (Fig. 6c) show a substantially better match to observations, particularly for western and southern aspects but also for flat terrain, with a rise in the WSL by up to 300 m relative to the baseline simulations with fsm_preop.

Figure 6 Fraction of wet-snow pixels at 150 m elevation bands and in eight aspect classes, from AlpSnow WSM (a), fsm_preop (b), and fsm_optim (c) over MEZ 11. The wet-snow line is displayed in red, and its altitude in flat terrain is indicated in the top left of each panel.

3.3 Time series of snow line and wet-snow line

Generalizing the approach, both WSL and SL were computed over the course of the melt season for all MEZs and all years. Results for MEZ 11 on descending orbits (05:00 UTC) are shown in Fig. 7. Results for ascending orbits (17:00 UTC) can be found in Fig. A1. Using fsm_preop, we see in the upper panel of Fig. 7 that the wet-snow line gradually rises to high elevations from March to May each year, both in the observations and in the model. From June onwards (and even in May in 2018 and 2020), the snowpack is wet up to high elevations, and no WSL can be defined; i.e. the signal is saturated both in the observations and in the model. In the northern sector, the match between observations and simulations is good, except in 2017 where the model shows a considerably delayed onset of melt for elevations between 2200 and 2400 m. For southerly exposures, characterized by significant inter-annual variability, the model consistently exhibits a prolonged delay throughout the season. The simulated wet snow tends to be frequently positioned about 300 m lower than observed values. From April onwards, fsm_optim shows a higher WSL than fsm_preop, usually by 200 to 300 m. The match with observations is therefore better, in particular on the south-exposed slopes.

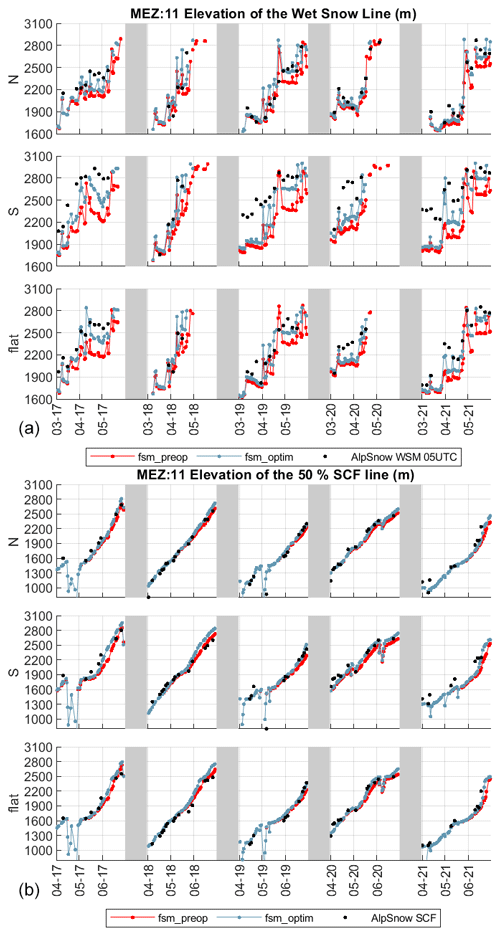
Figure 7 Time series of the wet-snow line (a) in the observations (black), fsm_preop (red), and fsm_optim (light blue) and snow lines (b) for the different aspects and seasons in MEZ 11. Only descending (05:00 UTC) Sentinel-1 tracks were used to determine the WSL.

Compared to the assessment of the WSL time series, the SL time series show much better agreement between observations and simulations (Fig. 7, right). Agreement between observations and fsm_preop is particularly good on the northerly slopes and in flat terrain, for almost all years. However some expositions show a snow line that is too high for the model (e.g. flat in 2018), and the snow line is mostly too low in the southern sector (in the years 2017, 2020, and 2021 in particular). The SL of fsm_optim becomes significantly higher (100–200 m) than that of fsm_preop from mid-May onwards. This results in an overall better match with the observations, with some exceptions (flat exposition in 2018 for example).

Comparing both the WSL and the SL products, we note that the years with the lowest SL bias for fsm_preop seem to coincide with the strongest WSL biases for that model version. Moreover, for a given elevation, there is a fairly consistent time lag between the WSL and the SL of 1 to 2 months.

3.4 Relationship between spring seasonal biases of WSL and SL

The time series of Fig. 7 show a persistence of WSL biases in fsm_preop across the entire season, suggesting a potential correlation with SL biases. In essence, our hypothesis posits that a delayed onset of melt in the model will likely lead to a delayed melt-out. To confirm this hypothesis, we conducted an analysis by computing the average model WSL bias and SL bias per year (over March–May and April–June, respectively), aspect, and MEZ. Figure 8a shows results for fsm_preop for all 5 years, all aspects, and MEZ 11. Overall, some correlation (R²=0.32) can be observed between the WSL and the SL biases, where often fsm_preop is too dry, coinciding with overestimated snow cover extent. WSL biases, however, are much higher in amplitude than SL biases (around −500 to 0 m vs. −200 to 100 m, respectively). The biases vary both between years and between aspect classes. For instance, 2021 exhibits overall strong biases, while 2018 is almost unbiased. The year 2019 stands out from the other years as it features a slightly higher SL bias. This anomaly is likely due to a single fresh-snow event in May during which the snow line was several hundred metres too high in the model (Fig. 7). Within each year, the WSL bias for fsm_preop is dominated by a north–south contrast. While the northern slopes (upward-pointing triangle) typically exhibit the least negative biases, the southern slopes (downward-pointing triangle) exhibit the most negative biases, in the range of −500 to −200 m. Similarly, the SL biases feature a northeast (square) to southwest (pentagram) contrast. This results in a very specific pattern: for each year, as we circle through the expositions clockwise, the bias values draw an ellipse in an anticlockwise direction.

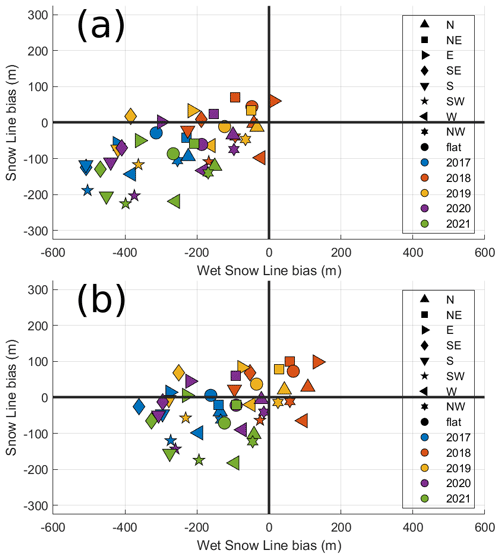
Figure 8 Snow-line bias as a function of wet-snow-line bias (at 05:00 UTC) for MEZ 11, across years and aspects.

The predominant factor contributing to the north–south disparity in ablation is likely the shortwave radiative input. Expectedly, a lower fresh-snow albedo value, as implemented in fsm_optim (see Sect. 2.3), could therefore induce an earlier melt in the model, while at the same time enhancing differential melting dynamics between north- and south-facing slopes. Results with fsm_optim show considerably reduced biases (Fig. 8b). Overall, with fsm_optim biases are better centred around zero, while the range of biases between aspects for any given year is reduced, particularly with regard to WSL biases. The correlation between biases in WSL and SL is also reduced from 0.32 to 0.13. Yet, the overall biases continue to vary between years. For instance, fsm_optim underpredicts both WSL and SL in 2021, while predominantly overpredicting WSL and SL in the year 2018. These results also hold when considering all the years and MEZs (Fig. 9). Despite the noticeable fluctuations between years, it is noteworthy that biases in WSL are considerably lower with fsm_optim compared to fsm_preop. This reduction also aligns with a significant decrease in the negative bias observed in SL.

Figure 9 Snow-line bias as a function of wet-snow-line bias (at 05:00 UTC) for all MEZs, across years and aspects.

4 Discussion

4.1 On the proposed wet-snow-line metric

In this study, we have evaluated the potential of Sentinel-1-based wet-snow maps for the performance assessment of snow-hydrological models in the ablation period. Leveraging the wet-snow-line concept facilitated a robust analysis of the information provided by Sentinel-1 wet-snow maps for high-spatial-resolution snowpack modelling. The topographic aggregation facilitated the direct comparison between remotely sensed observations and model simulations while achieving a good level of robustness against individual observation errors and data gaps as done in the literature (Mary et al., 2013; Karbou et al., 2022). Topographic aggregation makes the analysis more robust to missing or erroneous data in the observations, which is particularly important in the context of data assimilation (Cluzet et al., 2021). At the same time, while some relevant information from individual pixels may be lost, key spatial information was maintained by resolving biases in terms of region, elevation, aspect, and slope, which has been shown to be of critical relevance (Cluzet et al., 2020). Figures 3 and 6, as well as results from Karbou et al. (2021), suggest that this topographic aggregation can be further exploited to address shortcomings in the WSL retrievals (see Sect. 2.5 and Fig. 3): if a snowpack is wet at a given altitude, it will be wet at a lower altitude, all other factors being equal. The wet-snow line is therefore a condensed and potentially useful metric for both remote sensing and modelling, while the direct assimilation of binary products, such as wet-snow maps (or snow masks), into physically based snow models is typically seen as unfavourable (Baba et al., 2018; De Lannoy et al., 2012).

4.2 On the albedo correction

The wet-snow-line analysis evidenced a systematic dry bias in the pre-operational version of our model, fsm_preop (Fig. 8a). The comparison of observed versus simulated WSL revealed a systematic pattern, with model biases being particularly pronounced on the south-exposed slopes. This pattern indicated the need for a model adaptation that would accelerate the initiation of snowmelt, particularly in south-facing terrain, suggesting a mitigation strategy with a focus on shortwave radiation. Since FSM is driven by shortwave radiation per inclined surface (see Mott et al., 2023a), any reduction in the snow albedo will preferentially augment net shortwave radiation on south-exposed slopes. Indeed, the adjusted albedo parameterization in fsm_optim, while being closer to literature values (e.g. Gardner and Sharp, 2010), resulted in improved simulations of wet snow and snow cover fraction (Figs. 8 and 9) without incurring any considerable impairment of the excellent match between the observed and simulated snow depth at the stations (see Fig. 4). However, due to the lack of reliable spatialized albedo data in complex terrain (Largeron et al., 2020; Lamare et al., 2020; Cluzet et al., 2020), we can only speculate that this change actually addresses existing model deficiencies in the most efficient manner.

Simulated WSL and SL represent the equivalent elevation of two timing variables, i.e. the first occurrence of wet snow and the melt-out date. Both are a consequence of the coupled energy and mass balance equations and are affected by changes in the snow albedo in the same way: a reduction in the albedo will accelerate the timing of both events, providing a mechanism to explain why WSL and SL biases are correlated. Obviously, there are other factors that contribute to model biases of each so that such a correlation is not perfect. Apart from the energy turnover, there is also a direct link between the occurrence of wet snow and the progression of snowmelt. The occurrence of wet snow accelerates the albedo decay through wet metamorphism (see Sect. 2.3), which in turn increases the net shortwave input to the snowpack.

Observations indicate that both WSL and SL simulated by fsm_preop were typically biased low. Being able to improve both by decreasing the albedo is therefore expected. The remaining SL biases (Fig. 9) call for additional model improvements, requiring complementary data to the wet-snow maps exploited in this study, with spatially distributed and temporally resolved data of snow depth or SWE being the most obvious choice. Relying solely on snow cover fraction observations would have made it challenging to point out the details of the model deficiencies present in fsm_preop. The remaining bias patterns of fsm_optim (Figs. 8b, 9b and b) could be due to many reasons, e.g. biases in the subgrid parametrization for snow cover fraction (see Sect. 2.3), which derives modelled SCF from modelled snow mass (Helbig et al., 2021); biases in the observations (e.g. Aalstad et al., 2020); or biases in either simulated snow accumulation or melt. In this study, wet-snow observations helped to disentangle the causation by indicating a delayed melt, particularly on south-facing slopes. Further work can now focus on revealing other factors that contribute to the remaining snow-line biases.

4.3 Potential for data assimilation and model development

Significant biases, reaching up to approximately −350 m, persist in the modelled wet-snow line for fsm_optim (Fig. 8b). However, the extent to which additional information can be extracted from the observations remains uncertain. Observations are sensitive to wet-snow processes occurring at the subgrid scale, which are not accounted for in the model. The model itself has a coarse vertical resolution with three snow layers, which may not be enough to capture small surface melt events detected by SAR (Cristea et al., 2022; Lund et al., 2022). Further, the bucket approach used to route the liquid water through the snowpack is known to generate a slightly delayed onset of snowmelt runoff (Wever et al., 2014). On the other hand, wet-snow retrievals are not flawless either. SAR is sensitive to even very small amounts of liquid water and may misinterpret wet soil below a dry snowpack as wet snow (Marin et al., 2020). The retrievals are further known to be problematic in the presence of fractional snow cover and often report dry-snow conditions towards melt-out when this is clearly not the case (see Sect. 2.2). All these factors may contribute to an irreducible mismatch between observed and simulated wet-snow maps, which may undermine the utility of wet-snow maps beyond model assessment and optimization as demonstrated in this study.

However, several factors suggest that wet-snow maps contain further information, valuable for model evaluation and data assimilation in an operational model setting. First, it is interesting to note that even after model tuning, inter-annual variability dominates WSL and SL bias patterns, and their magnitudes show a strong correlation (Fig. 8). For example, the year 2018 exhibits positive biases of WSL and SL, while it is the opposite in 2021. Operational snowpack simulations are intrinsically dependent on numerical weather prediction models, which show variable performance and systematic biases between years (Winstral et al., 2019). In one year, a slight error in temperature might turn a major snowfall event into rain, while in another, early seasonal snowfall might be overpredicted, both causing snow model biases that will persist throughout the entire season. Such biases could be mitigated in real time through assimilation of wet-snow retrievals, since the transition from dry to wet snow happens during the season, not at the end of the season when optical remote sensing reports melt-out.

The potential for data assimilation of SCF has long been established, although most of the time in a reanalysis context (Margulis et al., 2015; Aalstad et al., 2018; Alonso-González et al., 2021) rather than in real time (Baba et al., 2018). As long as the snow cover fraction equals 1, the only information that can be derived is that the snow water equivalent is above a few tens of millimetres (e.g. Magand et al., 2014). This is not very informative as long as the model is not completely removed from reality (De Lannoy et al., 2012). Figure 7, however, frequently illustrates a persistent bias in the snow line throughout the ablation period. This pattern implies that information collected early at lower elevations could potentially be transferred to higher elevations through data assimilation using the propagation of information (Cluzet et al., 2021; Alonso-González et al., 2023). Such an approach has the potential to enhance the overall performance of the model. However, this may not be the case in the absence of systematic model biases. Figure 7 shows that once the systematic albedo bias has been fixed in fsm_optim, there is no longer a consistent snow-line bias throughout the season: there is a negative snow-line bias early in the season and then a positive one later in the season. In such a context, while reanalyses may be able to find optimal trajectories once the full time series of observations has been gathered, real-time data assimilation might result in degraded performance in the late season. SCF data assimilation could nevertheless be used to correct for the instances where the modelled fresh snow line is obviously wrong, as in May 2019 (Fig. 7).

The ellipsoidal patterns of the WSL and SL biases with respect to aspect (Fig. 8) demonstrate the potential of using WSL and SL retrievals in combination as a basis for a detailed model performance diagnosis. In most MEZs, SL biases with regard to the eastern slopes are often substantially higher compared to the western slopes by 50 to 200 m. The corresponding WSL biases, however, are of the same order of magnitude. This finding suggests a deficiency in the model's representation of wind-driven snow redistribution processes. In our climate, dominated by westerly winds, these processes typically lead to an uneven distribution of snow between west- and east-exposed slopes, a phenomenon that the model currently fails to adequately represent. Such a finding may motivate better inclusion of wind redistribution processes in FSM (e.g. Vionnet et al., 2021; Baron et al., 2024; Quéno et al., 2024) even at the considered spatial resolution of 250 m.

Conversely, the wet-snow-line bias in our simulations is still dominated by a south–north contrast with fsm_optim (Fig. 8b). Given the strong influence of albedo on the wet-snow line, we cannot exclude that further improvements are required with respect to the representation of snow albedo. Snow metamorphism and solar angle indeed have strong effects on the albedo, which are not accounted for in the model (e.g. Gardner and Sharp, 2010), and result in topographic variability of the albedo as evidenced by satellite imagery (e.g. Mary et al., 2013; Cluzet et al., 2020). The rather simplistic temperature-dependent time decay of albedo within FSM (Essery, 2015) cannot capture these processes in adequate detail, leaving potential for mitigation by way of data assimilation.

4.4 Complementarity with flat-field snow depth observations

As evidenced by Fig. 4, fsm_preop performs remarkably well against data measured at our 444 flat-field snow monitoring sites. There is little evidence and incentive to suggest that the model should be improved from these data alone. The remote sensing data reveal model shortcomings we would have remained unaware of. Wet-snow maps directed us towards a possible solution for an issue that was also visible in our snow-line comparisons, demonstrating the complementarity of all three datasets involved in our model performance assessment. Additionally, flat-field snow depth observations are scarce in alpine regions above 2500 m a.s.l. (e.g. Cluzet et al., 2022). Likewise, precipitation and air temperature measurements used to constrain meteorological input via assimilation or debiasing are scarce above these altitudes (Isotta et al., 2014; Vernay et al., 2022). Alpine areas are also where wind redistribution is prominent due to an enhanced exposition to winds (Dujardin and Lehning, 2022), not to mention steep terrain and glaciated areas. All in all, for these high elevations, the uncertain input data and rare validation measurements are a challenge for achieving accurate snowpack simulations. Therefore, wet-snow retrievals and snow cover fraction observations offer a unique opportunity to observe the snowpack where other data are typically scarce and provide key information to improve modelling and process understanding at high elevations. Nevertheless, a limitation arises from the challenges associated with distinguishing between snow-free and snow-covered glaciers in the snow cover fraction products.

Finally, Fig. 4 shows that the significant improvements we obtain with fsm_optim in terms of WSL and SL come at the cost of slightly deteriorating the model performance at flat-field snow depth stations in the ablation period. This is not necessarily a surprise, as fsm_preop inherits its tuning from model versions specifically calibrated against flat-field snow depth stations (Mott et al., 2023a). The performance of fsm_preop against snow depth observations already establishes high standards. Additionally, it is a well-known fact that snow depth tends to be higher in flat terrain compared to on the surrounding slopes (Grünewald and Lehning, 2015), a factor accounted for in our model through a precipitation multiplier (see Sect. 2.3). Further combining satellite observations of wet snow and snow cover fraction with flat-field snow depth observations could help refine the relative behaviour of models in flat terrain with respect to the complex topography that predominates in mountainous areas.

5 Conclusions

This work investigated the potential of wet-snow retrievals from Sentinel-1 SAR to inform operational snowpack simulations in alpine areas over large extents. We could demonstrate that a pre-operational version of the snow-hydrological model fsm_preop was well aligned with snow depth observations at hundreds of monitoring sites. However, notable discrepancies were observed between fsm_preop and wet-snow maps at the onset of the melting season over a span of 5 years. For an in-depth performance assessment, we used the wet-snow line (WSL) as an aspect-dependent elevation line across which the snowpack transitions from dry- to wet-snow conditions for a given hydrological unit. This metric provides a spatially aggregated summary of the information obtained from wet-snow maps, enabling the exploration of regional variations in moistening dynamics. This aggregation also mitigates data quality issues and data gaps at the pixel level that would hamper model evaluation. While the simulated WSL matched the observations well on northern slopes and in flat areas, the model had a substantial dry bias in the southern sector, suggesting a delay in the sun-induced melt. Snow lines (SLs) derived from Sentinel-2 snow cover fraction retrieval show that this dry bias coincides with a seasonal snowpack depletion that is too late. Both biases were substantially reduced when an update of the model albedo parametrization was applied.

Wet-snow maps provide valuable information about the snowpack state much earlier in the ablation season than snow cover fraction observations. This is an important asset of WSL data for operational applications. Snow cover fraction observations are much more detailed but come too late in the season to allow for mitigation of biases that arose much earlier during the winter. Our study demonstrates that wet-snow map and snow cover fraction observations can provide complementary information to that from flat-field snow depth observations, allowing us to evaluate snow-hydrological models from a new perspective. Satellite observations can be used to evaluate the simulations in diverse topographic conditions, contrary to flat-field snow depth observations. Finally, as snow depth observations are rare at high elevations, satellite imagery provides a unique opportunity to constrain models particularly at those altitudes.

Appendix A: Complementary figure

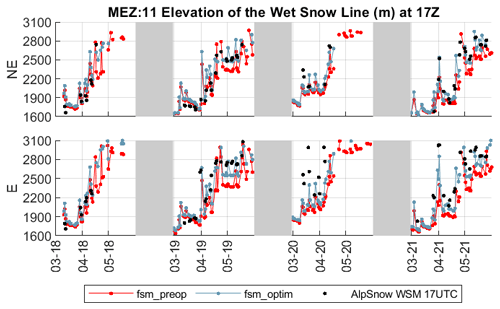
Figure A1 Time series of the wet-snow line in the observations (black), fsm_preop (red), and fsm_optim (light blue) for the different aspects and seasons in MEZ 11. Only ascending (17:00 UTC) Sentinel-1 tracks were used to determine the WSL. Note that for technical reasons, the year 2017 is not represented, as no model output was saved for this year at 17:00 UTC.