Brief communication: Stalagmite damage by cave ice flow quantitatively assessed by fluid–structure interaction simulations

Mechanical damage to stalagmites is commonly observed in mid-latitude caves. Former studies have identified thermoelastic ice expansion as a plausible mechanism for such damage. This study builds on these findings and investigates the role of ice flow along the cave bed as a possible second mechanism in stalagmite damage. Utilizing fluid–structure interaction models based on the finite-element method, forces created by ice flow are simulated for different stalagmite geometries. The resulting effects of such forces on the structural integrity of stalagmites are analyzed and presented. Our results suggest that structural failure of stalagmites caused by ice flow is possible, albeit unlikely.

1 Introduction

Secondary carbonate deposits such as stalactites and stalagmites, collectively referred to as speleothems, are abundant in caves worldwide and grow over extended periods of time, typically many thousands of years, thereby recording valuable proxy information about climate and vegetation outside the cave. Speleothems are therefore highly sought archives of paleoenvironmental change (e.g., Fairchild and Baker, 2012). Despite the fact that caves are typically well protected from processes such as weathering or erosion, some caves, particularly in the mid-latitudes, show naturally occurring mechanical damage to speleothems. Several processes have been discussed that cause damage to stalagmites and stalactites, including movement of stalagmites growing on a soft-sediment substrate, gravity-driven breakdown of cave ceilings, strong earthquakes, and the former presence of ice in these subterranean cavities. The latter process has been identified as a main cause for stalagmites being sheared off their bases (e.g., Gilli, 2004; Orvošová et al., 2012), as well as for sheet-like deposits known as flowstones showing a fractured appearance (e.g., Lundberg and McFarlane, 2012; see Fig. 1). Key to this interpretation is the coexistence of damaged speleothems with so-called cryogenic cave carbonates (Richter et al., 2011; Žak et al., 2018; Spötl et al., 2021). The former are indicators of the past presence of perennial ice in these caves and can be reliably dated using radiometric techniques (e.g., Dublyansky et al., 2024). In addition, damaged speleothems are often overgrown by younger calcite of Holocene age, which proves the glacial age of the damage (e.g., Žak et al., 2018; Spötl et al., 2021). In a recent study, Spötl et al. (2023) used numerical modeling combined with laboratory measurements to quantitatively assess which processes in former ice-filled caves led to damage of stalagmites. The results show that internal deformation within a cave ice body due to ice flow under gravity cannot fracture stalagmites, even on steep slopes. In contrast, thermoelastic stresses within an ice body due to temperature changes reach values partly exceeding the tensile strength of stalagmites. In this contribution we expand on the analysis of Spötl et al. (2023) by (a) examining not only the external forces exerted by ice flow but also their internal effect within stalagmites and (b) also including smaller stalagmite dimensions. Structural failure of stalagmites caused by ice flow was investigated using a fluid–structure interaction (FSI) model (e.g., Sigrist, 2015).

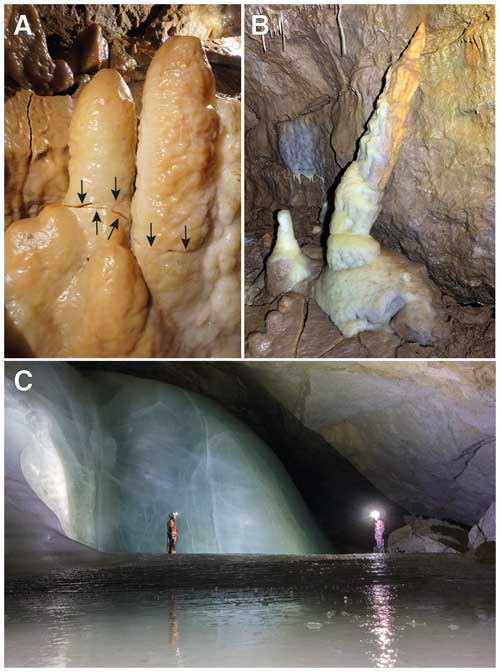
Figure 1 (a, b) Examples of stalagmites damaged by ice during the last glacial period as shown by the presence of cryogenically formed calcite deposits in these caves. (a) Two parallel stalagmites detached from their base along subhorizontal cracks (arrows), Obir Caves, Austria. Width of image 0.4 m. (b) Light-brown stalagmite broken near its base and tilted. Younger white calcite (of likely Holocene age) is growing over the lower part of this damaged speleothem and forms a smaller stalagmite to the left. Also note dark-brown flowstone in the foreground, likely fractured due to the former presence of ice. Shatter Cave, Mendip Hills, UK. Width of image 1.1 m. (c) Example of a modern ice cave with floor ice and thick ice deposits on the slope in the background. Feuertal Eishöhle, Austria. Images: Christoph Spötl (a, b) and Harald Zeitlhofer (d).

2 Methods

In order to be consistent with the study of Spötl et al. (2023), we chose to model the same ice domain with $-\mathrm{7}\le x\le \mathrm{14}$ m, $-\mathrm{3.5}\le y\le \mathrm{3.5}$ m and the stalagmite location at $x=y=\mathrm{0.0}$ m (cf. Fig. 3 in Spötl et al., 2023). However, we examined two ice thicknesses (h_ice=1.0 and 2.0 m), two slope angle values (β_ice=10 and 40°), three stalagmite diameters ($d_{\mathrm{s}}=\mathrm{0.15},\mathrm{0.25}$ and 0.4 m), two stalagmite heights (h_s=0.5 and 1.0 m), and full-slip and no-slip conditions at the cave base. We did not utilize any glaciological sliding laws, as we wanted to investigate the two end-member states (frictionless full sliding vs. no-slip). In total, 14 different configurations, which are summarized in Table 2, were examined. The cave walls (sidewalls of the ice domain) were assumed to be no-slip boundary conditions, and the ice surface was a stress-free boundary, allowing for free movement of ice. Stalagmites were modeled as cylinders with a fixed diameter d_s, except for configurations 13 and 14, which exhibited a conical shape ($d_{\mathrm{s}}^{\mathrm{base}}=\mathrm{0.25}$ m and $d_{\mathrm{s}}^{\mathrm{top}}=\mathrm{0.1}$ m). Our numerical mesh typically contains 100 000 tetrahedral elements with mesh element sizes varying between 0.3 m far away from the stalagmite and 0.02 m within the stalagmite.

2.1 FSI model

We assumed the deformation of ice to be fluid-like, with a non-Newtonian rheology following Glen's flow law (e.g., Glen, 1955). Driven by gravity, the cave ice flows downslope and exerts forces on the stalagmite's outer surface. The structural response of the stalagmite to these external forces was modeled as linearly elastic. In Spötl et al. (2023), laboratory experiment results were presented that identified the elastic properties of the stalagmite material. As we are interested in the stress distribution just before structural failure, linear elasticity (e.g., Zienkiewicz et al., 2013) is a reasonable choice for our model. Using the chosen FSI model approach, we simulated both the forces exerted by ice deformation (fluid) and the response of the stalagmite (solid structure) to these forces with a finite-element model. A summary of the relevant model parameters is given in Table 1.

Table 1 Model parameters.

We developed this simulation strategy using the open-source software Elmer FEM (e.g., Malinen and Råback, 2013), which includes well-established FSI routines (e.g., Järvinen et al., 2008). To include the non-linear flow behavior of ice in our model, we used Elmer/Ice (e.g., Gagliardini et al., 2013), which builds upon Elmer FEM.

Elmer FEM applies a partitioned approach to solving FSI problems, thus solving the equations governing non-linear fluid flow and elastic structural response with two different numerical solvers. Forces are coupled at the fluid–structure boundary (stalagmite outer surface), and the model performs iteration until a balance between fluid stress and the elastic response of the solid is found.

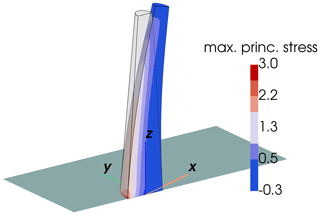
Figure 2 Maximum principal stress σ_max for the conical stalagmite of simulation 13 in 10⁶ Pa (displacements are scaled by a factor of 1000). Red colors on the upstream face indicate tensile stresses (σ_max>0). The z axis of the coordinate system is aligned vertically upward against gravity, while the x axis aligns with the downstream direction of the ice flow.

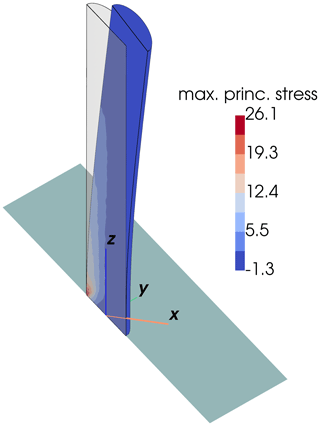
Figure 3 Maximum principal stress σ_max in the stalagmite pertaining to simulation 09 in 10⁶ Pa (displacements are scaled by a factor of 100). This simulation indicates stresses significantly exceeding the tensile strength of the stalagmite on its upstream side. The x axis points in the downstream direction of the ice flow.

3 Results

Solutions from the FSI simulations were analyzed for maximum (principal) tensile stresses σ_max in the stalagmite to identify cases where its tensile strength ($\mathrm{4.3}\times {\mathrm{10}}^{\mathrm{6}}\pm \mathrm{1.5}\times {\mathrm{10}}^{\mathrm{6}}$ Pa; Spötl et al., 2023) is exceeded. According to Rankine's theory (Rankine, 1857), this would result in structural failure of the stalagmite. Typically, the maximum tensile stresses were found to be caused by bending of the stalagmite and occurred at the upstream side of its base in the vertical direction (see Fig. 2). The results of the simulations are summarized in Table 2.

Table 2 Maximum principal stress max σ_max and maximum shear stress max $\left|{\mathit{\tau }}_{zx}\right|$ for all simulations. β_ice is the cave slope angle, h_ice the ice thickness, h_s the stalagmite height and d_s the stalagmite diameter. Boundary conditions (BCs) at the ice bed are listed as well. Bold simulation numbers indicate configurations for which the stalagmite would likely break due to the arising tensile stresses.

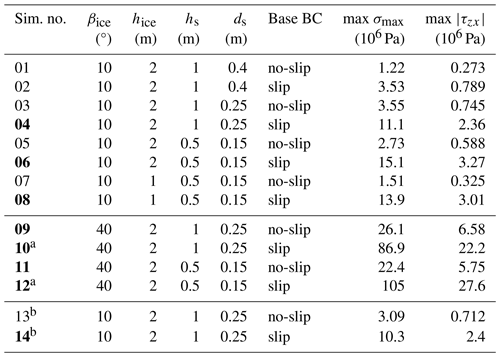
^a Maximum σ_max on the downslope side of the stalagmite exceeds the tensile strength of ice (cf. Sect. 3). ^b The configurations exhibiting a conical stalagmite shape.

For moderately sloping caves (β_ice=10°), only configurations exhibiting full-slip conditions at the ice–cave base interface (no bed friction) indicate failure (simulations 04, 06, 08 and 14). In the case of steeply sloping caves (β_ice=40°), all investigated configurations (simulations 09 to 12) exhibit maximum tensile stresses significantly exceeding the stalagmite's tensile strength.

We also investigated the effect of ice temperature, as all our simulations assume temperate ice (cf. A in Table 1). However, reducing the ice temperature to −5.0 °C only results in a reduction in the maximum tensile stress of less than 0.5 ‰ relative to the temperate case.

Ice thickness h_ice, and thereby how much ice overflows the stalagmite, significantly affects σ_max. Comparing simulations 05 (h_ice=2 m) and 07 (h_ice=1 m) reveals a reduction in σ_max by about 45 % in the case of no-slip conditions. In the case of full-slip conditions (simulations 06 and 08), however, only a small reduction in σ_max by about 8 % for the same 50 % reduction in h_ice is observed.

The stalagmite geometry is found to significantly influence the observed maximum tensile stresses. This is especially true for the stalagmite base diameter d_s and by extension its section modulus $S=\frac{\mathit{\pi }{d}_{\mathrm{s}}^{\mathrm{3}}}{\mathrm{32}}$. Even though a reduction in d_s reduces the surface area exposed to ice flow, σ_max for simulations 03 and 04 (d_s=0.25 m) is nearly 3 times higher than for simulations 01 and 02 (d_s=0.4 m) due to a disproportionate reduction in S. Given the same ice thickness of h_ice=2 m, small stalagmites (d_s=0.15 m and h_s=0.5 m; simulations 05 and 06) are more prone to failure than larger stalagmites (d_s=0.4 m and h_s=1 m; simulations 01 and 02). Conically shaped stalagmites (configurations 13 and 14) exhibit comparable, albeit slightly lower, maximum tensile stresses than cylindrical stalagmites (configurations 03 and 04).

For our simulations we assumed ice frozen to the stalagmite and thus a direct force coupling at the ice–stalagmite interface. Therefore, the modeled ice flow can potentially exert tensile forces on the downslope side of the stalagmite. By comparing the maximum principal tensile stress σ_max on the downslope ice–stalagmite interface with reported values for ice tensile strength (0.7×10⁶–3.1×10⁶ Pa; Petrovic, 2003), we identified two configurations (configurations 10 and 12) for which failure of the ice itself would likely occur. For these configurations the reported maximum σ_max values are definitely an overestimation as they assume full stress coupling between the ice and stalagmite on the downslope side. In reality, at such high stresses, the ice itself would fail and cracks would form which would decouple the ice body from the stalagmite at the downstream side. Our simulations do not account for such crack formations, and thus the results for configurations 10 and 12 have to be considered with caution.

High shear stresses within the stalagmite could also lead to structural failure; hence we report maximum absolute values of the base shear stress $\left|{\mathit{\tau }}_{zx}\right|$ in Table 2. However, maximum $\left|{\mathit{\tau }}_{zx}\right|$ amounts to less than 30 % of maximum σ_max for all investigated configurations. We therefore consider it unlikely that the stalagmite would fail due to the presence of shear stresses.

4 Discussion and conclusion

Ice caves exhibit complex geometries which comprise galleries, chambers and shafts. In addition, the floor of chambers and galleries is typically covered by coarse debris including variably large and angular blocks. These topographic intricate features render free-sliding (i.e., full-slip) interface conditions between the ice and the cave bed highly unlikely in reality. Most importantly, cave ice bodies are typically frozen to their substrate. They owe their existence to the strong cooling of the rock mass surrounding the cave as a consequence of strong (winter) cooling by airflow or the presence of permafrost (e.g., Luetscher, 2022).

Any zones of full-slip would be compensated for by ice being required to flow around and/or over complex bed topographies. Hence we regard our results with basal full-slip conditions (simulation numbers 02, 04, 06, 08, 10, 12 and 14) as highly unlikely upper-end-member cases for ice cave conditions. Conditions close to the no-slip simulations are regarded as most likely.

We found large tensile stresses on the upslope (i.e., upstream) side of stalagmites to be the main cause for structural failure. In contrast, a large influence of shear stresses near the stalagmite base is ruled out due to their comparatively small magnitude of less than 30 % of the observed tensile stresses.

Our results suggest that only in steeply sloping caves with large ice bodies (e.g., 14 m of cave ice, 2 m thick, upslope of a stalagmite) can forces exerted by ice flow become large enough to damage moderately large stalagmites. Only in one case with no-slip conditions (simulation number 09; see Fig. 3) did we find a configuration in which a moderately large stalagmite would be damaged.

This study confirms that vertical uplift of stalagmites due to thermoelastic stresses induced by expanding ice, as previously reported (Spötl et al., 2023), is still the most likely physical explanation for widespread damage to speleothems in mid-latitude caves during the cold periods of the Pleistocene. Even though our results rule out lateral ice flow as a main damage mechanism, which was previously often assumed, in extreme conditions (i.e., steeply sloping, large, ice-filled caves), large tensile stresses caused by ice flow can occur in stalagmites, which ultimately can also cause structural damage.