the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
The potential of in situ cosmogenic 14CO in ice cores as a proxy for galactic cosmic ray flux variations
Vasilii V. Petrenko
Segev BenZvi
Michael Dyonisius
Benjamin Hmiel
Andrew M. Smith
Christo Buizert
Galactic cosmic rays (GCRs) interact with matter in the atmosphere and at the surface of the Earth to produce a range of cosmogenic nuclides. Measurements of cosmogenic nuclides produced in surface rocks have been used to study past land ice extent as well as to estimate erosion rates. Because the GCR flux reaching the Earth is modulated by magnetic fields (solar and Earth's), records of cosmogenic nuclides produced in the atmosphere have also been used for studies of past solar activity. Studies utilizing cosmogenic nuclides assume that the GCR flux is constant in time, but this assumption may be uncertain by 30 % or more. Here we propose that measurements of 14C of carbon monoxide (14CO) in ice cores at low-accumulation sites can be used as a proxy for variations in GCR flux on timescales of several thousand years. At low-accumulation ice core sites, 14CO in ice below the firn zone originates almost entirely from in situ cosmogenic production by deep-penetrating secondary cosmic ray muons. The flux of such muons is almost insensitive to solar and geomagnetic variations and depends only on the primary GCR flux intensity. We use an empirically constrained model of in situ cosmogenic 14CO production in ice in combination with a statistical analysis to explore the sensitivity of ice core 14CO measurements at Dome C, Antarctica, to variations in the GCR flux over the past ≈ 7000 years. We find that Dome C 14CO measurements would be able to detect a linear change of 6 % over 7 ka, a step increase of 6 % at 3.5 ka or a transient 100-year spike of 190 % at 3.5 ka at the 3σ significance level. The ice core 14CO proxy therefore appears promising for the purpose of providing a high-precision test of the assumption of GCR flux constancy over the Holocene.
- Article
(1158 KB) - Full-text XML
- BibTeX
- EndNote
The galactic cosmic ray (GCR) flux at Earth is modulated by both the geomagnetic and the heliospheric (solar) magnetic fields. The heliospheric magnetic field strength is linked to solar activity and solar irradiance (e.g., Wu et al., 2018b; Steinhilber et al., 2009), with irradiance being a key climate driver. This has enabled the use of records of past cosmogenic nuclide production rates for studies of past solar variability (e.g., Adolphi et al., 2014; Bard et al., 2000; Steinhilber et al., 2009; Usoskin et al., 2016; Usoskin, 2023). The two main nuclides that have been used for these studies are 14C (mainly from tree rings, which record atmospheric ratio) and 10Be (from ice cores, which record the flux of 10Be at the snow deposition site). Measurements of cosmogenic nuclides have also been used extensively to study processes at the Earth's surface, such as the timing of glacial advance and retreat (e.g., Balco, 2020). In these applications, nuclides such as 10Be, 14C, 26Al and 36Cl that are produced in situ in surface rocks are of interest.
Cosmogenic nuclide-based reconstructions of past solar activity and ice extent have relied on the assumption that the GCR flux is constant in time (e.g., Balco, 2011; Gosse and Phillips, 2001; Muscheler, 2013). Measurements of cosmogenic radionuclides in meteorites provide arguably the strongest support for this assumption (e.g., Smith et al., 2019; Wieler et al., 2013). However, a number of important uncertainties are involved when interpreting these measurements, including meteoroid orbits, solar modulation of the GCR flux and break-up of meteoroids/fresh surface exposure on entry into the atmosphere. A review by Wieler et al. (2013) concluded that while overall the meteorite evidence indicates that the GCR flux is constant, this assumption is uncertain by 30 % or more. Measurements of cosmogenic nuclides in lunar rocks also indirectly indicate that the GCR flux could have been constant on million-year timescales, although there is still a confounding influence of solar modulation (e.g., Poluianov et al., 2018). Records of ratios in oceanic sediments and iron–manganese crusts (Willenbring and von Blanckenburg, 2010) have also been used to argue that the GCR flux is approximately constant on million-year timescales (Wieler et al., 2013). However, this approach also involves multiple confounding factors, such as solar and geomagnetic modulation of the GCR flux and 10Be transport, deposition, and oceanic cycling. Results from studies that have used cosmogenic 14C and 10Be to examine past solar activity also assume that there were no large changes in the GCR flux in the past few millennia (e.g., Knudsen et al., 2009; Steinhilber et al., 2012; Wu et al., 2018a). However, again, inferences about the GCR flux from such records are complicated by solar and geomagnetic modulation (e.g., Knudsen et al., 2008), carbon cycle (for 14C, e.g., Muscheler et al., 2007), and transport and deposition effects (for 10Be, e.g., Field et al., 2006).
Theoretical considerations also generally support the assumption that the GCR flux is constant, though small anisotropies are expected due to the effect of the nearest sources of GCRs and the diffusive propagation of cosmic rays in the galaxy (Erlykin and Wolfendale, 2006; Blasi and Amato, 2012; Ahlers and Mertsch, 2015; Mertsch and Funk, 2015). At energies above 100 GeV, the GCR flux at Earth today is isotropic to within 1 part in 1000, with the residual anisotropy characterized by a dipole plus statistically significant components on angular scales as small as 5° (e.g., Abeysekara et al., 2019, and references therein). The observations indicate that cosmic ray transport is dominated by diffusion in galactic magnetic fields, which should dampen the contributions of spatial and temporal point sources of cosmic rays. Nevertheless, significant GCR flux variations are in principle possible even on sub-millennial timescales. For example, Melott et al. (2017) and Thomas et al. (2016) consider the terrestrial effects of a supernova 50 parsecs from Earth and estimate that the production rate of atmospheric muons could increase by up to several orders of magnitude depending on how accelerated GCRs propagate through nearby galactic magnetic fields. While the predictions of such models should be understood to represent the extreme upper limit of possible effects, a number of observations suggest that supernova explosions in our galactic neighborhood do produce measurable effects on the local properties of GCRs. Such observations include the part-per-mille dipole anisotropy in the cosmic ray flux above 1 TeV (e.g., Abeysekara et al., 2019; Ahlers and Mertsch, 2015; Blasi and Amato, 2012; Erlykin and Wolfendale, 2006), the fluxes of positrons and antiprotons above 20 GeV and heavy nuclei above 1 TeV (e.g., Kachelriess et al., 2015), and the measurements of 60Fe in ocean sediments (Wallner et al., 2016) and Antarctic snow (Koll et al., 2019). Thus, high-precision tests of GCR flux variations that are free of the confounding factors discussed above for meteorites and for cosmogenic 10Be and 14C produced in the atmosphere would be valuable.
2.1 Overview of 14CO in glacial ice
We first provide an overview of the current understanding of the processes that control the abundance of in situ cosmogenic 14CO in glacial ice, which is needed to understand how the ice core 14CO proxy for GCR flux variations works. 14C in glacial ice originates from trapping of 14C-containing atmospheric gases such as carbon dioxide (CO2), methane (CH4) and carbon monoxide (CO) as well as from in situ cosmogenic production. In situ 14C is produced in glacial ice and firn via interactions of secondary cosmic ray neutrons and muons with 16O in the ice grains (Fig. 1a) (e.g., Lal et al., 1997; Petrenko et al., 2016; van der Kemp et al., 2002). Once produced, this 14C reacts rapidly to form predominantly 14CO2 and 14CO, with a small amount of 14CH4 and possibly other organics also being formed (e.g., Fang et al., 2021; Lal et al., 2000; Petrenko et al., 2013; van de Wal et al., 2007). 14C production rates are highest near the surface, where neutron-induced spallation of 16O is the main production mechanism. The neutron flux is attenuated rapidly with depth, however, and only affects the uppermost ≈ 20 m of the firn (or uppermost ≈ 10 m of solid ice) (e.g., Lal et al., 1987). Below these depths, production of 14C proceeds at lower rates and is dominated by negative muon capture as well as interactions with fast muons (Fig. 1b) (Petrenko et al., 2016; van der Kemp et al., 2002).
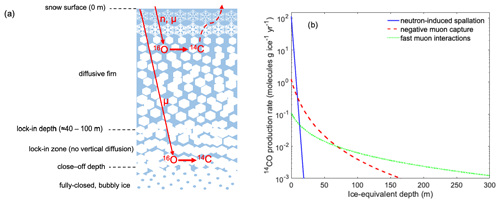
Figure 1Introduction to production and loss of 14C in firn and ice. (a) Simplified schematic of the firn column, illustrating in situ cosmogenic production 14C by neutrons (n) and muons (µ) and loss in the upper, diffusive part of the firn as well as 14C production by muons below the lock-in depth where all of the 14C is retained. (b) 14CO production rates calculated as described in Sect. 2.2. Here and fμf=0.0722, which are mid-range values from the range constrained by Hmiel et al. (2024).
The concentration of in situ 14C in glacial ice at accumulation sites is controlled by the 14C production rates (site and depth-dependent), the snow accumulation rate and the retention of 14C in the firn. Sites at higher altitudes have less atmospheric shielding from cosmic rays, resulting in higher 14C production rates at the surface (e.g., Lifton et al., 2014). At sites with low accumulation rates, ice layers spend more time at relatively shallower depths, allowing for more in situ 14C to be produced. Further, prior work has shown that most of the in situ cosmogenic 14C that is produced in the firn is rapidly lost to the atmosphere (de Jong et al., 2004; Hmiel et al., 2024; Petrenko et al., 2013). Because of this, the majority of the in situ cosmogenic 14C in glacial ice is from production below the firn zone. Of the 14C-containing gases in glacial ice, 14CO has the highest ratio of in situ cosmogenic to trapped atmospheric 14C. This is due to (1) atmospheric 14CO concentrations being lower than those for 14CO2 or 14CH4 (mainly because global mean mole fractions for CO (≈ 80 nmol mol−1) are much lower than those for CO2 (≈ 420 µmol mol−1) and CH4 (≈ 1920 nmol mol−1) (NOAA Global Monitoring Laboratory data viewer)) and (2) the relatively large fraction of in situ 14C that forms CO in ice (≈ 0.31; Dyonisius et al., 2023; Hmiel et al., 2024). This makes 14CO the best species for investigating the in situ cosmogenic component of 14C in ice.
In situ 14CO in glacial ice is present at very low concentrations (a few molecules per gram of ice is typical; see Figs. 2 and 3), making measurements very analytically challenging. Prior studies have either worked with relatively small (a few kg) ice samples available from a single shared ice core (e.g., van der Kemp et al., 2002), resulting in relatively large uncertainties, or required dedicated ice coring campaigns to obtain large ice amounts (100 kg or more) from multiple parallel ice cores for high-precision measurements (e.g., Dyonisius et al., 2023). Dry extraction of air from ice has been used for smaller ice samples (van der Kemp et al., 2002), and melt-extraction has been used for large samples (Dyonisius et al., 2023). CO in the extracted air is separated, it is combusted to CO2, this CO2 is subsequently converted to graphite, and then the or ratio is measured via accelerator mass spectrometry. A detailed description of the ice core 14CO measurement methodology can be found in Dyonisius et al. (2023).
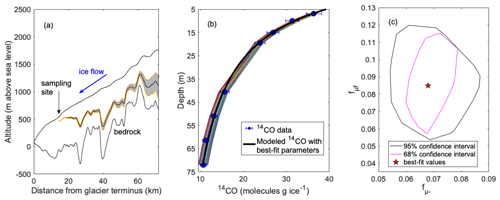
Figure 2Overview of 14CO results from Taylor Glacier. (a) Ice parcel back-trajectories for the deepest (72 m) Taylor Glacier 14CO sample. The solid black line shows the best-estimate flow trajectory, and the shaded envelope represents the 68 % confidence interval (CI). (b) Comparison of Taylor Glacier 14CO measurements with model predictions for accepted scenarios. (c) Accepted ranges of fμ− and fμf. Figures modified from Dyonisius et al. (2023).
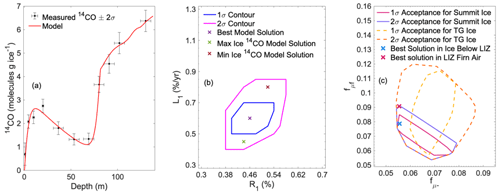
Figure 3Overview of 14CO results from Greenland Summit. (a) Measured 14CO content in ice grains and closed porosity along with a model fit. Horizontal error bars represent the depth range of firn and ice included in each sample. (b) Contour plot of the accepted ranges of the R1 (initial retention) and L1 (slow leakage) parameters in firn, together with the best-fit solution as well as solutions that result in maximum and minimum 14CO content in ice below the firn zone. (c) Contour plot of accepted ranges of fμ− and fμf from Taylor Glacier (dashed lines) and after further constraints from Greenland Summit measurements (solid lines).
2.2 Production of 14CO in glacial ice
Prior studies (Dyonisius et al., 2023; Hmiel et al., 2024) have presented detailed parameterizations of in situ cosmogenic 14CO production rates in glacial ice. This work uses the same parameterizations, which are described again here for the reader's convenience. The 14C production rate in ice via the neutron mechanism declines exponentially with depth, with the 14CO production rate calculated following Hmiel et al. (2024) as
In this equation, h is the mass-depth (in g cm−2), ΩCO is the fraction of total in situ 14C that forms CO (we use 0.31, following Hmiel et al., 2024) and Fn is an adjustable dimensionless parameter that allows for tuning the neutron mechanism production rate within uncertainties (0.9–1.1 range). Sn is the site-specific dimensionless scaling factor which describes the ratio of 14C production rate at the site of interest to 14C production rate at a sea-level high-latitude reference site; Sn is determined using the model of Lifton et al. (2014). Qc is a factor that translates 14C production rate from quartz to ice using the difference in oxygen atom density (atoms g−1) between ice and quartz (Qc=1.667). is the reference 14C production rate at the surface via the neutron mechanism in quartz at a sea-level high-latitude site; we use a value of 12.76 atoms g Qtz−1 yr−1 from the CRONUS-Earth project, which is defined for the 2001–2010 mean solar modulation and geomagnetic field conditions (Borchers et al., 2016). Λn is the absorption mean free path of neutrons in ice; we use a value of 150 g cm−2 (Lal et al., 1987; van de Wal et al., 2007).
For 14CO production by the muon mechanisms, we use a model developed by Balco et al. (2008) (“Balco model”), which incorporates parameterizations of Heisinger et al. (2002a, b). The 14C production rate via negative muon capture in these parameterizations is calculated using
where Rμ−(h) is the stopping rate of negative muons (muons g−1 yr−1) at mass-depth h, fC is the chemical compound factor representing the probability that the stopped muon is captured by one of the target atoms, fD is the probability that the negative muon does not decay in the K shell before nuclear capture and f∗ is the effective probability for production of the cosmogenic nuclide of interest after μ− capture by the target nucleus. For production of 14C from 16O in ice, fC=1, fD=0.1828 and (Heisinger et al., 2002a).
The 14C production rate via the fast muon mechanism is given by Heisinger et al. (2002b) as
where σ0 is the reference nuclear reaction cross section at a muon energy of 1 GeV (cm2), ϕ(h) is the total muon flux at mass-depth h (muons cm−2 yr−1 sr−1), is the mean muon energy at mass-depth h (GeV), α is a power factor that describes the energy dependence of the cross section (we use α=0.75, consistent with Dyonisius et al., 2023, and Heisinger et al., 2002b) and N is the number of target nuclei per gram target mineral (Hmiel et al., 2024). We use σ0=8.8 µb cm2 (Heisinger et al., 2002b) and N= (6.022×1023 atoms mol−1)(18.02 g mol−1) for ice. β(h) is a unitless depth dependence factor (≈ 0.9 at our depths of interest, with only a slight dependence on depth), given by Heisinger et al. (2002b) as
Heisinger et al. (2002b) also provide an approximate function for β(h), which is used in the Balco model and hence in our model:
The Balco model incorporates Eqs. (2) and (3) and also provides the muon fluxes and energies as a function of mass-depth h for a given site, using site atmospheric pressure as input.
2.3 Constraints on in situ 14CO production rates from measurements at Taylor Glacier, Antarctica
Recent studies at Taylor Glacier, Antarctica (an ice ablation site that exposes ancient ice at the surface), have provided measurements of 14C in ice older than 50 ka (Dyonisius et al., 2023; Petrenko et al., 2016). In such ice, any 14C from the snow accumulation site (from 14C-containing atmospheric gases trapped in air bubbles or from in situ cosmogenic production) has decayed away (14C half-life is 5700 years), and the only measurable 14C originates from relatively slow in situ cosmogenic production by muons as the glacier transports the ice at large depths and somewhat faster production as the ice gradually rises toward the surface via ablation. Due to the relatively fast ice ablation rate of ≈ 20 cm yr−1, the 14C contribution from the neutron production mechanism is negligible for ice deeper than 6 m. This presented an opportunity to use 14CO measurements in Taylor Glacier to constrain the muogenic 14CO production rates in ice in a natural setting.
Dyonisius et al. (2023) presented measurements of 14CO in Taylor Glacier ice between the surface and 72 m depth. An ice flowline model for Taylor Glacier (Buizert et al., 2012b) was used to reconstruct the possible range of trajectories for the sampled ice parcels (Fig. 2a). The Balco model was used to calculate 14CO production via the muon mechanisms as ice parcels followed the trajectories. As prior work suggested that muogenic 14C production rates from Heisinger et al. (2002a, b) may be too high when applied to ice (Petrenko et al., 2016), Dyonisius et al. (2023) introduced production rate adjustment factors fμ− and fμf into production rate equations as follows:
Here is the total 14C production rate (in atoms g−1 yr−1) in the Balco model for the respective muon mechanism at mass-depth h and surface pressure P. fμ− and fμf account for (1) the fraction of total 14C that forms 14CO (ΩCO) and (2) the adjustment factor for total 14C production rate.
To define the best-estimate 14CO production rate adjustment factors fμ− and fμf, Dyonisius et al. (2023) used a grid search approach, as follows. Using the best-estimate ice parcel back-trajectory (Fig. 2a), an expected 14CO depth profile was calculated for each combination of fμ− and fμf between 0 and 0.2 at 0.001 resolution. The model results were then compared to 14CO measurements (Fig. 2b) with mean depths of 6.85 m or deeper (to avoid significant effects from the neutron mechanism), and a χ2 metric was used to determine the goodness of fit. To define the possible range of fμ− and fμf, Dyonisius et al. (2023) used a Monte Carlo approach, as follows. First, 10 000 possible ice back-trajectories were generated by perturbing ablation rates along the glacier according to their uncertainties (Fig. 2a). Next, a wide prior distribution for fμ− and fμf was defined by starting with the best-estimate values and assuming a large and normally distributed 200 % uncertainty in these values. Thus, 100 000 Monte Carlo iterations of the model were then run, with each iteration randomly selecting a back-trajectory scenario and a pair of fμ− and fμf from the prior distribution described above. All pairs of fμ− and fμf that yielded 14CO depth profiles (Fig. 2b) that were within average measurement uncertainty (1σ or 2σ) from the best-fit solution were accepted (Fig. 2c).
2.4 Constraints on in situ 14CO retention and leakage in firn and production in ice at Greenland Summit
In situ cosmogenic 14C that is produced in the firn column above the lock-in depth can be lost to the atmosphere if it is able to leak out of the ice grains, resulting in low 14C retention into ice below the firn zone (e.g., de Jong et al., 2004; Petrenko et al., 2013, and references therein). Hmiel et al. (2024) used Greenland Summit to conduct the most comprehensive study to date of in situ cosmogenic 14C in the firn, with a focus on 14CO. This study measured 14CO in the ice grains in the firn matrix, in firn air, as well as in bubbly ice below the firn zone. Very large firn and ice samples (200–300 kg) were used for 14CO analysis, to provide sufficiently large numbers of 14C atoms for precise 14C measurements. Figure 3a shows the 14CO results for samples from the firn, firn-ice transition and bubbly ice below the firn zone. In the shallowest firn, 14CO increases rapidly with depth owing mainly to production by the neutron mechanism, reaching a peak in the 10–20 m depth range. Beyond 20 m, 14CO in the firn matrix declines gradually with depth in the diffusive part of the firn, reflecting leakage of in situ 14C from the ice grains. 14CO increases rapidly in the lock-in zone (≈ 70–80 m), reflecting addition of 14CO from trapped air. Below the lock-in zone, 14CO in the ice continues to increase gradually due to deeper production by the muon mechanisms.
To interpret the Greenland Summit 14CO results, Hmiel et al. (2024) employed a firn gas transport model that can also characterize trapped air in ice below the firn zone (Buizert et al., 2012a). Production of in situ 14C following the systematics described in Sect. 2.2 and tracking of 14C in ice grains and porosity was implemented in this model. With regard to 14C loss from ice grains in the firn, it was found that the model–data agreement was best if two separate loss processes were parameterized in the model: a fast process, with a timescale < 1 year and an additional slow process. This was described in the model using parameters R1 and L1. R1 represents the fraction of in situ 14C in the ice grains that is initially retained. The fraction of in situ 14C in ice grains that is lost rapidly, given by 1−R1, leaks out from the ice grains into the porosity at every model time step (0.5 year). L1 represents the fraction of the initially retained 14C that is lost more slowly from the ice grains over the course of 1 year. Hmiel et al. (2024) used a grid search approach to constrain the possible ranges of R1 and L1 at Greenland Summit (Fig. 3b), showing that > 99 % of in situ 14C is lost rapidly from the ice grains, while the remaining ≈ 0.5 % (R1) of in situ 14C continues to leak out slowly at a rate of ≈ 0.6 % yr−1 (L1). Hmiel et al. (2024) argued that the rapid loss is best explained by the process of gas diffusion through ice and suggested that the ≈ 0.5 % of 14C that is initially retained may be trapped in microbubbles or by impurities at dislocations or grain boundaries and is released via the process of recrystallization.
Greenland Summit 14CO measurements in ice below the firn zone also provided an opportunity to test muon mechanism 14CO production rate estimates from Taylor Glacier. For Greenland Summit ice samples, the contribution from trapped atmospheric 14CO is important (≈ 25 %–40 % of total), and uncertainties in the atmospheric 14CO history interfere with precise constraints on fμ− and fμf. Nevertheless, by trialing the Taylor Glacier sets of accepted fμ−–fμf pairs in combination with several possible atmospheric 14CO histories, Hmiel et al. (2024) were able to further narrow the possible ranges of fμ− and fμf (Fig. 3c).
3.1 Basic concept for using 14CO in ice cores as a GCR flux proxy
As the Greenland Summit 14CO results summarized above illustrate, the retention of in situ cosmogenic 14CO through the upper firn column is very low. This means that the majority of in situ 14CO found in ice below the firn zone originates from production by muons below the lock-in depth, where this 14CO can no longer escape to the atmosphere. If the firn layer is sufficiently thick (≈ 90–100 m actual depth or ≈ 65 m ice equivalent depth), the muons penetrating below the firn must have an energy of ≈ 15 GeV or greater at the surface (e.g., Rogers and Tristam, 1984). Such muons originate from primary GCR particles with energies of ≈ 100 GeV or greater (Gaisser et al., 2016). The part of the GCR flux possessing such energies is not affected appreciably by either the geomagnetic or the heliospheric magnetic fields. In situ cosmogenic 14CO content in ice cores drilled at such sites thus can serve as a proxy of variations in the primary GCR flux. This proxy is in principle free of the confounding effects discussed in the Introduction for other past GCR flux indicators.
Several considerations are important for site selection in order to increase the likelihood of success with this proxy. First, the in situ 14CO signal must be maximized to help with measurement sensitivity as well as to reduce interference from the trapped atmospheric 14CO component. Second, the site must have a thick firn column. This is needed to ensure that 14CO below the firn zone is produced only by muons originating from primary GCRs that are sufficiently energetic to be unaffected by solar magnetic field variations. Third, there should be as little in situ 14CO retained from the shallow firn as possible. 14CO produced in the shallow firn originates from neutrons or lower-energy muons that are affected by solar magnetic field variations and may complicate interpretation. Fourth, ideally the site must be glaciologically stable over time in terms of accumulation rate and lock-in depth. Large temporal variations in these parameters may introduce additional uncertainties in the interpretation, as they affect the predicted in situ 14CO content.
Considering the above, ice dome sites in the East Antarctica interior are most promising for attempting to examine past GCR flux variability using 14CO in ice cores. Low accumulation rates at such sites maximize cosmogenic exposure times and thereby the in situ 14CO signal. These sites also tend to have sufficiently thick firn columns (e.g., Buizert, 2013). The combination of low accumulation rate and thick firn column results in very long ice layer transit times through the firn, maximizing the chance that in situ 14CO produced by neutrons and low-energy muons in the shallow firn would be lost. Finally, dome sites are free of complications of upstream ice advection, and ice core water stable isotope records suggest that the interior East Antarctica climate has been stable over the last few thousand years (recent decades excepted) (e.g., Jouzel et al., 2001).
3.2 Using model predictions to explore Dome C, Antarctica, as a test case for the 14CO GCR flux proxy
Dome C, Antarctica, is a site that meets the criteria needed for the 14CO GCR flux proxy to be viable. It has been glaciologically very well characterized as a result of previous ice coring campaigns (e.g., EPICA Community Members, 2004) and has well-established logistical access owing to the permanent Concordia Station. Further, a scientific ice drilling expedition is planned for the near future to Dome C for the purpose of 14CO reconstruction at this site. We therefore use Dome C as an example site for more detailed model-based exploration of the 14CO past GCR flux proxy. We first applied the full firn-ice model mentioned above (Buizert et al., 2012a; Hmiel et al., 2024) to explore the (unwanted) contribution of 14CO originating from production in the shallow firn as well as trapped atmospheric 14CO to the overall 14CO signal in ice below the firn zone. In the model, we used an accumulation rate of 3.2 cm ice equivalent yr−1 and the firn density profile from the FIRETRACC project (EU FIRETRACC Campaign participants, 2006), and we tuned the firn gas diffusivity profile based on a combination of available CO2, CH4, CFC-11, CFC-12, CFC-113, CH3CCl3, SF6 and δ15N of N2 measurements (EU FIRETRACC Campaign participants, 2006). For parameters relevant to in situ 14CO, we used Fn=1.03, R1=0.44 % and L1=0.45 % yr−1 (see Sect. 2), which was the combination of values at Greenland Summit that maximized the amount of in situ 14CO produced in the shallow firn that is retained into ice below the firn zone (Fig. 3b). For muogenic 14CO production, we used fμ− = 0.065 and fμf=0.07, which are mid-range choices from the possible range of values that were consistent with both Taylor Glacier and Greenland Summit measurements (Fig. 3c). We used a constant concentration of 12 molecules cm−3 STP (standard temperature and pressure) for the atmospheric 14CO history, which is the average of the longest available Antarctic atmospheric 14CO record (Manning et al., 2005).
Figure 4a shows model-calculated 14CO content that represents the sum of 14CO in ice grains and closed porosity (this is what measurements done with a melt-extraction approach would provide). The solid black line shows results with both in situ and atmospheric 14CO included in the model. There is a sharp 14CO peak at ≈ 9 m depth that represents 14CO in ice grains and is driven by intense 14CO production by the neutron mechanism in near-surface firn. 14CO then declines to near zero by ≈ 70 m due to slow leakage out of ice grains (controlled by the L1 parameter in the model). At depths > 80 m, the amount of closed porosity starts to increase, and this increases 14CO by trapping of 14CO from open porosity and by allowing more in situ 14CO to be retained. This process further accelerates at ≈ 95 m, which is the lock-in depth at Dome C. Below the close-off depth at Dome C (≈ 100 m), 14CO content continues to increase due to production by muons, rising to 8.5 14CO molecules g−1 ice at the deepest modeled level (110 m).
The dashed blue line shows the expected contribution to total 14CO from in situ 14CO originating only from the shallower part of the firn. This was assessed by setting the atmospheric 14CO history to zero and setting in situ production rates to zero for depths > 54 m ice equivalent. This contribution is < 0.5 14CO molecules g−1 ice and is due to 14CO that leaks out from ice grains in the shallow firn, diffuses into the deep firn and is subsequently trapped in air bubbles. The contribution from trapped atmospheric 14CO (dotted pink line; assessed by turning off in situ production in the model) is < 1.2 14CO molecules g−1 ice. 14CO originating from the sum of shallow in situ cosmogenic production and air trapping (solid red line) is < 1.6 14CO molecules g−1 ice at all depths below the firn zone.
We next examined the in situ cosmogenic 14CO component at Dome C arising from production by deep-penetrating muons, as well as its suitability for detecting changes in the past GCR flux. As this approach involved generating thousands of simulated data sets (see Sect. 3.3 below), we created a simple and computationally efficient ice-only model of in situ cosmogenic 14CO for this test of the proxy concept. This ice-only model has its starting (shallowest) depth in the lock-in zone and assumes an initial 14CO content of zero. 14CO production in the model is implemented following parameterizations described above in Sect. 2, with production rates within the range constrained by Taylor Glacier and Greenland Summit results. The model assumes that all of the in situ 14CO is retained and also includes 14C radioactive decay. The model defines annual ice layers and shifts these layers downward on an annual basis following the ice layer age scale for Dome C from Buizert et al. (2018). For the purposes of this test of the proxy concept, we set the deepest model depth at 300 m, as this is the practical limit for light ice coring projects that do not use drilling fluid and the deepest depth in the planned fieldwork. The exact starting depth of the model was chosen by comparing predictions of this ice-only model with predictions from the full firn-ice model in the 100–110 m depth range (below close-off depth) when using the same muogenic 14CO production rates and setting atmospheric 14CO history to zero; using 96.5 m for the starting depth yields the best match.
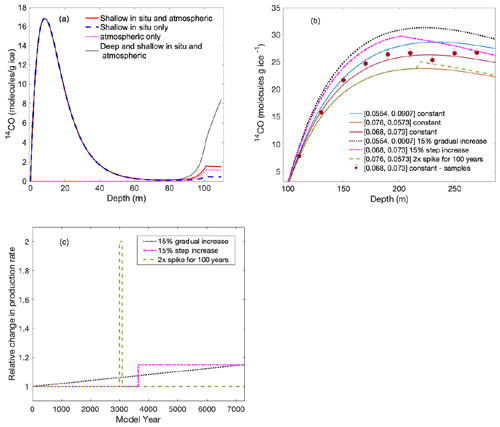
Figure 4Predicted 14CO content at Dome C. (a) Predicted 14CO content in ice grains + closed porosity (bubbles) from the full firn-ice model considering all 14CO contributions as well as contributions from individual 14CO components. (b) Predicted in situ 14CO content in ice below the firn zone from a simple ice-only model. The legend indicates the combination of [fμ−, fμf] values (see Sect. 2) used in each model run, as well as whether the production rate was assumed to be constant (solid lines) or variable (dashed and dotted lines) in time. Markers illustrate what sample measurements might look like assuming 20 m depth averaging and a random 1σ measurement error of 3 %. (c) Time-variable production rate scenarios used to generate the corresponding depth–14CO profiles in panel (b).
Figure 4b illustrates predictions of the simple ice model for a few scenarios involving different combinations of fμ− and fμf as well as different production rate histories (representing past GCR flux variations), and Fig. 4c illustrates the time-variable production rate scenarios reflected in Fig. 4b. Because in situ cosmogenic 14CO production takes place at the full range of modeled depths (with production rate declining with depth as illustrated in Fig. 1b), the 14CO values at each depth represent a time integral of production rate minus the 14C decay rate. As expected, 14CO content increases most rapidly at the shallowest depths, followed by a broad peak in the 200–250 m depth range. For deeper ice, the rate of 14CO removal via radioactive decay exceeds the rate of production by muons, and 14CO values gradually decline. The modeled ice layers at Dome C span an age range of 7283 years, meaning that an ice core 14CO record reaching 300 m depth could offer information about past GCR flux variations for most of the Holocene.
Predicted 14CO content originating from deep-penetrating muons is between 20 and 30 molecules g ice−1 for most of the modeled depth range. This means that the 14CO contribution arising from trapped atmospheric 14CO and 14CO production in shallow firn (< 1.6 molecules g ice−1; Fig. 4a) would contribute < 8 % of total 14CO and is unlikely to interfere with 14CO signal interpretation. We note that there were three prior 14CO measurements that were made on the Dome C ice core in the depth range we are considering (de Jong et al., 2004). Those measurements were made on much smaller (1–2 kg) samples than Taylor Glacier and Summit measurements and thus were associated with very large uncertainties (50 %–100 %, considering only uncertainty reported for 14C activities). That said, de Jong et al. (2004) reported 14CO values in the 15–30 molecules g ice−1 range for these three samples and concluded that there was no detectable in situ 14C retention from the firn, consistent with our model predictions.
Figure 4b illustrates that the absolute 14CO content in the ice as well as the depth of the 14CO peak depend on the balance of production rates from the negative muon capture and fast muon mechanisms (solid lines); this is controlled by the fμ− and fμf parameters in the model. In the modeled depth range, the fast muon mechanism is relatively more important (Fig. 1b), so maximizing fμf at the expense of fμ− (within the range in Fig. 3c) increases total 14CO and shifts the peak slightly deeper. Despite these differences, the shape of the depth–14CO curves remains largely similar. Figure 4b also illustrates a few scenarios where the production rates (controlled by GCR flux) vary in time (dashed and dotted lines). For time-variable production rates for the purpose of this illustration (Fig. 4c), we trialed (1) a scenario where production by each muon mechanism increases at a linear rate over the entire duration of the model run, reaching 15 % higher rates by the end of the run (black dotted line), (2) a scenario where there is a 15 % step increase in production rates halfway through the model run (pink dash-dot line) and (3) a scenario where there is a 2 times transient step increase in production rates that takes places between 3000 and 3100 years in the model run (dashed green line). As can be seen, all of these types of variations produce depth–14CO profiles that are distinct in their shape from the constant production rate scenarios.
3.3 Analysis of sensitivity of ice core 14CO measurements at Dome C to variations in past GCR flux
We compare several time-varying scenarios to the baseline model of a constant GCR flux with muonic production rates (fμ−, fμf) that are consistent with ice core 14CO measurements in both Dyonisius et al. (2023) and Hmiel et al. (2024). As shown in Fig. 4b, deviations from the baseline model can be produced by temporal variations in the GCR flux. However, in the presence of a steady-state flux, uncertainties in the muonic production rates also create deviations from the baseline model. While the normalization of the depth–14CO profile is affected by both the temporal variations in the GCR flux and the production rates, the shape of the profile is more sensitive to temporal variations in the flux. Therefore, we develop an analysis that is sensitive to the shape of the 14CO profile as a function of depth.
To discriminate the steady-state GCR scenario H0 from the time-varying scenario H1, we construct a test statistic using a Bayes factor (Jeffreys, 1998; Kass and Raftery, 1995):
In this expression, c={c(hj)} is a 14CO profile measured as a function of discrete depths . The Bayes factor computes the ratio of the marginal probabilities of measuring 14CO profile c given the steady-state and time-varying scenarios H0 and H1. If the data provide greater evidence for the steady-state hypothesis H0, B01>1, and if the time-varying hypothesis is supported, B01<1.
During the calculation of B01, each marginal probability, P(c|Hi), can be factorized into two terms: a conditional probability P(c|θi,Hi), where θi lists the free parameters of GCR flux model Hi, and a “prior” probability distribution P(θi|Hi). To complete the calculation, we integrate over the possible values of the parameters θi in each model Hi. The prior probabilities specify the allowed ranges of parameters θi in model Hi and allow us to weight the calculation toward more probable values of the model parameters. Note that we are free to choose the functional form of the prior distributions using theoretical considerations, past measurements or even our subjective degree of belief in the most likely values of the parameters of a given model. In this work, we use non-informative (or flat) prior distributions that do not favor any particular values of the model parameters, beyond restricting their ranges to physically motivated regions.
In the sensitivity calculation, the muonic production rates (fμ−, fμf) are nuisance parameters folded into both θ0 and θ1. Using the confidence intervals on (fμ−, fμf) from Dyonisius et al. (2023) and Hmiel et al. (2024), we can factorize the prior probability P(θi|Hi) for model i into a joint prior ) and a set of independent priors dependent on the parameters of the model. For example, the joint prior ) is given by the “2σ acceptance from Summit ice” contour in Fig. 3c. If we wish to test a cosmic ray model H1 with a flux that varies linearly in time, the model includes an additional free parameter a representing the rate of change of the flux as a function of time. In the calculation of the Bayes factor, the prior distribution of a is a uniform probability density function:
Here amin and amax represent the allowed range of values we consider for the rate of change of the flux. We use a uniform distribution for P(a|H1) because it is unbiased, giving equal weight to all values of a between amin and amax.
Table 1Simulated sensitivity to temporal changes in the GCR flux. We report the magnitude of GCR flux changes in time-varying models required to produce a 3σ or 5σ detection in at least 50 % of simulated data sets, assuming 2 % (3 %) relative uncertainties in the 14CO measurements. For example, to produce a 3σ detection of a linearly increasing or decreasing GCR flux, the rate of change of the flux must be at least 6 % (7 %) over 7 ka.

Our calculation assumes the ice core 14CO measurements are depth-averaged over 20 m, and each measurement has independent Gaussian uncertainties with relative sizes of 2 % at 1σ. The 20 m depth averaging is assumed because this would provide the needed amount of ice for high-precision 14CO measurements (≈ 140 kg with a 10 cm diameter ice core). Recent improvements in analytical techniques for ice core and atmospheric 14CO measurements (Petrenko et al., 2023, 2021) make 2 % uncertainties achievable, although for completeness we also repeat the calculations assuming 3 % 1σ uncertainties. The conditional probability of observing a 14CO profile c given GCR model Hi with parameters θi is
Here ) is the expected 14CO profile at depth hj, which we compute using the model, while cj=c(hj) is the observed 14CO concentration at depth hj. Since the measurement uncertainties are independent and Gaussian, the probability is the product of N independent Gaussian probability density functions over the N measurements in the depth profile. Multiplying this probability by the prior distributions of the nuisance parameters (fμ−, fμf) and the allowed prior ranges of the model parameters (such as the slope of the linear change in the GCR flux) allows us to account for both systematic and statistical uncertainties in the measurement.
We calculate our sensitivity to a given GCR scenario as follows:
-
We produce 5×106 random realizations of the 14CO profile at Dome C, assuming a constant production rate but accounting for the systematic uncertainties in (fμ−, fμf). The profiles are generated with depth averaging of 20 m, and relative measurement uncertainties of % and 3 % are both investigated.
-
For each time-varying model under consideration, we compute a distribution of Bayes factors B01 using the random constant-flux data sets. This provides us with a distribution of the Bayes factor when the null constant-flux hypothesis H0 is true.
-
We next produce a large set of independent 14CO profiles assuming the alternative time-varying hypothesis H1 is true and compute the Bayes factor for each simulated data set. We expect that will be much smaller than B01, on average, since P(c|H1)>P(c|H0) when the alternative hypothesis H1 is true.
-
For each , we compute the tail probability, or p value, that gives the probability that a constant flux model will produce a Bayes factor smaller than the time-varying model purely by a chance statistical fluctuation, i.e.,
The reported sensitivity of a given model is the value of the model parameter(s) in which at least 50 % of simulated data sets yield (3σ evidence against the steady-state model). We also report the value of the model parameter(s) yielding , corresponding to a 5σ discovery of a time-varying flux. This “calibration” of the Bayes factor accounts for the chance probability that a steady-state flux could produce a false positive report of a time-varying flux.
We investigated scenarios involving (1) a linear GCR flux increase over the entire duration of the record, (2) a step-like increase at approximately the mid-point of the record and (3) a brief (100-year) burst in the GCR flux. The scenarios start at a common point in model year 0 (≈7 ka) and diverge during the model run (toward present day). The results are reported in Table 1. For a scenario H1 where the GCR flux increases linearly with time and assuming 2 % (3 %) relative uncertainties in the measured 14CO profile, a flux increase a=6 % (7 %) over 7 ka is required to produce a 3σ evidence of a non-steady flux in at least 50 % of simulated data sets. For a 5σ detection, the rate of change of the flux must be at least a=8 % (10 %). We also investigated and found similar sensitivities for a scenario involving a step-like increase in the GCR flux at 3.5 ka. Much larger GCR flux changes are required for detection in the impulsive burst scenario: 190 % (240 %) for 3σ evidence. This is likely due to the large amount of temporal averaging (≈ 700 years) that is imposed by the 20 m depth averaging for the measurements and the fact that the 14CO content at each depth level represents a time integral of production rates. We further note that improving the relative uncertainty in the 14CO measurement from 3 % to 2 % has a minor effect on the sensitivity to linear and step-like increases in the GCR flux, but the change in sensitivity to burst-like increases in the flux is substantial.
14CO in ice cores at low-accumulation sites such as Dome C, Antarctica, has a good potential to provide a test of the assumption of GCR flux constancy over the Holocene and to serve as a proxy for past variations in the GCR flux on timescales of a few thousand years. 14CO measurements in the proposed approach would be most sensitive to gradual linear or step-like changes in the GCR flux, in principle allowing us to test the assumption of GCR flux constancy to 7 % or better. This would represent a large improvement over the ≈ 30 % uncertainty associated with constraints from meteorite measurements. Because our approach involves a large amount of temporal averaging, sensitivity to short-lived GCR bursts is much worse. However, such bursts (if present) would have been captured by high-resolution records of other cosmogenic nuclides such as ice core 10Be and tree-ring 14C.
We note that cosmogenic nuclides produced in the atmosphere such as 10Be are primarily sensitive to the GCR flux below 10 GeV, while the 14CO proxy discussed here is sensitive to the flux above 100 GeV. The extent to which temporal variations in the GCR flux above 100 GeV would produce proportional changes below 10 GeV, while beyond the scope of this paper, is an interesting question to consider, as the answer depends on the origin of the temporal variations. Since the diffusion length of cosmic rays increases with energy, it is reasonable to expect that a constant GCR flux at high energy is likely to imply a constant GCR flux below 10 GeV, while a time-varying flux above 100 GeV could still be consistent with a constant flux at or below 10 GeV.
For the most precise results, the 14CO proxy approach requires an ice dome site that is glaciologically stable (accumulation rate, lock-in depth) over the duration of the GCR flux reconstruction. Although our work indicates that the 14CO GCR flux proxy is likely to provide useful results for most of the Holocene, we expect that GCR flux reconstructions beyond the Holocene with this approach would be more challenging, owing to (1) the need for drilling fluid to obtain ice below ≈ 300 m, which would greatly increase logistical requirements and introduce added challenges of CO contamination from the drilling fluid; (2) glaciological changes beyond the Holocene; and (3) reduced 14CO signal at greater depths due to 14C radioactive decay.
Code for the firn and ice models as well as for the statistical analysis used in this study is available from https://github.com/14CO/Dome-C-Sensitivity (last access: July 2024) and Zenodo (https://doi.org/10.5281/zenodo.12667033, Petrenko et al., 2024).
The simulated data sets created as part of the statistical analysis in this study are available from https://github.com/14CO/Dome-C-Sensitivity.
VVP and SB developed the 14CO GCR flux proxy concept. VVP wrote the code for the simple ice model and performed firn and ice model simulations. SB developed the approach, wrote the code for and performed statistical analyses. CB provided firn model tuning and ice layer age scale for Dome C. VVP and SB wrote the paper, with input from all other authors.
The contact author has declared that none of the authors has any competing interests.
Publisher’s note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
This article is part of the special issue “Ice core science at the three poles (CP/TC inter-journal SI)”. It is not associated with a conference.
This work was funded by the University of Rochester Bridging Fellowship (to Vasilii V. Petrenko) and US NSF Award OPP-2146131 (to Vasilii V. Petrenko and Segev BenZvi). We thank Ilya Usoskin, Raimund Muscheler, Greg Balco, John Stone and Nathaniel Lifton for helpful discussions and Walter Cook for assistance with the statistical analyses.
This research has been supported by the University of Rochester (Bridging Fellowship to Vasilii V. Petrenko) and the National Science Foundation (grant no. OPP-2146131).
This paper was edited by Hubertus Fischer and reviewed by Ilya Usoskin and one anonymous referee.
Abeysekara, A. U., Alfaro, R., Alvarez, C., et al., HAWC Collaboration, Aartsen, M. G., Ackermann, M., Adams, J. et al., IceCube Collaboration: All-sky Measurement of the Anisotropy of Cosmic Rays at 10 TeV and Mapping of the Local Interstellar Magnetic Field, Astrophys. J., 871, 96, https://doi.org/10.3847/1538-4357/aaf5cc, 2019.
Adolphi, F., Muscheler, R., Svensson, A., Aldahan, A., Possnert, G., Beer, J., Sjolte, J., Bjorck, S., Matthes, K., and Thieblemont, R.: Persistent link between solar activity and Greenland climate during the Last Glacial Maximum, Nat. Geosci., 7, 662–666, 2014.
Ahlers, M. and Mertsch, P.: Small-Scale Anisotropies of Cosmic Rays from Relative Diffusion, Astrophys. J. Lett., 815, L2, https://doi.org/10.1088/2041-8205/815/1/L2, 2015.
Balco, G.: Contributions and unrealized potential contributions of cosmogenic-nuclide exposure dating to glacier chronology, 1990-2010, Quaternary Sci. Rev., 30, 3–27, 2011.
Balco, G.: Glacier Change and Paleoclimate Applications of Cosmogenic-Nuclide Exposure Dating, Annu. Rev. Earth Pl. Sci., 48, 21–48, 2020.
Balco, G., Stone, J. O., Lifton, N. A., and Dunai, T. J.: A complete and easily accessible means of calculating surface exposure ages or erosion rates from Be-10 and Al-26 measurements, Quatern. Geochronol., 3, 174–195, 2008.
Bard, E., Raisbeck, G., Yiou, F., and Jouzel, J.: Solar irradiance during the last 1200 years based on cosmogenic nuclides, Tellus B, 52, 985–992, 2000.
Blasi, P. and Amato, E.: Diffusive propagation of cosmic rays from supernova remnants in the Galaxy. II: anisotropy, J. Cosmol. Astropart. Phys., 11, https://doi.org/10.1088/1475-7516/2012/01/011, 2012.
Borchers, B., Marrero, S., Balco, G., Caffee, M., Goehring, B., Lifton, N., Nishiizumi, K., Phillips, F., Schaefer, J., and Stone, J.: Geological calibration of spallation production rates in the CRONUS-Earth project, Quatern. Geochronol., 31, 188–198, 2016.
Buizert, C.: Studies of Firn Air, in: The Encyclopedia of Quaternary Science, edited by: Elias, S. A., Elsevier, Amsterdam, ISBN 978-0-444-53642-6, 2013.
Buizert, C., Martinerie, P., Petrenko, V. V., Severinghaus, J. P., Trudinger, C. M., Witrant, E., Rosen, J. L., Orsi, A. J., Rubino, M., Etheridge, D. M., Steele, L. P., Hogan, C., Laube, J. C., Sturges, W. T., Levchenko, V. A., Smith, A. M., Levin, I., Conway, T. J., Dlugokencky, E. J., Lang, P. M., Kawamura, K., Jenk, T. M., White, J. W. C., Sowers, T., Schwander, J., and Blunier, T.: Gas transport in firn: multiple-tracer characterisation and model intercomparison for NEEM, Northern Greenland, Atmos. Chem. Phys., 12, 4259–4277, https://doi.org/10.5194/acp-12-4259-2012, 2012a.
Buizert, C., Petrenko, V. V., Kavanaugh, J. L., Cuffey, K. M., Lifton, N. A., Brook, E. J., and Severinghaus, J. P.: In situ cosmogenic radiocarbon production and 2-D ice flow line modeling for an Antarctic blue ice area, J. Geophys. Res., 117, F02029, https://doi.org/10.1029/2011JF002086, 2012b.
Buizert, C., Sigl, M., Severi, M., Markle, B. R., Wettstein, J. J., McConnell, J. R., Pedro, J. B., Sodemann, H., Goto-Azuma, K., Kawamura, K., Fujita, S., Motoyama, H., Hirabayashi, M., Uemura, R., Stenni, B., Parrenin, F., He, F., Fudge, T. J., and Steig, E. J.: Abrupt ice-age shifts in southern westerly winds and Antarctic climate forced from the north, Nature, 563, 681–685, 2018.
de Jong, A. F. M., Alderliesten, C., van der Borg, K., van der Veen, C., and van De Wal, R. S. W.: Radiocarbon analysis of the EPICA Dome C ice core: no in situ C-14 from the firn observed, Nucl. Instrum. Meth. B, 223–224, 516–520, 2004.
Dyonisius, M. N., Petrenko, V. V., Smith, A. M., Hmiel, B., Neff, P. D., Yang, B., Hua, Q., Schmitt, J., Shackleton, S. A., Buizert, C., Place, P. F., Menking, J. A., Beaudette, R., Harth, C., Kalk, M., Roop, H. A., Bereiter, B., Armanetti, C., Vimont, I., Englund Michel, S., Brook, E. J., Severinghaus, J. P., Weiss, R. F., and McConnell, J. R.: Using ice core measurements from Taylor Glacier, Antarctica, to calibrate in situ cosmogenic 14C production rates by muons, The Cryosphere, 17, 843–863, https://doi.org/10.5194/tc-17-843-2023, 2023.
EPICA Community Members: Eight glacial cycles from an Antarctic ice core, Nature, 429, 623–628, 2004.
Erlykin, A. D. and Wolfendale, A. W.: The anisotropy of galactic cosmic rays as a product of stochastic supernova explosions, Astropart. Phys., 25, 183–194, 2006.
EU FIRETRACC Campaign participants, Atlas, E. B., Barnola, J.-M., Brenninkmeijer, C., Mulvaney, R., Schwander, J., Sturges, W. T., Penkett, M., Penkett, S. A., Chappellaz, J., and Jouzel, J.: Firn Record of Trace Gases Relevant to Atmospheric Chemical Change over 100 yrs (FIRETRACC/100), NCAS British Atmospheric Data Centre, https://catalogue.ceda.ac.uk/uuid/41a6e20ba98c4913ea6893e2fcb5aec5 (last access: December 2021), 2006.
Fang, L., Jenk, T. M., Singer, T., Hou, S., and Schwikowski, M.: Radiocarbon dating of alpine ice cores with the dissolved organic carbon (DOC) fraction, The Cryosphere, 15, 1537–1550, https://doi.org/10.5194/tc-15-1537-2021, 2021.
Field, C. V., Schmidt, G. A., Koch, D., and Salyk, C.: Modeling production and climate-related impacts on Be-10 concentration in ice cores, J. Geophys. Res., 111, D15107, https://doi.org/10.1029/2005JD006410, 2006.
Gaisser, T. K., Engel, A., and Resconi, E.: Cosmic Rays and Particle Physics, Cambridge University Press, https://doi.org/10.1017/CBO9781139192194, 2016.
Gosse, J. C. and Phillips, F. M.: Terrestrial in situ cosmogenic nuclides: theory and application, Quaternary Sci. Rev., 20, 1475–1560, 2001.
Heisinger, B., Lal, D., Jull, A. J. T., Kubik, P., Ivy-Ochs, S., Knie, K., and Nolte, E.: Production of selected cosmogenic radionuclides by muons: 2. Capture of negative muons, Earth Planet. Sc. Lett., 200, 357–369, 2002a.
Heisinger, B., Lal, D., Jull, A. J. T., Kubik, P., Ivy-Ochs, S., Neumaier, S., Knie, K., Lazarev, V., and Nolte, E.: Production of selected cosmogenic radionuclides by muons 1. Fast muons, Earth Planet. Sc. Lett., 200, 345–355, 2002b.
Hmiel, B., Petrenko, V. V., Buizert, C., Smith, A. M., Dyonisius, M. N., Place, P., Yang, B., Hua, Q., Beaudette, R., Severinghaus, J. P., Harth, C., Weiss, R. F., Davidge, L., Diaz, M., Pacicco, M., Menking, J. A., Kalk, M., Faïn, X., Adolph, A., Vimont, I., and Murray, L. T.: Characterization of in situ cosmogenic 14CO production, retention and loss in firn and shallow ice at Summit, Greenland, The Cryosphere, 18, 3363–3382, https://doi.org/10.5194/tc-18-3363-2024, 2024.
Jeffreys, H.: Theory of Probability, Oxford University Press, Oxford, U.K., ISBN 9780198503682, 1998.
Jouzel, J., Masson, V., Cattani, O., Falourd, S., Stievenard, M., Stenni, B., Longinelli, A., Johnsen, S. J., Steffenssen, J. P., Petit, J. R., Schwander, J., Souchez, R., and Barkov, N. I.: A new 27 ky high resolution East Antarctic climate record, Geophys. Res. Lett., 28, 3199–3202, 2001.
Kachelriess, M., Neronov, A., and Semikoz, D. V.: Signatures of a Two Million Year Old Supernova in the Spectra of Cosmic Ray Protons, Antiprotons, and Positrons, Phys. Rev. Lett., 115, 181103, https://doi.org/10.1103/PhysRevLett.115.181103, 2015.
Kass, R. E. and Raftery, A. E.: Bayes Factors, J. Am. Stat. Assoc., 90, 773–795, 1995.
Knudsen, M. F., Riisager, P., Donadini, F., Snowball, I., Muscheler, R., Korhonen, K., and Pesonen, L. J.: Variations in the geomagnetic dipole moment during the Holocene and the past 50 kyr, Earth Planet. Sc. Lett., 272, 319–329, 2008.
Knudsen, M. F., Riisager, P., Jacobsen, B. H., Muscheler, R., Snowball, I., and Seidenkrantz, M. S.: Taking the pulse of the Sun during the Holocene by joint analysis of (14)C and (10)Be, Geophys. Res. Lett., 36, L16701, https://doi.org/10.1029/2009gl039439, 2009.
Koll, D., Korschinek, G., Faestermann, T., Gomez-Guzman, J. M., Kipfstuhl, S., Merchel, S., and Welch, J. M.: Interstellar Fe-60 in Antarctica, Phys. Rev. Lett., 123, 072701, https://doi.org/10.1103/PhysRevLett.123.072701, 2019.
Lal, D., Nishiizumi, K., and Arnold, J. R.: Insitu Cosmogenic H-3, C-14, and Be-10 for Determining the Net Accumulation and Ablation Rates of Ice Sheets, J. Geophys. Res., 92, 4947–4952, 1987.
Lal, D., Jull, A. J. T., Burr, G. S., and Donahue, D. J.: Measurements of in situ C-14 concentrations in Greenland Ice Sheet Project 2 ice covering a 17-kyr time span: Implications to ice flow dynamics, J. Geophys. Res., 102, 26505–26510, 1997.
Lal, D., Jull, A. J. T., Burr, G. S., and Donahue, D. J.: On the characteristics of cosmogenic in situ C-14 in some GISP2 Holocene and late glacial ice samples, Nucl. Instrum. Meth. B, 172, 623–631, 2000.
Lifton, N., Sato, T., and Dunai, T. J.: Scaling in situ cosmogenic nuclide production rates using analytical approximations to atmospheric cosmic-ray fluxes, Earth Planet. Sc. Lett., 386, 149–160, 2014.
Manning, M. R., Lowe, D. C., Moss, R. C., Bodeker, G. E., and Allan, W.: Short-term variations in the oxidizing power of the atmosphere, Nature, 436, 1001–1004, 2005.
Melott, A. L., Thomas, B. C., Kachelriess, M., Semikoz, D. V., and Overholt, A. C.: A Supernova at 50 pc: Effects on the Earth's Atmosphere and Biota, Astrophys. J., 840, 105, https://doi.org/10.3847/1538-4357/aa6c57, 2017.
Mertsch, P. and Funk, S.: Solution to the Cosmic Ray Anisotropy Problem, Phys. Rev. Lett. 114, 021101, https://doi.org/10.1103/PhysRevLett.114.021101, 2015.
Muscheler, R.: 10Be and Cosmogenic Radionuclides in Ice Cores, in: Encyclopedia of quaternary science, edited by: Mock, C., Elsevier, ISBN 978-0-444-53642-6, 2013.
Muscheler, R., Joos, F., Beer, J., Muller, S. A., Vonmoos, M., and Snowball, I.: Solar activity during the last 1000 yr inferred from radionuclide records, Quaternary Sci. Rev., 26, 82–97, 2007.
Petrenko, V. V., Severinghaus, J. P., Smith, A. M., Riedel, K., Baggenstos, D., Harth, C., Orsi, A., Hua, Q., Franz, P., Takeshita, Y., Brailsford, G. W., Weiss, R. F., Buizert, C., Dickson, A., and Schaefer, H.: High-precision C-14 measurements demonstrate production of in situ cosmogenic (CH4)-C-14 and rapid loss of in situ cosmogenic (CO)-C-14 in shallow Greenland firn, Earth Planet. Sc. Lett., 365, 190–197, 2013.
Petrenko, V. V., Severinghaus, J. P., Schaefer, H., Smith, A. M., Kuhl, T., Baggenstos, D., Hua, Q., Brook, E. J., Rose, P., Kulin, R., Bauska, T., Harth, C., Buizert, C., Orsi, A., Emanuele, G., Lee, J. E., Brailsford, G., Keeling, R., and Weiss, R. F.: Measurements of C-14 in ancient ice from Taylor Glacier, Antarctica constrain in situ cosmogenic (CH4)-C-14 and (CO)-C-14 production rates, Geochim. Cosmochim. Ac., 177, 62–77, 2016.
Petrenko, V. V., Smith, A. M., Crosier, E. M., Kazemi, R., Place, P., Colton, A., Yang, B., Hua, Q., and Murray, L. T.: An improved method for atmospheric 14CO measurements, Atmos. Meas. Tech., 14, 2055–2063, https://doi.org/10.5194/amt-14-2055-2021, 2021.
Petrenko, V., Neff, P., Etheridge, D., Smith, A., Buizert, C, Murray, L., Trudinger, C., Shi, M., Crosier, E., Hmiel, B., Thornton, D., Jong, L., van Ommen, T., Curran, M., Moy, A., Plummer, C., Nation, M., Beaudette, R., Harth, Langenfelds, R., Mitrevski, B., Dyonisius, M., Ng, J., Severinghaus, J. P., and Weiss, R.: Insights into the preindustrial atmospheric methane sources and sinks from 14CH4 and 14CO measurements at Law Dome, Antarctica, AGU Fall Meeting, https://agu.confex.com/agu/fm23/meetingapp.cgi/Paper/1391486 (July 2024), 2023.
Petrenko, V., BenZvi, S., Dyonisius, M., Hmiel, B., Smith, A., and Buizert, C.: Sensitivity Calculations for Measurement of the Cosmic Ray Flux using Carbon-14 at Dome C in Antarctica (v1.0.0), Zenodo [code], https://doi.org/10.5281/zenodo.12667033, 2024.
Poluianov, S., Kovaltsov, G. A., and Usoskin, I. G.: Solar energetic particles and galactic cosmic rays over millions of years as inferred from data on cosmogenic 26Al in lunar samples, Astron. Astrophys., 618, A96, https://doi.org/10.1051/0004-6361/201833561, 2018.
Rogers, I. W. and Tristam, M.: The Absolute Depth Intensity Curve for Cosmic-Ray Muons Underwater and the Integral Sea-Level Momentum Spectrum in the Range 1-100 Gev/C, J. Phys. G. Nucl. Phys., 10, 983–1001, 1984.
Smith, T., Cook, D. L., Merchel, S., Pavetich, S., Rugel, G., Scharf, A., and Leya, I.: The constancy of galactic cosmic rays as recorded by cosmogenic nuclides in iron meteorites, Meteorit. Planet. Sci., 54, 2951–2976, 2019.
Steinhilber, F., Beer, J., and Frohlich, C.: Total solar irradiance during the Holocene, Geophys. Res. Lett., 36, L19704, https://doi.org/10.1029/2009gl040142, 2009.
Steinhilber, F., Abreu, J. A., Beer, J., Brunner, I., Christl, M., Fischer, H., Heikkila, U., Kubik, P. W., Mann, M., McCracken, K. G., Miller, H., Miyahara, H., Oerter, H., and Wilhelms, F.: 9,400 years of cosmic radiation and solar activity from ice cores and tree rings, P. Natl. Acad. Sci. USA, 109, 5967–5971, 2012.
Thomas, B. C., Engler, E. E., Kachelriess, M., Melott, A. L., Overholt, A. C., and Semikoz, D. V.: Terrestrial Effects of Nearby Supernovae in the Early Pleistocene, Astrophys. J. Lett., 826, L3, https://doi.org/10.3847/2041-8205/826/1/L3, 2016.
Usoskin, I. G.: A history of solar activity over millennia, Liv. Rev. Solar Phys., 20, 2, https://doi.org/10.1007/s41116-023-00036-z, 2023.
Usoskin, I. G., Gallet, Y., Lopes, F., Kovaltsov, G. A., and Hulot, G.: Solar activity during the Holocene: the Hallstatt cycle and its consequence for grand minima and maxima, Astron. Astrophys., 587, A150, https://doi.org/10.1051/0004-6361/201527295, 2016.
van der Kemp, W. J. M., Alderliesten, C., van der Borg, K., de Jong, A. F. M., Lamers, R. A. N., Oerlemans, J., Thomassen, M., and van de Wal, R. S. W.: In situ produced C-14 by cosmic ray muons in ablating Antarctic ice, Tellus B, 54, 186–192, 2002.
van de Wal, R. S. W., Meijer, H. A. J., de Rooij, M., and van der Veen, C.: Radiocarbon analyses along the EDML ice core in Antarctica, Tellus B, 59, 157–165, 2007.
Wallner, A., Feige, J., Kinoshita, N., Paul, M., Fifield, L. K., Golser, R., Honda, M., Linnemann, U., Matsuzaki, H., Merchel, S., Rugel, G., Tims, S. G., Steier, P., Yamagata, T., and Winkler, S. R.: Recent near-Earth supernovae probed by global deposition of interstellar radioactive Fe-60, Nature, 532, 69–72, 2016.
Wieler, R., Beer, J., and Leya, I.: The Galactic Cosmic Ray Intensity over the Past 10(6)-10(9) Years as Recorded by Cosmogenic Nuclides in Meteorites and Terrestrial Samples, Space Sci. Rev., 176, 351–363, 2013.
Willenbring, J. K. and von Blanckenburg, F.: Long-term stability of global erosion rates and weathering during late-Cenozoic cooling, Nature, 465, 211–214, 2010.
Wu, C. J., Usoskin, I. G., Krivova, N., Kovaltsov, G. A., Baroni, M., Bard, E., and Solanki, S. K.: Solar activity over nine millennia: A consistent multi-proxy reconstruction, Astron. Astrophys., 615, A93, https://doi.org/10.1051/0004-6361/201731892, 2018a.
Wu, C. J., Krivova, N., Solanki, S. K., and Usoskin, I. G.: Solar total and spectral irradiance reconstruction over the last 9000 years, Astron. Astrophys., 620, A120, https://doi.org/10.1051/0004-6361/201832956, 2018b.
- Abstract
- Introduction
- Systematics of in situ cosmogenic 14CO in glacial ice
- In situ cosmogenic 14CO in ice cores as a possible proxy for GCR flux variability
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Systematics of in situ cosmogenic 14CO in glacial ice
- In situ cosmogenic 14CO in ice cores as a possible proxy for GCR flux variability
- Conclusions
- Code and data availability
- Author contributions
- Competing interests
- Disclaimer
- Special issue statement
- Acknowledgements
- Financial support
- Review statement
- References





