Brief communication: Non-linear sensitivity of glacier mass balance to climate attested by temperature-index models

Temperature-index models have been widely used for glacier-mass projections spanning the 21st century. The ability of temperature-index models to capture non-linear responses of glacier surface mass balance (SMB) to high deviations in air temperature and solid precipitation was recently discussed in the context of mass-balance simulations employing advanced machine-learning techniques. Here, we performed numerical experiments with a classic temperature-index model and confirmed that such models are capable of detecting non-linear responses of glacier SMB to temperature and precipitation changes. Non-linearities derive from the change in the degree-day factor over the ablation season and from the lengthening of the ablation season.

1 Introduction

Glacier surface-mass-balance (SMB) projections in response to climate change up to the end of the 21st century can be analysed via physical approaches using energy-balance calculations and empirical approaches linking simple meteorological variables to SMB such as temperature-index models. Most glacier-mass projections in response to climate change in large-scale studies spanning the 21st century have been based on temperature-index models (Huss and Hock, 2015; Fox-Kemper et al., 2021), given the lack of available or reliable information on detailed future meteorological variables (Réveillet et al., 2018). The deep artificial-neural-network (ANN) approach is a promising new empirical approach to simulate SMB in the future (Bolibar et al., 2020). A neural network is a collection of interconnected simple processing elements called neurons. These processing elements are assigned coefficients or weights, which constitute the neural-network structure. Each weight is generated by the training process for the ANN (Agatonovic-Kustrin and Beresford, 2000).

Recently, Bolibar et al. (2022) analysed the sensitivity of glacier SMB to future climate change using a deep ANN. They write that their deep-learning approach captures non-linear responses of glacier SMB to high deviations in air temperature and solid precipitation, improving the representation of extreme SMBs. Bolibar et al. (2022) argue that temperature-index models, widely used to simulate the large-scale evolution of glaciers, can be suitable for steep mountain glaciers but may be less suitable for some scenarios and flatter glaciers and ice caps due to linear sensitivities in such mass-balance models. In this paper we perform numerical experiments with a classic and simple temperature-index model. Our unique purpose is to demonstrate that temperature-index models are able to capture non-linear responses of glacier mass balance (MB) to high deviations in air temperature and solid precipitation.

2 Data

For our numerical experiments, we selected two very different glaciers in the French Alps. The first, the Argentière Glacier, is located in the Mont Blanc range (45^∘55^′ N, 6^∘57^′ E). Its surface area was approximately 10.9 km² in 2018. The glacier extends from an altitude of approximately 3400 m a.s.l. at the upper bergschrund down to 1600 m a.s.l. at the snout. It faces north-west, except for a large part of the accumulation area (south-west-facing tributaries). The second, the Sarennes Glacier, is a small south-facing glacier (0.51 km²) with a limited altitude range between 2820 and 3160 m (mean values over the period used for the present study) located in the Grande Rousses range (45^∘07^′ N, 6^∘07^′ E). The field SMB observations of the Argentière and Sarennes glaciers come from the French glacier-monitoring programme GLACIOCLIM (Les GLACIers, un Observatoire du CLIMat; https://glacioclim.osug.fr/, last access: 25 April 2023). Annual SMBs were monitored in the ablation area of the Argentière Glacier between 1975 and 1993 using 20 to 30 ablation stakes. Since 1993, systematic winter and summer mass-balance measurements (May and September respectively) have been carried out over the entire surface of the glacier. Approximately 40 sites were selected at various elevations representative of the whole surface. Moreover, geodetic mass balances have been calculated using digital elevation models on the basis of an old map from 1905 and photogrammetric measurements carried out in 1949, 1980, 1993, 1998, 2003, 2008, and 2019 (Vincent et al., 2009). Since 1949, systematic winter and summer mass-balance measurements have been carried out on the Sarennes Glacier, from which annual balances are calculated (Thibert et al., 2013).

We used the atmospheric temperature and precipitation data from the SAFRAN (Système d'Analyse Fournissant des Renseignements Adaptés à la Nivologie analysis system for the provision of information for snow research) reanalysis process that are available from 1958 to date (Durand et al., 2009; Verfaillie et al., 2018). SAFRAN disaggregates large-scale meteorological analyses and observations in the French Alps. The analyses provide hourly meteorological data as a function of seven slope exposures (N, S, E, W, SE, SW, and flat) and altitude (at 300 m intervals up to 3600 m a.s.l.) that differ for each mountain range (e.g. the Mont Blanc, Vanoise, and Grandes Rousses ranges).

3 Method

We ran numerical experiments with a classic simple temperature-index model (Hock, 2003; Reveillet et al., 2017) and using SAFRAN reanalysis data (Durand et al., 2009; Verfaillie et al., 2018). These numerical experiments were run on the two very different French glaciers, Argentière and Sarennes, observed over several decades (Thibert et al., 2013; Vincent et al., 2009). The SMB model was run for each day using the equation

$$\mathrm{SMB}={\mathrm{DDF}}_{\mathrm{snow}/\mathrm{ice}}\cdot T+k\cdot P,$$

where T is the difference between the mean daily air temperature and the melting point, DDF${}_{\mathrm{snow}/\mathrm{ice}}$ is the degree-day factor for snow and ice, DDF = 0 if T<0 ^∘C, P is the precipitation (m w.e.), k is a ratio between snow accumulation and precipitation, and k=0 if T>0 ^∘C.

The degree-day factors for snow and ice were 0.0035 and 0.0055 m w.e. K⁻¹ d⁻¹ for the Argentière Glacier (Reveillet et al., 2017) and 0.0041 and 0.0068 m w.e. K⁻¹ d⁻¹ for the Sarennes Glacier (Thibert et al., 2013). The point mass balances were calculated for each elevation for the Argentière and Sarennes glaciers. In addition, we calculated the glacier-wide mass balance of the Argentière Glacier using the point mass balances for the elevation range and the geodetic mass balances (Vincent et al., 2009). Parameter k depends on the site elevation in accounting for the precipitation gradient and is determined from the winter-balance measurements and precipitation data.

Other enhanced temperature-index models including potential direct solar radiation could be used for our study, but here the purpose is to show that responses in SMB are not linear to temperature or precipitation changes even when using a simple degree-day model.

4 Results

The reconstruction of the glacier-wide MBs of these glaciers from our simple temperature-index model shows good agreement with data (Fig. 1). Using these reconstructed MBs, we calculated the SMB sensitivities to temperature and winter precipitation at 2750 and 3100 m on the Argentière and Sarennes glaciers respectively (Fig. 2). These altitudes were selected because they correspond to the approximate centre of the glaciers. For each day of each series, we calculated an annual SMB anomaly by adding a temperature anomaly or a precipitation anomaly. The anomaly was generated as a shift (increment/decrement) in the mean of the distribution of the original data in temperatures and winter balances. The distribution around the means was unchanged (same year-to-year variability as found in the original data).

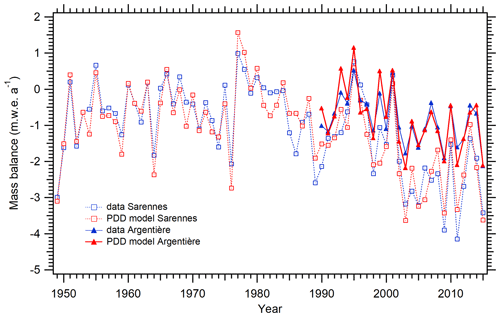
Figure 1 Glacier-wide mass balance of the Argentière Glacier (1990–2015) and the Sarennes Glacier (1949–2015). Observations and simulations from the simple degree-day model used in our experiments.

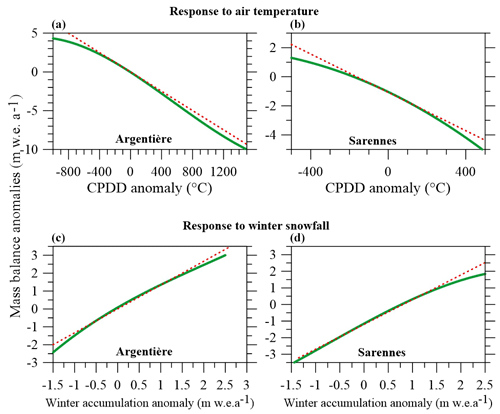
Figure 2 Response of mass balance to climate forcing using a temperature-index model (green line) at 2750 and 3100 m on the Argentière (a, c) and Sarennes (b, d) glaciers respectively. The red dashed lines are the best linear fit. Note that, in such graphs, the sensitivity of the mass balance to temperature and winter accumulation changes is the slope of the curves.

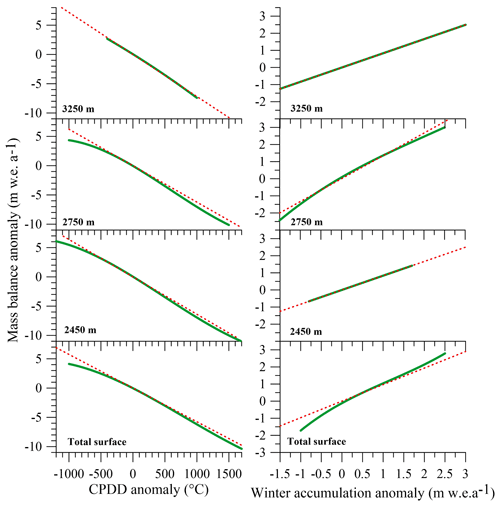
Figure 3 Response of annual mass balance to air temperature (left panel) and to winter accumulation (right panel) using a temperature-index model (green line) on the Argentière Glacier. The red dashed lines are the best linear fit forced through the origin.

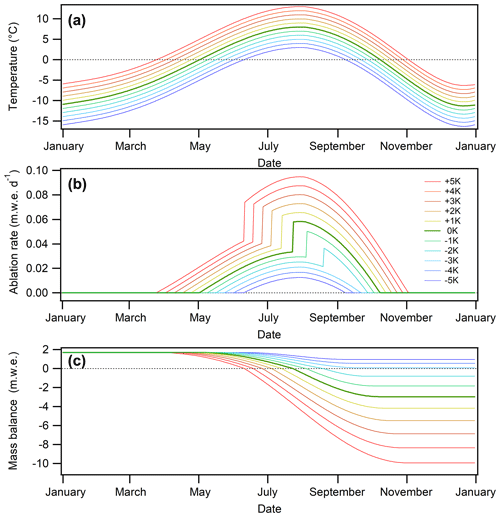
Figure 4 Positive degree-day model running on synthetic data (response to air temperature). Evolution of air temperatures (a), ablation rates (b), and mass balance (c) over the year, according to different temperature scenarios, calculated at 2800 m. Note the jump in ablation rates when ablation shifts from snow to ice. This occurs earlier with temperature forcing. Note also the lengthening of the ablation season with a rise in temperature.

We report the results in Fig. 2 to mirror Fig. 3 of Bolibar et al. (2022) and make the comparison easier. We also ran these numerical experiments at different altitudes and over the entire glacier surface of the Argentière Glacier (Fig. 3).

From our experiments, we found first that the response of SMB to temperature, using a temperature-index model, is not linear. As expected, the sensitivity of annual SMB (i.e. the slope of the green curves in the graphs of Fig. 2) increases with the positive-degree-day (PDD) anomaly. To explain the physical processes involved in non-linearity, we again used our PDD model but with synthetic data for atmospheric temperature changes over a year (Fig. 4a). The reference scenario (unforced temperature and winter-balance reference conditions) of synthetic data is typical for a location in the upper ablation area of an Alpine glacier (cumulative PDD of 800 degree-days from early May to early October; 1700 mm of winter balance). We use increments of ±1 K (−5 K; +5 K) to analyse the response of SMB. PDD factors for snow and ice come from Thibert et al. (2013). As shown in Fig. 4, the non-linearity with respect to temperature forcing (the spread between SMB plots in Fig. 4c) comes from (i) the lengthening of the ablation season (Fig. 4a) and (ii) the earlier disappearance of the winter snow cover which increases the ablation rate due to the change in the degree-day factor from snow to ice (Fig. 4b).

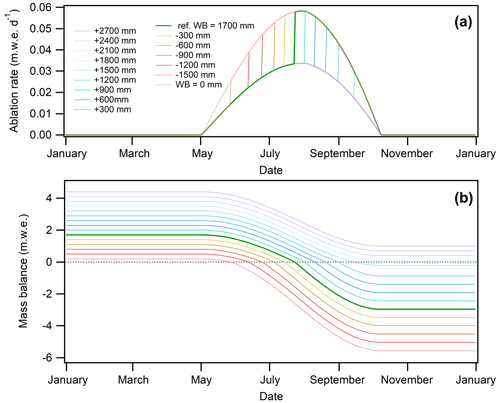
Figure 5 Positive degree-day model running on synthetic data (response to winter balance). Change in ablation rates (a) and mass balance (b) over the year according to different winter-balance scenarios calculated at 2800 m. Note the jump in ablation rates when ablation shifts from snow to ice. This occurs earlier under lower winter-balance conditions. Note that the duration of the ablation season is unchanged under variable winter-balance conditions.

Concerning the winter balance, runs of our PDD model on synthetic data under different conditions of winter balance (Fig. 5) used a reference scenario of 1700 mm of winter balance changed by increments of ±300 mm in precipitation. We found a non-linear response of SMBs to winter precipitation with our PDD model. For instance, with winter accumulation decreased by −1500 mm, ice ablation starts very early (by the end of May), and the annual MB is −5.55 m w.e. a⁻¹ in October. With winter accumulation increased by +1500 mm, ice ablation starts in mid-September and the annual MB is −0.21 m w.e. a⁻¹ in October. This asymmetry clearly shows that the response to winter accumulation is not linear. Results show that the increase in sensitivity can be physically explained by the earlier disappearance of the winter snow cover. The earlier and abrupt increase in the ablation rate under lower conditions of winter balance (Fig. 5a) results in non-linearity attested by the spread between SMB plots in Fig. 5b. We detect sensitivity to winter accumulation, contrary to the Bolibar et al. (2022) findings using their ANN (Figs. 2 and 3). Indeed, MB sensitivity increases with low winter-accumulation anomalies using our model but decreases in the deep-learning model of Bolibar et al. (2022). Our results are consistent with direct in situ observations (Six and Vincent, 2014) and are also consistent with the results reported by Réveillet et al. (2018) from observations and energy-balance modelling. The opposite results obtained from the deep-learning model may be due to an issue in the calibration of the model.

Summing up, the ability of PDD models to provide non-linear sensitivity to air temperature and solid precipitation is due to the different ablation rates and the associated change in the degree-day factor that can be involved depending on snow or ice conditions at the glacier surface. An additional non-linearity to temperature forcing is caused by changes in the ablation duration.

Another question arises in the discussion section of Bolibar et al. (2022) concerning the comparison between their results and those from other studies. According to this paper, all glacier models in the Glacier Model Intercomparison Project (GlacierMIP) (Hock et al., 2019) rely on SMB models with linear relationships between PDDs, melt, and precipitation. The authors argue that these PDD models present behaviour very similar to the linear-build statistical Least Absolute Shrinkage and Selection Operator (LASSO) model. However, most of the temperature-index models used in GlacierMIP include two degree-day factors. Consequently, they cannot provide a linear response to climate forcing as shown above. In the Bolibar et al. (2022) paper, the MB anomalies in response to climate forcing were obtained using a linear LASSO SMB model, which is based on a regularized multi-linear regression, although the authors also used the Global Glacier Evolution Model (GloGEMflow) model in their paper (see their discussion section), which is a temperature-index model widely used for glacier projections (Zekollari et al., 2019).

5 Conclusions

From numerical experiments with a classic and simple temperature-index model, our results highlight that temperature-index models are able to capture non-linear responses of glacier mass balance (MB) to high deviations in air temperature and solid precipitation, unlike the Bolibar et al. (2022) study.

Bolibar et al. (2022) compared the response of SMB to climate forcing (air temperature, winter and summer snowfall) using a deep-learning approach and a LASSO model. From this comparison, they conclude that deep learning provides a non-linear response, contrary to the LASSO model. The conclusions of Bolibar et al. (2022) may be due to the use of a linear LASSO SMB model instead of a temperature-index model. We would suggest testing the capability of an ANN to capture non-linearity by comparing its results with that of the GloGEM PDD model that they used in their paper.

Regarding specifically SMB changes due to solid precipitation, the deep-learning model used by Bolibar et al. (2022) foresees decreasing sensitivity under low winter-accumulation conditions. We point out that this result directly contradicts PDD model outcomes. We explain in physical terms why a PDD model projects higher sensitivity to low winter accumulation but do not yet understand why the approach of Bolibar et al. (2022) does not.

Given that detailed meteorological variables are highly unpredictable in the future, most glacier-mass projections in response to climate change in large-scale studies spanning the 21st century are still today based on temperature-index models with simple temperature and precipitation variables. It follows that the questions raised here relative to the non-linear responses of surface SMB to meteorological variables are crucial.