Glacier Image Velocimetry: an open-source toolbox for easy and rapid calculation of high-resolution glacier velocity fields

We present Glacier Image Velocimetry (GIV), an open-source and easy-to-use software toolkit for rapidly calculating high-spatial-resolution glacier velocity fields. Glacier ice velocity fields reveal flow dynamics, ice-flux changes, and (with additional data and modelling) ice thickness. Obtaining glacier velocity measurements over wide areas with field techniques is labour intensive and often associated with safety risks. The recent increased availability of high-resolution, short-repeat-time optical imagery allows us to obtain ice displacement fields using “feature tracking” based on matching persistent irregularities on the ice surface between images and hence, surface velocity over time. GIV is fully parallelized and automatically detects, filters, and extracts velocities from large datasets of images. Through this coupled toolchain and an easy-to-use GUI, GIV can rapidly analyse hundreds to thousands of image pairs on a laptop or desktop computer. We present four example applications of the GIV toolkit in which we complement a glaciology field campaign (Glaciar Perito Moreno, Argentina) and calculate the velocity fields of small mid-latitude (Glacier d'Argentière, France) and tropical glaciers (Volcán Chimborazo, Ecuador), as well as very large glaciers (Vavilov Ice Cap, Russia). Fully commented MATLAB code and a stand-alone app for GIV are available from GitHub and Zenodo (see https://doi.org/10.5281/zenodo.4624831, Van Wyk de Vries, 2021a).

1 Introduction

Satellite imagery revolutionized our ability to study changes in glacier extent, volume, and surface velocities and is an effective tool for communicating these changes to the broader public (Scambos et al., 1992; Rignot et al., 2011; Heid and Kääb, 2012a; Stocker et al., 2013; Howat et al., 2019). Glacier velocity measurements enable scientists to map glacier divides and drainage basins (Davies and Glasser, 2012; Pfeffer et al., 2014; Mouginot and Rignot, 2015), track changes in surface melt production and accumulation (Mote, 2007; Sneed and Hamilton, 2007), and address key questions about ice dynamics and the future of glaciers under a changing climate (Stearns et al., 2008; van de Wal et al., 2008; Rignot et al., 2011; Willis et al., 2018; Millan et al., 2019; Altena et al., 2019). Even the earliest glaciologists identified that glaciers may flow as viscous fluids (Forbes, 1840, 1846; Bottomley, 1879; Nye, 1952) and later that glacier surface motions reflect a complex interplay between internal deformation, basal sliding, and deformation of subglacial sediments (Deeley and Parr, 1914; Weertman, 1957; Kamb and LaChapelle, 1964; Nye, 1970; Fowler, 2010). Such changes reflect a combination of glacier mass balance and basal conditions – including time-varying hydrology – both of which may respond to climate. Widespread measurement of glacier surface velocities, a key constraint on glacier dynamics, has however only become possible with the advent of satellite-based remote sensing (e.g. Bindschadler and Scambos, 1991; Scambos et al., 1992).

Deriving glacier velocities from satellite imagery is possible through an image analysis technique known as “feature tracking”, “image cross correlation”, or “particle image velocimetry” (PIV). The latter term, particle image velocimetry, describes a well-established technique in fluid dynamics typically involving the use of a high-speed digital camera to track the motion of tracers within a fluid in a laboratory setting (Buchhave, 1992; Grant, 1997; Raffel et al., 2018). These ideas were first carried over to the field of glaciology by Bindschadler and Scambos (1991) and Scambos et al. (1992) to evaluate the flow velocity of a portion of an Antarctic ice stream. Since that time, the increasing abundance and availability of imagery has facilitated the expanded use of feature-tracking-based velocimetry techniques. With the release of the full Landsat data archive and launch of Sentinel-2, 10–30 m pixel resolution imagery of any given location is now available at sub-weekly repeat coverage intervals. A number of studies apply this exceptional archive to map velocity fields across the major ice sheets, as well as those of many glaciers around the world (Gardner et al., 2018; Millan, 2019).

Prior to the advent of remote sensing, spatially distributed measurements of glacier flow velocities required lengthy field campaigns (Meier and Tangborn, 1965; Hooke et al., 1989; Chadwell, 1999; Mair et al., 2003). Nowadays full 2D flow-velocity maps may be readily calculated from a variety of optical- and radar-based satellite imagery (Heid and Kääb, 2012b; Fahnestock et al., 2016). For this toolbox we focus on optical imagery products due to their ease of access, limited need for pre-processing, and high spatial and temporal resolution (Drusch et al., 2012; Heid and Kääb, 2012b, a; Kääb et al., 2016; Darji et al., 2018).

A number of tools exist to derive displacements from imagery, as partially reviewed by Heid and Kääb (2012a), Jawak et al. (2018), and Darji et al. (2018). These include CARST (Cryosphere and Remote Sensing Toolkit; Willis et al., 2018), COSI-corr (Co-registration of Optically Sensed Images and Correlation; Leprince et al., 2007b), AutoRIFT (Autonomous Repeat Image Feature Tracking; Gardner et al., 2018), ImGRAFT (Image Georectification and Feature Tracking; Messerli and Grinsted, 2015), and SenDiT (the Sentinel-2 Displacement Toolbox; Nagy and Andreassen, 2019; Nagy et al., 2019). CARST contains a mixture of Python and Bash scripts used to monitor changes in glaciers and includes feature-tracking and ice-elevation-change-monitoring tools (Willis et al., 2018; Zheng et al., 2018, 2019a). COSI-Corr is a flexible co-registration and feature-tracking tool written in IDL, implemented in the ENVI GIS package, and initially used for measuring co-seismic deformation. Auto-RIFT is a Python-based feature-tracking algorithm (Gardner et al., 2018). ImGRAFT is a MATLAB-based toolbox for georectifying and feature tracking of ground-based imagery and may also be used on satellite imagery. SenDiT provides a platform to automatically download and generate velocity maps based on Sentinel-2 data using a Python interface with bindings to the C- and Fortran-based imcorr toolbox (Scambos et al., 1992) for feature-tracking calculations. In addition, near-global ice velocity maps are calculated in near real time from Landsat and other freely available satellite data sources: GoLIVE using PyCorr (Scambos, 2016) and ITS_LIVE using Auto-RIFT (Gardner et al., 2020).

Gardner et al. (2018)Zheng et al. (2019a)Kääb and Vollmer (2000)Leprince et al. (2007a)Schwalbe and Maas (2017)Minchew et al. (2017)Scambos et al. (1992)Messerli and Grinsted (2015)Sveen (2004)Thielicke and Stamhuis (2014)James et al. (2016)Fahnestock et al. (2016)How et al. (2020)Nagy et al. (2019)Shean (2019)

Table 1 Non-exhaustive list of codes and toolboxes that may be used for feature tracking and associated references. For availability, 1 = fully available, 2 = available but relies on commercial software, and 3 = not available. A spreadsheet with download links is available in the Supplement.

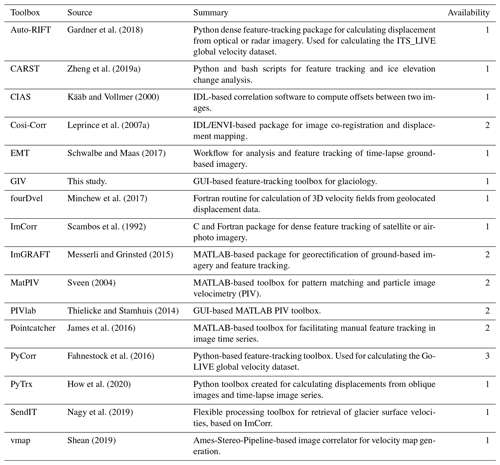
Table 1 presents a non-exhaustive list of feature-tracking software packages. In some circumstances, GIV will not be the most suitable feature-tracking tool depending on the user's requirements. For example, users who need to manually perform prior image co-registration (e.g. with airphotos) may wish to use the built-in workflow in COSI-Corr. The objective of the Glacier Image Velocimetry (GIV) toolbox presented here is not to compete with or replace these other tools. Rather, GIV aims to provide an easy-to-use, flexible, and robust alternative. GIV may be used to derive high spatial and temporal resolution surface-velocity maps of glaciers of all scales. The following section will run through the basics of the image-feature-tracking techniques and advances built into GIV.

2 Methods and model setup

The fundamental idea of feature tracking is based on techniques used to co-register images: the properties of two images are compared in order to identify the best-fit location of one image within the other (Scambos et al., 1992; Thielicke and Stamhuis, 2014; Messerli and Grinsted, 2015). In feature tracking, including in GIV, individual images are divided into a grid of smaller images (referred to as “chips”). We compare each individual chip from the first image (I1) to a surrounding portion within a second image (I2) and find the best matching portion of I2. If no displacement has occurred between the two images, the best-fitting portion of I2 will have the same location as the original chip on I1 (excluding any georeferencing or distortion-related errors). However, if any motion has occurred between the two images, the corresponding best matching chip within I2 will be displaced relative the original location within I1. We may then determine the bulk displacement in pixels between the original I1 chip and best matching I2 chip. The correlation coefficients between the original chip and surrounding area within I2 are also calculated. This allows a Gaussian curve to be fit to this grid in order to determine the peak location at sub-pixel accuracy. Repeating this routine for every chip within the original image allows a 2D surface velocity field to be derived.

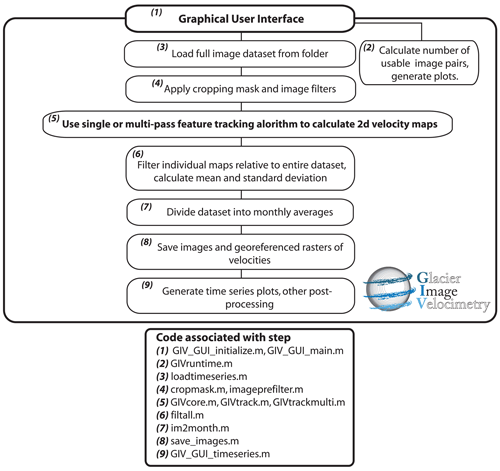
Figure 1 Flowchart describing the Glacier Image Velocimetry toolbox design. Names of the code files associated with each step are given for reference (and are available in the linked Zenodo repository). The feature-tracking step is shown in bold. Note that the source code is open source but that accessing it is not necessary for running GIV. Users may enter all parameter options into fields in the user interface, with subsequent steps automatically performed by the toolbox.

While initially developed for use in laboratory-based fluid dynamics, the camera, lighting, and tracer-particle conditions were all closely constrained (Grant, 1997; Raffel et al., 2018). On glaciers, features change over time as crevasses open and close, snow drifts, and ablation exposes new surfaces. In addition, the satellite may acquire imagery from slightly different locations and angles with each pass, and lighting conditions depend strongly on the time of day and year, as well as degree of shadowing and local weather conditions (Berthier et al., 2005; Kääb et al., 2016). This complexity raises additional problems in the use of this technique for deriving glacier velocities and makes it entirely unusable in some cases (e.g. images too far spaced in time relative to the speed of the glacier for image pairs to retain any coherence). These problems can be mitigated though a combination of image pre-filtering, comparison between adjacent velocity maps, and outlier filtering. We also refer readers to Sects. 2 and 4 of Altena (2018) for a detailed discussion on these topics. The Glacier Image Velocimetry toolbox makes use of these methods, with a particular emphasis on noise reduction in individual velocity map outputs through the use of large datasets. Figure 1 presents the overall model setup and order of operations.

2.1 Model pre-processing

Prior to running the feature-tracking algorithms, the satellite images are first loaded into the workspace and filtered. The user interface will prompt the user to enter the coordinates of the images (minimum and maximum latitude and longitude) and to select a given folder in which the images are stored. These images can be .png, .jpg, or .geotiff files of the area, with each file name being the date of image acquisition (in yyyymmdd format). In the case of a GeoTIFF input, GIV will automatically load the geographic information from the input. GIV will then extract the dates from the file names, calculate time between images, and load the raw image data into an array for further processing. The user also inputs a modified image with glaciers of interest converted to pure white (RGB 255, 255, 255). This image is loaded by GIV and converted into a binary mask with areas within (1) and outside (0) the computational region. The size and resolution of images are also automatically calculated and resampled to a common resolution such that images from different satellites may be combined in the same dataset.

Figure 2 Comparison between raw optical images, band-summed images, and NAOF-filtered images for a clear image (a, d, g), a heavily shadowed image (b, e, h), and a cloudy image (c, f, i) of Amalia glacier, Patagonia (−50.92^∘ S, −73.56^∘ W). Note how despite the complexity, the NAOF images recover a clear and easily traceable feature pattern on the surface of the glacier that is suitable for obtaining velocities. The shadow line leaves an artefact in (h) but is a marked improvement on the lack of features in the shaded area in (e). Images from Sentinel-2.

Following this, GIV filters the images according to user-defined settings. GIV includes a range of filters in order to reduce the effect of unwanted noise (e.g. clouds and shadows) and emphasize trackable features (e.g. crevasses, snowdrifts, supraglacial debris). In particular we include high-pass, Sobel, and Laplacian filter options to emphasize short-wavelength features and edges, as well as intensity-capping and contrast-limited histogram-equalization filters to improve image contrast (Sveen, 2004; Thielicke and Stamhuis, 2014; Gardner et al., 2018). We also include a variation of the orientation filter (Fitch et al., 2002) named “near anisotropic orientation filter” (NAOF). We define this filter as follows:

$$\begin{array}{}\text{(1)}& {\mathbf{I}}_{\mathrm{f}}=\sum _{i=\mathrm{1}}^{\mathrm{4}}\cos \left[\arctan \mathrm{2}({\mathbf{I}}_{\mathrm{o}}\cdot {\mathit{\alpha }}_i,{\mathbf{I}}_{\mathrm{o}}\cdot R[{\mathit{\alpha }}_i\left]\right)\right],\end{array}$$

with I_f being the filtered image and I_o the original image, α representing four different convolution matrices oriented at 45^∘ from each other using the eight adjacent pixels, arctan 2(x,y) representing the four-quadrant arctangent (also called the two-argument arctangent), x×y representing a 2D matrix convolution, and R[x] representing a 90^∘ matrix rotation. This filter works by summing differently angled orientation filters together in order to recover a “pseudo-feature” with the same location as the original feature but with an increased contrast between the feature and the background and homogenized magnitude (Fitch et al., 2002; Kobayashi and Otsu, 2008). Information on absolute pixel colour magnitude is discarded, with only information on colour gradients preserved. A similar result may be obtained by convolving the original image with a single convolution matrix summing the four directional filters, but this normalizes all features to a single magnitude and results in a larger number of false matches. The NAOF has the advantages of (a) strongly increasing the contrast between features and background; (b) removing contrast differences between clouded, shadowed, and clear areas; and (c) preserving feature location and uniqueness. Figure 2 shows examples of how this filter is able to recover features from challenging images. Many glaciated areas remain cloud covered and shadowed for much of the year, so being able to recover partial velocity fields from these images can greatly increase the size of potential datasets. Note that no amount of filtering can improve certain images, such as those in which cloud cover is too thick for the glacier surface to be visible. An evaluation of the quality of velocity maps derived from different image filters is provided in the Supplement (Figs. S1–S16 in the Supplement). These show that NAOF, contrast-limited histogram equalization, and high-pass filtering provide a major improvement over raw imagery.

2.2 Velocity calculations

2.2.1 Frequency domain matching

The central part of any feature-tracking code involves matching a small region of one image (chip) with a surrounding region of a second image (“search area”). The chip is matched to the search area through 2D cross correlation, which may be performed in the spatial or frequency domain (Thielicke and Stamhuis, 2014; Altena, 2018). Matching in the spatial domain (“normalized cross correlation”) may better account for feature distortion or shear and may have a higher accuracy (Thielicke and Stamhuis, 2014). Frequency domain methods (“frequency cross correlation”) generally benefit from a greater computational efficiency as the correlation matrix is calculated across the whole domain in one operation. We implement frequency domain matching in GIV as feature distortion is minimal in most glaciers and it has been found to perform well in prior studies (e.g. Heid and Kääb, 2012a). We refer readers to Thielicke and Stamhuis (2014) and Sect. 4 of Altena (2018) for more details on these topics.

Frequency cross correlation involves calculating the correlation between the chip and search area in the frequency domain. This is done by converting both the chip and search area to the frequency domain using a fast Fourier transform (FFT), calculating the pointwise product between these two matrices, and converting the resulting similarity matrix back to the spatial domain with an inverse FFT. This step is repeated on each chip within the original image and is the most computationally expensive of the entire process.

GIV is written in MATLAB. Despite being a high-level interpreted programming language, MATLAB performs FFT calculations using pre-compiled C and Fortran bindings for the FFTW library (Frigo and Johnson, 1998, 2005). Due to this being the rate-limiting step in feature-tracking calculations (> 90 % of computation time in most cases), such code may be written in MATLAB with few performance issues relative to other programming languages.

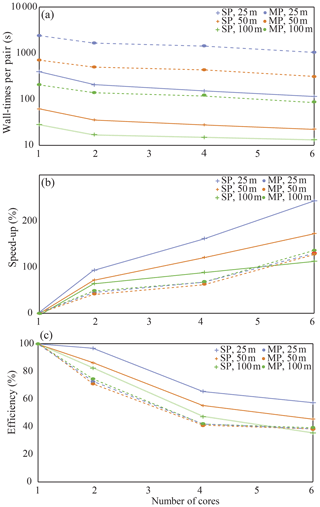
Figure 3 MP = multi-pass; SP = single-pass. Test conducted on a 12-image dataset of 10 m resolution, 1.7 million pixel images of Amalia Glacier, Chile, using a Dell XPS 15 laptop (2 × 16 GB DDR4 2666 MHz memory, 6-core Intel i7-8750H 2.20 GHz processor). In all cases, parallelization decreases runtime, and going from one to two cores improves runtime by 1.4–1.9×. Fine-resolution multi-pass runs usually yield the best velocity fields, and (b) shows that these benefit from the largest speed-up when parallelized.

2.2.2 Parallel computing

As the feature-tracking correlation between two images inherently requires a large number of FFT and inverse FFT (IFFT) operations, this step has limited potential for further optimization. Computation time may instead be decreased by deriving displacement fields from different image pairs in parallel rather than in series. This requires a slightly different code design. First, GIV detects the number of physical cores on the user's computer and starts a parallel pool; alternatively, users may start their own parallel pool with a chosen number of cores. It then decomposes the full sequence of image pairs into sub-sequences, each containing a number of image pairs equal to the number of cores. Finally, displacements are calculated in parallel on the image pairs within each sub-sequence (each on a different core in the computer). Figure 3 shows the increase in computation speed with number of cores used in different scenarios. This enables large datasets to be processed more rapidly, even on standard laptop and desktop computers.

2.2.3 Single- and multi-pass approaches

Displacements may be derived from an image pair either with a single pass across the images or with multiple passes with gradually reducing window sizes (Thielicke and Stamhuis, 2014; Raffel et al., 2018). Single-pass methods generally have the advantage of generally being faster at coarse resolutions and are less at risk of smearing one erroneous value over a larger area. Multi-pass methods update displacement estimates over multiple iterations, refining initial coarse-window-size displacement calculations using progressively smaller window sizes. Multi-pass methods combine the advantages of better feature matching at large window sizes with the higher spatial resolution of small window sizes. Both methods are integrated into GIV, with a single-pass method based on ImGRAFT (Messerli and Grinsted, 2015) and a three-iteration multi-pass algorithm modified from MatPIV (Sveen, 2004). Both functions have been tested in a number of previous studies, with MatPIV being used extensively in fluid-dynamics research (e.g. Sveen and Cowen, 2004; Sveen, 2004; Lee et al., 2017; Oertel and Süfke, 2020). An experiment evaluating the difference between a normalized cross-correlation algorithm and the multi-pass frequency domain cross correlation in GIV is given in the Supplement. We find that the multi-pass frequency domain algorithm produces velocity maps with a higher signal to noise ratio than the normalized cross-correlation algorithm across test scenarios with a range of cloud cover.

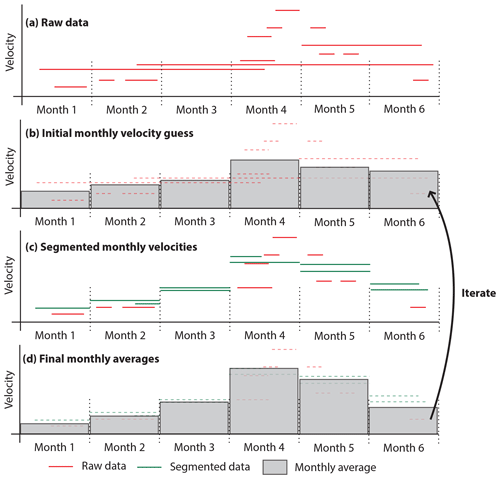
Figure 4 Schematic description of the techniques used to derive monthly velocities. The raw data (a) are combined in a weighted average to make an initial guess of monthly averages (b). The monthly averages are then used to segment longer time period velocity maps into their different monthly contributions (c). These are used to recalculate the monthly averages (d). Finally, GIV iterates over steps (b–d) for a number of times (e.g. 10) provided by user inputs. Note that an estimate may be made for the average velocity in “Month 3” despite this month having no imagery available.

2.2.4 Non-consecutive images

GIV may also calculate velocity maps for pairs of non-consecutive images, which we refer to as “temporal oversampling”, resulting in much larger final datasets. The user inputs maximum and minimum temporal separations for image pairs, and GIV extracts all suitable pairs, including those that are not consecutive. For a dataset of n images, this theoretically enables a total of $(n^{\mathrm{2}}-n)/\mathrm{2}$ image pairs. For example, this would produce 19,900 image pairs from a 200-satellite-image time series. For heavily clouded datasets this also has the advantage of increasing the likelihood of forming cloud-free image pairs.

2.2.5 Velocity map filtering and improvement

Apart from some scenarios and positions, such as surges, spring speed-ups, and the margins of ice streams, glacier velocity gradients vary gradually in both space (low lateral velocity gradients) and time (low acceleration). Therefore, the accuracy of individual velocity measurements can be evaluated by comparing them to their immediate neighbours in both space and time. Sudden jumps in space or time most likely represent erroneous velocities due to mismatches within the feature-tracking algorithm. This property is used in the GIV toolbox to improve the final velocity maps through the following workflow.

Firstly, GIV filters each individual velocity map through user-prescribed limits on velocity and flow direction, as well as outlier detection functions. This finds values that differ by more than 50 % from their immediate neighbours (four surrounding cells) and 200 % from the mean of their larger local area (25 surrounding cells), removes these outlier values, and interpolates across these now-empty pixels using the remaining values. Secondly, GIV calculates the mean, standard deviation, and median, minimum, and maximum velocities through time at each grid cell in the dataset. It then compares each individual value to the mean value at that location for the entire dataset. Any values more than 1.5 standard deviations away from this mean are considered outliers. This process is carried out for the x and y components of velocity and flow-speed and flow-direction grids, and only values within the threshold for all velocity and flow direction components are conserved. This provides an additional check as erroneous values are unlikely to coincidentally match both the velocity and flow direction. Finally, the entire dataset may be smoothed and interpolated in space or time and space according to the user's choices. This allows missing values at one time step to be linearly infilled from neighbouring times. In addition, the displacement of each image pair may be normalized to the displacement of a user-defined stable ground mask to correct for systematic georeferencing errors.

2.2.6 Temporal resampling

Variable satellite repeat intervals and the exclusion of entirely clouded or otherwise unusable images lead to unevenly spaced velocity time series that are more difficult to interpret. In order to reduce this challenge, GIV includes a function that automatically averages the data and resamples it to monthly intervals. This is easy when all individual velocity maps cover periods of less than 1 month and do not overlap between months but become more complex when they do. In many cases, image pairs with the shortest lag times (< 7–10 d) are excluded because displacement over such a short time may be obscured by offsets due to distortion and/or georeferencing errors. For the slowest-moving glaciers, this lower bound may be extended to several weeks or months. Lag times as long as the available imagery time series may be used so long as the surface of the glacier retains coherence in the image pairs.

GIV can determine monthly values by averaging across all image pairs that overlap with a given month. However, this produces an artificially smoothed dataset due to the influence of velocities measured across the boundaries of months. In order to make use of longer lag-time pairs, we develop an iterative strategy for calculating monthly values. In the first place, GIV takes a weighted mean of all velocities covering that month to make an initial guess at monthly velocities. The weighting parameter is determined by the proportion of the individual map contained within a given month. For instance, a velocity entirely within 1 month will be weighted 1, while a velocity spread evenly over 4 months will be weighted 0.25. This initial estimate is then used to iterate between monthly averages and raw data values, with raw values covering more than 1 month split into monthly values by subtracting the previous iteration's estimate of monthly averages from them (Fig. 4). This procedure may extract average monthly velocities even for months lacking any images. Outlier detection and maximum velocity filters are implemented based on user-provided maximum velocity and comparison to neighbouring pixels. This prevents noise in the raw data from being accentuated by the iterations but may also lead to loss of data if too large a proportion of the initial dataset is inaccurate. Due to this limitation, the iterative calculations are not adapted for some noisy datasets for which the partial loss of temporal resolution by weighted averaging will be preferable. Monthly averaging is performed as a post-processing step and so may be repeated without the need to recalculate any raw velocity maps. Time series may also be generated from the raw data if monthly averaging is not desirable.

Figure 5 Mean flow velocity (m yr⁻¹) (a) and direction (degrees) (b) of Glaciar Perito Moreno, Argentina, for the first 3 months of 2020. Figure panels have been automatically generated from GIV, labels have been added, and the colour bars moved.

2.2.7 Georeferencing and plotting

As a final step, GIV will automatically georeference the velocity grids and save .geotiff files to the user's computer. The toolbox also contains mapping tools that allow for the automatic generation of publication-quality images of the velocity and flow-direction maps (Fig. 5). Flow direction maps are plotted with a circular colourmap, and all colour maps used are colour-blind friendly based on Crameri et al. (2020) and may be modified according to user preferences. In the following section we will examine some case studies of real glaciers and scenarios for which this model may be useful.

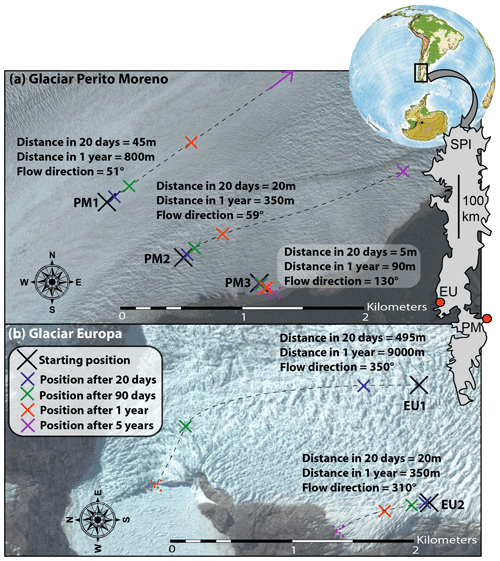
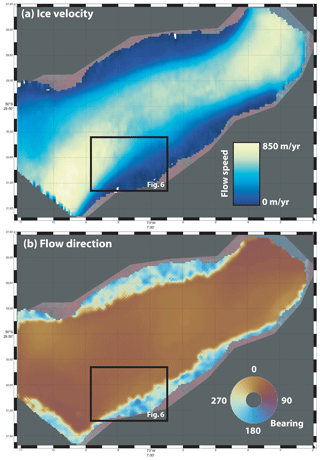
Figure 6 (a) Position of a point on Glaciar Perito Moreno (PM) with the time for three different starting locations within 2 km of the glacier's southern margin. At PM1, ice speeds reach 800 m yr⁻¹, and any equipment will be rapidly displaced. At PM3 ice-flow speeds are < 100 m yr⁻¹ and oriented towards the valley edge. (b) Identical plot for two points on Glaciar Europa (EU). Any equipment installed at EU1 will be displaced several kilometres and lost to calving in less than 6 months. The inlay shows an outline of the Southern Patagonian Icefield (SPI) with the locations of the two glaciers. Imagery © Google Earth.

3 Results and examples

Ice velocity measurements supply essential information for studies of glacier dynamics, thickness, subglacial hydrology, and mass balance. With its GUI-based inputs and potential for parallelization, GIV can calculate a monthly velocity field for any glacier around the world with only a few hours of work. As such, it may also be run alongside field-based expeditions in order to understand the current conditions of the glacier and aid in instrumentation positioning.

We present four case studies. The first is of Glaciar Perito Moreno (50.48^∘ S, 73.11^∘ W), where we use GIV to determine the displacement of automated ablation stakes in conjunction with fieldwork in Spring 2020. The second is Glacier d'Argentière (45.95^∘ N, 06.97^∘ E), a small and well-studied valley glacier located in the French Alps. The third is Vavilov Ice Cap (79.32^∘ N, 94.34^∘ E), located on October Revolution Island in the Arctic Ocean off the mainland Russian coast, whose western outlet glacier is now surging. Here we evaluate GIV against published results (Zheng et al., 2019b) using another image-based ice velocity tool, CARST (Zheng et al., 2019a). Finally, we compute ice-flow velocities across the glaciers on Volcán Chimborazo (01.45^∘ S, 78.82^∘ W) in Ecuador.

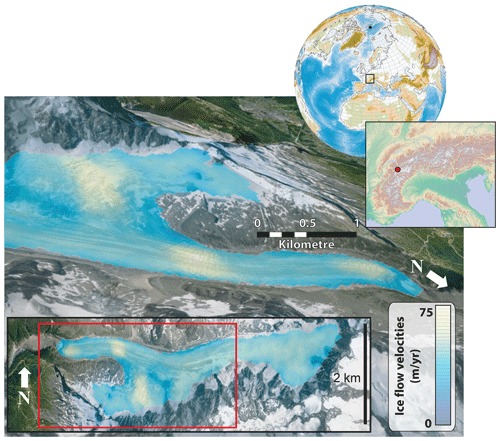
Figure 7 Perspective view of mean flow velocities of Glacier d'Argentière, France, over the period March 2019–March 2020. Imagery is from © Google Earth, and scale is for near margin of glacier.

3.1 Field campaign support: Glaciar Perito Moreno and the Southern Patagonian Icefield

A team from the University of Minnesota installed three automated weather stations and three automated ablation stakes near the southern flank of Glaciar Perito Moreno in order to better understand the local conditions of this glacier and construct temperature-index and energy-balance models for glacier ablation. We installed the automated ablation stakes, based on designs by Wickert (2014) and Wickert et al. (2019) and tested by Saberi et al. (2019) and Armstrong and Anderson (2020), for 20 d between 23 February and 14 March, 2020. In slow-moving glaciers, ice flow may be largely neglected when considering equipment recovery. In rapidly flowing glaciers such as Perito Moreno, however, it may be relevant to consider the movement of the glacier when planning equipment recovery. This is particularly relevant where intense crevassing makes both access and visibility difficult. Figure 6 shows how different positioning decisions may influence ease of recovery: ablation stakes installed in position PM1 will move tens of metres towards the glacier calving front in less than a month, whereas stakes in position PM3 will move less than 5 m towards the glacier flank. In our survey, stakes were installed around position PM3 for ease of access.

Figure 6b also presents the case of Glaciar Europa, which drains the adjacent portion of the Southern Patagonian Icefield in Chile. We also derived the mean velocity field of this glacier over the past 3 years using Sentinel-2 imagery (195 image pairs). GIV velocity measurements reveal that the central portion of Glaciar Europa at its outlet flows nearly 10 000 m yr⁻¹. If an ablation stake were installed in this area (point EU1), it would be displaced almost half a kilometre over the course of a 20 d survey. If it were instead placed at an alternative location 1 km to the west (EU2), it would be displaced only 20 m in the same time period. This is an extreme case, and the flow speeds of most glaciers are orders of magnitude slower, but it showcases the potential importance of deriving glacier surface velocity fields for the success of a glaciological field campaign.

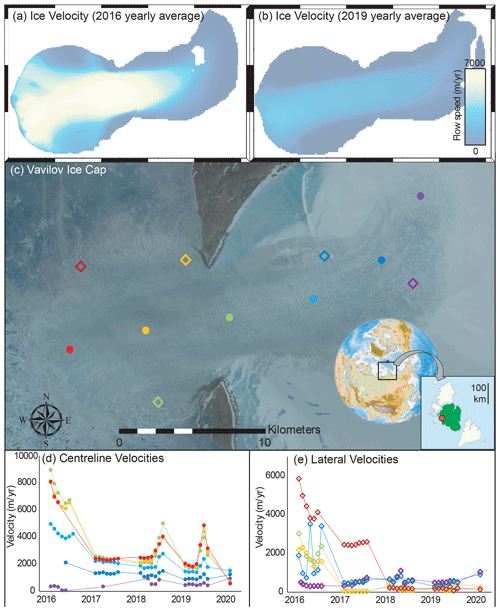
Figure 8 (a, b) 100 m resolution annual mean velocities for the western outlet glacier of Vavilov Ice Cap. (c) A 2019 Sentinel-2 image showing the main features of this outlet and the locations used to derive monthly time series. (d, e) Monthly resolution velocity time series along the glacier centreline and flanks using Sentinel-2 imagery.

3.2 Valley-glacier velocity distribution: Glacier d'Argentière

In order to evaluate the effectiveness of GIV on smaller glaciers, we calculate a velocity field for a well-studied valley glacier in the Mont Blanc massif, Glacier d'Argentière (Benoit et al., 2015). We download 1-year worth of Sentinel-2 data (March 2019–March 2020), containing over 1000 image pairs. These images are then used to derive a 25 m resolution mean ice velocity map, shown in Fig. 7. The sparsity of features transverse to flow direction on Glacier d'Argentière make it difficult for feature-tracking methods to calculate velocities. Nevertheless, the resulting flow-velocity map is comparable to those derived using a SPOT satellite image pair from 2003 (Berthier et al., 2005; Rabatel et al., 2018), synthetic-aperture radar (SAR), and ground-based photogrammetry (Benoit et al., 2015) and a different feature-tracking routine based on a modified version of ampcor (Millan et al., 2019). The velocity map highlights accelerated ice flow at the terminus icefall and on the steep tributary glacier to the south-west of the main trunk (Fig. 7). Main-trunk velocities are on the order of 45–70 m yr⁻¹, slightly slower than SPOT values from Berthier et al. (2005) but in line with values from Benoit et al. (2015). Our values represent the mean over an entire year, including the slower winter velocities not captured by Berthier et al. (2005). It is also possible that glacier thinning has reduced its flow velocity, but our data are not sufficient to evaluate this.

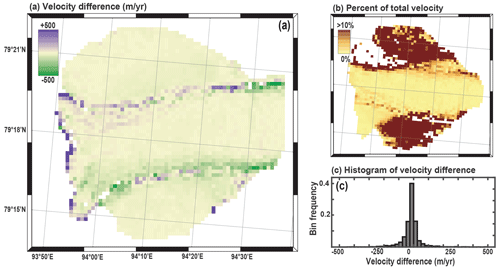
Figure 9 Comparison between the velocity maps of Zheng et al. (2019b) for Vavilov Ice Cap (Pair037_20170506_20170522) and results from GIV (May 2017 average). (a) Difference map, corresponding to the velocity minus GIV velocity from Zheng et al. (2019b), (b) percentage of the total velocity this difference represents (absolute value of the difference shown in (a) divided by GIV velocity), and (c) histogram of the difference values. The mean difference between the two velocity maps is less than 20 m yr⁻¹ or less than 1 % of the total velocity for much of the area.

3.3 Vavilov Ice Cap dynamics

Arctic land-ice melt, including both the Greenland Ice Sheet and all Arctic glaciers, has contributed more than 20 mm to global sea level rise since the 1970s (Box et al., 2018). Most of these large glaciers remain remote and difficult to access, and high spatial and temporal resolution surface velocity maps provide one important tool to assess their response to changing environmental conditions.

Vavilov Ice Cap is a 1700 km³ glacier on October Revolution Island in the Severnaya Zemlya archipelago located in the Russian high arctic (Bassford et al., 2006). Until the 2010s, Vavilov Ice Cap exhibited surface velocities of only a few tens of metres per year, typical of many cold-based high-arctic ice masses. In 2013, a large portion of the marine-terminating western flank surged, with the ice front reaching more than 10 km beyond its prior grounding line by 2016 (Willis et al., 2018; Zheng et al., 2019b). This sudden shift in ice behaviour was not accompanied by any dramatic climatic shift, and the exact triggers are a matter of active debate (Willis et al., 2018, and references therein). Willis et al. (2018) proposed that the dramatic acceleration is related to the glacier overriding weak marine sediments in the Kara Sea, which can deform easily and substantially increase ice velocity. The glacier margin is also no longer frozen to bedrock, leading to the associated removal of resistive stresses at the ice front (Willis et al., 2018). Rapid ice flow initiates a set of internal feedbacks to further increase ice velocity, including strain softening of the ice itself, shear heating that produces meltwater capable of reducing the effective normal stress of the ice and hence its friction against the bed, and potential infiltration of this water into the bed material, increasing its deformability (Sevestre and Benn, 2015; Willis et al., 2018, and references therein). With no direct data on subglacial conditions prior to or during the surge, the exact processes involved remain difficult to determine. We may, however, monitor surface ice velocities to examine the ongoing changes in ice kinematics.

Optical satellite imagery from Vavilov Ice Cap is available only for summer months (March to September) due to darkness during the high-latitude boreal winter. We use GIV to derive a 100 m resolution ice velocity map of a 365 km² area of the western flank of the glacier using all Sentinel-2 imagery from 2016 to 2020. Figure 8a and b present two average yearly velocity maps for the apex of the surge in 2016 and in 2019. Figure 8d and e presents time series of monthly velocities over the period from March 2016 to March 2020 at the locations shown in Fig. 8c.

Velocities of the centreline points converge over the time period considered: although the velocities near the ice front decrease from the 2016 peak (red, orange, and green circles), velocities of regions most distant from the coast show a steady increase (purple points). The central portion of this newly formed outlet glacier shows distinct late-summer accelerations in both 2018 and 2019, reaching around double its spring and early summer rates and rapidly decaying (Fig. 7d). Within the newly formed western frontal lobe, extruded beyond the prior grounding line, flow has concentrated into a single branch with well-developed shear margins separating a central region with rapid ice flow from slow-moving lateral portions of the glacier (Zheng et al., 2019b).

Extraction of high-resolution ice velocities in this region using GIV confirms the findings of Willis et al. (2018) and Zheng et al. (2019b) that the western portion of Vavilov has entered into a new fast-flow regime. The late summer velocity peaks in both 2018 and 2019 may shed some light on the driving forces behind this acceleration if associated changes in climatic, ice surface, or ice basal conditions are identified. Ongoing monitoring will help to determine whether a similar peak occurs in subsequent years, and this can be performed in near real time using GIV.

We compare our GIV-derived results against a velocity map of the front of the western outlet glacier generated by Zheng et al. (2019b) using CARST (Zheng et al., 2019a). Zheng et al. (2019b) generated their velocity map based on a single Landsat 8 pair dated 6 and 22 May 2017. We compared the ice-surface velocity magnitude calculated from this pair to the May 2017 average velocity map generated from Sentinel-2 imagery using GIV through the approach described above. We georeferenced the two velocity maps using the glacier margins and other notable features. The difference map (Fig. 9a) displays the highest amplitude anomalies along the margins of the central high-velocity band. Differences between the GIV- and CARST-derived velocity maps are normally distributed, with a mean difference of −16 m yr⁻¹ (Fig. 9c). This mean difference is ≤ 1 % of the speed across the majority of the glacier surface (Fig. 9b). In this region of the glacier surface, the annual variability in ice-surface velocities is on the order of several hundred metres per year (Fig. 8d and e), and this difference may result from the slightly different dates covered or differing image resolutions (10 m for Sentinel-2 compared to 15–30 m for Landsat). The high-magnitude difference bands on either side of the fast-moving central region may also result in whole or in part from georeferencing errors in GIV, in CARST, or in our work to georeference these two velocity maps to one another.

3.4 Ice velocity of a small tropical glacier: Chimborazo

Many tropical glaciers have limited to no ice-flow data from direct field measurements (Thompson et al., 2011). These are important water sources to millions of people (Bury et al., 2011; Chevallier et al., 2011; La Frenierre and Mark, 2017). Vergara et al. (2007) estimated the economic cost of glacier retreat on water use to be in the hundreds of millions of US dollars and the impact on Peru's electrical utility to be ∼ 1.5 billion. High-resolution estimates of ice velocity provide information on glacier state and can contribute to practical decision-making in the tropical Andes.

Chimborazo is a 6268 m high stratovolcano in Ecuador covered with 17 glaciers. On Chimborazo's north-eastern flank, glacier meltwater drives nearly all of the discharge variability, and the disappearance of the prominent Reschreiter Glacier could decrease the discharge of the watershed's outlet stream by up to 50 % (Saberi et al., 2019). Due to its high elevation and steep slopes that are unstable in regions of recent ice retreat, the glaciers on Chimborazo are difficult to survey (Saberi et al., 2019). No field measurements of glacier surface velocity have been conducted.

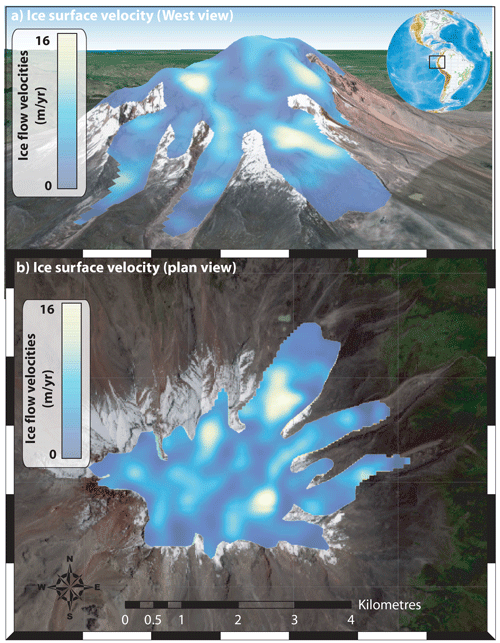
Figure 10 Ice-surface-velocity map for the Chimborazo glaciers calculated with GIV. Imagery © Google Earth and Sentinel-2.

Chimborazo poses challenges to feature-tracking-based ice velocimetry as its glaciers are small, regularly feature-poor or snow covered, very slow moving, and cloud covered for large parts of the year. The velocity limitations are mitigated by using only images with large temporal separation (acquisition dates more than 6 months apart). GIV is also well suited for extracting velocities from partially clouded imagery. We run GIV on the full Sentinel-2 dataset, which is comprised of 91 individual partially or fully cloud-free images. These were cropped to Chimborazo, resulting in 3062 image pairs separated by at least 6 months. Resultant ice velocities for each pair were corrected for the mean displacement of a stable, non-glaciated region surrounding the glaciers. Results are shown in Fig. 10.

Figure 11 Main graphical user interface for GIV showing the main input fields. This interface may either be run through MATLAB or as an independent desktop app with no licensing requirements.

4 Discussion and conclusions

These four examples underline GIV's flexibility, ease of use, and ability to rapidly process large datasets for calculating ice velocities in a range of environments. Most regular laptop and desktop computers now include at least four cores, which GIV uses to speed up calculations by a factor of 2 or more (Fig. 3). This makes velocity-field calculations with hundreds to tens of thousands of image pairs practical on regular computers. The inclusion of “temporal oversampling” allows much larger datasets to be generated than via simple consecutive image comparison; a dataset of 100 images may in fact include several thousand usable image pairs. We combine methodological advances in feature tracking and image processing from both geoscience and engineering toolboxes and develop new filtering techniques to improve the quality of the final surface-velocity maps. GIV provides a rapid and easy-to-use interface (shown in Fig. 11) and a user manual and may also be of use to communities who would not generally be involved with glacier remote sensing (Van Wyk de Vries, 2021a, b).

GIV is easily learned and is not computationally time-consuming, and the results derived with it are easy to reproduce. GIV allows users to modify image-processing and feature-tracking parameters based on their expert knowledge of particular glaciers without the need for specific computational knowledge. GIV may be run either directly through MATLAB functions, through a MATLAB graphical user interface (Van Wyk de Vries, 2021a), or as an independent desktop app that may be run with no MATLAB license (Van Wyk de Vries, 2021b). GIV has been tested and successfully run on Windows, Mac, and Linux operating systems.

In summary, GIV is a versatile, GUI-based, and fully parallelized toolbox that enables the rapid calculation of glacier velocity fields from satellite imagery. GIV builds upon recent improvements in optical satellite imagery availability and resolution to extract high temporal and high spatial resolution velocity maps, and it uses novel and pre-existing filters to optimize the quality of these velocity maps. GIV has been successfully tested on a wide range of environments, including small valley glaciers (Glacier d'Argentière, France), tropical glaciers (Volcán Chimborazo, Ecuador), and large outlet glaciers (Glaciar Perito Moreno, Argentina, and outflow from Vavilov Ice Cap, Russia). We show that ice velocity datasets are versatile and may be used to complement field campaigns and study the dynamics of large and small glaciers. Source code and pre-compiled binary executables for GIV are available from Van Wyk de Vries (2021a) and Van Wyk de Vries (2021b).