Use of Sentinel-1 radar observations to evaluate snowmelt dynamics in alpine regions

Knowing the timing and the evolution of the snow melting process is very important, since it allows the prediction of (i) the snowmelt onset, (ii) the snow gliding and wet-snow avalanches, (iii) the release of snow contaminants, and (iv) the runoff onset. The snowmelt can be monitored by jointly measuring snowpack parameters such as the snow water equivalent (SWE) or the amount of free liquid water content (LWC). However, continuous measurements of SWE and LWC are rare and difficult to obtain. On the other hand, active microwave sensors such as the synthetic aperture radar (SAR) mounted on board satellites are highly sensitive to LWC of the snowpack and can provide spatially distributed information with a high resolution. Moreover, with the introduction of Sentinel-1, SAR images are regularly acquired every 6 d over several places in the world. In this paper we analyze the correlation between the multitemporal SAR backscattering and the snowmelt dynamics. We compared Sentinel-1 backscattering with snow properties derived from in situ observations and process-based snow modeling simulations for five alpine test sites in Italy, Germany and Switzerland considering 2 hydrological years. We found that the multitemporal SAR measurements allow the identification of the three melting phases that characterize the melting process, i.e., moistening, ripening and runoff. In particular, we found that the C-band SAR backscattering decreases as soon as the snow starts containing water and that the backscattering increases as soon as SWE starts decreasing, which corresponds to the release of meltwater from the snowpack. We discuss the possible reasons of this increase, which are not directly correlated to the SWE decrease but to the different snow conditions, which change the backscattering mechanisms. Finally, we show a spatially distributed application of the identification of the runoff onset from SAR images for a mountain catchment, i.e., the Zugspitze catchment in Germany. Results allow us to better understand the spatial and temporal evolution of melting dynamics in mountain regions. The presented investigation could have relevant applications for monitoring and predicting the snowmelt progress over large regions.

1 Introduction

Seasonal snowpack is one of the most important water resources present in nature. It stores water during the winter and releases it in spring during the melt. In mountain regions, snow storage is essential for the freshwater supply of the lowlands, making the mountains the water towers of the downstream regions (Viviroli and Weingartner, 2004). In fact, the temporally delayed release of the water from the head watersheds to the forelands is essential for a large number of human activities such as agriculture irrigation, drinking water supply and hydropower production (Beniston et al., 2018). In particular, in the Alps, discharges in May and June are largely dictated by snowmelt, while from July to September they are influenced by glacier melt (Wehren et al., 2010) and liquid precipitation. On the other hand, wet snow may contribute to natural disasters such as wet-snow avalanches (Bellaire et al., 2017) or wet-snow gliding (Fromm et al., 2018). Moreover, in case of accumulated contaminant release from a snowpack, initial runoff meltwater can be highly enriched and is able to cause severe impact on the water quality (Hürkamp et al., 2017). In this context, knowing the temporal and spatial evolution of the snow melting process is very important for a proactive management of the water resources and for hazard mitigation.

The melt period can be generally separated in three phases (Dingman, 2015): (i) moistening, (ii) ripening and (iii) runoff. The moistening is the initial phase of the snowmelt. The air temperature and solar radiation increase, and due to heat exchanges and/or rain the superficial layers of the snowpack start melting. The ripening phase begins when the maximum retention capacity of the pores is exceeded. The wetting front penetrates through the snowpack, driven by repeated cycles of melting and refreezing, but the meltwater is not yet released. During this phase, the snowpack becomes isothermal, and when no more liquid water can be retained, the runoff phase starts. The snowmelt process is a nonlinear process affected by the strong variability of both the snowpack characteristics and the meteorological forcings that affect the snow. In order to obtain useful information about the progression of the melting process, noninvasive techniques that allow performing multiple measurements at the same location should be exploited. For this purpose, measurements of meteorological variables such as air temperature, snow temperature, relative humidity, wind speed, precipitation and solar radiation are usually employed to extract information on snowmelt dynamics (Kinar and Pomeroy, 2015). However, the most significant state variables to properly identify the three melting phases are the snow water equivalent (SWE), i.e. the total mass of liquid and solid water stored in the form of snow; and the liquid water content (LWC), i.e. the mass of liquid water inside the snowpack. An increase in LWC in time indicates that a moistening process is ongoing. The downward penetration of the water front into the snowpack leads first to a partial and later to a complete isothermal state. This leads to the generation of water runoff and consequently to a significant decrease in SWE.

Continuous measurements of SWE and LWC are therefore essential to monitor the snowpack melting dynamics. So far, the most common method to manually measure SWE is using snow sampling tubes, while the most spread techniques for automatic SWE measurement include snow pillows and snow scales (Kinar and Pomeroy, 2015). The installation and the maintenance of these kinds of measurements are very costly and a relatively limited number of continuous measurements of SWE are available in the Alps. Direct measurements of LWC are usually performed through empirical estimations (e.g., the hand test) or indirect assessments based on snow temperature. Recently, some promising systems that exploit the dielectric properties of the snow in the microwave region of the electromagnetic (EM) spectrum have been presented to allow the continuous and nondestructive measuring of LWC. In particular, three systems have demonstrated to be effective and robust in operational conditions: (i) the snowpack analyzer (SPA) (Stähli et al., 2004), (ii) the snow sense (Koch et al., 2014) based on GPS signals, and (iii) the upward-looking ground-penetrating radar (upGPR) (Schmid et al., 2014). All of them are commercial systems buried under the snowpack and rely on different methods for the dielectric constant estimation. Interestingly, these EM devices can be used to measure the SWE as well. However, all these ground-based measurements are limited in application to a single point; require calibration to relate the dielectric constant to volumetric snow LWC; and some of them are expensive, power intensive and laborious to install and maintain. These limitations complicate the possibility to monitor and understand the meltwater runoff and the snow stability considering also the spatial variability of the snowmelt dynamics.

To mitigate these limitations, energy-based, multilayer physically based snow models can simulate SWE and LWC at high spatial and temporal resolution (Essery et al., 2013). Such kinds of models account for shading, shortwave and longwave radiation, and turbulent fluxes of sensible and latent heat (Mott et al., 2011) but can differ in the way they parametrize snow metamorphism, grain size evolution, snow layering and liquid water percolation (Wever et al., 2014). They can range from very detailed approaches with a Lagrangian representation of snow layers such as avalanche-forecasting models like CROCUS (Brun et al., 1992) or SNOWPACK/ALPINE3D (Bartelt and Lehning, 2002; Lehning et al., 2006) to more simplified approaches such as the ones of hydrologically oriented Eulerian models like AMUNDSEN (Strasser et al., 2011) or GEOtop (Endrizzi et al., 2014). Therefore, snow models can provide detailed information about the snow properties starting from observed meteorological conditions, which can be reliably acquired especially at the plot scale. However, model performances are affected by uncertainties and errors related to model structure (Avanzi et al., 2016), meteorological forcing (Raleigh et al., 2015) and model parametrizations (Engel et al., 2017; Günther et al., 2019). Therefore, there is the need of snow observations with high temporal and spatial resolution, distributed over a large area and systematically acquired.

In the past years, synthetic aperture radar (SAR) was shown to be a valid tool to identify the wet snow, i.e., snow that contains a given amount of free liquid water (Nagler and Rott, 2000; Dong, 2018). In fact, SAR measurements are highly sensitive to the liquid water in the snowpack, and the increase in the LWC causes a high dielectric loss that increases the absorption coefficient generating backscattered signal with low intensity (Long and Ulaby, 2015). This physical principle has been exploited for the generation of wet-snow maps by the bitemporal algorithm proposed by Nagler and Rott (2000) and further improved in Nagler et al. (2016). However, the increase in the liquid water content explains only partially the decrease in the backscattering coefficient. Indeed, as pointed out in Shi and Dozier (1995) and Baghdadi et al. (2000), the relationship between the coefficient of backscattering and the snow wetness can cause an increment of the backscattering value depending on the conditions of the snow roughness, snow density, snow layering, snow grain size and local incidence angle. This large number of unknowns, upon which the SAR backscattering is dependent, defines a complex multiparametric problem that is difficult or even impossible to solve without introducing some simplification assumptions. So, even though some works have been presented that try to extract the LWC using C-band SAR images (Shi and Dozier, 1995; Longepe et al., 2009), to the best of our knowledge there are no attempts to use the SAR as source of information for describing the multitemporal evolution of the snow melting process. Progress has been hampered by (i) the lack of ground truth information, (ii) the relatively high number of sources of uncertainty of the SAR signal, and (iii) the difficulty in accessing SAR data in the past. This has changed since 2014 with the introduction of the Sentinel-1 (S-1) mission from the European Space Agency (ESA) and the European Commission (EC) guaranteeing the availability of C-band SAR images free of charge. Specifically, S-1 is a constellation made up of two near-polar sun-synchronous satellites that acquire images early in the morning and late in the afternoon, with a revisit time of 6 d at the Equator. Moreover, as discussed before, an increasing number of data on relevant snow parameters related to the snowmelt are collected by operational systems (e.g., by SPA) or derived by physically based snow models. The information on SWE and LWC provided by independent sources opens new opportunities for better understanding the relationship between the snowpack properties during the melting phase and the multitemporal SAR backscattering.

The aim of this work is to evaluate the information that S-1 can provide on monitoring the snowmelt dynamics. In particular, we provide the theoretical EM background for understanding the impact on the multitemporal SAR backscattering of a melting snowpack. Then, we analyze the relationship between the multitemporal SAR signal acquired from S-1 and in situ measurements of LWC and SWE in the Alps. Given the limited number of point-related continuous SWE and LWC measurements available in the test area, we made use of the physically based model SNOWPACK to simulate the snow properties in other locations where only meteorological data and snow depth were available. This allowed us to define five test sites at different altitudes in the Alps, where the interactions of S-1 backscattering with the snowpack were studied in detail during two melting seasons. On the basis of the outcomes of the study, we propose an interpretation scheme to be applied to multitemporal dual polarization C-band SAR data in order to identify the different snow melting phases of moistening, ripening and runoff. Finally, we demonstrate the effectiveness of the proposed approach in a real application scenario to provide a spatially distributed information about the melting phases of the snowpack in alpine terrain, which can be used for monitoring and predicting the snowmelt progress over large regions.

2 Background

In this section we report the theoretical background on which this work is based. First, the snow melting process is explained from a physical point of view, and the different phases are identified considering the information of LWC and SWE. Then, the response of the SAR backscattering to the wet snow is described in detail.

2.1 Snow melting process

Figure 1 illustrates the snow cover development during the melting season considering the snow status in the morning and in the afternoon, when the S-1 descending and ascending data are acquired respectively. Hypothetical values of LWC and SWE are reported on the right side of the figure. In general, the liquid water is introduced in the snow by rain and/or melt due to heat exchange and the incoming flux of shortwave radiation flux, which varies with slope, aspect and elevation. In both cases, the snowpack starts melting at the surface (Techel and Pielmeier, 2011). This superficial moistening phase can be identified by comparing observations from the coldest and warmest period of the day; i.e., a diurnal cycle is visible. Interestingly, the SAR acquisitions are approximately acquired around these two periods. The liquid water released or absorbed from the superficial layers gets in contact with the subfreezing snow present underneath and freezes. This releases latent heat that causes the snowpack to warm up, starting the process of snow ripening. Repeated cycles of partial melting during the day and refreezing during the night induce the development of the wetting front into the snow. This is generally not uniform, since infiltrations usually start through isolated “flow fingers” which enlarge into meltwater channels due to the passing of time. Therefore, the ripening of the snowpack may be different year by year or considering different areas. In fact, climatic factors or snowpack stratifications may induce different behaviors. At the point of full water saturation, the snow layer cannot retain any more liquid water. Further absorption of energy produces water output, which, depending on soil properties, ice and water content, could infiltrate the soil or appear as surface runoff (DeWalle and Rango, 2008). The runoff phase is characterized by a significant decrease in SWE.

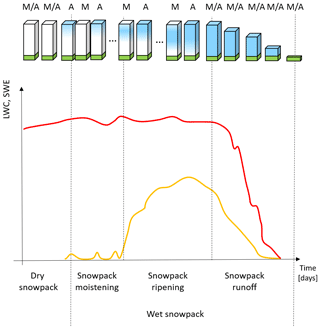
Figure 1 Example of transitions in snow status during the melting season obtained by sampling the snow in the morning (M), when the S-1 descending observations are taken, and in the evening (A), when the S-1 ascending data are taken. The upper part of the figure illustrates the simplified temporal transportation of the free liquid water (blue area) in the dry snowpack (white area). The lower part of the figure illustrates the respective temporal evolution of LWC (yellow line) and SWE (red line). Specifically, by starting from a dry situation, the liquid water is introduced into the snowpack by either a rain event or the melt due to the incoming flux of shortwave radiation. In this moistening phase the LWC (yellow line) varies with a diurnal cycle. Repeated cycles of partial melting and refreezing conduct the snowpack to the isothermal state. During the ripening period, a combination of different situations can occur depending on the weather conditions, but an increasing trend of the LWC is visible. Once the snowpack is isothermal and it cannot retain water anymore, it starts to produce water output until it melts totally. This last phase starts with a significant decrease in the SWE (red line).

During the melting, the presence of liquid water inside the snowpack directly affects the grain size, the grain shape and the density of the pack (Pomeroy and Brun, 2001). Indeed, during the melt process the snow undergoes to a rapid metamorphism that leads to a growing and a rounding of the grains linked to an increase in the snow density. Moreover, it is important to underline that during the melt season a general increase in the roughness of the snow surface is observed (Fassnacht et al., 2009) due to localized melting pattern (i.e., flow fingers) and rain-on-snow events.

2.2 SAR backscattering response to wet snow

From an EM point of view, the snowpack is an inhomogeneous medium composed of scattering elements with different sizes, shapes, orientations and permittivity values. The backscattering σ⁰ produced by an EM wave generated by SAR over such a medium can be modeled as an incoherent sum of three contributions (Shi and Dozier, 1995; Long and Ulaby, 2015): the surface scattering produced at the air–snow interface, ${\mathit{\sigma }}_{\sup }^{\mathrm{0}}$; the surface scattering produced at the snow–ground interface attenuated by the snowpack, ${\mathit{\sigma }}_{\mathrm{grd}}^{\mathrm{0}}$; and the volumetric scattering of the snowpack, ${\mathit{\sigma }}_{\mathrm{vol}}^{\mathrm{0}}$. The intensity of these contributions depends on parameters related to (i) the sensors, i.e., frequency, local incidence angle (LIA) and polarization; (ii) the snowpack properties, i.e., liquid water content, density (DS), ice particle size and shape (GS), and surface roughness (RS), which is usually described by the standard deviation of the height and the correlation length of the surface; and (iii) the ground properties. In this paper we focus on the use of the C-band SAR mounted on board S-1, and therefore all the parameters related to the sensor are known. Nonetheless, deriving the theoretical behavior of the time series of σ⁰ for a given LIA for 1 hydrological year is complex. Indeed, the relationship between the backscattering and the snow parameters forms a nonlinear system of equations. In the following we identify the main scattering mechanisms isolating the contribution of each parameter to the total backscattering.

During the accumulation period, dry snow is almost transparent for the C band, and the radar echo can penetrate the snow for several meters. In this situation, the main scattering source is the snow–ground interface (see Fig. 2), and the backscattering is almost insensitive to different snow parameters (Rott and Mätzler, 1987; Shi and Dozier, 1993). During the melting period, the increase in the free liquid water inside the snowpack causes high dielectric losses, which increase the absorption coefficient. By considering a sufficiently thick snowpack, this leads to a rapid decrease in ${\mathit{\sigma }}_{\mathrm{grd}}^{\mathrm{0}}$, which can then be neglected. By assuming all the parameters but the LWC to be constant, the increase in LWC causes the volume scattering to decrease and the backscattering becomes sensitive to surface roughness (Shi and Dozier, 1995). When the surface is smooth, for example, according to the Fraunhofer criterion (Long and Ulaby, 2015), volume scattering dominates and therefore the increase in LWC results in a decrease in the total backscattering, whereas when the surface is rough the surface scattering dominates; thus with the increase in LWC the total backscattering tends to increase. The amount of wetness from which the surface scattering becomes predominant depends mainly on the surface roughness and LIA and may vary from about 1 % to 6 % of the total volume (Magagi and Bernier, 2003). However, other parameters play a role in this mechanism: by assuming all the parameters but the snow density to be constant, the volume scattering decreases as the snow density increases, if all the other parameters are kept fixed. In contrast, the grain size increases the volume scattering. Finally, it is worth stressing the fact that the response to the wet snow becomes more complex in case of the snowpack in forest (Koskinen et al., 2010). In this case the total backscattering σ⁰ is also a function of the forest stem volume. This can be estimated and taken into account; nonetheless in this work we focus on the identification of the snow melting phase in open areas.

Figure 2 Main SAR backscattering mechanisms in presence of dry and wet snow at the C band. The dry snow is almost transparent, and the radar echo can penetrate the snow for several meters. The presence of LWC causes high dielectric loss, which increases the absorption coefficient.

The main scattering mechanisms and their influence on the backscattering, as studied in the literature, are reported in Table 1. Even though the table reports the main backscattering mechanisms of the different snow conditions during the melting process, the complete multitemporal behavior that characterizes the three phases of moistening, ripening and runoff has not yet been studied. In particular, from an EM modeling point of view or real-data analysis, the implications of the wet-snow metamorphism – i.e., increase in LWC, density, snow grain size and superficial roughness – remain mainly unsolved. Indeed, state-of-the-art radiative transfer (RT) models, particularly designed for studying the snow melting process, such as Shi and Dozier (1995), Nagler and Rott (2000), and Magagi and Bernier (2003), are not able to model the microstructure scattering interactions, whereas RT models that take into account the microstructure interactions, such as the models developed in SMRT (Picard et al., 2018) or MEMLS3&a (Proksch et al., 2015), are not able to model the contribution from the superficial roughness and have never been specifically tested for the characterization of the melting phases. Therefore, without further research and validation activities, this invalidates the possibility of using state-of-the-art RT models to better understand the multitemporal EM mechanisms during the snowmelt at the C band (e.g., Veyssière et al., 2018, found a significant deviation between observations and simulations with MEMLS3&a during the melting period).

Table 1 Simplified SAR backscattering response to wet snow divided in volumetric, ${\mathit{\sigma }}_{\mathrm{vol}}^{\mathrm{0}}$, and surface backscattering, ${\mathit{\sigma }}_{\sup }^{\mathrm{0}}$, contributions. Considering a sufficiently thick snowpack the contribution of ${\mathit{\sigma }}_{\mathrm{grd}}^{\mathrm{0}}$ can be neglected.

In the following, as first attempt to fill this gap, we will consider the real time series of backscattering recorded by S-1 during 2 hydrological years in the proximity of five test sites where LWC and SWE were measured or simulated. The outcome of this study will be exploited to (i) understand if a characteristic relation can be recognized from the comparison between the multitemporal SAR signal and the melting phases and (ii) define some rules to automatically identify the beginning of each melting phase from the time series of σ⁰.

3 Dataset description

In this section, we present the experimental sites, and we describe the collected in situ data, the SNOWPACK setup and S-1 data.

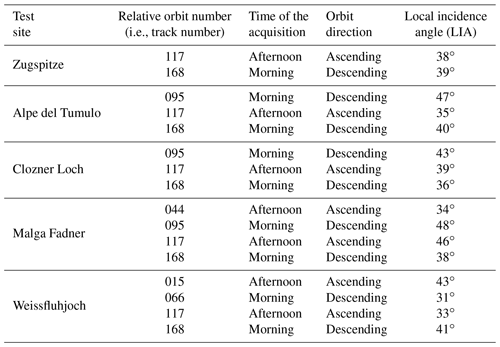
3.1 Test site description and in situ data

For ground truth and as input for the simulations with SNOWPACK, we consider five snow and meteorological weather stations with a different location in terms of place and altitude in the European Alps, equipped with different installed sensors. Among these, one is located in Bavaria (Germany), three in South Tyrol (Italy) and one in Graubünden (also known as Grisons, Switzerland). Specifically, the considered parameters are wind velocity (VW), wind direction (DW), air temperature (TA), relative humidity (RH), snow depth (HS), snow temperature at different depths (TS), surface temperature (TSS), soil temperature (TSG), incoming shortwave radiation (ISWR), incoming longwave radiation (ILWR), outgoing shortwave radiation (OSWR), snow water equivalent (SWE), snow density (DS), liquid water content (LWC) and ice content (IC). The considered data records started from 1 October 2016 in order to cover the two winter seasons 2016/2017 and 2017/2018. An overview of the location of the stations is presented in Fig. 3, and a summary with the available parameters is presented in Table 2.

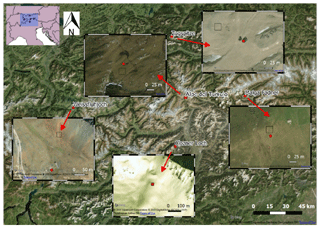
Figure 3 Overview map with the five stations used for the presented study (© 2019 Microsoft Corporation, © 2019 Digital Globe, © CNES (2019) Distribution Airbus DS). The red points indicate the exact location of the stations. The black squares indicate the S-1 footprints. The footprints were selected in order to minimize any possible interference of the EM wave with the homemade structures but maintaining a certain correlation with the in situ measurements. The panoramic images give an idea about the land cover type and the topography around the stations.

Table 2 Details of the meteorological and snow parameters measured at each station. Wind velocity (VW), wind direction (DW), air temperature (TA), relative humidity (RH), snow depth (HS), snow temperature at different depths (TS), surface temperature (TSS), soil temperature (TSG), incoming shortwave radiation (ISWR), incoming longwave radiation (ILWR), outgoing shortwave radiation (OSWR), snow water equivalent (SWE), snow density (DS), liquid water content (LWC) and ice content (IC).

3.1.1 Zugspitze (Werdenfelser Alps, Germany)

The station is located in the northern Calcareous Werdenfelser Alps, being part of the Zugspitze massif. It is part of the snow monitoring stations network of the Bavarian Avalanche Warning Service (Lawinenwarnzentrale Bayern) and located on a flat plateau at the southern slope of the Zugspitze summit (2962 m a.s.l.), the so-called Zugspitzplatt (1500–2700 m a.s.l.), which is surrounded by several summits in the north, south and west and drained by the Partnach river to the east. In addition to being a standard meteorological station, the site is equipped with a snow scale and a snow pack analyzer to record SWE, DS, LWC and IC. The SPA uses a time-domain reflectometer (TDR) at high frequencies and a low-frequency impedance analyzer. By exploiting different frequencies, the SPA is able to determine the volumetric ice, air, and water content as well as the density by measurement of the complex impedance of the snow layer. The EM pulse propagates along three 5 m long sensor bands, horizontally installed at 10, 30 and 50 cm above ground in 2016/2017. In 2017/2018 the heights of the bands were changed to 10, 20 and 30 cm due to a frequent failure of the uppermost sensor in the preceding years. This allows the measurement of the bulk properties of the snowpack rather than a point measurement as well as a tracking of the downward-penetrating water front inside the snowpack. Combined with information on the snow height bulk, LWC is determined. The SPA has not been calibrated for the test site, but it is used with standard setup parameters and an internal calibration by the manufacturer. This results in unreliable LWC values of about 2 %–3 % when the snowpack is dry. Moreover, given that no bulk information of LWC for the total thickness of the snowpack is provided by the SPA, we did not use the SPA LWC in this study. Snow height is recorded by an ultrasound sensor, installed at 6 m height. The sensors for the meteorological parameters are installed at a crossbar of the 6 m mast too, besides the wind sensor, which is at a 6.5 m height. The maximum snow height was 3.3 m during winter 2016/2017 and 3.9 m in January 2018. The area is continuously covered by snow between December and May each year. During the accumulation period, the station records showed that no significant snowmelt runoff at the snow base occurred at any time since 2012 (Hürkamp et al., 2019). During the observed winter seasons the mean monthly wind velocity exceeded 3 ms⁻¹ in the winter months; therefore wind drift could likely alter snow accumulation. The amount of mean annual precipitation is ∼2000 mm.

3.1.2 Alpe del Tumulo (South Tyrol, Italy)

The station is located on an alpine pasture in the north of Val Passiria. For this and the other South Tyrolean stations, the temperature sensor is installed at a 2.8 m height and the wind sensor at 5.5 m. The site is weakly windy, with mean monthly velocity usually around 2 ms⁻¹. The maximum snow height was around 1.5 m during winter 2016/2017 and around 2 m during the winter 2017/2018. No continuous measurements of LWC and SWE are available for this and the other South Tyrolean stations.

3.1.3 Clozner Loch (South Tyrol, Italy)

The station is located in Laurein (Lauregno, Alta Val di Non) on an almost flat site. The mean monthly wind velocity seldom exceeds 2 ms⁻¹. The snow height never exceeded 1 m during the winter 2016/2017, and the maximum height reached during the winter 2017/2018 was around 1.5 m.

3.1.4 Malga Fadner (South Tyrol, Italy)

The station is located on an alpine pasture in Ahrntal (Valle Aurina). The mean monthly wind velocity never exceeds 2 ms⁻¹. The maximum snow height was less than 1.5 m during winter 2016/2017 and around 2 m during the winter 2017/2018.

3.1.5 Weissfluhjoch (Graubünden, Switzerland)

The automatic weather station is located at Weissfluhjoch, Davos, Switzerland. It is maintained by the WSL Institute for Snow and Avalanche Research SLF. The data are regularly updated and made freely available (WSL Institute for Snow and Avalanche Research SLF, 2015). The wind sensor is installed at 5.5 m and the temperature sensor at 4.5 m. The site is quite windy, with mean monthly velocity usually around 2 ms⁻¹ or sometimes greater than this value. The maximum snow height was around 2 m during winter 2016/2017 and around 3 m during the winter 2017/2018. In this study, SWE GPS-derived measurements are used (Koch et al., 2019), which are also freely made available upon request.

3.2 SNOWPACK model setup

As described in the introduction, the proper identification of the melting phases requires a precise understanding of the evolution of LWC and SWE. However, these parameters are not always available for the selected test sites. For this reason, there is the need to set up snowpack simulations for obtaining the missing parameters. In this work we used the physically based model SNOWPACK, a one-dimensional (1-D) model developed by the WSL Institute for Snow and Avalanche Research SLF (Bartelt and Lehning, 2002). The model solves 1-D partial differential equations governing the mass, energy and momentum conservation. Heat transfer, water transport, vapor diffusion and mechanical deformation of a phase-changing snowpack are modeled assuming snow to be a three-component (ice, water and air) porous material. Meteorological data are used as input for the model. Required parameters are air temperature, relative humidity, wind velocity, incoming longwave radiation and/or outgoing shortwave radiation, incoming longwave radiation and/or surface temperature, precipitation and/or snow depth, and soil temperature. The data were taken or derived from the in situ measurements at the test sites. MeteoIO (Bavay and Egger, 2014) is used as a preprocessing tool to check erroneous data, fill the gaps and generate missing parameters. In the current case, the ground temperature is generated as a constant value assumed to be equal to the melting temperature if missing, and the incoming longwave radiation is calculated through an all-sky parametrization, which makes use of air temperature and humidity (Unsworth and Monteith, 1975; Dilley and O'brien, 1998). Fresh snowfall must be provided as an initial condition. Since direct snow precipitation measurements are not available, the amount of new snow is forced by subtracting the model snow depth from the measured snow depth. This difference is assumed to be fresh snow only if reliable humidity and temperature conditions are verified, using the approach proposed and validated by Mair et al. (2016) and implemented in the SNOWPACK model. This approach has been validated against snow pillow observations and proves to be more reliable compared to heated tipping-bucket rain gauges, which may underestimate solid precipitation up to 40 % (Sevruk et al., 2009). The energy exchanges on the snowpack surface are imposed either using a Neumann boundary condition (BC) – i.e. the energy fluxes are forced – or a Dirichlet BC – i.e., imposing the surface temperature, except during ablation when again a Neumann BC is imposed. Additionally, a Dirichlet BC is imposed at the ground interface. A neutral atmospheric surface layer using the Monin–Obukhov similarity theory is imposed. The used water transport model is the NIED scheme proposed by Hirashima et al. (2010). A typical time step of 15 min is used for the simulations.

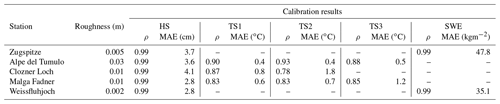
Since the SNOWPACK simulations are used in this work as reference data to be compared against the SAR backscattering, we calibrated the model considering the best agreement in the analyzed years 2016–2018 with in situ snow depth; snow temperatures at three different depths – TS1 (0 m from the ground), TS2 (0.2 m from the ground) and TS3 (0.5 m from the ground); and SWE, when available. The Pearson correlation coefficient (ρ) and the mean absolute error (MAE) have been computed for these variables. Roughness is used as a calibration parameter. The results are reported in Table 3.

Table 3 SNOWPACK calibration results for each test site. The Pearson correlation coefficient (ρ) and the mean absolute error (MAE) have been computed for snow depth (HS); snow temperatures at three different depths – TS1 (0 m from the ground), TS2 (0.2 m from the ground), and TS3 (0.5 m from the ground); and SWE, according to the availability of the in situ data.

Table 4 List of the Sentinel-1 acquisitions and their main characteristics over the five test sites.

3.3 Remote sensing observations

S-1 is a two-satellite constellation with a revisit time of 6 d with the same acquisition geometry and is able to acquire dual polarimetric C-band (central frequency of 5.405 GHz) SAR images with a nominal resolution of 2.7 m×22 m to 3.5 m×22 m in Interferometric Wide swath mode (IW). S-1 works in a preprogrammed way in order to build a consistent long-term data archive of images all around the world. IW acquisitions have a swath of about 250 km. This, together with the cycle length of the satellites of 175 orbits, allows the acquisition of more tracks over a given location at the middle latitudes such as the Alps. Therefore, in 6 d more than one acquisition may be available for the area of interest. Table 4 indicates the most relevant parameters related to the data acquisition for each of the selected locations. For the five test sites a total of about 1300 acquisitions were considered. The data used for the presented study are level-1 ground-range-detected data, consisting of focused SAR data that have been detected, multilooked and projected to ground range using an earth ellipsoid model by the data provider. The resulting products have approximately square spatial spacing of 10 m by 10 m. Phase information is lost for these data. These data can be downloaded free of charge from the Copernicus data hub (https://scihub.copernicus.eu/, last access: 5 March 2020). In order to correct the complex topographic terrain, typical of mountain regions, and to reduce the speckle noise that affects SAR acquisitions, a tailored preprocessing has been applied for all the analyzed data. Specifically, the preprocessing operations are performed using the tools included in SNAP (Sentinel Application Platform) version 6.0 and some custom tools developed in Python. In particular, the S-1 backscatter preprocessing operations are the following (S indicates the SNAP tool and C indicates the custom tool):

• application of the precise Sentinel orbit to the data (S),

• removal of the thermal noise present in the images (S),

• removal of the noise present at the border of the images (C),

• beta nought calibration (S),

• assembly of the S-1 tiles coming from the same track (S),

• coregistration of the multitemporal images (S),

• multitemporal filtering with a window size of 11 pixels by 11 pixels (C),

• gamma-MAP spatial filtering 3 pixels by 3 pixels (S),

• geocoding and sigma nought calibration (S), and

• masking of the layover and shadow by considering the local incidence angle (LIA) for each pixel (C).

It is worth noting that we use the multitemporal filter proposed by Quegan and Yu (2001). This filter, which is suited for long time series, allows a suppression of the speckle noise by preserving at the same time the geometrical detail. The final spatial resolution of the geocoded S-1 images is 20 m by 20 m.

4 Data analysis and proposed approach to the melting phases' identification from S-1

In this section, the time series of SWE, LWC and σ⁰ for the identification of the melting phases are compared. From this analysis and the background information described in Sect. 2, we present the general temporal evolution of the backscattering during the melting process. Finally, on the basis of this analysis we propose a set of simple rules for the derivation of the onsets of each snow melting phase.

4.1 Data analysis

Figure 4 shows the time series of the backscattering coefficient against the measured and/or modeled SWE and LWC for the five test sites during the hydrological years 2016/2017 (left column) and 2017/2018 (right column). Yellow, red and green areas highlight the moistening, ripening and runoff phases respectively. These phases have been identified from the SWE and LWC data according to Sect. 2.1. Specifically, the moistening phase onset is identified by looking at the liquid water content of the snowpack. We empirically established a threshold of 1 kg m⁻² that has to be satisfied for at least 2 consecutive days. In other words, a significant melting (and refreezing) cycle should be observed within 2 d. Among all the isolated moistening events, in this work we focus only on the moistening preceding a ripening phase. However, this does not mean that the SAR cannot detect isolated peaks of melting, if the acquisitions are performed simultaneously to those events. Regarding the ripening phase, we impose the rule to observe an increase in LWC exceeding 5 kg m⁻² and not decreasing to 0 kg m⁻² during the diurnal cycles. If the LWC returns to 0 kg m⁻² for a timing of at least 5 d, we assume that the ripening phase is interrupted. Otherwise, we assume that there is enough penetration of the waterfront into the snowpack to initiate the ripening. Finally, the runoff phase is identified when SWE starts decreasing from its maximum (after the ripening phase is activated). In the event we have both measured and modeled SWE available, we consider measured SWE as reference. The runoff phase ends when SWE has a value of 0 kg m⁻². The rules are shown in pseudocode in Algorithm 1.

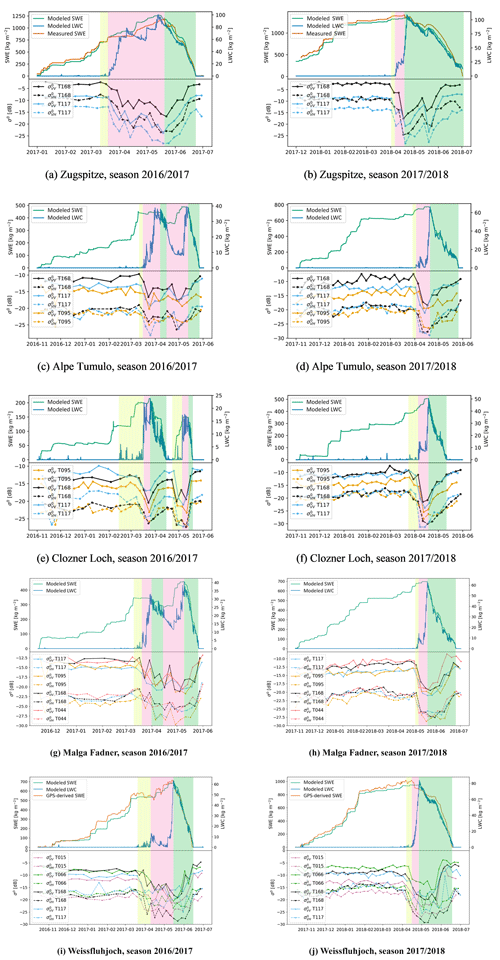
Figure 4 Temporal evolution of the coefficient of backscattering acquired over the five test sites compared to LWC and SWE measured in situ at the stations (when available) and modeled with SNOWPACK (contains modified Copernicus Sentinel data, 2016/2018, processed by Eurac Research). The three phases during the melting have been identified from the in situ/modeled data. The first phase of moistening is reported in light yellow, the ripening phase in light red and the runoff in light green. For all the test sites we found that the multitemporal SAR measurements confirm the identification of the three melting phases. In particular, we systematically found that the SAR backscattering decreases as soon the snow starts containing water and increases as soon as SWE starts decreasing, which corresponds to the release of meltwater from the snowpack.

In the following, for each of the five test sites, i.e., Zugspitze, Alpe del Tumulo, Clozner Loch, Malga Fadner and Weissfluhjoch, we will present the detailed comparison of LWC, SWE and the S-1 σ⁰ time series during the melting process. This will allow the derivation of important information about the possibility to identify the three melting phases in general. In the next section, the outcome of this comparison will be exploited to describe the characteristic behavior of the multitemporal SAR signal during the melting process.

4.1.1 Zugspitze

For this station, SWE was both measured and simulated, and LWC was simulated with SNOWPACK. The temporal evolution of SWE measured by the snow scale and the one simulated with SNOWPACK shows a good agreement. For this station, the tracks T168 (descending, morning) and T117 (ascending, afternoon) are available. The local incidence angle for the two tracks differs by about 1^∘. For the hydrological year 2016/2017 the backscattering remains almost constant during the accumulation phase until the beginning of the moistening phase (Fig. 4a). Here, as described in Sect. 2.2, the increase in the LWC is accompanied by a decrease in the backscattering from −8.5 and −12.7 to −14.3 and −20.0 dB for respectively VV and VH polarizations of the afternoon track T117 between 19 and 25 March 2017 and from −5.8 and −12.7 to −12.5 and −18.1 dB for respectively VV and VH of the morning track T168 between 27 March and 4 April. The difference in the dropping of the signal acquired by the morning and afternoon track is due to the diurnal melting and refreezing cycles. After this phase, the ripening phase began with oscillations of the backscattering coefficient which on average presented low values. As described in Sect. 2.2 the oscillations are due to the snowpack metamorphism, snow stratification and the meteorological conditions. Since the ripening phase is characterized by an increase in the LWC, the time series of the backscattering presents a decreasing trend. Interestingly, the minimum of σ⁰ is reached at the end of the ripening phase and the beginning of the runoff phase, i.e., 20 May 2017. The runoff is instead characterized by a monotonic increase in the backscattering until all snow is melted. This characteristic behavior can be interpreted as follows: when the considered snowpack reaches its saturation condition in terms of the LWC, snow density and internal structure, the backscattering recorded in the C band reaches its minimum value. These snowpack conditions seem to represent the isothermal condition before the release of meltwater, i.e., the end of the ripening phase. After the saturation point is reached, the monotonic increase in σ⁰ could be explained by a dominance of the superficial scattering that becomes more and more prominent due to a monotonic increase in the LWC per volume (see Sect. 2.2). This behavior continues until the snow disappears. This period corresponds to the runoff formation phase, when SWE starts decreasing. In Sect. 4.2 we will discuss a possible explanation of this behavior. Regarding the winter 2017/2018 similar observations were made, but here the snow ripening phase was limited to a very short period and the runoff started very early in mid-April due to strong insolation and high mean daily temperatures up to 5 ^∘C the days before. Interestingly, during the runoff phase, σ⁰ started increasing as expected, then it decreased due to a snow fall (probably wet) followed by a relatively colder period which lasted some days at the end of May 2018, and finally it increased again until the end of the snow season (Fig. 4b).

It is worth noting that the two polarizations acquired by S-1 provided coherent information. However, few cases in which there is a depolarization of the signal can be spotted during the ripening phase. Here the repeated cycles of melting and refreezing can generate ice layers (Kattelmann and Dozier, 1999), which affect the polarization in different ways.

4.1.2 Alpe del Tumulo

For this station, the information about the LWC and SWE was derived through SNOWPACK. The calibration of the model was performed in order to achieve a high agreement in terms of snow height and snow temperature (see Table 3). For this station, the tracks T168 (descending, morning), T117 (ascending, afternoon) and T095 (descending, morning) are available. The LIAs for the three tracks are 40, 35 and 47^∘, respectively.

A very short moistening phase can be identified in both years from the modeled LWC and SWE time series (Fig. 4c, d). These phases are well identified in the σ⁰ time series by a drop of the morning and afternoon signal. The situation of the runoff phase 2016/2017 looks similar to Zugspitze for the season 2017/2018: from the LWC and SWE time series two modes are visible, suggesting that the runoff was stopped by a cold period (with a new snowfall). This situation is reflected in the time series of the S-1 backscattering by the two characteristic U-shaped behaviors indicating that a first runoff started after the first minimum of σ⁰ and continued for some days following the monotonic increase in σ⁰, but then the process was stopped by a new wet snowfall that forced the backscattering to a new minimum. Finally, the runoff phase restarted, and the SAR signal increased again. However, the runoff phases identified from the SAR local minima seem to be anticipated by about 2 weeks with respect to the modeling results. Regarding the season 2017/2018, the runoff phase showed a more linear behavior which is represented by the characteristic shape of σ⁰ time series as the one identified in the Zugspitze test site. Finally, it is worth noting that the three tracks (T095 and T168, descending, and T117, ascending) acquired with different LIAs show very similar trends.

4.1.3 Clozner Loch

For this station, the information about the LWC and SWE was simulated with the SNOWPACK model. The calibration of the model was performed in order to achieve a high agreement in terms of snow height and snow temperature (see Table 3). The tracks T168 (descending, morning), T117 (ascending, afternoon) and T095 (descending, morning) are available for this station. The LIAs for the three tracks are 43, 36 and 39^∘, respectively.

The season 2016/2017 is characterized by two melting phases (Fig. 4e). In fact, the snow was completely melted in the first half of April with a new fresh snowfall at the end of the month. For this reason, we highlighted the moistening–ripening–runoff snowpack alteration sequence two different times. Interestingly, the time series of the backscattering seems to properly follow the two melting processes with two characteristic U-shaped behaviors. The melting process for the season 2017/2018 was more linear (Fig. 4f), and the σ⁰ time series of the three tracks provides coherent information with the one extracted by analyzing the time series of LWC and SWE.

4.1.4 Malga Fadner

For this station, the information about the LWC and SWE was derived through the SNOWPACK model. The calibration of the model was performed in order to achieve a high agreement in terms of snow height and snow temperature (see Table 3). Four tracks are available for this station: T168 (descending, morning), T117 (ascending, afternoon), T044 (ascending, afternoon) and T095 (descending, morning). The LIAs for the three tracks are 46, 48, 38 and 34^∘, respectively.

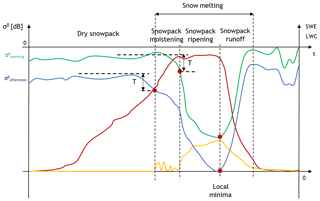
Figure 5 Schematic representation of the evolution of the backscattering coefficient acquired in the morning (green line) and in the afternoon (blue line) compared with LWC (yellow line) and SWE (red line) evolution. The offset between the morning and afternoon signals is due to the generally different local incidence angle of the ascending and descending acquisitions in mountainous regions. The three melting phases are identified from the LWC and SWE information. Correspondingly, the rules for the identification of each phase from the time series of σ⁰ are highlighted: a decrease of at least T (dB) from the mean value in dry snow conditions applied to the afternoon and morning signals identifies the moistening and ripening onsets respectively. The local minima of the signals indicate the runoff onset.

The trend of the melting process over the two seasons looks similar to Alpe del Tumulo. The season 2016/2017 is characterized by a consistent snowfall, which happened after an initial runoff phase of the snowpack. This together with a cold period stopped the process, which was resumed in May (Fig. 4g). The time series of the four tracks recorded by S-1 backscattering showed two characteristic U-shaped behaviors indicating that a first runoff started after the first minimum of σ⁰ and continued for some days following the monotonic increase in σ⁰, but then the process was stopped by a new wet snowfall that forced the backscattering again to the minimum. Nonetheless, the timings are different from the one identified with the modeled data of LWC and SWE. The strong depolarization may indicate a complex structure of the snowpack with different ice layers. The melting process for the season 2017/2018 was more linear, and the σ⁰ time series of the four tracks provides coherent information with the one extracted by analyzing the time series of LWC and SWE (Fig. 4e).

4.1.5 Weissfluhjoch

For this station, the information about the LWC and SWE was simulated with SNOWPACK; in addition, SWE GPS-derived measurements were available. The calibration of the model was performed in order to achieve a high agreement in terms of snow height and SWE (see Table 3). The tracks T168 (descending, morning), T117 (ascending, afternoon), T015 (ascending, afternoon) and T066 (descending, morning) are available for this station. The LIAs for the three tracks are 41, 33, 43 and 31^∘, respectively.

The season 2016/2017 is characterized by an initial moistening phase, followed by a ripening phase that was delayed by a cold period, when the LWC decreases almost to 0 (Fig. 4i). In the middle of May a runoff phase started. The backscattering followed the different phases as expected. The season 2017/2018 is more regular, with a monotonic increasing of LWC indicating a short moistening followed by a regular ripening and the runoff. In this case the measured SWE anticipated the runoff onset of about 1 week with respect to the modeled SWE, which seems more in accordance with the S-1 data. The backscattering shows a similar behavior of other previously discussed cases with the characteristic U-shaped signal except for the T066 that present several oscillations in the VH polarization.

4.2 Temporal evolution of the backscattering

From the comparison carried out in the previous section and by taking into account the main backscattering mechanisms described in Sect. 2.2, it is possible to derive and explain the temporal behavior of σ⁰ generated by a C-band SAR over a sufficiently deep snowpack located in an open space that presents a linear transition between the three melting phases. By analyzing the backscattering time series of the same pixel, the contribution of the LIA is always the same, making the values of the time series comparable. Figure 5 shows an illustrative evolution of σ⁰ for a complete hydrological year that summarizes both the state-of-the-art background and the observations done on real data. As described later, this conceptual time signature will allow us to derive a set of rules for the identification of the melting phases also in time series of backscattering never observed before or in independent datasets (e.g., Veyssière et al., 2018; Lievens et al., 2019).

Before the snow cover the terrain σ⁰ is influenced by the fluctuation of the soil moisture (Ulaby et al., 1996). Then, generally the first snow fall is wet or it covers relatively warm terrain, resulting in a wet snowpack. This generates low backscattering values in the SAR response. This situation, which in alpine environments usually lasts for short periods, ends either with a significant decrease in the temperature that brings the snowpack to a dry condition or with a complete melting of the snowpack. It is also possible that the soil freezes before the first snowfalls. In this case the coefficient of backscattering decreases and stabilizes around a given value not being affected by the soil moisture anymore.

As soon as the snowpack starts incorporating liquid water, the melting period starts. It can be divided into three important phases as described in Sect. 2.1, i.e., the moistening, the ripening and the runoff phases. The first phase is related to the initial moistening of the snowpack. As discussed previously, the liquid water is introduced in the snow by rain and/or melt due to temperature and the incoming flux of shortwave radiation. At the beginning of the process the value of LWC is low and therefore the SAR backscattering experiences a relevant decrease in its value since the volumetric scattering dominates the total backscattering. The drop of the signal is recognizable by imposing a given threshold T. During the moistening, the wetting front may be visible only during the afternoon and not in the morning since the snowpack is still subjected to the diurnal cycles of melting and refreezing. As soon as the wetting front has penetrated the superficial insulating layer of the snowpack, the wet snow becomes visible also in the SAR early morning acquisitions. Please note that the systematic offset between the morning and afternoon signals represents the generally different local incidence angle of the ascending and descending acquisitions in mountainous region. At this point the phase of snowpack ripening starts. In this phase, the wetting front keeps penetrating the snowpack conducting it to an isothermal condition. During the ripening phase, which is influenced by the weather and the snowpack conditions, σ⁰ varies according to the snow conditions but with an overall decreasing trend due to the increase in LWC.

We observed that the minimum of σ⁰ is reached at the end of the ripening phase and the beginning of the runoff phase for all the 10 time series observed (see Sect. 5). The runoff is instead characterized by a monotonic increase in the backscattering until all the snow is melted. To our knowledge, this characteristic behavior has never been observed in the literature before. Our interpretation is as follows: when the considered snowpack reaches its saturation condition in terms of LWC and snow structure, the backscattering recorded in the C band reaches its minimum value. This snowpack condition seems to correspond with the isothermal condition, i.e., the end of the ripening phase. After the saturation point is reached, the monotonic increase in σ⁰ could be explained by one or the combination of the following factors: (i) an increase in the superficial roughness; (ii) a change in the snow structure, i.e., increase in the density and increase in grain size; and (iii) at the end of the melting the presence of patchy snow creates a situation of mixed contribution inside the resolution cell of the SAR, and therefore a further increase in the total backscattering is recorded.

On the basis of this analysis, we propose here a simple set or rules to identify the snow melting phases on the basis of the multitemporal SAR signal. The start of the melting process can be identified by a decrease in the multitemporal SAR signal recorded in the afternoon of 2 dB or more with respect to the general winter trend. This threshold has been successfully used in Nagler et al. (2016) for detecting wet snow from S-1 images. As soon as the time series of morning backscattering also decreases by 2 dB or more, the ripening phase begins. This phase, characterized by several oscillations, ends when both the morning and afternoon σ⁰ values reach their local minimum. We propose the mean date among the local minima as the start of the runoff phase, which is characterized by a monotonic increase in the coefficient of backscattering. These rules are summarized in Algorithm 2. It is worth noting that the rules are not calibrated on the observations done in Sect. 4.1, but reflect the literature background.

In the next section we applied these simple sets of rules in order to identify the melting phases for each of the five considered test sites. Moreover, the same rules are used to identify the runoff onset for each SAR pixel in the topographically well defined catchment of the Zugspitzplatt obtaining a spatially distributed map of the runoff timing.

5 Application of the proposed approach to 1-D and 2-D cases

In this section, we present the results obtained for the snow melting phases' identification from the time series of backscattering recorded from S-1 over the five selected alpine test sites. The results are compared with the derivation of the melting phases considering the observed and modeled measurements of LWC and SWE. Finally, we present the result of the runoff onset identification in the two-dimensional (2-D) space of the original 20 m SAR images for the Zugspitze catchment.

5.1 Identification of snow phases from Sentinel-1 in the five alpine test sites

Table 5 reports the comparison of the onset dates for the melting phases for each of the considered test sites. The phases were identified from the backscattering time series according to the rules expressed in the previous section. If more than two acquisitions, i.e., ascending and descending, are available for one test site, the first date representing the onset for the moistening and ripening phase among all available tracks is selected. The runoff onset is identified as the mean date among the local minima. These rules can be automatically applied without any human supervision.

Table 5 Onset times for the melt phases identified in the five test sites using the LWC and SWE (reference) and Sentinel-1 with the method proposed in the previous section.

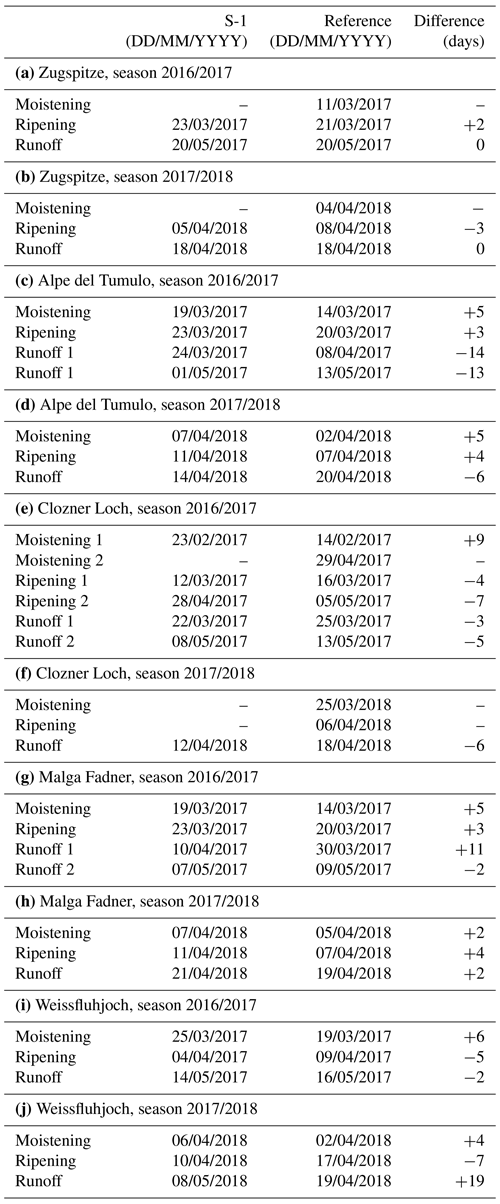
On average, the moistening phase was identified with a rms error of 6.5 d. For the ripening phase the SAR time series allowed the identification with 4.5 d of rms error. Finally, the runoff was identified with a rms of 8 d (4 d rms error without considering Alpe del Tumulo for the years 2016/2017 and Weissfluhjoch for the years 2017/2018 where the runoff process were articulated). Considering the repetition frequency provided by S-1 and the possible uncertainty of the SNOWPACK modeling (Wever et al., 2015), the produced results demonstrate the effectiveness of using the SAR for characterizing the snowmelt process.

In some cases, the proposed rules could not be applied and the onset could not be identified from the S-1 data. This is mainly due to the short melting or ripening periods that occurred during some years in the selected test sites. In these cases, the 6 d repetitions provided by S-1 are not adequate to sample this situation and it happens that the moistening phase is captured by the morning acquisition before the afternoon acquisition (i.e., Zugspitze season 2016/2017 and 2017/2018, Clozner Loch season 2016/2017 second moistening phase and 2017/2018) or the first signal drop is reached at the same time of the local minima (i.e., Clozner Loch season 2017/2018). One can also notice that, for the first runoff identified in the season 2016/2017 for Malga Fadner, the proposed rules failed since for T168 no local minimum was clearly identified (Fig. 4g).

5.2 Extension to a 2-D analysis of the runoff onset: the Zugspitzplatt catchment

In this section we evaluate how the identification of the runoff onset is performed at a catchment scale. In particular, we considered the multitemporal behavior of each pixel acquired by S-1 over the Zugspitzplatt during the hydrological year 2017/2018. The plateau (1500–2700 m a.s.l.) on the southern slope of the Zugspitze summit (2962 m a.s.l.) is well suited for this application scenario, since it is proven that all surface and ground water is drained to the Reintal valley in the east by the Partnach river (Rappl et al., 2010). With regard to a potential transport of contaminants that are stored in the snowpack and released with the first snowmelt (Hürkamp, Tafelmeier and Tschiersch, 2017), the knowledge of the runoff onset can provide important information for the scope of action concerning the management of countermeasures or planning actions to mitigate potential soil and water contamination.

As illustrated in the previous section, the runoff onset was identified by locating the minimum of the backscattering time series. In order to increase the robustness of the detection, we considered the mean of the backscattering of the close pixel presenting the same characteristics in terms of altitude, exposition and slopes. In particular, belts of 100 m were considered for the altitude. Slope was divided in three classes between 0 and 20, 20 and 40, and 40 and 60^∘. Four aspect classes were considered, i.e. north, east, south and west. Finally, a local incidence angle ranging from 25 to 65^∘ was divided in eight classes with a 5^∘ span, avoiding layover and shadow effects. All the homogeneous classes generated by the different combinations were aggregated. The forested areas were masked using the Copernicus tree cover density map (https://land.copernicus.eu/pan-european/high-resolution-layers/forests/tree-cover-density/status-maps/2015, last access: 5 March 2020). Moreover, since in this illustrative example we are interested in the main runoff contribution, the proposed algorithm is looking for local minima of the backscattering time series only after January 2018. This is to exclude isolated wet snowfalls or complete early melting events typical of the beginning of the seasons.

Figure 6 shows the runoff onset identified by the proposed method. As one can see, the regions at lower altitude started the runoff phase before the areas at higher altitude. The same consideration can be performed for the north-exposed pixels versus the south-exposed ones. Interestingly, the last areas that start the runoff phase in the catchment are the glacierized areas (Northern and Southern Schneeferner glacier) and north-facing slope areas. A selection of the backscattering time series is reported at the bottom of the Fig. 6 for six points selected at different altitudes. As one can see, the characteristic behavior described in Sect. 4.2 is always visible in the real data even though they were not analyzed before.

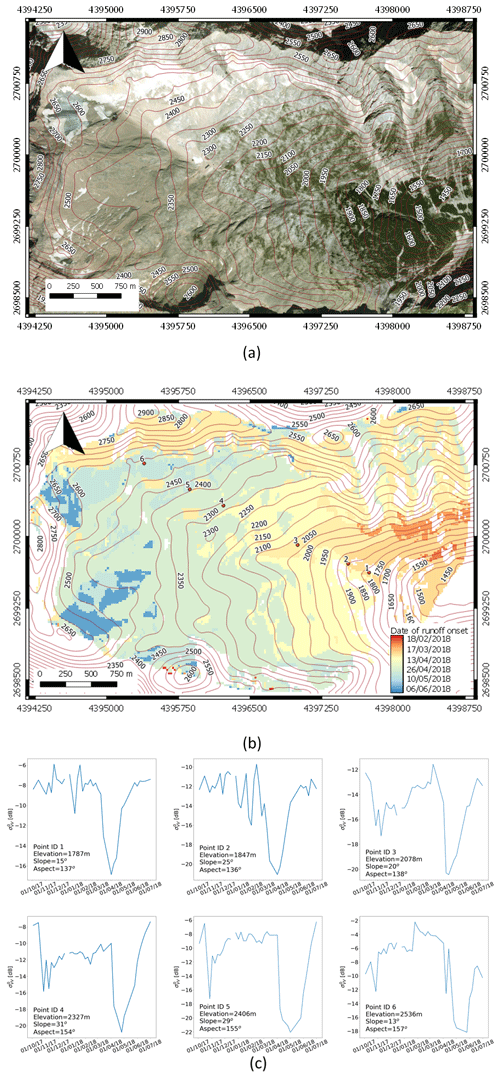
Figure 6 Runoff onset for the Zugspitzplatt catchment. (a) Test site presentation (© 2019 Microsoft Corporation, © 2019 Digital Globe, © CNES (2019) Distribution Airbus DS). (b) Map of the runoff onset (contains modified Copernicus Sentinel data, 2018, processed by Eurac Research). The runoff started at lower altitude and at the south-exposed slopes. The last areas to have the runoff in the catchment are the high-altitude, the north-exposed and glacierized areas. (c) The multitemporal backscattering time series extracted from track T117 for the selected points identified in (b). All the time series present the characteristic U-shaped pattern.

6 Discussion

Snow monitoring and/or prediction systems are typically based on real-time snow ground observations (e.g., WSL Swiss monitoring system, https://www.slf.ch/en/avalanche-bulletin-and-snow-situation/snow-maps.html, last access: 5 March 2020), snow hydrological models (e.g., Mysnowmaps for the European Alps, https://www.mysnowmaps.com/, last access: 5 March 2020), optical and passive microwave remote sensing observations (e.g., ESA Snow Climate Change Initiative (CCI) project, http://cci.esa.int/snow, last access: 5 March 2020), or the combination of different sources (e.g., the US National Operational Hydrologic Remote Sensing Center (NOHRSC), https://www.nohrsc.noaa.gov/, last access: 5 March 2020). The accuracy of such systems varies but in general is limited by the poor information on snow precipitation, especially in mountain areas. This could lead to errors of several days, and even weeks, in the estimation of the snow disappearance time (Engel et al., 2017). The approach described in this paper allowed the identification of the melting phases for the five considered test sites with an RMSE of 6 d for the 510 moistening phase, 4 d for the ripening phase and 7 d for the runoff phase. Therefore, it could be potentially useful to improve the performances of snow monitoring.

It is important to underline that, in order to predict runoff, further hydrological modeling is needed in addition to the information provided by the proposed approach. While the runoff production below the snowpack starts quickly, with snow being permeable to water, the streamflow production can be delayed by several days, and even weeks, depending on catchment size and hydrological behavior (Rinaldo et al., 2011). Therefore, even if we do not propose a real-time implementation, we think that, combining the information on the snow melting phases based on the principles presented in Sect. 4.2 and easily available real-time and historical auxiliary data such as temperature or historical streamflow, it is possible to develop an algorithm to extract valuable information for the anticipation of the peak stream runoff phase.

Knowing the snow melting phases with just a few days delay can have very important applications for water resources management (e.g., hydropower production or irrigation administration). In particular, the information provided by the proposed approach can be ingested in operational hydrological modeling systems. The ingestion of remote sensing information for improving snow modeling and monitoring has been extensively applied in the past (e.g., Molotch and Margulis, 2008). So far, the most common variable assimilated is snow cover fraction from optical sensors since this is the most available information acquired using remote sensing. In our case, we would need to assimilate either information on the presence/absence of snow liquid water content or on the snow depletion curve, which can be computed for the first time from the real beginning of the melting (i.e., runoff onset) from high-resolution remote sensing data. From a theoretical point of view, this is feasible. However, if the assimilated variable is snow liquid water content, only snow models which explicitly simulate snow liquid water content can be used. Usually physically based, energy-based snow models such as GEOtop (Endrizzi et al., 2014), AMUNDSEN (Strasser et al., 2011), CROCUS (Brun et al., 1992) or SNOWPACK/ALPINE3D (Bartelt and Lehning, 2002; Lehning et al., 2006) are suitable for this purpose.

The possibility of using state-of-the-art radiative transfer models to simulate the multitemporal behavior of the backscattering presented in Sect. 4.2 has also been investigated. Although wet snow is of great importance for many applications, the most widely used models have been tested and applied mainly in dry snow conditions (Picard et al., 2018; Proksch et al., 2015). In particular, during the melting process the increase in superficial roughness, LWC, and density and the coarsening of the snow grains play an important role on the backscattering mechanisms. Indeed, when the LWC increases, the absorption coefficient increases, the penetration depth decreases, and the total backscattering is influenced more and more by the superficial roughness of the snow. As discussed in the background Sect. 2.2, to the best of our knowledge only few works have specifically addressed the wet-snow modeling at the C band (i.e., Shi and Dozier, 1995; Nagler and Rott, 2000; Magagi and Bernier, 2003). Differently from more advanced models such as SMRT (Picard et al., 2018) or MEMLS3&a (Proksch et al., 2015), these models assume independent scattering. Even though Shi and Dozier (1995) and Magagi and Bernier (2003) indicate a positive correlation between largely wet snowpack and the superficial roughness, Kendra et al. (1998) on the basis of ground experimental analysis expressed some doubts on the realistic behavior of such models. Therefore, wet-snow RT modeling requires dedicated efforts and validation campaigns, which have never been systematically conducted for characterizing the multitemporal snow roughness, which is out of the scope of this paper and will be left to future work.

Finally, it is worth noting that the availability of multitemporal data, acquired regularly over the entire globe and freely accessible, opens new opportunities to monitor dynamic phenomena. In particular, monitor snow depth and snow water equivalent in a systematic and spatially distributed manner would be crucial for a proactive management of the water resources. The recent paper by Lievens et al. (2019) proposes an empirical algorithm for snow depth retrieval from S-1 at 1 km resolution. The authors suggest a C-band sensibility to snow height generated by the cross-polarized information. This was never fully recognized before in the literature. Even though the focus of our research is only on the snowmelt, by considering the 20 m multitemporal S-1 data acquired over the five test sites studied in the presented work, we provide some remarks that may be useful for future works in this context. If all the backscattering time series in the two polarizations shown in the paper by Lievens et al. (2019) exhibit the characteristic shape identified and analyzed in the presented study, at least in our five test sites – which comprise a restricted and very specific dataset with respect to the global one considered by Lievens et al. (2019) – the ratio σ_VH∕σ_VV does not seem to provide clear evidence that the cross polarization is sensitive to the increase (or decrease) in snow depth (or SWE) during both the accumulation and melting period (see Fig. 4). However, this does not exclude the fact that different manipulation of the S-1 data (e.g., spatial and temporal averaging) and the empirical incidence angle normalization proposed in Lievens et al. (2019), which were not taken into account in our experiments, may contribute to the increase in the sensitivity of the backscattering to the snow height by possibly removing the source of noise. In conclusion, despite the lack of a generally accepted physical explanation, this work shows how the rich amount of SAR data made available with a high repetition interval can allow the monitoring of the complex processes related to the snow evolution in a manner that was never addressed before. We believe this will be one of the most interesting research topics in the future.

7 Conclusions

In this paper, we analyzed the correlation between the multitemporal SAR backscattering and the snowmelt dynamics. We compared Sentinel-1 backscattering with LWC and SWE measurements derived from in situ observations and process-based snow modeling simulations for five alpine test sites in Italy, Germany and Switzerland considering 2 hydrological years. We found that the multitemporal SAR measurements allow the identification of the three melting phases that characterize the melting process, i.e., moistening, ripening and runoff with a good agreement considering the revisit time of Sentinel-1. In particular, we found that in the considered sites the SAR backscattering decreases as soon as the snow starts containing water and that the backscattering increases as soon as SWE starts decreasing, which corresponds to the release of meltwater from the snowpack. We discuss the possible reasons of this increase, which are not directly correlated to the SWE decrease but most probably to the different snow conditions, which change the backscattering mechanisms. From this study we define a set of simple rules that can be applied to the multitemporal SAR backscattering in order to identify the melting phases. We showed that by applying these rules the identification of the melting phases was possible for the five considered test sites with an RMSE of 6 d for the moistening phase, 4 d for the ripening phase and 7 d for the runoff phase. Moreover, the same rules were applied for the identification of the runoff onset for the entire Zugspitzplatt catchment, with reasonable results even if further hydrological analyses have to be performed. The presented investigation could have relevant application for monitoring and predicting the snowmelt progress over large regions. A better understanding of the spatial and temporal evolution of melting dynamics in mountain regions and the knowledge of the onset of meltwater runoff can help to predict floods and define the scope of action to mitigate potential contaminant distributions in soils and surface water.

As future developments, we plan to develop and test an automatic method to identify the three melting phases of a snowpack using a larger validation dataset (e.g., SNOTEL), which will allow us to properly discuss the spatial and temporal evolution of snow water content and runoff in mountainous regions. Moreover, we investigate the reasons of the increase in the backscattering that follows the decrease in SWE through in situ experiments that take into account the hypothesis expressed in this paper. This will help the development of the RT models in wet-snow conditions.