Brief communication: The influence of mica-rich rocks on the shear strength of ice-filled discontinuities

A temperature- and stress-dependent failure criterion for ice-filled rock (limestone) joints was proposed in 2018 as an essential tool to assess and model the stability of degrading permafrost rock slopes. To test the applicability to other rock types, we conducted laboratory tests with mica schist and gneiss, which provide the maximum expected deviation of lithological effects on the shear strength due to strong negative surface charges affecting the rock–ice interface. Retesting 120 samples at temperatures from −10 to −0.5 ^∘C and normal stress of 100 to 400 kPa, we show that even for controversial rocks the failure criterion stays unaltered, suggesting that the failure criterion is transferable to mostly all rock types.

1 Introduction

Climate-related changes in the thermal conditions in steep bedrock permafrost can lead to rock slope destabilization or failure (e.g. Gruber and Haeberli, 2007), potentially triggering large-scale hazards via process chains (Huggel et al., 2012). A number of failures in bedrock permafrost have exposed residual ice at their shear and detachment planes (Keuschnig et al., 2015; Phillips et al., 2017; Ravanel et al., 2017; Weber et al., 2018; Walter et al., 2020). These observations indicate the occurrence of ice-filled rock discontinuities and their importance as a controlling factor for the stability of degrading permafrost rock slopes. While the shear strength of rock joints can be increased by ice fillings due to adhesion and rock–ice interlocking (Gruber and Haeberli, 2007), warming can reduce the strength of ice-filled joints (Krautblatter et al., 2013). To improve attempts to accurately assess the stability of rock slopes with degrading permafrost due to climate change, we will have to better understand the effect of warming on the shear strength of ice-filled joints.

So far, the shear failure of ice-filled rock joints has been studied in a number of direct shear tests using samples of concrete and ice (Davies et al., 2000; Günzel, 2008). Mamot et al. (2018) added a series of constant strain shear tests with real rock samples. The ice-filled rock joints were represented by “sandwich”-like limestone–ice–limestone samples. Normal stresses of 100, 200 and 400 kPa were applied to the ice-filled discontinuities, which simulated rock overburdens of 4, 8 and 15 m, respectively. A brittle failure criterion was developed for these overburdens and validated for rock temperatures from −8 to −0.5 ^∘C. The failure criterion is based on Mohr–Coulomb (a combination of Coulomb, 1776, and Mohr, 1900) and contains temperature- and stress-dependent cohesion and friction which decrease upon warming. When warming from −1 or −0.5 ^∘C leads to thawing and a subsequent loss of the ice infill, the shear strength of unfrozen joints reduces slightly by approximately 100 kPa (Krautblatter et al., 2013; Mamot et al., 2018). However, the unfrozen shear strength is 400–1000 kPa lower when compared with the one of ice-filled joints at temperatures between −2 and −10 ^∘C.

Mamot et al. (2018) postulate that their failure criterion can be applied to shear planes in all rock types, even though they solely used limestone in their laboratory experiments. The authors discussed potential influences of the rock type on the shear strength, and they emphasized the need to study a potential rock type dependency with additional laboratory tests. An inventory of rock slope failures in the central European Alps by Fischer et al. (2012) shows that the rock types, in which failure occurred and which potentially include the fracturing of ice-filled rock joints, are not only limestone but also gneiss and granite. Most of the detachment zones are likely affected by permafrost and roughly follow the assumed lower altitudinal boundary of permafrost for the respective area. Rock slopes within this boundary are expected to respond sensitively to warming and a related reduction in stability (Nötzli et al., 2010) and predominantly consist of gneiss, limestone or schist at altitudes from 2000 to 3000$\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ and mostly of gneiss or granite at altitudes $>\mathrm{3000}\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$ (Fischer et al., 2012).

Among the rock types observed to be involved in permafrost rock slope failures, gneiss and schist are metamorphic rocks with a pronounced foliation and typically show bands with a concentrated abundance of aligned, platy mica. These bands can form weak zones where shear planes develop more easily (Shea and Kronenberg, 1993). Furthermore, basal cleavage surfaces of mica carry a strong negative surface charge compared to other minerals like quartz, feldspar or calcite. When in contact with water, this leads to the formation of a common but specifically strong electrical double layer (Fenter et al., 2000; Bourg and Sposito, 2011). Such an electrical double layer causes a homogenous alignment of at first water molecules, and, with freezing, structural integrity in ensuing ice crystals (Dosch et al., 1996). As a result, adhesion at the interface is increased and the process of phase change upon warming is delayed. While the mean equilibrium freezing point in permafrost rocks is depressed to $-\mathrm{0.7}\pm \mathrm{0.4}$ ^∘C (Krautblatter, 2009), mica-rich rocks with strongly attractive surfaces are observed to increase the freezing temperature (Alba-Simionesco et al., 2006). Close below the melting point, this results in a crystalline contact layer on mica-rich surfaces while inner layers remain fluid. In contrast, a liquid layer forms along the rock–ice interface on weakly attractive silica-rich surfaces while the absorbed water in the mineral is crystalline (Alba-Simionesco et al., 2006). Consequently, one would theoretically expect a stronger adhesion at the rock–ice interface for mica-rich rocks, presumably leading to a higher shear strength close below 0 ^∘C.

Therefore, this study aims to verify if the failure criterion by Mamot et al. (2018) accounts for (i) the relevance of gneiss for permafrost rock slope failures, (ii) the abundance of gneiss and schist within the lower permafrost boundary, and (iii) the potentially significant effects of foliated metamorphic rocks with high mica content on the shear strength of ice-filled joints. For this, we performed 120 shear tests on ice-filled joints in gneiss and mica schist, rerunning the sample preparation, test setup and procedure of Mamot et al. (2018). In the present article we address the following question: is the failure criterion for ice-filled rock joints by Mamot et al. (2018) valid for rocks with different mineral composition, specifically containing mica?

2 Methods

Two different rock types with a considerable mica content were selected for this study: gneiss that originates from the Matterhorn (45^∘${\mathrm{58}}^{\prime }{\mathrm{52}}^{\prime \prime }$ N, 07^∘${\mathrm{40}}^{\prime }{\mathrm{14}}^{\prime \prime }$ E, $\mathrm{3218}\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$), Switzerland, and mica schist that was involved in the Ramnanosi landslide, close to the village of Flåm (60^∘${\mathrm{49}}^{\prime }{\mathrm{41}}^{\prime \prime }$ N, 07^∘${\mathrm{08}}^{\prime }{\mathrm{59}}^{\prime \prime }$ E, $\mathrm{750}\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$), Norway (Fig. 1a). The limestone samples used for the precedent laboratory tests by Mamot et al. (2018), to which this study refers, were picked from the Zugspitze (47^∘${\mathrm{25}}^{\prime }{\mathrm{21}}^{\prime \prime }$ N, 10^∘${\mathrm{59}}^{\prime }{\mathrm{13}}^{\prime \prime }$ E, $\mathrm{2900}\mathrm{m}\mathrm{a}.\mathrm{s}.\mathrm{l}.$), Germany.

A thin section analysis was added to the direct shear tests to determine the mineral composition and the amount of mica in the rock samples. The thin sections were taken from the same rock blocks from which the cylinders for the shear tests were cored. Two thin sections were prepared of each, the gneiss and the mica schist; the results were averaged per rock type. One thin section was produced of the limestone. To account for the anisotropic nature of both gneiss and mica schist, all samples (Sect. 2.1 and 2.2) were prepared from cuts parallel to the foliation of the rocks. As such, we assume a similar mica content for both the thin sections and the sample surfaces in the shear tests.

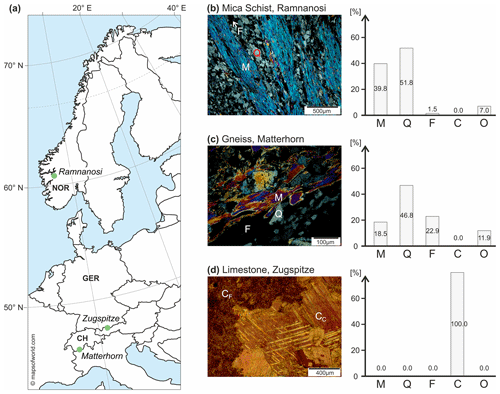
Figure 1 (a) Map showing the locations where samples for this study and the previous one by Mamot et al. (2018) were collected. Panels (b), (c) and (d) show associated results of thin section analyses, where M refers to mica, Q to quartz, F to feldspar, C to calcite (C_F: fine grains; C_C: coarse grains) and O to others.

2.1 Petrographical analysis

The thin section analysis was conducted through cross polarized light microscopy with an Olympus DP26 microscope which is standardized according to the DIN ISO 8576 (2002). The proportionate mineral compositions were recorded in a PELCON automatic point counter for a point-counter analysis as recommended by Chayes (1949). Two point-counter tracks of at least 100 points were indexed on each thin section. We estimated the mica content on sample surfaces via image histogram analysis.

2.2 Shear experiments

The sample preparation, setup and procedure of the tests were conducted according to Mamot et al. (2018) to guarantee comparability: (i) each rock–ice–rock sandwich sample consisted of two pieces of rock with a surface roughness of 80 grains per inch and its gap is filled with a 3.5±0.5 mm thin ice layer. (ii) We used the same custom-built shear apparatus installed in a temperature-controlled cooling box. (iii) We applied a constant strain rate of $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{3}}{\mathrm{s}}^{-\mathrm{1}}$, provoking brittle fracture of ice and thereby representing the well-advanced stage of rock slope failure.

Tests were performed at temperatures of −10, −6, −2, −1 and −0.5 ^∘C and at normal stress levels of 100, 200 and 400 kPa. Four tests were conducted per rock type and per combination of temperature and normal stress, leading to a total of 120 tests. As in the tests by Mamot et al. (2018), the type of failure was identified qualitatively by visual inspection of the failure surfaces immediately after removing them from the shear apparatus. Samples which did not allow a definite failure type classification were assigned to the mixed failure.

3 Results and interpretation

3.1 Mineral composition relevant for rock–ice interfaces

The mica schist is a fine-grained rock with well-developed foliation. Layers of dark mica, predominantly biotite, and light quartz and plagioclase alternate in the rock. In the thin section analysis (Fig. 1b) the mica schist shows very distinct bands of mica (39.8 %) in a ground mass mostly comprised of quartz (51.8 %). Other minerals identified in the sample are feldspar and chlorite as well as possibly sillimanite and amphibole. An average porosity of 1.3 % was determined in the thin section analysis. The gneiss is clearly laminated and shows bands of mica (18.5 %), yet it is less distinctly layered than the mica schist (Fig. 1c). The main components are quartz (46.8 %) and feldspar (22.9 %); other minerals identified in the sample are chloritoid and epidote as well as traces of chlorite, amphibole and rutile. Furthermore, the porosity of the gneiss is considerably low (0.9 %, Draebing and Krautblatter, 2012) compared to the mica schist. Both rock types show a high abundance of mica minerals at the sample surfaces, presumably leading to a higher concentration of negative surface charges than at limestone surfaces. The latter is only constituted of calcite without any occurrence of mica (Fig. 1d).

3.2 Shear tests of rock–ice interfaces with mica-rich rocks

Mamot et al. (2018) subdivided the paths of shear stress and shear strain into five distinct stages including (i) consolidation, (ii) adjustment to the sample holder, (iii) build-up of the shear stress, (iv) failure and (v) post-failure behaviour. The same pattern can be identified by the presented laboratory tests with mica-rich rocks. We also observe a general decrease in peak shear stress with increasing temperature from −10 to −0.5 ^∘C at all tested normal stress levels, without any systematic difference between the samples of mica schist and gneiss (Fig. 2). Overall, the measured peak shear stresses of this study lie well within, or close to, the range of the failure criterion (dark blue area in Fig. 2). Even the laboratory tests conducted at −10 ^∘C fit mostly within the expected values of the same failure criterion, although they are outside the valid temperature range proposed. Nevertheless, the measured peak shear stresses tend to fall below the failure criterion for the same temperature and at a normal stress of 400 kPa. This pattern is also noted in the previous tests with limestone (grey triangles in Fig. 2) and in the concrete–ice shear experiments by Günzel (2008), possibly due to the beginning transition from brittle to ductile failure with higher rock overburden leading to a lower shear strength (Renshaw and Schulson, 2001). When approaching the melting point of the ice, above −2 ^∘C, the measured peak shear stresses slightly exceed the calculated range of the failure criterion.

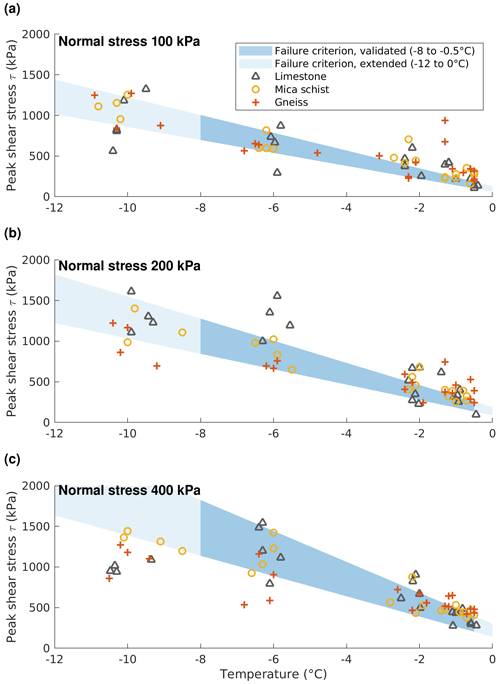
Figure 2 Peak shear strength across sub-zero temperature of ice-filled rock joints constituted of gneiss (red crosses), mica schist (orange circles) and limestone (grey triangles). The relationships are plotted for normal stresses of (a) 100, (b) 200 and (c) 400 kPa. The limestone data are added from previous tests by Mamot et al. (2018). The validated range of the failure criterion by Mamot et al. (2018) is marked in dark blue while an extended section to −12 and to 0 ^∘C is displayed in light blue.

Figure 3 illustrates the temperature-dependent ratio of failure types that were observed in the shear tests for distinguishing rocks with and without mica content. Failure within the ice is very dominant for mica-rich rocks in the temperature range from −10 to −1 ^∘C, but absent at −0.5 ^∘C. In contrast, rock without mica (limestone) shows a gradual decrease in the ratio of failure within the ice and a gradual increase in the ratio of failure along the rock–ice interface with warming. Overall, it is remarkable that the fracture along the rock–ice interface and mixed fracture are the only failure types at −0.5 ^∘C for limestone and mica-rich rocks.

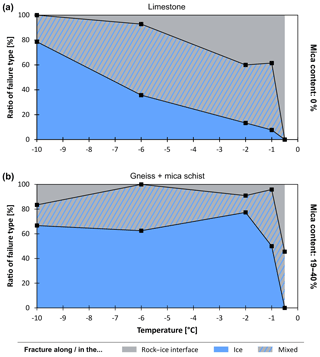
Figure 3 Ratios of failure types versus temperature for (a) mica-free (0 %) and (b) mica-rich (19 %–40 %) surfaces in ice-filled rock joints. Failure in mica-rich joints is dominated by fracturing inside the ice layer, whereas at temperatures warmer than −1 ^∘C failure is controlled by fracturing along the rock–ice interface and the mixed type. However, in mica-free joints the proportion of ice fracturing decreases gradually when approaching the melting point of ice while rock–ice fracturing gains importance, especially at temperatures warmer than −1 ^∘C.

4 Discussion

In Mamot et al. (2018) the question remained open if the failure criterion for ice-filled rock joints was transferable to rock types other than limestone. As Fischer et al. (2012) demonstrated that gneiss and schist are among the most relevant rock types involved in rock slope failures within the Alpine mountain permafrost belt, this study aims at testing the applicability of the failure criterion for those rock types. Furthermore, gneiss and schist were selected since they are characterized by foliation with high mica content, which may potentially affect the shear strength of ice-filled joints close to 0 ^∘C.

We quantified the shear strength of ice-filled discontinuities in mica-rich rocks, which fits well to the temperature- and normal stress-dependent failure criterion (Fig. 2), thereby indicating its validity for mica-rich rocks. It is remarkable that the failure criterion seems to be conservative for conditions close to 0 ^∘C compared to the shear tests with mica-rich rocks. However, this underestimation of shear strength does not state a problem for any purpose of rock slope stability assessment and, hence, does not diminish the applicability of the failure criterion. The higher shear strength close to 0 ^∘C for mica-rich rocks has been expected by the authors and may be explained by the higher adhesion at the rock–ice interface, the delayed phase change upon warming and the absence of a liquid layer along mica-rich joint surfaces close to the melting point of ice. The strengthening effect of the rock–ice contact by mica also becomes evident when looking at the temperature-dependent distribution of failure types (Fig. 3): while in mica-rich rocks failures along the rock–ice interface only dominate at temperatures warmer than −1 ^∘C, in limestone (without mica) the same failure type gradually gains in importance at temperatures warmer than −6 ^∘C.

Previous publications on the shear strength of ice-filled rock joints relate to a small number of tests on samples with ice and concrete, generally not below −5 ^∘C (Günzel, 2008; Davies et al., 2000). Krautblatter et al. (2013) developed a first failure criterion which was based on the experiments by Günzel (2008). About 5 years later, Mamot et al. (2018) proposed an improved failure criterion which refers to rock–ice–rock samples and covers a broader range of bedrock temperatures. This study demonstrates that the failure criterion by Mamot et al. (2018) is surprisingly resilient as it can be applied to (i) different failure types including the fracture in ice and along the rock–ice contact, (ii) a wide range of temperatures relevant for bedrock permafrost (−0.5 to −8 ^∘C), (iii) a wide range of relevant stress conditions (100–400 kPa) and (iv) mostly all rock types relevant for permafrost rock slope failures in the Alps, as the metamorphic mica-rich rocks tested in this study represent the expected maximum deviation of potential lithological effects on the shear strength of ice-filled rock joints. This strong deviation is established due to three characteristics of the tested rock types.

• (i)

  They are foliated and typically have a high amount of mica aligned subparallel within major shear planes. This property and the resulting effect of the surface charge are expected to be more emphasized along natural joints than along the tested surfaces, as these were cut within intact rock samples.

• (ii)

  The platy and subparallelly aligned mica grains lead to a very low surface roughness, potentially reducing the shear strength. This effect will become more relevant at temperatures close to 0 ^∘C where we observe a higher proportion of fractures along the rock–ice interface. As it is hard to define a representative surface roughness for typically diverse natural fractures, and to guarantee reproducibility of the laboratory rock surfaces, we standardized the joint surface roughness in our tests. Therefore, we assume the effect of varying surface roughness and its dependence on the rock type to be visible in natural fractures, but not in our tests.

• (iii)

  The strong negative surface charge results in an elevated adhesion and equilibrium freezing point which likely leads to a higher peak shear strength.

Due to the uniform surface roughness in the presented tests, we are not able to determine the extent to which the reduction in shear strength by a lower surface roughness (see ii) may offset the increase in shear strength by a strong negative surface charge (see iii). But, overall, we expect the observed mica-dependent higher shear strength close to 0 ^∘C to be suppressed slightly.

5 Conclusions

In this study, we carried out 120 constant strain rate shear tests on ice-filled joints in gneiss and mica schist to investigate a potential influence of metamorphic foliated rocks with a high amount of mica on the shear resistance of ice-filled discontinuities. Based on the laboratory tests, we could demonstrate a slight increase in peak shear strength at temperatures close to 0 ^∘C, which is most likely caused by the presence of mica. However, overall our data correspond well with the failure criterion for ice-filled rock joints introduced by Mamot et al. (2018). As the tested mica-rich rocks represent the expected maximum deviation of potential lithological effects on the shear strength, we conclude that the failure criterion is transferable to a wide variety of rock types relevant for permafrost rock slope failures in the Alps.