An estimate of ice wedge volume for a High Arctic polar desert environment, Fosheim Peninsula, Ellesmere Island

Quantifying ground-ice volume on a regional scale is necessary to assess the vulnerability of permafrost landscapes to thaw-induced disturbance like terrain subsidence and to quantify potential carbon release. Ice wedges (IWs) are a ubiquitous ground-ice landform in the Arctic. Their high spatial variability makes generalizing their potential role in landscape change problematic. IWs form polygonal networks that are visible on satellite imagery from surface troughs. This study provides a first approximation of IW ice volume for the Fosheim Peninsula, Ellesmere Island, a continuous permafrost area characterized by polar desert conditions and extensive ground ice. We perform basic GIS analyses on high-resolution satellite imagery to delineate IW troughs and estimate the associated IW ice volume using a 3-D subsurface model. We demonstrate the potential of two semi-automated IW trough delineation methods, one newly developed and one marginally used in previous studies, to increase the time efficiency of this process compared to manual delineation. Our methods yield acceptable IW ice volume estimates, validating the value of GIS to estimate IW volume on much larger scales. We estimate that IWs are potentially present on 50 % of the Fosheim Peninsula (∼3000 km²), where 3.81 % of the top 5.9 m of permafrost could be IW ice.

1 Introduction

Arctic temperatures have increased twice as fast as the rest of the world over the past 50 years; a pattern that is expected to continue for the next century (IPCC, 2013; AMAP, 2017). Permafrost is perennially cryotic ground that is estimated to underlie up to 24 % of the Earth's land surface (French, 2018), including vast areas in the Arctic that are threatened by climate change. Potential feedbacks of thawing permafrost include widespread landscape instability, accelerated coastal erosion and a massive release of carbon into the atmosphere, thus adding to the forcing on Earth's climate through the greenhouse-gas effect (Schuur et al., 2015). The Canadian High Arctic permafrost is vulnerable to even a slight temperature increase because it lacks thermal protection from vegetation, a substantial surface organic soil layer, or thick snow cover. Subsequent melting of ground ice reinforces the disturbance on permafrost's thermal equilibrium. These effects are already seen in the form of increased subsidence and rapid melting events (Pollard et al., 2015). Ice wedges (IWs), wedge-shaped bodies of nearly pure ice, are a ground-ice type ubiquitous in the High Arctic and in areas of continuous permafrost in general. Investigating the response of IWs to climate change is a necessity to understand future permafrost degradation.

Figure 1 Thermokarst processes in the Eureka Sound Lowlands. (a) Retrogressive thaw slump headwall with an exposed ice wedge (∼6 m depth) with no surface expression, Axel Heiberg Island, July 2016. Helicopter and person for scale. (b) Aerial view of an active melt out along ice wedge troughs and the resultant dissected landscape, Fosheim Peninsula, July 2015. (c) Example of backwasting of ice wedges melting out, Fosheim Peninsula, July 2013. (d) Rapid melt out of ice wedges where massive ice is present, Fosheim Peninsula, July 2017.

1.1 Ice wedges and thermokarst

The main factors controlling permafrost occurrence and depth of the active layer are air temperature, vegetation cover, soil type, snow cover and topography (French, 2018). Thermokarst refers to all the processes related to permafrost degradation involving subsidence, erosion, collapse and instability resulting from thawing of ice-rich permafrost or the melting of massive ice (van Everdingen, 1998). Ice-rich permafrost typically contains ice contents well in excess of the saturated moisture content of the sediments under natural unfrozen conditions (van Everdingen, 1998); the volume of ice in excess of saturation is called excess ice. Thermokarst is initiated when the thermal equilibrium of permafrost is disrupted as a result of increasing ground surface temperature, which causes warming in the upper part of the permafrost and increases the depth of the active layer. Thermokarst alters surface hydrology, favouring pond formation and gully formation, further causing permafrost erosion and thaw (Godin and Fortier, 2012). The magnitude of thermokarst-driven geomorphic change is highly dependent on ground-ice content (Couture and Pollard, 2007; Kokelj and Jorgenson, 2013; Pollard et al., 2015). Thermokarst features can be geomorphologically significant in landscapes containing massive ground-ice and IW ice. These permafrost features have the highest excess ice contents since they are usually composed of almost pure ice (Couture and Pollard, 1998) (Fig. 1).

Figure 2 Ice wedge surface expression. (a) Representation of an epigenetic ice wedge. (b) Aerial view of ice wedge polygons on the Fosheim Peninsula, Ellesmere Island.

During the freezing season, rapid cooling of soil can lead to thermal contraction and result in the formation of cracks in frozen ground. At the beginning of the thaw season, contraction cracks are filled with meltwater that freezes to form a vertical vein of ice. Over hundreds of years, re-forming cracks create polygonal patterns and form large IWs that are widespread in the Arctic and for this reason have been the subject of abundant research (e.g. Leffingwell, 1915; Lachenbruch, 1962; Black, 1976; Mackay, 1990).

Three types of IWs are identified based on their growth direction relative to the ground surface: epigenetic, syngenetic and anti-syngenetic wedges (Mackay, 1990). Epigenetic IWs typically grow on stable surfaces in pre-existing permafrost (Fig. 2). Their V-shapes denote their tapered growth as cracks tend to form in the middle of the wedge. Syngenetic IWs grow upward as a response to surface aggradation of sediments. They are typically located in floodplains, where fluvial sedimentation occurs, in areas of eolian sedimentation and on lower segment of slopes as a result of mass wasting. They are often nested in a chevron pattern. Anti-syngenetic IWs are characterized by a gradual downward growth pattern because of an incremental removal of surface material, for example on upper slope segments affected by denudation from slow mass wasting. They penetrate deeper each year if thermal contraction cracking keeps pace with ice vein formation and their tops are truncated by thaw (Mackay, 1990). In the Canadian High Arctic polar desert, epigenetic IWs are most typical and reflect a dynamic balance between climate and geomorphology, whereas the other types are less common and occur in areas of geomorphic change (e.g. deposition and erosion). The distinct polygonal patterns produced by networks of IWs reflect the complex interaction between climate, materials and topography. In general, two polygonal morphotypes are recognized, namely high- and low-centred polygons depending on the microtopographic relationship between polygon edges and polygon centres (Mackay, 2000). In this study, our analysis is concerned with epigenetic IWs, most commonly expressed as high-centered polygons in this polar desert environment.

As IWs grow, a shallow trough often develops over the ice body reflecting the quasi-stable relationship between the active layer and the IW top. In some cases, ridges parallel to the IW trough develop, creating low-centred polygons with raised rims often higher than 50 cm (French, 2018). Preferential thaw of IW happens when snowmelt and run-off collect and flow in IW troughs creating a thermal perturbation. Changes in microtopography related to the evolution of high- and low-centred IW polygons play an important role in surface process by influencing drainage, snow distribution and vegetation. These changes generate feedbacks that accentuate polygon morphology and eventually their vulnerability to thawing (Liljedahl et al., 2016).

1.2 High Arctic climate change

Climate change in the Arctic will impact the three most important environmental factors dictating permafrost and ground-ice state, namely air temperature, vegetation characteristics and snow cover. Regional interaction between these biological and physical dimensions make it difficult to generalize the permafrost response to increased temperatures on a local scale. Decreasing albedo due to diminishing snow cover, glacier ice and sea ice extent affects atmospheric and oceanic circulation, amplifying the increase in temperatures in the northern polar region (IPCC, 2013). In the Canadian High Arctic, the increase in air temperature has largely resulted in winter and autumn warming, and sites with little snow cover exposed to winds are therefore more responsive to changes in air temperature (Smith et al., 2012). An increase in annual snow accumulation is also projected for high latitudes due to warmer temperatures (AMAP, 2017). Since the 1980s, permafrost temperatures have risen in most regions, but this increase is particularly strong (0.4 to 1 ^∘C decade⁻¹) in continuous cold permafrost regions such as the High Arctic (AMAP, 2017). This rise in ground temperature is disturbing the thermal equilibrium of permafrost and results in changes in the active layer thickness and surface conditions. Increased thermokarst processes will enhance the permafrost carbon feedback through the release of greenhouse gases from a previously frozen organic pool (IPCC, 2013). The release of these large carbon and methane reserves will have an important effect on global temperatures on a millennial timescale (IPCC, 2013; Schuur et al., 2015). It is currently estimated that permafrost regions contain twice as much carbon than there is in the atmosphere (Schuur et al., 2015). However, the Canadian High Arctic permafrost is underrepresented in terms of datasets for carbon stocks (Brummell et al., 2014; Schuur et al., 2015). This region is dominated by a polar desert landscape (Walker et al., 2002), where the cold dry soils contain a smaller carbon pool than tundra and it is uncertain whether it will stay as a carbon sink (Brummell et al., 2014; Schuur et al., 2015). No clear increase in thermokarst activity linked to climate change in the Arctic has been observed in the past decade (AMAP, 2017). However, widespread IW degradation has been observed in the Canadian Arctic Archipelago, Alaska and Siberia in recent decades and linked to climate change (Liljedahl et al., 2016). As climate change projections specific for the High Arctic polar deserts are poorly constrained due to a lack of data (Pollard et al., 2015), many uncertainties remain about their response to increases in temperature and permafrost stability.

1.3 Ground-ice volume estimation

Analysis of permafrost and modelled disturbance due to an increase in ground temperature shows that the degree of response, specifically the magnitude of ground subsidence, is a direct function of the volume of excess ice (Couture and Pollard, 2007). Ground-ice content is a key property of permafrost terrain (Gogineni et al., 2014) and its estimation is necessary to predict the sensitivity of a particular area to disturbance (Gilbert et al., 2016), which is important for engineering and environmental evaluations. It is also crucial for quantifying carbon pools and potential fluxes in the atmosphere (Kuhry et al., 2013; Strauss et al., 2013; Ulrich et al., 2014). Understanding the cryostratigraphy and estimating ground-ice-type proportions also helps to reconstruct geomorphic history (Couture and Pollard, 2007; Gilbert et al., 2016). One of the first regional ground-ice approximation study was performed by Pollard and French (1980) for Richards Island in the Mackenzie Delta, Northwest Territories, Canada. Estimation of ground-ice in the upper 10 m of permafrost was completed using drill log data, aerial photographs and topographic maps. Intensive field studies that characterize IW terrain and estimate ground-ice content have recently been carried out in the Mackenzie Delta by Morse and Burn (2013) and on the Beaufort Sea coast in Alaska by Kanevskiy et al. (2013). The lack of detailed field data for large and basically unstudied areas in the Arctic explains why ground-ice distribution is often estimated on small regional scales.

Pore ice and segregated ice volumes can be determined from permafrost sample analysis but not large ice bodies like wedges and massive ice. To specifically conduct IW volume estimations, knowledge of IW morphology as well as IW polygons geometry are required. Point measurement data from exposed IWs, excavation and/or boreholes help to constrain IW type, shape and mean IW width and depth for a specific site (e.g. Pollard and French, 1980; Morse and Burn, 2013; Jorgenson et al., 2015). Geophysical techniques such as ground-penetrating radar (GPR) and electrical resistivity tomography (ERT) have also been used to investigate IW morphology (e.g. Munroe et al., 2007; Bode et al., 2008; De Pascale et al., 2008; Léger et al., 2017). IW are often approximated to be an inverted isosceles triangle and mean cross-sectional area of IWs is estimated with the use of width-to-depth ratios based on field observations. This works well for epigenetic and anti-syngenetic IWs but would underestimate syngenetic ice volume due to their chevron pattern (Morse and Burn, 2013). Many other assumptions are often made which lead to over-/underestimation of wedge ice. For example, Kanevskiy et al. (2013) assumed that IW polygons were square and did not take into account the active layer thickness. Pollard and French (1980) adapted their IW volume estimation for areas with less developed polygons to come up with an overall volume for Richard Island, Northwest Territories. Bearing in mind the assumptions made possibility yield large errors, these studies give some crucial information on the relative proportion of IW volume as a first approximation.

IW polygon geometry, mainly perimeter and total length of troughs for a defined surface area, can be manually calculated on a small scale from air photos (e.g. Pollard and French, 1980; Couture and Pollard, 1998). Improvements in remote-sensing capabilities for this task are needed to characterize various permafrost regions (Jorgenson and Grosse, 2016). In the review of recent advances in the study of ground ice by Gilbert et al. (2016), the use of satellite imagery has been recognized as the main contemporary method used to determine IW polygon geometry on larger scales. Access to remotely sensed high-resolution imagery encouraged the development of techniques to measure polygon geometries using Geographic Information Systems (GIS). Ulrich et al. (2014) proposed a method to estimate IW volume from high-resolution satellite images and limited ground data using 3-D GIS tools. Polygon networks are delineated from satellite imagery and converted into a triangular irregular network (TIN). Average IW width and depth from previous field surveys serve as inputs to a 3-D subsurface model of polygons, enabling wedge ice volume calculation. Their method was used in Yedoma deposits (Pleistocene-age ice-rich permafrost) and Holocene thermokarst basins in Siberia and Alaska. Two procedures were used to digitize the centre lines of troughs in their study: manual delineation and Thiessen polygon delineation. Compared to previous estimation methods, the volume accuracy is increased as the actual polygon dimensions are used. The study by Ulrich et al. (2014) establishes that GIS is an appropriate tool with which to conduct estimates of geometrically irregular features on a large scale but recognizes that precise field data are necessary.

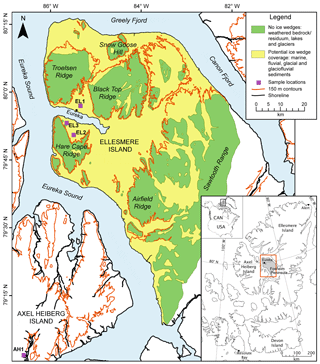
Figure 3 Sample locations of this study and potential coverage area of ice wedges on the Fosheim Peninsula in the Canadian High Arctic, shown in inset. Surficial geology data have been simplified and are from a map produced by Bell (1992). The 150 m contours (CanVec data, Natural Resources Canada, 2016) are a proxy for the Holocene sea level on the Peninsula (Bell, 1996). Coordinate system: NAD 1983 UTM 16N. Projection: Transverse Mercator.

IWs often have a distinct surface expression that can be mapped using high-resolution satellite imagery (Gilbert et al., 2016). Previous studies have shown that IWs occur literally everywhere in unconsolidated sediments in the continuous permafrost zone and that their subsurface geometry is relatively consistent and closely related to terrain conditions and surficial geology (Couture and Pollard, 2007). Given the predicted changes in Arctic climate and our current understanding about nature and distribution of IWs, it is safe to assume that IW melt will contribute greatly to High Arctic geomorphic change with feedbacks that will reinforce permafrost instability. Semi-automated techniques that delineate IW polygons on satellite images greatly improve the time efficiency and coverage area of wedge ice volume estimates compared to manual delineation (Ulrich et al., 2014). In this study, we build upon the methodology introduced by Ulrich et al. (2014) by testing GIS-based methods to delineate IW troughs and present a new semi-automated method based on watershed segmentation principles. We then provide a first approximation of IW ice volume in a High Arctic polar desert environment, the Fosheim Peninsula, to assess its sensitivity to thermokarst processes as a response to climate change.

Table 1 Definition of the sample locations and satellite imagery used.

2 Study area: Fosheim Peninsula

Our study focusses on the Fosheim Peninsula of Ellesmere Island (Fig. 3), which lies within the Eureka Sound Lowlands (ESL). The ESL region roughly covers 750 km² on central Ellesmere and Axel Heiberg Islands in the northernmost part of the Canadian Arctic Archipelago and is bordered by the Sawtooth Mountains to the east and the Mueller Ice cap to the west (Pollard et al., 2015). An Environment Canada weather station located at Eureka (80^∘00^′ N, 85^∘55^′ W) is in the centre of the ESL on the Fosheim Peninsula. The area is mostly flat to gently rolling with elevations below 300 m a.s.l., except for several ridges that rise to a maximum of 840 m a.s.l. where outcrops of intact bedrock occur (Bell, 1996). The surficial geology of the area is dominated (∼60 %) by unconsolidated ice-rich silty-clay marine sediments below ∼150 m a.s.l., but local fluvial, glacial and glaciofluvial deposits are present. The area is underlain by continuous permafrost ∼500 m deep. As a polar desert, it is one of the driest regions in Canada, with a mean annual precipitation of 68 mm recorded at Eureka for the period 1980–2015 (Pollard et al., 2015). The mean annual air temperature is −18.8 ^∘C with the lowest mean monthly temperature in February of −37.4 ^∘C and highest in July of 6.2 ^∘C for the same period. The thaw season varies between 3 and 6 weeks in length (Pollard et al., 2015). The mountains surrounding the ESL limit cold air masses from the ocean and create relatively warm July temperatures for this latitude, and a general warming trend has been noted for this month since 1980 (Pollard et al., 2015). Sparse vegetation (patchy low shrubs) and very low snowfall in this polar desert region suggests that the climate drivers are fairly consistent across the ESL. The mean active layer thickness is 60 cm and ranges between 30 and 100 cm. IW polygons are nearly continuous in unconsolidated sediments across the ESL and exposures of thick tabular massive ice bodies are numerous (Pollard et al., 2015). Couture and Pollard (1998) estimated that the volume of ground ice in the uppermost 5.9 m of permafrost comprises 1.8 %–3.5 % of wedge ice and up to 30.8 % with all ground-ice types combined. Average IW width is 1.46 m and depth is 3.23 m from a survey of 150 exposed IWs by Couture and Pollard (1998). Extreme polar latitudes often lack thermokarst features but with ice content often exceeding 60–70 % in the fine marine sediments, the ESL is an exception (Pollard et al., 2015; French, 2018). Due to a generally thin active layer, IWs are commonly close to the surface. This makes them vulnerable to an increase in the active layer thickness as a result of an increase in ground temperature. The response of High Arctic polar desert to projected climate change was modelled by Couture and Pollard (2007) with the climatic and geologic conditions of the ESL. They outlined two scenarios of +4.9 and +6.6 ^∘C mean annual air temperature increase in the 2040–2060 period compared to mean annual air temperature from the 1948–1997 period. These led to a lengthening of the thaw season by 26 days and increased thaw depths of 17–20 cm. Comparison with modelled and past disturbance values reveal that ground subsidence would be of the order of 1 m in the vicinity of IWs and greater than 1 m for massive ground-ice bodies.

Figure 4 Original satellite image and delineation outputs with percentage of ice wedge volume in the top 5.9 m of permafrost for each method for each sample location.

3 Methodology

3.1 Data sources and sample locations

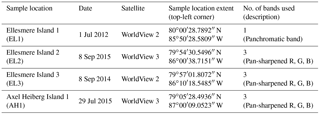
To assess the best techniques for IW trough delineation, we first identified a series of suitable sample locations from a detailed analysis of four high-resolution (0.5 m pixels) WorldView 2 and 3 satellite images. Like Ulrich et al. (2014) we defined the sample locations as squares of 250 × 250 m. Four sample locations, three on Ellesmere Island (EL1, 2 and 3) and one on Axel Heiberg Island (AH1), with different polygon size, morphology, density and width of troughs were selected (Table 1 and Fig. 3). All sample locations are characterized by random orthogonal polygons formed by epigenetic IWs on relatively flat surfaces (Fig. 4). The high-centred polygons on the Ellesmere Island sample locations have well-developed troughs (approximately 2–6 m wide). Wedge hierarchy reflected by variability in trough width is most visible in sample location EL1. EL2 was chosen due to its dominance of rectilinear polygons, while EL3 was chosen for the high number of polygons with small areas and their proximity to polygons with much larger areas. In contrast, AH1 was chosen because of polygons with large areas and narrow troughs where cracking is assumed to be less frequent. AH1 is the only sample location where IW cracks not forming closed polygons are visible.

3.2 Delineation of polygons

At each sample location, the following three delineating methods were performed once using built-in tools in ArcGIS (ESRI, version 10.3.1): (1) manual delineation, (2) Thiessen polygons and (3) watershed segmentation. In our method, we use and refer to specific ArcGIS tools but most GIS packages contain similar tools and functions that could be used to replicate our analysis.

3.2.1 Manual delineation

Following the Ulrich et al. (2014) methodology, we manually digitized polygons at each sample location by creating a line dataset of the troughs centre lines. Only lines enclosing complete polygons falling within the sample location were kept and visible IW cracks not enclosing any polygons were also mapped.

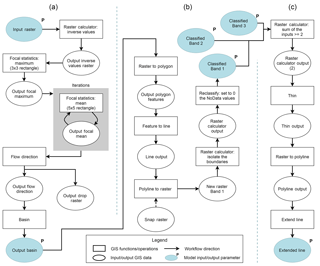
Figure 5 Models developed with ArcGIS Model Builder for the watershed segmentation method. (a) Watershed creation: the inputs are the raster image as well as the maximum and minimum values needed to inverse the pixel values. The treatment of each site differed in the number of iterations run by the focal statistic mean tool for a satisfying basin segmentation output. The output is a basin raster, and every pixel has the value of its corresponding watershed. (b) Converting basin output to a raster of the watershed borders: watershed boundaries are classified as a raster where the value of 1 represent boundaries. The snap raster is the initial band image clipped to the sample location. (c) Combination of the bands: all the classified watershed boundaries of each band are converted to a line feature that can be manually edited. A detailed description of the tools can be found at http://desktop.arcgis.com/en/arcmap/10.3/main/tools/a-quick-tour-of-geoprocessing-tool-references.htm (last access: 14 November 2018).

3.2.2 Thiessen polygons

The second method involved the semi-automated delineation of polygons based on the creation of Thiessen (or Voronoi) polygons. This approach was used in Ulrich et al. (2014) to estimate the volume of a relict IW network in baydzherakhs landforms, where IWs had melted and only raised polygon centres remained, and was compared at other sites with manual delineation. Thiessen polygons are defined mathematically as the perpendicular bisectors of the lines between all input points. Then, the area inside one Thiessen polygon is closer to its associated input point than any other input point (Aurenhammer, 1991). The tool “create Thiessen polygon” was used to create Thiessen polygons from manually chosen centre points of IW polygons, hereafter called the “approximated” centre points. Following this creation, polygons near the outer boundaries of the sample squares were necessarily defined by having these boundaries as vertices. To avoid those edge effects, we created approximated centre points for polygons up to 30 m away from the sample locations before the creation of the Thiessen polygons. All resulting polygons that were not completely inside the sample locations were then deleted, and the remaining polygons were converted to a line dataset. Approximated centre points were created without the visible manual delineation lines to test the ability of the analyst to identify IW polygon centres.

3.2.3 Watershed segmentation

Delineating IW polygons has many similarities with detecting grain boundaries in thin sections for petrographic analysis because both involve detecting edges. In a study by Barraud (2006) grain boundaries are detected using a watershed segmentation algorithm in image segmentation software. The basic principles of this segmentation process were reproduced in this study with the Spatial Analyst Hydrology toolbox from ArcGIS.

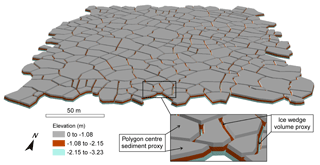
Figure 6 Example of a 3-D subsurface model. The TIN surface represents the entire EL3 sample location (250 m × 250 m). The elevation of zero corresponds to the base of the active layer. This model is based on the methodology developed in Ulrich et al. (2014).

This third delineation method is based on the interpretation of the value of each pixel as a height function, i.e. as if it was a digital elevation model (DEM). If the IW troughs have higher pixel values (brighter) than the polygon centres they will act as “mountains” and polygon centres as “valleys”. If this topography was to be flooded, the water would accumulate in each polygon centre valley delineated by the trough boundary mountains. In the WorldView images, the polygon centres have higher value pixels and the troughs lower value; therefore we inverted the pixel values before using the hydrology tools.

Watersheds were first obtained using the flow direction tool to calculate the flow direction of each pixel in the image, and then the basin tool was used to delineate the smallest possible watersheds where water could accumulate. We converted the multiple steps of this method into a semi-automated process by implementing them in ArcGIS Model Builder (Fig. 5), which increased time efficiency and required few interventions from the analyst. Filtering and smoothing of the image is required before the flow direction and basin tool outputs can provide watershed outlines that are representative of the IW polygons (Fig. 5a). To enhance troughs pattern, we used the focal statistic maximum tool followed by the focal statistic mean tool to reduce noise in the polygon centres. The later had to be performed multiple times to generate watersheds that were not oversegmented, i.e. too many watersheds representing one actual IW polygon. Watersheds were created after each focal mean iteration and evaluated against the manually digitized polygons lines. The iterations were stopped when some watersheds started to merge and to include two or more manually digitized polygons. At this point, approximately one to eight watersheds represented each actual IW polygon.

The hydrology tools were used on all of the available bands in WorldView imagery at each sample location (Table 1) before being combined into a single-line dataset per sample location. The same number of focal mean iterations were performed on all the bands and they were then combined to create the final IW polygon delineation lines. For each band, watershed outlines were extracted as lines and were converted into a raster format (Fig. 5b). The three raster datasets of each band were summed, and pixels which were classified as boundaries (IW troughs) in two or more of the bands were kept (Fig. 5c). For these steps, the pixel size was increased from 0.5 to 1 m to get a better chance of the watershed outlines overlapping. To convert the boundary pixel raster into a clean-line dataset, the output raster was thinned, watershed boundary pixels were converted to polylines, and the extend line tool was used with a maximum extension distance of 5 m (10 original pixels) to obtain a maximum number of closed polygons.

The clean trough centre-line datasets representing IW polygon outlines were visually assessed and edited to improve their accuracy. With the initial WorldView image visible, lines oversegmenting the IW polygons were deleted and lines were added where polygons when some boundaries were not closed. All lines outside the sample locations were also deleted. Manually delineated polygons were included in these edited datasets to be consistent with the initial choice of the analyst. The remaining dangling lines were erased using the trim line tool. Finally, the simplify line tool with the point remove option and a tolerance of 1.5 m (3 pixels) was used to smooth any lines which had sharp edges due to the contouring of pixels form the conversion of raster to polyline format.

3.3 Three-dimension subsurface model for ice wedge and sediment volume calculation

Similarly to Ulrich et al. (2014), field data of mean IW depth and width were used to estimate IW volume from Couture and Pollard (1998). A buffer was created around the delineated lines of half the mean width of an IW (0.73 m) and then the buffer extent was cut out of the polygons with the erase tool. The resulting polygons therefore did not include the IW troughs. All polygons, even the edge ones, are then considered to be surrounded by half an IW.

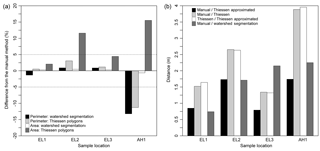
Figure 7 Delineation method for comparison metrics. (a) Difference in mean area and perimeter of delineated polygons for the semi-automated methods with the manual delineation method. Data from Table 2. (b) Mean distance between the centres of polygons created by the semi-automated delineation methods compared to the manual delineation method. The near tool was used with a search radius of 10 m (20 pixels). Two sets of centre points were considered for the Thiessen polygons method: the approximated centre point to create the polygons initially and the resulting centre points of the created Thiessen polygons.

Volume calculations were performed in a 3-D subsurface model by creating a Triangulated Irregular Network (TIN) dataset, which is a network of mass points representing a surface terrain. Assuming that the IWs are inverted isosceles triangles, the elevation of −3.23 m (mean IW depth) was assigned to the trough centre lines and an elevation of 0 m was assigned to the polygons corresponding to the base of the active layer (see legend for elevation in Fig. 6). An elevation of −3.23 m was also assigned to a dissolved polygon extent. The TIN was created from those three datasets with the Delaunay triangulation constrained for each segment (lines and polygon vertices) to be added as an edge in the TIN.

The IW volume and sediment volume were calculated using the surface volume tool. The IW volume was calculated from a plane above the TIN at 0 m. In order to compare the results of this study with the values found in Couture and Pollard (1998), the thickness of frozen soil considered in their study (5.9 m) was used to calculate sediment volume. It was calculated from a plane at this depth below the TIN (−5.9 m). The percent volume of IWs at each sample location was calculated by dividing the IW volume by the total frozen material (sediment and IWs) volume.

3.4 Fosheim Peninsula ice wedge volume estimation

We estimated the cumulative coverage area of IW polygons for the Fosheim Peninsula based on the surficial geology map from Bell (1992), which differentiates between surficial sediments of marine, fluvial, glaciofluvial and glacial origin and indicates weathered bedrock and residuum areas. The map was digitized with reference to the shoreline and contour datasets of CanVec Series dataset from Natural Resource Canada (2016). As it is rare for IW polygons to occur in bedrock (French, 2018), it was assumed that they can be located in all the unconsolidated surficial sediment classes (marine, fluvial, glaciofluvial and glacial). The potential area occupied by IWs was determined by subtracting the area of the large lakes and areas identified as bedrock from the total area of the peninsula. The 150 m CanVec contour was isolated, as this provides a proxy for the Holocene marine limit on the Fosheim Peninsula because IWs are ubiquitous below this elevation (Bell, 1996; Couture and Pollard, 1998). We assumed that the mean of the IW percent volume of our sample locations was representative of the geomorphological settings where IWs are present on Fosheim Peninsula and used it to calculate the equivalent IW ice volume over the entire peninsula.

4 Results

4.1 Delineation of polygons

To compare the accuracy of the two semi-automated delineation methods against the manual method, the mean perimeter and area of polygons (Fig. 7a) as well as the total length of delineated troughs (Table 2) were calculated. It is expected that a more efficient method would have a mean perimeter and mean centre point distance close to the manual delineation method values. While we recognize the importance of assessing variance in polygon size at the sample locations, it could not be treated quantitatively herein, but can be assessed qualitatively by examining Fig. 4.

Table 2 Summary of the delineation results for each method at each sample location and corresponding proportion of ice wedge volume.

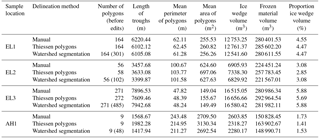
All the delineation methods provided polygon outlines for the four sample locations, although the accuracy of the outlines is variable. We assume that the manual method provides the best outlines because troughs can be detected by the analyst regardless of their width and intersection with other troughs. Manually delineating the troughs was most difficult at EL3 where polygons were small and contrast was very low, especially on the left side of the sample location (Fig. 4). The presence of IW troughs that do not form closed polygons in AH1 was also difficult to detect as the troughs themselves were thin. When compared with the manual trough centre lines, the Thiessen polygons do not agree very well as they simplify the actual polygon shapes. Some edge effects remain on the Thiessen polygon boundaries, mostly caused by the proximity of polygons with large area difference (Fig. 4). The number of polygons were slightly increased at EL2 (+3.57 %) and EL3 (+0.04 %) and equal at EL1 and AH1 for the Thiessen polygons method (Table 2). The edited trough centre lines from the watershed segmentation method are generally in good agreement with the manually digitized trough centre lines (Fig. 4). The watershed segmentation technique overestimates the number of polygons, by as much as 5 times in the case of AH1 but around two times for the three Ellesmere Island sample locations (Table 2). This result is anticipated, as watershed oversegmentation is preferred to undersegmentation before editing, because outlines of smaller polygons would disappear when watersheds start to merge.

The mean distance between the centre points of the polygons for the different methods was calculated as an indicator of the similarity between the delineated polygons, particularly for the Thiessen approximated centre points versus the manual centre points (Fig. 7b). At all sample locations, this mean distance is <4 m, equivalent to <8 pixels. The maximum distance encountered was 9.5 m for a polygon on the edge of EL2 for the Thiessen polygons method. Two patterns in the mean distance between the centre points seem to emerge: (1) the grouping of manual and Thiessen-approximated methods with manual and watershed-segmentation methods and of Thiessen–Thiessen-approximated methods with manual–Thiessen methods due to their value closeness, and (2) the fact that the last group has higher values. The only exception to this observation is the manual–watershed-segmentation mean distance being the highest value for EL3.

The majority of mean perimeter and polygon areas of the Thiessen and watershed segmentation methods have a difference of <5 % with the manual method at a given sample location (Fig. 7a). Exceptions occur at larger polygon sample locations with the Thiessen polygons method, where polygon area is overestimated by 11.6 % and 15.5 % for EL2 and AH1, respectively (Fig. 6a). Another exception occurs for the mean perimeter of polygons at AH1, which is underestimated by >10 % for each method (Fig. 7a). The Thiessen method overestimates the mean polygon area at each sample location, with proportionally greater overestimations for sample locations with larger polygons. The watershed segmentation area estimation is more precise, being <1 % different than the mean area for the manually delineated polygons at all sample locations.

4.2 Ice wedge volume

An example of the TIN output for the IW volume calculation can be found in Fig. 6. The percent volume of IWs in the top 5.9 m of frozen material ranges from 1.41 % for the lowest polygon density AH1 to 5.88 % for the highest polygon density sample location EL3, all delineation methods included (Table 2). IW volumes for the watershed segmentation and Thiessen methods are slightly lower or equal to the manual method estimate. The largest difference occurs at AH1 where there is a difference of −0.31 in the percent IW volume, which is equivalent at this sample location to 7.23 m³ of IW ice. At each sample location, the IW volume estimate from the Thiessen polygons method is the lowest, except in the case of EL1, where it is equal to the watershed segmentation method but still lower than the manual method estimates (Table 2).

Based on digitization of the Bell (1992) map, approximately half of the Fosheim Peninsula surface area contains IWs, corresponding to an area of ∼3000 km² (Fig. 3). Considering only the top 5.9 m of permafrost, this is equivalent to a volume of frozen material of 17.7 km³. The total IW ice volume is 6.7×10⁸ m³ when assuming an IW volume of 3.81 % by averaging the results from the manual delineation method at the four sample locations in Table 2. Slightly lower estimates are obtained when averaging the IW volume of the two other semi-automated methods: 6.4×10⁸ m³ with 3.61 % for the Thiessen method and 6.6×10⁸ m³ with 3.74 % for the watershed segmentation method.

5 Discussion

5.1 Semi-automated delineation methods

The use of the Thiessen method on four sample locations with various polygon morphologies reveals its strength for volume estimation but not for trough identification. The main problem with this method is that curved troughs could not be delineated properly because the create Thiessen polygon tool can only output straight lines. This is reflected by the overestimation of polygon area (Fig. 7a). It is anticipated that better results would be obtained for hexagonal or rectangular polygonal patterns, rather than the orthogonal polygons tested in this study. This method is the least time consuming, but overall underestimates IW volume by differing between 0.1 % and 0.3 % from the percent IW volumes from manual delineation (Table 2). The Thiessen method was judged by Ulrich et al. (2014) to be “visually similar” to manual digitization. However, their study areas had a majority of rectilinear polygons, for which the approximation of centre point is easier than for more complex shapes found in the sample locations of this study.

The watershed segmentation method developed for this study with ArcGIS Hydrology tools was the most accurate in terms of locating trough centre lines and IW volume for every sample location. The poor agreement along the margins of sample location EL3 can be attributed to the lack of contrast in this part of the image (Fig. 4) and explains why the mean distance between the automatically vs. manually derived centre points is the highest at this sample location (Fig. 7a). With minimal editing, the results of IW volume calculations using the watershed segmentation were equal to the manual method values for two sample locations (Table 2). The method accuracy can be improved by editing the sharp angles at boundaries that are not completely smoothed with the simplify line tool. These are most prevalent at sample location AH1 where the XY tolerance for simplifying the lines (1.5 m) was the smallest compared to the length of the polygon vertices. The accuracy of the trough centre-line positions was reduced when increasing the pixel resolution to 1 m in the polyline-to-raster conversion but does not make a large difference in IW volume as the troughs are overwhelmingly larger than 1 m (2 pixels) at every sample location.

The effect of larger polygon size is visible in the results of sample location AH1 with the greatest differences in mean perimeter and area of polygons compared to manual delineation, and this was independent of the method used. This can also be attributed to the thin troughs at this sample location and to the difficulty of differentiating what seems like dry run-off channels from IW troughs (Fig. 4).

This study focussed on the development of two methodologies to delineate IW polygons based on only four sample locations. However, we are confident that both methods are applicable to delineating polygons for much larger areas. Thiessen polygons can readily be generated for larger areas and are manually edited along the boundaries to reduce edge effects. The watershed segmentation method can also be used for larger areas by choosing a number of focal mean iterations that will preserve the boundary details of the smallest polygons present. Even if oversegmented, this method preserves the largest polygon outlines corresponding to the darker zones of the images, interpreted as higher elevation when creating watersheds. The applicability of this methodology to terrain with complex contrast patterns in satellite imagery has not yet been tested. We suspect that presence of water bodies within IW polygons or in troughs, or of prominent vegetation at lower Arctic latitudes, would impact the proper detection of IW troughs. Hence, we suggest that it could be applied to high-resolution DEMs (≤0.5 m pixels with centimetre scale horizontal and vertical accuracy) instead of high-resolution satellite images. Then, the watershed segmentation method could be applied with more confidence on a wider range of Arctic terrain. The need for higher-resolution DEMs has been identified for the study of permafrost degradation in general, specifically to monitor surface subsidence and thermokarst processes (Jorgenson and Grosse, 2016). Promising remote sensing methods to detect topographic and subsurface change and to map ground-ice distribution include airborne light detection and ranging (lidar), interferometric radar (InSAR), airborne ground-penetrating radar and structure-from-motion technology (Gogineni et al., 2014; Jorgenson and Grosse, 2016). High resolution terrain models can be derived from these methods that are needed to monitor surface subsidence on a smaller scale and to estimate ground-ice distribution over large areas (Gogineni et al., 2014). These data could be acquired from unmanned aerial vehicles (UAVs) or other airborne platforms and would require fieldwork. This highlights the strength of our relatively simple methodology, relying on high-resolution satellite images and minimal field data, which can be applied on remote locations without the need of extensive fieldwork to create DEMs.

There are other semi-automated delineation methods that could be used to improve the delineation process of IW polygons on satellite images. One potential technique is the method described by Li et al. (2008), which was used to delineate grain boundaries in thin sections. In this method, edge detection is based on the abrupt change in pixel values, representing brightness, at the boundary between two grains. However, this method was deemed unsuitable for delineation of IW polygons since it requires considerable manual editing, and image classification algorithms could also not be applied due to the lack of contrast in some of our satellite images. Another approach would be to build on the methodology of Skurikhin et al. (2013), who classified Arctic tundra drainage network components including IW troughs with image segmentation and shape-based classification.

5.2 Ice wedge volume calculations

IW volume at the four sample locations of this study, derived from manual delineation and both of the semi-automated methods, is similar to the results of Couture and Pollard (1998) on the Fosheim Peninsula. Their study concluded that, for low-density polygonal terrain, IW ice comprised 1.8 % of the top 5.9 m of permafrost and high-density polygonal terrain 3.5 %. Their low density sample is very close to sample location AH1 (1.73 %), which confirms that the sample location on Axel Heiberg Island is representative of parts of the Fosheim Peninsula. Even if our values from EL2 are very similar to the high-density values in their study, EL1 and EL3 have a much higher IW ice volume percentage, redefining high-density polygonal terrain on the Fosheim Peninsula. This may be due to the choice of sample locations of 250 × 250 m for estimating IW volume. This surface area was found by Ulrich et al. (2014) to provide a representative scale where polygon diameter showed only small variations. Although the polygon density and shapes of sites in Siberia used by Ulrich et al. (2014) may not be comparable to the sites tested here, this size was chosen in our study as a manageable area for manual delineation and development of methodologies to delineate polygons. In future studies, the effect of the scale of the extent considered on the IW perimeter, area and IW volume should be assessed to refine the IW volume estimation.

Multiple necessary assumptions are made when calculating IW volume with TINs and here we consider their potential effect in estimating IW volume on large scales. The most critical is probably the assumption that IW width and depth do not vary significantly between polygonal terrains. A lack of subsurface data meant that using mean IW width and depth was the best approximation we could use for our calculations. The small variability in estimations of IW volume for the entire peninsula from the three delineation methods suggests that more error might be introduced in our estimate from the assumption of a fixed IW geometry than by the technique used to derive IW length in a specific area. Differences in IW width at our sample locations are obvious in Fig. 4, where multiple troughs are greater than the 1.46 m average used (e.g. EL2) and likely relate to sub-regional variation in geological history. Using these visible differences in surface expression as information on IW width would require another assumption that cannot be validated with the limited field data available: trough width is approximately IW width. Multiple sample locations in each surficial geology class presented by Bell (1992) would have permitted the calculation of IW volume on a sub-regional basis and the definition of IW parameters such as apparent width and polygon density for each surficial geology class. A specific example in which assuming a fixed IW geometry is not valid on the Fosheim Peninsula is in the surficial geology unit of the thin veneer of glacial sediments defined by Bell (1992). The thickness of this geological unit over bedrock is defined as 2 m, which is less than the 3.23 m mean IW depth used here. It is important to mention that the IW width and depth used in our calculations are minimal estimates because only exposed IWs were measured by Couture and Pollard (1998). As with this earlier study, we used the depth of 5.9 m below the active layer to calculate the IW volume because no IWs were observed below this depth.

The fixed geometry of IWs, assumed to be isosceles triangles, also impacts our IW volume calculation. It is the general shape of epigenetic IWs recognized by Mackay (1990) and the shape used in previous IW volume estimates (e.g. Pollard and French, 1980; Couture and Pollard, 1998; Bode et al., 2008; Ulrich et al., 2014). Even though IWs can be irregularly shaped in cross section, an inverted isosceles triangle with its base corresponding to the IW width is the best approximation of the shape for a calculation of this nature. Based on nearly 20 years of fieldwork on the Fosheim Peninsula, we have found syngenetic IWs to be relatively uncommon and limited to areas of active sedimentation like glacial forelands (floodplains), alluvial fans and deltas. Thus, we assumed that most IWs in the Fosheim Peninsula are epigenetic and that our sample locations are representative of the ESL and should therefore not greatly affect our IW volume calculation.

IWs may contain gas inclusions, small amounts of sediment as disseminated grains and discontinuous veins of silt and fine sand (French, 2018). The inclusion of this factor in our volume calculation is not realistic for this first-approximation study so it was assumed that all IWs were composed of pure ice. This has also been assumed by Ulrich et al. (2014) and most previous studies (e.g. Pollard and French, 1980; Couture and Pollard, 1998; Bode et al., 2008). Delineating IW polygons on satellite images implicitly assumes that all IWs have a visible surface expression (i.e. a trough structure). Field observations in the ESL show that this is not always the case because many of the factors leading to trough development (e.g. vegetation coverage and surface hydrology) do not always apply in very cold and relatively dry polar desert environments. Commonly, no trough structure is visible when the top of an IW is in equilibrium with the thin active layer depth (Fig. 1a) (Pollard et al., 2015). This assumption would lead to an underestimation of IW volumes on the Fosheim Peninsula. The opposite is also true as there might not be an IW below every crack and trough, but our estimates can only be based on what is detectable in the satellite imagery.

Given the potential errors discussed above associated with assumptions of width, depth and surface expression of IWs on the Fosheim Peninsula, we refer to our estimate of total IW volume as a first approximation and are confident it is a reasonable minimum estimate for this regional scale.

5.3 Impacts of melting ice wedges

IWs are the most widespread ground-ice phenomenon in areas of continuous permafrost. By virtue of their formative processes, the top of the active IW in many cases corresponds with the base of the active layer. Since they are in a quasi-stable relationship with maximum seasonal thaw depth, then any increase in the active layer depth will result in subsidence of the ground surface over the top of the IW. Under stable permafrost conditions, networks of shallow IW troughs will interact with snow distribution, surface vegetation and surface hydrology, in some cases contributing locally to additional deepening and surface ponding (Jorgenson et al., 2006, 2015). Over time, however, warm summers may produce small amounts of thaw at the top of the wedge leading to deepening of the trough. Thus, the localized degradation of IWs may be part of the normal evolution of permafrost landscapes. However, the widespread deepening of the active layer under projected Arctic climate change scenarios is expected to lead to dramatic regional changes in landscapes marked by increased local topography and changes in surface hydrology (Liljedahl et al., 2016). As IWs melt out, the sides of the IW polygons collapse into the open trough, producing a highly dissected landscape characterized by mounds at the former polygon centres and networks of deep channels and shallow ponds along the former IW troughs (Fig. 1; Couture and Pollard, 2007).

There is evidence that our local observations relate directly to widespread permafrost thaw and development of thermokarst terrain on the Fosheim Peninsula. An increase in thermokarst processes and retrogressive thaw slump retreat in the ESL over the past 25 years has been documented by Pollard et al. (2015). Unlike IW degradation associated mainly with thermal erosion by running water (e.g. Fortier et al., 2007), the instability of IWs in this region is related initially to thaw-induced surface collapse, but undoubtedly running water will play a role at some point. The active melt out seen in Fig. 1b gives an indication of how rapidly these changes may occur once the system becomes unstable. There is not only subsidence in the IW troughs, but also widespread backwasting of exposed IWs, similar to the headwall retreat in a retrogressive thaw slump (Fig. 1a). There is also evidence of shallow active layer detachments along IW troughs in the ESL (Fig. 1b). In some cases, on the Fosheim Peninsula we have observed rapid melt out of IWs contributing to the formation of much larger retrogressive thaw slumps in areas where massive ground ice is present (Fig. 3a, d). The net result will be a period of landscape instability amplified by feedbacks associated with run-off (surface hydrology), snow accumulation, changing vegetation, thermokarst from massive ground ice, mass wasting and microclimate. In principle, the new landscape will develop a deeper active layer consistent with the summer thaw conditions, though it may take a long time for the new active layer depth to stabilize, prolonging the period of thermokarst activity and subsidence. The new landscape will be quite different, and depending on the topographic and geologic setting not unlike badlands. For other areas, the new landscape will reflect a geomorphic system affected not only by IW degradation but other changes to the permafrost system and surface hydrology.

6 Conclusion

IWs are the most common form of ground ice in areas underlain by continuous permafrost. The occurrence of IWs increases the biophysical complexity of permafrost landscapes. Their widespread nature will contribute to significant permafrost instability once thermokarsts processes are initiated. IWs exist in a quasi-stable equilibrium with seasonal thaw as defined by the depth of the active layer. Accordingly, a climate-change-driven increase in active layer depths will likely produce widespread instability of landscapes associated with melting IWs. To better understand the potential impact of widespread destabilization of polygonal terrains there is a need to assess the volume and extent of IW ice. In the absence of detailed field observations, the analysis of IW polygons using high-resolution satellite imagery and GIS-based tools is the most logical solution. Based on our analysis of IW polygons for the Fosheim Peninsula, we present three main conclusions. Firstly, compared to manual delineation, two GIS-based semi-automated techniques – the Thiessen polygons methodology presented in Ulrich et al. (2014) and the watershed segmentation methodology, newly developed in this study – permit an acceptable approximation of IW volume in remote Arctic locations. Implementation of these methods in a coded process accelerated the polygon delineation and demonstrates their potential to be applied to much larger areas in an efficient manner. Time constraint and required level of precision in the estimation of IW volume are two criteria to be considered when choosing one of these methods for future application in other sample locations. Secondly, IWs potentially cover an area of ∼3000 km² on the Fosheim Peninsula where 3.81 % of the upper 5.9 m of permafrost could be IW ice. This first approximation is based on limited field validation data and sample locations that constrain it to the Fosheim Peninsula; however we are confident that our results are applicable to the entire ESL. Thirdly, further study in the ESL should focus on estimating IW volume for other sample locations using one of the semi-automated methods to increase the statistical significance of the results. Fieldwork in the ESL region could improve the IW volume estimates by linking surficial geology and physiographic units with IW characteristics. Associated with estimations of other ground ice type and carbon content, IW volume estimates will help to assess the vulnerability of High Arctic permafrost to climate change.